Sofia Airport Visibility Estimation with Two Machine-Learning Techniques
Abstract
:1. Introduction
2. Data and Methods
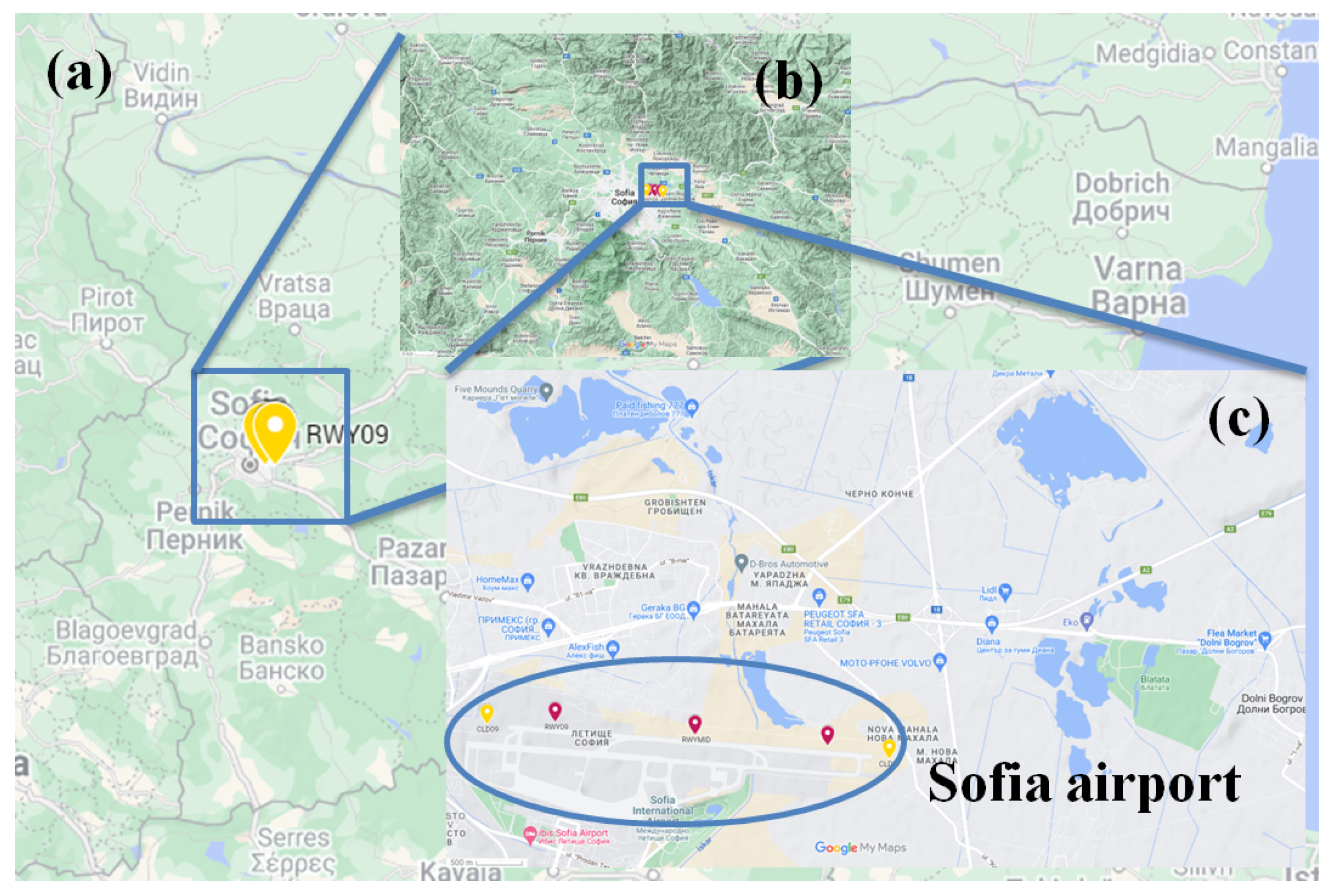
2.1. Study Area
2.2. Data
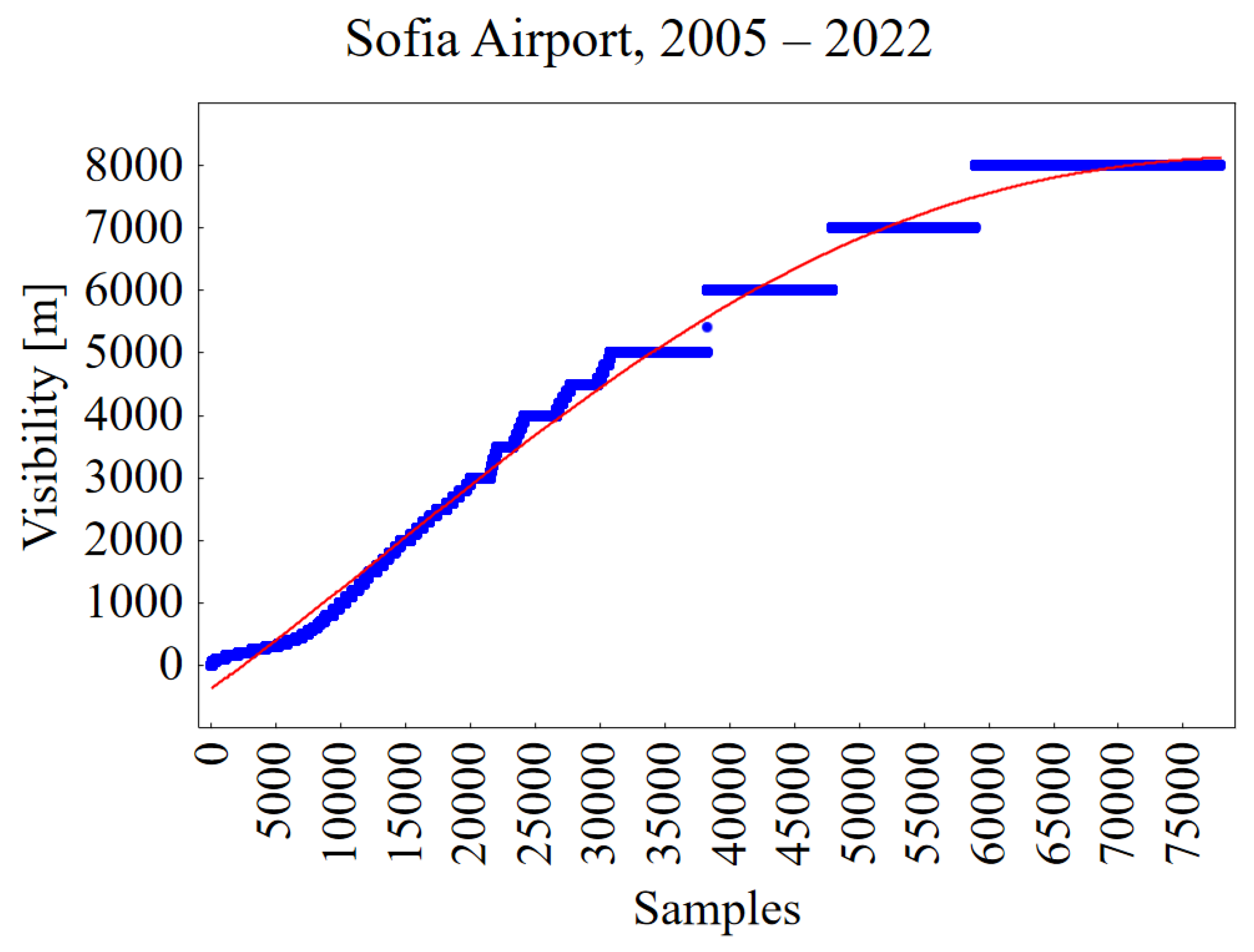
Data Pre-Processing
2.3. Random Forest Model
RF Model Training
2.4. Long Short-Term Memory Model (LSTM)
LSTM Model Training
2.5. R2, MAE, RMSE
2.6. POD, FAR, CSI, TSS
3. Results
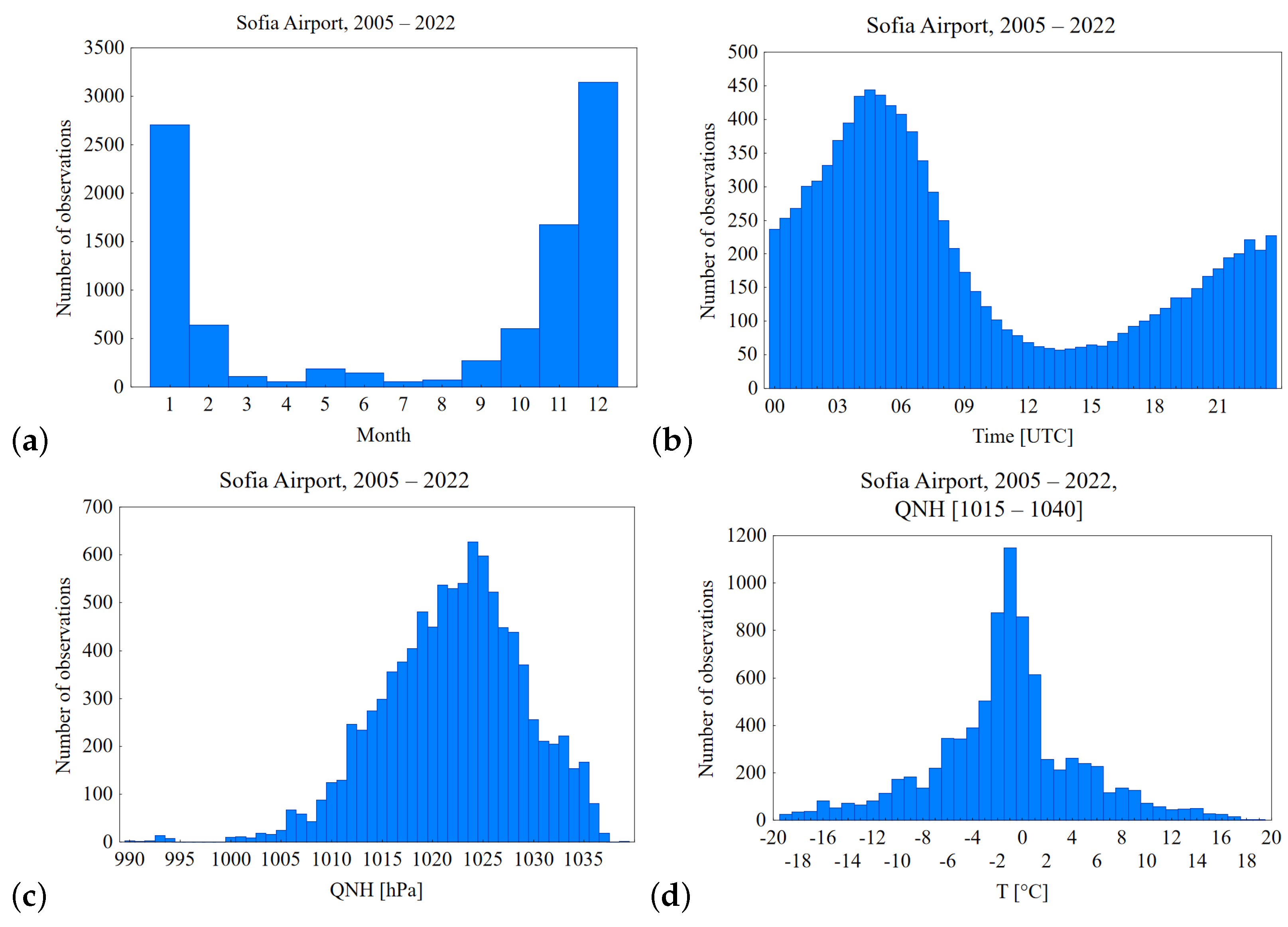
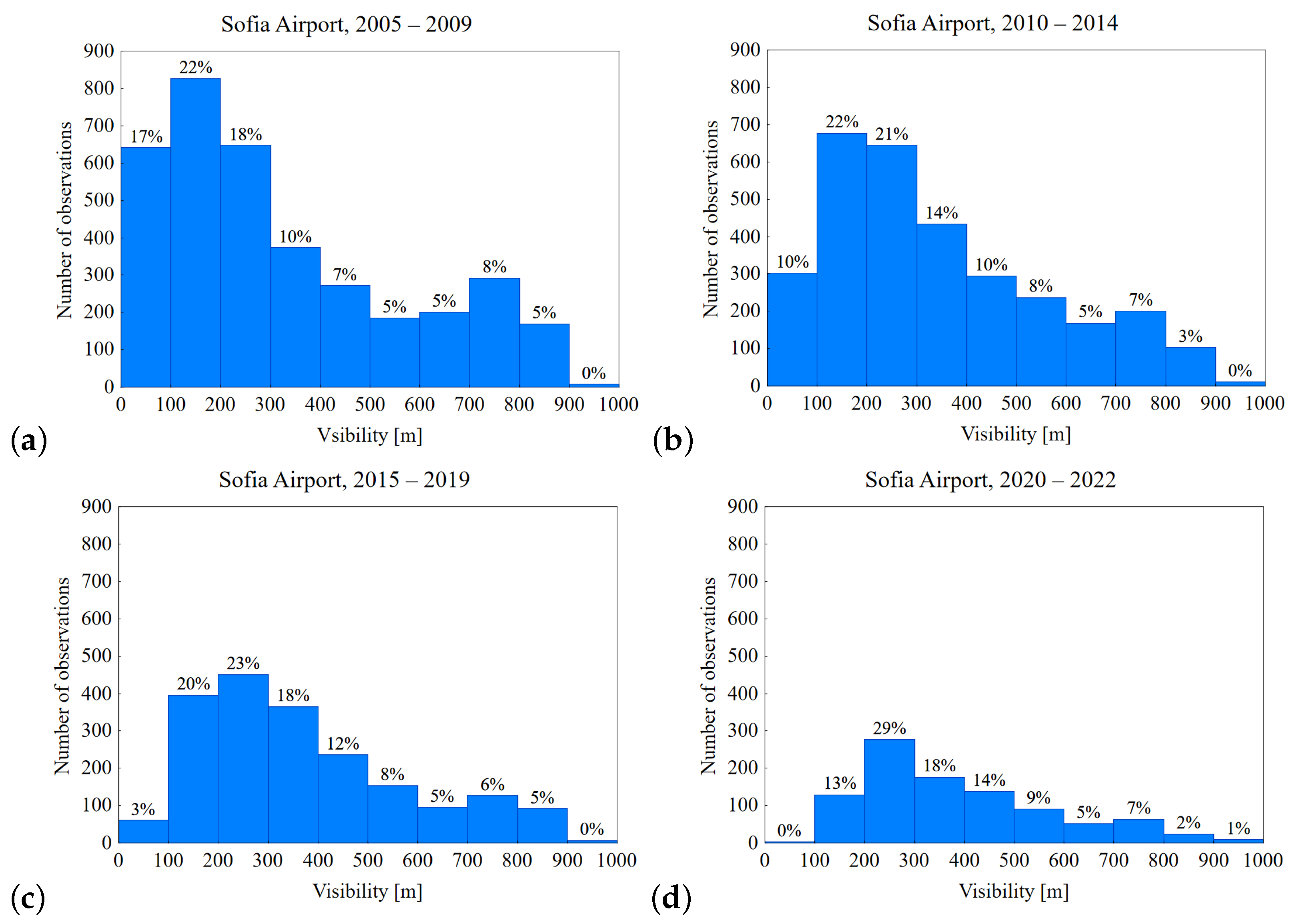
3.1. Sofia Airport Fog Characteristics: 2005–2022
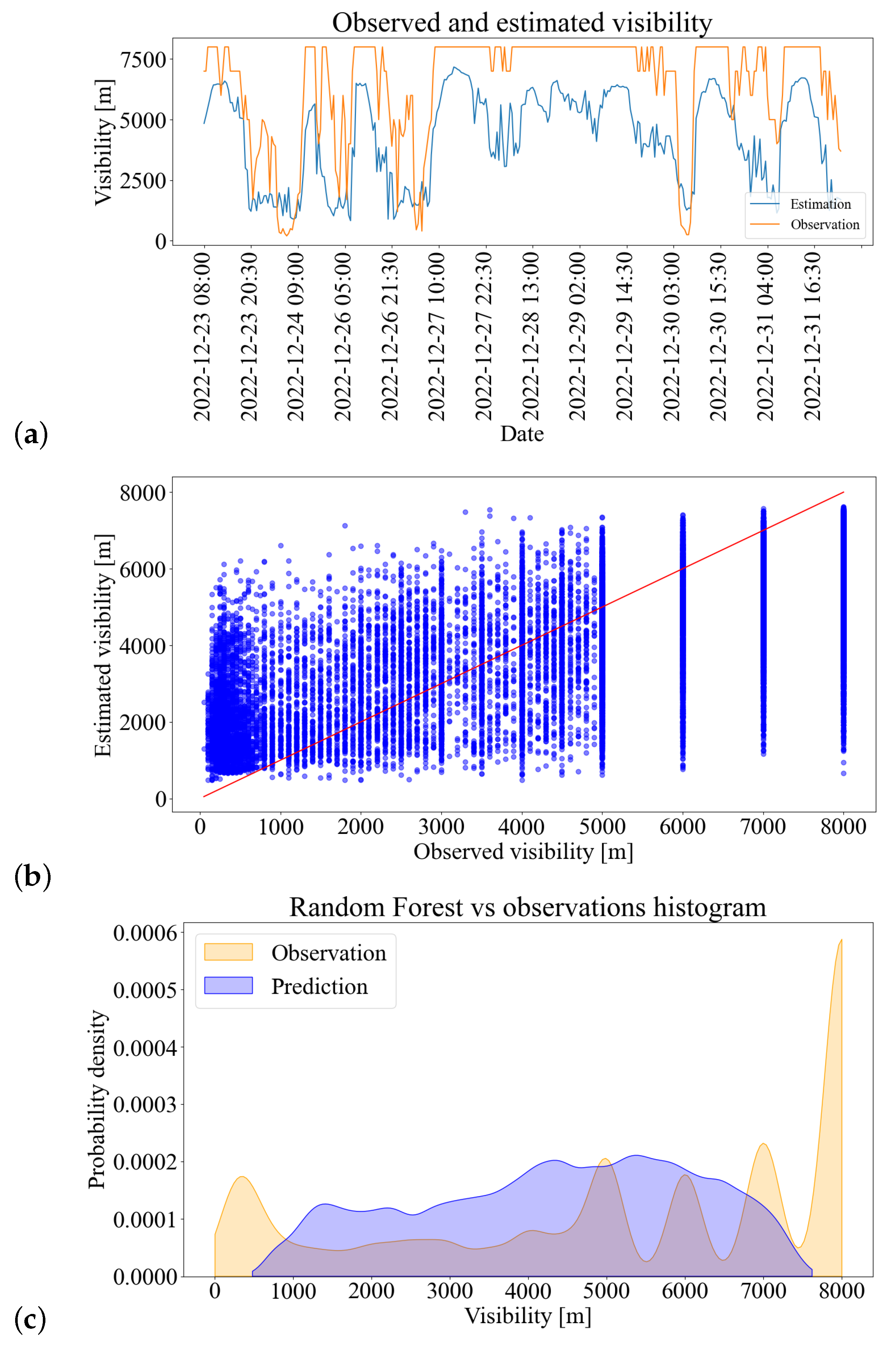
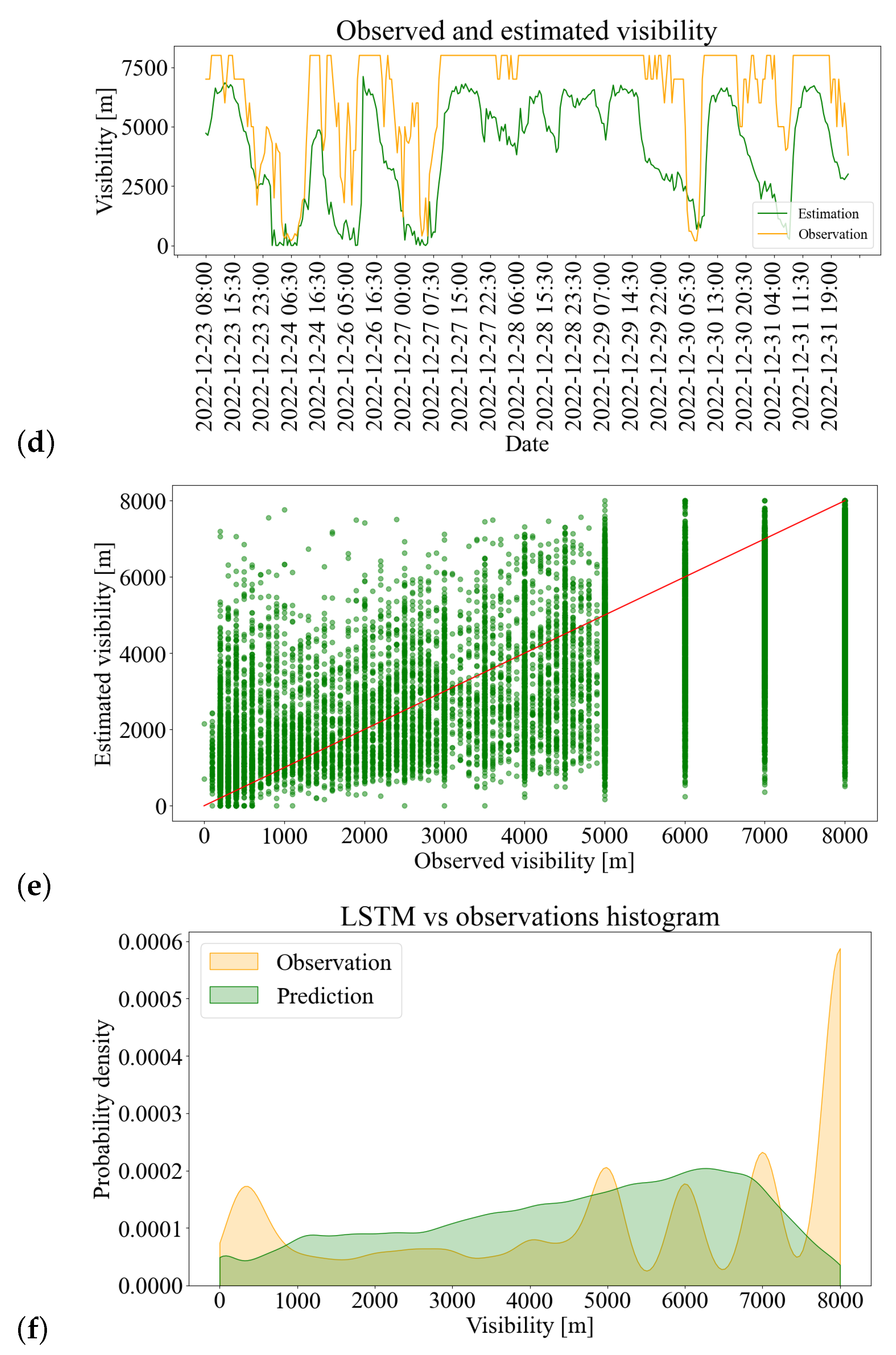
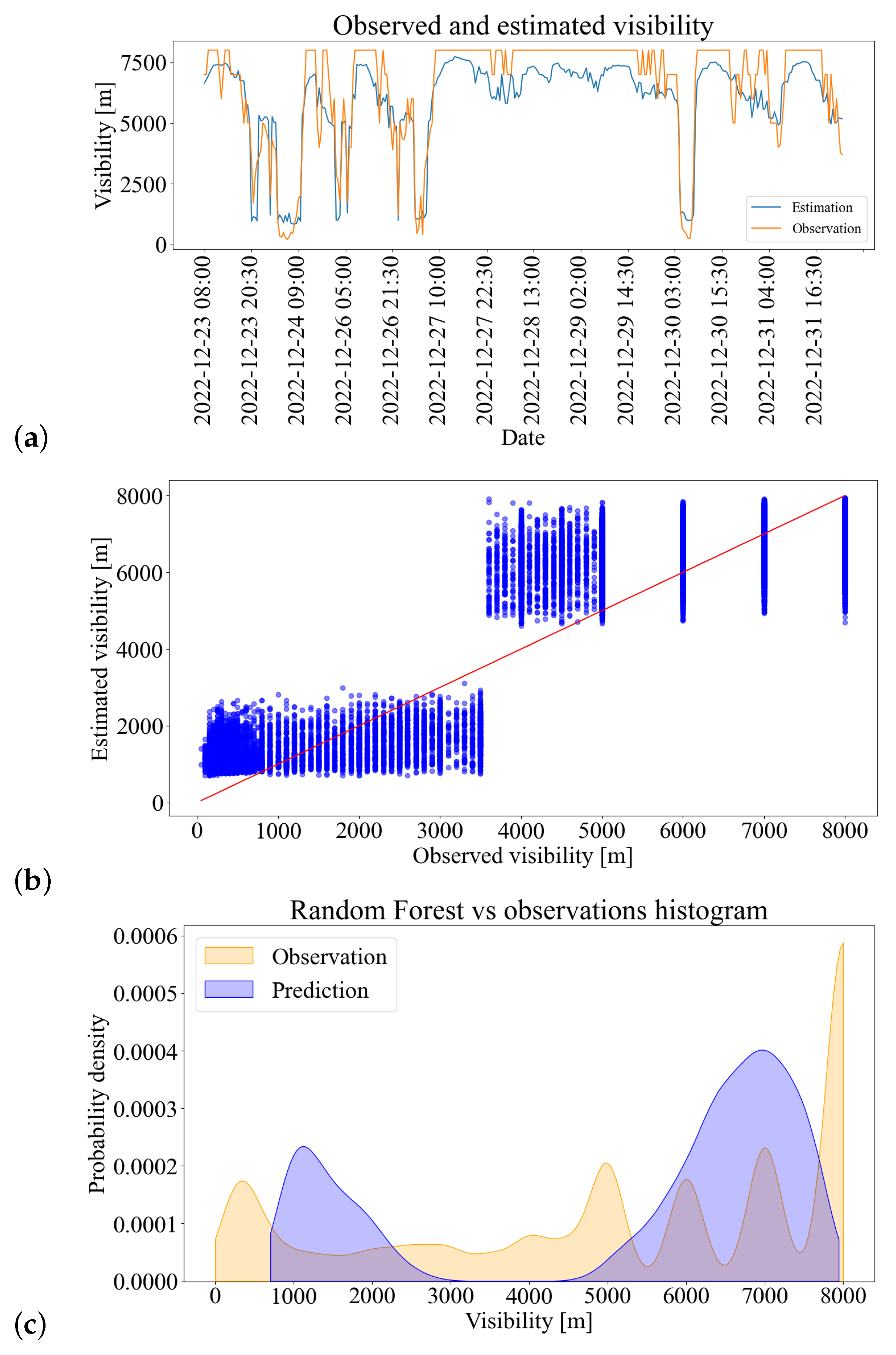
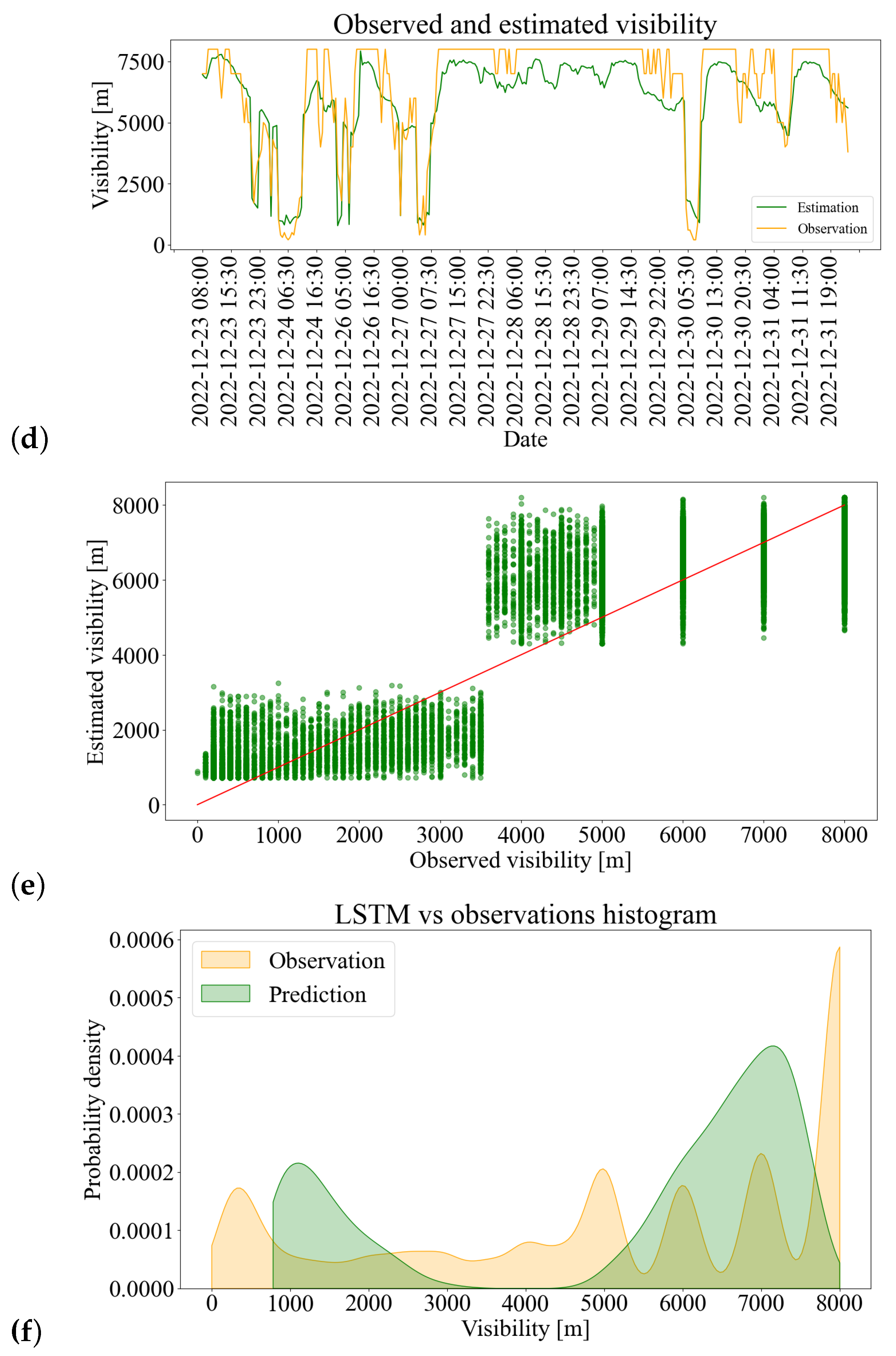
3.2. Random Forest and LSTM Visibility Estimation
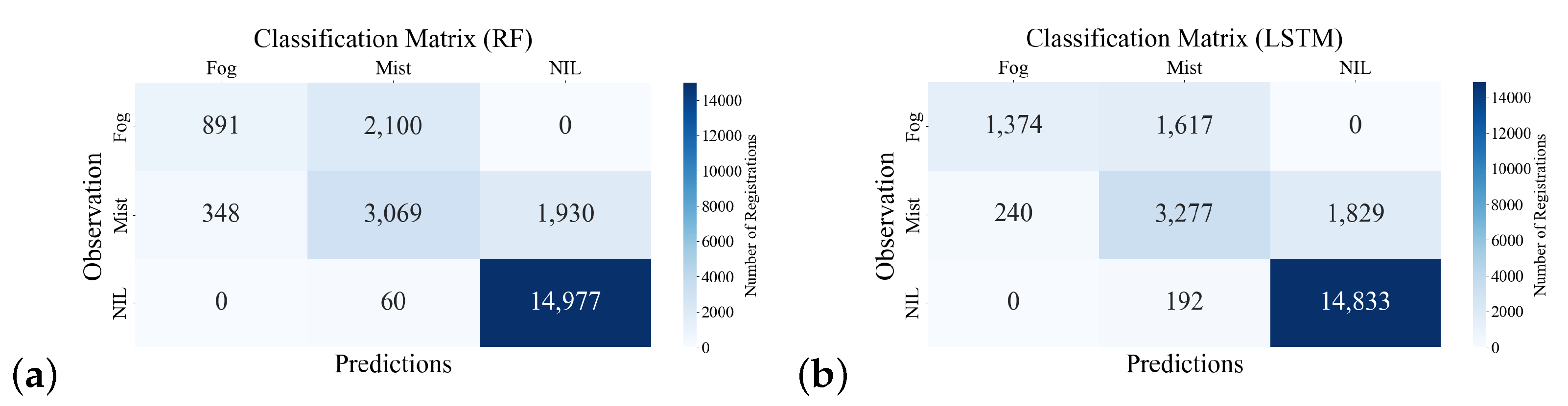
3.2.1. Results Post-Processing and Model Evaluation
3.2.2. Feature Importance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gultepe, I.; Sharman, R.; Williams, P.D.; Zhou, B.; Ellrod, G.; Minnis, P.; Trier, S.; Griffin, S.; Yum, S.S.; Gharabaghi, B.; et al. A review of high impact weather for aviation meteorology. Pure Appl. Geophys. 2019, 176, 1869–1921. [Google Scholar] [CrossRef]
- Belo-Pereira, M.; Santos, J. A persistent wintertime fog episode at Lisbon airport (Portugal): Performance of ECMWF and AROME models. Meteorol. Appl. 2016, 23, 353–370. [Google Scholar] [CrossRef]
- Liu, D.; Niu, S.; Yang, J.; Zhao, L.; Lü, J.; Lu, C. Summary of a 4-year fog field study in northern Nanjing, Part 1: Fog boundary layer. Pure Appl. Geophys. 2012, 169, 809–819. [Google Scholar] [CrossRef]
- Román-Cascón, C.; Yagüe, C.; Sastre, M.; Maqueda, G.; Salamanca, F.; Viana, S. Observations and WRF simulations of fog events at the Spanish Northern Plateau. Adv. Sci. Res. 2012, 8, 11–18. [Google Scholar] [CrossRef]
- Smith, D.K.; Renfrew, I.A.; Dorling, S.R.; Price, J.D.; Boutle, I.A. Sub-km scale numerical weather prediction model simulations of radiation fog. Q. J. R. Meteorol. Soc. 2021, 147, 746–763. [Google Scholar] [CrossRef]
- Jia, X.; Quan, J.; Zheng, Z.; Liu, X.; Liu, Q.; He, H.; Liu, Y. Impacts of anthropogenic aerosols on fog in North China Plain. J. Geophys. Res. Atmos. 2019, 124, 252–265. [Google Scholar] [CrossRef]
- Yan, S.; Zhu, B.; Huang, Y.; Zhu, J.; Kang, H.; Lu, C.; Zhu, T. To what extents do urbanization and air pollution affect fog? Atmos. Chem. Phys. 2020, 20, 5559–5572. [Google Scholar] [CrossRef]
- Boutle, I.; Price, J.; Kudzotsa, I.; Kokkola, H.; Romakkaniemi, S. Aerosol–fog interaction and the transition to well-mixed radiation fog. Atmos. Chem. Phys. 2018, 18, 7827–7840. [Google Scholar] [CrossRef]
- Bergot, T.; Escobar, J.; Masson, V. Effect of small-scale surface heterogeneities and buildings on radiation fog: Large-eddy simulation study at Paris–Charles de Gaulle airport. Q. J. R. Meteorol. Soc. 2015, 141, 285–298. [Google Scholar] [CrossRef]
- Shao, N.; Lu, C.; Jia, X.; Wang, Y.; Li, Y.; Yin, Y.; Zhu, B.; Zhao, T.; Liu, D.; Niu, S.; et al. Radiation fog properties in two consecutive events under polluted and clean conditions in the Yangtze River Delta, China: A simulation study. Atmos. Chem. Phys. 2023, 23, 9873–9890. [Google Scholar] [CrossRef]
- Arun, S.; Chaurasia, S.; Misra, A.; Kumar, R. Fog Stability Index: A novel technique for fog/low clouds detection using multi-satellites data over the Indo-Gangetic plains during winter season. Int. J. Remote Sens. 2018, 39, 8200–8218. [Google Scholar] [CrossRef]
- Holtslag, M.; Steeneveld, G.; Holtslag, A. Fog forecasting: “Old fashioned” semi-empirical methods from radio sounding observations versus “modern” numerical models. In Proceedings of the 5th International Conference on Fog, Fog Collection and Dew (FOGDEW2010), Münster, Germany, 25–30 July 2010. [Google Scholar]
- Song, Y.; Yum, S.S. Development and verification of the fog stability index for Incheon international airport based on the measured fog characteristics. Atmosphere 2013, 23, 443–452. [Google Scholar] [CrossRef]
- Stoycheva, A.; Evtimov, S. Studying the fogs in Sofia with Cherni vrah-Sofia Stability Index. Bulg. Geophys. J. 2014, 40, 23–32. [Google Scholar]
- Penov, N.; Stoycheva, A.; Guerova, G. Fog in Sofia 2010–2019: Objective circulation classification and fog indices. Atmosphere 2023, 14, 773. [Google Scholar] [CrossRef]
- Lui, G.N.; Hon, K.K.; Liem, R.P. Weather impact quantification on airport arrival on-time performance through a Bayesian statistics modeling approach. Transp. Res. Part C Emerg. Technol. 2022, 143, 103811. [Google Scholar] [CrossRef]
- Schultz, M.; Reitmann, S.; Alam, S. Predictive classification and understanding of weather impact on airport performance through machine learning. Transp. Res. Part C Emerg. Technol. 2021, 131, 103119. [Google Scholar] [CrossRef]
- Bari, D.; Bergot, T.; Tardif, R. Fog Decision Support Systems: A Review of the Current Perspectives. Atmosphere 2023, 14, 1314. [Google Scholar] [CrossRef]
- Kim, J.; Kim, S.H.; Seo, H.W.; Wang, Y.V.; Lee, Y.G. Meteorological characteristics of fog events in Korean smart cities and machine learning based visibility estimation. Atmos. Res. 2022, 275, 106239. [Google Scholar] [CrossRef]
- Castillo-Botón, C.; Casillas-Pérez, D.; Casanova-Mateo, C.; Ghimire, S.; Cerro-Prada, E.; Gutierrez, P.; Deo, R.; Salcedo-Sanz, S. Machine learning regression and classification methods for fog events prediction. Atmos. Res. 2022, 272, 106157. [Google Scholar] [CrossRef]
- Peláez-Rodríguez, C.; Pérez-Aracil, J.; de Lopez-Diz, A.; Casanova-Mateo, C.; Fister, D.; Jiménez-Fernández, S.; Salcedo-Sanz, S. Deep learning ensembles for accurate fog-related low-visibility events forecasting. Neurocomputing 2023, 549, 126435. [Google Scholar] [CrossRef]
- Dewi, R.; Harsa, H. Fog prediction using artificial intelligence: A case study in Wamena Airport. J. Phys. Conf. Ser. 2020, 1528, 012021. [Google Scholar] [CrossRef]
- Bartok, J.; Šišan, P.; Ivica, L.; Bartoková, I.; Malkin Ondík, I.; Gaál, L. Machine learning-based fog nowcasting for aviation with the aid of camera observations. Atmosphere 2022, 13, 1684. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife annals of statistics. Ann. Statist. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations (iclr’15), San Diego, CA, USA, 7–9 May 2015; Volume 500. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io/ (accessed on 24 September 2023).
- Hanssen, A.; Kuipers, W. On the Relationship between the Frequency of Rain and Various Meteorological Parameters. (With Reference to the Problem of Objective Forecasting); Koninklijk Nederlands Meteorologisch Instituut: Utrecht, The Netherlands, 1965. [Google Scholar]
- StatSoft Inc. Statistica (Data Analysis Software System), 6th ed.; StatSoft Inc.: Tulsa, OK, USA, 2001; p. 150. Available online: www.statsoft.com (accessed on 23 April 2023).
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.L. Seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P. Control of recent European surface climate change by atmospheric flow. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Stoev, K.; Post, P.; Guerova, G. Synoptic circulation patterns associated with foehn days in Sofia in the period 1979–2014. IdŐJÁRÁS/Q. J. Hung. Meteorol. Serv. 2022, 126, 545–566. [Google Scholar] [CrossRef]
- Maurer, M.; Klemm, O.; Lokys, H.L.; Lin, N.H. Trends of fog and visibility in Taiwan: Climate change or air quality improvement? Aerosol Air Qual. Res. 2019, 19, 896–910. [Google Scholar] [CrossRef]
- Hunova, I.; Brabec, M.; Maly, M.; Valerianova, A. Long-term trends in fog occurrence in the Czech Republic, Central Europe. Sci. Total. Environ. 2020, 711, 135018. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.Y.; Cha, J.W.; Chang, K.H.; Lee, C. Visibility prediction over South Korea based on random forest. Atmosphere 2021, 12, 552. [Google Scholar] [CrossRef]
- Choi, W.; Park, J.; Kim, D.; Park, J.; Kim, S.; Lee, H. Development of two-dimensional visibility estimation model using machine learning: Preliminary results for South Korea. Atmosphere 2022, 13, 1233. [Google Scholar] [CrossRef]

| Parameter | Trees | Max Features | Max Depth | Min Samples |
|---|---|---|---|---|
| Value | 2000 | sqrt | 10 | 10 |
| Parameter | Units | Steps | Optimizer | Learning Rate | Activation | Loss Function | Epochs |
|---|---|---|---|---|---|---|---|
| Value | 150 | 12 | Adam | Exponential decay | ReLU | Mean squared error | 10 |
| R2 | MAE [m] | RMSE [m] | |
|---|---|---|---|
| RF | 0.38 | 1752 | 2123 |
| RF* | 0.81 | 984 | 1178 |
| LSTM | 0.44 | 1600 | 2024 |
| LSTM* | 0.82 | 955 | 1154 |
| RF | RF* | LSTM | LSTM* | |
|---|---|---|---|---|
| POD [%] | 12 | 30 | 29 | 37 |
| FAR [%] | 0.7 | 1.7 | 0.9 | 1 |
| CSI [%] | 11 | 27 | 27 | 35 |
| TSS [%] | 11 | 28 | 28 | 36 |
| Variable | Importance |
|---|---|
| FSI | 0.34 |
| Dew-point deficit | 0.23 |
| Cloud base | 0.11 |
| Temperature | 0.09 |
| Wind speed | 0.08 |
| Day of year | 0.06 |
| Dew point | 0.04 |
| Hour | 0.02 |
| Pressure | 0.02 |
| Wind direction | 0.01 |
| Cloud coverage | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penov, N.; Guerova, G. Sofia Airport Visibility Estimation with Two Machine-Learning Techniques. Remote Sens. 2023, 15, 4799. https://doi.org/10.3390/rs15194799
Penov N, Guerova G. Sofia Airport Visibility Estimation with Two Machine-Learning Techniques. Remote Sensing. 2023; 15(19):4799. https://doi.org/10.3390/rs15194799
Chicago/Turabian StylePenov, Nikolay, and Guergana Guerova. 2023. "Sofia Airport Visibility Estimation with Two Machine-Learning Techniques" Remote Sensing 15, no. 19: 4799. https://doi.org/10.3390/rs15194799
APA StylePenov, N., & Guerova, G. (2023). Sofia Airport Visibility Estimation with Two Machine-Learning Techniques. Remote Sensing, 15(19), 4799. https://doi.org/10.3390/rs15194799









