Performance Assessment of a High-Frequency Radar Network for Detecting Surface Currents in the Pearl River Estuary
Abstract
1. Introduction
2. Materials and Methods
2.1. High-Frequency Radar: OSMAR-S100
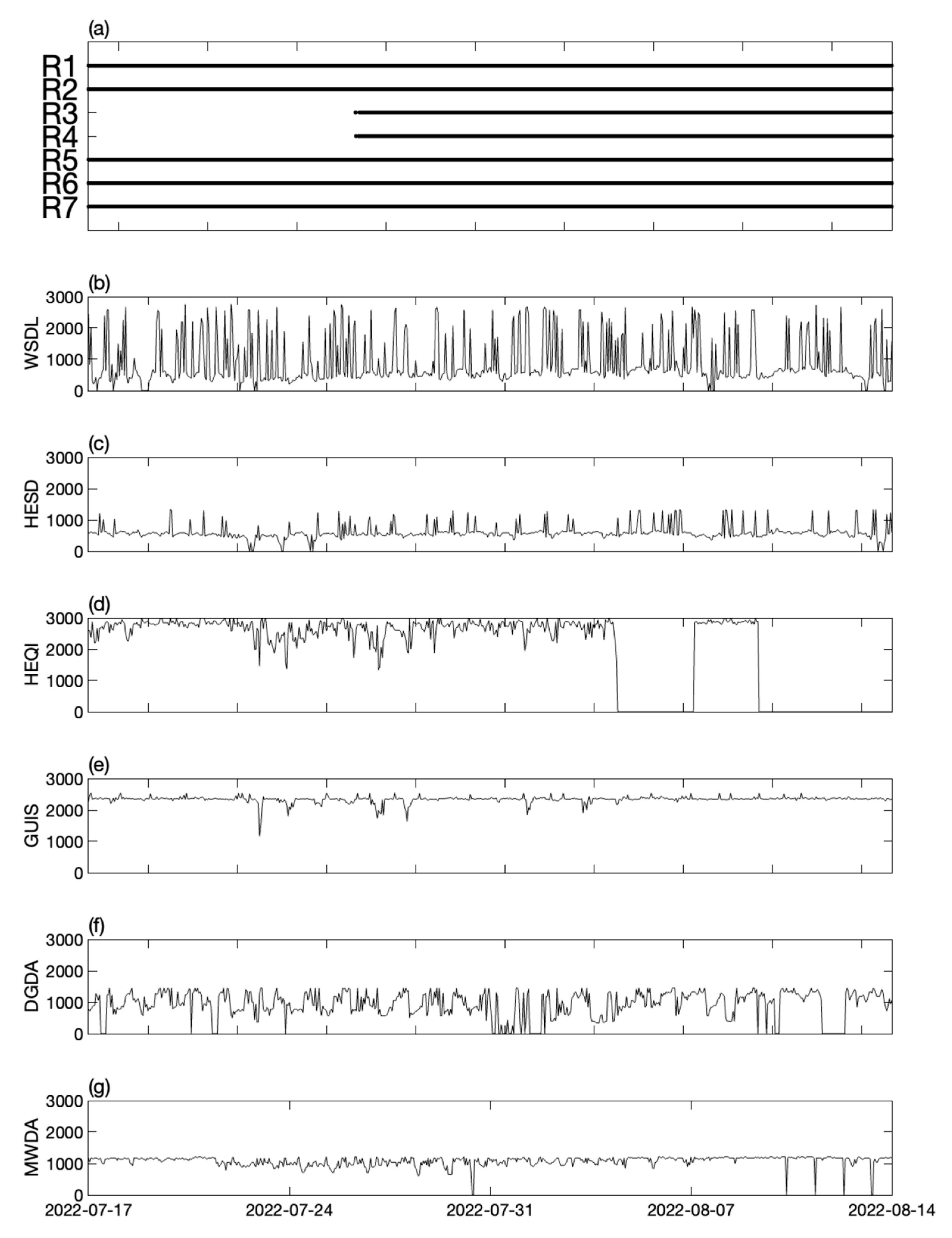
2.2. Mooring Instruments and Data Coverage Variations
2.3. Statistical Metrics
3. Results
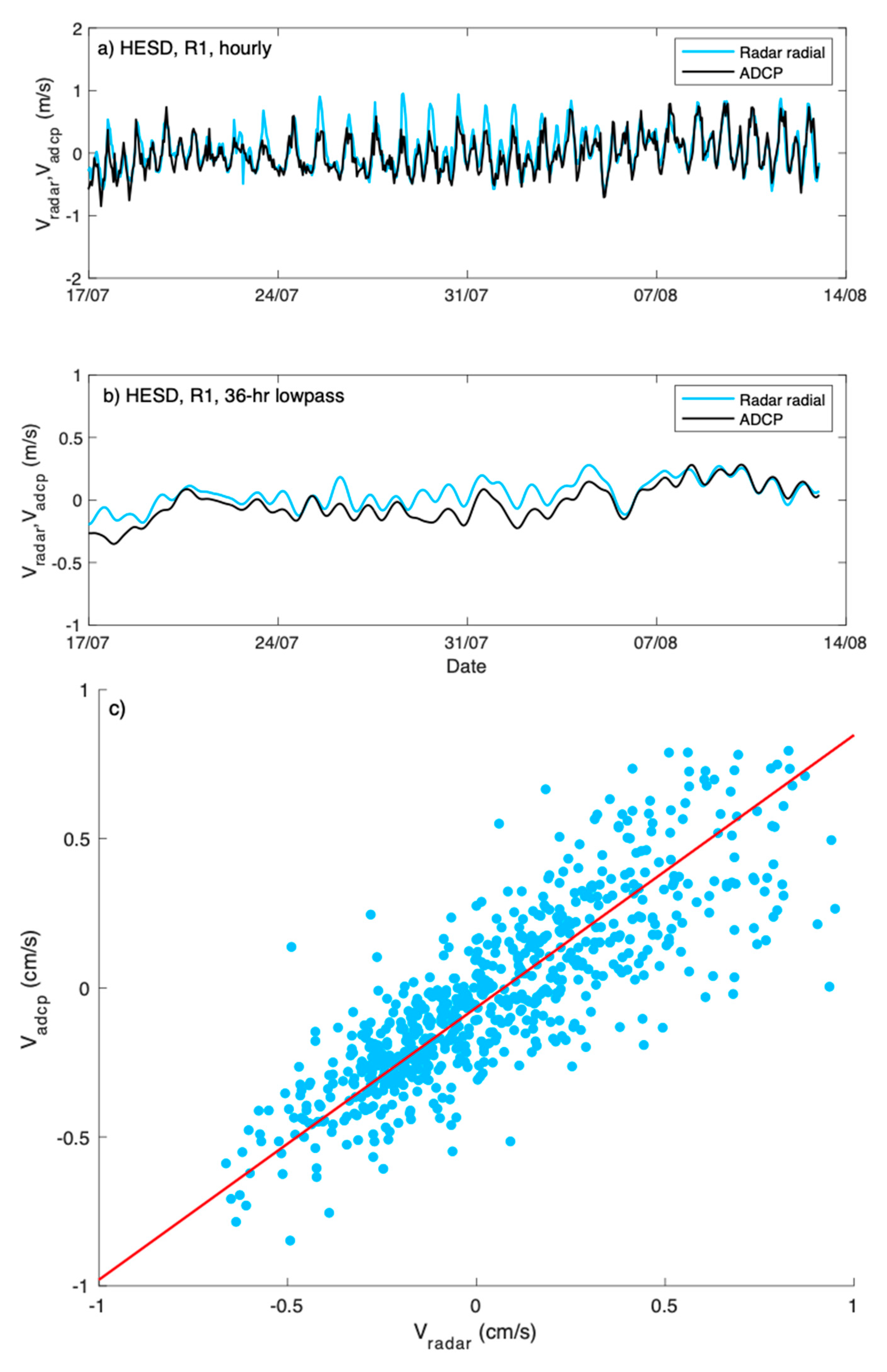
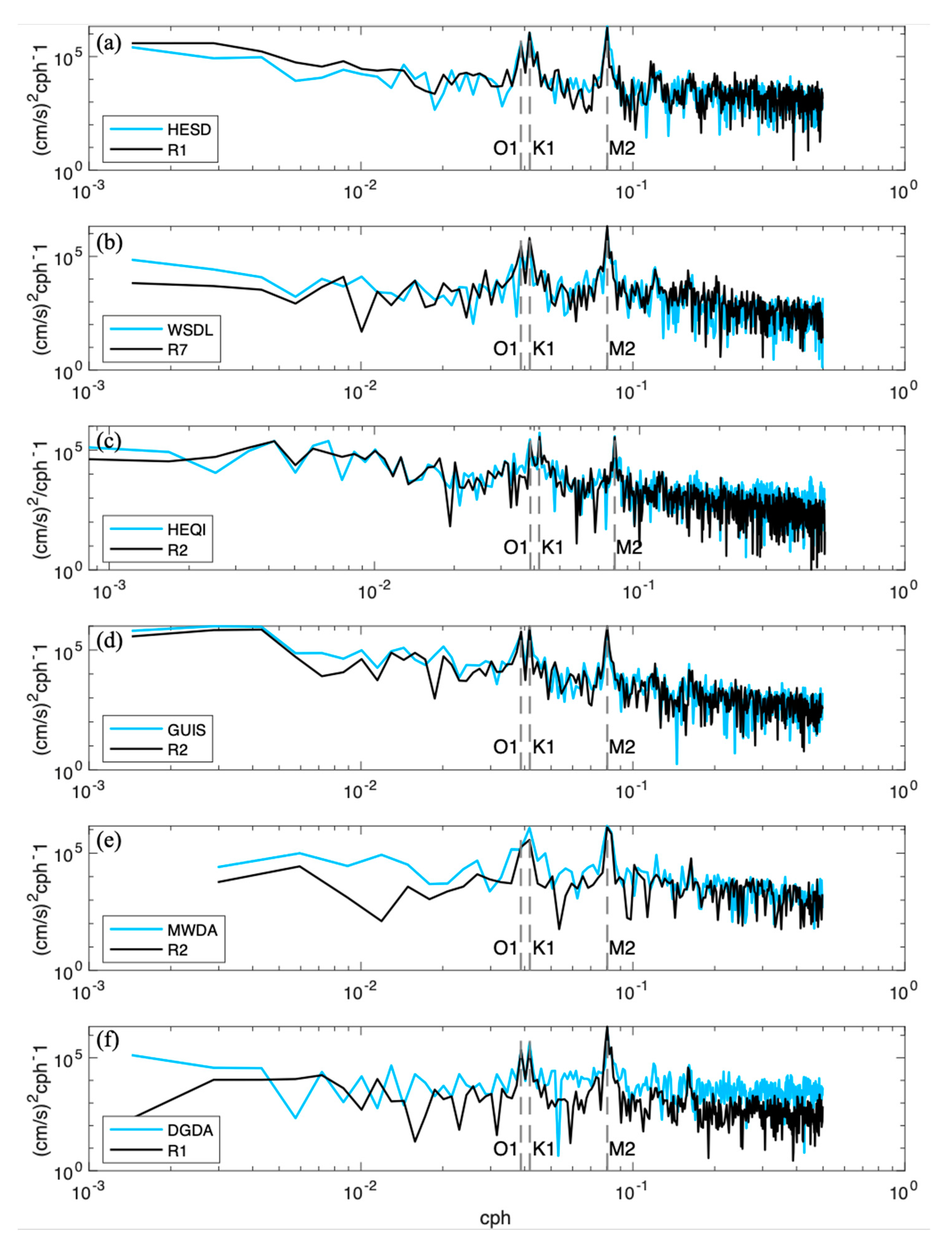
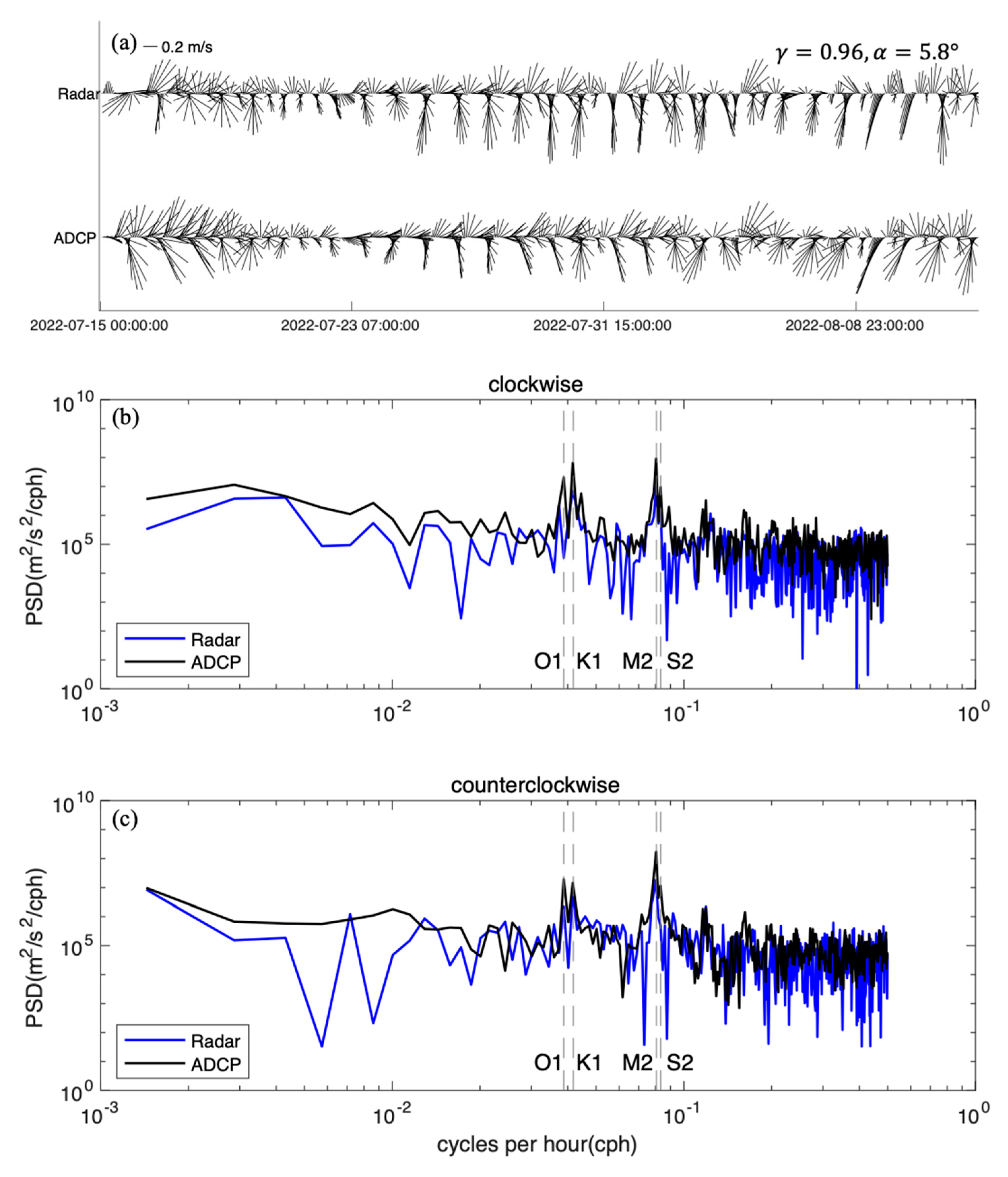
3.1. Radial Velocity
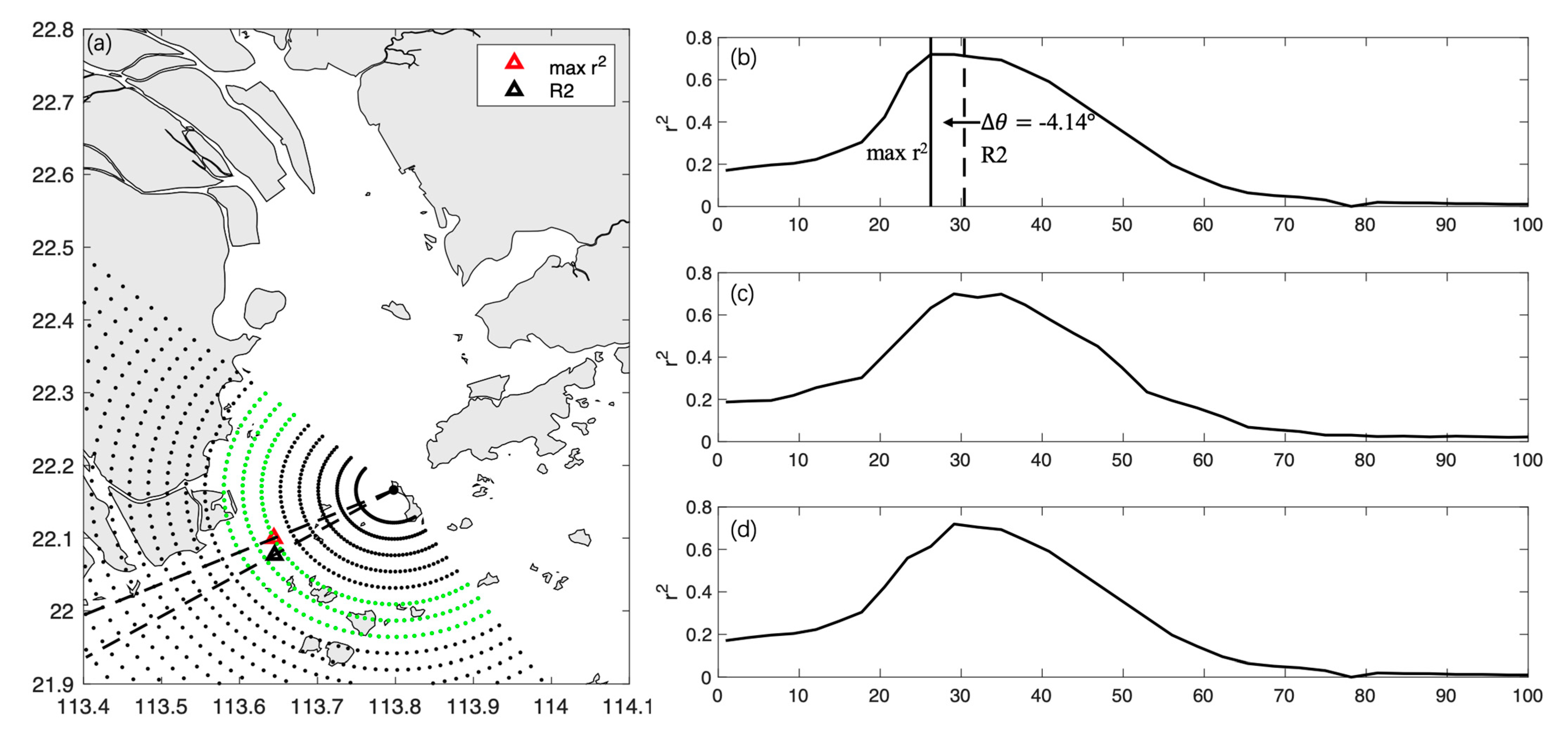
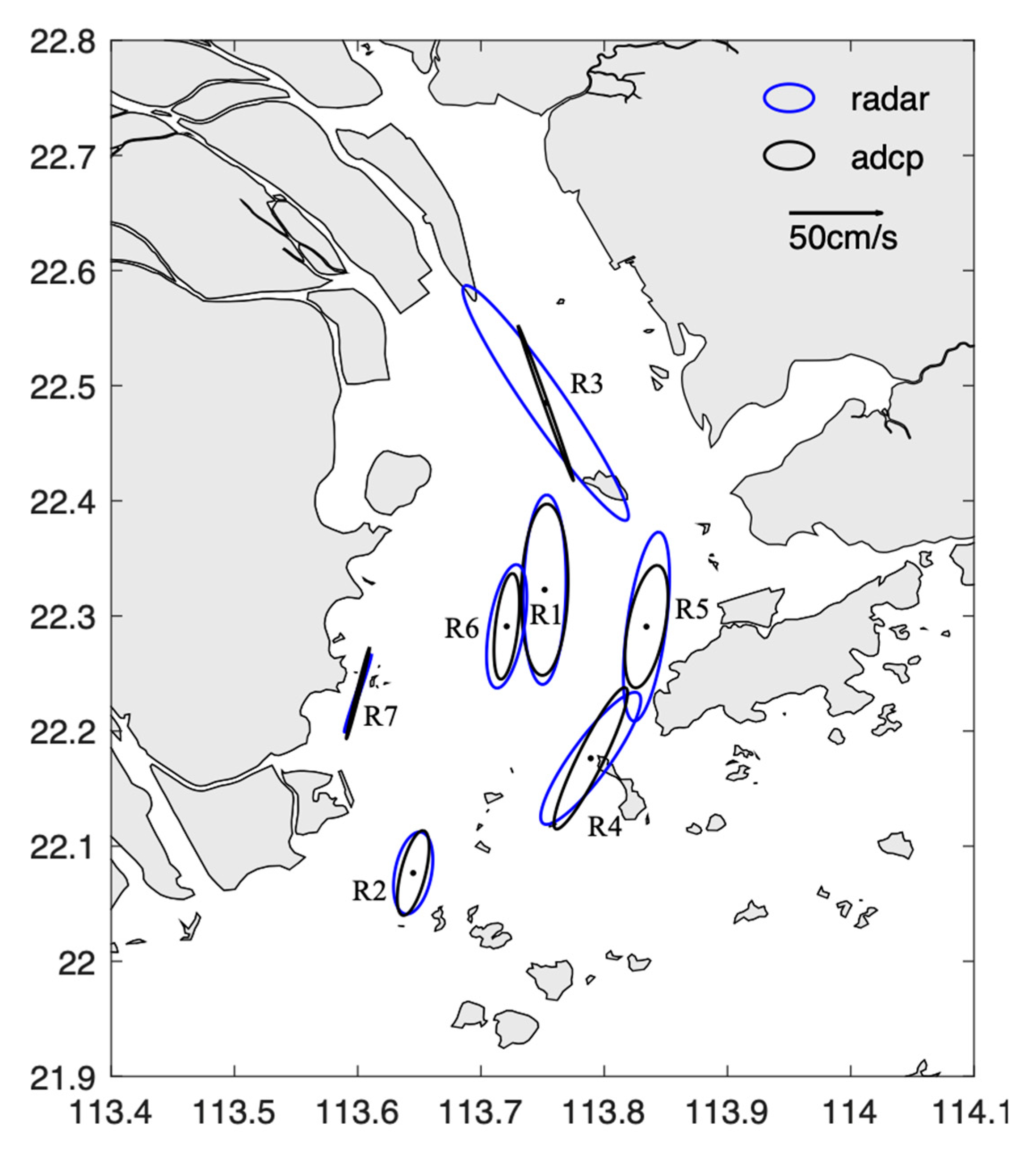
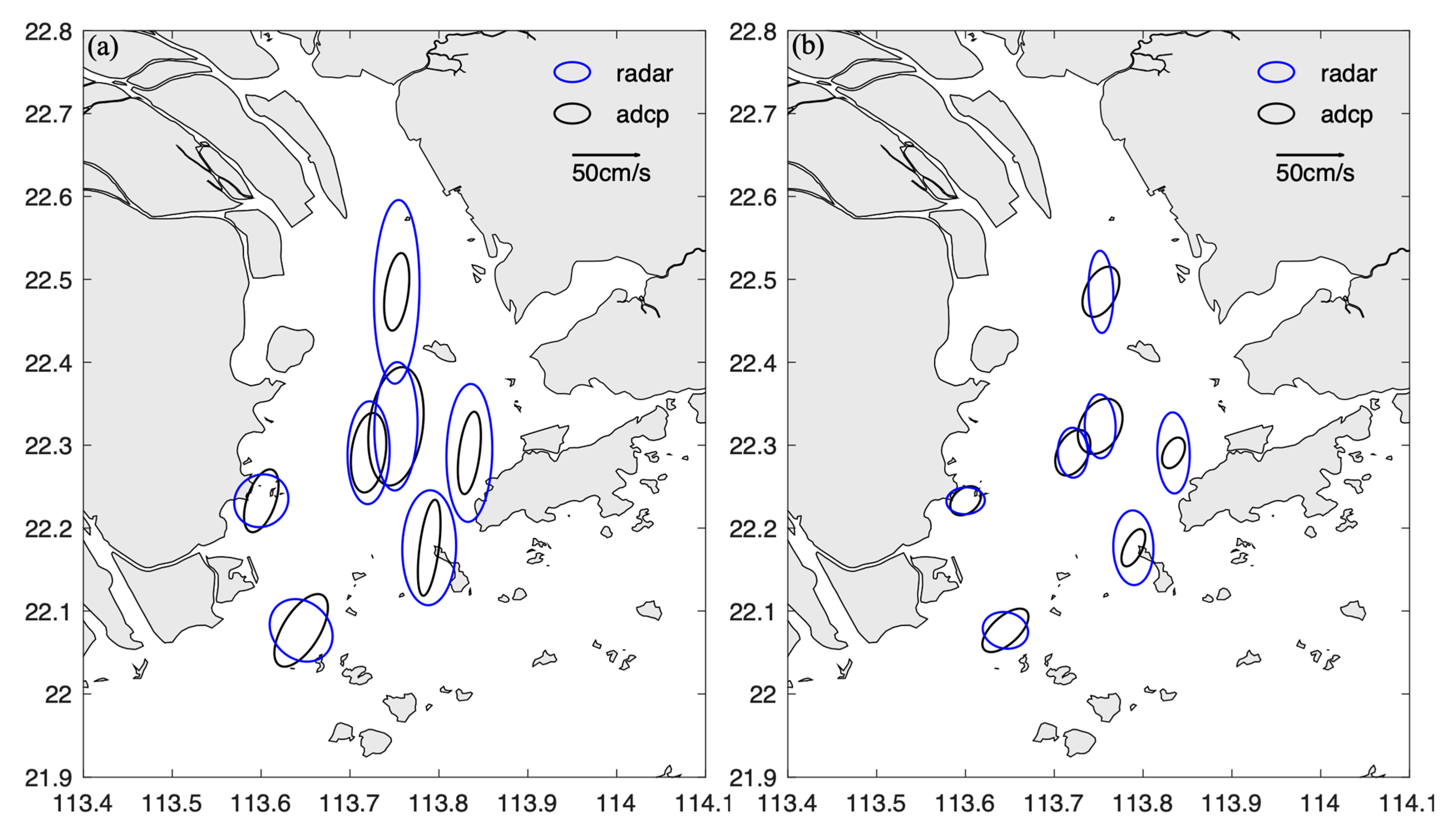
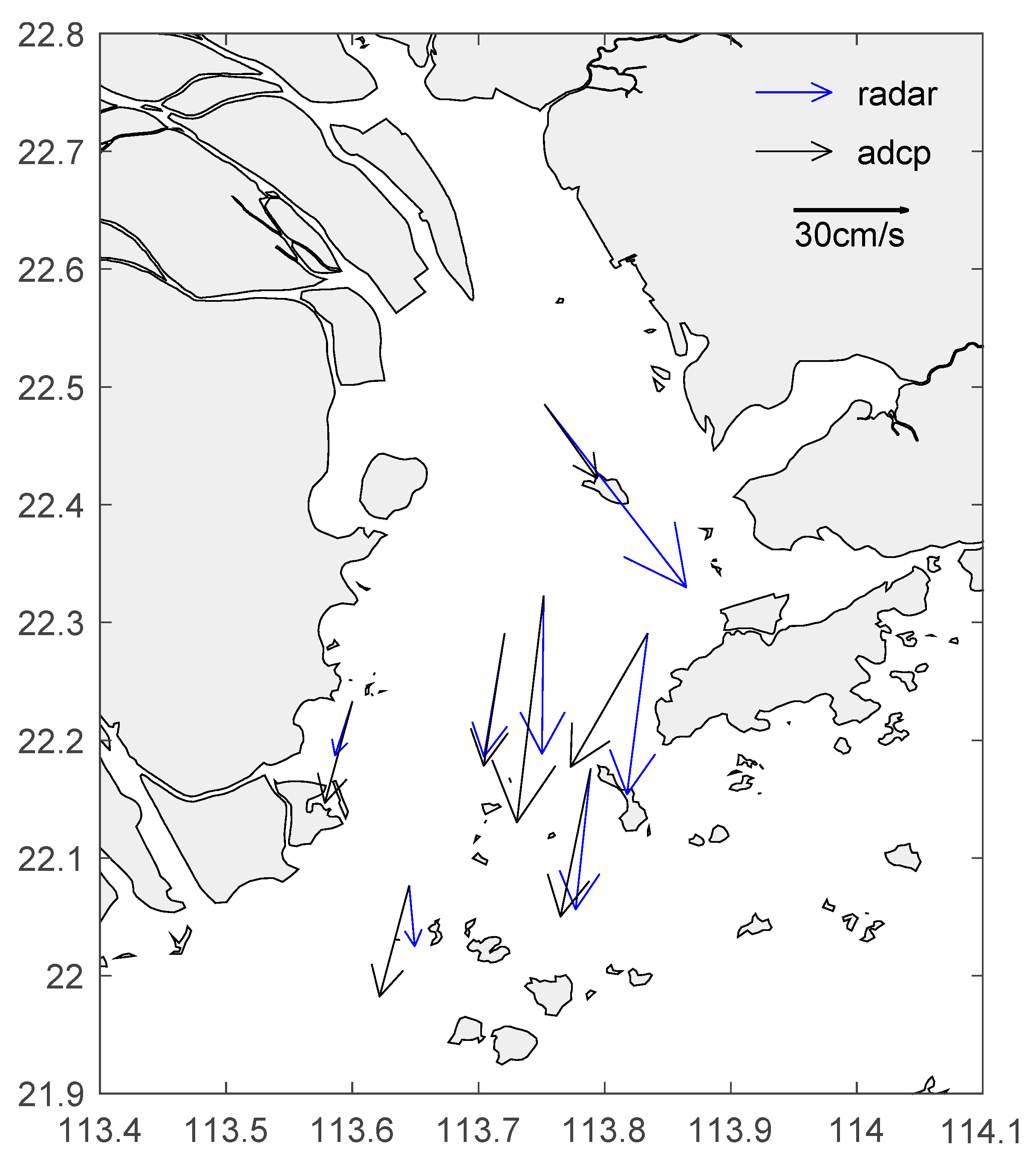
3.2. Total Velocity
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crombie, D.D. Doppler Spectrum of Sea Echo at 13.56 Mc./s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Barrick, D.E.; Evans, M.W.; Weber, B.L. Ocean Surface Currents Mapped by Radar. Science 1977, 198, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Lipa, B.J.; Barrick, D.E. Least-Squares Methods for the Extraction of Surface Currents from CODAR Crossed-Loop Data: Application at ARSLOE. IEEE J. Ocean. Eng. 1983, 8, 226–253. [Google Scholar] [CrossRef]
- Paduan, J.D.; Washburn, L. High-Frequency Radar Observations of Ocean Surface Currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef] [PubMed]
- Stewart, R.H.; Joy, J.W. HF Radio Measurements of Surface Currents. Deep Sea Res. Oceanogr. Abstr. 1974, 21, 1039–1049. [Google Scholar] [CrossRef]
- Teague, C.C.; Vesecky, J.F.; Fernandez, D.M. HF Radar Instruments, Past to Present. Oceanography 1997, 10, 40–44. [Google Scholar] [CrossRef]
- Gurgel, K.W.; Antonischki, G.; Essen, H.H.; Schlick, T. Wellen Radar (WERA): A New Ground-Wave HF Radar for Ocean Remote Sensing. Coast. Eng. 1999, 37, 219–234. [Google Scholar] [CrossRef]
- Hammond, T.M.; Pattiaratchi, C.B.; Eccles, D.; Osborne, M.J.; Nash, L.A.; Collins, M.B. Ocean Surface Current Radar (OSCR) Vector Measurements on the Inner Continental Shelf. Cont. Shelf Res. 1987, 7, 411–431. [Google Scholar] [CrossRef]
- Barrick, D.E.; Lipa, B.J.; Crissman, R.D. Mapping Surface Currents with Codar. Sea Technol. 1985, 26, 43–48. [Google Scholar]
- Hou, J.; Wu, S.; Yang, Z.; Qiu, C.; Wen, B.; Shi, Z.; Wu, Q.; Guan, R.; Wang, S. Remote Sensing of Ocean Surface Currents by HF Radar. Acta Geophys. Sin. 1997, 40, 18–26. [Google Scholar]
- Frisch, A.S.; Weber, B.L. A New Technique for Measuring Tidal Currents by Using a Two-Site HF Doppler Radar System. J. Geophys. Res. Ocean. 1980, 85, 485–493. [Google Scholar] [CrossRef]
- Holbrook, J.R.; Frisch, A.S. A Comparison of Near-Surface CODAR and VACM Measurements in the Strait of Juan De Fuca, August 1978. J. Geophys. Res. 1981, 86, 10908–10912. [Google Scholar] [CrossRef]
- Paduan, J.D.; Rosenfeld, L.K. Remotely Sensed Surface Currents in Monterey Bay from Shore-Based HF Radar (Coastal Ocean Dynamics Application Radar). J. Geophys. Res. Ocean. 1996, 101, 20669–20686. [Google Scholar] [CrossRef]
- Yoshikawa, Y.; Masuda, A.; Marubayashi, K.; Ishibashi, M.; Okuno, A. On the Accuracy of HF Radar Measurement in the Tsushima Strait. J. Geophys. Res. Ocean. 2006, 111, C04009. [Google Scholar] [CrossRef]
- Emery, B.M.; Washburn, L.; Harlan, J.A. Evaluating Radial Current Measurements from CODAR High-Frequency Radars with Moored Current Meters*. J. Atmos. Ocean. Technol. 2004, 21, 1259–1271. [Google Scholar] [CrossRef]
- Matthews, J.P.; Simpson, J.H.; Brown, J. Remote Sensing of Shelf Sea Currents Using a High-Frequency Ocean Surface Current Radar System. J. Geophys. Res. Ocean. 1988, 93, 2303–2310. [Google Scholar] [CrossRef]
- Chapman, R.D.; Shay, L.K.; Graber, H.C.; Edson, J.B.; Karachintsev, A.; Trump, C.L.; Ross, D.B. On the Accuracy of HF Radar Surface Current Measurements: Intercomparisons with Ship-Based Sensors. J. Geophys. Res. Ocean. 1997, 102, 18737–18748. [Google Scholar] [CrossRef]
- Graber, H.C.; Haus, B.K.; Chapman, R.D.; Shay, L.K. HF Radar Comparisons with Moored Estimates of Current Speed and Direction: Expected Differences and Implications. J. Geophys. Res. Ocean. 1997, 102, 18749–18766. [Google Scholar] [CrossRef]
- Kosro, M.; Barth, J.; Strub, T. The Coastal Jet: Observations of Surface Currents Over the Oregon Continental Shelf From HF Radar. Oceanography 1997, 10, 53–56. [Google Scholar] [CrossRef]
- Shay, L.K.; Graber, H.C.; Ross, D.B.; Chapman, R.D. Mesoscale Ocean Surface Current Structure Detected by High-Frequency Radar. J. Atmos. Ocean. Technol. 1995, 12, 881–900. [Google Scholar] [CrossRef][Green Version]
- Shay, L.K.; Lentz, S.J.; Graber, H.C.; Haus, B.K. Current Structure Variations Detected by High-Frequency Radar and Vector-Measuring Current Meters. J. Atmos. Ocean. Technol. 1998, 15, 237–256. [Google Scholar] [CrossRef]
- Essen, H.-H.; Gurgel, K.-W.; Schlick, T. On the Accuracy of Current Measurements by Means of HF Radar. IEEE J. Ocean. Eng. 2000, 25, 472–480. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Merz, C.R.; Lichtenwalner, S.; Kirkpatrick, G.J. HF Radar Performance in a Low-Energy Environment: CODAR Seasonde Experience on the West Florida Shelf. J. Atmos. Ocean. Technol. 2010, 27, 1689–1710. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Merz, C.R. Assessment of CODAR Seasonde and WERA HF Radars in Mapping Surface Currents on the West Florida Shelf. J. Atmos. Ocean. Technol. 2014, 31, 1363–1382. [Google Scholar] [CrossRef]
- Mau, J.C.; Wang, D.P.; Ullman, D.S.; Codiga, D.L. Comparison of Observed (HF Radar, ADCP) and Model Barotropic Tidal Currents in the New York Bight and Block Island Sound. Estuar. Coast. Shelf Sci. 2007, 72, 129–137. [Google Scholar] [CrossRef]
- Mau, J.C.; Wang, D.P.; Ullman, D.S.; Codiga, D.L. Model of the Long Island Sound Outflow: Comparison with Year-Long HF Radar and Doppler Current Observations. Cont. Shelf Res. 2008, 28, 1791–1799. [Google Scholar] [CrossRef]
- Paduan, J.D.; Kim, K.C.; Cook, M.S.; Chavez, F.P. Calibration and Validation of Direction-Finding High-Frequency Radar Ocean Surface Current Observations. IEEE J. Ocean. Eng. 2006, 31, 862–875. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, T.; Yang, F.; Liu, B.; Wu, L.; Wei, J. Comparisons of Tidal Currents in the Pearl River Estuary between High-Frequency Radar Data and Model Simulations. Appl. Sci. 2022, 12, 6509. [Google Scholar] [CrossRef]
- Laws, K.E.; Fernandez, D.M.; Paduan, J.D. Simulation-Based Evaluations of HF Radar Ocean Current Algorithms. IEEE J. Ocean. Eng. 2000, 25, 481–491. [Google Scholar] [CrossRef]
- Kohut, J.; Glenn, S.; Barrick, D. SeaSonde Is Integral to Coastal Flow Model Development. Hydro Int. 1999, 3, 32–35. [Google Scholar]
- Shaolin, Y.; Hengyu, K.; Jiechang, H.; Shicai, W.; Zijie, Y.; Biyang, W.; Xiongbin, W. Super-Resolution Ocean Surface Current Algorithm Based on MUSIC for OSMAR2000. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No.01CH37295), Honolulu, HI, USA, 5–8 November 2001; Volume 2, pp. 930–941. [Google Scholar]
- Lai, Y.; Zhou, H.; Wen, B. Surface Current Characteristics in the Taiwan Strait Observed by High-Frequency Radars. IEEE J. Ocean. Eng. 2017, 42, 449–457. [Google Scholar] [CrossRef]
- Lai, Y.; Zhou, H.; Zeng, Y.; Wen, B. Accuracy Assessment of Surface Current Velocities Observed by OSMAR-S High-Frequency Radar System. IEEE J. Ocean. Eng. 2018, 43, 1068–1074. [Google Scholar] [CrossRef]
- Shicai, W.; Zijie, Y.; Biyang, W.; Zhenhua, S.; Jiansheng, T.; Huotao, G.; Xiongbin, W.; Hengyu, K. Test of HF Ground Wave Radar OSMAR2000 at the Eastern China Sea. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No.01CH37295), Honolulu, HI, USA, 5–8 November 2001; Volume 1, pp. 646–648. [Google Scholar]
- Wu, X.; Li, L.; Shao, Y.; Li, Y.; Guo, T. Experimental Determination of Significant Waveheight by OSMAR071: Comparison with Results from Buoy. Wuhan Univ. J. Nat. Sci. 2009, 14, 499–504. [Google Scholar] [CrossRef]
- Shen, W.; Wen, B.; Wu, S.; Bai, L.; Zhou, H.; Yang, J. HF Radar Receiver Designed for Surface Current Radar System. In Proceedings of the 2006 10th IET International Conference on Ionospheric Radio Systems and Techniques (IRST 2006), London, UK, 18–21 July 2006; pp. 240–243. [Google Scholar]
- Zhu, L.; Yang, F.; Yang, Y.; Xiong, Z.; Wei, J. Designing Theoretical Shipborne ADCP Survey Trajectories for High-Frequency Radar Based on a Machine Learning Neural Network. Appl. Sci. 2023, 13, 7208. [Google Scholar] [CrossRef]
- Kundu, P.K. Ekman Veering Observed near the Ocean Bottom. J. Phys. Oceanogr. 1976, 6, 238–242. [Google Scholar] [CrossRef]
- Essen, H.-H.; Breivik, Ø.; Günther, H.; Gurgel, K.-W.; Johannessen, J.; Klein, H.; Schlick, T.; Stawarz, M. Comparison of Remotely Measured and Modelled Currents in Coastal Areas of Norway and Spain. J. Atmos. Ocean Sci. 2003, 9, 39–64. [Google Scholar] [CrossRef]
- Kaplan, D.M.; Largier, J.; Botsford, L.W. HF Radar Observations of Surface Circulation off Bodega Bay (Northern California, USA). J. Geophys. Res. Ocean. 2005, 110, C10020. [Google Scholar] [CrossRef]
- Parks, A.B.; Shay, L.K.; Johns, W.E.; Martinez-Pedraja, J.; Gurgel, K.-W. HF Radar Observations of Small-Scale Surface Current Variability in the Straits of Florida. J. Geophys. Res. Ocean. 2009, 114, C08002. [Google Scholar] [CrossRef]
- Shay, L.K.; Martinez-Pedraja, J.; Cook, T.M.; Haus, B.K.; Weisberg, R.H. High-Frequency Radar Mapping of Surface Currents Using WERA. J. Atmos. Ocean. Technol. 2007, 24, 484–503. [Google Scholar] [CrossRef]
- Weisberg, R.H.; He, R. Local and Deep-Ocean Forcing Contributions to Anomalous Water Properties on the West Florida Shelf. J. Geophys. Res. Ocean. 2003, 108, 3184. [Google Scholar] [CrossRef]
- Zheng, L.; Weisberg, R.H. Modeling the West Florida Coastal Ocean by Downscaling from the Deep Ocean, across the Continental Shelf and into the Estuaries. Ocean Model. 2012, 48, 10–29. [Google Scholar] [CrossRef]
- Mooers, C.N.K. A Technique for the Cross Spectrum Analysis of Pairs of Complex-Valued Time Series, with Emphasis on Properties of Polarized Components and Rotational Invariants. Deep Sea Res. Oceanogr. Abstr. 1973, 20, 1129–1141. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, C.; Yang, F.; Lu, T.; Zhu, L.; Wei, J. A Machine Learning-Based Correction Method for High-Frequency Surface Wave Radar Current Measurements. Appl. Sci. 2022, 12, 12980. [Google Scholar] [CrossRef]


| Parameter | Setting |
|---|---|
| Transmit frequency (MHz) | 13/16 |
| Equivalent isotropic radiated power (EIRP) peak (dBW) | <25 |
| Transmit bandwidth (kHz) | 30/60/120 |
| Harmonic suppression (dBc) | >60 |
| Maximum detection range (km) | 120 |
| Sweep period (s) | 0.38 |
| Nominal range resolution (km) | 2.5 |
| Nominal bearing resolution (degree) | 3 |
| Radial current resolution (cm/s) | 5.5 |
| Time resolution (min) | 20 |
| Number of transmit antenna elements | 1 |
| Number of receive antenna elements | 3 |
| Average transmitter power (W) | 100 |
| Transmitted waveform | FMICW |
| Technique of azimuthal resolution | Direction finding |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| HF site | Mooring | r2 | Bias | ||||
| WSDL | R1 | 0.42 | 14 | 2.5 | 16.1 | 0.77 | −0.02 |
| WSDL | R4 | 0.64 | 18.0 | −7 | 1.2 | 0.87 | 0.11 |
| HESD | R1 | 0.78 | 16.6 | 6 | −2.7 | 0.80 | −0.06 |
| HESD | R3 | 0.65 | 12.7 | 5.8 | −4.8 | 0.50 | −0.06 |
| HEQI | R2 | 0.60 | 17.5 | 4.7 | −3.9 | 0.71 | 0.05 |
| DGDA | R1 | 0.61 | 14.6 | 1 | 8.7 | 0.73 | 0.02 |
| DGDA | R2 | 0.59 | 13.0 | 7 | 7.6 | 0.57 | −0.06 |
| GUIS | R2 | 0.74 | 12.4 | 6.9 | −4.1 | 0.93 | −0.08 |
| MWDA | R4 | 0.43 | 21.6 | 8.7 | 13.4 | 0.79 | −0.08 |
| HESD | R5 | 0.57 | 13 | 8 | 1.7 | 0.54 | −0.04 |
| HESD | R6 | 0.55 | 11 | 9 | −3.4 | 0.37 | −0.03 |
| WSDL | R7 | 0.71 | 11.8 | −1.9 | 5.6 | 0.81 | 0.01 |
| Site | Statistic Metrics | |
|---|---|---|
| Mooring Site | (°) | |
| R1 | 0.96 | 5.8 |
| R2 | 0.95 | −9.7 |
| R3 | 0.62 | −24.3 |
| R4 | 0.84 | 7.8 |
| R5 | 0.93 | 14.3 |
| R6 | 0.91 | −1.4 |
| R7 | 0.63 | 17.8 |
| Constituents | Site | Radar | Mooring Observation | ||||
|---|---|---|---|---|---|---|---|
| Semi-Major (cm/s) | Semi-Minor (cm/s) | Orientation (°) | Semi-Major (cm/s) | Semi-Minor (cm/s) | Orientation (°) | ||
| M2 | R1 | 54.90 | −11.54 | 88.75 | 49.64 | −12.59 | 88.47 |
| R2 | 24.08 | −9.92 | 80 | 25.15 | −6.71 | 77.08 | |
| R3 | 80.80 | −10.58 | 122.91 | 47.36 | −1.14 | 108.46 | |
| R4 | 45.67 | −10.62 | 55.88 | 45.06 | −7.01 | 65.20 | |
| R5 | 55.14 | −10.53 | 82.90 | 35.96 | −10.13 | 79.51 | |
| R6 | 36.19 | −9.47 | 81.12 | 30.78 | 6.11 | 83.93 | |
| R7 | 23.68 | −1.02 | 72.10 | 27.18 | −0.87 | 76.69 | |
| S2 | R1 | 16.43 | −3.5 | 88.06 | 15.38 | −2.54 | 103.50 |
| R2 | 8.11 | −3.09 | 114.14 | 5.38 | −1.71 | 78.76 | |
| R3 | 20.64 | −5.04 | 124.72 | 22.6 | −2.2 | 99.31 | |
| R4 | 13.92 | −6.45 | 34.3 | 18.29 | −0.13 | 85.40 | |
| R5 | 16.09 | −2.75 | 77.52 | 12.73 | −0.46 | 56.78 | |
| R6 | 12.95 | −3.5 | 75.89 | 10.44 | −3.02 | 99.63 | |
| R7 | 5.91 | −3.94 | 54.08 | 7.21 | −1.92 | 97.54 | |
| K1 | R1 | 24.2 | −6.26 | 81.08 | 25.34 | −5.25 | 73.41 |
| R2 | 15.4 | −11.93 | 106.15 | 18.8 | −3.13 | 64.39 | |
| R3 | 34.97 | 6.02 | 119.11 | 22.78 | 4.59 | 81.92 | |
| R4 | 18.1 | −9.2 | 34.45 | 13.61 | 0.85 | 94.44 | |
| R5 | 27.64 | −7.51 | 76.57 | 17.85 | −0.5 | 59.33 | |
| R6 | 24.04 | −6.01 | 69.65 | 14.79 | −0.71 | 80.46 | |
| R7 | 12.66 | −8.26 | 40.62 | 13.93 | 0.57 | 73.32 | |
| O1 | R1 | 14.91 | −2.41 | 85.54 | 15.53 | −5.32 | 86.47 |
| R2 | 9.34 | −8.05 | 25.61 | 13.67 | −4.05 | 66.85 | |
| R3 | 24.27 | −1.89 | 124.41 | 25.39 | 2.48 | 82.45 | |
| R4 | 8.89 | 1.93 | 45.59 | 11.19 | 0.4 | 94.42 | |
| R5 | 16.07 | −2.01 | 74.29 | 10.17 | 0.02 | 65.04 | |
| R6 | 13.01 | −1.69 | 75.4 | 7.26 | 0.23 | 87.05 | |
| R7 | 9.56 | −5.81 | 29.79 | 8.37 | −0.82 | 71.81 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Lu, T.; Yang, F.; Wei, C.; Wei, J. Performance Assessment of a High-Frequency Radar Network for Detecting Surface Currents in the Pearl River Estuary. Remote Sens. 2024, 16, 198. https://doi.org/10.3390/rs16010198
Zhu L, Lu T, Yang F, Wei C, Wei J. Performance Assessment of a High-Frequency Radar Network for Detecting Surface Currents in the Pearl River Estuary. Remote Sensing. 2024; 16(1):198. https://doi.org/10.3390/rs16010198
Chicago/Turabian StyleZhu, Langfeng, Tianyi Lu, Fan Yang, Chunlei Wei, and Jun Wei. 2024. "Performance Assessment of a High-Frequency Radar Network for Detecting Surface Currents in the Pearl River Estuary" Remote Sensing 16, no. 1: 198. https://doi.org/10.3390/rs16010198
APA StyleZhu, L., Lu, T., Yang, F., Wei, C., & Wei, J. (2024). Performance Assessment of a High-Frequency Radar Network for Detecting Surface Currents in the Pearl River Estuary. Remote Sensing, 16(1), 198. https://doi.org/10.3390/rs16010198





