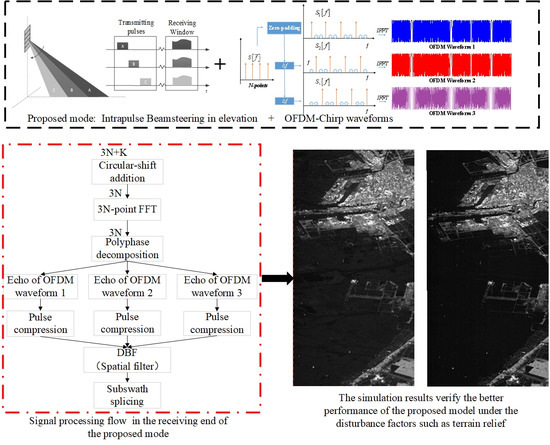
A Novel Intrapulse Beamsteering SAR Imaging Mode Based on OFDM-Chirp Signals
Abstract
:1. Introduction
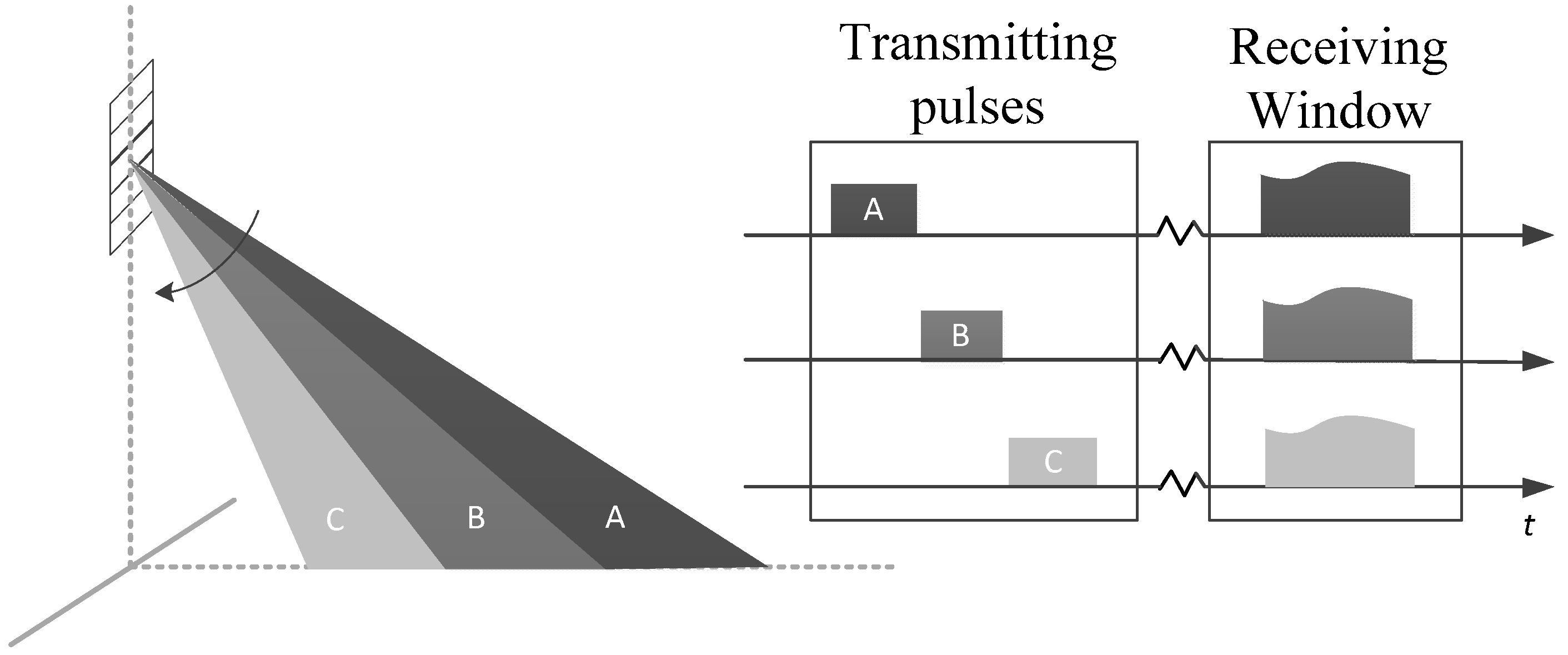
2. Intrapulse Beamsteering in Elevation
2.1. Principles
- Echoes from different subswaths overlap at the receiving end, leading to a substantial reduction in the time width of receiving window, so that the duty ratio of the transmitting signal can be increased, thereby improving both the echo SNR (Signal-to-Noise Ratio) and the working distance of the system;
- Due to the freedom of transmission, signals with different bandwidths can be transmitted for different subpulses, therefore, that different subswaths can have different range resolutions, which can enhance the system’s multi-range-resolution observation ability;
- It uses array weighting to form narrow beams in the elevation direction, so the gain of each narrow beam is higher and then the transmission power requirements for the transmitter can be reduced;
- Through phase weighting, the gains of different directions in each subswath are almost uniform, and the gain attenuation at the edge of the swath is alleviated.
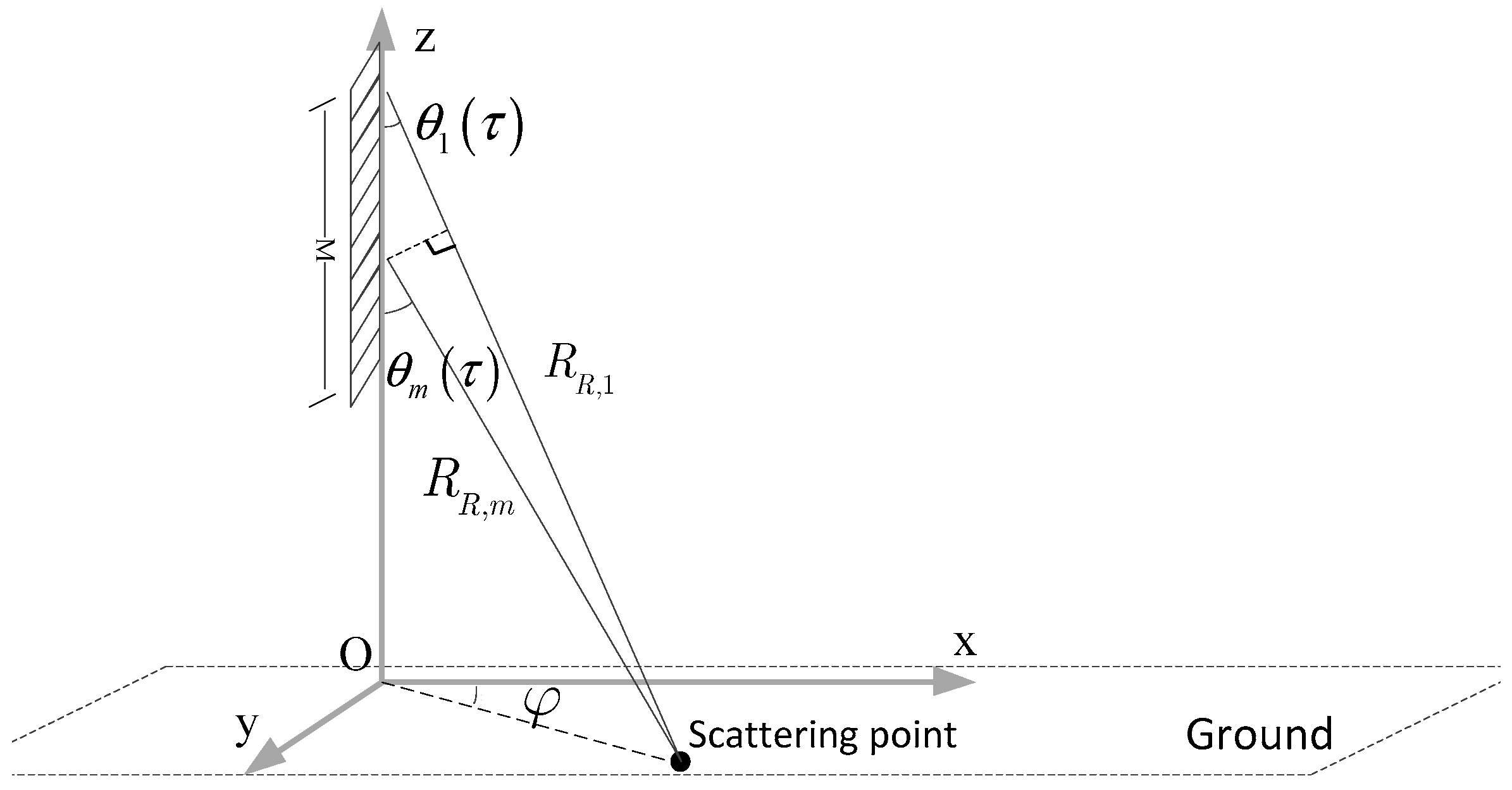
2.2. Signal Model
3. Intrapulse Beamsteering Based on OFDM-Chirp Signals
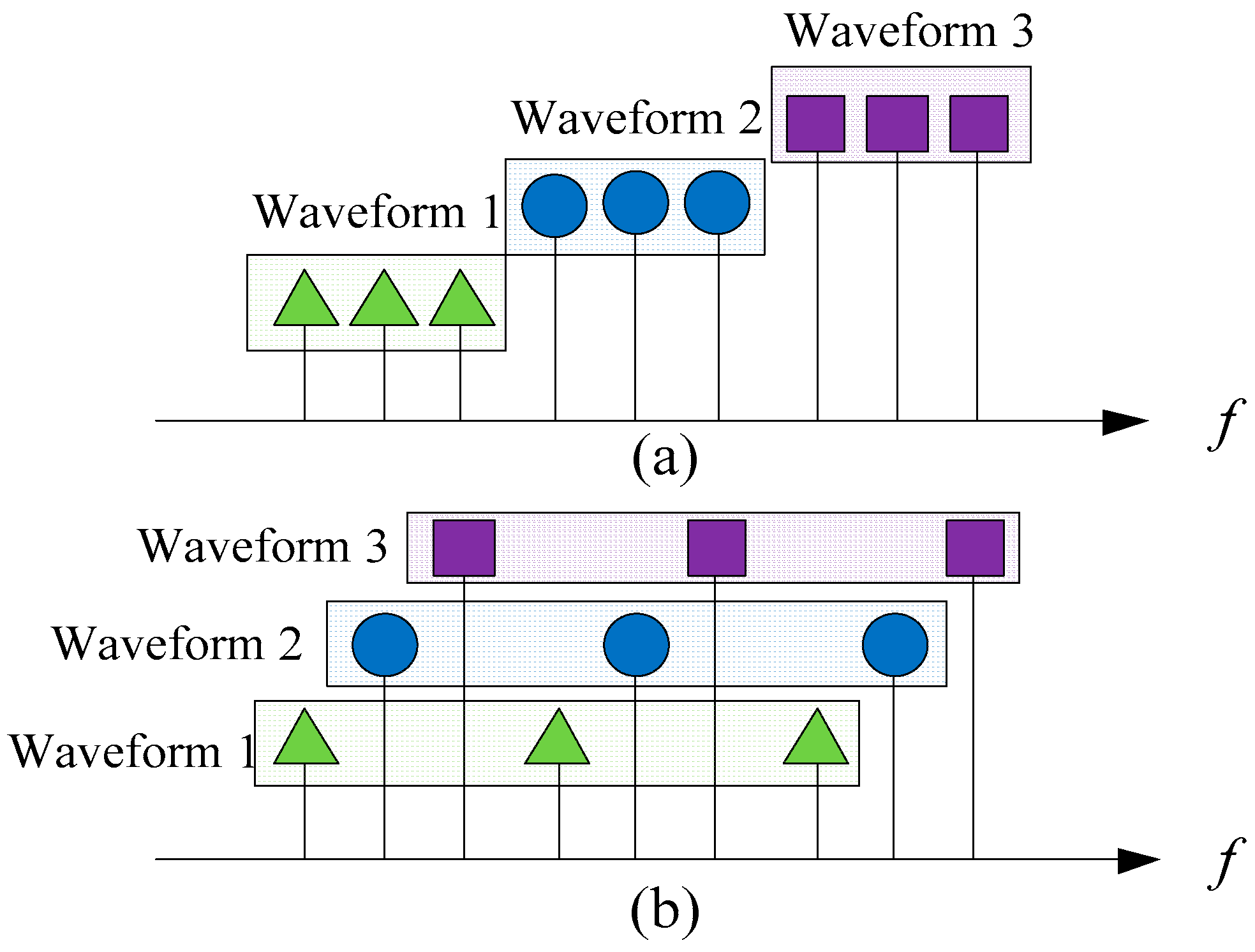
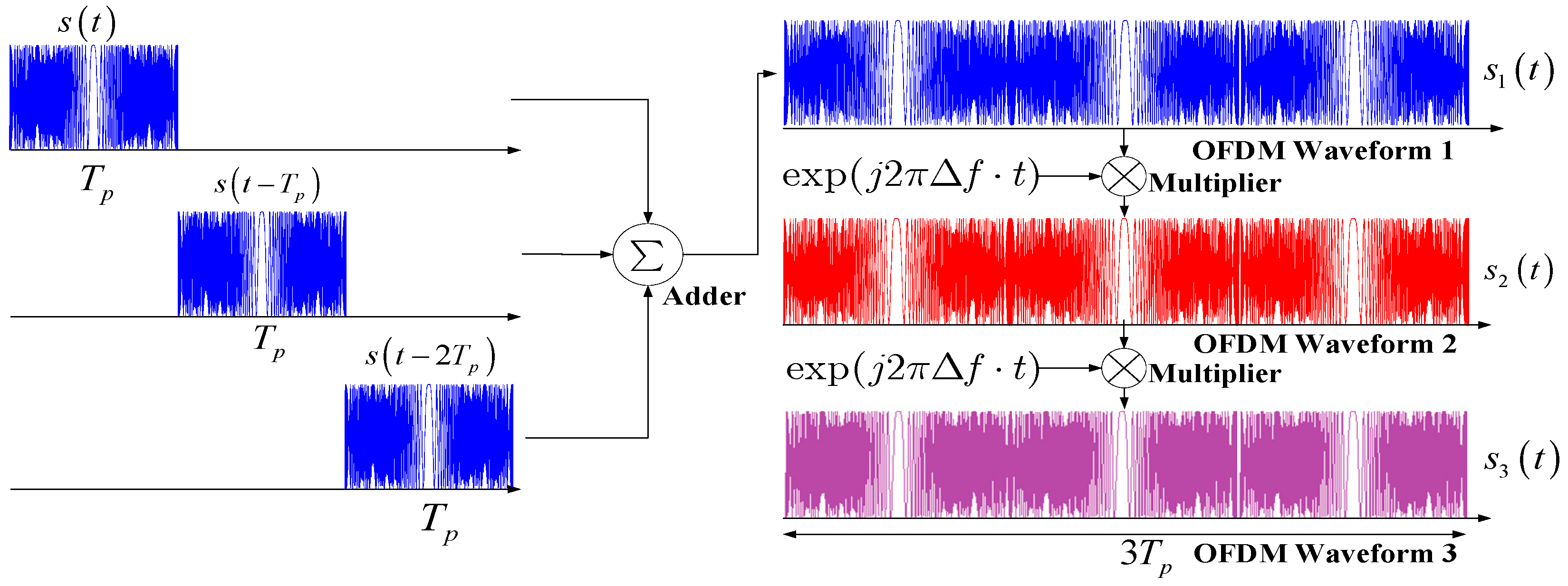
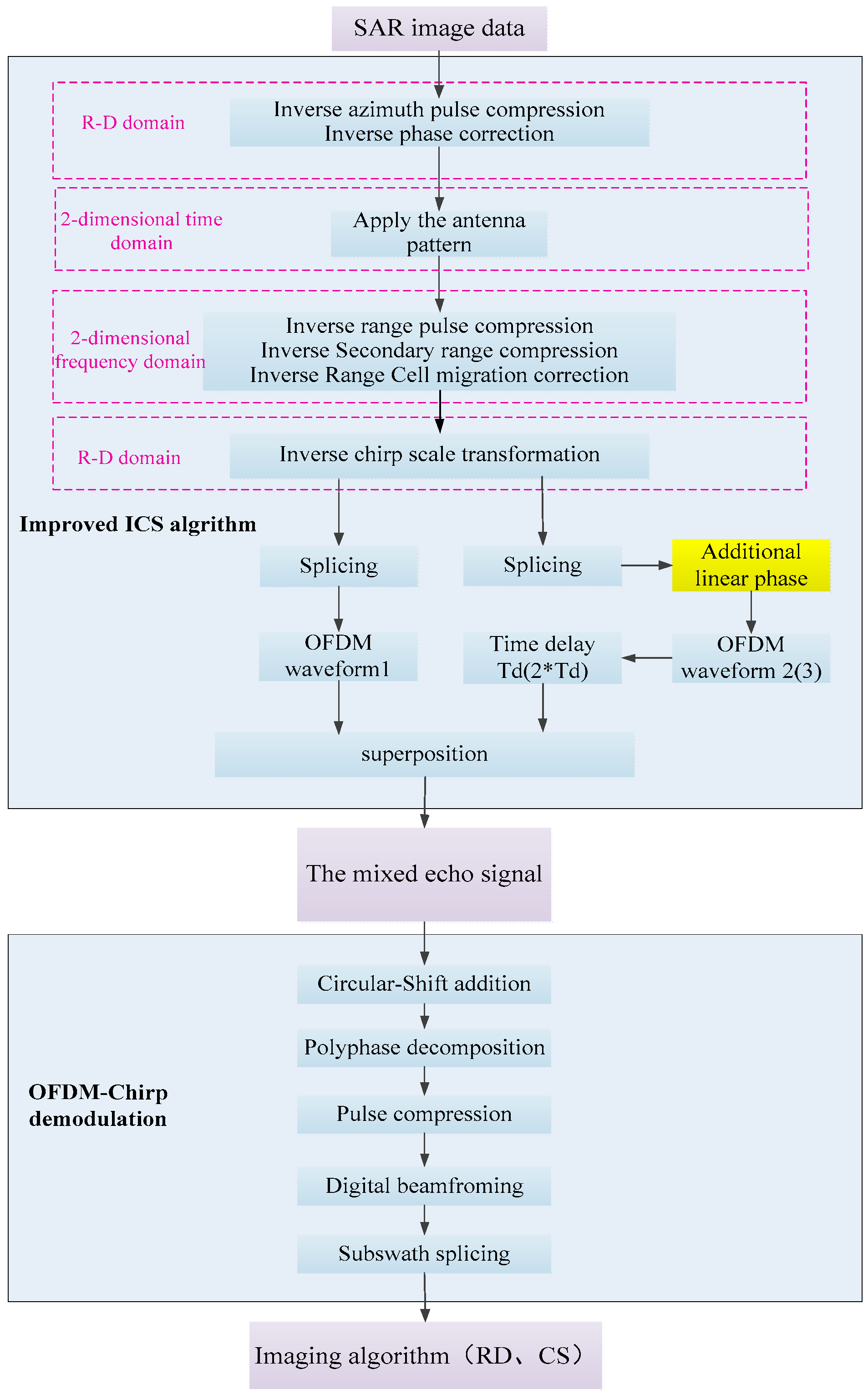
3.1. OFDM-Chirp Signal Modulation
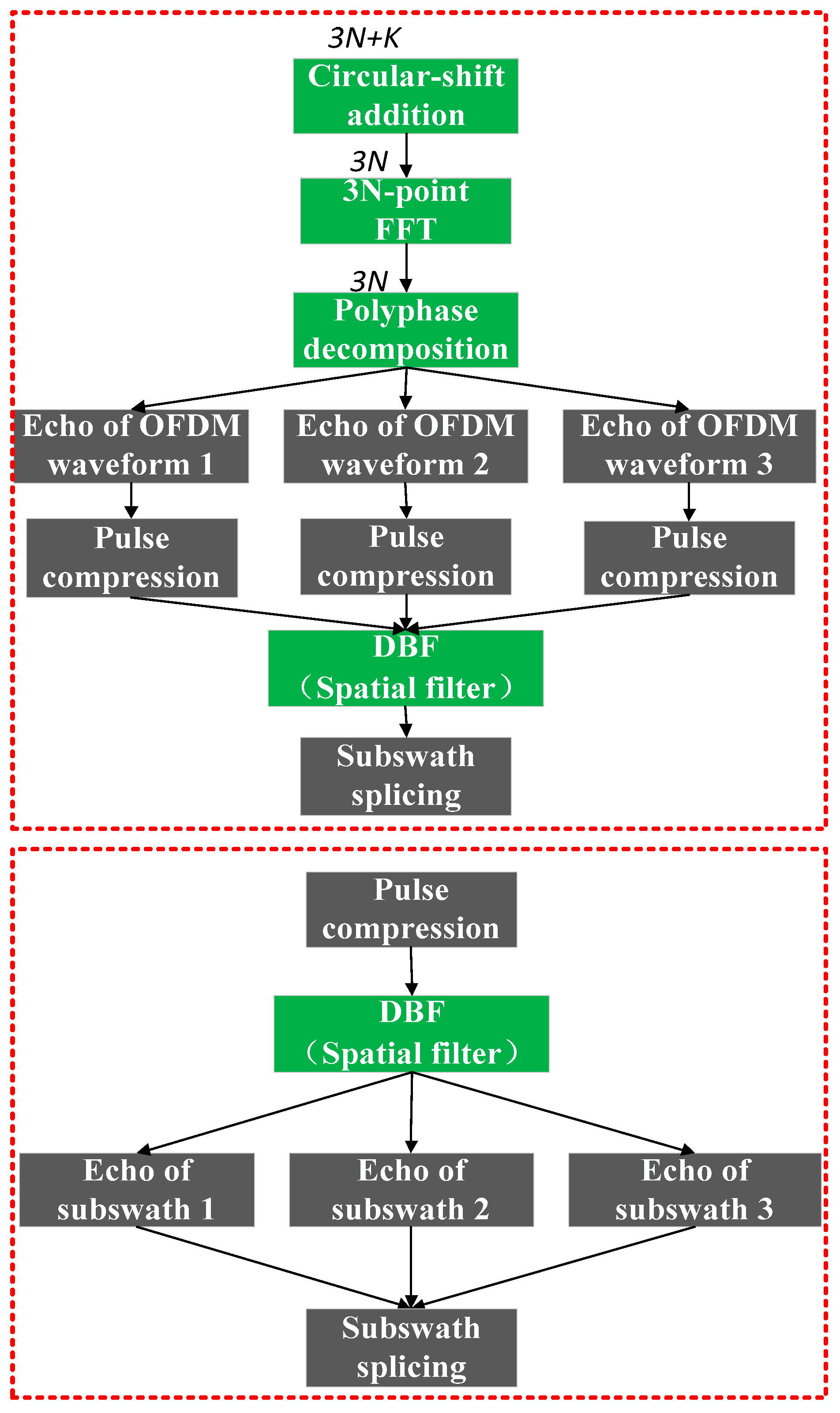
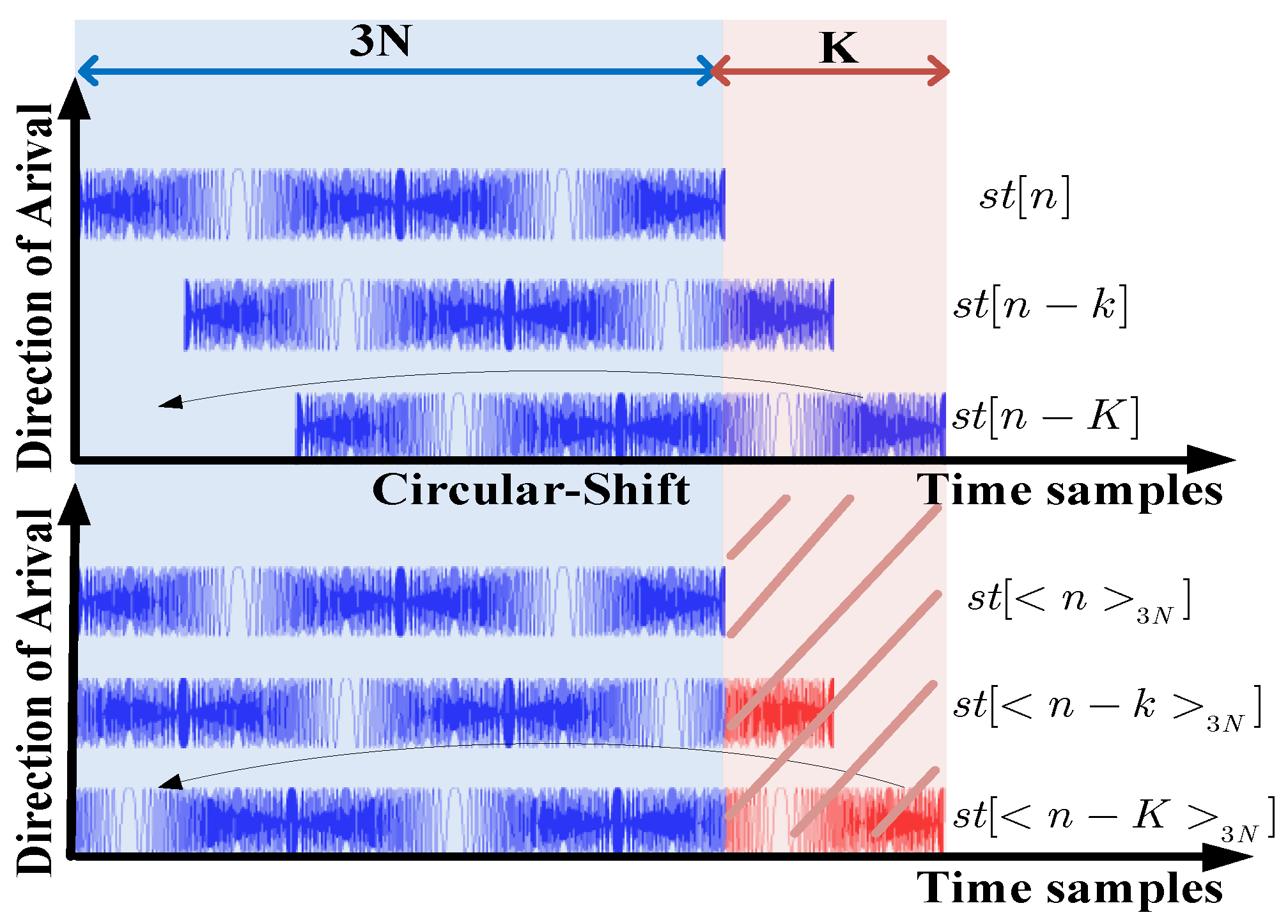
3.2. Circular-Shift Addition
3.3. Demodulation of 3N-Points
3.4. DBF for Further Processing
4. Simulations
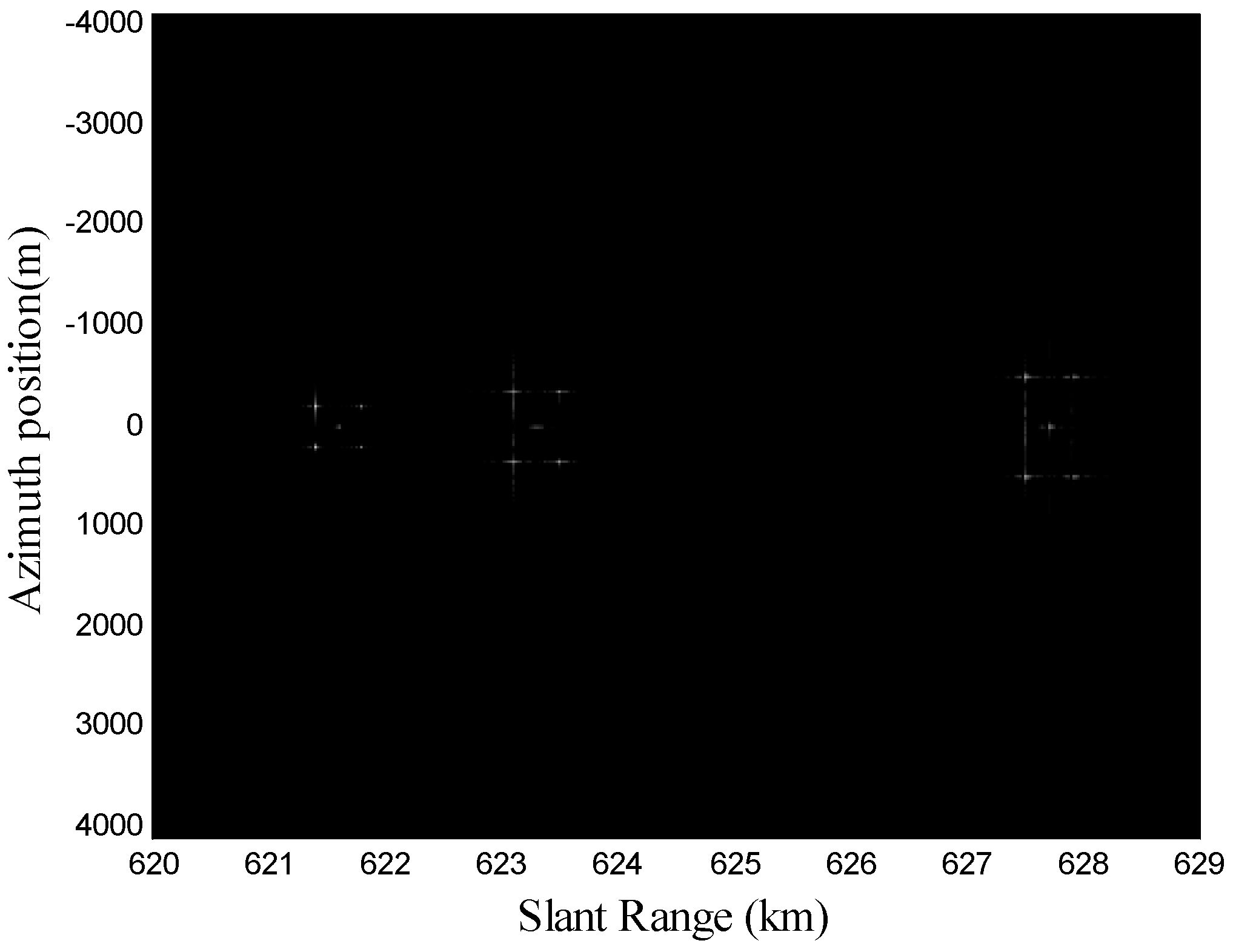
4.1. Point Targets Simulation
4.2. Distributed Targets Simulation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bliss, D.; Forsythe, K. Environmental issues for MIMO capacity. IEEE Trans. Signal Process. 2002, 50, 2128–2142. [Google Scholar] [CrossRef]
- Fishler, E. MIMO RADAR: An idea whose time has come. In Proceedings of the 2004 IEEE Radar Conference (IEEE Cat. No.04CH37509), Philadelphia, PA, USA, 29 April 2004; pp. 71–78. [Google Scholar]
- Wang, W. MIMO SAR imaging: Potential and challenges. IEEE Aerosp. Electron. Syst. Mag. 2013, 28, 18–23. [Google Scholar] [CrossRef]
- Younis, M.; Krieger, G.; Moreira, A. MIMO SAR techniques and trades. In Proceedings of the 2013 European Radar Conference, Nuremberg, Germany, 9–11 October 2013; pp. 141–144. [Google Scholar]
- Kim, J.; Ossowska, A.; Wiesbeck, W. Investigation of MIMO SAR for interferometry. In Proceedings of the European Radar Conference, Munich, Germany, 10–12 October 2007. [Google Scholar]
- Krieger, G. MIMO-SAR: Opportunities and Pitfalls. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2628–2645. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, H.; Sun, H.; Ying, W. Multireceiver SAS imagery based on monostatic conversion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10835–10853. [Google Scholar] [CrossRef]
- Wang, J.; Chen, L.Y.; Liang, X.D. Orthogonal waveform separation based on echo compression for airborne MIMO-SAR systems. J. Eng. 2019, 19, 6336–6340. [Google Scholar] [CrossRef]
- Gebert, N.; Krieger, G.; Moreira, A. Digital beamforming on receive: Techniques and optimization strategies for high-resolution wideswath SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 564–592. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional Waveform Encoding: A New Digital Beamforming Technique for Synthetic Aperture Radar Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2008, 46, 31–46. [Google Scholar] [CrossRef]
- Tang, F.; Ji, Y.; Zhang, Y.; Dong, Z.; Wang, Z.; Zhang, Q.; Zhao, B.; Gao, H. Drifting ionospheric scintillation simulation for L-band geosynchronous SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 852–854. [Google Scholar] [CrossRef]
- Rommel, T.; Younis, M.; Krieger, G. An Orthogonal Waveform for Fully Polarimetric MIMO-SAR. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0887–0891. [Google Scholar]
- Wang, S.; Sun, Y.; He, F.; Sun, Z.; Li, P.; Dong, Z. DBF Processing in Range-Doppler Domain for MWE SAR Waveform Separation Based on Digital Array-Fed Reflector Antenna. Remote Sens. 2020, 12, 3161. [Google Scholar] [CrossRef]
- He, F.; Ma, X.; Dong, Z.; Liang, D. Digital Beamforming on Receive in Elevation for Multidimensional Waveform Encoding SAR Sensing. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2173–2177. [Google Scholar]
- Zhu, J.; Song, Y.; Jiang, N.; Xie, Z.; Fan, C.; Huang, X. Enhanced Doppler Resolution and Sidelobe Suppression Performance for Golay Complementary Waveforms. Remote Sens. 2023, 15, 2452. [Google Scholar] [CrossRef]
- Stoica, P.; Wang, Z.; Li, J. Robust Capon beamforming. IEEE Signal Process. Lett. 2003, 10, 172–175. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Liu, T.; Chen, H.; Wang, Y. Detector design and performance analysis for target detection in subspace interference. IEEE Signal Process. Lett. 2023, 30, 618–622. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Younis, M. Advanced Synthetic Aperture Radar Based on Digital Beamforming and Waveform Diversity. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar]
- Lueders, C. Theory and Applications of OFDM and CDMA: Wideband Wireless Communications; John Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Kim, J.; Younis, M.; Moreira, A. A Novel OFDM Chirp Waveform Scheme for Use of Multiple Transmitters in SAR. IEEE Geosci. Remote Sens. Lett. 2013, 10, 568–572. [Google Scholar] [CrossRef]
- Wang, S.; He, F.; Sun, Z.; Li, P.; Dong, Z. The intrapulse beamsteering radar based on ofdm chirp signals. J. Phys. Conf. Ser. 2020, 1607, 012061. [Google Scholar] [CrossRef]

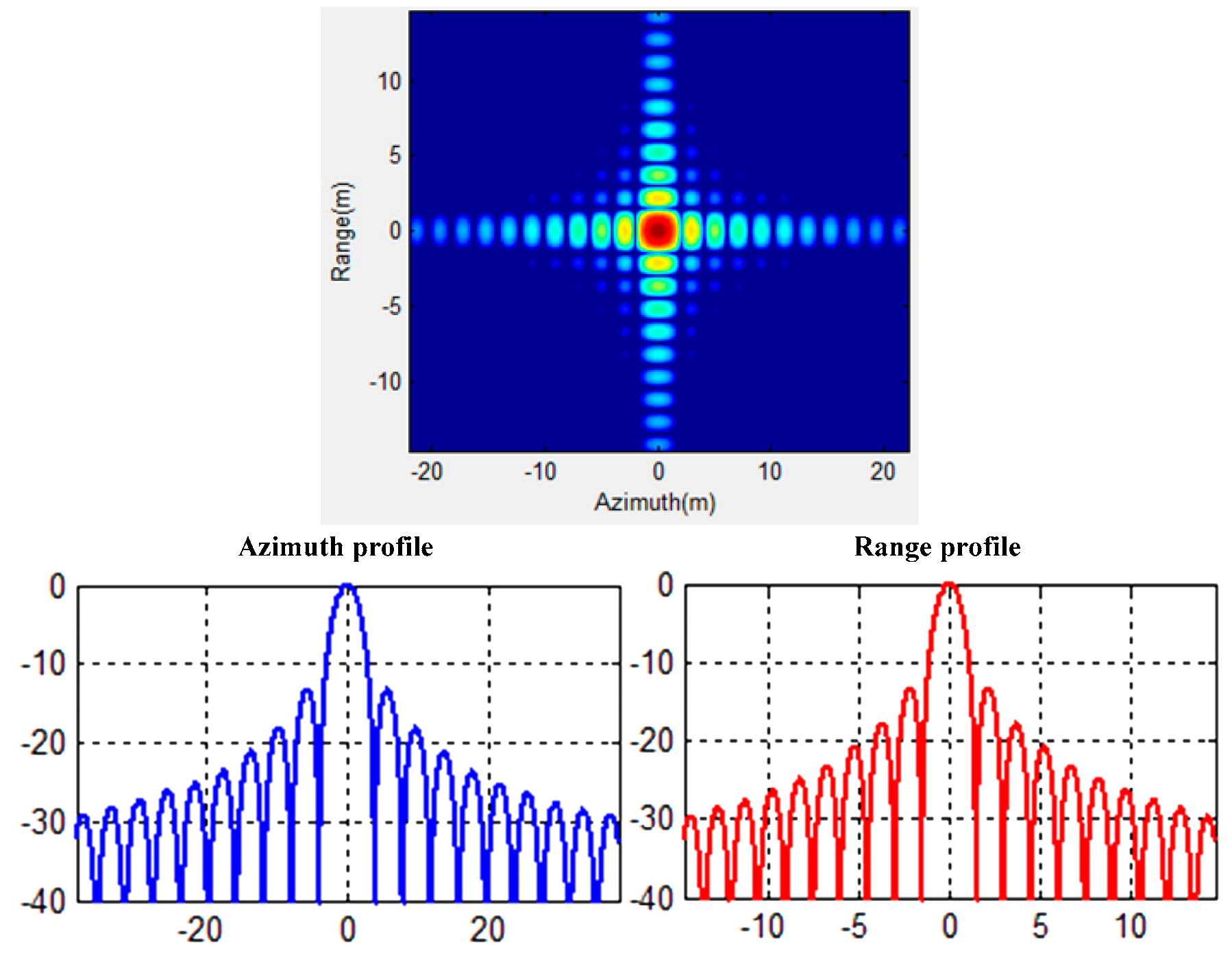


| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Platform height | 600 Km | Antenna length | 5 m |
| Platform flight speed | 7557 m/s | Aperture angle | 0.61° |
| Carrier frequency | 5.6 GHz | Antenna height | 2.5 m |
| Chirp bandwidth | 100 MHz | Subaperture number | 10 |
| Subpulse width | 60 us | Subswath 1 | (620~623 Km) |
| Subpulse number | 3 | Subswath 2 | (623~626 Km) |
| Subswath number | 3 | Subswath 3 | (626~629 Km) |
| Target | Location | Target | Location |
|---|---|---|---|
| A1 | (621.8 Km, 200 m) | B1 | (623.1 Km, 350 m) |
| A2 | (621.8 Km, −200 m) | B2 | (623.1 Km, −350 m) |
| A3 | (621.4 Km, 200 m) | B3 | (623.5 Km, 350 m) |
| A4 | (621.4 Km, −200 m) | B4 | (623.5 Km, −350 m) |
| A5 | (621.6 Km, 0 m) | B5 | (623.3 Km, 0 m) |
| C1 | (627.5 Km, −500 m) | C4 | (627.9 Km, −500 m) |
| C2 | (627.5 Km, 500 m) | C5 | (627.9 Km, 500 m) |
| C3 | (627.7 Km, 0 m) | --- | --- |
| Target | Azimuth Direction | Range Direction | ||||
|---|---|---|---|---|---|---|
| PSLR (dB) | ISLR (dB) | Resolution (m) | PSLR (dB) | ISLR (dB) | Resolution (m) | |
| A1 | −13.115 | −9.267 | 1.807 | −13.160 | −9.334 | 1.315 |
| A2 | −13.358 | −9.419 | 1.807 | −13.239 | −9.289 | 1.317 |
| A3 | −13.087 | −9.122 | 1.806 | −13.119 | −9.420 | 1.317 |
| A4 | −13.156 | −9.238 | 1.807 | −12.874 | −9.018 | 1.315 |
| A5 | −13.473 | −9.682 | 1.807 | −13.012 | −9.241 | 1.315 |
| B1 | −13.084 | −9.311 | 1.805 | −12.243 | −8.703 | 1.305 |
| B2 | −13.073 | −9.304 | 1.805 | −12.745 | −8.669 | 1.313 |
| B3 | −13.215 | −9.748 | 1.805 | −12.264 | −8.394 | 1.305 |
| B4 | −13.117 | −9.578 | 1.805 | −12.356 | −8.637 | 1.313 |
| B5 | −13.070 | −9.299 | 1.805 | −12.242 | −8.700 | 1.305 |
| C1 | −13.094 | −9.389 | 1.799 | −13.228 | −10.034 | 1.332 |
| C2 | −13.432 | −9.649 | 1.793 | −13.229 | −10.040 | 1.332 |
| C3 | −13.221 | −9.750 | 1.799 | −13.217 | −9.764 | 1.324 |
| C4 | −13.103 | −9.395 | 1.799 | −12.997 | −9.560 | 1.324 |
| C5 | −13.435 | −9.661 | 1.799 | −13.000 | −9.569 | 1.324 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Platform height | 600 Km | Antenna length | 4 m |
| Platform flight speed | 7557 m/s | Aperture angle | 0.77° |
| Carrier frequency | 5.6 GHz | Antenna height | 5 m |
| Chirp bandwidth | 100 MHz | Subswath 1 | (620~623 Km) |
| Subpulse width | 60 us | Subswath 2 | (623~626 Km) |
| Subpulse number | 3 | Subswath 3 | (626~629 Km) |
| Subaperture number | 5 | Random height error | 0~800 m |
| Random Height | (LFM) | (OFDM-Chirp) |
|---|---|---|
| 0 m | 0 | 0 |
| 0~100 m | 0.030 | 0.006 |
| 0~500 m | 0.140 | 0.030 |
| 0~800 m | 0.201 | 0.047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; He, F.; Dong, Z. A Novel Intrapulse Beamsteering SAR Imaging Mode Based on OFDM-Chirp Signals. Remote Sens. 2024, 16, 126. https://doi.org/10.3390/rs16010126
Wang S, He F, Dong Z. A Novel Intrapulse Beamsteering SAR Imaging Mode Based on OFDM-Chirp Signals. Remote Sensing. 2024; 16(1):126. https://doi.org/10.3390/rs16010126
Chicago/Turabian StyleWang, Shenjing, Feng He, and Zhen Dong. 2024. "A Novel Intrapulse Beamsteering SAR Imaging Mode Based on OFDM-Chirp Signals" Remote Sensing 16, no. 1: 126. https://doi.org/10.3390/rs16010126
APA StyleWang, S., He, F., & Dong, Z. (2024). A Novel Intrapulse Beamsteering SAR Imaging Mode Based on OFDM-Chirp Signals. Remote Sensing, 16(1), 126. https://doi.org/10.3390/rs16010126