Spatial Estimation of Daily Growth Biomass in Paddy Rice Field Using Canopy Photosynthesis Model Based on Ground and UAV Observations
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Description
2.1.1. Light Distribution under Canopy
2.1.2. Canopy Photosynthesis Model
2.2. Experimental Site
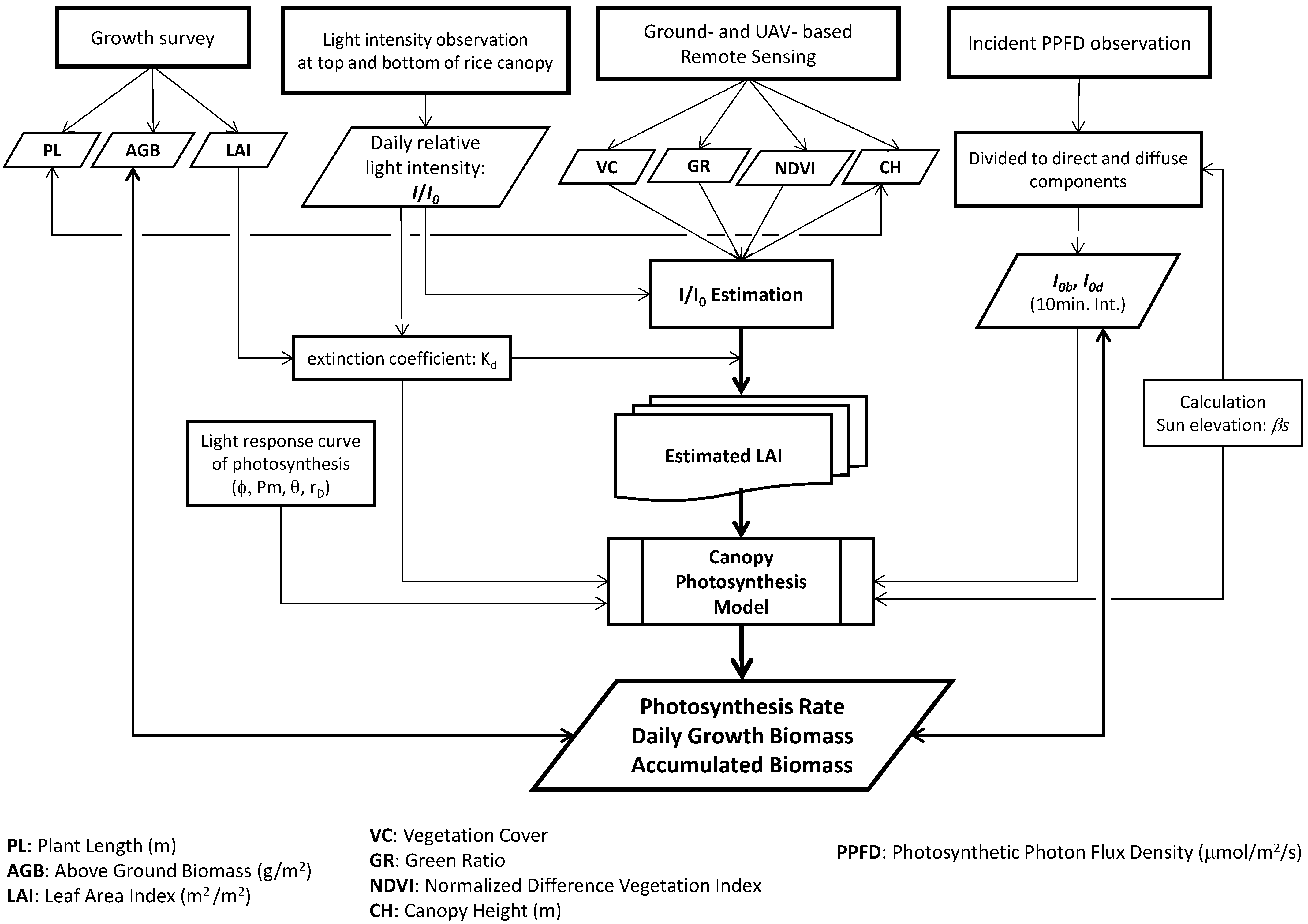
2.3. Estimation Procedures of Daily Growth Biomass
2.4. Observation Data
2.4.1. Relative Light Intensity under Rice Canopy
2.4.2. Incident Photosynthetic Photon Flux Density (PPFD)
2.4.3. Ground-Based Remote Sensing
2.4.4. UAV-Based Remote Sensing
2.4.5. Rice Growth Survey
2.5. LAI Estimations
2.6. Direct and Diffuse Light Intensity Divided from Incident Global PPFD
3. Results and Discussion
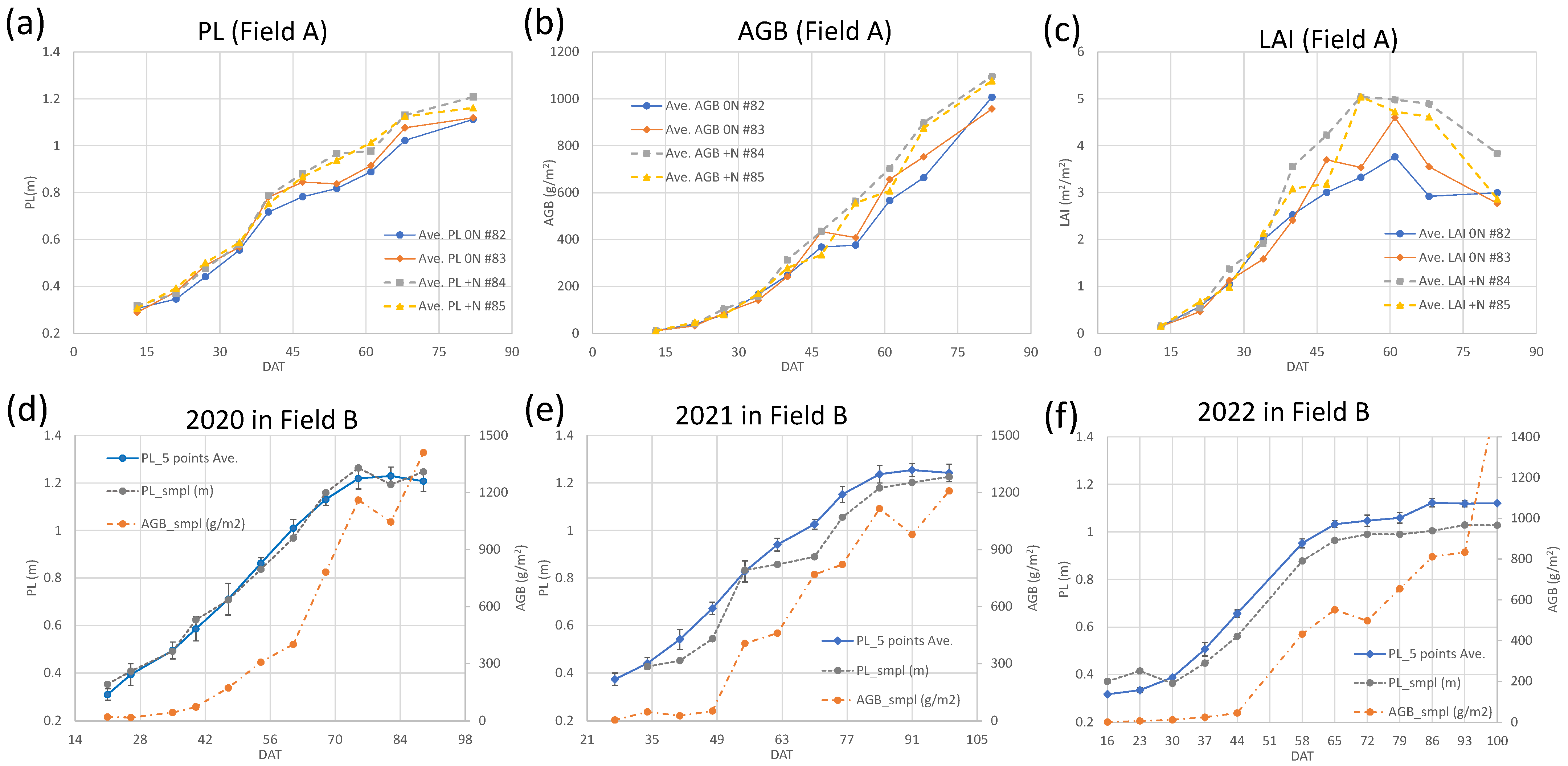
3.1. Rice Growth Survey
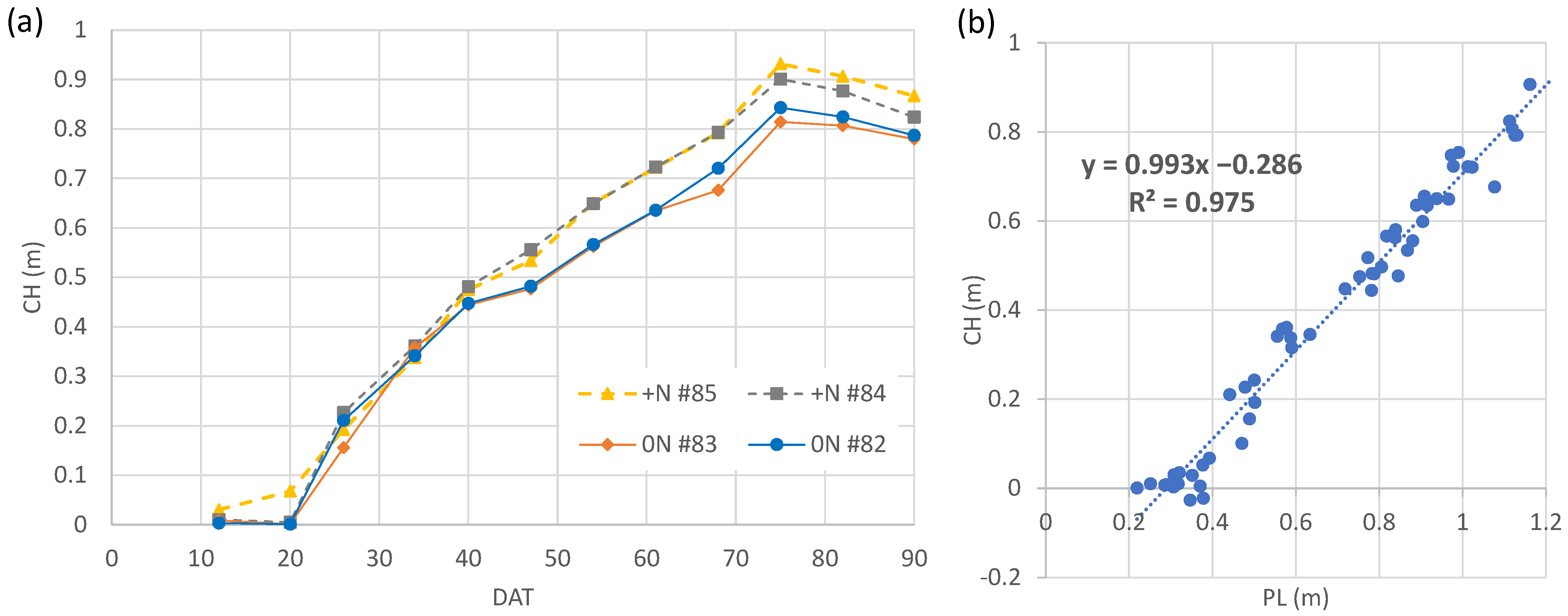
3.2. Weekly Change in Canopy Height Calculated from Canopy Surface Models
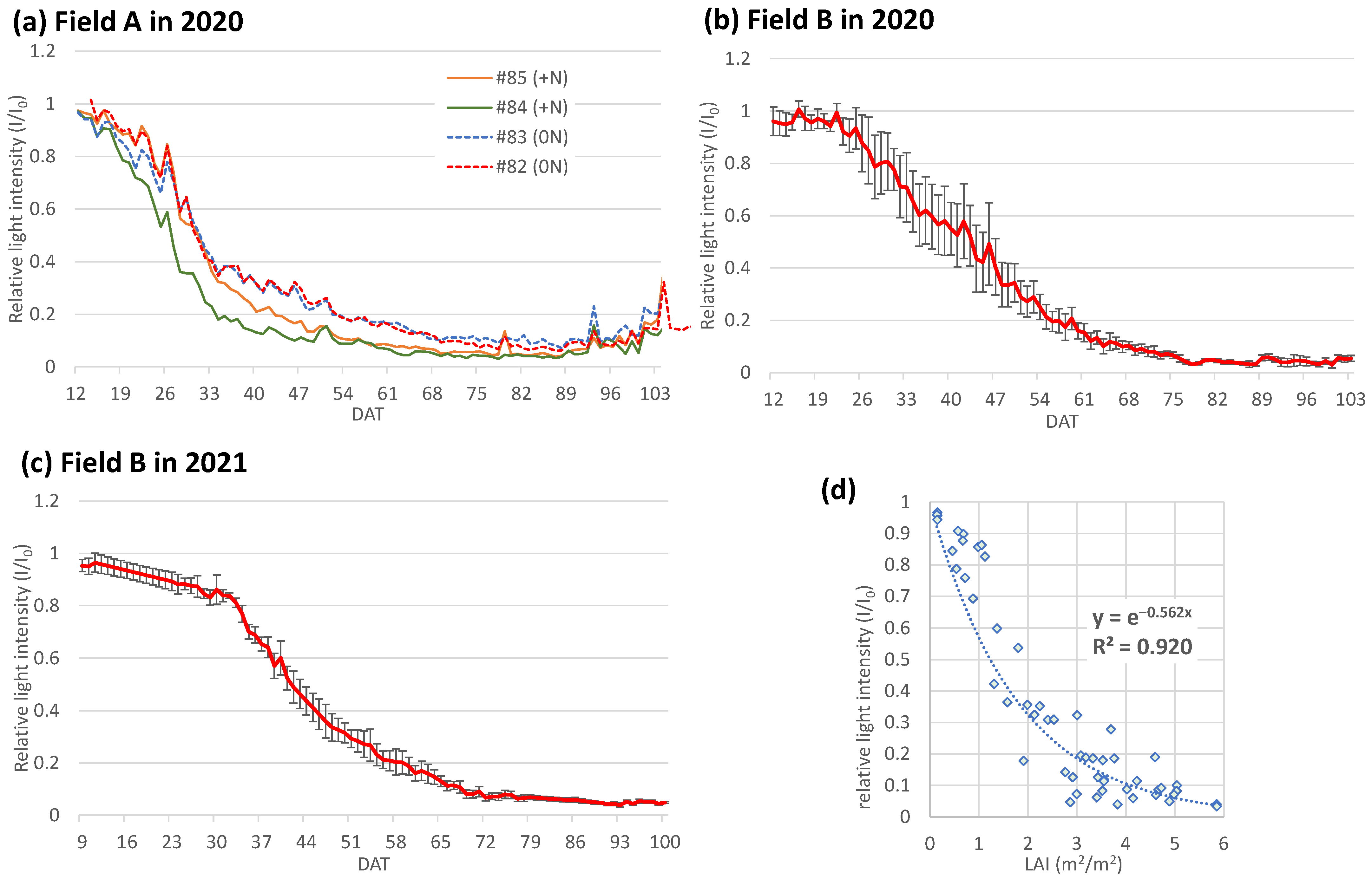
3.3. Daily Change in Relative Light Intensity (I/I0) and the Extinction Coefficient (Kd)
3.4. Relations of Relative Light Intensity with the Parameters of Ground- and UAV-Based Observations
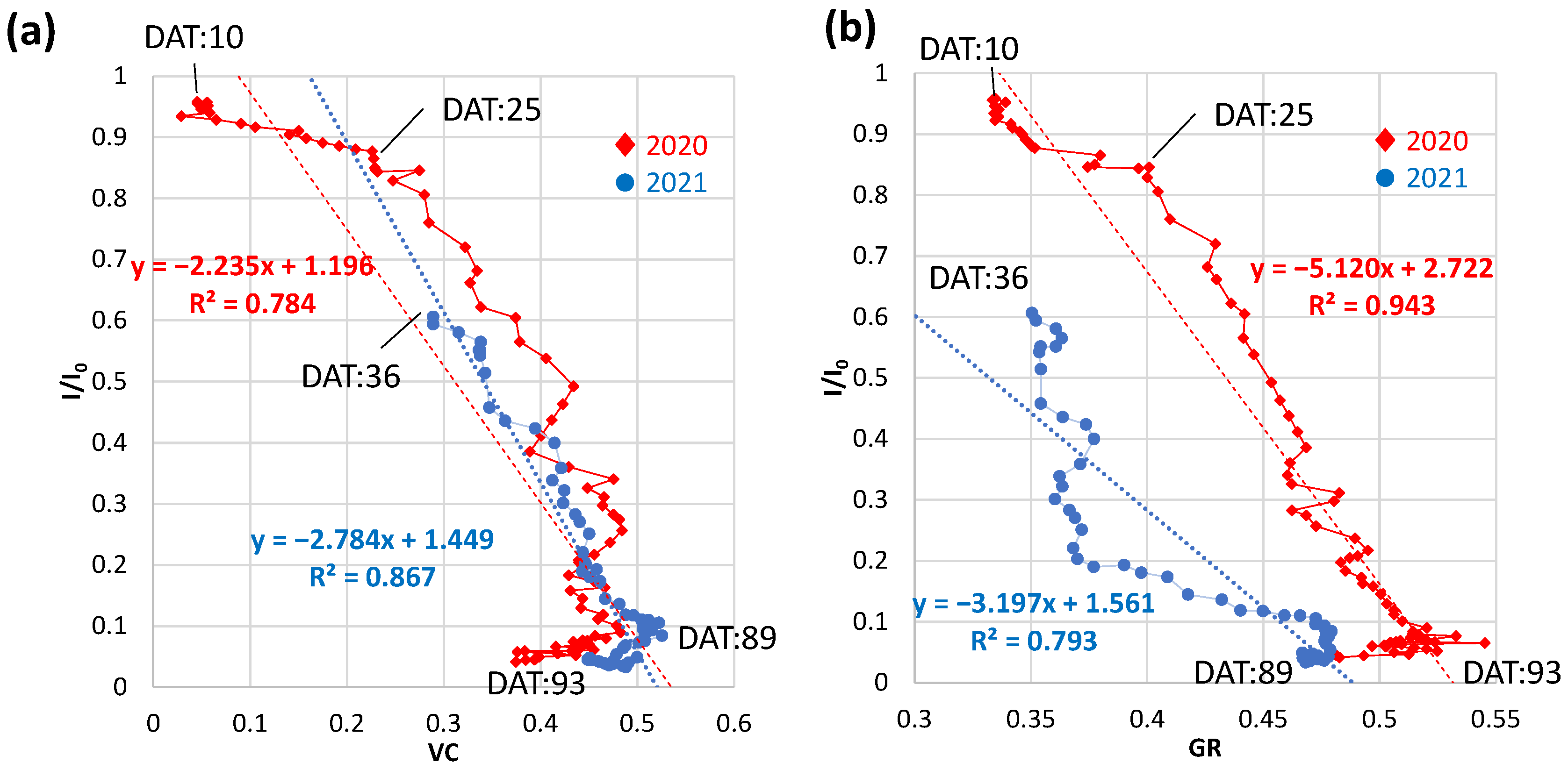
3.4.1. Daily VC and GR at Field B in 2020 and 2021
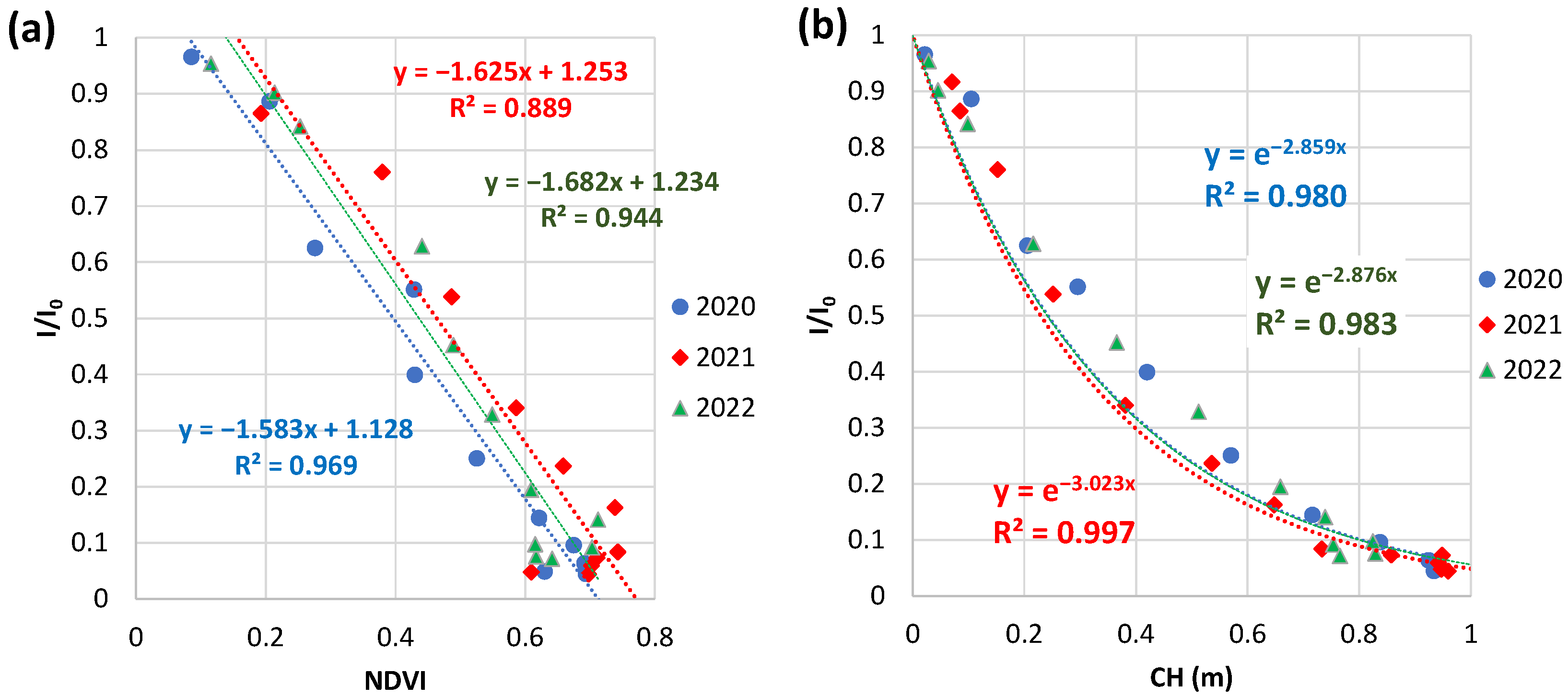
3.4.2. Weekly NDVI and CH at Field B in 2020 to 2022
3.4.3. Weekly NDVI and CH from UAV-Based Observation at Field A in 2020
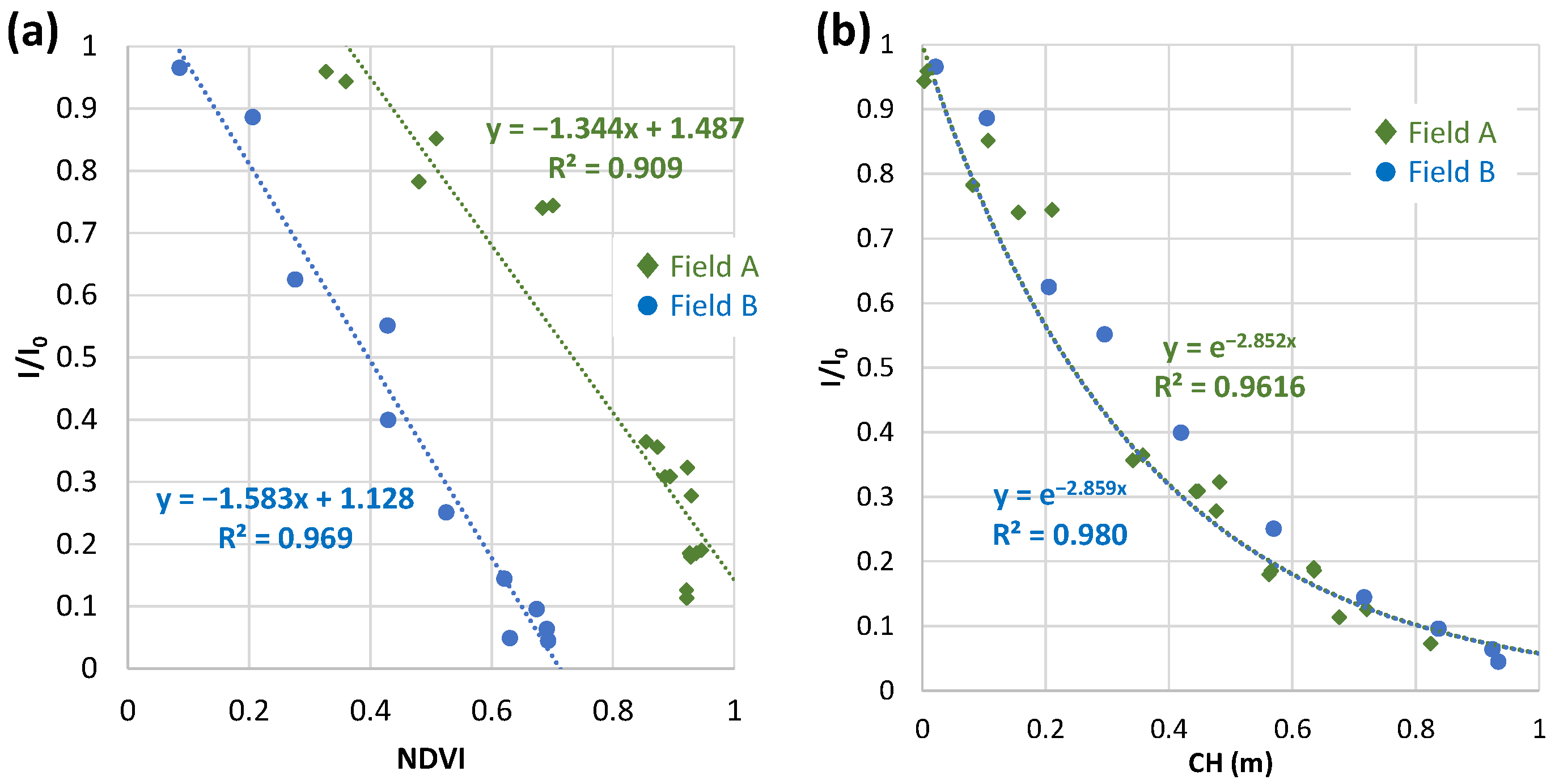
3.4.4. Comparison with Field A and Field B in 2020
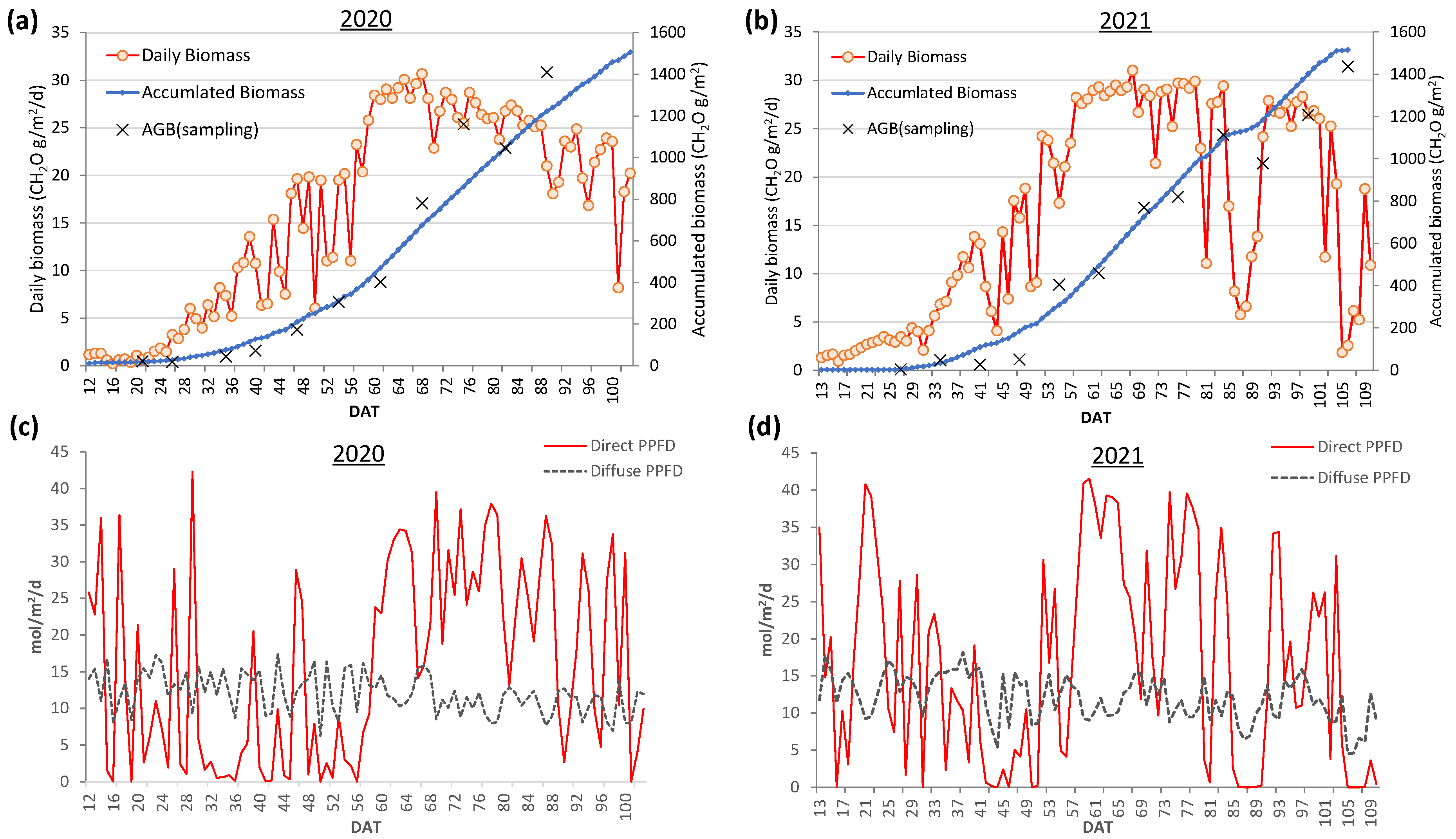
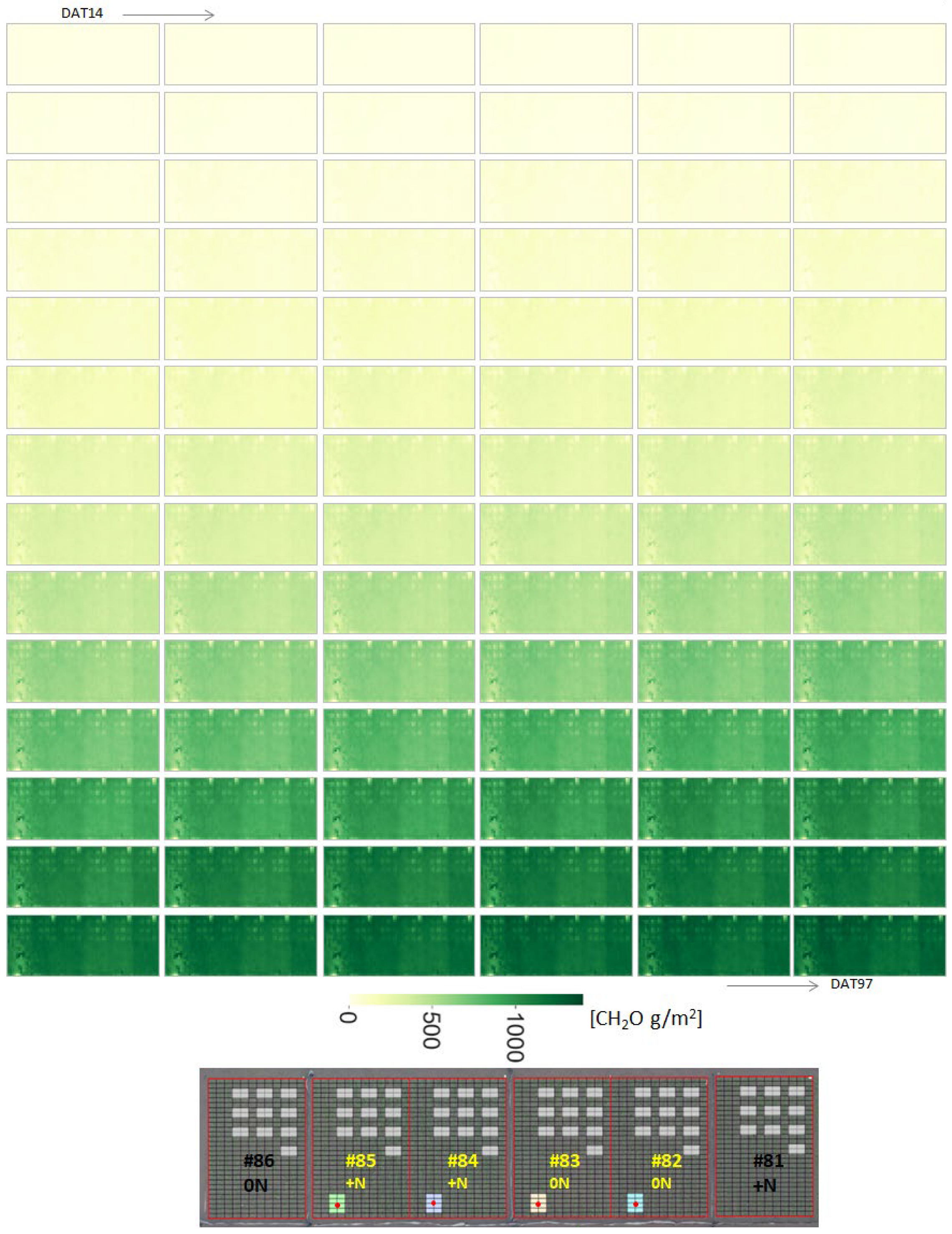
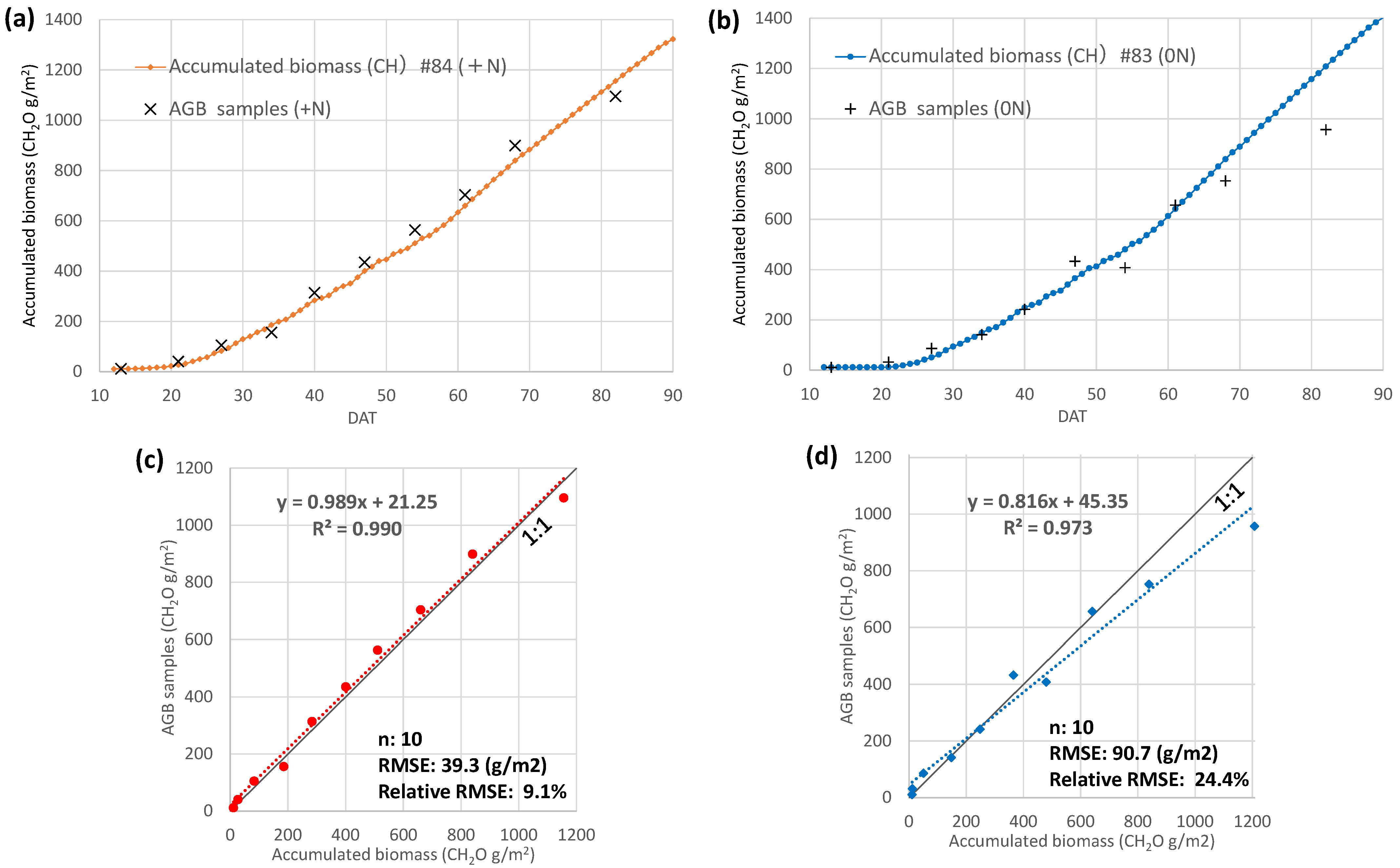
3.5. Daily Biomass Estimation at the Field Scale
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Molotoks, A.; Smith, P.; Dawson, T.P. Impacts of Land Use, Population, and Climate Change on Global Food Security. Food Energy Secur. 2021, 10, e261. [Google Scholar] [CrossRef]
- FAO; IFAD; UNICEF; WFP; WHO. Urbanization, agrifood systems transformation and healthy diets across the rural–urban continuum. In The State of Food Security and Nutrition in the World 2023; FAO: Rome, Italy, 2023. [Google Scholar] [CrossRef]
- FAO. World Food and Agriculture—Statistical Yearbook 2020; FAO: Rome, Italy, 2020. [Google Scholar] [CrossRef]
- Dworak, V.; Selbeck, J.; Dammer, K.H.; Hoffmann, M.; Zarezadeh, A.A.; Bobda, C. Strategy for the Development of a Smart NDVI Camera System for Outdoor Plant Detection and Agricultural Embedded Systems. Sensors 2013, 13, 1523–1538. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.J.; Lee, B.W. Estimation of Rice Growth and Nitrogen Nutrition Status Using Color Digital Camera Image Analysis. Eur. J. Agron. 2013, 48, 57–65. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Perspectives for Remote Sensing with Unmanned Aerial Vehicles in Precision Agriculture. Trends Plant Sci. 2019, 24, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Duan, S.B.; Li, Z.L.; Wu, H.; Tang, B.H.; Ma, L.; Zhao, E.; Li, C. Inversion of the PROSAIL Model to Estimate Leaf Area Index of Maize, Potato, and Sunflower Fields from Unmanned Aerial Vehicle Hyperspectral Data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Zhou, X.; Zheng, H.B.; Xu, X.Q.; He, J.Y.; Ge, X.K.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.X.; Tian, Y.C. Predicting Grain Yield in Rice Using Multi-Temporal Vegetation Indices from UAV-Based Multispectral and Digital Imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 246–255. [Google Scholar] [CrossRef]
- Li, S.; Yuan, F.; Ata-UI-Karim, S.T.; Zheng, H.; Cheng, T.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Combining Color Indices and Textures of UAV-Based Digital Imagery for Rice LAI Estimation. Remote Sens. 2019, 11, 1763. [Google Scholar] [CrossRef]
- Zermas, D.; Morellas, V.; Mulla, D.; Papanikolopoulos, N. 3D Model Processing for High Throughput Phenotype Extraction—The Case of Corn. Comput. Electron. Agric. 2019, 172, 105047. [Google Scholar] [CrossRef]
- Comba, L.; Biglia, A.; Ricauda Aimonino, D.; Tortia, C.; Mania, E.; Guidoni, S.; Gay, P. Leaf Area Index Evaluation in Vineyards Using 3D Point Clouds from UAV Imagery. Precis. Agric. 2020, 21, 881–896. [Google Scholar] [CrossRef]
- Qiao, L.; Gao, D.; Zhao, R.; Tang, W.; An, L.; Li, M.; Sun, H. Improving Estimation of LAI Dynamic by Fusion of Morphological and Vegetation Indices Based on UAV Imagery. Comput. Electron. Agric. 2022, 192, 106603. [Google Scholar] [CrossRef]
- Monsi, M.; Saeki, T. Uber den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung fiir die Stoffproduktion. Jap. J. Bot. 1953, 14, 22–52. [Google Scholar]
- Stenberg, P.; Linder, S.; Smolander, H.; Flower-Ellis, J. Performance of the LAI-2000 Plant Canopy Analyzer in Estimating Leaf Area Index of Some Scots Pine Stands. Tree Physiol. 1994, 14, 981–995. [Google Scholar] [CrossRef] [PubMed]
- Kume, A.; Nasahara, K.N.; Nagai, S.; Muraoka, H. The Ratio of Transmitted Near-Infrared Radiation to Photosynthetically Active Radiation (PAR) Increases in Proportion to the Adsorbed PAR in the Canopy. J. Plant Res. 2011, 124, 99–106. [Google Scholar] [CrossRef]
- Kuroiwa, S. Theoretical Analysis of Light Factor and Photosynthesis in Plant Communities (3) Total photosynthesis of a foliage under parallel light in comparison with that under isotropic light condition. J. Agric. Meteorol. 1968, 24, 85–90. [Google Scholar] [CrossRef][Green Version]
- Gourdriaan, J. The bare bones of leaf angle distribution in radiation models for canopy photosynthesis and energy exchange. Agric. For. Meteorol. 1988, 43, 155–169. [Google Scholar] [CrossRef]
- Anten, N.P.R. Modeling canopy photosynthesis using parameters determined from simple non-destructive measurements. Ecol. Res. 1997, 12, 77–88. [Google Scholar] [CrossRef]
- Oikawa, S. Structure of herbaceous plant stands and canopy photosynthesis models. Low Temp. Sci. 2009, 67, 103–112. [Google Scholar]
- He, M.; Ju, W.; Zhou, Y.; Chen, J.; He, H.; Wang, S.; Wang, H.; Guan, D.; Yan, J.; Li, Y.; et al. Development of a Two-Leaf Light Use Efficiency Model for Improving the Calculation of Terrestrial Gross Primary Productivity. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Xin, Q.; Gong, P.; Suyker, A.E.; Si, Y. Effects of the Partitioning of Diffuse and Direct Solar Radiation on Satellite-Based Modeling of Crop Gross Primary Production. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 51–63. [Google Scholar] [CrossRef]
- Ito, A.; Oikawa, T. A Simulation Model of the Carbon Cycle in Land Ecosystems (Sim-CYCLE): A Description Based on Dry-Matter Production Theory and Plot-Scale Validation. Ecol. Model. 2002, 151, 143–176. [Google Scholar] [CrossRef]
- Hirose, T.; Werger, M.J.A. Maximizing Daily Canopy Photosynthesis with Respect to the Leaf Nitrogen Allocation Pattern in the Canopy. Oecologia 1987, 72, 520–526. [Google Scholar] [CrossRef] [PubMed]
- Ohsumi, A.; Hamasaki, A.; Nakagawa, H.; Yoshida, H.; Shiraiwa, T.; Horie, T. A model explaining genotypic and ontogenetic variation of leaf photosynthetic rate in rice (Oryza sativa) based on leaf nitrogen content and stomatal conductance. Ann. Bot. 2007, 99, 265–273. [Google Scholar] [CrossRef] [PubMed]
- Ohkubo, S.; Tanaka, Y.; Yamori, W.; Adachi, S. Rice Cultivar Takanari Has Higher Photosynthetic Performance under Fluctuating Light than Koshihikari, Especially under Limited Nitrogen Supply and Elevated CO2. Front. Plant Sci. 2020, 11, 1308. [Google Scholar] [CrossRef] [PubMed]
- Messier, C.; Puttonen, P. Spatial and temporal variation in the Bight environment of developing Scots pine stands: The basis for a quick and efficient method of characterizing Bight. Can. J. For. Res. 1995, 25, 343–354. [Google Scholar] [CrossRef]
- Muraoka, H.; Kaci, N. (Eds.) The Society for the Study of Species Biology. Introduction to Plant Physiological Ecology; Bun-ichi So go Shuppan Co.: Tokyo, Japan, 2005. [Google Scholar]
- Peprah, C.O.; Yamashita, M.; Yamaguchi, T.; Sekino, R.; Takano, K.; Katsura, K. Spatio-Temporal Estimation of Biomass Growth in Rice Using Canopy Surface Model from Unmanned Aerial Vehicle Images. Remote Sens. 2021, 13, 2388. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Jourdan, R.C. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- Orgill, J.F.; Hollands, K.G.T. Correlation equation for hourly diffuse radiation on a horizontal surface. Sol. Energy 1977, 19, 357–359. [Google Scholar] [CrossRef]
- Erbs, D.G.; Klein, S.A.; Duffie, J.A. Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy 1982, 28, 293–302. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Tymvios, F.S.; Assimakopoulos, V.D.; Kaltsounides, N.A. The Dependence of Global and Diffuse PAR Radiation Components on Sky Conditions at Athens, Greece. Agric. For. Meteorol. 2007, 143, 277–287. [Google Scholar] [CrossRef]
- Ohmura, A.; Dutton, E.G.; Forgan, B.; Fröhlich, C.; Gilgen, H.; Hegner, H.; Heimo, A.; König-Langlo, G.; McArthur, B.; Müller, G.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New Precision Radiometry for Climate Research. Bull. Am. Meteorol. Soc. 1998, 79, 2115–2136. [Google Scholar] [CrossRef]
- Thuillier, G.; Hers, M.; Simon, P.C.; Labs, D.; Mandel, H.; Gillotay, D. Observation of the Solar Spectral Irradiance from 200 Nm to 870 Nm during the ATLAS 1 and ATLAS 2 Missions by the SOLSPEC Spectrometer. Metrologia 2003, 35, 689–695. [Google Scholar] [CrossRef]
- Yamashita, M.; Yoshimura, M. Estimation of Global and Diff Use Photosynthetic Photon Flux Density under Various Sky Conditions Using Ground-Based Whole-Sky Images. Remote Sens. 2019, 11, 932. [Google Scholar] [CrossRef]
- Soda, K.; Ookawa, T.; Motobayashi, T.; Hirasawa, T. Quick Estimation of Varietal Differences in Light Extinction Coefficient of the Canopy through the Inclination Angle of Leaf Blade in Rice. Jpn. J. Crop Sci. 2010, 79, 174–183. [Google Scholar] [CrossRef][Green Version]
- Chakraborty, P.K.; Banerjee, S.; Mukkherijee, A.; Nath, R.; Samanta, S. Extinction coefficient and photosynthetically active radiation use efficiency of summer rice as influenced by transplanting dates. J. Environ. Biol. 2018, 39, 467–471. [Google Scholar] [CrossRef]
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-Based Multispectral Remote Sensing for Precision Agriculture: A Comparison between Different Cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Sunoj, S.; Igathinathane, C.; Saliendra, N.; Hendrickson, J.; Archer, D. Color Calibration of Digital Images for Agriculture and Other Applications. ISPRS J. Photogramm. Remote Sens. 2018, 146, 221–234. [Google Scholar] [CrossRef]
- Yamashita, M.; Shinomiya, Y.; Yoshimura, M. Development of Methodology for Plant Phenology Monitoring By Ground-Based Observation Using Digital Camera. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, IV-3/W1, 65–70. [Google Scholar] [CrossRef]
- Kim, M.; Ko, J.; Jeong, S.; Yeom, J.M.; Kim, H.O. Monitoring Canopy Growth and Grain Yield of Paddy Rice in South Korea by Using the GRAMI Model and High Spatial Resolution Imagery. GISci. Remote Sens. 2017, 54, 534–551. [Google Scholar] [CrossRef]
- Inoue, Y. Satellite- and Drone-Based Remote Sensing of Crops and Soils for Smart Farming—A Review. Soil Sci. Plant Nutr. 2020, 66, 798–810. [Google Scholar] [CrossRef]
- dela Torre, D.M.G.; Gao, J.; Macinnis-Ng, C. Remote Sensing-Based Estimation of Rice Yields Using Various Models: A Critical Review. Geo-Spat. Inf. Sci. 2021, 24, 580–603. [Google Scholar] [CrossRef]
- Wali, E.; Tasumi, M.; Moriyama, M. Combination of Linear Regression Lines to Understand the Response of Sentinel-1 Dual Polarization SAR Data with Crop Phenology—Case Study in Miyazaki, Japan. Remote Sens. 2020, 12, 189. [Google Scholar] [CrossRef]
- Yang, H.; Li, H.; Wang, W.; Li, N.; Zhao, J.; Pan, B. Spatio-Temporal Estimation of Rice Height Using Time Series Sentinel-1 Images. Remote Sens. 2022, 14, 546. [Google Scholar] [CrossRef]
- Tan, C.W.; Zhang, P.P.; Zhou, X.X.; Wang, Z.X.; Xu, Z.Q.; Mao, W.; Li, W.X.; Huo, Z.Y.; Guo, W.S.; Yun, F. Quantitative Monitoring of Leaf Area Index in Wheat of Different Plant Types by Integrating NDVI and Beer-Lambert Law. Sci. Rep. 2020, 10, 929. [Google Scholar] [CrossRef] [PubMed]
- Baar, S.; Kobayashi, Y.; Horie, T.; Sato, K.; Suto, H.; Watanabe, S. Non-Destructive Leaf Area Index Estimation via Guided Optical Imaging for Large Scale Greenhouse Environments. Comput. Electron. Agric. 2022, 197, 106911. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A Review of Data Assimilation of Remote Sensing and Crop Models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
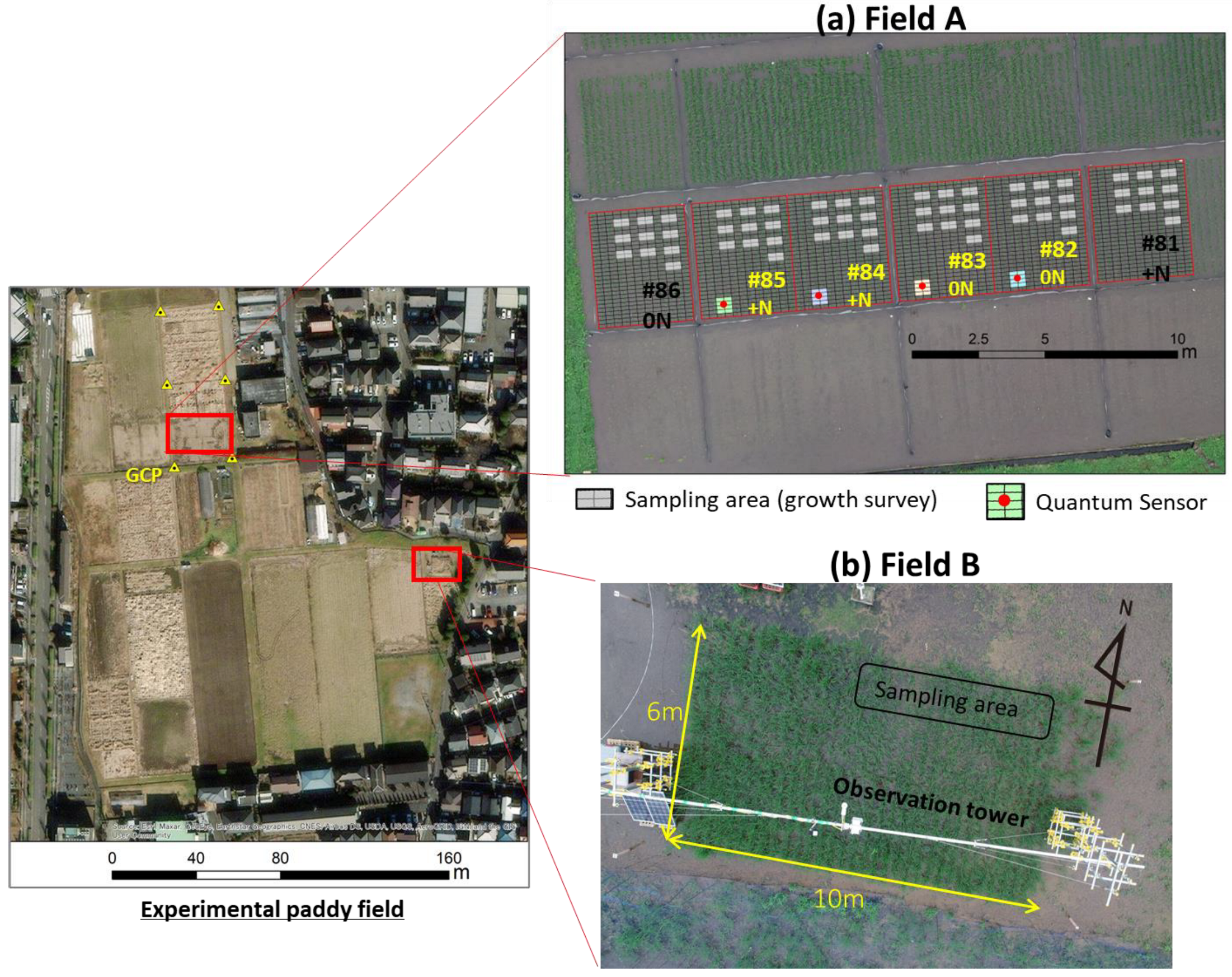



| Field A | Field B | |
|---|---|---|
| Observation year | 2020 | 2020, 2021, 2022 * |
| Relative light intensity under the canopy (daily) | 4 plots | 5 points |
| Incident PPFD (10-min) | Downward and upward PPFD (μmol/m2/s) | |
| Ground-based remote sensing (daily/weekly) | - | VC, GR, NDVI |
| UAV-based remote sensing (weekly) | CH (m), GR, NDVI | - |
| Growth survey (weekly) | PL (m), AGB (g/m2), LAI (m2/m2) | PL(m), AGB (g/m2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamashita, M.; Kaieda, T.; Toyoda, H.; Yamaguchi, T.; Katsura, K. Spatial Estimation of Daily Growth Biomass in Paddy Rice Field Using Canopy Photosynthesis Model Based on Ground and UAV Observations. Remote Sens. 2024, 16, 125. https://doi.org/10.3390/rs16010125
Yamashita M, Kaieda T, Toyoda H, Yamaguchi T, Katsura K. Spatial Estimation of Daily Growth Biomass in Paddy Rice Field Using Canopy Photosynthesis Model Based on Ground and UAV Observations. Remote Sensing. 2024; 16(1):125. https://doi.org/10.3390/rs16010125
Chicago/Turabian StyleYamashita, Megumi, Tomoya Kaieda, Hiro Toyoda, Tomoaki Yamaguchi, and Keisuke Katsura. 2024. "Spatial Estimation of Daily Growth Biomass in Paddy Rice Field Using Canopy Photosynthesis Model Based on Ground and UAV Observations" Remote Sensing 16, no. 1: 125. https://doi.org/10.3390/rs16010125
APA StyleYamashita, M., Kaieda, T., Toyoda, H., Yamaguchi, T., & Katsura, K. (2024). Spatial Estimation of Daily Growth Biomass in Paddy Rice Field Using Canopy Photosynthesis Model Based on Ground and UAV Observations. Remote Sensing, 16(1), 125. https://doi.org/10.3390/rs16010125





