High-Resolution Precipitation Modeling in Complex Terrains Using Hybrid Interpolation Techniques: Incorporating Physiographic and MODIS Cloud Cover Influences
Abstract
1. Introduction
2. Materials and Methods
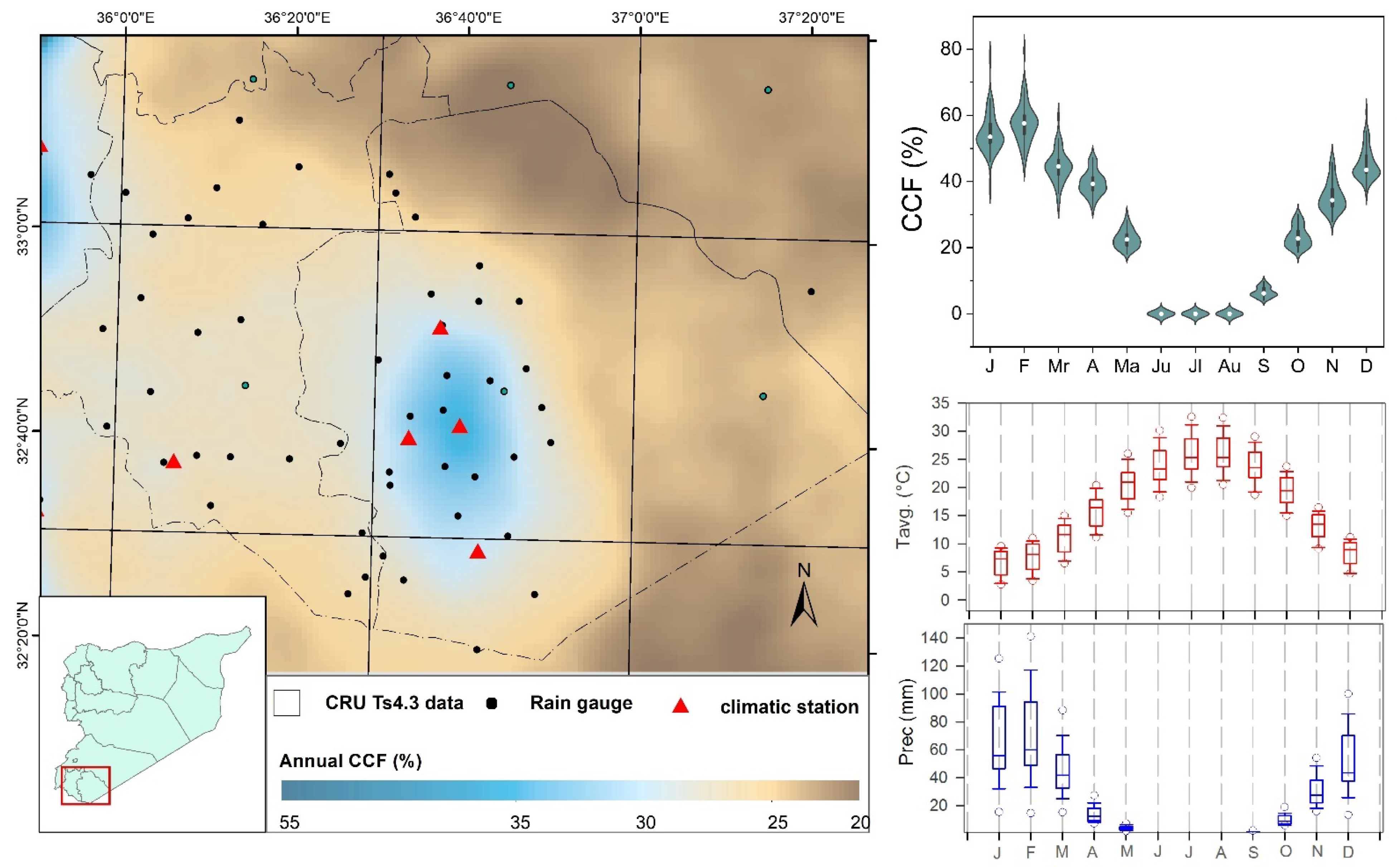
2.1. Study Area and Data Collection
2.1.1. Monthly Observed Precipitation Data
2.1.2. Auxiliary Remote Sensing Data
2.2. Data Analysis
2.2.1. Preliminary Analysis of Monthly Precipitation Series
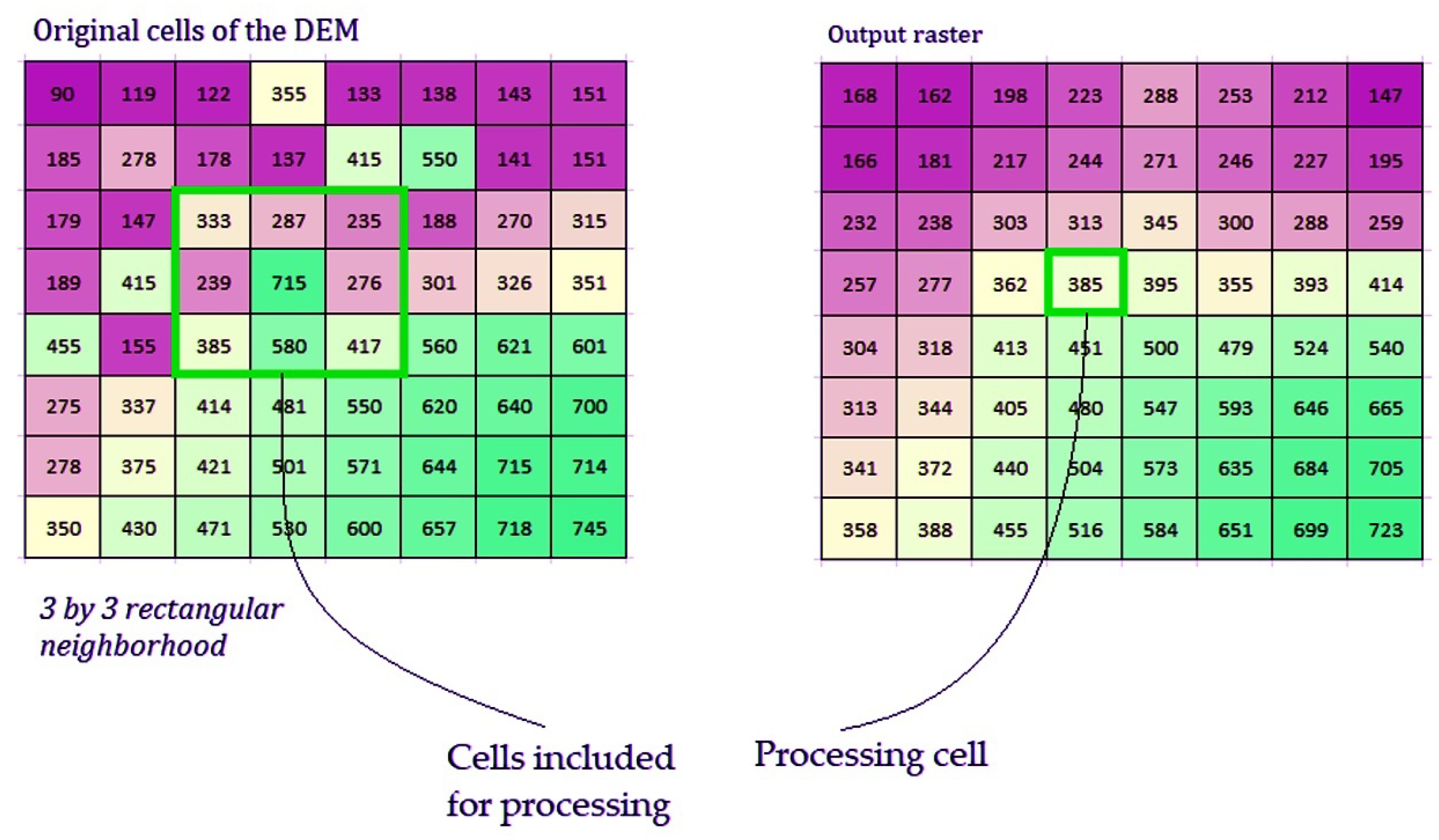
2.2.2. Preprocessing of Explanatory Variables
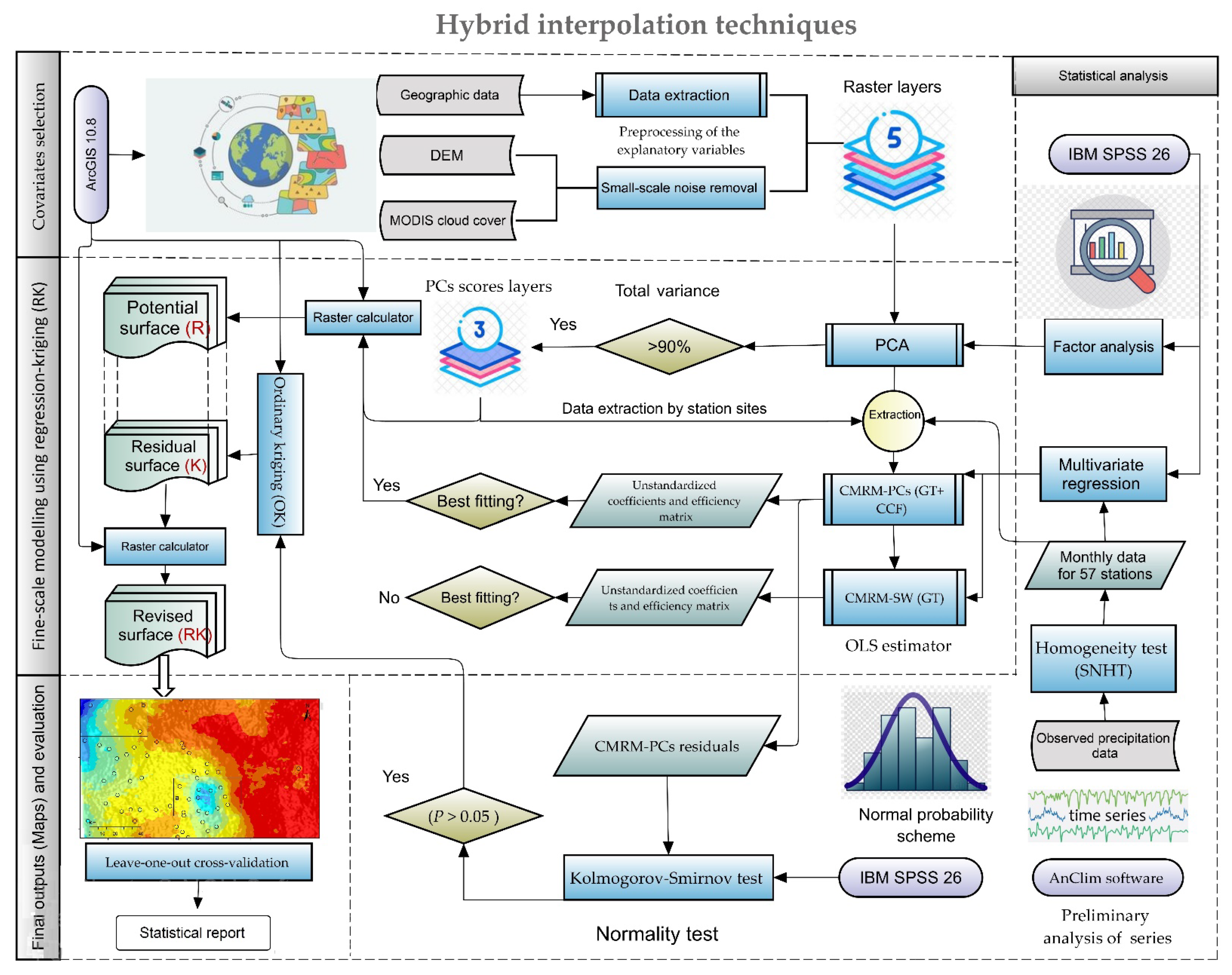
2.2.3. Fine-Scale Modeling Using Regression-Kriging (RK)
2.2.4. Steps Involved in Fitting, Calculating, and Assessing the CMRM and RK Models
| Model | Description | Included Variables | Benefits |
|---|---|---|---|
| Regression model: CMRM-SW (GT) | Fitting the CMRM function using the stepwise regression (SW) method. | Both geographical and topographical factors (elevation, longitude, latitude, and distance to the coast) by including only significant independent variables. | Calculating geographical and topographical contribution (GT) in precipitation modeling. |
| Regression model: CMRM-PCs (GT+ CCF) | Using the extracted PC scores from the PCA to fit the CMRM function. | Geographical and topographical factors (elevation, longitude, latitude, and distance to the coast) were included, besides the CCF data. The extracted PC scores from the PCA. | Calculating remotely sensed CCF contribution in precipitation modeling besides GT effects. |
| Hybrid model: RK (GT + CCF) | Using the extracted PC scores from the PCA to fit the CMRM function and then adding the CMRM’s residuals using OK with exponential variogram model. | As presented in the CMRM-PC (GT + CCF) scheme. | CMRM’s residual correction to improve the outputs. |
3. Results
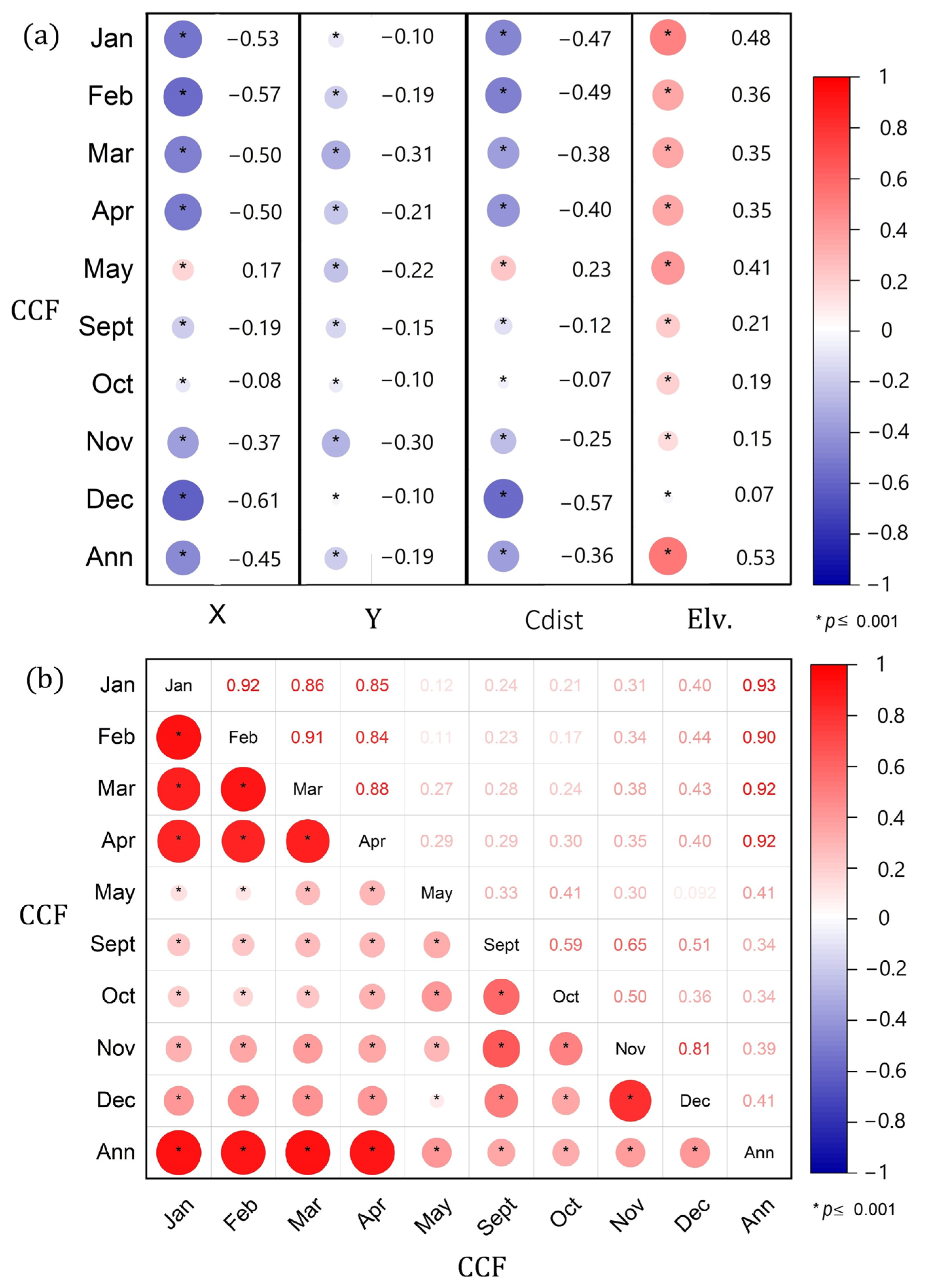
3.1. Effect of Topographical–Geographical Factors on the Spatial Variability of Precipitation
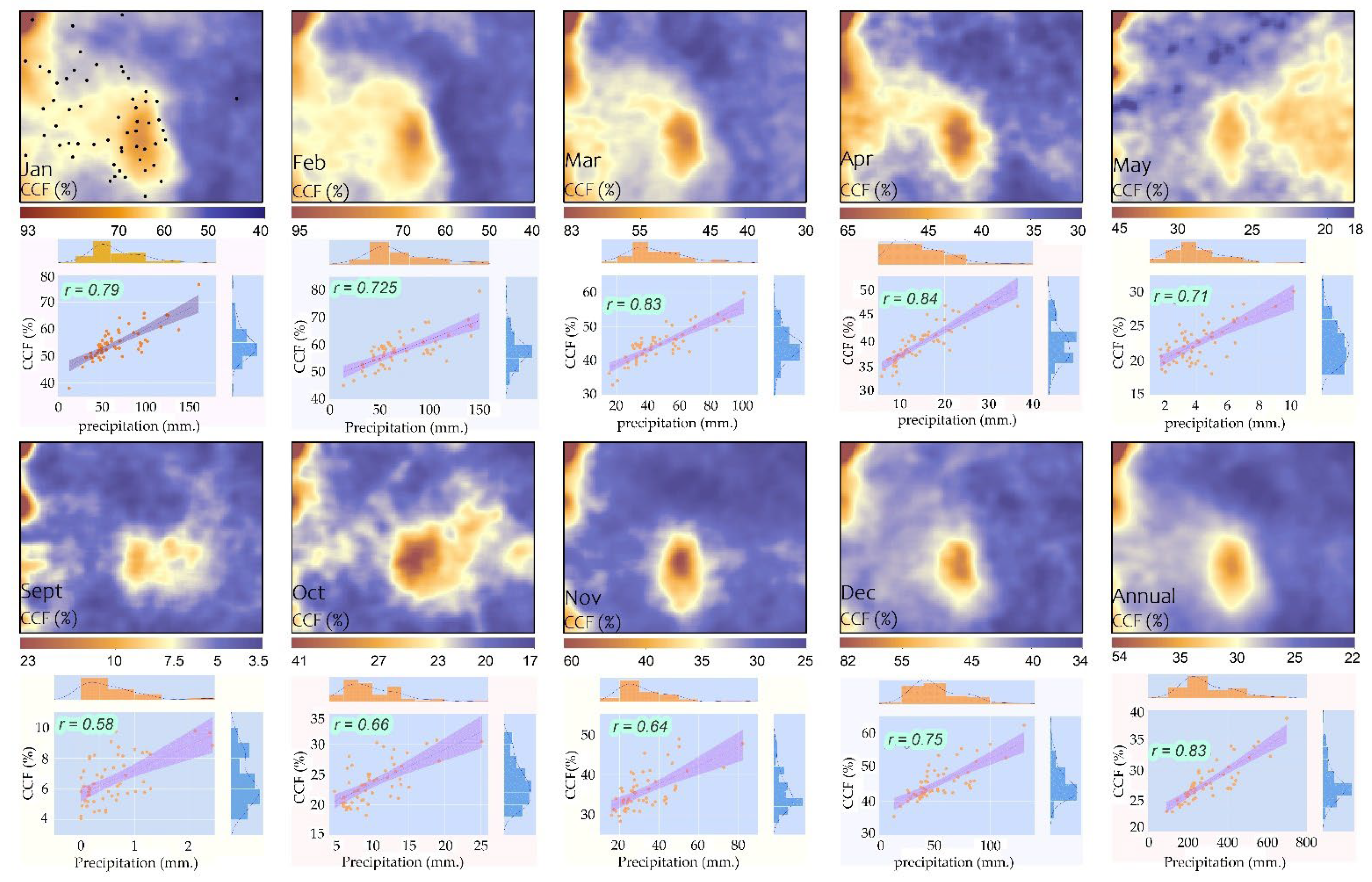
3.2. Spatial Distribution of CCF and Its Effect on the Average Monthly Precipitation
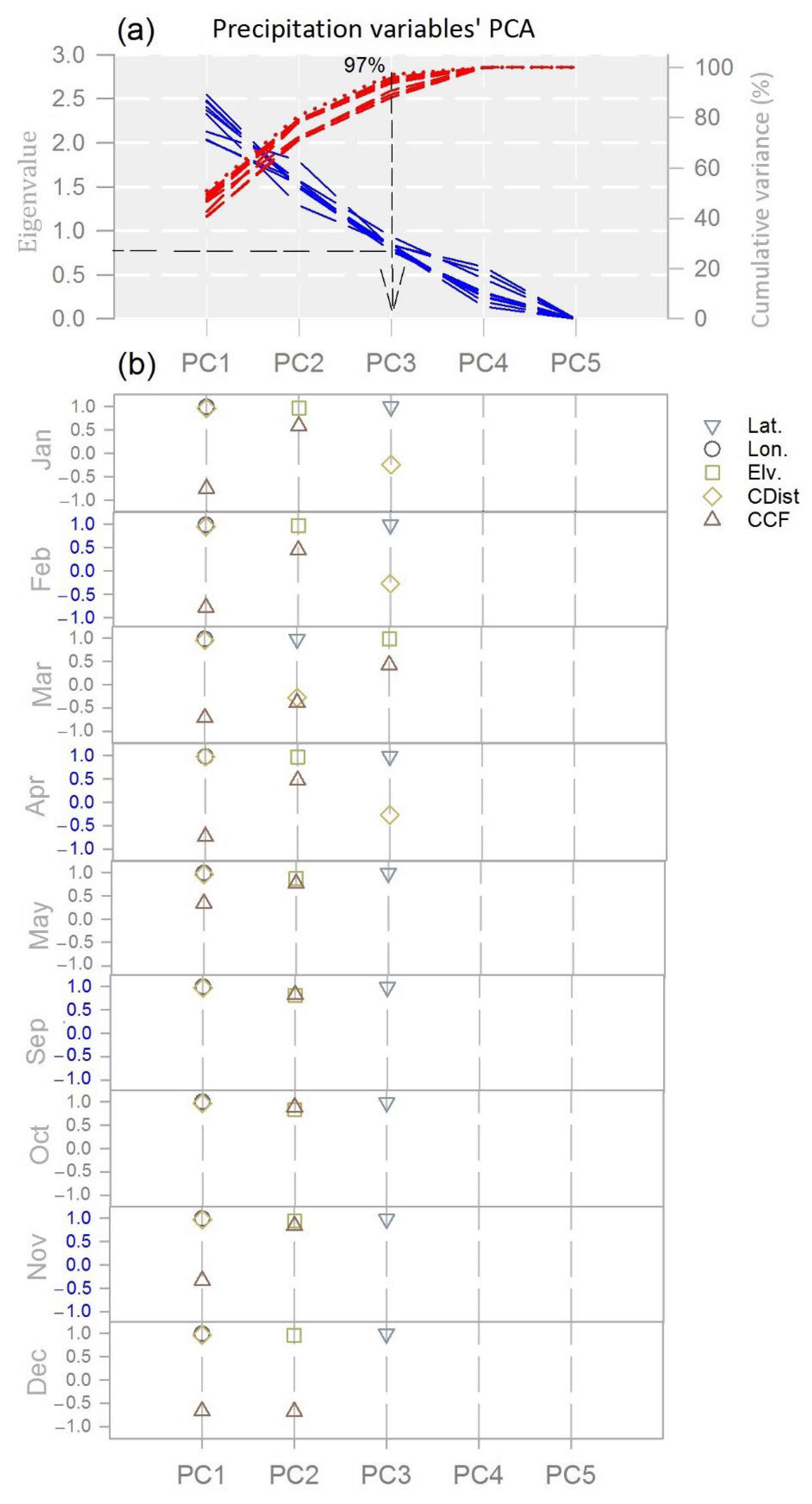
3.3. Interrelationships between Explanatory Variables and PC Analysis
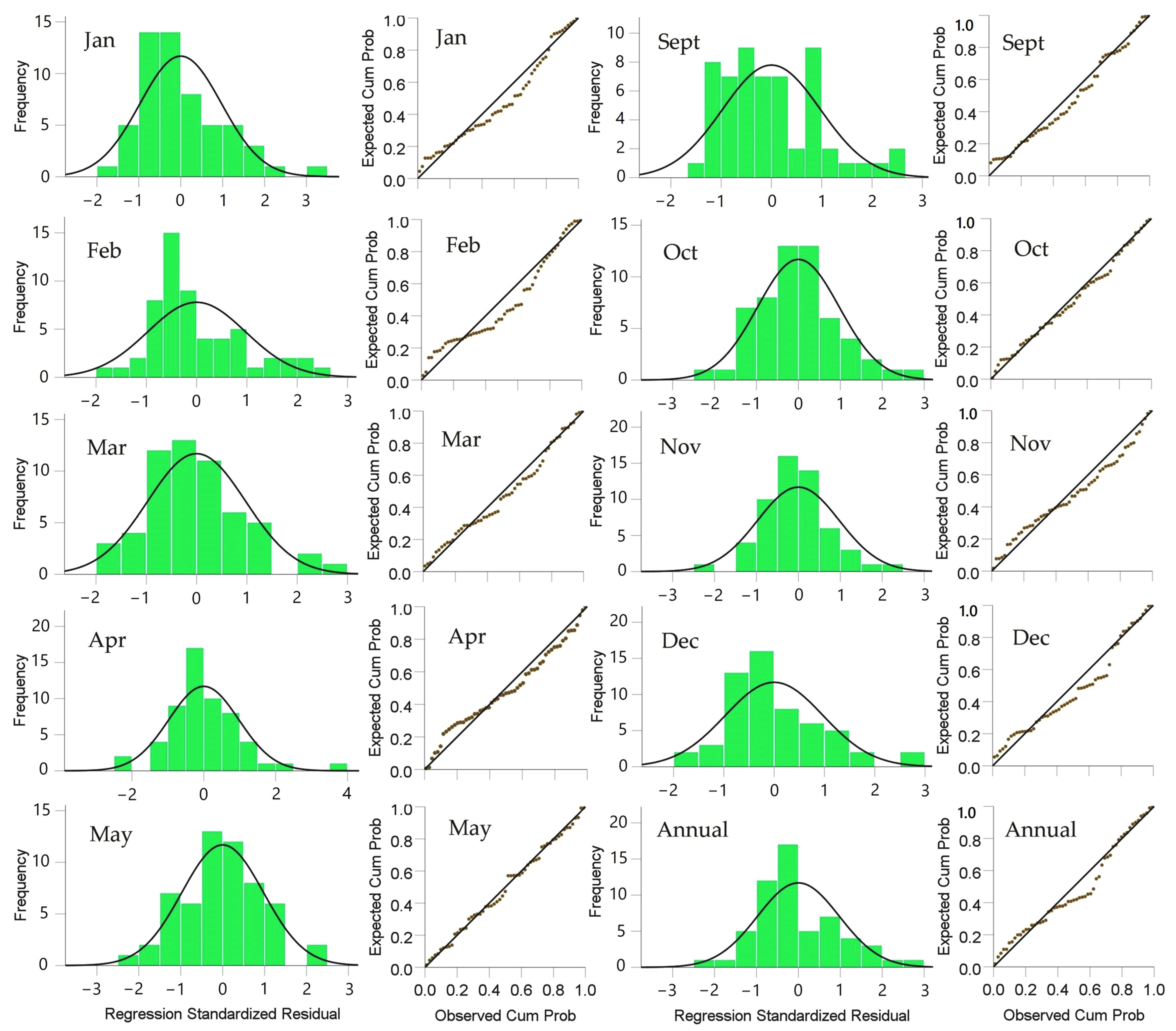
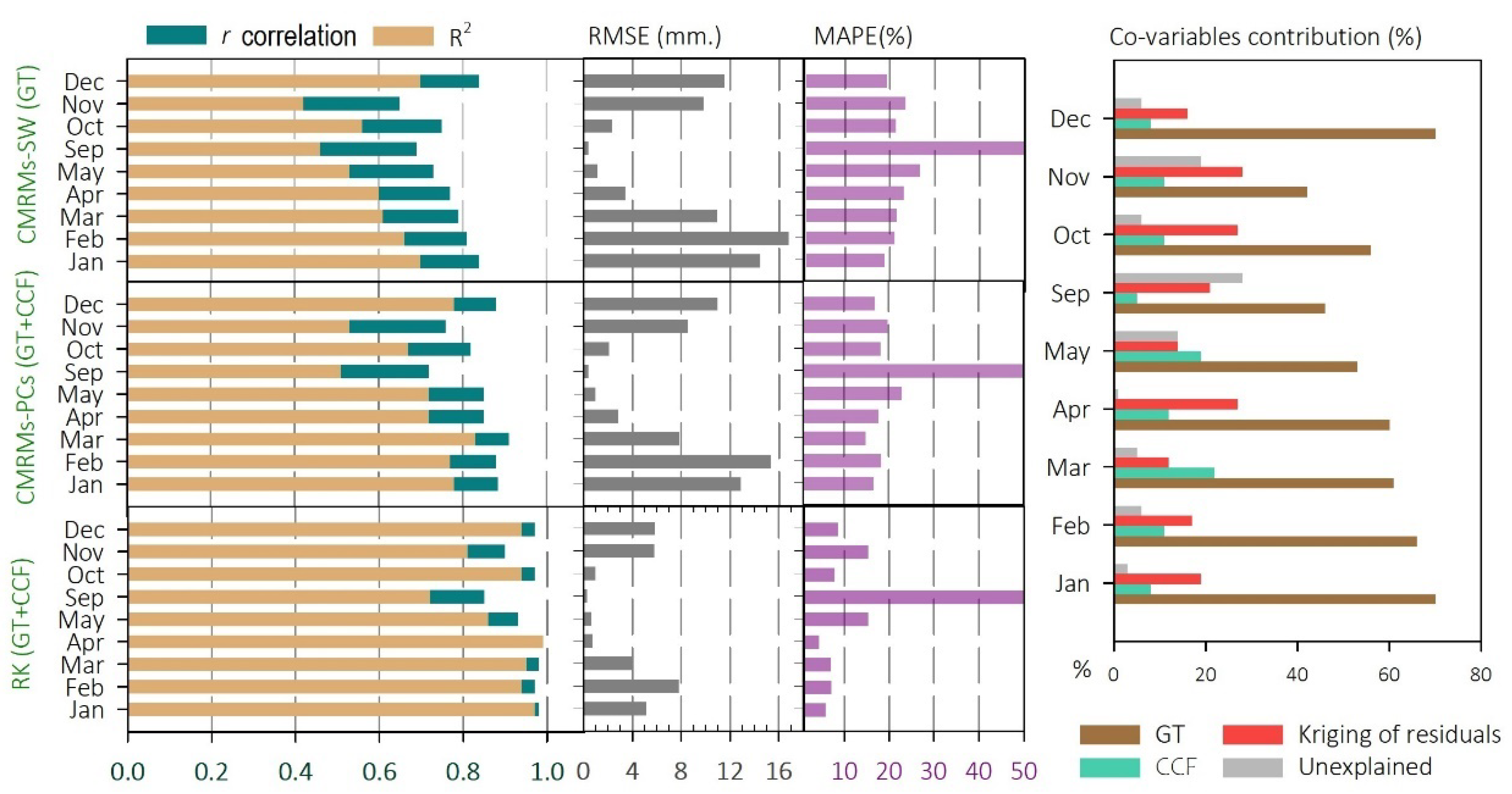
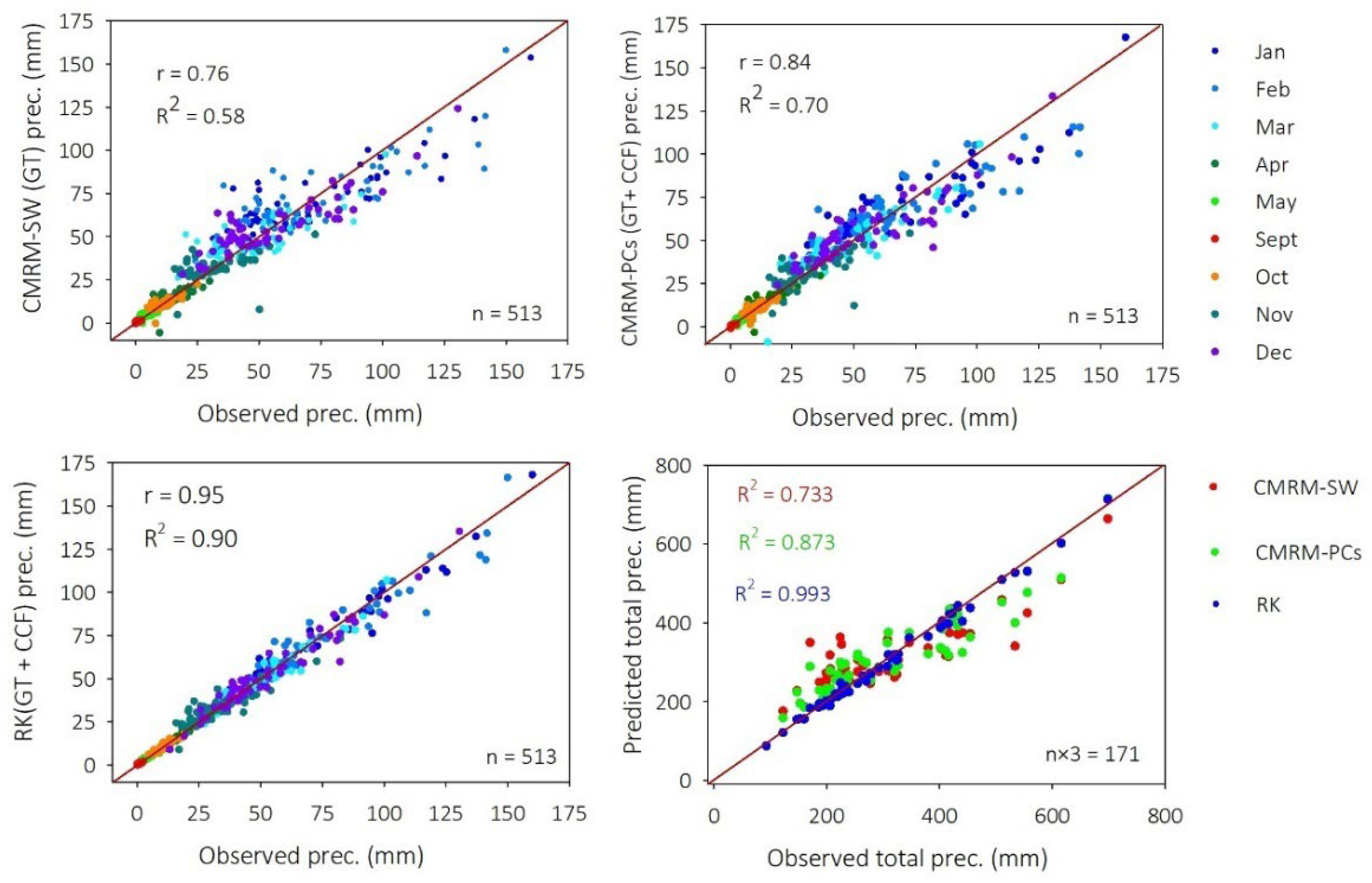
3.4. Modeling of Monthly Precipitation Using the CMRM
3.5. Interpolation of the CMRM’s Residuals
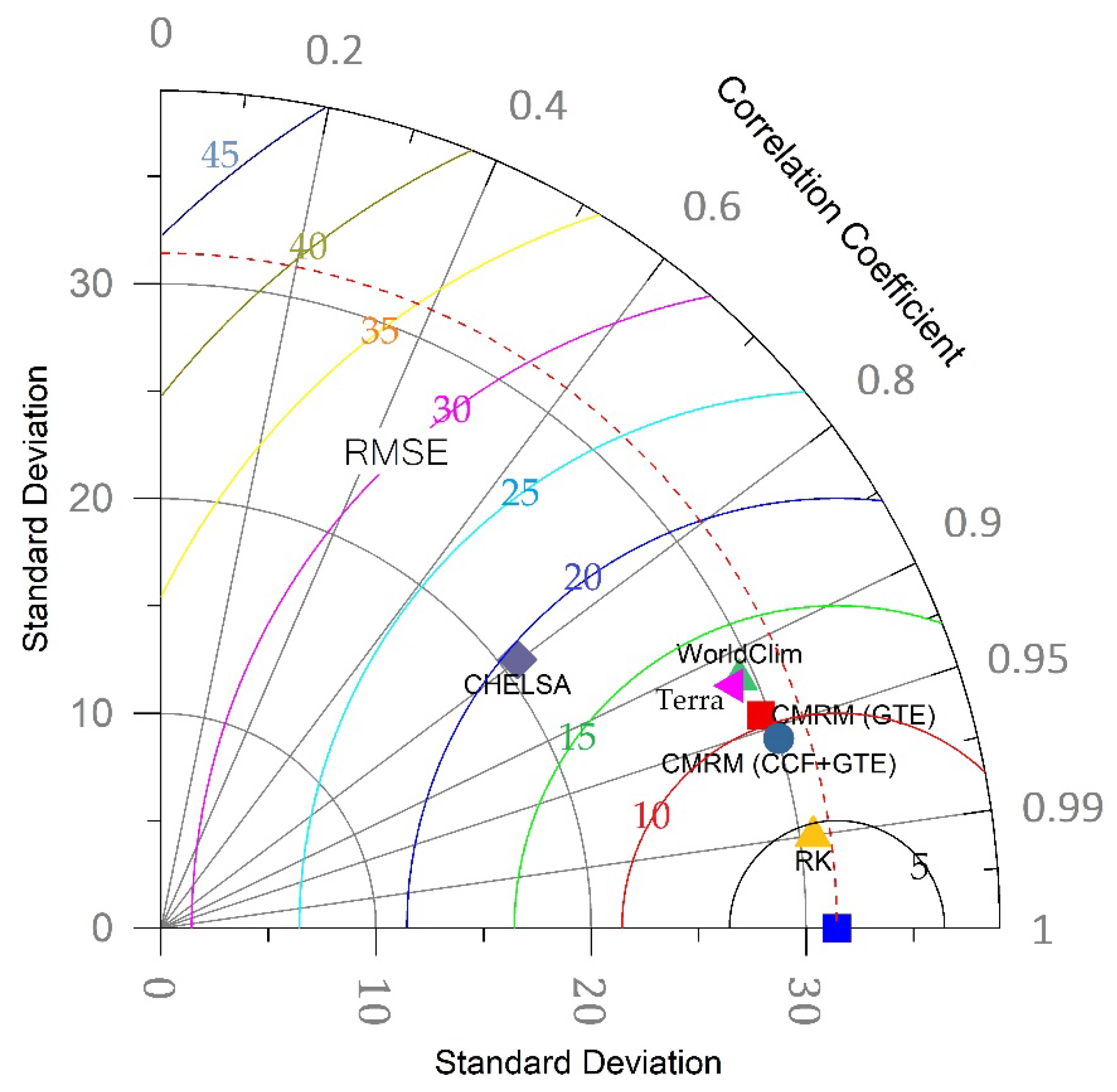
3.6. Performance of CMRMs and RK Models in the Prediction of Precipitation
4. Discussion
5. Conclusions
- The optimal MODIS-CCF surface effects on monthly precipitation patterns are most significant at a horizontal scale of 7 km, and the maximum correlations are in April and March (r > 0.8, p < 0.05).
- The RK method outperforms the single methods, i.e., the multivariate regression models.
- The geographical and topographical factors can explain 42–70% of the total spatial variance in precipitation. Incorporating CCF as a covariate significantly improves the interpolation accuracy by 5–20%. The kriging of the CMRMs’ residuals significantly improves the interpolation accuracy by 12–28%.
- Both the single and the hybrid models are better than the global models (WorldCim, CHELSA, and TerraClimate) in estimating regional precipitation in terms of all statistical indicators.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alsafadi, K.; Mohammed, S.; Habib, H.; Kiwan, S.; Hennawi, S.; Sharaf, M. An Integration of Bioclimatic, Soil, and Topographic Indicators for Viticulture Suitability Using Multi-Criteria Evaluation: A Case Study in the Western Slopes of Jabal Al Arab—Syria. Geocarto Int. 2020, 35, 1466–1488. [Google Scholar] [CrossRef]
- Moreira, R.M.; dos Santos, B.C.; Sanches, R.G.; Bourscheidt, V.; de Sales, F.; Sieber, S.; de Souza, P.H. Precipitation Variability for Protected Areas of Primary Forest and Pastureland in Southwestern Amazônia. Climate 2023, 11, 27. [Google Scholar] [CrossRef]
- Ray, R.L.; Sishodia, R.P.; Tefera, G.W. Evaluation of Gridded Precipitation Data for Hydrologic Modeling in North-Central Texas. Remote Sens. 2022, 14, 3860. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Geostatistical Interpolation of Daily Rainfall at Catchment Scale: The Use of Several Variogram Models in the Ourthe and Ambleve Catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Durre, I.; Arguez, A.; Schreck, C.J.; Squires, M.F.; Vose, R.S. Daily High-Resolution Temperature and Precipitation Fields for the Contiguous United States from 1951 to Present. J. Atmos. Ocean. Technol. 2022, 39, 1837–1855. [Google Scholar] [CrossRef]
- Sun, R.; Zhang, B.P.; Tan, J. A Multivariate Regression Model for Predicting Precipitation in the Daqing Mountains. Mt. Res. Dev. 2008, 28, 318–325. [Google Scholar] [CrossRef]
- Kumari, M.; Singh, C.K.; Bakimchandra, O.; Basistha, A. Geographically Weighted Regression Based Quantification of Rainfall-Topography Relationship and Rainfall Gradient in Central Himalayas. Int. J. Climatol. 2017, 37, 1299–1309. [Google Scholar] [CrossRef]
- Arowolo, A.O.; Bhowmik, A.K.; Qi, W.; Deng, X. Comparison of spatial interpolation techniques to generate high-resolution climate surfaces for Nigeria. Int. J. Climatol. 2017, 37, 179–192. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall Spatial Estimations: A Review from Spatial Interpolation to Multi-Source Data Merging. Water 2019, 11, 579. [Google Scholar] [CrossRef]
- New, M.; Lister, D.; Hulme, M.; Makin, I. A high-resolution data set of surface climate over global land areas. Clim. Res. 2002, 21, 1–25. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Kriticos, D.J.; Webber, B.L.; Leriche, A.; Ota, N.; Macadam, I.; Bathols, J.; Scott, J.K. CliMond: Global High-Resolution Historical and Future Scenario Climate Surfaces for Bioclimatic Modelling. Methods Ecol. Evol. 2012, 3, 53–64. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km Spatial Resolution Climate Surfaces for Global Land Areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the earth’s land surface areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a High-Resolution Global Dataset of Monthly Climate and Climatic Water Balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef]
- Cuervo-Robayo, A.P.; Téllez-Valdés, O.; Gómez-Albores, M.A.; Venegas-Barrera, C.S.; Manjarrez, J.; Martínez-Meyer, E. An update of high-resolution monthly climate surfaces for Mexico. Int. J. Climatol. 2014, 34, 2427–2437. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically Sensitive Mapping of Climatological Temperature and Precipitation across the Conterminous United States. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Daly, C.; Slater, M.E.; Roberti, J.A.; Laseter, S.H.; Swift, L.W. High-Resolution Precipitation Mapping in a Mountainous Watershed: Ground Truth for Evaluating Uncertainty in a National Precipitation Dataset. Int. J. Climatol. 2017, 37, 124–137. [Google Scholar] [CrossRef]
- Ninyerola, M.; Pons, X.; Roure, J.M. Monthly Precipitation Mapping of the Iberian Peninsula Using Spatial Interpolation Tools Implemented in a Geographic Information System. Theor. Appl. Climatol. 2007, 89, 195–209. [Google Scholar] [CrossRef]
- Rockel, B. The Regional Downscaling Approach: A Brief History and Recent Advances. Curr. Clim. Change Rep. 2015, 1, 22–29. [Google Scholar] [CrossRef]
- Crespi, A.; Lussana, C.; Brunetti, M.; Dobler, A.; Maugeri, M.; Tveito, O.E. High-resolution monthly precipitation climatologies over Norway (1981–2010): Joining numerical model data sets and in situ observations. Int. J. Climatol. 2019, 39, 2057–2070. [Google Scholar] [CrossRef]
- Karger, D.N.; Wilson, A.M.; Mahony, C.; Zimmermann, N.E.; Jetz, W. Global Daily 1 Km Land Surface Precipitation Based on Cloud Cover-Informed Downscaling. Sci. Data 2021, 8, 307. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Chen, Q.; Qin, B.; Zhao, S.; Duan, Z. Comparison of Different Methods for Spatial Downscaling of GPM IMERG V06B Satellite Precipitation Product Over a Typical Arid to Semi-Arid Area. Front. Earth Sci. 2020, 8, 536337. [Google Scholar] [CrossRef]
- Gutmann, E.D.; Rasmussen, R.M.; Liu, C.; Ikeda, K.; Gochis, D.J.; Clark, M.P.; Dudhia, J.; Thompson, G. A Comparison of Statistical and Dynamical Downscaling of Winter Precipitation over Complex Terrain. J. Clim. 2012, 25, 262–281. [Google Scholar] [CrossRef]
- Schneider, R.; Koch, J.; Troldborg, L.; Henriksen, H.J.; Stisen, S. Machine-Learning-Based Downscaling of Modelled Climate Change Impacts on Groundwater Table Depth. Hydrol. Earth Syst. Sci. 2022, 26, 5859–5877. [Google Scholar] [CrossRef]
- Serifi, A.; Günther, T.; Ban, N. Spatio-Temporal Downscaling of Climate Data Using Convolutional and Error-Predicting Neural Networks. Front. Clim. 2021, 3, 656479. [Google Scholar] [CrossRef]
- Wang, F.; Tian, D.; Lowe, L.; Kalin, L.; Lehrter, J. Deep Learning for Daily Precipitation and Temperature Downscaling. Water Res. 2021, 57, e2020WR029308. [Google Scholar] [CrossRef]
- Salimi, A.H.; Masoompour Samakosh, J.; Sharifi, E.; Hassanvand, M.R.; Noori, A.; von Rautenkranz, H. Optimized Artificial Neural Networks-Based Methods for Statistical Downscaling of Gridded Precipitation Data. Water 2019, 11, 1653. [Google Scholar] [CrossRef]
- Coulibaly, M.; Becker, S. Spatial Interpolation of Annual Precipitation in South Africa-Comparison and Evaluation of Methods. Water Int. 2007, 32, 494–502. [Google Scholar] [CrossRef]
- Chutsagulprom, N.; Chaisee, K.; Wongsaijai, B.; Inkeaw, P.; Oonariya, C. Spatial Interpolation Methods for Estimating Monthly Rainfall Distribution in Thailand. Theor. Appl. Climatol. 2022, 148, 317–328. [Google Scholar] [CrossRef]
- Vargas-Guzman, J.A.; Warrick, A.W. Geostatistics for Natural Resources Evaluation: Pierre Goovaerts; Oxford University Press: Madison Avenue, NY, USA, 1997; 483p, ISBN 0-19-511538-4. [Google Scholar]
- Ahrens, B. Distance in Spatial Interpolation of Daily Rain Gauge Data. Hydrol. Earth Syst. Sci. 2006, 10, 197–208. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Feki, H.; Slimani, M.; Cudennec, C. Incorporating elevation in rainfall interpolation in Tunisia using geostatistical methods. Hydrol. Sci. J. 2012, 57, 1294–1314. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for Enhanced Spatial Interpolation of Rainfall in Two Australian Catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A Review of Comparative Studies of Spatial Interpolation Methods in Environmental Sciences: Performance and Impact Factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Herrera, S.; Kotlarski, S.; Soares, P.M.M.; Cardoso, R.M.; Jaczewski, A.; Gutiérrez, J.M.; Maraun, D. Uncertainty in Gridded Precipitation Products: Influence of Station Density, Interpolation Method and Grid Resolution. Int. J. Climatol. 2019, 39, 3717–3729. [Google Scholar] [CrossRef]
- Bostan, P.A.; Heuvelink, G.B.M.; Akyurek, S.Z. Comparison of Regression and Kriging Techniques for Mapping the Average Annual Precipitation of Turkey. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 115–126. [Google Scholar] [CrossRef]
- Brunsdon, C.; McClatchey, J.; Unwin, D.J. Spatial Variations in the Average Rainfall-Altitude Relationship in Great Britain: An Approach Using Geographically Weighted Regression. Int. J. Climatol. 2001, 21, 455–466. [Google Scholar] [CrossRef]
- Lloyd, C. Nonstationary models for exploring and mapping monthly precipitation in the United Kingdom. Int. J. Climatol. 2010, 30, 390–405. [Google Scholar] [CrossRef]
- Kumari, M.; Singh, C.K.; Basistha, A.; Dorji, S.; Tamang, T.B. Nonstationary modelling framework for rainfall interpolation in complex terrain. Int. J. Climatol. 2017, 37, 4171–4185. [Google Scholar] [CrossRef]
- Aalto, J.; Pirinen, P.; Heikkinen, J.; Venäläinen, A. Spatial Interpolation of Monthly Climate Data for Finland: Comparing the Performance of Kriging and Generalized Additive Models. Theor. Appl. Climatol. 2013, 112, 99–111. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M. Geographically Weighted Summary Statistics—A Framework for Localised Exploratory Data Analysis. Comput. Environ. Urban Syst. 2002, 26, 501–524. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and Temporally Weighted Regression for Modeling Spatio-Temporal Variation in House Prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Doulamis, A.; Doulamis, N. Comparison of Machine Learning Algorithms for Merging Gridded Satellite and Earth-Observed Precipitation Data. Water 2023, 15, 634. [Google Scholar] [CrossRef]
- Rigol, J.P.; Jarvis, C.H.; Stuart, N. Artificial Neural Networks as a Tool for Spatial Interpolation. Int. J. Geogr. Inf. Sci. 2001, 15, 323–343. [Google Scholar] [CrossRef]
- Kalteh, A.M.; Berndtsson, R. Interpolating Monthly Precipitation by Self-Organizing Map (SOM) and Multilayer Perceptron (MLP). Hydrol. Sci. J. 2007, 52, 305–317. [Google Scholar] [CrossRef]
- Kajornrit, J.; Wong, K.W.; Fung, C.C. An Interpretable Fuzzy Monthly Rainfall Spatial Interpolation System for the Construction of Aerial Rainfall Maps. Soft Comput. 2016, 20, 4631–4643. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.M.; Nikolić, M.; Bajat, B. Random Forest Spatial Interpolation. Remote Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Chen, C.; Hu, B.; Li, Y. Easy-to-Use Spatial Random-Forest-Based Downscaling-Calibration Method for Producing Precipitation Data with High Resolution and High Accuracy. Hydrol. Earth Syst. Sci. 2021, 25, 5667–5682. [Google Scholar] [CrossRef]
- Pour, S.H.; Shahid, S.; Chung, E.S. A hybrid model for statistical downscaling of daily rainfall. Procedia Eng. 2016, 154, 1424–1430. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Copula-Based Stochastic Uncertainty Analysis of Satellite Precipitation Products. J. Hydrol. 2019, 570, 739–754. [Google Scholar] [CrossRef]
- Álvarez-Rodríguez, J.; Llasat, M.C.; Estrela, T. Development of a Hybrid Model to Interpolate Monthly Precipitation Maps Incorporating the Orographic Influence. Int. J. Climatol. 2019, 39, 3962–3975. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, D.; Zheng, S.; Liu, S.; Loáiciga, H.A.; Li, W. Regional Precipitation Model Based on Geographically and Temporally Weighted Regression Kriging. Remote Sens. 2020, 12, 2547. [Google Scholar] [CrossRef]
- Alsafadi, K.; Mohammed, S.; Mokhtar, A.; Sharaf, M.; He, H. Fine-Resolution Precipitation Mapping over Syria Using Local Regression and Spatial Interpolation. Atmos. Res. 2021, 256, 105524. [Google Scholar] [CrossRef]
- Guan, H.; Hsu, H.H.; Makhnin, O.; Xie, H.; Wilson, J.L. Examination of Selected Atmospheric and Orographic Effects on Monthly Precipitation of Taiwan Using the ASOADeK Model. Int. J. Climatol. 2009, 29, 1171–1181. [Google Scholar] [CrossRef]
- Guan, H.; Wilson, J.L.; Makhnin, O. Geostatistical Mapping of Mountain Precipitation Incorporating Autosearched Effects of Terrain and Climatic Characteristics. J. Hydrometeorol. 2005, 6, 1018–1031. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Further Results on Prediction of Soil Properties from Terrain Attributes: Heterotopic Cokriging and Regression-Kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Rossiter, D.G. About Regression-Kriging: From Equations to Case Studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, Y.; Huang, S.; Guo, C. Mapping the Mean Annual Precipitation of China Using Local Interpolation Techniques. Theor. Appl. Climatol. 2014, 119, 171–180. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Singh, V.P. Estimating spatial precipitation using regression kriging and artificial neural network residual kriging (RKNNRK) hybrid approach. Water Resour. Manag. 2015, 29, 2189–2204. [Google Scholar] [CrossRef]
- Kisi, O.; Mohsenzadeh Karimi, S.; Shiri, J.; Keshavarzi, A. Modelling long-term monthly rainfall using geographical inputs: Assessing heuristic and geostatistical models. Meteorol. Appl. 2019, 26, 698–710. [Google Scholar] [CrossRef]
- Lei, J.; Quan, Q.; Li, P.; Yan, D. Research on monthly precipitation prediction based on the least square support vector machine with multi-factor integration. Atmosphere 2021, 12, 1076. [Google Scholar] [CrossRef]
- Tan, J.; Xie, X.; Zuo, J.; Xing, X.; Liu, B.; Xia, Q.; Zhang, Y. Coupling random forest and inverse distance weighting to generate climate surfaces of precipitation and temperature with multiple-covariates. J. Hydrol. 2021, 598, 126270. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Nanni, T.; Simolo, C.; Spinoni, J. High-resolution temperature climatology for Italy: Interpolation method intercomparison. Int. J. Climatol. 2014, 34, 1278–1296. [Google Scholar] [CrossRef]
- Wang, M.; He, G.; Zhang, Z.; Wang, G.; Zhang, Z.; Cao, X.; Wu, Z.; Liu, X. Comparison of spatial interpolation and regression analysis models for an estimation of monthly near surface air temperature in China. Remote Sens. 2017, 9, 1278. [Google Scholar] [CrossRef]
- Cristóbal, J.; Ninyerola, M.; Pons, X. Modeling air temperature through a combination of remote sensing and GIS data J. Geophys. Res. Atmos. 2008, 113, D13106. [Google Scholar] [CrossRef]
- Antal, A.; Guerreiro, P.M.; Cheval, S. Comparison of spatial interpolation methods for estimating the precipitation distribution in Portugal. Theor. Appl. Climatol. 2021, 145, 1193–1206. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Rutten, M.M.; Droogers, P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lű, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Lu, X.; Tang, G.; Wang, X.; Liu, Y.; Wei, M.; Zhang, Y. The development of a two-step merging and downscaling method for satellite precipitation products. Remote Sens. 2020, 12, 398. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G.M.; Rutten, M.M. Validation of surface soil moisture from AMSR-E using auxiliary spatial data in the transboundary Indus Basin. J. Hydrol. 2011, 405, 137–149. [Google Scholar] [CrossRef]
- Richards, F.; Arkin, P. On the relationship between satellite-observed cloud cover and precipitation. Mon. Weather Rev. 1981, 109, 1081–1093. [Google Scholar] [CrossRef]
- Arkin, P.A.; Meisner, B.N. The relationship between large-scale convective rainfall and cold cloud over the western hemisphere during 1982–84. Mon. Weather Rev. 1987, 115, 51–74. [Google Scholar] [CrossRef]
- Betts, A.K.; Tawfik, A.B.; Desjardins, R.L. Revisiting Hydrometeorology Using Cloud and Climate Observations. J. Hydrometeorol. 2017, 18, 939–955. [Google Scholar] [CrossRef]
- Alsafadi, K.; Bi, S.; Abdo, H.G.; Almohamad, H.; Alatrach, B.; Srivastava, A.K.; Al-Mutiry, M.; Bal, S.K.; Chandran, M.A.S.; Mohammed, S. Modeling the Impacts of Projected Climate Change on Wheat Crop Suitability in Semi-Arid Regions Using the AHP-Based Weighted Climatic Suitability Index and CMIP6. Geosci. Lett. 2023, 10, 20. [Google Scholar] [CrossRef]
- Wilson, A.M.; Jetz, W. Remotely sensed high-resolution global cloud dynamics for predicting ecosystem and biodiversity distributions. PLoS Biol. 2016, 14, e1002415. [Google Scholar] [CrossRef]
- Danielson, J.J.; Gesch, D.B. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); US Department of the Interior, US Geological Survey: Reston, VA, USA, 2011; p. 101. 26p. [Google Scholar]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Štěpánek, P.; Zahradníček, P.; Skalák, P. Data quality control and homogenization of air temperature and precipitation series in the area of the Czech Republic in the period 1961–2007. Adv. Sci. Res. 2009, 3, 23–26. [Google Scholar] [CrossRef]
- Zhu, X.; Qiu, X.; Zeng, Y.; Ren, W.; Tao, B.; Pan, H.; Gao, T.; Gao, J. High-resolution precipitation downscaling in mountainous areas over China: Development and application of a statistical mapping approach. Int. J. Climatol. 2018, 38, 77–93. [Google Scholar] [CrossRef]
- Daly, C.; Smith, J.W.; Smith, J.I.; McKane, R.B. High-Resolution Spatial Modeling of Daily Weather Elements for a Catchment in the Oregon Cascade Mountains, United States. J. Appl. Meteorol. Climatol. 2007, 46, 1565–1586. [Google Scholar] [CrossRef]
- Portalés, C.; Boronat, N.; Pardo-Pascual, J.E.; Balaguer-Beser, A. Seasonal precipitation interpolation at the Valencia region with multivariate methods using geographic and topographic information. Int. J. Climatol. 2010, 30, 1547–1563. [Google Scholar] [CrossRef]
- Qi, W.W.; Zhang, B.P.; Yao, Y.H.; Zhao, F.; Zhang, S.; He, W.H. A topographical model for precipitation pattern in the Tibetan Plateau. J. Mt. Sci. 2016, 13, 763–773. [Google Scholar] [CrossRef]
- Drogue, G.; Humbert, J.; Deraisme, J.; Mahr, N.; Freslon, N. A statistical–topographic model using an omnidirectional parameterization of the relief for mapping orographic rainfall. Int. J. Climatol. 2002, 22, 599–613. [Google Scholar] [CrossRef]
- Lloyd, C. Assessing the effect of integrating elevation data into the estimation of monthly precipitation in Great Britain. J. Hydrol. 2005, 308, 128–150. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling Satellite Precipitation Estimates with Multiple Linear Regression, Artificial Neural Networks, and Spline Interpolation Techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef]
- Zandi, O.; Zahraie, B.; Nasseri, M.; Behrangi, A. Stacking machine learning models versus a locally weighted linear model to generate high-resolution monthly precipitation over a topographically complex area. Atmos. Res. 2022, 272, 106159. [Google Scholar] [CrossRef]
- Bartholomew, D.J. Principal Components Analysis, 3rd ed.; Peterson, P., Baker, E., McGaw, B., Eds.; Elsevier: Oxford, UK, 2010; pp. 374–377. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. WIREs Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Sulaiman, M.S.; Abood, M.M.; Sinnakaudan, S.K.; Shukor, M.R.; You, G.Q.; Chung, X.Z. Assessing and solving multicollinearity in sediment transport prediction models using principal component analysis. ISH J. Hydraul. Eng. 2021, 27 (Suppl. 1), 343–353. [Google Scholar] [CrossRef]
- Chen, T.; Ren, L.; Yuan, F.; Yang, X.; Jiang, S.; Tang, T.; Liu, Y.; Zhao, C.; Zhang, L. Comparison of Spatial Interpolation Schemes for Rainfall Data and Application in Hydrological Modeling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- Abreu, M.C.; de Souza, A.; Lyra, G.B.; Pobocikova, I.; Cecílio, R.A. Analysis of Monthly and Annual Rainfall Variability Using Linear Models in the State of Mato Grosso Do Sul, Midwest of Brazil. Int. J. Climatol. 2021, 41, E2445–E2461. [Google Scholar] [CrossRef]
- Tveito, O.E.; Wegehenkel, M.; Wel, F.V.D. The use of geographic information systems in climatology and meteorology. In Cost Action 719; EU Publications: Luxembourg, 2008. [Google Scholar] [CrossRef]
- Faurès, J.M.; Goodrich, D.C.; Woolhiser, D.A.; Sorooshian, S. Impact of small-scale spatial rainfall variability on runoff modeling. J. Hydrol. 1995, 173, 309–326. [Google Scholar] [CrossRef]
- Michaelides, S.C.; Tymvios, F.S.; Michaelidou, T. Spatial and temporal characteristics of the annual rainfall frequency distribution in Cyprus. Atmos. Res. 2009, 94, 606–615. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumari, N.; Dharpure, J.K.; Mokhtar, A.; Alsafadi, K.; Kumar, M.; Mehdinejadiani, B.; Ramezani Etedali, H.; Brouziyne, Y.; Towfiqul Islam, A.R.M.; et al. Prediction of combined terrestrial evapotranspiration index (CTEI) over large river basin based on machine learning approaches. Water 2021, 13, 547. [Google Scholar] [CrossRef]
- Mokhtar, A.; Jalali, M.; He, H.; Al-Ansari, N.; Elbeltagi, A.; Alsafadi, K.; Abdo, H.G.; Sammen, S.S.; Gyasi-Agyei, Y.; Rodrigo-Comino, J. Estimation of SPEI meteorological drought using machine learning algorithms. IEEE Access 2021, 9, 65503–65523. [Google Scholar] [CrossRef]
- Li, X.; He, X.; Li, X.; Du, Y.; Yang, G.; Tian, H.; Yu, J. Construction of high-resolution precipitation dataset and its implication to drought over the Tianshan Mountains, China. Front. Earth Sci. 2023, 11, 1128990. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.; Huffman, G. Evaluation of the potential of NASA multi-satellite precipitation analysis in global landslide hazard assessment. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Ceron, W.L.; Andreoli, R.V.; Kayano, M.T.; Canchala, T.; Carvajal-Escobar, Y.; Souza, R.A. Comparison of spatial interpolation methods for annual and seasonal rainfall in two hotspots of biodiversity in South America. An. Acad. Bras. Cienc. 2021, 93, e20190674. [Google Scholar] [CrossRef]
- Alsafadi, K.; Bi, S.; Abdo, H.G.; Al Sayah, M.J.; Ratonyi, T.; Harsanyi, E.; Mohammed, S. Spatial–temporal dynamic impact of changes in rainfall erosivity and vegetation coverage on soil erosion in the Eastern Mediterranean. Environ. Sci. Pollut. Res. 2022, 1–19. [Google Scholar] [CrossRef]
- Huang, Z.; Derin, Y.; Kirstetter, P.E.; Li, Y. Multigraph Convolutional Networks for Rainfall Estimation in Complex Terrain. EEE Geosci. Remote Sens. Lett. 2022, 19, 1506005. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, M.; Pandey, R.; ZhiGuo, Y.; Cabral-Pinto, M. Forest Soil Nutrient Stocks along Altitudinal Range of Uttarakhand Himalayas: An Aid to Nature Based Climate Solutions. Catena 2021, 207, 105667. [Google Scholar] [CrossRef]
- Bhardwaj, D.R.; Tahiry, H.; Sharma, P.; Pala, N.A.; Kumar, D.; Kumar, A.; Bharti. Influence of Aspect and Elevational Gradient on Vegetation Pattern, Tree Characteristics and Ecosystem Carbon Density in Northwestern Himalayas. Land 2021, 10, 1109. [Google Scholar] [CrossRef]
- Camera, C.; Bruggeman, A.; Hadjinicolaou, P.; Pashiardis, S.; Lange, M.A. Evaluation of interpolation techniques for the creation of gridded daily precipitation (1× 1 km2); Cyprus, 1980–2010. J. Geophys. Res. Atmos. 2014, 119, 693–712. [Google Scholar] [CrossRef]
- Geiss, A.; Hardin, J.C. Inpainting Radar Missing Data Regions with Deep Learning. Atmos. Meas. Tech. 2021, 14, 7729–7747. [Google Scholar] [CrossRef]
- Sun, B.; Groisman, P.Y.; Mokhov, I.I. Recent changes in cloud-type frequency and inferred increases in convection over the United States and the former USSR. J. Clim. 2001, 14, 1864–1880. [Google Scholar] [CrossRef]
- Mishra, A.K. Investigating changes in cloud cover using the long-term record of precipitation extremes. Meteorol. Appl. 2019, 26, 108–116. [Google Scholar] [CrossRef]
- Zhong, X.; Liu, S.C.; Liu, R.; Wang, X.; Mo, J.; Li, Y. Observed trends in clouds and precipitation (1983–2009): Implications for their cause(s). Atmos. Chem. Phys. 2021, 21, 4899–4913. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Dewan, A.; Shahid, S.; Bhuian, M.H.; Hossain, S.M.J.; Nashwan, M.S.; Chung, E.S.; Hassan, Q.K.; Asaduzzaman, M. Developing a high-resolution gridded rainfall product for Bangladesh during 1901–2018. Sci. Data 2022, 9, 471. [Google Scholar] [CrossRef]
- Pellicone, G.; Caloiero, T.; Modica, G.; Guagliardi, I. Application of several spatial interpolation techniques to monthly rainfall data in the Calabria region (southern Italy). Int. J. Climatol. 2018, 38, 3651–3666. [Google Scholar] [CrossRef]
- Doran, J.C.; Zhong, S.; Liljegren, J.C.; Jakob, C. A comparison of cloud properties at a coastal and inland site at the North Slope of Alaska. J. Geophys. Res. Atmos. 2002, 107, ACL-5. [Google Scholar] [CrossRef]
- Ye, Y. Marine Geographic and Geological Environment of China. Mar. Geo-Hazards China 2017, 10, 35–75. [Google Scholar] [CrossRef]
- Prijith, S.S.; Lima, C.B.; Ramana, M.V.; Sai, M.S. Intra-seasonal contrasting trends in clouds due to warming induced circulation changes. Sci. Rep. 2021, 11, 16985. [Google Scholar] [CrossRef]
- Pielke Sr, R.A.; Adegoke, J.; BeltraáN-Przekurat, A.; Hiemstra, C.A.; Lin, J.; Nair, U.S.; Niyogi, D.; Nobis, T.E. An overview of regional land-use and land-cover impacts on rainfall. Tellus B Chem. Phys. Meteorol. 2007, 59, 587–601. [Google Scholar] [CrossRef]
- Yu, H.; Wang, L.; Yang, R.; Yang, M.; Gao, R. Temporal and spatial variation of precipitation in the Hengduan Mountains region in China and its relationship with elevation and latitude. Atmos. Res. 2018, 213, 1–16. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, Z.; Borders, B.E. Assessment of Regression Kriging for Spatial Interpolation—Comparisons of Seven GIS Interpolation Methods. Cartogr. Geogr. Inf. Sci. 2013, 40, 28–39. [Google Scholar] [CrossRef]
- Mishra, P.K.; Nath, S.K.; Sen, M.K.; Fasshauer, G.E. Hybrid Gaussian-cubic radial basis functions for scattered data interpolation. Comput. Geosci. 2018, 22, 1203–1218. [Google Scholar] [CrossRef]
- Khedhaouiria, D.; Bélair, S.; Fortin, V.; Roy, G.; Lespinas, F. Using a hybrid optimal interpolation–ensemble Kalman filter for the Canadian Precipitation Analysis. Nonlinear Process. Geophys. 2022, 29, 329–344. [Google Scholar] [CrossRef]

| Variable | Data Type | Number of Stations/Points | Spatial Resolution | Reference Period | Source |
|---|---|---|---|---|---|
| Observed precipitation (mm) | Rain gauge and climatic stations (Historical) | 57 | – | 1984–2015 | SMA SMOAAR JMD |
| CRU Ts4.3 precipitation (mm) | Gridded data (Historical) | 9 gridded points | 0.5 degree | 1984–2015 | https://crudata.uea.ac.uk/cru/data/hrg/, (accessed on 7 September 2022) |
| TerraClimate precipitation (mm) | Gridded data (Monthly average) | – | ~4 km (2.5 arc. min) | 1970–2000 | https://www.climatologylab.org/, (accessed on 7 September 2022) |
| WorldClim V. 2.1 precipitation (mm) | Gridded data (Monthly average) | – | ~1 km (30 arc-second) | 1981–2010 | https://www.worldclim.org/, (accessed on 7 September 2022) |
| CHELSA V1.0 precipitation (mm) | Gridded data (Monthly average) | – | ~1 km (30 arc-second) | 1979–2016 | https://chelsa-climate.org/, (accessed on 7 September 2022) |
| PCs/Prc. | January | February | March | April | May | June | July | August | September | October | November | December | Annual |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PC1 | −0.415 | −0.39 | −0.38 | −0.45 | −0.35 | – | – | – | −0.34 | −0.30 | −0.36 | −0.42 | −0.36 |
| PC2 | 0.47 | 0.51 | 0.005 | 0.49 | 0.64 | – | – | – | 0.12 | 0.55 | 0.46 | 0.46 | 0.55 |
| PC3 | 0.14 | 0.13 | 0.56 | 0.13 | 0.30 | – | – | – | 0.27 | 0.34 | 0.33 | 0.17 | 0.17 |
| Variables | January | February | March | April | May | June | July | August | September | October | November | December | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Constant | 3303 | 3013 | 1706 | 600 | 4.8 | – | – | – | 51.1 | 13.5 | 44.9 | 2610 | |
| Elv. | 0.083 | 0.088 | 0.053 | 0.017 | 0.005 | – | – | – | 0.001 | 0.010 | 0.025 | 0.064 | |
| Lon. | −85.4 | −83 | −46.9 | −16.5 | – | – | – | – | −1.42 | – | – | −71.8 | |
| Lat. | – | – | – | – | – | – | – | – | – | – | – | – | |
| CDist. | – | – | – | – | –0.04 | – | – | – | – | −0.10 | −0.28 | – | |
| r correlation | 0.84 | 0.81 | 0.79 | 0.77 | 0.73 | – | – | – | 0.69 | 0.75 | 0.65 | 0.843 | |
| Adj. R2 | 0.70 | 0.66 | 0.61 | 0.6 | 0.53 | – | – | – | 0.46 | 0.56 | 0.42 | 0.71 | |
| RMSE (mm.) | 16.25 | 18.4 | 11.8 | 4.1 | 1.25 | – | – | – | 0.42 | 2.6 | 10.2 | 13.3 | |
| Sig. value (p) | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | – | – | – | <0.01 | <0.01 | <0.01 | <0.01 | |
| Variables | January | February | March | April | May | June | July | August | September | October | November | December | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Constant | 33.4 | 36.6 | 26.2 | 8.05 | 2.8 | – | – | – | 0.18 | 6.8 | 23.7 | 28 | |
| 1CP | −37.7 | −37.4 | −21.5 | −9.6 | −1.62 | – | – | – | −0.47 | −3.6 | −11 | −29.1 | |
| 2CP | 18.8 | 18.9 | 2.02 | 3.54 | 1.03 | – | – | – | 0.31 | 2.35 | 6.74 | 15.3 | |
| 3CP | −0.09 | 1.1 | 12.3 | 0.13 | 0.14 | – | – | – | −0.01 | 0.42 | 1.9 | −1.6 | |
| r correlation | 0.885 | 0.88 | 0.91 | 0.85 | 0.856 | – | – | – | 0.72 | 0.82 | 0.76 | 0.88 | |
| Adj. R2 | 0.781 | 0.77 | 0.83 | 0.72 | 0.73 | – | – | – | 0.51 | 0.67 | 0.53 | 0.78 | |
| RMSE (mm.) | 14.37 | 15.7 | 8.3 | 3.5 | 0.98 | – | – | – | 0.42 | 2.4 | 9.0 | 11.8 | |
| Sig. value (p) | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | – | – | – | <0.01 | <0.01 | <0.01 | <0.01 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsafadi, K.; Bi, S.; Bashir, B.; Sharifi, E.; Alsalman, A.; Kumar, A.; Shahid, S. High-Resolution Precipitation Modeling in Complex Terrains Using Hybrid Interpolation Techniques: Incorporating Physiographic and MODIS Cloud Cover Influences. Remote Sens. 2023, 15, 2435. https://doi.org/10.3390/rs15092435
Alsafadi K, Bi S, Bashir B, Sharifi E, Alsalman A, Kumar A, Shahid S. High-Resolution Precipitation Modeling in Complex Terrains Using Hybrid Interpolation Techniques: Incorporating Physiographic and MODIS Cloud Cover Influences. Remote Sensing. 2023; 15(9):2435. https://doi.org/10.3390/rs15092435
Chicago/Turabian StyleAlsafadi, Karam, Shuoben Bi, Bashar Bashir, Ehsan Sharifi, Abdullah Alsalman, Amit Kumar, and Shamsuddin Shahid. 2023. "High-Resolution Precipitation Modeling in Complex Terrains Using Hybrid Interpolation Techniques: Incorporating Physiographic and MODIS Cloud Cover Influences" Remote Sensing 15, no. 9: 2435. https://doi.org/10.3390/rs15092435
APA StyleAlsafadi, K., Bi, S., Bashir, B., Sharifi, E., Alsalman, A., Kumar, A., & Shahid, S. (2023). High-Resolution Precipitation Modeling in Complex Terrains Using Hybrid Interpolation Techniques: Incorporating Physiographic and MODIS Cloud Cover Influences. Remote Sensing, 15(9), 2435. https://doi.org/10.3390/rs15092435











