Development of a Machine Learning Forecast Model for Global Horizontal Irradiation Adapted to Tibet Based on Visible All-Sky Imaging
Abstract
1. Introduction
2. Data
2.1. General Information of the Study Area
2.2. Irradiance Data
2.3. Ground-Based Cloud Image Data
2.4. Data Set Settings
3. Methodology
3.1. Cloud Cover Estimation
3.1.1. Image Preprocessing
3.1.2. Cloud Detection
3.1.3. Characteristics of Cloud Cover in the Yangbajing Region
3.2. RF Prediction Model
3.2.1. Data Transformation and Feature Extraction
3.2.2. Parameter Tuning (Model Optimization)
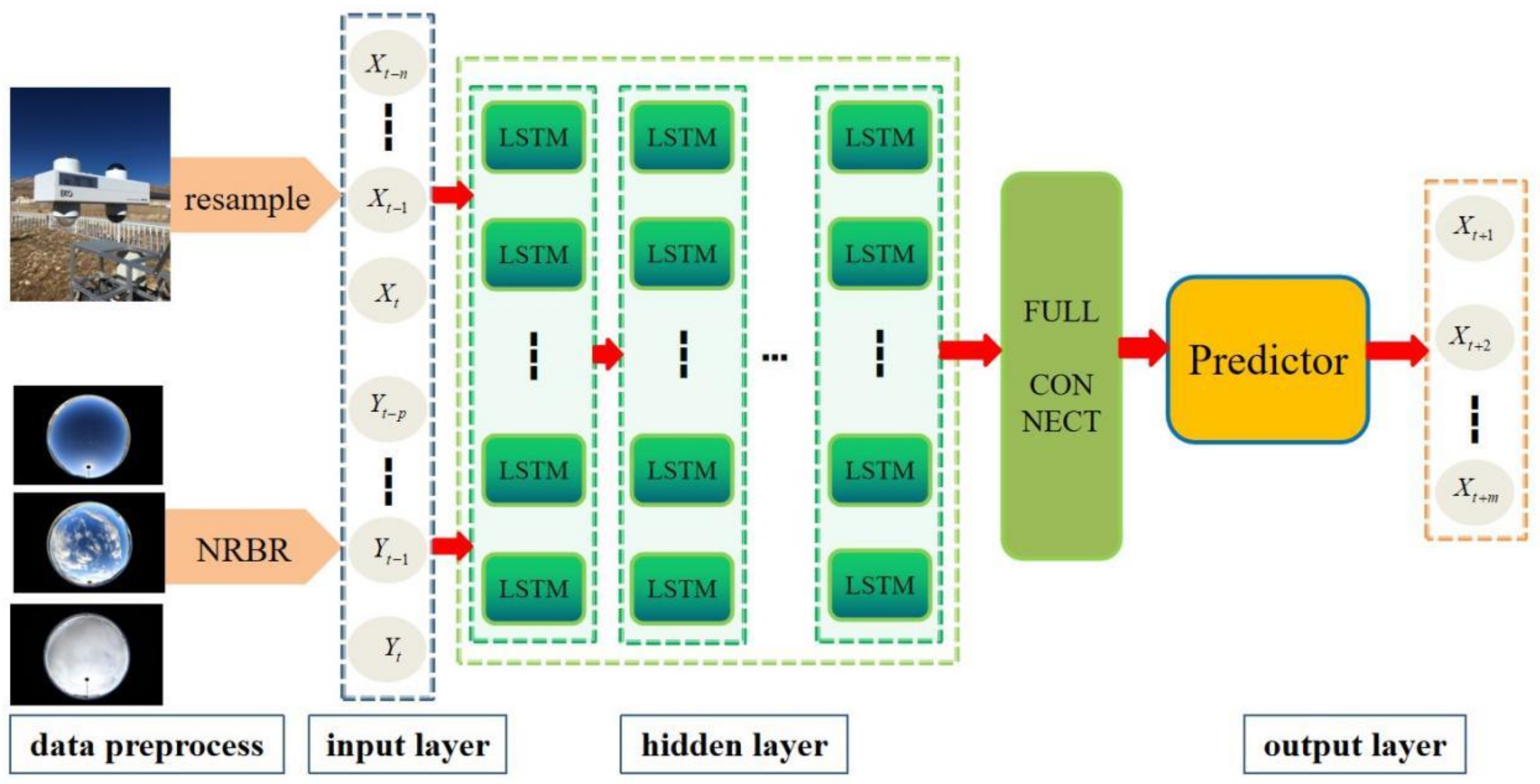
3.3. LSTM Prediction Model
3.4. Evaluation Index
4. Results
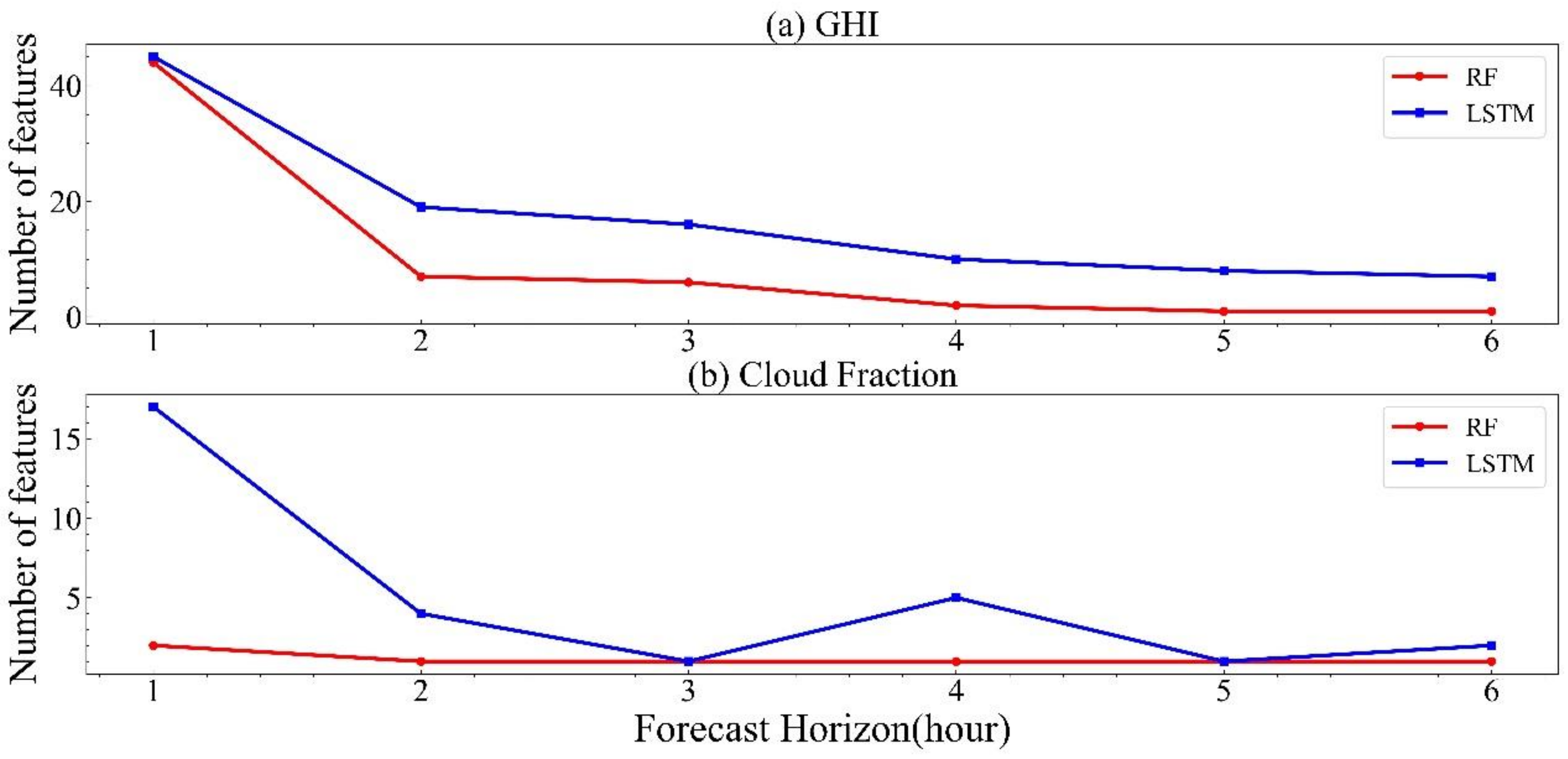
4.1. Model Input Feature Analysis
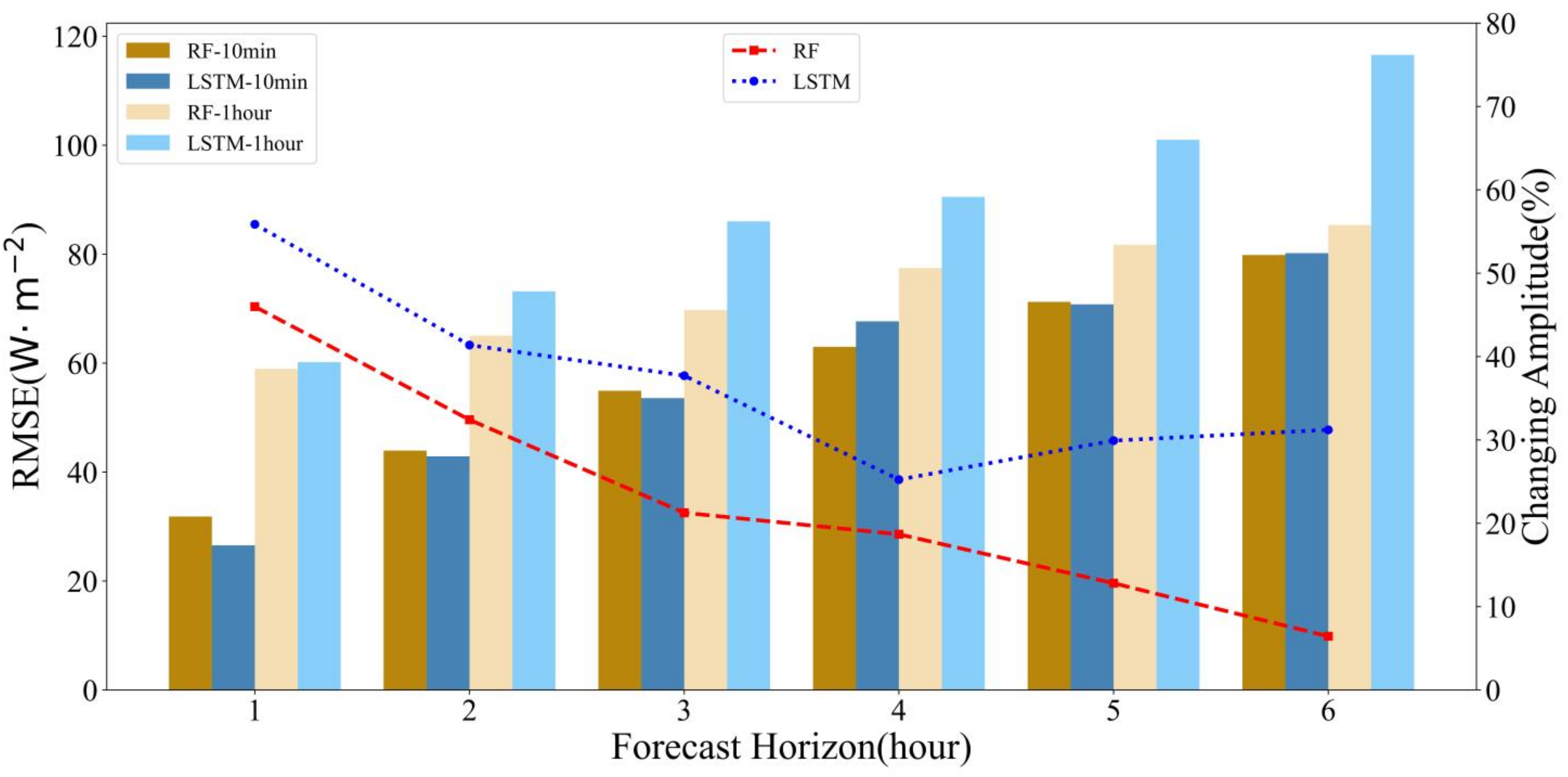
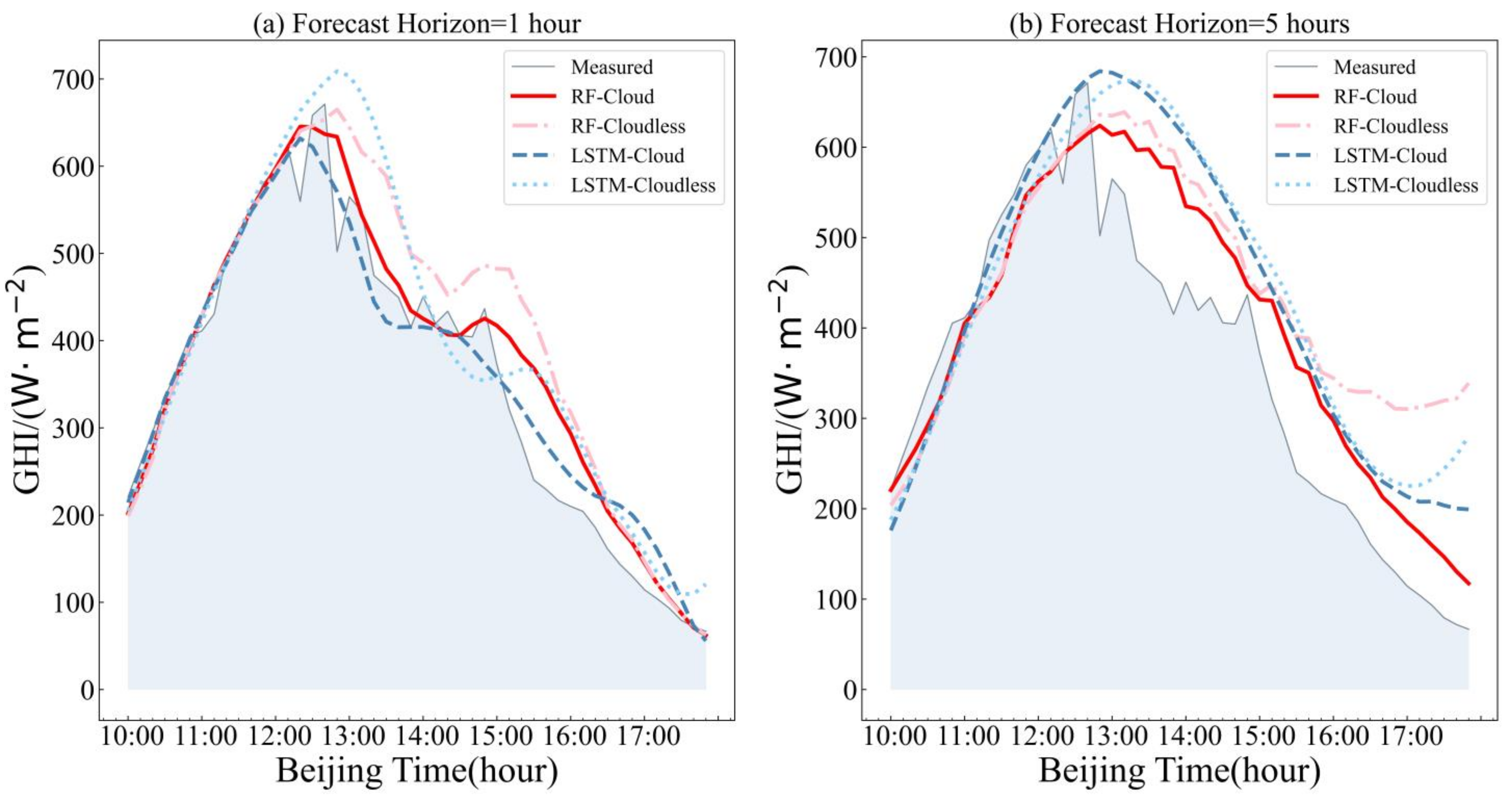
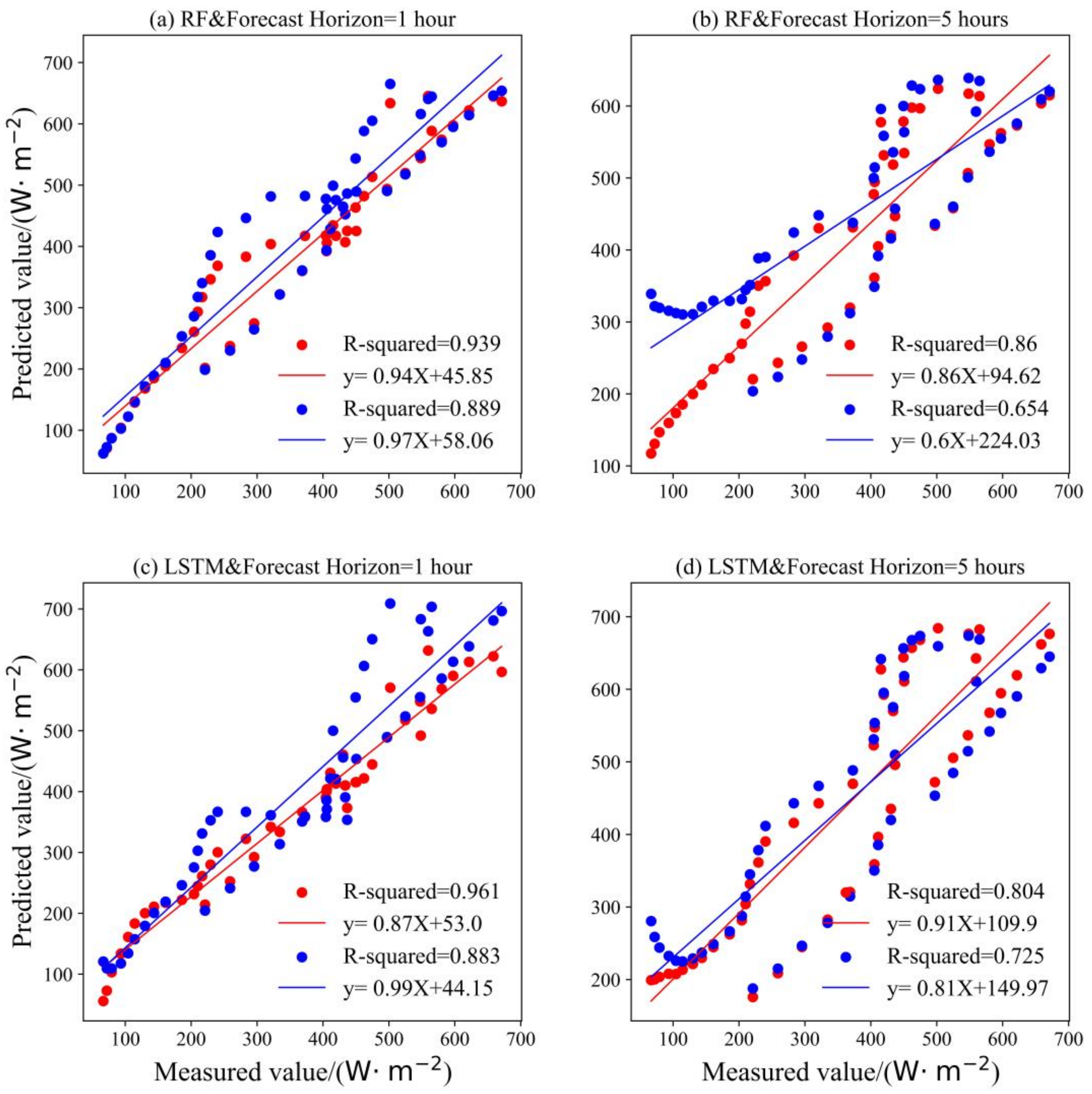
4.2. Analysis of the Forecast Horizon and Step Size
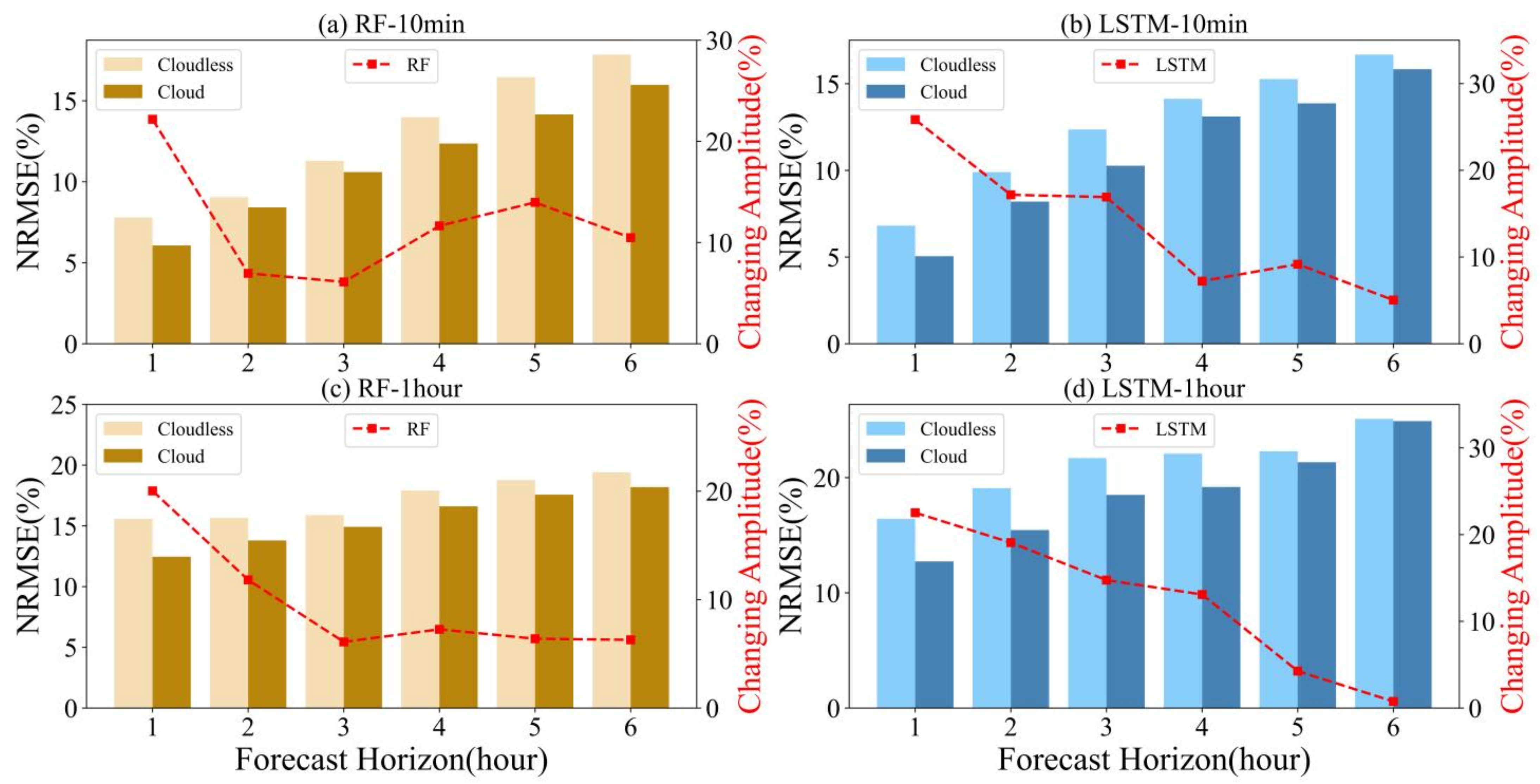
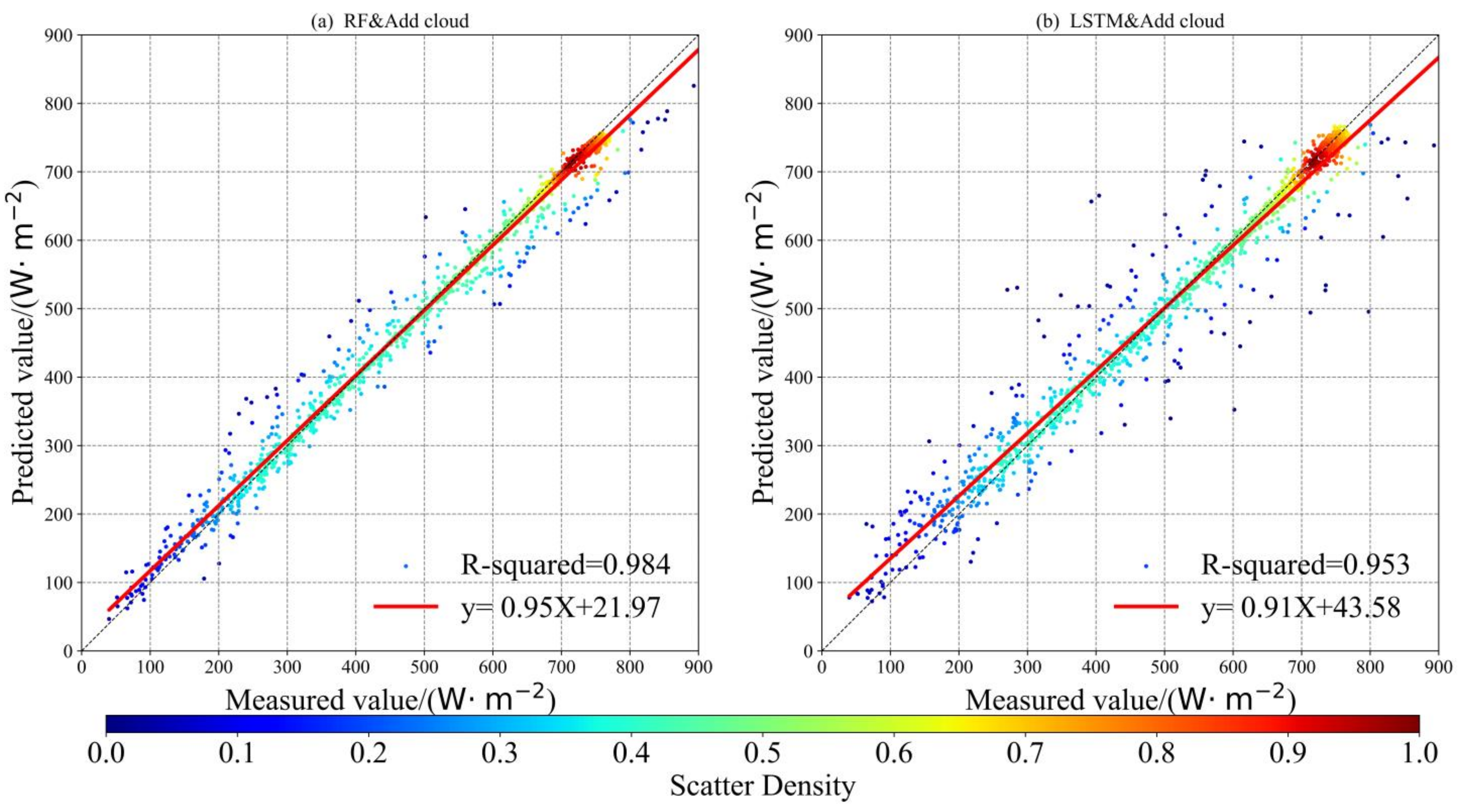
4.3. Influence of Cloud Cover on Model Accuracy
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Wang, M.; Wei, Z.; Sun, G. Estimation and validation of daily global solar radiation by day of the year-based models for different climates in China. Renew. Energy 2019, 135, 984–1003. [Google Scholar] [CrossRef]
- Urban, F.; Geall, S.; Wang, Y. Solar PV and solar water heaters in China: Different pathways to low carbon energy. Renew. Sustain. Energy Rev. 2016, 64, 531–542. [Google Scholar] [CrossRef]
- Murata, A.; Ohtake, H.; Oozeki, T. Modeling of uncertainty of solar irradiance forecasts on numerical weather predictions with the estimation of multiple confidence intervals. Renew. Energy 2018, 117, 193–201. [Google Scholar] [CrossRef]
- Yang, Z.; Mourshed, M.; Liu, K.; Xu, X.; Feng, S. A novel competitive swarm optimized RBF neural network model for short-term solar power generation forecasting. Neurocomputing 2020, 397, 415–421. [Google Scholar] [CrossRef]
- Yang, L.; Gao, X.; Li, Z.; Jia, D.; Jiang, J. Nowcasting of Surface Solar Irradiance Using FengYun-4 Satellite Observations over China. Remote Sens. 2019, 11, 1984. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Wang, F.; Zhen, Z.; Liu, C.; Mi, Z.; Hodge, B.; Shafie-khah, M.; Catalão, J.P.S. Image phase shift invariance based cloud motion displacement vector calculation method for ultra-short-term solar PV power forecasting. Energy Convers. Manag. 2018, 157, 123–135. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, G.; Li, D.; Zhou, J.; Li, L.; Li, L. Application and development of solar energy in building industry and its prospects in China. Energy Policy 2007, 35, 4121–4127. [Google Scholar] [CrossRef]
- Wild, M. Global dimming and brightening: A review. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, H.; Yang, S.; Chen, Q.; Zhou, X.; Shi, G.; Cheng, Y.; Wild, M. Potential Driving Factors on Surface Solar Radiation Trends over China in Recent Years. Remote Sens. 2021, 13, 704. [Google Scholar] [CrossRef]
- Yang, K.; Ding, B.; Qin, J.; Tang, W.; Lu, N.; Lin, C. Can aerosol loading explain the solar dimming over the Tibetan Plateau? Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent climate changes over the Tibetan Plateau and their impacts on energy and water cycle: A review. Glob. Planet. Chang. 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Fountoulakis, I.; Kosmopoulos, P.; Papachristopoulou, K.; Raptis, I.; Mamouri, R.; Nisantzi, A.; Gkikas, A.; Witthuhn, J.; Bley, S.; Moustaka, A.; et al. Effects of Aerosols and Clouds on the Levels of Surface Solar Radiation and Solar Energy in Cyprus. Remote Sens. 2021, 13, 2319. [Google Scholar] [CrossRef]
- Wu, H.; Ying, W. Benchmarking Machine Learning Algorithms for Instantaneous Net Surface Shortwave Radiation Retrieval Using Remote Sensing Data. Remote Sens. 2019, 11, 2520. [Google Scholar] [CrossRef]
- Sun, H.; Gui, D.; Yan, B.; Liu, Y.; Liao, W.; Zhu, Y.; Lu, C.; Zhao, N. Assessing the potential of random forest method for estimating solar radiation using air pollution index. Energy Convers. Manag. 2016, 119, 121–129. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Hou, N.; Zhang, X.; Zhang, W.; Wei, Y.; Jia, K.; Yao, Y.; Jiang, B.; Cheng, J. Estimation of Surface Downward Shortwave Radiation over China from Himawari-8 AHI Data Based on Random Forest. Remote Sens. 2020, 12, 181. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Peng, T.; Zhang, C.; Zhou, J.; Nazir, M.S. An integrated framework of Bi-directional long-short term memory (BiLSTM) based on sine cosine algorithm for hourly solar radiation forecasting. Energy 2021, 221, 119887. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Zhang, T.; Han, Y.; Zhou, X.; Xie, Y.; Yoo, S. Use of physics to improve solar forecast: Part II, machine learning and model interpretability. Sol. Energy 2022, 244, 362–378. [Google Scholar] [CrossRef]
- Yang, D.; Wang, W.; Xia, X. Related articles that may interest you. Adv. Atmos. Sci. 2022, 8, 1239–1251. [Google Scholar] [CrossRef]
- Qin, J.; Jiang, H.; Lu, N.; Yao, L.; Zhou, C. Enhancing solar PV output forecast by integrating ground and satellite observations with deep learning. Renew. Sustain. Energy Rev. 2022, 167, 112680. [Google Scholar] [CrossRef]
- Caldas, M.; Alonso-Suárez, R. Very short-term solar irradiance forecast using all-sky imaging and real-time irradiance measurements. Renew. Energy 2019, 143, 1643–1658. [Google Scholar] [CrossRef]
- Chu, Y.; Li, M.; Pedro, H.T.C.; Coimbra, C.F.M. Real-time prediction intervals for intra-hour DNI forecasts. Renew. Energy 2015, 83, 234–244. [Google Scholar] [CrossRef]
- King, J.C. Longwave atmospheric radiation over Antarctica. Antarct. Sci. 1996, 8, 105–109. [Google Scholar] [CrossRef]
- Long, C.N.; Sabburg, J.M.; Calbo, J.; Pages, D. Retrieving Cloud Characteristics from Ground-Based Daytime Color All-Sky Images. J. Atmos. Ocean. Technol. 2006, 23, 633–652. [Google Scholar] [CrossRef]
- Zhang, J.; Verschae, R.; Nobuhara, S.; Lalonde, J. Deep photovoltaic nowcasting. Sol. Energy 2018, 176, 267–276. [Google Scholar] [CrossRef]
- Jiang, J.; Lv, Q.; Gao, X. The Ultra-Short-Term Forecasting of Global Horizonal Irradiance Based on Total Sky Images. Remote Sens. 2020, 12, 3671. [Google Scholar] [CrossRef]
- Heinle, A.; Macke, A.; Srivastav, A. Automatic cloud classification of whole sky images. Atmos. Meas. Tech. 2010, 3, 557–567. [Google Scholar] [CrossRef]
- Li, Q.; Lu, W.; Yang, J. A Hybrid Thresholding Algorithm for Cloud Detection on Ground-Based Color Images. J. Atmos. Ocean. Technol. 2011, 28, 1286–1296. [Google Scholar] [CrossRef]
- Shields, J.; Karr, M.E.; Burden, A.; Johnson, R.W.; Hodgkiss, W.S. Continuing Support of Cloud Free Line of Sight Determination Including Whole Sky Imaging of Clouds; University of California: San Diego, CA, USA, 2007. [Google Scholar]
- Ghonima, M.S.; Urquhart, B.; Chow, C.W.; Shields, J.E.; Cazorla, A.; Kleissl, J. A method for cloud detection and opacity classification based on ground based sky imagery. Atmos. Meas. Tech. 2012, 5, 2881–2892. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Jang, J.; Sohn, E.; Park, K. Estimating Hourly Surface Solar Irradiance from GK2A/AMI Data Using Machine Learning Approach around Korea. Remote Sens. 2022, 14, 1840. [Google Scholar] [CrossRef]
- Azimi, R.; Ghayekhloo, M.; Ghofrani, M. A hybrid method based on a new clustering technique and multilayer perceptron neural networks for hourly solar radiation forecasting. Energy Convers. Manag. 2016, 118, 331–344. [Google Scholar] [CrossRef]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 8, 1735–1780. [Google Scholar] [CrossRef]
- Yu, L.; Qu, J.; Gao, F.; Tian, Y. A Novel Hierarchical Algorithm for Bearing Fault Diagnosis Based on Stacked LSTM. Shock Vib. 2019, 2019, 2756284. [Google Scholar] [CrossRef]
- Srivastava, S.; Lessmann, S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Sol. Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Gneiting, T. Making and Evaluating Point Forecasts. J. Am. Stat. Assoc. 2011, 494, 746–762. [Google Scholar] [CrossRef]
- Chu, Y.; Urquhart, B.; Gohari, S.M.I.; Pedro, H.T.C.; Kleissl, J.; Coimbra, C.F.M. Short-term reforecasting of power output from a 48 MWe solar PV plant. Sol. Energy 2015, 112, 68–77. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Yang, D.; Jirutitijaroen, P.; Walsh, W.M. Hourly solar irradiance time series forecasting using cloud cover index. Sol. Energy. 2012, 86, 3531–3543. [Google Scholar] [CrossRef]
- Blaga, R. The impact of temporal smoothing on the accuracy of separation models. Sol. Energy 2019, 191, 371–381. [Google Scholar] [CrossRef]
- Gallucci, D.; Romano, F.; Cimini, D.; Di Paola, F.; Gentile, S.; Larosa, S.; Nilo, S.T.; Ricciardelli, E.; Ripepi, E.; Viggiano, M.; et al. Improvement of Hourly Surface Solar Irradiance Estimation Using MSG Rapid Scanning Service. Remote Sens. 2019, 11, 66. [Google Scholar] [CrossRef]
- Pyrina, M.; Hatzianastassiou, N.; Matsoukas, C.; Fotiadi, A.; Papadimas, C.D.; Pavlakis, K.G.; Vardavas, I. Cloud effects on the solar and thermal radiation budgets of the Mediterranean basin. Atmos. Res. 2015, 152, 14–28. [Google Scholar] [CrossRef]


| [0, 0.1) | [0.1, 0.2) | [0.2, 0.3) | [0.3, 0.4) | [0.4, 0.5) | [0.5, 0.6) | [0.6, 0.7) | [0.7, 0.8) | [0.8, 0.9) | [0.9, 1] | |
|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 3885 | 1510 | 975 | 774 | 730 | 672 | 627 | 799 | 931 | 5872 |
| Proportion (%) | 23.16 | 9.00 | 5.81 | 4.61 | 4.35 | 4.01 | 3.74 | 4.76 | 5.55 | 35.00 |
| January | February | March | April | May | June | July | August | September | October | November | December | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean value | 0.56 | 0.49 | 0.64 | 0.72 | 0.79 | 0.66 | 0.78 | 0.63 | 0.55 | 0.12 | 0.29 | 0.28 |
| Standard deviation | 0.41 | 0.39 | 0.37 | 0.32 | 0.31 | 0.31 | 0.28 | 0.36 | 0.36 | 0.19 | 0.39 | 0.38 |
| Forecast Horizon | 1 h | 2 h | 3 h | 4 h | 5 h | 6 h | |
|---|---|---|---|---|---|---|---|
| GHI | RF | 44 | 7 | 6 | 2 | 1 | 1 |
| LSTM | 45 | 19 | 16 | 10 | 8 | 7 | |
| Cloud fraction | RF | 2 | 1 | 1 | 1 | 1 | 1 |
| LSTM | 17 | 4 | 1 | 5 | 1 | 2 |
| RF | LSTM | |||||
|---|---|---|---|---|---|---|
| Step Size = 1 h (W/m2) | Step Size = 10 min (W/m2) | Amplitude Change (%) | Step Size = 1 h (W/m2) | Step Size = 10 min (W/m2) | Amplitude Change (%) | |
| 1 h | 58.95 | 31.84 | 45.99 | 60.18 | 26.56 | 55.87 |
| 2 h | 65.03 | 43.95 | 32.42 | 73.17 | 42.89 | 41.38 |
| 3 h | 69.76 | 54.93 | 21.26 | 86.02 | 53.58 | 37.71 |
| 4 h | 77.46 | 62.99 | 18.68 | 90.53 | 67.68 | 25.24 |
| 5 h | 81.72 | 71.25 | 12.81 | 101.01 | 70.79 | 29.92 |
| 6 h | 85.35 | 79.85 | 6.44 | 116.58 | 80.19 | 31.21 |
| Step Size = 10 min | Step Size = 1 h | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RF | LSTM | RF | LSTM | |||||||||
| No Cloud (%) | Add Cloud (%) | Amplitude Change (%) | No Cloud (%) | Add Cloud(%) | Amplitude Change (%) | No Cloud (%) | Add Cloud (%) | Amplitude Change (%) | No Cloud (%) | Add Cloud (%) | Amplitude Change (%) | |
| 1 h | 7.80 | 6.07 | 22.18 | 6.81 | 5.05 | 25.84 | 15.58 | 12.46 | 20.03 | 16.43 | 12.73 | 22.52 |
| 2 h | 9.05 | 8.42 | 6.96 | 9.90 | 8.20 | 17.17 | 15.65 | 13.80 | 11.82 | 19.09 | 15.45 | 19.07 |
| 3 h | 11.29 | 10.60 | 6.11 | 12.36 | 10.27 | 16.91 | 15.89 | 14.92 | 6.10 | 21.70 | 18.50 | 14.75 |
| 4 h | 13.99 | 12.36 | 11.65 | 14.13 | 13.11 | 7.22 | 17.91 | 16.61 | 7.26 | 22.08 | 19.19 | 13.09 |
| 5 h | 16.46 | 14.16 | 13.97 | 15.27 | 13.87 | 9.17 | 18.77 | 17.57 | 6.39 | 22.29 | 21.34 | 4.26 |
| 6 h | 17.85 | 15.98 | 10.48 | 16.68 | 15.84 | 5.04 | 19.41 | 18.19 | 6.29 | 25.10 | 24.91 | 0.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Chen, T.; Ciren, N.; Wang, D.; Meng, H.; Li, M.; Zhao, W.; Luo, J.; Hu, X.; Jia, S.; et al. Development of a Machine Learning Forecast Model for Global Horizontal Irradiation Adapted to Tibet Based on Visible All-Sky Imaging. Remote Sens. 2023, 15, 2340. https://doi.org/10.3390/rs15092340
Wu L, Chen T, Ciren N, Wang D, Meng H, Li M, Zhao W, Luo J, Hu X, Jia S, et al. Development of a Machine Learning Forecast Model for Global Horizontal Irradiation Adapted to Tibet Based on Visible All-Sky Imaging. Remote Sensing. 2023; 15(9):2340. https://doi.org/10.3390/rs15092340
Chicago/Turabian StyleWu, Lingxiao, Tianlu Chen, Nima Ciren, Dui Wang, Huimei Meng, Ming Li, Wei Zhao, Jingxuan Luo, Xiaoru Hu, Shengjie Jia, and et al. 2023. "Development of a Machine Learning Forecast Model for Global Horizontal Irradiation Adapted to Tibet Based on Visible All-Sky Imaging" Remote Sensing 15, no. 9: 2340. https://doi.org/10.3390/rs15092340
APA StyleWu, L., Chen, T., Ciren, N., Wang, D., Meng, H., Li, M., Zhao, W., Luo, J., Hu, X., Jia, S., Liao, L., Pan, Y., & Wang, Y. (2023). Development of a Machine Learning Forecast Model for Global Horizontal Irradiation Adapted to Tibet Based on Visible All-Sky Imaging. Remote Sensing, 15(9), 2340. https://doi.org/10.3390/rs15092340






