Improving Solar Radiation Nowcasts by Blending Data-Driven, Satellite-Images-Based and All-Sky-Imagers-Based Models Using Machine Learning Techniques
Abstract
1. Introduction
1.1. Importance of Solar Radiation Nowcasting
1.2. Nowcasting Solar Radiation Methods
1.3. Models Blending
1.4. Aim of This Paper
2. Dataset and Models Input Description
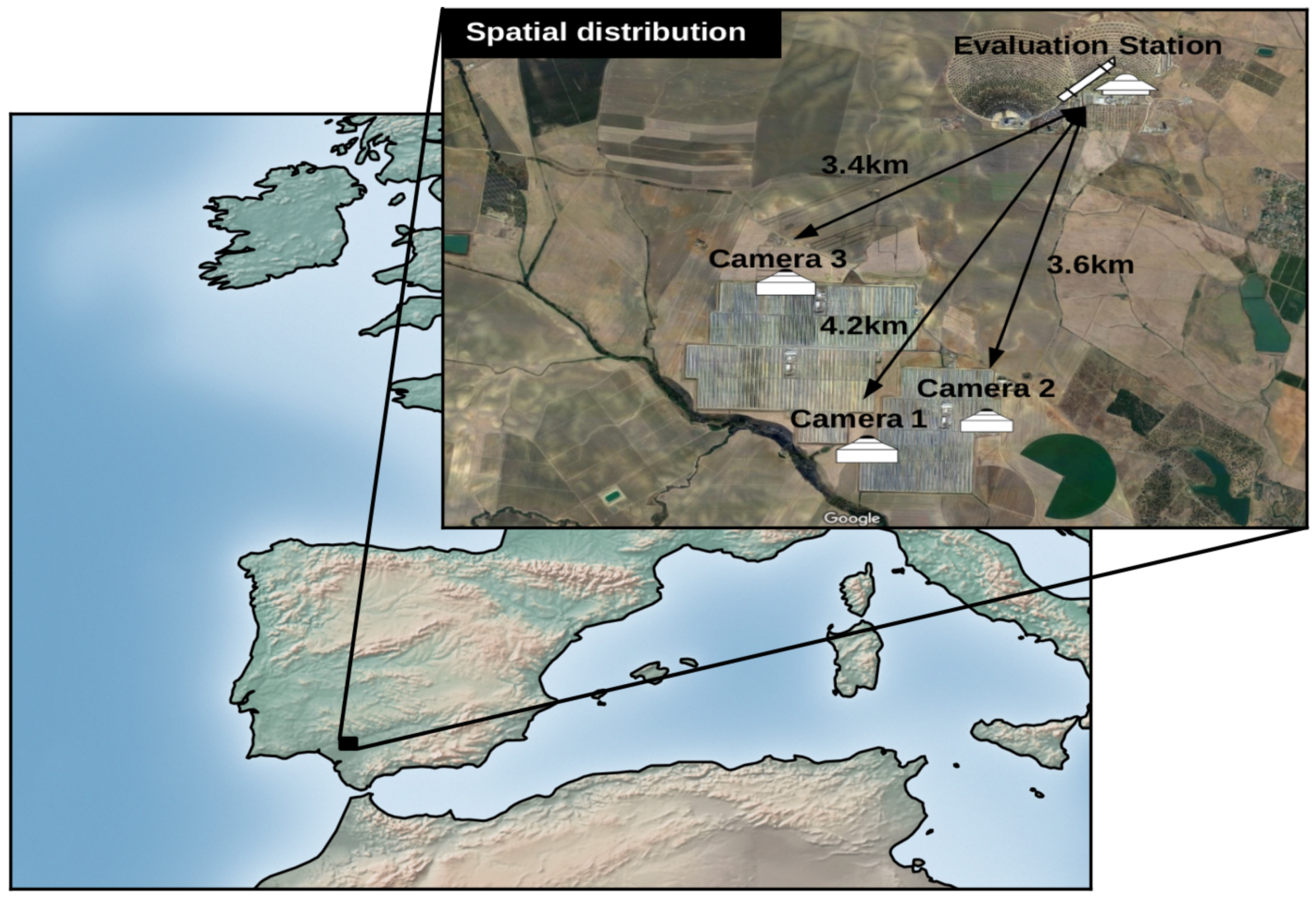
2.1. Dataset and Study Region
2.2. Models Input Description
3. Methods
3.1. Horizon and General Approaches
3.2. Machine Learning Algorithms
3.3. Model Blending Experiments
3.4. Evaluation Procedure
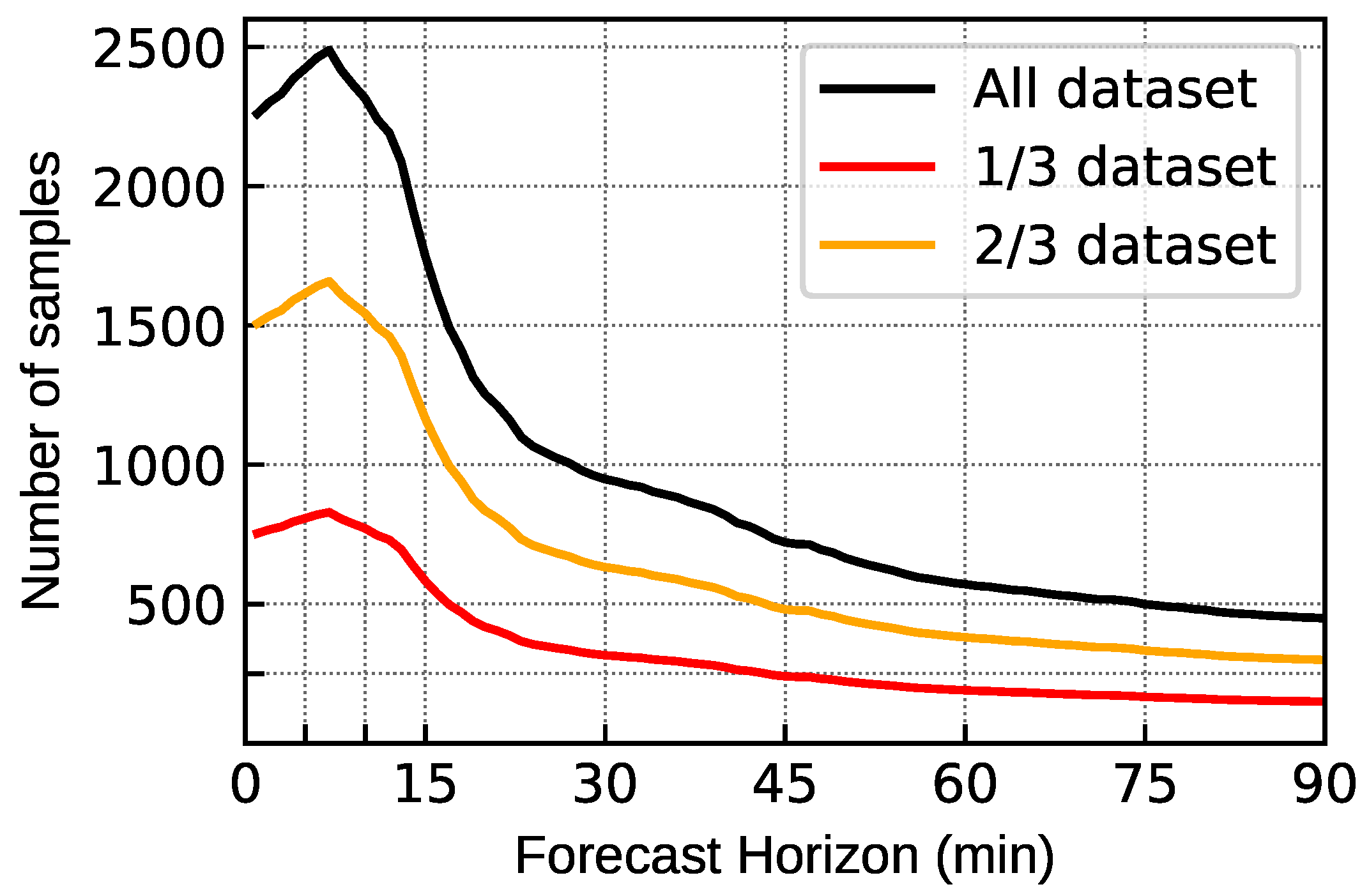
3.4.1. Training and Evaluation Datasets
3.4.2. Evaluation Metrics
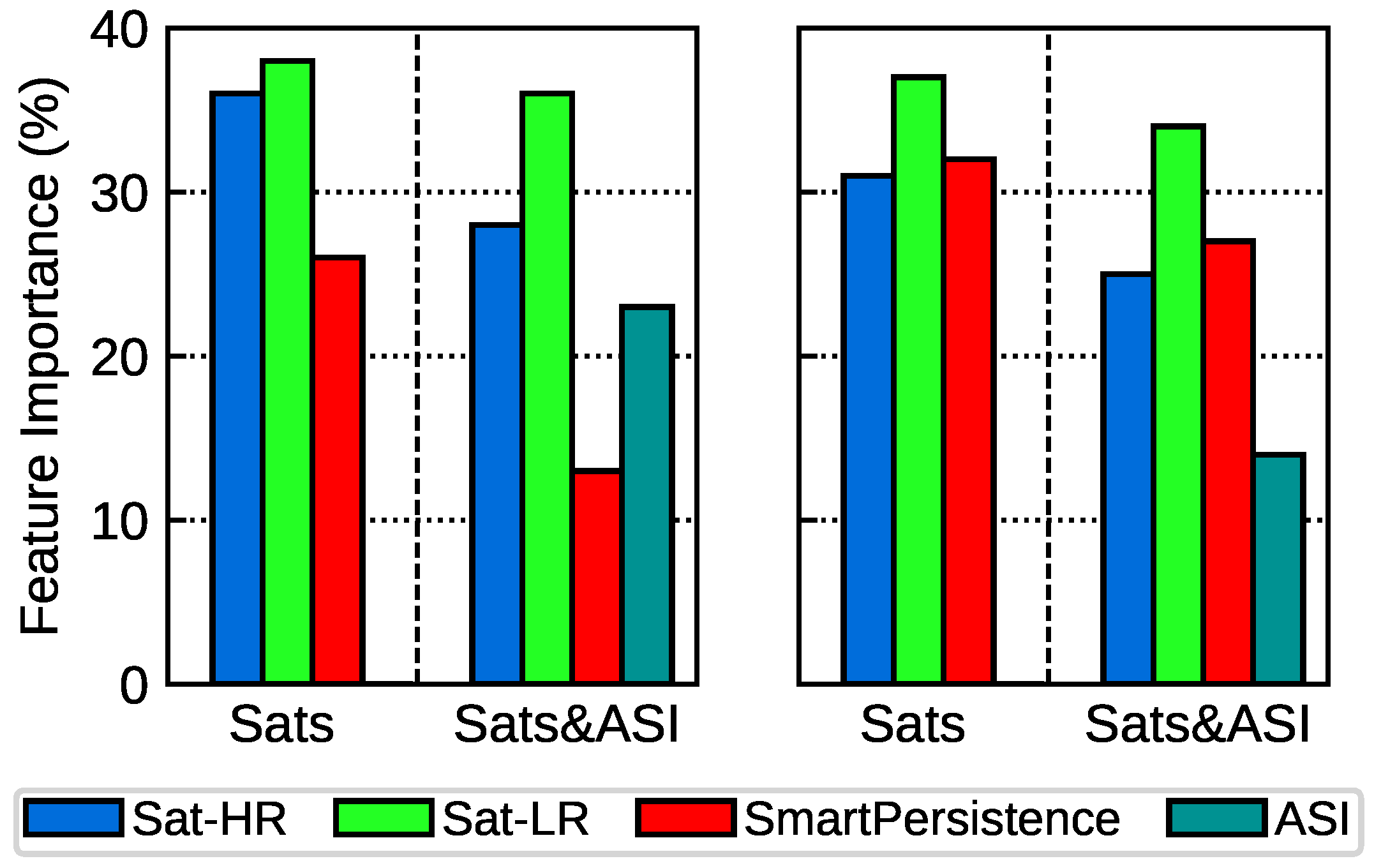
3.4.3. Feature Importance
4. Results and Discussion
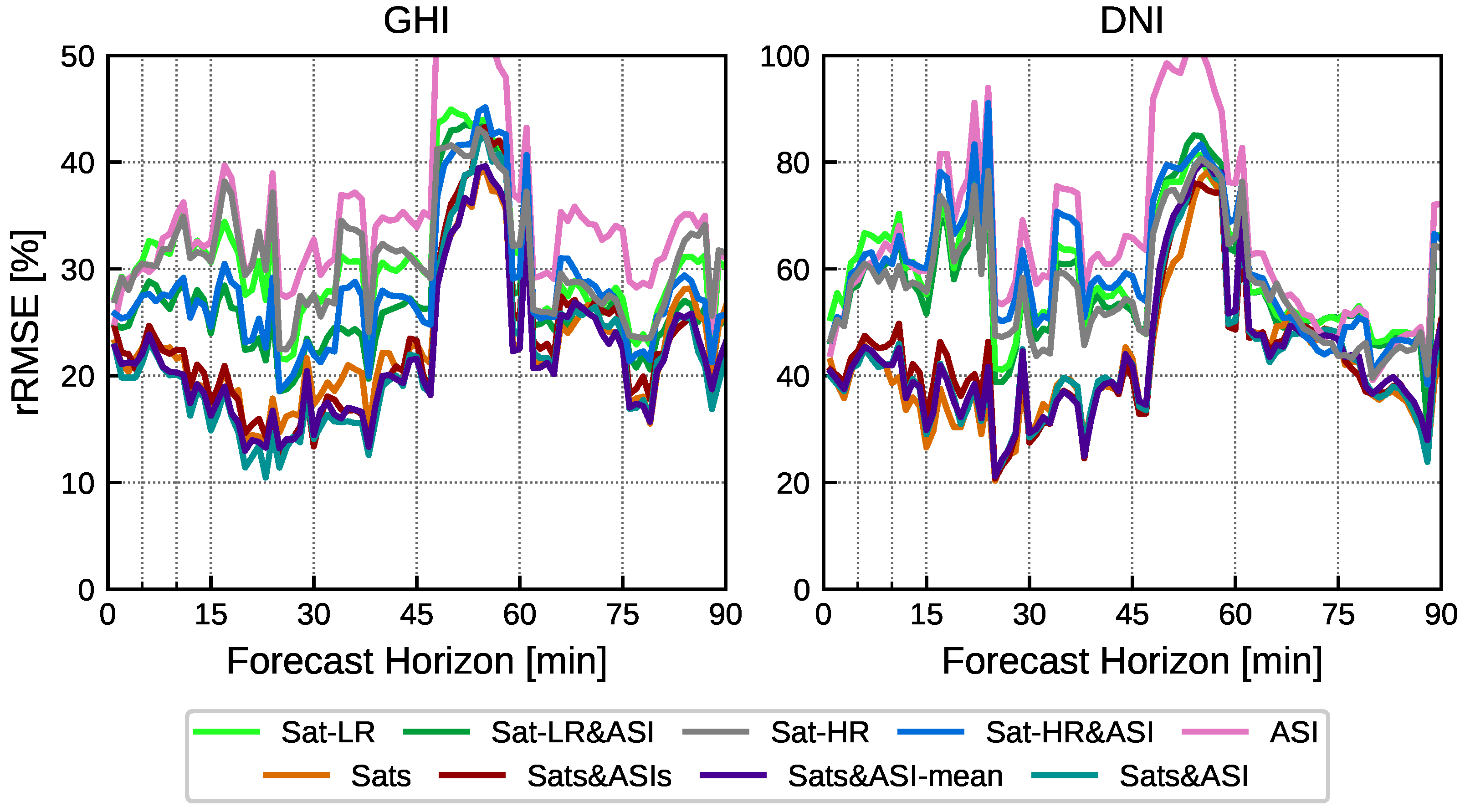
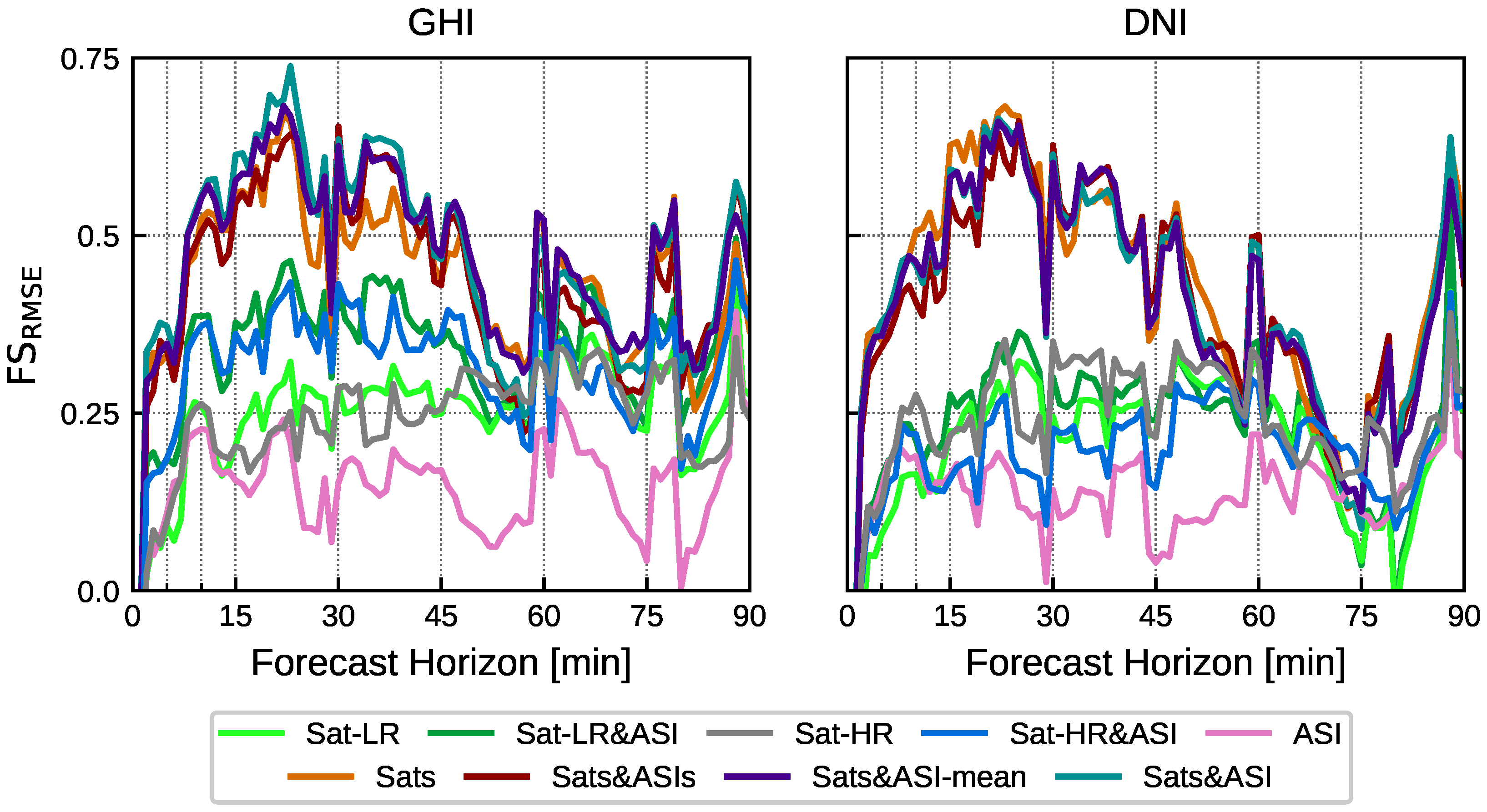
4.1. Assessment of Blending Approaches And Models
4.2. Assessment of the Importance of the Models Inputs
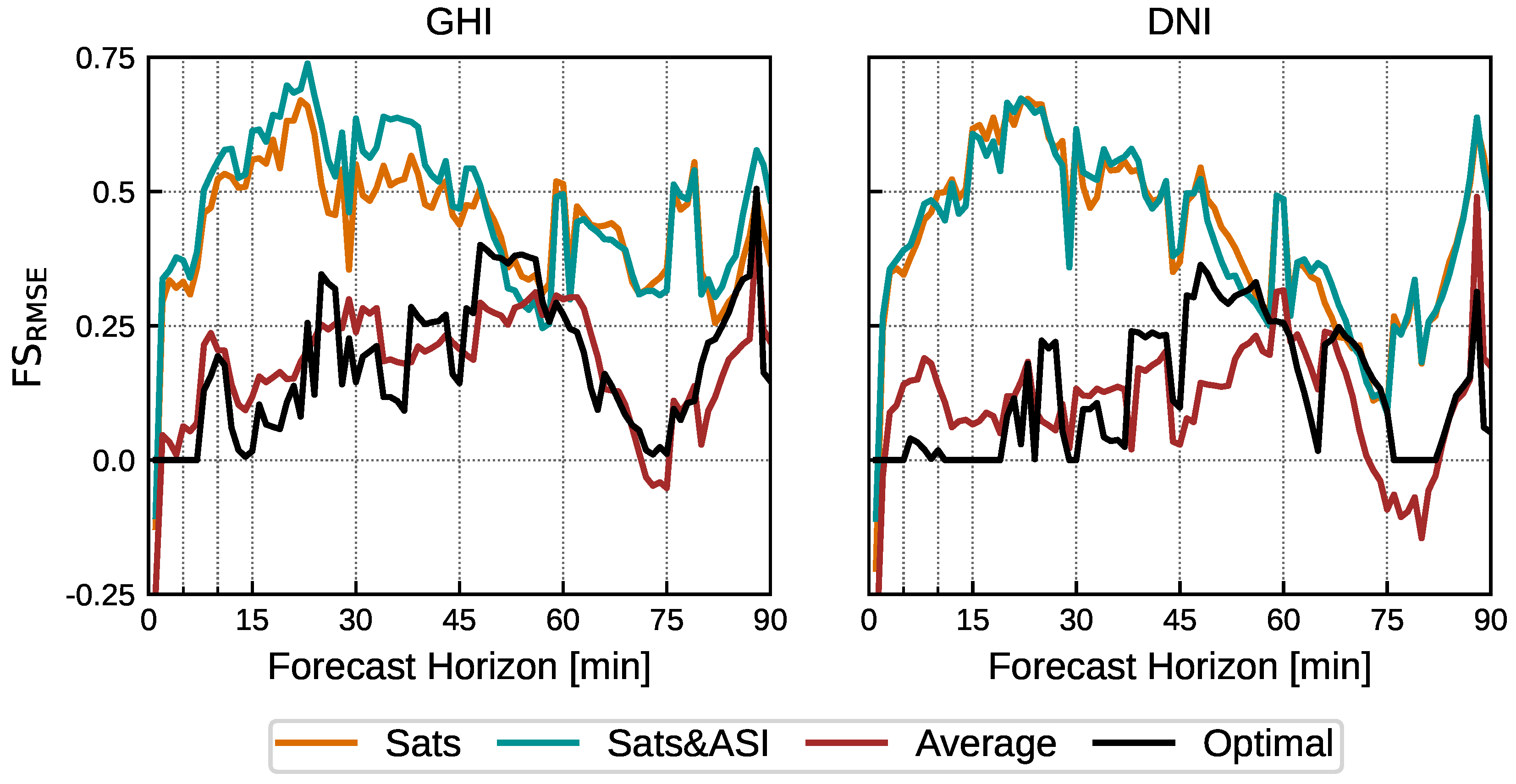
4.3. Forecasting Horizon Dependency
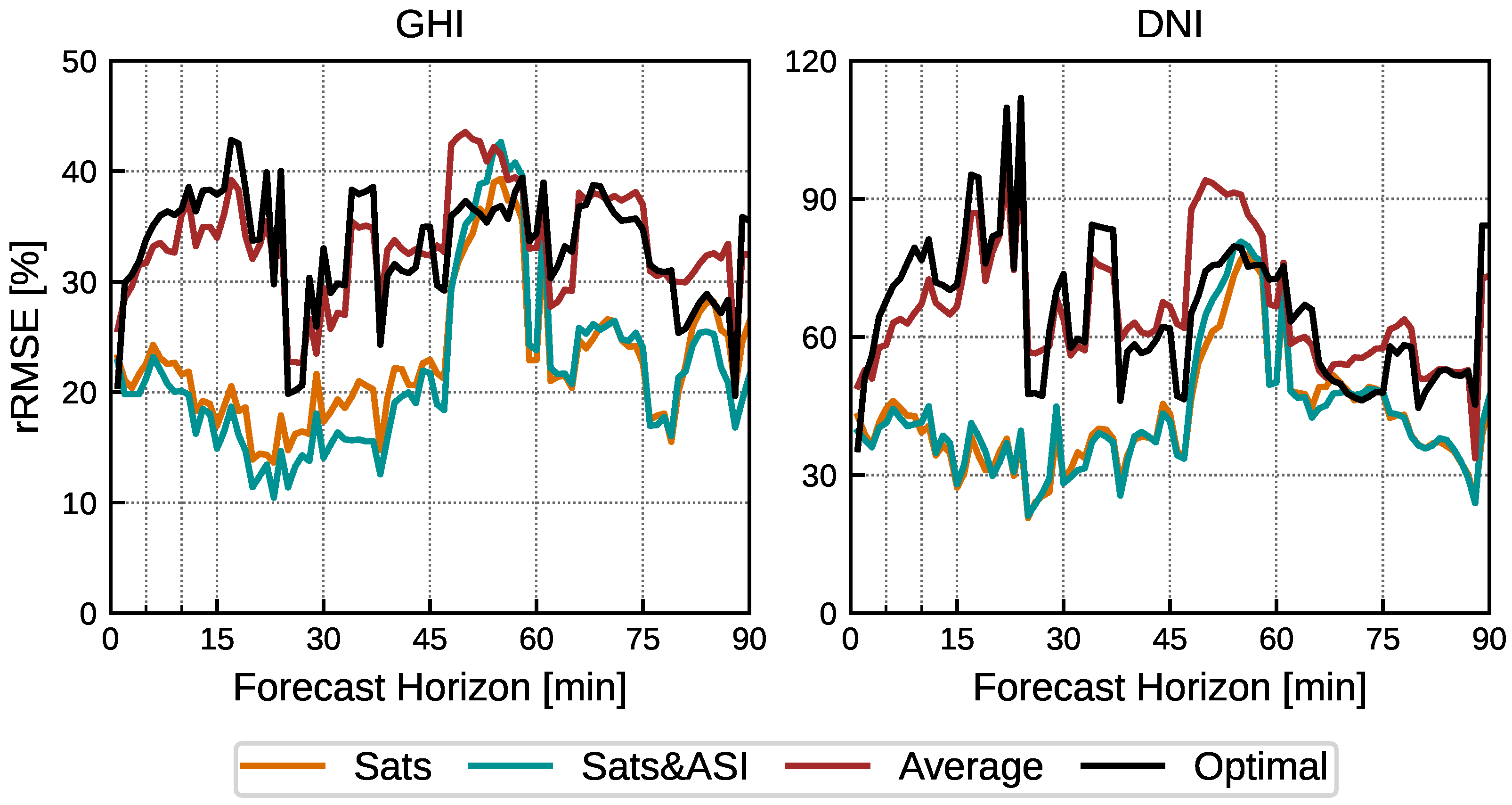
4.4. Model Blending Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Horizon and General Approaches
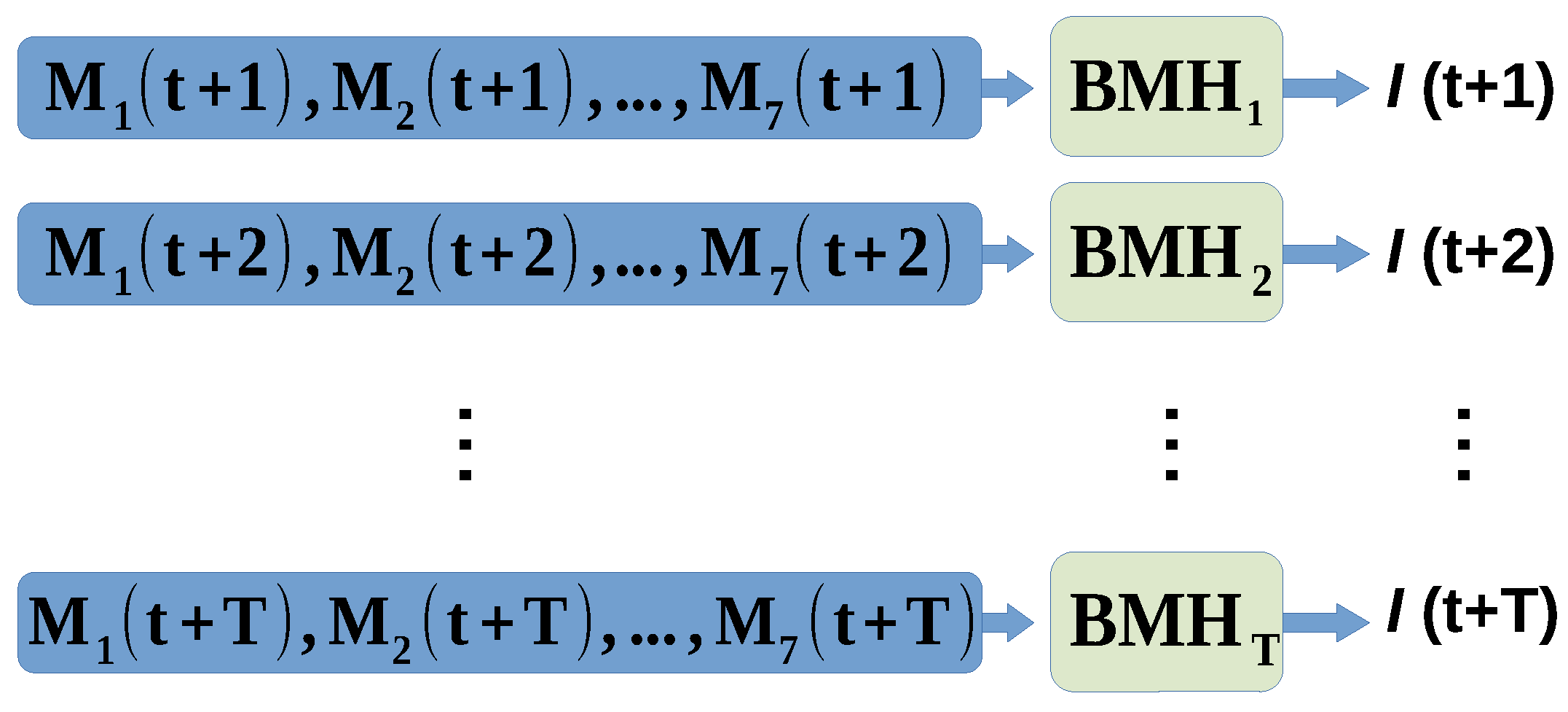
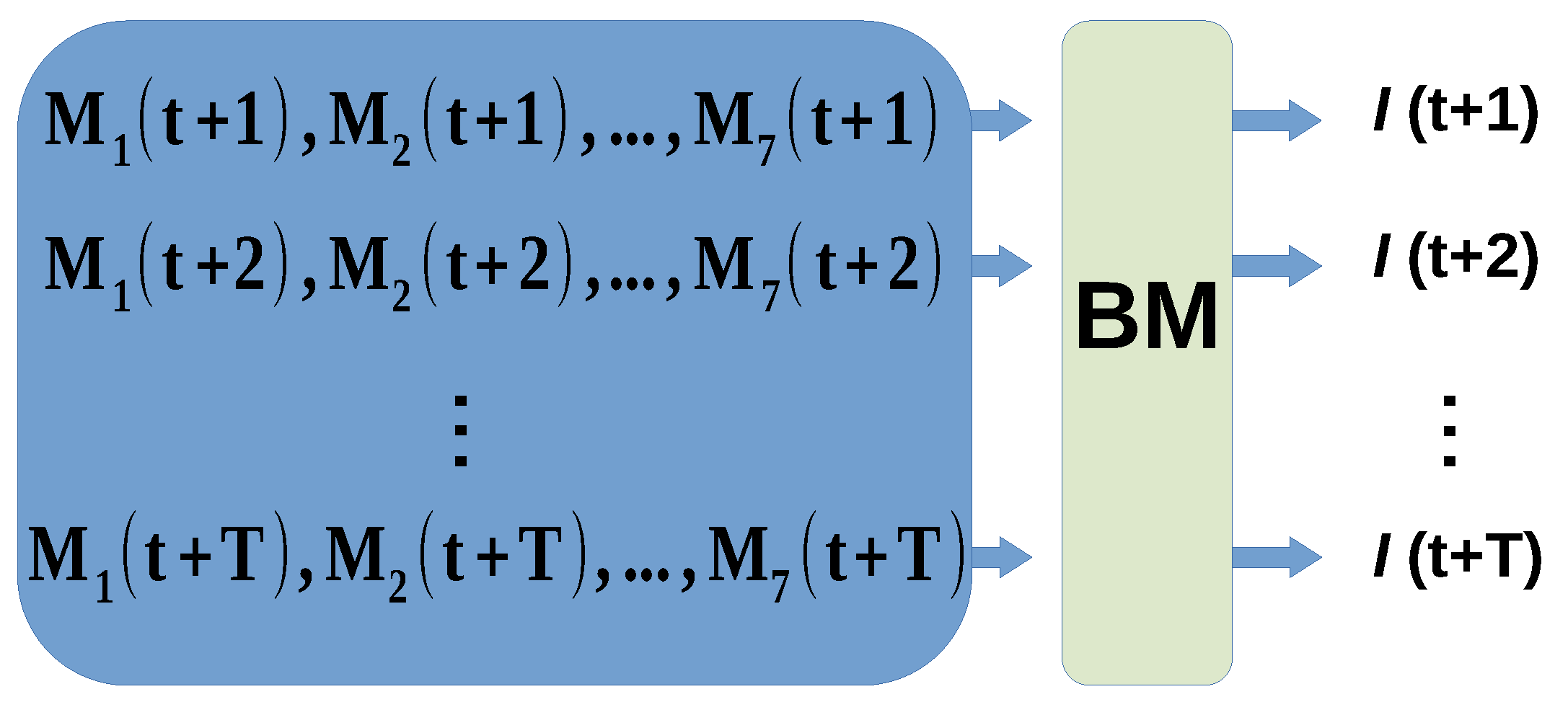
Appendix B. Linear and RF algorithms
- The number of trees N was sampled from a uniform distribution between 50 and 5000 trees.
- The size of the random feature subset m was sampled out of two values, and , as these two values are commonly used in the literature.
- The maximum depth was sampled from a uniform distribution between 5 and 50.
- The minimum number of samples was in the range of 2–20.

References
- Murdock, H.E.; Gibb, D.; Andre, T.; Sawin, J.L.; Brown, A.; Ranalder, L.; Collier, U.; Dent, C.; Epp, B.; Hareesh Kumar, C.; et al. Renewables 2021-Global Status Report. 2021. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2021_Full_Report.pdf (accessed on 2 February 2023).
- Renné, D.S. Emerging meteorological requirements to support high penetrations of variable renewable energy sources: Solar energy. In Weather Matters for Energy; Springer: Berlin/Heidelberg, Germany, 2014; pp. 257–273. [Google Scholar]
- Haupt, S.E. Short-range forecasting for energy. In Weather & Climate Services for the Energy Industry; Palgrave Macmillan: Cham, Switzerland, 2018; pp. 97–107. [Google Scholar]
- Yang, D.; Wang, W.; Gueymard, C.A.; Hong, T.; Kleissl, J.; Huang, J.; Perez, M.J.; Perez, R.; Bright, J.M.; Xia, X.; et al. A review of solar forecasting, its dependence on atmospheric sciences and implications for grid integration: Towards carbon neutrality. Renew. Sustain. Energy Rev. 2022, 161, 112348. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Inman, R.H.; Pedro, H.T.; Coimbra, C.F. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.; Coimbra, C.F. History and trends in solar irradiance and PV power forecasting: A preliminary assessment and review using text mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Samu, R.; Calais, M.; Shafiullah, G.; Moghbel, M.; Shoeb, M.A.; Nouri, B.; Blum, N. Applications for solar irradiance nowcasting in the control of microgrids: A review. Renew. Sustain. Energy Rev. 2021, 147, 111187. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer energy trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- Agoua, X.G.; Girard, R.; Kariniotakis, G. Short-term spatio-temporal forecasting of photovoltaic power production. IEEE Trans. Sustain. Energy 2017, 9, 538–546. [Google Scholar] [CrossRef]
- Heng, J.; Wang, J.; Xiao, L.; Lu, H. Research and application of a combined model based on frequent pattern growth algorithm and multi-objective optimization for solar radiation forecasting. Appl. Energy 2017, 208, 845–866. [Google Scholar] [CrossRef]
- Urquhart, B.; Ghonima, M.; Nguyen, D.A.; Kurtz, B.; Chow, C.W.; Kleissl, J. Chapter 9—Sky-Imaging Systems for Short-Term Forecasting. In Solar Energy Forecasting and Resource Assessment; Kleissl, J., Ed.; Academic Press: Boston, MA, USA, 2013; pp. 195–232. [Google Scholar] [CrossRef]
- Kazantzidis, A.; Tzoumanikas, P.; Blanc, P.; Massip, P.; Wilbert, S.; Ramirez-Santigosa, L. 5-Short-term forecasting based on all-sky cameras. In Renewable Energy Forecasting; Kariniotakis, G., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Shaxton, UK, 2017; pp. 153–178. [Google Scholar] [CrossRef]
- Rodríguez-Benítez, F.J.; López-Cuesta, M.; Arbizu-Barrena, C.; Fernández-León, M.M.; Pamos-Ureña, M.Á.; Tovar-Pescador, J.; Santos-Alamillos, F.J.; Pozo-Vázquez, D. Assessment of new solar radiation nowcasting methods based on sky-camera and satellite imagery. Appl. Energy 2021, 292, 116838. [Google Scholar] [CrossRef]
- Peng, Z.; Yu, D.; Huang, D.; Heiser, J.; Yoo, S.; Kalb, P. 3D cloud detection and tracking system for solar forecast using multiple sky imagers. Sol. Energy 2015, 118, 496–519. [Google Scholar] [CrossRef]
- Schmidt, T.; Kalisch, J.; Lorenz, E.; Heinemann, D. Evaluating the spatio-temporal performance of sky-imager-based solar irradiance analysis and forecasts. Atmos. Chem. Phys 2016, 16, 3399–3412. [Google Scholar] [CrossRef]
- Nouri, B.; Wilbert, S.; Kuhn, P.; Hanrieder, N.; Schroedter-Homscheidt, M.; Kazantzidis, A.; Zarzalejo, L.; Blanc, P.; Kumar, S.; Goswami, N.; et al. Real-Time Uncertainty Specification of All Sky Imager Derived Irradiance Nowcasts. Remote Sens. 2019, 11, 1059. [Google Scholar] [CrossRef]
- Dittmann, A.; Holland, N.; Lorenz, E. A new sky imager based global irradiance forecasting model with analyses of cirrus situations. Meteorol. Z. 2021, 101–113. [Google Scholar] [CrossRef]
- Fernández-León, M.; Pacheco, G.; Bolinaga, B.; Campa, L.; Lara-Fanego, V.; Valenzuela, J.M. Solar thermal energy predictability for the grid (STEP4Grid). In Proceedings of the AIP Conference Proceedings, Cape Town, South Africa, 13–16 October 2016; AIP Publishing LLC: Melville, NY, USA, 2016; Volume 1734, p. 080001. [Google Scholar]
- Nouri, B.; Noureldin, K.; Schlichting, T.; Wilbert, S.; Hirsch, T.; Schroedter-Homscheidt, M.; Kuhn, P.; Kazantzidis, A.; Zarzalejo, L.; Blanc, P.; et al. Optimization of parabolic trough power plant operations in variable irradiance conditions using all sky imagers. Sol. Energy 2020, 198, 434–453. [Google Scholar] [CrossRef]
- Schmidt, T.; Calais, M.; Roy, E.; Burton, A.; Heinemann, D.; Kilper, T.; Carter, C. Short-term solar forecasting based on sky images to enable higher PV generation in remote electricity networks. Renew. Energy Environ. Sustain. 2017, 2, 23. [Google Scholar] [CrossRef]
- Anagnostos, D.; Schmidt, T.; Cavadias, S.; Soudris, D.; Poortmans, J.; Catthoor, F. A method for detailed, short-term energy yield forecasting of photovoltaic installations. Renew. Energy 2019, 130, 122–129. [Google Scholar] [CrossRef]
- Lorenz, E.; Heinemann, D. Prediction of Solar Irradiance and Photovoltaic Power. In Comprehensive Renewable Energy; Sayigh, A., Ed.; Elsevier: Oxford, UK, 2012; pp. 239–292. [Google Scholar] [CrossRef]
- Blanc, P.; Remund, J.; Vallance, L. Short-term solar power forecasting based on satellite images. In Renewable Energy Forecasting; Elsevier: Amsterdam, The Netherlands, 2017; pp. 179–198. [Google Scholar]
- Ramírez, L.; Vindel, J. Forecasting and nowcasting of DNI for concentrating solar thermal systems. In Advances in Concentrating Solar Thermal Research and Technology; Blanco, M.J., Santigosa, L.R., Eds.; Woodhead Publishing Series in Energy; Woodhead Publishing: Shaxton, UK, 2017; pp. 293–310. [Google Scholar] [CrossRef]
- Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Huertas-Tato, J.; Aler-Mur, R.; Galván-León, I.; Pozo-Vázquez, D. A short-term solar radiation forecasting system for the Iberian Peninsula. Part 1: Models description and performance assessment. Sol. Energy 2020, 195, 396–412. [Google Scholar] [CrossRef]
- Holmlund, K.; Grandell, J.; Schmetz, J.; Stuhlmann, R.; Bojkov, B.; Munro, R.; Lekouara, M.; Coppens, D.; Viticchie, B.; August, T.; et al. Meteosat Third Generation (MTG): Continuation and innovation of observations from geostationary orbit. Bull. Am. Meteorol. Soc. 2021, 102, 1–71. [Google Scholar] [CrossRef]
- Prasad, A.A.; Kay, M. Prediction of Solar Power Using Near-Real Time Satellite Data. Energies 2021, 14, 5865. [Google Scholar] [CrossRef]
- Antonanzas, J.; Urraca, R.; de Pison, F.M.; Antonanzas, F. Optimal solar tracking strategy to increase irradiance in the plane of array under cloudy conditions: A study across Europe. Sol. Energy 2018, 163, 122–130. [Google Scholar] [CrossRef]
- Dersch, J.; Schroedter-Homscheidt, M.; Gairaa, K.; Hanrieder, N.; Landelius, T.; Lindskog, M.; Mueller, S.C.; Santigosa, L.R.; Sirch, T.; Wilbert, S. Impact of DNI nowcasting on annual revenues of CSP plants for a time of delivery based feed in tariff. Meteorol. Z. 2019, 28, 235–253. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Polo, J.; Ballestrín, J.; Batlles, F.; Portillo, C. Impact of DNI forecasting on CSP tower plant power production. Renew. Energy 2019, 138, 368–377. [Google Scholar] [CrossRef]
- Litjens, G.; Worrell, E.; van Sark, W. Assessment of forecasting methods on performance of photovoltaic-battery systems. Appl. Energy 2018, 221, 358–373. [Google Scholar] [CrossRef]
- Haupt, S.E.; Casado, M.G.; Davidson, M.; Dobschinski, J.; Du, P.; Lange, M.; Miller, T.; Mohrlen, C.; Motley, A.; Pestana, R.; et al. The use of probabilistic forecasts: Applying them in theory and practice. IEEE Power Energy Mag. 2019, 17, 46–57. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Srinivasan, D. Automatic hourly solar forecasting using machine learning models. Renew. Sustain. Energy Rev. 2019, 105, 487–498. [Google Scholar] [CrossRef]
- Vislocky, R.L.; Fritsch, J.M. Improved model output and statistics through model consensus. Bull. Am. Meteorol. Soc. 1995, 76, 1157–1164. [Google Scholar] [CrossRef]
- Lorenz, E.; Kühnert, J.; Heinemann, D. Short term forecasting of solar irradiance by combining satellite data and numerical weather predictions. In Proceedings of the 27th European PV Solar Energy Conference (EU PVSEC), Frankfurt, Germany, 24–28 September 2012; Volume 2428, p. 44014405. [Google Scholar]
- Haupt, S.E.; Kosović, B.; Jensen, T.; Lazo, J.K.; Lee, J.A.; Jiménez, P.A.; Cowie, J.; Wiener, G.; McCandless, T.C.; Rogers, M.; et al. Building the Sun4Cast System: Improvements in Solar Power Forecasting. Bull. Am. Meteorol. Soc. 2018, 99, 121–136. [Google Scholar] [CrossRef]
- Nouri, B.; Blum, N.; Wilbert, S.; Zarzalejo, L.F. A Hybrid Solar Irradiance Nowcasting Approach: Combining All Sky Imager Systems and Persistence Irradiance Models for Increased Accuracy. Solar RRL 2022, 6, 2100442. [Google Scholar] [CrossRef]
- Boukabara, S.A.; Krasnopolsky, V.; Penny, S.G.; Stewart, J.Q.; McGovern, A.; Hall, D.; Hoeve, J.E.T.; Hickey, J.; Huang, H.L.A.; Williams, J.K.; et al. Outlook for Exploiting Artificial Intelligence in the Earth and Environmental Sciences. Bull. Am. Meteorol. Soc. 2021, 102, E1016–E1032. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Wang, D.; Liu, X.; Wang, Y. A review on global solar radiation prediction with machine learning models in a comprehensive perspective. Energy Convers. Manag. 2021, 235, 113960. [Google Scholar] [CrossRef]
- Pedro, H.T.; Coimbra, C.F.; David, M.; Lauret, P. Assessment of machine learning techniques for deterministic and probabilistic intra-hour solar forecasts. Renew. Energy 2018, 123, 191–203. [Google Scholar] [CrossRef]
- Sun, Y.; Venugopal, V.; Brandt, A.R. Short-term solar power forecast with deep learning: Exploring optimal input and output configuration. Sol. Energy 2019, 188, 730–741. [Google Scholar] [CrossRef]
- Fouilloy, A.; Voyant, C.; Notton, G.; Motte, F.; Paoli, C.; Nivet, M.L.; Guillot, E.; Duchaud, J.L. Solar irradiation prediction with machine learning: Forecasting models selection method depending on weather variability. Energy 2018, 165, 620–629. [Google Scholar] [CrossRef]
- Dewangan, C.L.; Singh, S.; Chakrabarti, S. Combining forecasts of day-ahead solar power. Energy 2020, 202, 117743. [Google Scholar] [CrossRef]
- Wolff, B.; Kühnert, J.; Lorenz, E.; Kramer, O.; Heinemann, D. Comparing support vector regression for PV power forecasting to a physical modeling approach using measurement, numerical weather prediction, and cloud motion data. Sol. Energy 2016, 135, 197–208. [Google Scholar] [CrossRef]
- Aguiar, L.M.; Pereira, B.; Lauret, P.; Díaz, F.; David, M. Combining solar irradiance measurements, satellite-derived data and a numerical weather prediction model to improve intra-day solar forecasting. Renew. Energy 2016, 97, 599–610. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Huertas-Tato, J.; Aler, R.; Galván, I.M.; Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Pozo-Vázquez, D. A short-term solar radiation forecasting system for the Iberian Peninsula. Part 2: Model blending approaches based on machine learning. Sol. Energy 2020, 195, 685–696. [Google Scholar] [CrossRef]
- Long, C.N.; Dutton, E.G. BSRN Global Network Recommended QC Tests, V2. x. 2010. Available online: https://epic.awi.de/id/eprint/30083/1/BSRN_recommended_QC_tests_V2.pdf (accessed on 2 February 2023).
- Li, Q.; Lu, W.; Yang, J. A Hybrid Thresholding Algorithm for Cloud Detection on Ground-Based Color Images. J. Atmos. Ocean. Technol. 2011, 28, 1286–1296. [Google Scholar] [CrossRef]
- Weinzaepfel, P.; Revaud, J.; Harchaoui, Z.; Schmid, C. DeepFlow: Large displacement optical flow with deep matching. In Proceedings of the ICCV-IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1385–1392. [Google Scholar] [CrossRef]
- Rigollier, C.; Bauer, O.; Wald, L. On the clear sky model of the ESRA—European Solar Radiation Atlas—with respect to the Heliosat method. Sol. Energy 2000, 68, 33–48. [Google Scholar] [CrossRef]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An introduction to Meteosat second generation (MSG). Bull. Am. Meteorol. Soc. 2002, 83, 977–992. [Google Scholar] [CrossRef]
- Rigollier, C.; Lefèvre, M.; Wald, L. The method Heliosat-2 for deriving shortwave solar radiation from satellite images. Sol. Energy 2004, 77, 159–169. [Google Scholar] [CrossRef]
- Liberzon, A.; Gurka, R.; Taylor, Z. Openpiv Home Page. 2009. Available online: https://openpiv.sourceforge.net/ (accessed on 2 February 2023).
- Nonnenmacher, L.; Coimbra, C.F. Streamline-based method for intra-day solar forecasting through remote sensing. Sol. Energy 2014, 108, 447–459. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, Y. Ensemble Machine Learning: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Louppe, G.; Wehenkel, L.; Sutera, A.; Geurts, P. Understanding variable importances in forests of randomized trees. Adv. Neural Inf. Process. Syst. 2013, 26, 431–439. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hammer, A.; Kühnert, J.; Weinreich, K.; Lorenz, E. Short-term forecasting of surface solar irradiance based on Meteosat-SEVIRI data using a nighttime cloud index. Remote Sens. 2015, 7, 9070–9090. [Google Scholar] [CrossRef]
- Romano, F.; Cimini, D.; Cersosimo, A.; Di Paola, F.; Gallucci, D.; Gentile, S.; Geraldi, E.; Larosa, S.; Nilo, S.T.; Ricciardelli, E.; et al. Improvement in surface solar irradiance estimation using HRV/MSG data. Remote Sens. 2018, 10, 1288. [Google Scholar] [CrossRef]
- Aksakal, S.K. Geometric accuracy investigations of SEVIRI high resolution visible (HRV) level 1.5 Imagery. Remote Sens. 2013, 5, 2475–2491. [Google Scholar] [CrossRef]
- Debaecker, V.; Kocaman, S.; Saunier, S.; Garcia, K.; Bas, S.; Just, D. On the geometric accuracy and stability of MSG SEVIRI images. Atmos. Environ. 2021, 262, 118645. [Google Scholar] [CrossRef]
- Miller, S.D.; Rogers, M.A.; Haynes, J.M.; Sengupta, M.; Heidinger, A.K. Short-term solar irradiance forecasting via satellite/model coupling. Sol. Energy 2018, 168, 102–117. [Google Scholar] [CrossRef]
- Sirch, T.; Bugliaro, L.; Zinner, T.; Möhrlein, M.; Vazquez-Navarro, M. Cloud and DNI nowcasting with MSG/SEVIRI for the optimized operation of concentrating solar power plants. Atmos. Meas. Tech. 2017, 10, 409–429. [Google Scholar] [CrossRef]
- López-Cuesta, M.; Jiménez-Garrote, A.; Aler-Mur, R.; Galván-León, I.; Tovar-Pescador, J.; Pozo-Vazquez, D. Improving ASI-Based Solar Radiation Nowcasting by Using Automatic Cloud Type Recognition Methods (No. EMS2022-166). Technical Report. In Proceedings of the Copernicus Meetings, Bonn, Germany, 4–9 September 2022. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Meinshausen, N.; Ridgeway, G. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]

| Model Input Acronym | Model Main Characteristics |
|---|---|
| ASI-1, ASI-2 and ASI-3 | Single ASI-based, forecasts spatial resolution ∼meters |
| ASI-mean | Mean of the ASI-1, ASI-2 and ASI-3 models forecasts |
| Sat-LR | Low Resolution satellite-images-based forecasts, 5 km spatial resolution |
| Sat-HR | High resolution satellite-images-based forecasts, 1 km spatial resolution |
| Smart-Persistence | Smart persistence (data-driven) model, no error at lead time 0 |
| Name of Input Models Set | Models Input Involved |
|---|---|
| Sat-LR | Sat-LR, Smart-Persistence |
| Sat-HR | Sat-HR, Smart-Persistence |
| ASI | ASI-1, Smart-Persistence |
| Sat-LR & ASI | Sat-HR, ASI-1, Smart-Persistence |
| Sat-HR & ASI | Sat-HR, ASI-1, Smart-Persistence |
| Sats | Sat-LR, Sat-HR, Smart-Persistence |
| Sats & ASI | ASI-1, Sat-LR, Sat-HR, Smart-Persistence |
| Sats & ASIs | ASI-1, ASI-2, ASI-3, Sat-LR, Sat-HR, Smart-Persistence |
| Sats & ASI-mean | ASI-mean, Sat-LR, Sat-HR, Smart-Persistence |
| Models Input Set | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Blending Model | Blending Approach | Sat-LR | Sat-HR | ASI | Sat-LR & ASI | Sat-HR & ASI | Sats | Sats & ASI | Sats & ASIs | Sats & ASI-mean | |
| GHI | RF | General | 30.7 | 31.0 | 35.1 | 27.1 | 28.1 | 22.9 | 21.8 | 22.8 | 21.9 |
| Horizon | 33.7 | 34.7 | 37.9 | 33.0 | 34.0 | 32.5 | 32.9 | 32.4 | 32.5 | ||
| Linear | General | 32.9 | 33.0 | 35.8 | 32.6 | 32.8 | 31.9 | 31.8 | 31.7 | 31.7 | |
| Horizon | 32.8 | 33.6 | 36.9 | 33.0 | 34.2 | 32.7 | 33.0 | 33.3 | 32.9 | ||
| DNI | RF | General | 58.8 | 56.5 | 65.0 | 57.2 | 60.0 | 42.2 | 43.2 | 43.6 | 43.5 |
| Horizon | 63.5 | 67.0 | 70.2 | 64.7 | 67.2 | 62.2 | 64.3 | 64.1 | 63.0 | ||
| Linear | General | 62.3 | 63.3 | 67.3 | 62.2 | 62.7 | 61.2 | 61.0 | 60.8 | 60.5 | |
| Horizon | 61.5 | 63.9 | 70.8 | 63.4 | 65.9 | 61.0 | 62.6 | 62.4 | 61.3 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Cuesta, M.; Aler-Mur, R.; Galván-León, I.M.; Rodríguez-Benítez, F.J.; Pozo-Vázquez, A.D. Improving Solar Radiation Nowcasts by Blending Data-Driven, Satellite-Images-Based and All-Sky-Imagers-Based Models Using Machine Learning Techniques. Remote Sens. 2023, 15, 2328. https://doi.org/10.3390/rs15092328
López-Cuesta M, Aler-Mur R, Galván-León IM, Rodríguez-Benítez FJ, Pozo-Vázquez AD. Improving Solar Radiation Nowcasts by Blending Data-Driven, Satellite-Images-Based and All-Sky-Imagers-Based Models Using Machine Learning Techniques. Remote Sensing. 2023; 15(9):2328. https://doi.org/10.3390/rs15092328
Chicago/Turabian StyleLópez-Cuesta, Miguel, Ricardo Aler-Mur, Inés María Galván-León, Francisco Javier Rodríguez-Benítez, and Antonio David Pozo-Vázquez. 2023. "Improving Solar Radiation Nowcasts by Blending Data-Driven, Satellite-Images-Based and All-Sky-Imagers-Based Models Using Machine Learning Techniques" Remote Sensing 15, no. 9: 2328. https://doi.org/10.3390/rs15092328
APA StyleLópez-Cuesta, M., Aler-Mur, R., Galván-León, I. M., Rodríguez-Benítez, F. J., & Pozo-Vázquez, A. D. (2023). Improving Solar Radiation Nowcasts by Blending Data-Driven, Satellite-Images-Based and All-Sky-Imagers-Based Models Using Machine Learning Techniques. Remote Sensing, 15(9), 2328. https://doi.org/10.3390/rs15092328








