Inter-Comparison of Landsat-8 and Landsat-9 during On-Orbit Initialization and Verification (OIV) Using Extended Pseudo Invariant Calibration Sites (EPICS): Advanced Methods
Abstract
1. Introduction
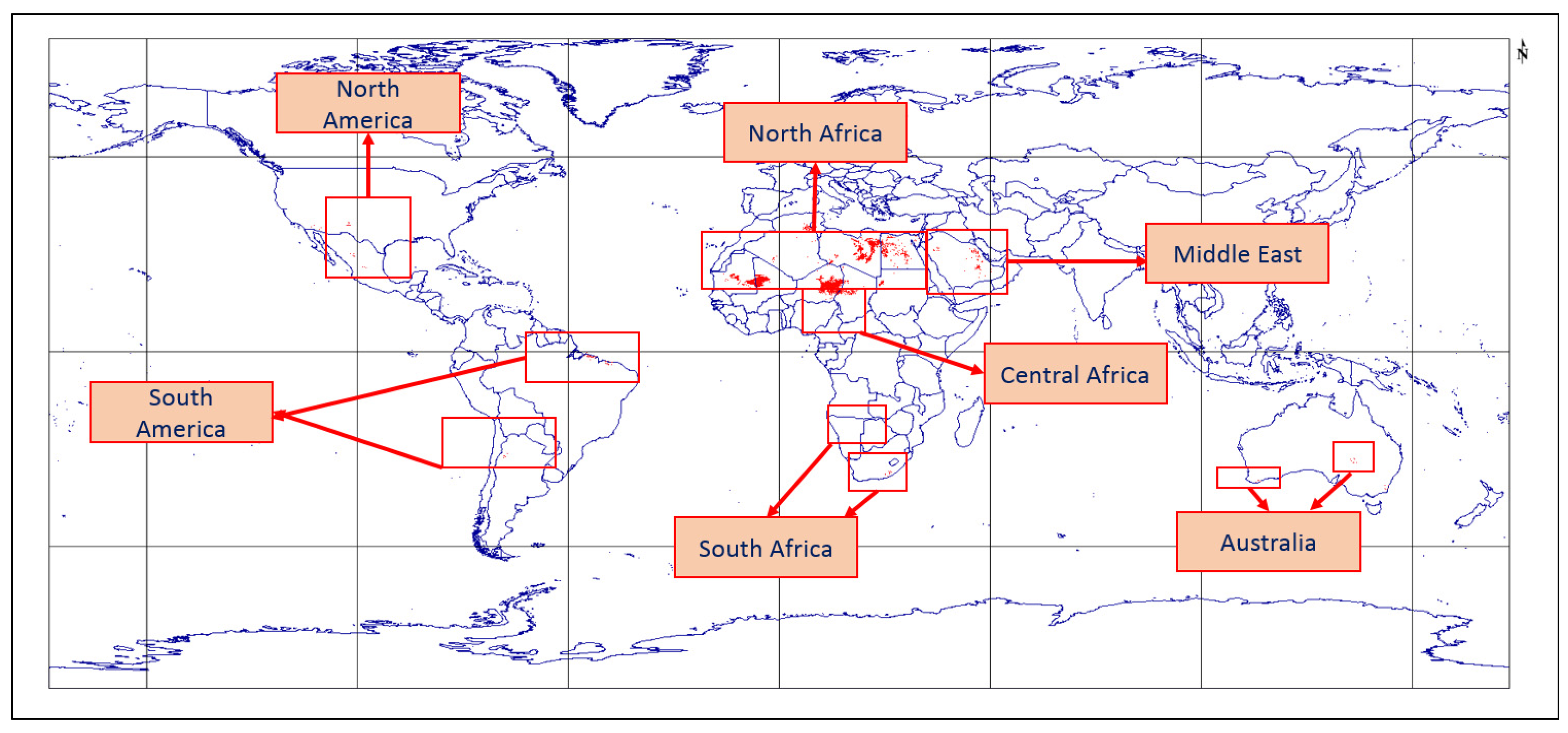
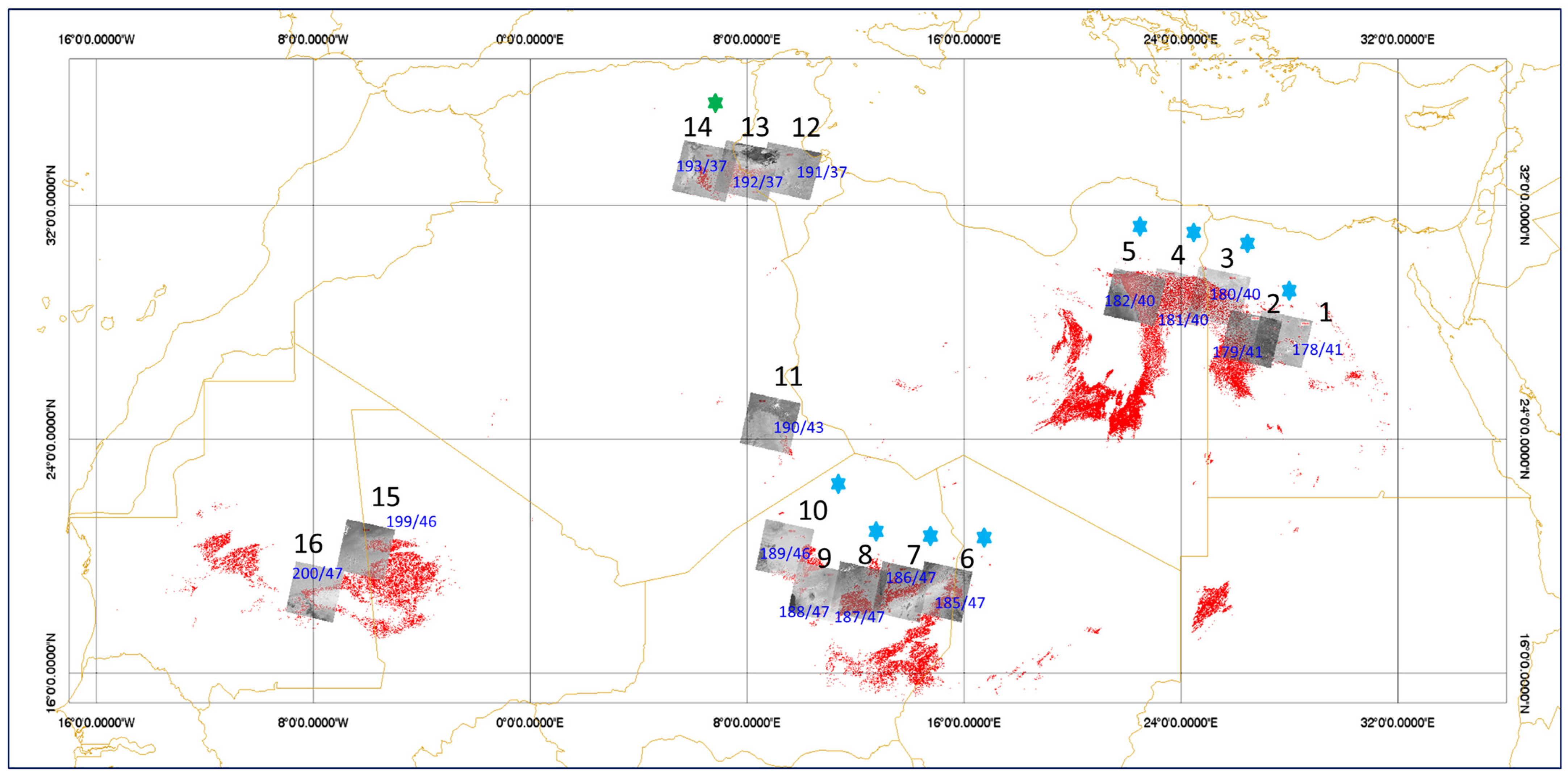
1.1. Extended Pseudo Invariant Calibration Site in North African Desert Sites (EPICS-NA) and a Global Scale (EPICS-Global)
1.2. Extended PICS Absolute Calibration Model (ExPAC Model)
2. The Development of Extended PICS Absolute Calibration Model (ExPAC Model)
2.1. Data
2.1.1. Landsat-7, 8, 9
2.1.2. EO-1 Hyperion
2.1.3. Sentinel-2A, Sentinel-2B (S2A, S2B)
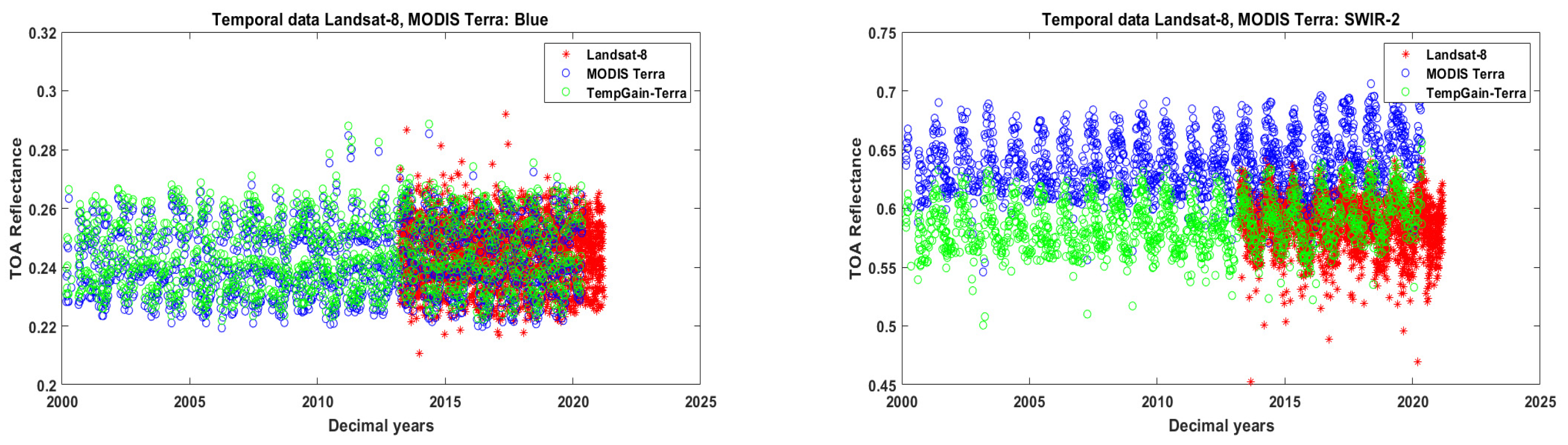
2.1.4. MODIS Terra and Aqua
2.2. The ExPAC BRDF Model
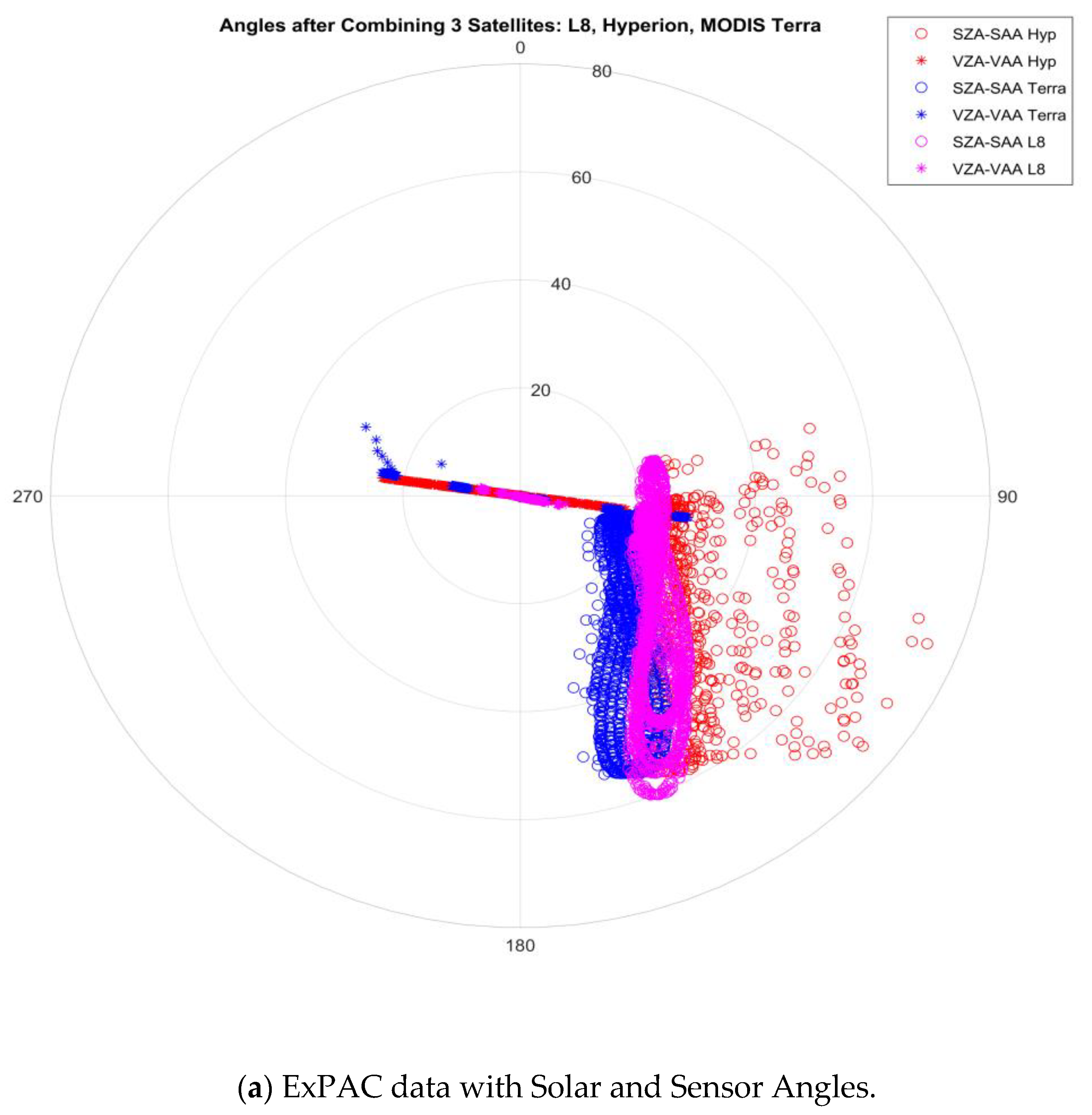
2.2.1. The ExPAC Data: Hyperion EO-1, Landsat-8 Data and MODIS TERRA
2.2.2. The Generation of the 4-Angle BRDF Model
2.2.3. The Adjustment Factor for ExPAC Model
2.2.4. The Extended PICS Absolute Calibration Model–ExPAC Model
3. EPICS-Based Cross-Calibration
3.1. Spectral Band Adjustment Function (SBAF)
3.2. Bidirectional Reflection Distribution Function (BRDF)
3.3. The EPICS-Based Cross-Calibration Ratio
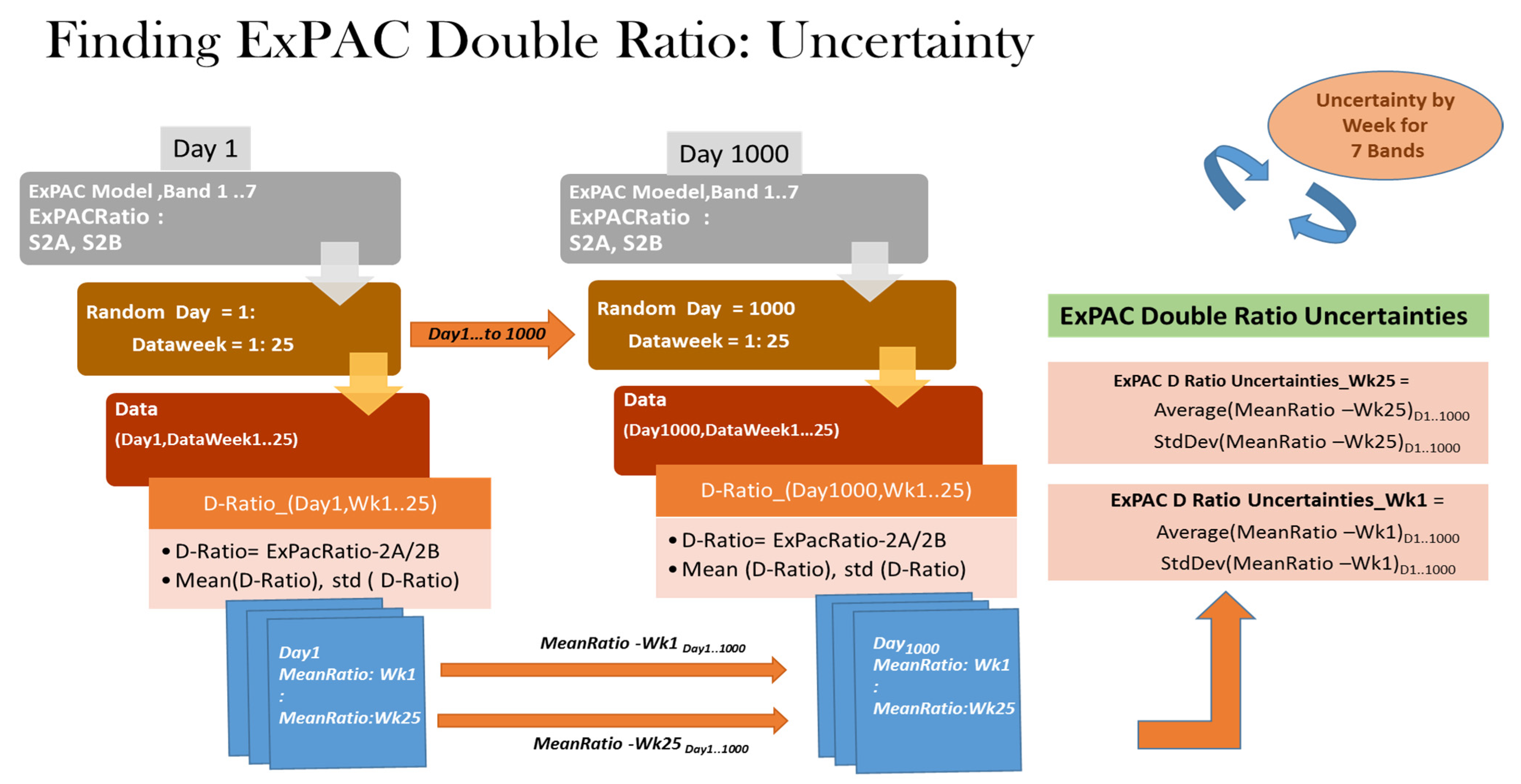
4. The ExPAC Double Ratio and the EPICS-Based Cross-Calibration Uncertainties Analysis
4.1. The ExPAC Double Ratio Uncertainties Analysis
4.2. The EPICS-Based Cross-Calibration Ratio Uncertainties Analysis
5. Results and Discussion
5.1. Validation of the ExPAC Model
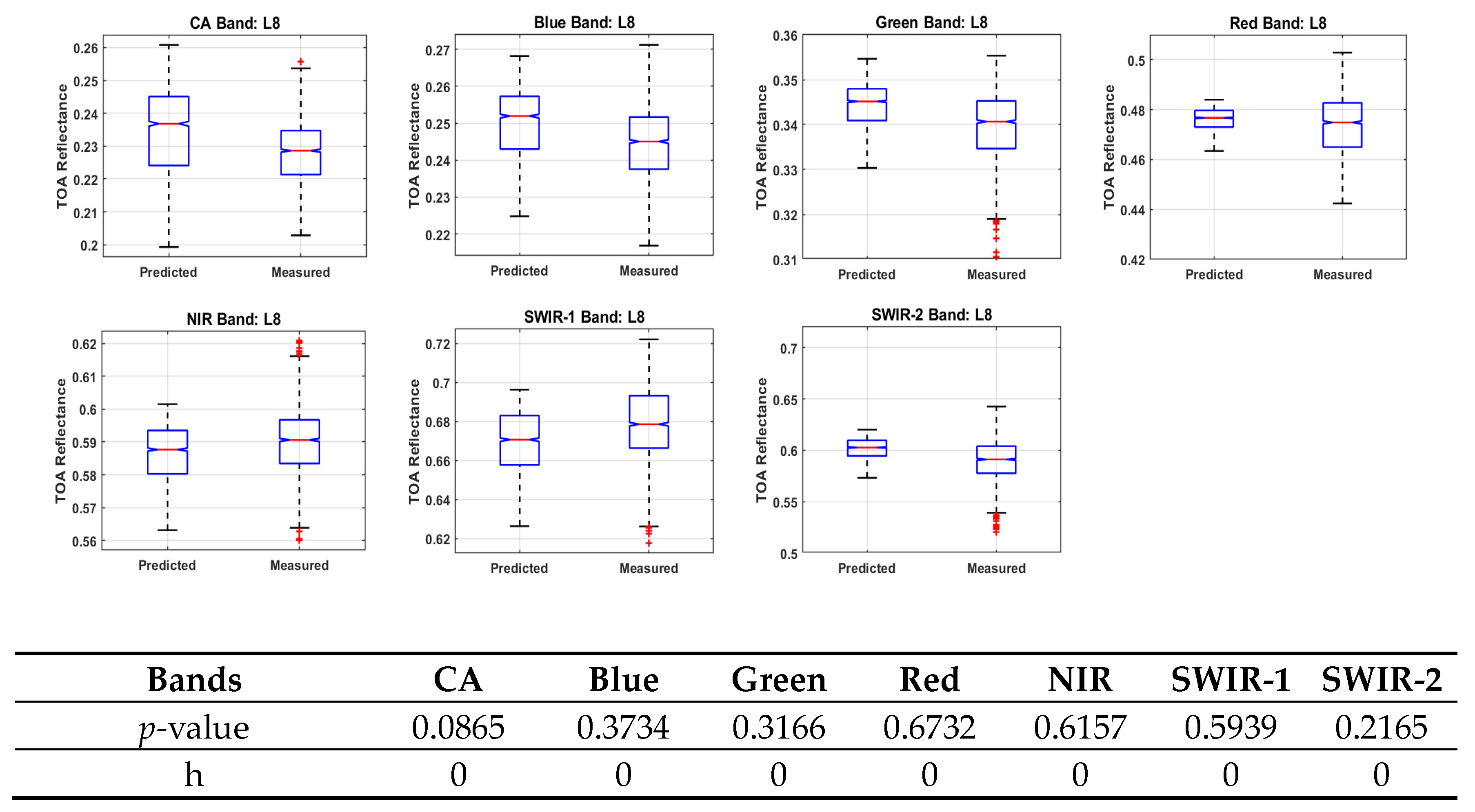
5.1.1. The Validation of ExPAC Model with Landsat-8 Collection-2 Data
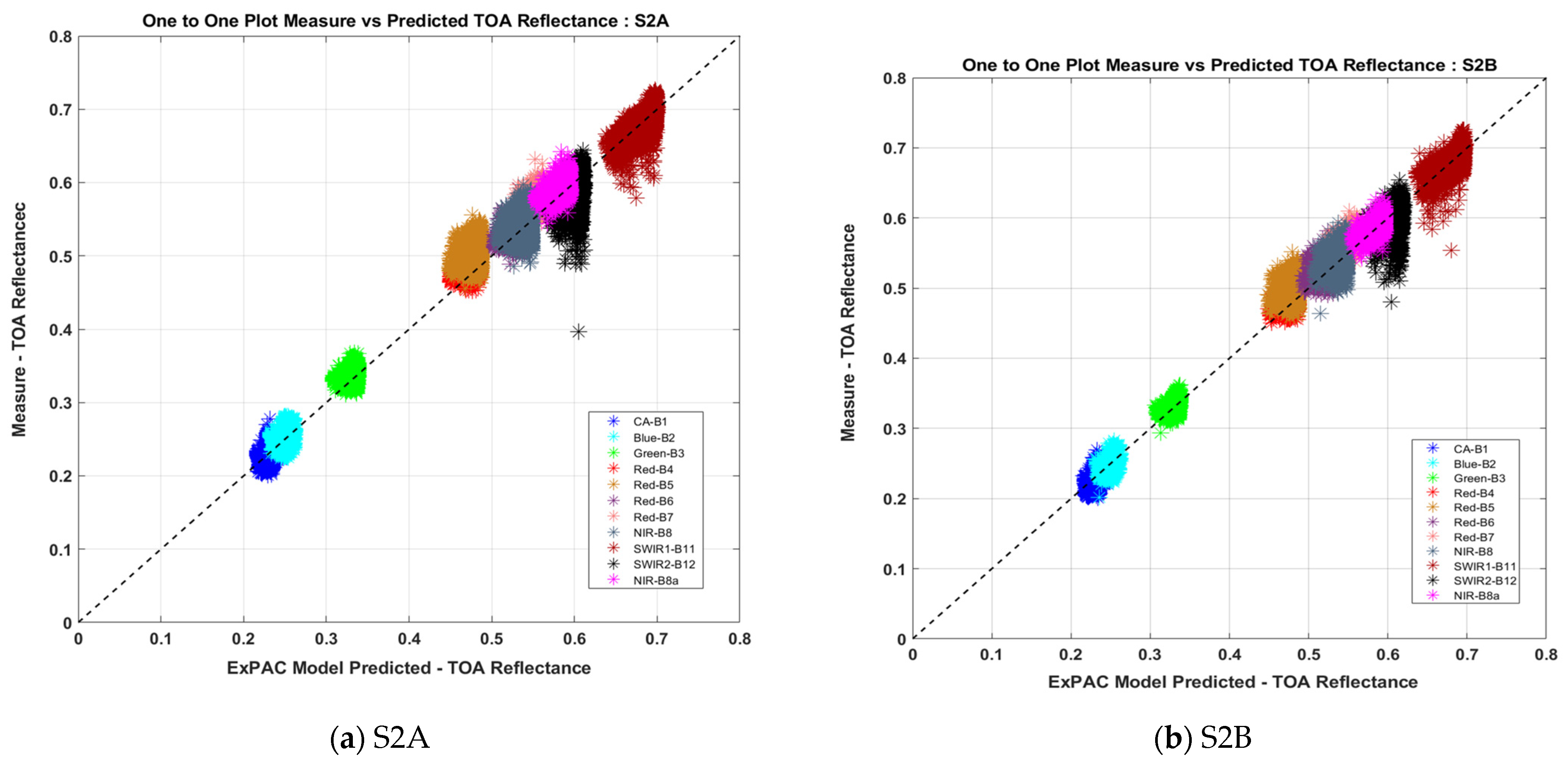
5.1.2. The Validation of ExPAC Model Using Satellite Measurements
5.1.3. The ExPAC Model vs. Non-Landsat-8 Equivalent Spectral Bands
5.2. The Application of the ExPAC Model
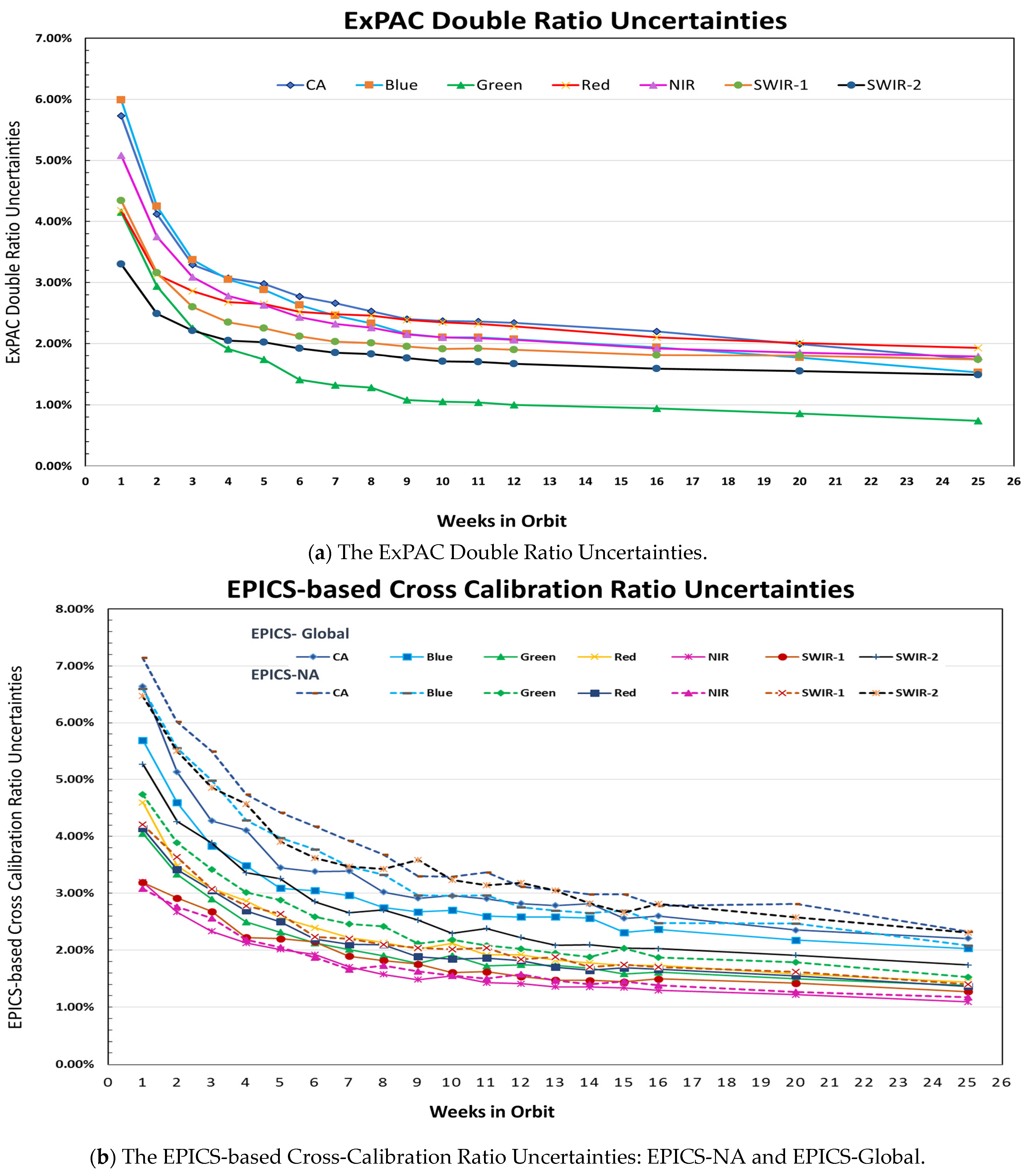
5.2.1. The ExPAC Double Ratio
5.2.2. The ExPAC Double Ratio for Sentinel 2A–2B with 11 Bands and Inter-Comparison Results
5.3. The Inter-Comparison of Landsat Missions vs. Sentinel-2 Missions Results
5.3.1. The EPICS-Based Cross-Calibration Results
5.3.2. The Inter-Comparison Landsat-8 vs. Landsat-9 during OIV with the Three Advanced Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| The Wilcoxon Rank Sum Test (p-Value) | The Wilcoxon Rank Sum Test (h) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Terra | Aqua | L7 | L8 | S2A | S2B | Terra | Aqua | L7 | L8 | S2A | S2B | |
| CA | -- | -- | -- | 0.087 | 0.085 | 0.456 | -- | -- | -- | 0 | 0 | 0 |
| Blue | 0.094 | 0.084 | 0.084 | 0.373 | 0.097 | 0.849 | 0 | 0 | 0 | 0 | 0 | 0 |
| Green | 0.100 | 0.086 | 0.277 | 0.317 | 0.238 | 0.777 | 0 | 0 | 0 | 0 | 0 | 0 |
| Red | 0.085 | 0.193 | 0.412 | 0.673 | 0.416 | 0.411 | 0 | 0 | 0 | 0 | 0 | 0 |
| NIR | 0.091 | 0.305 | 0.736 | 0.616 | 0.090 | 0.139 | 0 | 0 | 0 | 0 | 0 | 0 |
| SWIR-1 | 0.870 | -- | 0.305 | 0.594 | 0.460 | 0.110 | 0 | -- | 0 | 0 | 0 | 0 |
| SWIR-2 | 0.921 | 0.398 | 0.340 | 0.217 | 0.422 | 0.341 | 0 | 0 | 0 | 0 | 0 | 0 |
| Coefficient | Estimate | Standard Error | T-Statistics | p-Value Statistical | Statistical Response |
|---|---|---|---|---|---|
| Intercept | 0.7005 | 0.0003 | 2361.149 | 0 | Significant |
| Y1 | 0.0000 | 0.0003 | <0 | 1 | Insignificant |
| X1 | 0.0000 | 0.0003 | <0 | 1 | Insignificant |
| Y2 | 0.0000 | 0.0037 | <0 | 1 | Insignificant |
| X2 | 0.0000 | 0.0006 | <0 | 1 | Insignificant |
| X1Y1 | 0.0000 | 0.0008 | <0 | 1 | Insignificant |
| Y1Y2 | 0.1754 | 0.0155 | 11.293 | <0 | Significant |
| X1Y2 | 0.0000 | 0.0181 | <0 | 1 | Insignificant |
| X2Y1 | 0.0000 | 0.0026 | <0 | 1 | Insignificant |
| X1X2 | 0.0094 | 0.0029 | 3.2460 | 0.001 | Significant |
| X2Y2 | 0.0000 | 0.0117 | <0 | 1 | Insignificant |
| −0.0727 | 0.0006 | −117.254 | 0 | Significant | |
| −0.0588 | 0.0015 | −40.519 | 0 | Significant | |
| −1.9655 | 0.1240 | −15.845 | <0 | Significant | |
| 0.0722 | 0.0038 | 19.183 | <0 | Significant |
| Satellites | No. of Images | ||
|---|---|---|---|
| EPICS-NA | EPICS-Global | Data Till | |
| Landsat-7 | 2168 | 7510 | 31 August 2022 |
| Landsat-8 | 2751 | 4910 | 31 August 2022 |
| Landsat-9 | 266 | 420 | 31 August 2022 |
| Sentinel-2A | 3329 | 5113 | 31 August 2022 |
| Sentinel-2B | 2484 | 3495 | 31 August 2022 |
References
- Shrestha, M.; Hasan, M.N.; Leigh, L.; Helder, D. Extended Pseudo Invariant Calibration Sites (EPICS) for the Cross-Calibration of Optical Satellite Sensors. Remote Sens. 2019, 11, 1676. [Google Scholar] [CrossRef]
- Hasan, M.N.; Shrestha, M.; Leigh, L.; Helder, D. Evaluation of an Extended PICS (EPICS) for Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 1755. [Google Scholar] [CrossRef]
- Kaewmanee, M. Pseudo Invariant Calibration Sites: PICS Evolution. In Proceedings of the CalCon 2018, Logan, UT, USA, 18–20 June 2018. [Google Scholar]
- Fajardo Rueda, J.; Leigh, L.; Teixeira Pinto, C.; Kaewmanee, M.; Helder, D. Classification and Evaluation of Extended PICS (EPICS) on a Global Scale for Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2021, 13, 3350. [Google Scholar] [CrossRef]
- Kaewmanee, M.; Vuppula, H.; Helder, D. Improved Temporal Resolution of Pseudo Invariant Calibration Sites (PICS) through Development of the PICS Normalization Process (PNP); Utah State University: Logan, UT, USA, 2017. [Google Scholar]
- Teixeira Pinto, C.; Haque, M.O.; Micijevic, E.; Helder, D.L. Landsats 1–5 Multispectral Scanner System Sensors Radiometric Calibration Update. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7378–7394. [Google Scholar] [CrossRef]
- Mishra, N.; Helder, D.; Barsi, J.; Markham, B. Continuous Calibration Improvement in Solar Reflective Bands: Landsat 5 through Landsat 8. Remote Sens. Environ. 2016, 185, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Kaewmanee, M.; Micijevic, E.; Helder, D.; Haque, O.; Barsi, J. Radiometric Comparison of Sentinel 2A, Sentinel 2B and Landsat-8: Lifetime Trending, Cross Calibration and Absolute Calibration Assessment Over the Libya 4 PICS JACIE Workshop By. In Proceedings of the JACIE, Brussels, Belgium, 30 November 2018. [Google Scholar]
- Raut, B.; Kaewmanee, M.; Angal, A.; Xiong, X.; Helder, D. Empirical Absolute Calibration Model for Multiple Pseudo-Invariant Calibration Sites. Remote Sens. 2019, 11, 1105. [Google Scholar] [CrossRef]
- Das Chaity, M.; Kaewmanee, M.; Leigh, L.; Pinto, C.T.; Pignatti, S. Remote Sensing Hyperspectral Empirical Absolute Calibration Model Using Libya 4 Pseudo Invariant Calibration Site. Remote Sens. 2021, 8, 1538. [Google Scholar] [CrossRef]
- Gross, G.; Helder, D.; Begeman, C.; Leigh, L.; Kaewmanee, M.; Shah, R. Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underfly Event. Remote Sens. 2022, 14, 2418. [Google Scholar] [CrossRef]
- Nagaraja Rao, C.R.; Chen, J. Post-Launch Calibration of the Visible and Near-Infrared Channels of the Advanced Very High Resolution Radiometer on the NOAA-14 Spacecraft. Int. J. Remote Sens. 1996, 17, 2743–2747. [Google Scholar] [CrossRef]
- Smith, D.L.; Mutlow, C.T.; Nagaraja Rao, C.R. Calibration Monitoring of the Visible and Near-Infrared Channels of the Along-Track Scanning Radiometer-2 by Use of Stable Terrestrial Sites. Appl. Opt. 2002, 41, 515–523. [Google Scholar] [CrossRef] [PubMed]
- Cosnefroy, H.; Leroy, M.; Briottet, X. Selection and Characterization of Saharan and Arabian Desert Sites Forthe Calibration of Optical Satellite Sensors. Remote Sens. Environ. 1996, 58, 101–114. [Google Scholar] [CrossRef]
- Markham, B.L.; Helder, D.L. Forty-Year Calibrated Record of Earth-Reflected Radiance from Landsat: A Review. Remote Sens. Environ. 2012, 122, 30–40. [Google Scholar] [CrossRef]
- Vuppula, H. Normalization of Pseudo-Invariant Calibration Sites for Increasing the Temporal Resolution and Long-Term Trending; South Dakota State University: Brookings, SD, USA, 2017. [Google Scholar]
- Ozen, H.; Fox, N.; Deadman, A.; Behnert, I.; Harris, P.; Gurbuz, S.; Yuan, L.; Griffith, D.; Kaewmanee, M.; Prakobya, A.; et al. Comparison of Radiometric Gain of Optical Satellite Sensors Using Tuz Golu Radiometrically Calibrated Test Site. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: New York, NY, USA, 2012; pp. 1120–1123. [Google Scholar]
- Leigh, L.; Shrestha, M.; Hasan, N.; Kaewmanee, M. Classification of North Africa for Use as an Extended Pseudo Invariant Calibration Site for Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors. In Proceedings of the CALCON 2019, Logan, UT, USA, 19–21 September 2019; Utah State University: Logan, UT, USA, 2019. [Google Scholar]
- Shrestha, M.; Leigh, L.; Helder, D. Classification of North Africa for Use as an Extended Pseudo Invariant Calibration Sites (EPICS) for Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 875. [Google Scholar] [CrossRef]
- Rueda, J.F.; Kaewmanee, M.; Shah, R.; Leigh, L. Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors Using Global Extended Pseudo Invariant Calibration Sites (During Landsat 9 OIV). In Proceedings of the PECROA 2022, Denver, CO, USA, 24–27 October 2022. [Google Scholar]
- Mishra, N.; Helder, D.; Angal, A.; Choi, J.; Xiong, X. Absolute Calibration of Optical Satellite Sensors Using Libya 4 Pseudo Invariant Calibration Site. Remote Sens. 2014, 6, 1327–1346. [Google Scholar] [CrossRef]
- Kaewmanee, M.; Helder, D. Refined Absolute PICS Calibration Model Over Libya-4 Using Sentinel2A and Landsat 8 Collection-1 Data for Validation. In Proceedings of the PECROA 20, Sioux Falls, SD, USA, 14–16 November 2017. [Google Scholar]
- USGS Using-Usgs-Landsat-Level-1-Data-Product@www.usgs.gov. Available online: https://www.usgs.gov/core-science-systems/nli/landsat/using-usgs-landsat-level-1-data-product (accessed on 20 February 2023).
- Farhad, M.M.; Kaewmanee, M.; Leigh, L.; Helder, D. Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A. Remote Sens. 2020, 12, 806. [Google Scholar] [CrossRef]
- Farhad, M.M. Cross Calibration and Validation of Landsat 8 OLI and Sentinel 2A MSI; South Dakota State University: Brookings, SD, USA, 2018. [Google Scholar]
- USGS Landsat 7 End of Mission Activities. Available online: https://www.usgs.gov/landsat-missions/landsat-7 (accessed on 20 February 2023).
- Morfitt, R.; Barsi, J.; Levy, R.; Markham, B.; Micijevic, E.; Ong, L.; Scaramuzza, P.; Vanderwerff, K. Landsat-8 Operational Land Imager (OLI) Radiometric Performance On-Orbit. Remote Sens. 2015, 7, 2208–2237. [Google Scholar] [CrossRef]
- USGS Landsat Collection 2. Available online: https://www.usgs.gov/landsat-missions/landsat-collection-2-level-1-data (accessed on 20 February 2023).
- USGS Landsat 9 Bands. Available online: https://landsat.gsfc.nasa.gov/satellites/landsat-9/landsat-9-bands/ (accessed on 20 February 2023).
- Franks, S.; Neigh, C.S.R.; Campbell, P.K.; Sun, G.; Yao, T.; Zhang, Q.; Huemmrich, K.F.; Middleton, E.M.; Ungar, S.G.; Frye, S.W. EO-1 Data Quality and Sensor Stability with Changing Orbital Precession at the End of a 16 Year Mission. Remote Sens. 2017, 9, 412. [Google Scholar] [CrossRef]
- Jing, X.; Leigh, L.; Helder, D.; Teixeira Pinto, C.; Aaron, D. Lifetime Absolute Calibration of the EO-1 Hyperion Sensor and Its Validation. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9466–9475. [Google Scholar] [CrossRef]
- Revel, C.; Lonjou, V.; Marcq, S.; Desjardins, C.; Fougnie, B.; Coppolani-Delle Luche, C.; Guilleminot, N.; Lacamp, A.-S.; Lourme, E.; Miquel, C.; et al. Sentinel-2A and 2B Absolute Calibration Monitoring. Eur. J. Remote Sens. 2019, 52, 122–137. [Google Scholar] [CrossRef]
- Barsi, J.A.; Alhammoud, B.; Czapla-Myers, J.; Gascon, F.; Haque, M.O.; Kaewmanee, M.; Leigh, L.; Markham, B.L. Sentinel-2A MSI and Landsat-8 OLI Radiometric Cross Comparison over Desert Sites. Eur. J. Remote Sens. 2018, 51, 822–837. [Google Scholar] [CrossRef]
- Xiong, X.; Butler, J.J. MODIS and VIIRS Calibration History and Future Outlook. Remote Sens. 2020, 12, 2523. [Google Scholar] [CrossRef]
- Lee, S.; Meister, G.; Franz, B. MODIS Aqua Reflective Solar Band Calibration for NASA’s R2018 Ocean Color Products. Remote Sens. 2019, 11, 2187. [Google Scholar] [CrossRef]
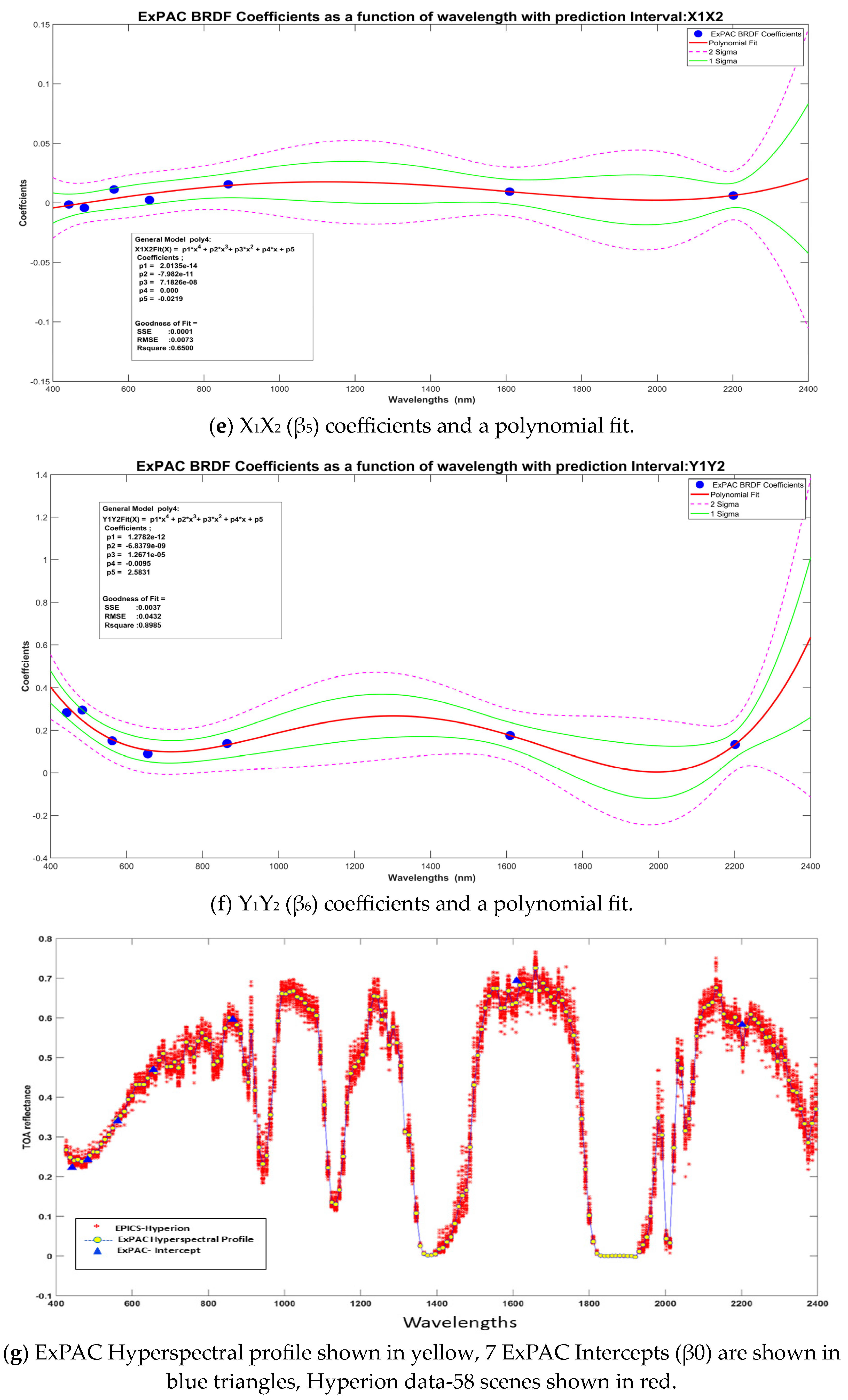
- Shrestha, M.; Hasan, N.; Leigh, L.; Helder, D. Derivation of Hyperspectral Profile of Extended Pseudo Invariant Calibration Sites (EPICS) for Use in Sensor Calibration. Remote Sens. 2019, 11, 2279. [Google Scholar] [CrossRef]
- Khadka, N.; Teixeira Pinto, C.; Leigh, L. Detection of Change Points in Pseudo-Invariant Calibration Sites Time Series Using Multi-Sensor Satellite Imagery. Remote Sens. 2021, 13, 2079. [Google Scholar] [CrossRef]
- Helder, D.; Thome, K.J.; Mishra, N.; Chander, G.; Xiong, X.; Angal, A.; Choi, T. Absolute Radiometric Calibration of Landsat Using a Pseudo Invariant Calibration Site. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1360–1369. [Google Scholar] [CrossRef]
- Barsi, J.; Haque, M.O.; Markham, B.L.; Montanaro, M.; McCorkel, J.T.; Gerace, A.; Pedelty, J.; Hook, S.; Raqueno, N.; Anderson, C. Landsat-8 on-Orbit and Landsat-9 Pre-Launch Sensor Radiometric Characterization. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization V, Honolulu, HI, USA, 25–26 September 2018; Xiong, X., Kimura, T., Eds.; SPIE: Bellingham, WA, USA, 2018; p. 3. [Google Scholar]
- Teixeira Pinto, C.; Shrestha, M.; Helder, D.; Leigh, L.; Hasan, N. SBAF for Cross-Calibration of Landsat-8 OLI and Sentinel-2 MSI over North African PICS; SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A.; et al. Copernicus Sentinel-2A Calibration and Products Validation Status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef]
- Team, S.M.E. Data Quality Report Sentinel-2 L1C MSI June 2022. Available online: https://sentinels.copernicus.eu/documents/247904/4766914/OMPC.CS.DQR.001.05-2022+-+i76r0+-+MSI+L1C+DQR+June+2022.pdf (accessed on 20 February 2023).
- Markham, B.L.; Barsi, J.A. Landsat-8 Operational Land Imager on-Orbit Radiometric Calibration. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 4205–4207. [Google Scholar]
- Sentinel Sentinel-2 MSI Processing Baseline. Available online: https://sentinels.copernicus.eu/web/sentinel/technical-guides/sentinel-2-msi/processing-baseline (accessed on 20 February 2023).
- Sterckx, S.; Wolters, E. Radiometric Top-of-Atmosphere Reflectance Consistency Assessment for Landsat 8/OLI, Sentinel-2/MSI, PROBA-V, and DEIMOS-1 over Libya-4 and RadCalNet Calibration Sites. Remote Sens. 2019, 11, 2253. [Google Scholar] [CrossRef]
- Gil, J.; Rodrigo, J.F.; Salvador, P.; Gómez, D.; Sanz, J.; Casanova, J.L. An Empirical Radiometric Intercomparison Methodology Based on Global Simultaneous Nadir Overpasses Applied to Landsat 8 and Sentinel-2. Remote Sens. 2020, 12, 2736. [Google Scholar] [CrossRef]
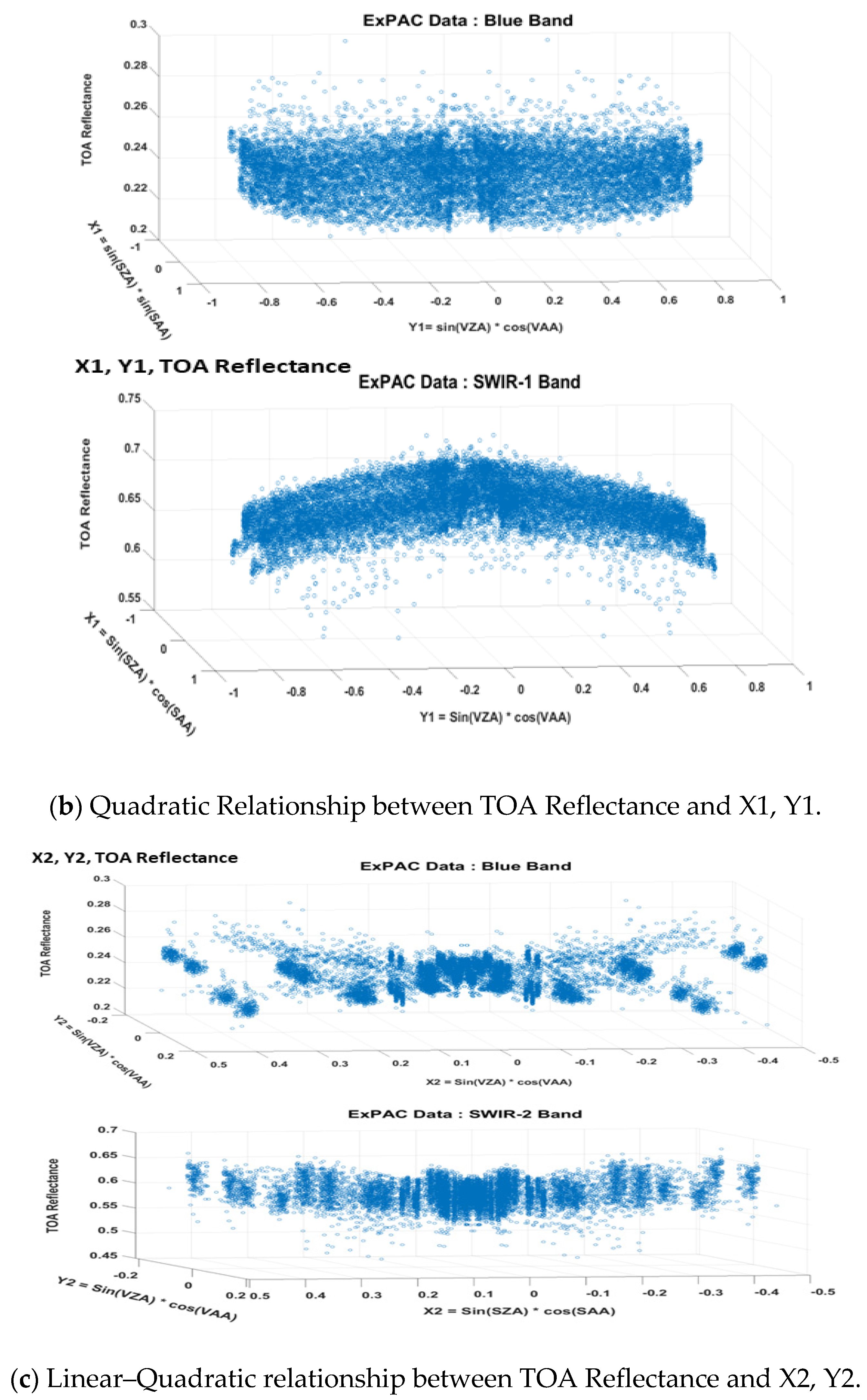
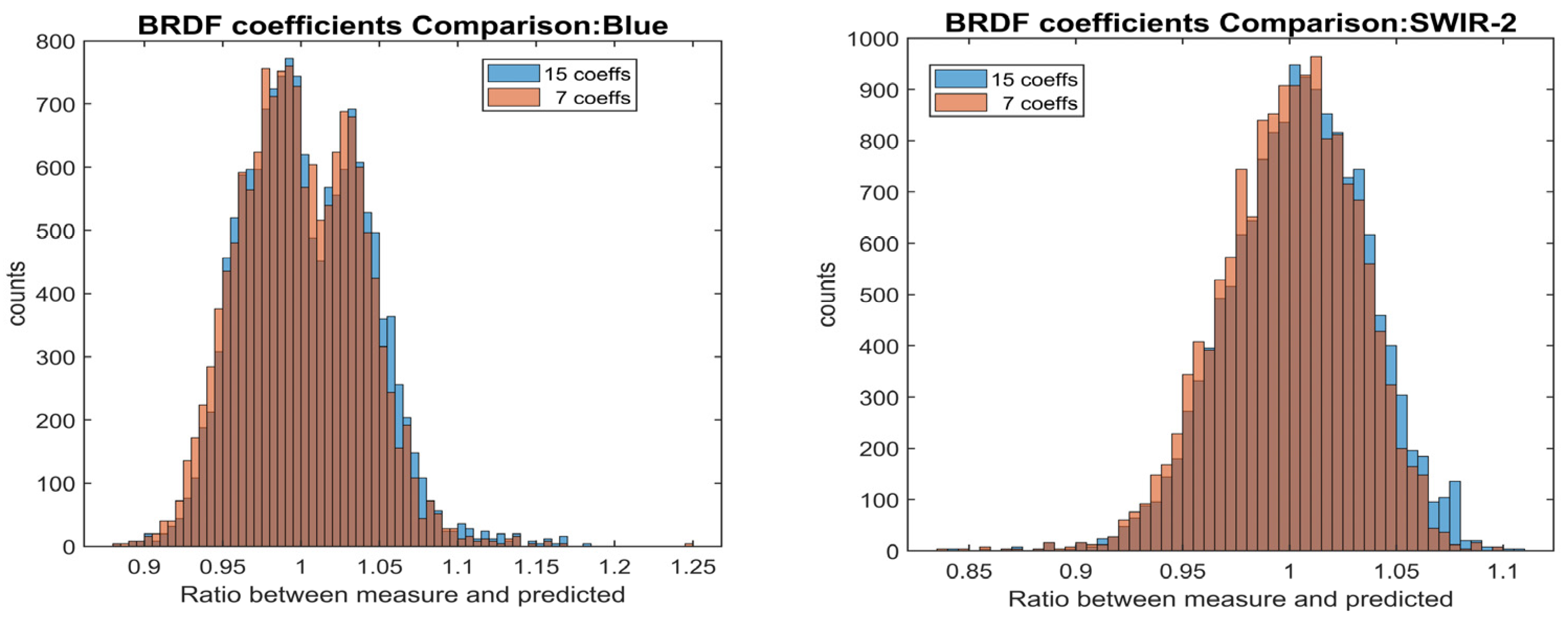


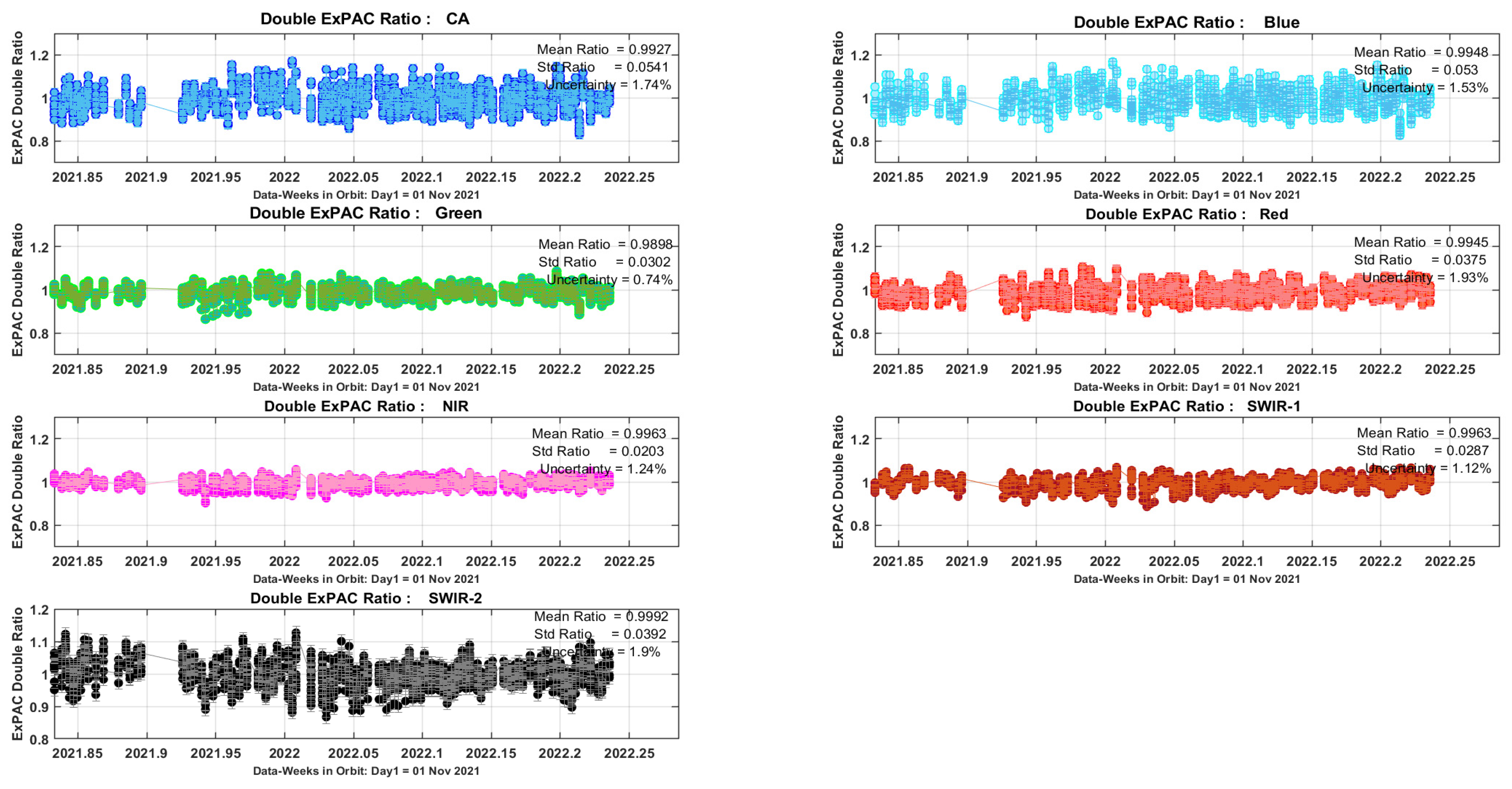
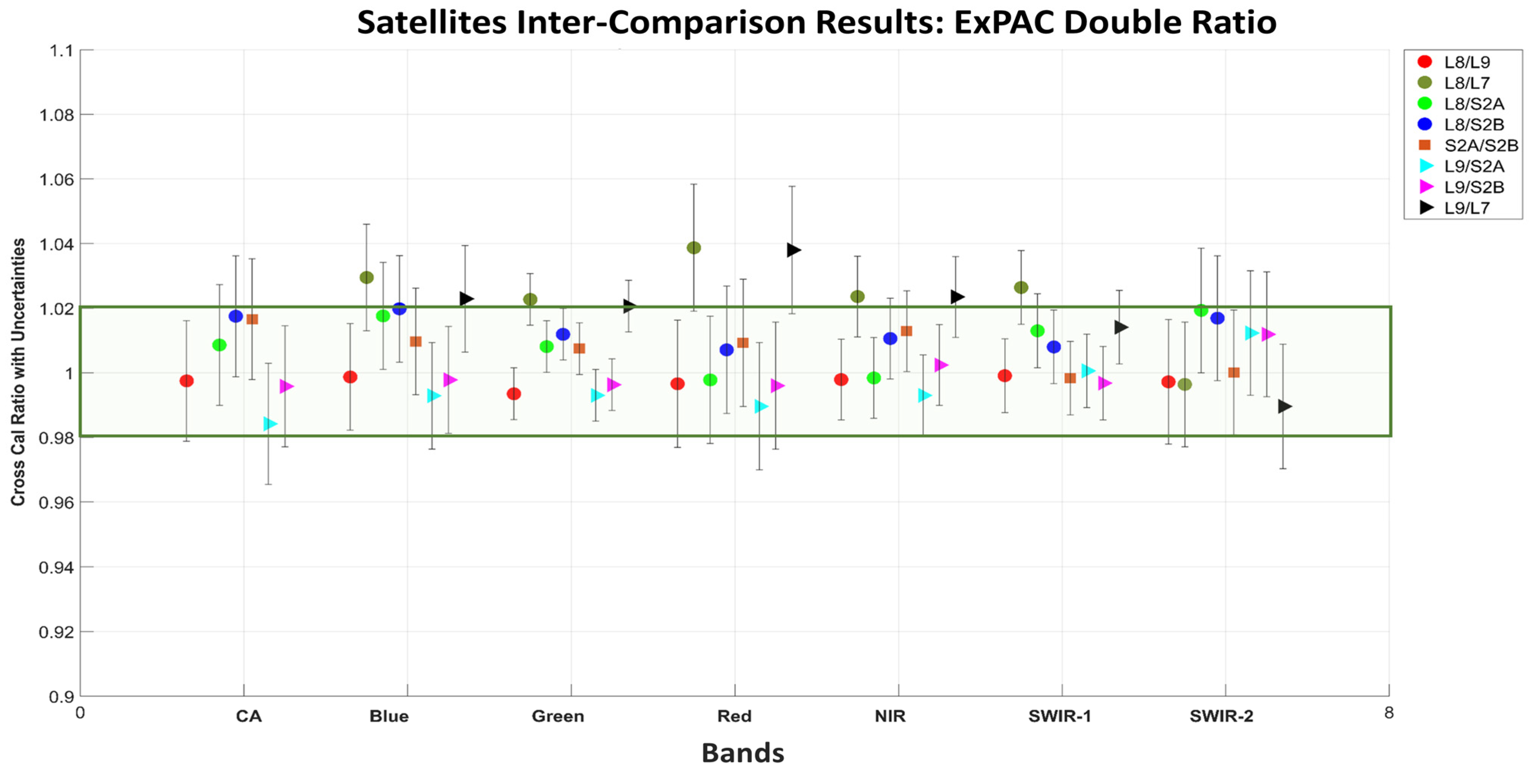
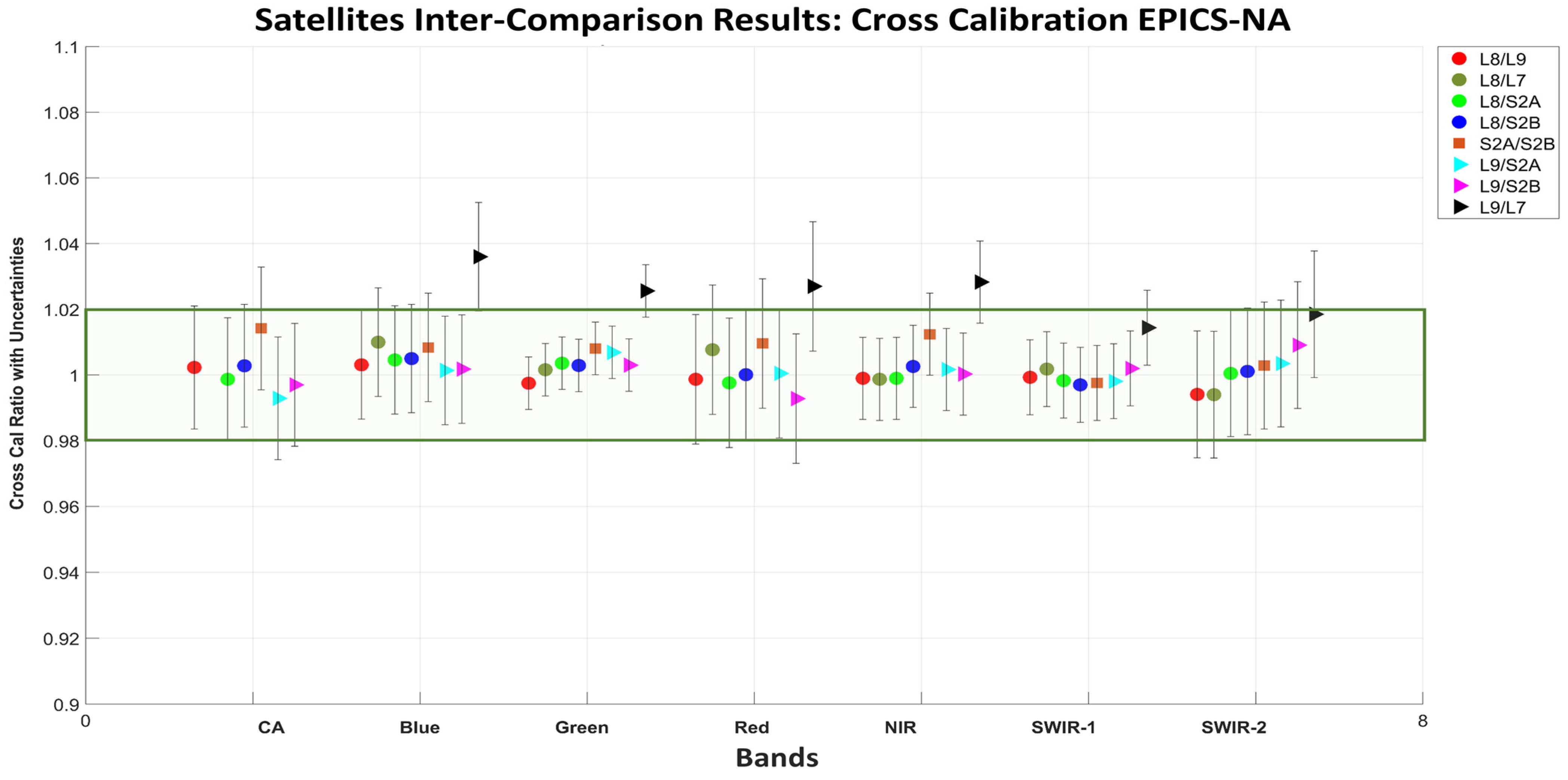


| Satellite Names | Launch Date | VZA | VAA | SZA | SAA | No. Scenes | Remarks |
|---|---|---|---|---|---|---|---|
| Landsat-8 | 11 February 2013 | 3° to 8° | 90° to 98° 270° to 280° | 20° to 60° | 73° to 160° | 2741 | 16 sites |
| Landsat-7 | 15 April 1999 | 3° to 8° | 90° to 98° 270° to 298° | 19° to 58° | 73° to 158° | 1952 | 9 sites |
| Sentinel-2A | 23 June 2015 | 2° to 12° | 90° to 97° 270° to 296° | 15° to 59° | 71° to 167° | 3583 | 16 sites |
| Sentinel-2B | 7 Mar 2017 | 2° to 12° | 90° to 98° 270° to 291° | 15° to 9° | 71° to 167° | 1784 | 16 sites |
| MODIS Terra | 18 December 1999 | 1° to 30° | 90° to 98° 270° to 291° | 12° to 55° | 81° to 167° | 1285 | 1 site-Libya-4 |
| MODIS Aqua | 4 May 2002 | 1° to 9° | 200° to 260° | 16° to 56° | 79° to 83° 90° to 102° | 1573 | 1 site-Libya-4 |
| EO-1 Hyperion | 21 November 2000 | 0° to 25° | 90° to 98° 270° to 291° | 21° to 77° | 70° to160° | 667 | 16 Sites |
| Temporal Gain | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|
| Hyp to L8 | 0.9326 ± 0.031 | 0.9766 ± 0.0274 | 0.9890 ± 0.018 | 1.0103 ± 0.030 | 0.9965 ± 0.025 | 1.0346 ± 0.032 | 1.0079 ± 0.035 |
| Terra to L8 | -- | 1.0115 ± 0.002 | 1.0371 ± 0.003 | 1.0651 ± 0.006 | 1.0310 ± 0.001 | 0.9668 ± 0.002 | 0.9171 ± 0.007 |
| ExPAC Data | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|
| Hyp-L8 | 0.2283 | 0.2447 | 0.3396 | 0.4733 | 0.5896 | 0.6770 | 0.5883 |
| Terra-L8 | NA | 0.2441 | 0.3352 | 0.4877 | 0.6066 | 0.6784 | 0.5724 |
| Landsat-8 | 0.2281 | 0.2445 | 0.3400 | 0.4736 | 0.5904 | 0.6814 | 0.5938 |
| Mean | 0.2282 | 0.2444 | 0.3382 | 0.4782 | 0.5956 | 0.6789 | 0.5848 |
| Std. Dev | 0.0001 | 0.0003 | 0.0027 | 0.0082 | 0.0096 | 0.0023 | 0.0112 |
| CV (%) | 0.06% | 0.13% | 0.79% | 1.72% | 1.61% | 0.34% | 1.91% |
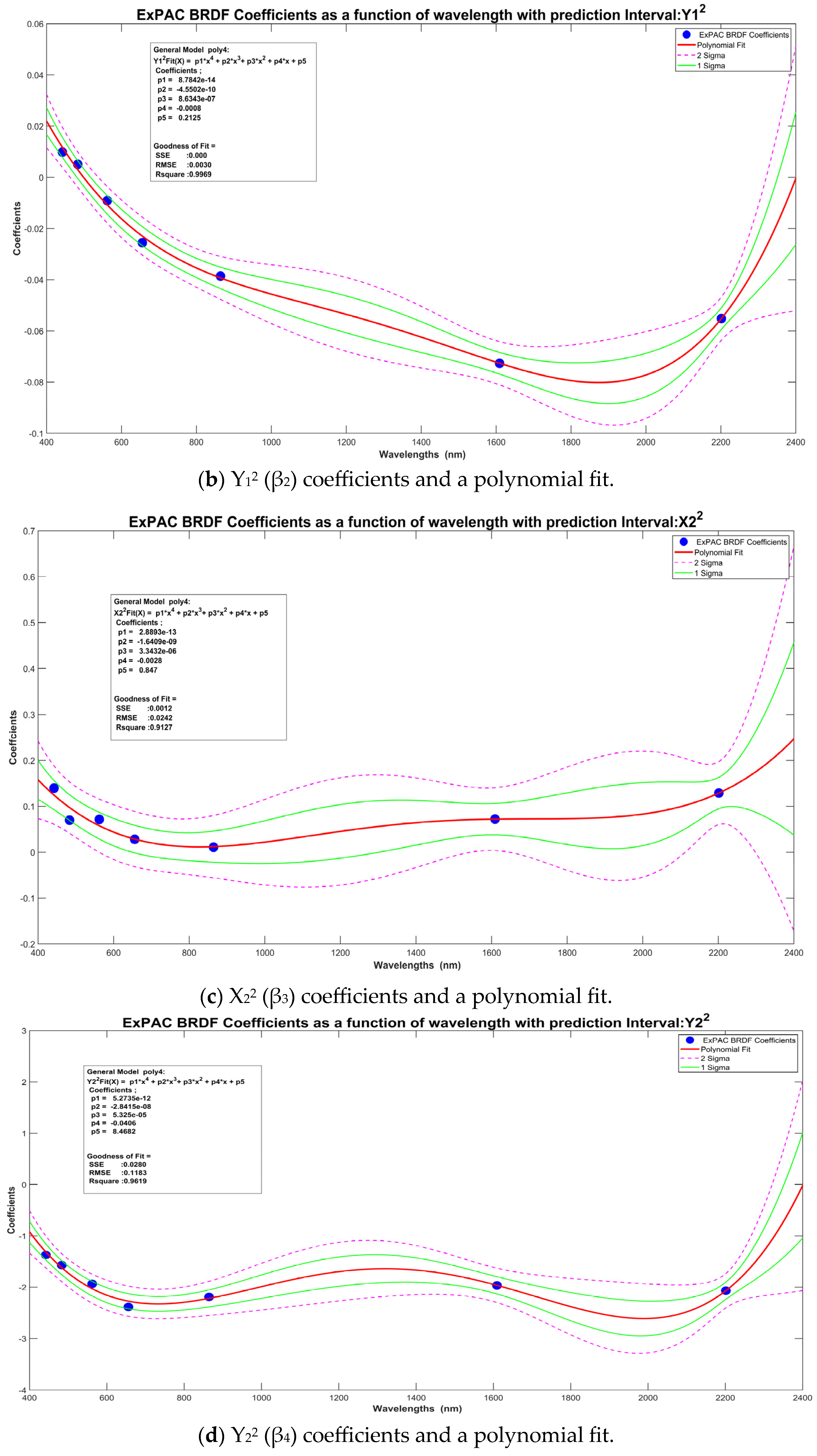
| Center Wavelength (nm) | CA (440) | Blue (480) | Green (545) | Red (655) | NIR (865) | SWIR-1 (1610) | SWIR-2 (2200) |
|---|---|---|---|---|---|---|---|
| X12 | 0.0234 | 0.0511 | 0.0162 | 0.0530 | 0.0253 | −0.0588 | −0.0724 |
| Y12 | 0.0098 | 0.0051 | −0.0091 | −0.0255 | −0.0386 | −0.0727 | −0.0552 |
| X22 | 0.1396 | 0.0699 | 0.0715 | 0.0280 | 0.0108 | 0.0722 | 0.1289 |
| Y22 | −1.3725 | −1.5704 | −1.9356 | −2.3844 | −2.1897 | −1.9655 | −2.0677 |
| X1X2 | −0.0014 | −0.0042 | 0.0113 | 0.0024 | 0.0156 | 0.0094 | 0.0063 |
| Y1Y2 | 0.2828 | 0.2949 | 0.1510 | 0.0894 | 0.1375 | 0.1754 | 0.1331 |
| Intercept | 0.2235 | 0.2335 | 0.3381 | 0.4671 | 0.5890 | 0.7005 | 0.6141 |
| CA | Blue | Green | Red | NIR | SWIR-1 | SWIR2 | |
|---|---|---|---|---|---|---|---|
| 0.9148 | 0.9334 | 0.9837 | 0.9972 | 0.9946 | 1.0645 | 1.0435 | |
| Std. Dev. | 0.030 | 0.026 | 0.017 | 0.030 | 0.024 | 0.032 | 0.036 |
| CV(%) | 3.27% | 2.81% | 1.77% | 3.01% | 2.46% | 3.04% | 3.44% |
| CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 | |
|---|---|---|---|---|---|---|---|
| SBAF | 1.000 | 1.000 | 1.005 | 1.002 | 1.000 | 1.000 | 1.001 |
| Std. Dev. | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 |
| RMSE (Reflectance Units) | Precison (Reflectance Units) | |||||||||||
| Terra | Aqua | L7 | L8 | S2A | S2B | Terra | Aqua | L7 | L8 | S2A | S2B | |
| CA | -- | -- | -- | 0.012 | 0.021 | 0.021 | -- | -- | -- | 0.013 | 0.020 | 0.020 |
| Blue | 0.007 | 0.011 | 0.027 | 0.014 | 0.016 | 0.016 | 0.007 | 0.010 | 0.018 | 0.017 | 0.015 | 0.014 |
| Green | 0.015 | 0.011 | 0.028 | 0.013 | 0.009 | 0.011 | 0.009 | 0.010 | 0.018 | 0.020 | 0.008 | 0.009 |
| Red | 0.029 | 0.013 | 0.041 | 0.014 | 0.017 | 0.011 | 0.016 | 0.011 | 0.027 | 0.020 | 0.013 | 0.011 |
| NIR | 0.029 | 0.016 | 0.024 | 0.012 | 0.025 | 0.013 | 0.016 | 0.014 | 0.021 | 0.019 | 0.016 | 0.011 |
| SWIR-1 | 0.021 | -- | 0.020 | 0.016 | 0.029 | 0.034 | 0.015 | -- | 0.017 | 0.019 | 0.021 | 0.024 |
| SWIR-2 | 0.023 | 0.022 | 0.027 | 0.019 | 0.024 | 0.024 | 0.022 | 0.021 | 0.022 | 0.020 | 0.021 | 0.021 |
| Model Accuracy (%) | The Wilcoxon Rank Sum Test (h) | |||||||||||
| Terra | Aqua | L7 | L8 | S2A | S2B | Terra | Aqua | L7 | L8 | S2A | S2B | |
| CA | -- | -- | -- | −0.75 | 0.43 | 1.85 | -- | -- | -- | 0 | 0 | 0 |
| Blue | −0.63 | 0.65 | 3.51 | −2.22 | −0.20 | 0.50 | 0 | 0 | 0 | 0 | 0 | 0 |
| Green | 2.12 | 0.89 | 2.25 | −2.41 | −1.56 | −1.04 | 0 | 0 | 0 | 0 | 0 | 0 |
| Red | 3.20 | 0.88 | 2.11 | −1.71 | −1.47 | −1.39 | 0 | 0 | 0 | 0 | 0 | 0 |
| NIR | 2.45 | 0.89 | 0.57 | −1.38 | −1.23 | −0.78 | 0 | 0 | 0 | 0 | 0 | 0 |
| SWIR-1 | 1.17 | -- | 1.48 | −0.93 | 1.25 | −0.22 | 0 | -- | 0 | 0 | 0 | 0 |
| SWIR-2 | −0.52 | 0.53 | −0.94 | −0.42 | −1.23 | 1.42 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sentinel-2 Bands | Model Accuracy (%) | RMSE (Reflectance Units) | Precision (Reflectance Units) | ExPAC D_Ratio | |||
|---|---|---|---|---|---|---|---|
| S2A | S2B | S2A | S2B | S2A | S2B | S2A/S2B | |
| CA | 1.92 | 0.33 | 0.010 | 0.010 | 0.013 | 0.010 | 1.016 |
| Blue | 0.77 | −0.21 | 0.010 | 0.010 | 0.010 | 0.010 | 1.009 |
| Green | −0.74 | −1.59 | 0.009 | 0.011 | 0.010 | 0.014 | 1.008 |
| Red | −1.11 | −2.10 | 0.012 | 0.016 | 0.016 | 0.024 | 1.011 |
| RE-1 | −4.52 | −5.59 | 0.027 | 0.032 | 0.048 | 0.059 | 1.010 |
| RE-2 | −1.27 | −1.27 | 0.016 | 0.015 | 0.020 | 0.019 | 1.000 |
| RE-3 | −2.93 | −3.92 | 0.020 | 0.025 | 0.035 | 0.046 | 1.011 |
| NIR | −0.81 | −1.32 | 0.016 | 0.018 | 0.018 | 0.022 | 1.006 |
| SWIR-1 | 0.03 | 0.56 | 0.015 | 0.015 | 0.015 | 0.017 | 0.994 |
| SWIR-2 | 2.01 | 2.25 | 0.023 | 0.025 | 0.031 | 0.034 | 0.998 |
| NIR-8A | −0.34 | −1.56 | 0.010 | 0.013 | 0.011 | 0.021 | 1.012 |
| GAINS | The EPICS-Based Cross-Calibration Ratio and the ExPAC Double Ratio Results | ||||||
|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR-1 | SWIR-2 | |
| EPICS-NA | 0.994 | 0.994 | 0.992 | 0.997 | 0.998 | 0.997 | 1.001 |
| Std. Dev | 0.048 | 0.046 | 0.029 | 0.037 | 0.021 | 0.028 | 0.039 |
| Uncertainty (%) | 2.21% | 2.03% | 1.38% | 1.44% | 1.09% | 1.27% | 1.74% |
| EPICS-Global | 0.994 | 0.994 | 0.994 | 1.003 | 1.001 | 0.998 | 0.998 |
| Std. Dev. | 0.049 | 0.052 | 0.035 | 0.051 | 0.034 | 0.033 | 0.046 |
| Uncertainty (%) | 1.66% | 1.58% | 1.20% | 1.33% | 1.01% | 1.26% | 1.53% |
| ExPAC D Ratio | 0.993 | 0.995 | 0.999 | 0.995 | 0.996 | 0.996 | 0.999 |
| Std. Dev. | 0.054 | 0.053 | 0.030 | 0.038 | 0.020 | 0.029 | 0.039 |
| Uncertainty (%) | 1.87% | 1.65% | 0.80% | 1.97% | 1.25% | 1.14% | 1.93% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaewmanee, M.; Leigh, L.; Shah, R.; Gross, G. Inter-Comparison of Landsat-8 and Landsat-9 during On-Orbit Initialization and Verification (OIV) Using Extended Pseudo Invariant Calibration Sites (EPICS): Advanced Methods. Remote Sens. 2023, 15, 2330. https://doi.org/10.3390/rs15092330
Kaewmanee M, Leigh L, Shah R, Gross G. Inter-Comparison of Landsat-8 and Landsat-9 during On-Orbit Initialization and Verification (OIV) Using Extended Pseudo Invariant Calibration Sites (EPICS): Advanced Methods. Remote Sensing. 2023; 15(9):2330. https://doi.org/10.3390/rs15092330
Chicago/Turabian StyleKaewmanee, Morakot, Larry Leigh, Ramita Shah, and Garrison Gross. 2023. "Inter-Comparison of Landsat-8 and Landsat-9 during On-Orbit Initialization and Verification (OIV) Using Extended Pseudo Invariant Calibration Sites (EPICS): Advanced Methods" Remote Sensing 15, no. 9: 2330. https://doi.org/10.3390/rs15092330
APA StyleKaewmanee, M., Leigh, L., Shah, R., & Gross, G. (2023). Inter-Comparison of Landsat-8 and Landsat-9 during On-Orbit Initialization and Verification (OIV) Using Extended Pseudo Invariant Calibration Sites (EPICS): Advanced Methods. Remote Sensing, 15(9), 2330. https://doi.org/10.3390/rs15092330






