Exploring the Optimal 4D-SfM Photogrammetric Models at Plot Scale
Abstract
1. Introduction
2. Materials and Methods
2.1. Testing Experiment Site
2.2. Physical Measurement for Accuracy Assessment
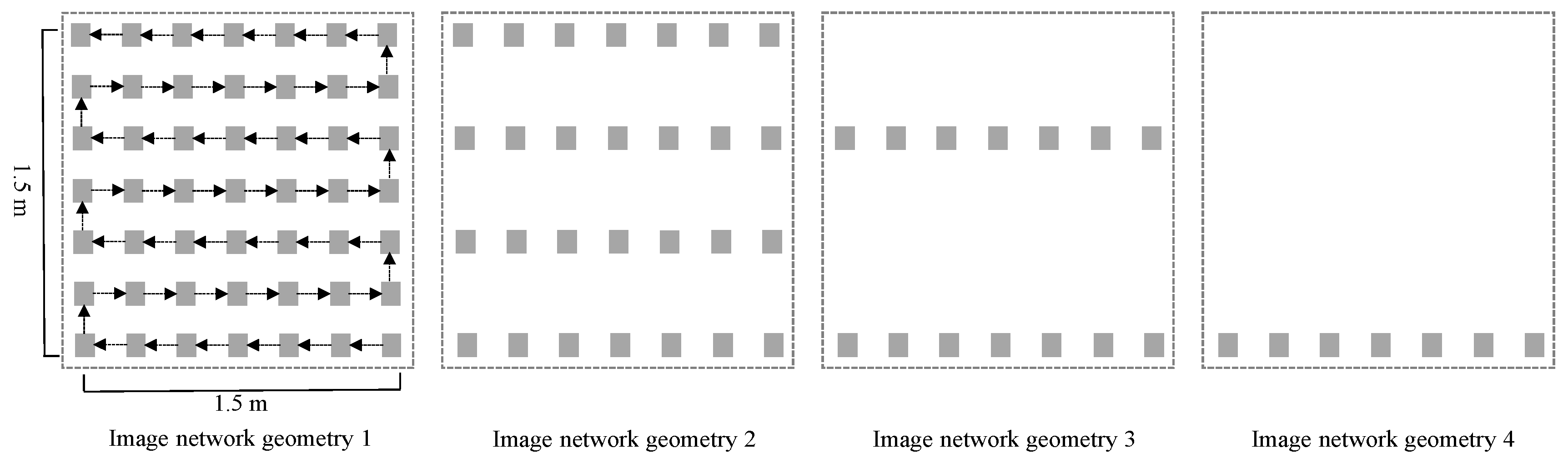
2.3. The One-Camera Time-Lapse 4D-SfM Photogrammetry
2.4. The Strategies for 4D-Data Reconstruction
2.5. The Performance of 8 Different 4D-SfM Models in Terms of the Tie Points and Dense Clouds
2.6. The Uncertainty of the 8 4D-SfM Models
2.7. The Influence of Wet and Dry Condition on the Model Accuracy
2.8. The Absolute Accuracy of the 8 4D-SfM Models
3. Results
3.1. The Number of Tie Points, Dense Clouds of the 8 4D-SfM Models
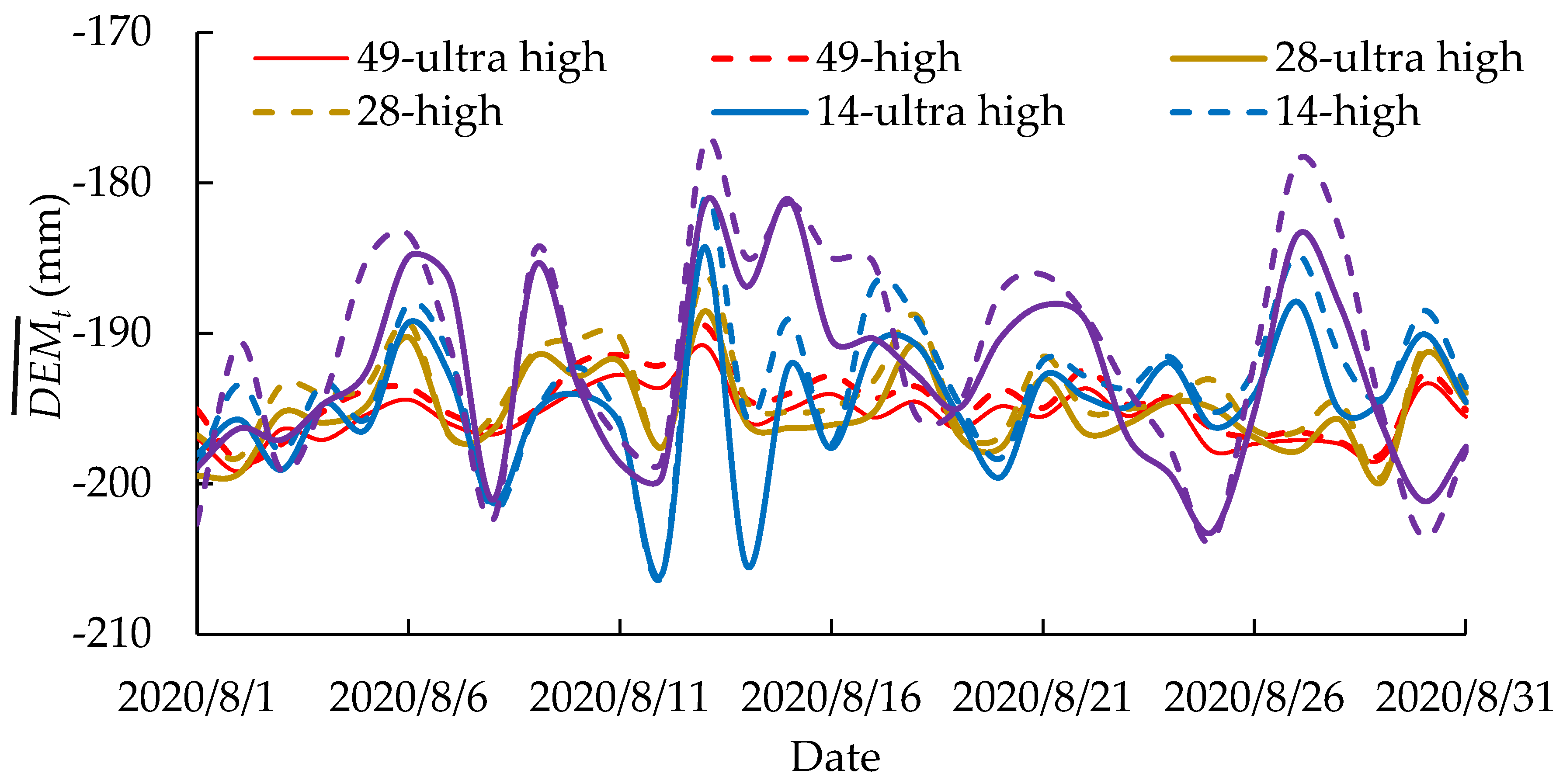
3.2. The Similarity and Difference of the 8 4D-SfM Models for Reconstructed DEM
3.3. The Stability of the 8 4D-SfM Models
3.4. The Assessment of the Model Accuracy
4. Discussion
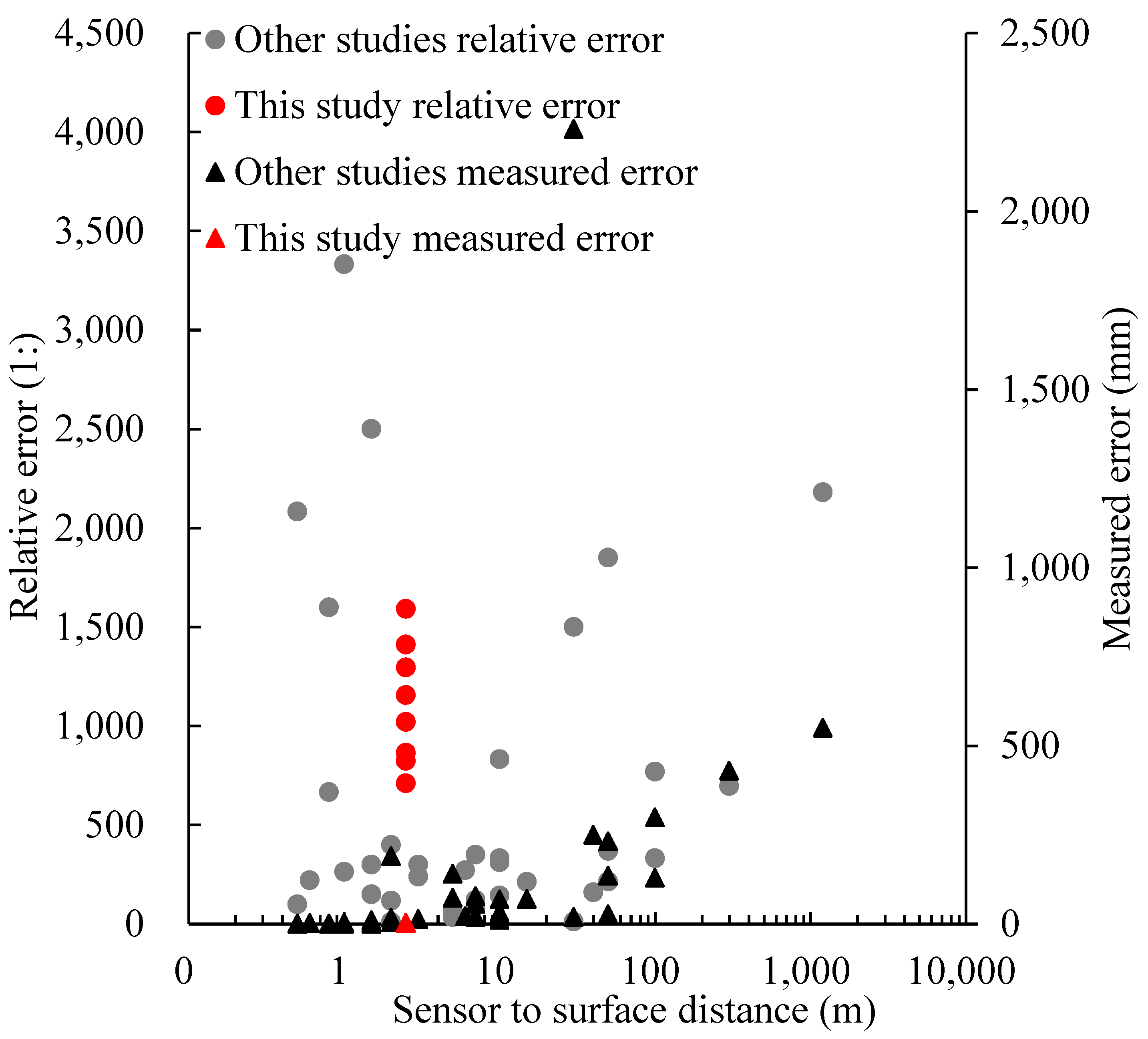
4.1. Accuracy of 4D-SfM and Other Ground-Based Photogrammetry Studies
| References (Terrestrial) | Distance (m) | Measurement Error (mm) | Relative Error |
|---|---|---|---|
| Castillo et al., 2012 [38] | 7 | 20 | 350.0 |
| Castillo et al., 2014 [39] | 6 | 22 | 273.0 |
| Castillo et al., 2015 [40] | 10 | 69 | 145.0 |
| Favalli et al., 2012 [41] | 1 | 0.3–3.8 | 367–3333.3 |
| Fonstad et al., 2013 [42] | 40 | 250 | 160.0 |
| Frankl et al., 2015 [43] | 2 | 17–190 | 10.5, 117.6 |
| Gómez-Gutiérrez et al., 2014 [44] | 300 | 280, 210 | 1071, 1429 |
| Kaiser et al., 2014 [45] | 5 | 73, 141 | 68.5, 35.5 |
| Leon et al., 2015 [46] | 1.5 | 0.6 | 2500.0 |
| Nouwakpo et al., 2015 [47] | 2 | 5 | 400.0 |
| Piermattei et al., 2015 [48] | 7 | 57–300 | 23.3–122.8 |
| Ružić et al., 2014 [49] | 15 | 70 | 214.0 |
| Smith et al., 2014 [50] | 50 | 135 | 370.0 |
| Snapir et al., 2014 [51] | 0.6 | 2.7 | 222.0 |
| Stumpf et al. 2014 [20] | 50 | 27, 232 | 1851.9, 215.5 |
| Rodríguez et al., 2022 [24] | 0.8 | 0.5, 1.2 | 1600, 666.7 |
| Morgan, 2019 [23] | 0.5 | 0.24 | 2083.3 |
| Eltner et al., 2017 [1] | 3 | 12.5 | 240.0 |
| Gómez-Gutiérrez et al., 2020 [52] | 10 | 30 | 333.3 |
| Irvine-Fynn et al., 2022 [36] | 1.5 | 5, 10 | 300, 150 |
| He et al., 2022 [5] | 0.5 | 1.8 | 100.0 |
| Chakra et al., 2019 [26] | 30 | 20, 2230 | 1500, 13.5 |
| Filhol et al., 2019 [37] | 1200 | 550 | 2181.8 |
| Liu et al., 2021 [25] | 3 | 14 | 214.3 |
| This study, 49-ultra high | 2.5 | 1.57 | 1592.4 |
| This study, 49-high | 2.5 | 2.45 | 1020.4 |
| This study, 28-ultra high | 2.5 | 1.77 | 1412.4 |
| This study, 28-high | 2.5 | 2.89 | 865.1 |
| This study, 14-ultra high | 2.5 | 1.93 | 1295.3 |
| This study, 14-high | 2.5 | 3.03 | 825.1 |
| This study, 7-ultra high | 2.5 | 2.16 | 1157.4 |
| This study, 7-high | 2.5 | 3.51 | 712.3 |
4.2. The Effect of Surface Conditions on Measurement Accuracy
4.3. The Potential Application of 4D-SfM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eltner, A.; Kaiser, A.; Abellan, A.; Schindewolf, M. Time lapse structure-from-motion photogrammetry for continuous geomorphic monitoring. Earth Surf. Process. Landf. 2017, 42, 2240–2253. [Google Scholar] [CrossRef]
- Ryan, J.C.; Hubbard, A.L.; Box, J.E.; Todd, J.; Christoffersen, P.; Carr, J.R.; Holt, T.; Snooke, N. UAV photogrammetry and structure from motion to assess calving dynamics at store glacier, a large outlet draining the Greenland ice sheet. Cryosphere 2015, 9, 1–11. [Google Scholar] [CrossRef]
- Revuelto, J.; López-Moreno, J.I.; Alonso-González, E. Light and shadow in mapping alpine snowpack with unmanned aerial vehicles in the absence of ground control points. Water Resour. Res. 2021, 57, e2020WR028980. [Google Scholar] [CrossRef]
- Gomez, C.; Hayakawa, Y.; Obanawa, H. A study of Japanese landscapes using structure from motion derived DSMs and DEMs based on historical aerial photographs: New opportunities for vegetation monitoring and diachronic geomorphology. Geomorphology 2015, 242, 11–20. [Google Scholar] [CrossRef]
- He, T.; Yang, Y.; Shi, Y.; Liang, X.; Fu, S.; Xie, G.; Liu, B.; Liu, Y. Quantifying spatial distribution of interrill and rill erosion in a loess at different slopes using structure from motion (SfM) photogrammetry. Int. Soil Water Conserv. Res. 2022, 10, 393–406. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating biomass of barley using crop surface models (CSMs) derived from UAV-based RGB imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Cunliffe, A.; Anderson, K. Measuring above-Ground Biomass with Drone Photogrammetry: Data Collection Protocol, 2 January 2019, PROTOCOL (Version 1). Protocol Exchange. Available online: https://www.researchgate.net/publication/330096533_Measuring_Above-ground_Biomass_with_Drone_Photogrammetry_Data_Collection_Protocol (accessed on 22 April 2023).
- Cunliffe, A.M.; Anderson, K.; Boschetti, F.; Brazier, R.E.; Graham, H.A.; Myers-Smith, I.H.; Astor, T.; Boer, M.M.; Calvo, L.G.; Clark, P.E.; et al. Global application of an unoccupied aerial vehicle photogrammetry protocol for predicting above ground biomass in non-forest ecosystems. Remote Sens. Ecol. Conserv. 2022, 8, 57–71. [Google Scholar] [CrossRef]
- Forsmoo, J.; Anderson, K.; Macleod, C.J.A.; Wilkinson, M.E.; Brazier, R. Drone-based structure-from-motion photogrammetry captures grassland sward height variability. J. Appl. Ecol. 2018, 55, 2587–2599. [Google Scholar] [CrossRef]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; O’Connor, J.; Rosette, J. Structure from Motion photogrammetry in forestry: A review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef]
- Eltner, A.; Sofia, G. Structure from motion photogrammetric technique, 1st ed. In Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2020; Volume 23, pp. 1–22. [Google Scholar]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellan, A. Image-based surface reconstruction in geomorphometry—Merits, limits and developments. Earth Surf. Dynam. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from motion photogrammetry in physical geography. Prog. Phys. Geogr. 2016, 40, 247–275. [Google Scholar] [CrossRef]
- James, M.; Chandler, J.; Eltner, A.; Fraser, C.; Miller, P.; Mills, J.; Noble, T.; Robson, S.; Lane, S. Guidelines on the use of structure from motion photogrammetry in geomorphic research. Earth Surf. Process. Landf. 2019, 44, 2081–2084. [Google Scholar] [CrossRef]
- Westoby, M.J.J.; Brasington, J.; Glasser, N.F.F.; Hambrey, M.J.J.; Reynolds, J.M.M. “Structure-from-motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Griffiths, D.; Burningham, H. Comparison of pre- and selfcalibrated camera calibration models for UAS-derived nadir imagery for a SfM application. Prog. Phys. Geogr. 2019, 43, 215–235. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Sequential digital elevation models of active lava flows from ground-based stereo time-lapse imagery. ISPRS J. Photogramm. Remote Sens. 2014, 97, 160–170. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Straightforward reconstruction of 3-D surfaces and topography with a camera: Accuracy and geoscience application. J. Geophys. Res. 2012, 117, F03017. [Google Scholar] [CrossRef]
- Senn, J.A.; Mills, J.; Walsh, C.L.; Addy, S.; Peppa, M. On-site geometric calibration of RPAS mounted sensors for SfM photogrammetric geomorphological surveys. Earth Surf. Process. Landf. 2022, 47, 1615–1634. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.-P.; Allemand, P.; Pierrot-Deseilligny, M.; Skupinski, G. Ground-based multi-view photogrammetry for the monitoring of landslide deformation and erosion. Geomorphology 2014, 231, 130–145. [Google Scholar] [CrossRef]
- Gaiani, M.; Remondino, F.; Apollonio, F.I.; Ballabeni, A. An advanced pre-processing pipeline to improve automated photogrammetric reconstructions of Architectural scenes. Remote Sens. 2016, 8, 178. [Google Scholar] [CrossRef]
- Forsmoo, J.; Anderson, K.; Macleod, C.J.A.; Wilkinson, M.E.; BeBell, L.; Brazier, R. Structure from motion photogrammetry in ecology: Does the choice of software matter? Ecol. Evol. 2019, 9, 12964–12979. [Google Scholar] [CrossRef]
- Morgan, B.; Ford, A.L.J.; Smith, M.J. Standard methods for creating digital skeletal models using structure-from-motion photogrammetry. Am. J. Phys. Anthropol. 2019, 169, 152–160. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, R.F.; Ponte, M.; Bento, R.; Cardoso, R. Potential of mobile application based on structure from motion (SfM) photogrammetry to monitor slope fast erosion by runoff water. Catena 2022, 216, 106359. [Google Scholar] [CrossRef]
- Liu, J.; Chen, R.; Ding, Y.; Han, C.; Ma, S. Snow process monitoring using time-lapse structure-from-motion photogrammetry with a single camera. Cold Reg. Sci. Technol. 2021, 190, 103355. [Google Scholar] [CrossRef]
- Chakra, C.A.; Gascoin, S.; Somma, J.; Fanise, P.; Drapeau, L. Monitoring the snowpack volume in a Sinkhole on Mount Lebanon using time lapse photogrammetry. Sensors 2019, 19, 3890. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Mallalieu, J.; Carrivick, J.L.; Quincey, D.J.; Smith, M.W.; James, W.H.M. An integrated structure-from-motion and time-lapse technique for quantifying ice-margin dynamics. J. Glaciol. 2017, 63, 937–949. [Google Scholar] [CrossRef]
- Galland, O.; Bertelsen, H.S.; Guldstrand, F.; Girod, L.; Johannessen, R.F.; Bjugger, F.; Burchardt, S.; Mair, K. Application of open-source photogrammetric software MicMac for monitoring surface deformation in laboratory models. J. Geophys. Res. Solid Earth 2016, 121, 2852–2872. [Google Scholar] [CrossRef]
- Young, D.J.N.; Koontz, M.J.; Weeks, J. Optimizing aerial imagery collection and processing parameters for drone-based individual tree mapping in structurally complex conifer forests. Methods Ecol. Evol. 2022, 13, 1447–1463. [Google Scholar] [CrossRef]
- Gerke, M.; Przybilla, H. Accuracy analysis of photogrammetric UAV image blocks: Influence of on board RTK-GNSS and cross flight patterns. Photogramm. Fernerkund. Geoinf. 2016, 17–30. [Google Scholar] [CrossRef]
- Bayley, D.T.I.; Mogg, A.O.M. A protocol for the large-scale analysis of reefs using structure from Motion photogrammetry. Methods Ecol. Evol. 2020, 11, 1410–1420. [Google Scholar] [CrossRef]
- Agisoft, LLC. PhotoScan User Manual, Professional Edition, Version 1.4. 2008. Available online: https://www.agisoft.com/pdf/photoscan-pro_1_4_en.pdf (accessed on 22 April 2023).
- Deliry, S.I.; Avdan, U. Accuracy of Unmanned Aerial Systems Photogrammetry and Structure from Motion in Surveying and Mapping: A Review. J. Indian Soc. Remote Sens. 2021, 49, 1997–2017. [Google Scholar] [CrossRef]
- Morel, J.M.; Yu, G. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Irvine-Fynn, T.D.L.; Holt, T.O.; James, T.D.; Smith, M.W.; Rutter, N.; Porter, P.R.; Hodson, A.J. Time-lapse photogrammetry reveals hydrological controls of fine-scale High-Arctic glacier surface roughness evolution. Earth Surf. Process. Landf. 2022, 47, 1635–1652. [Google Scholar] [CrossRef]
- Filhol, S.; Perret, A.; Girod, L.; Sutter, G.; Schuler, T.V.; Burkhart, J.F. Time-Lapse Photogrammetry of distributed snow depth during snowmelt. Water Resour. Res. 2019, 55, 7916–7926. [Google Scholar] [CrossRef]
- Castillo, C.; James, M.R.; Redel-Macías, M.D.; Pérez, R.; Gómez, J.A. SF3M software: 3-D photo-reconstruction for nonexpert users and its application to a gully network. Soil 2015, 1, 583–594. [Google Scholar] [CrossRef]
- Castillo, C.; Pérez, R.; James, M.R.; Quinton, J.N.; Taguas, E.V.; Gómez, J.A. Comparing the Accuracy of Several Field Methods for Measuring Gully Erosion. Soil Sci. Soc. Am. J. 2012, 76, 1319–1332. [Google Scholar] [CrossRef]
- Castillo, C.; Taguas, E.V.; Zarco-Tejada, P.; James, M.R.; Gómez, J.A. The normalized topographic method: An automated procedure for gully mapping using GIS. Earth Surf. Process. Landf. 2014, 39, 2002–2015. [Google Scholar] [CrossRef]
- Favalli, M.; Fornaciai, A.; Isola, I.; Tarquini, S.; Nannipieri, L. Multiview 3-D reconstruction in geosciences. Comput. Geosci. 2012, 44, 168–176. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic structure from motion: A new development in photogrammetric measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- Frankl, A.; Stal, C.; Abraha, A.; Nyssen, J.; Rieke-Zapp, D.; De Wulf, A.; Poesen, J. Detailed recording of gully morphology in 3-D through image-based modelling PhotoScan Digital Elevation Model (DEM) Soil pipes Structure from M otion–Multi View Stereo (SfM–MVS) Volume calculation. Catena 2015, 127, 92–101. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, Á.; de Sanjosé-Blasco, J.J.; de Matías Bejarano, J.; Berenguer-Sempere, F. Comparing Two Photo Reconstruction Methods to Produce High Density Point Clouds and DEMs in the Corral del Veleta Rock Glacier (Sierra Nevada, Spain). Remote Sens. 2014, 6, 5407–5427. [Google Scholar] [CrossRef]
- Kaiser, A.; Neugirg, F.; Rock, G.; Müller, C.; Haas, F.; Ries, J.; Schmidt, J. Small-Scale Surface Reconstruction and Volume Calculation of Soil Erosion in Complex Moroccan Gully Morphology Using Structure from Motion. Remote Sens. 2014, 6, 7050–7080. [Google Scholar] [CrossRef]
- Leon, J.X.; Roelfsema, C.M.; Saunders, M.I.; Phinn, S.R. Measuring coral reef terrain roughness using “Structure-from-Motion” close-range photogrammetry. Geomorphology 2015, 242, 21–28. [Google Scholar] [CrossRef]
- Nouwakpo, S.K.; James, M.R.; Weltz, M.A.; Huang, C.-H.; Chagas, I.; Lima, L. Evaluation of structure from motion for soil microtopography measurement. Photogramm. Rec. 2014, 29, 297–316. [Google Scholar] [CrossRef]
- Piermattei, L.; Carturan, L.; Guarnieri, A. Use of terrestrial photogrammetry based on structure from motion for mass balance estimation of a small glacier in the Italian Alps. Earth Surf. Process. Landf. 2015, 40, 1791–1802. [Google Scholar] [CrossRef]
- Ružić, I.; Marovic, I.; Benac, C.; Ilic, S. Coastal cliff geometry derived from structure-from-motion photogrammetry at Stara Baka, Krk Island, Croatia. Geo Mar. Lett. 2014, 34, 555–565. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Hooke, J.; Kirkby, M.J. Reconstructing flash flood magnitudes using “Structure-from-Motion”: A rapid assessment tool. J. Hydrol. 2014, 519, 1914–1927. [Google Scholar] [CrossRef]
- Snapir, B.; Hobbs, S.; Waine, T.W. Roughness measurements over an agricultural soil surface with Structure from Motion. ISPRS J. Photogramm. Remote Sens. 2014, 96, 210–223. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, Á.; Biggs, T.; Gudino-Elizondo, N.; Errea, P.; Alonso-González, E.; Nadal Romero, E.; de Sanjosé Blasco, J. Using visibility analysis to improve point density and processing time of SfM-MVS techniques for 3D reconstruction of landforms. Earth Surf. Process. Landf. 2020, 45, 2524–2539. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Smith, M.W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Process. Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Agueera-Vega, F.; Carvajal-Ramirez, F.; Martinez-Carricondo, P.; López, J.S.; Mesas-Carrascosa, F.J.; Garcia-Ferrer, A.; Pérez-Porras, F.J. Reconstruction of extreme topography from UAV structure from motion photogrammetry. Measurement 2018, 121, 127–138. [Google Scholar] [CrossRef]
- Rusnák, M.; Sládek, J.; Kidová, A.; Lehotský, M. Template for high-resolution river landscape mapping using UAV technology. Measurement 2018, 115, 139–151. [Google Scholar] [CrossRef]
- Hood, E.; Williams, M.; Cline, D. Sublimation from a seasonal snowpack at a continental, mid-latitude alpine site. Hydrol. Process. 1999, 13, 1781–1797. [Google Scholar] [CrossRef]
- Marks, D.; Dozier, J. Climate and energy exchanges at the snow surface in the alpine region of the Sierra Nevada: 2. Snow cover energy balance. Water Resour. Res. 1992, 28, 3043–3054. [Google Scholar] [CrossRef]
- Stössel, F.; Guala, M.; Fierz, C.; Manes, C.; Lehning, M. Micrometeorological and morphological observations of surface hoar dynamics on a mountain snow cover. Water Resour. Res. 2010, 46, 1–11. [Google Scholar] [CrossRef]
- Li, S.; Yao, T.; Yang, W.; Yu, W.; Zhu, M. Glacier energy and mass balance in the inland Tibetan Plateau: Seasonal and interannual variability in relation to atmospheric changes. J. Geophys. Res. Atmos. 2018, 123, 6390–6490. [Google Scholar] [CrossRef]




| Model | Tie Points | Dense Cloud Number | Time Consumed (h) | Overlap at Front Direction | Overlap at Lateral Direction |
|---|---|---|---|---|---|
| 49-ultra high | 9040 | 4.50 × 107 | 10.5 | 85% | 85% |
| 49-high | 8430 | 1.03 × 107 | 6.4 | 85% | 85% |
| 28-ultra high | 5987 | 3.63 × 107 | 4.32 | 80% | 85% |
| 28-high | 5846 | 8.19 × 106 | 2.21 | 80% | 85% |
| 14-ultra high | 5987 | 3.63 × 107 | 1.32 | 70% | 85% |
| 14-high | 5846 | 8.19 × 106 | 0.21 | 70% | 85% |
| 7-ultra high | 5740 | 3.20 × 107 | 0.33 | 0 | 85% |
| 7-high | 5650 | 7.21 × 106 | 0.12 | 0 | 85% |
| Mode | 49-Ultra High | 49-High | 28-Ultra High | 28-High | 14-Ultra High | 14-High | 7-Ultra High | 7-High |
|---|---|---|---|---|---|---|---|---|
| (mm) | −195.50 | −194.61 | −195.19 | −194.01 | −194.88 | −193.29 | −192.75 | −191.38 |
| 49-Ultra High | 49-High | 28-Ultra High | 28-High | 14-Ultra High | 14-High | 7-Ultra High | 7-High | |
|---|---|---|---|---|---|---|---|---|
| 49-ultra high | 1.00 | |||||||
| 49-high | 0.96 | 1.00 | ||||||
| 28-ultra high | 0.68 | 0.60 | 1.00 | |||||
| 28-high | 0.65 | 0.61 | 0.97 | 1.00 | ||||
| 14-ultra high | 0.24 | 0.17 | 0.47 | 0.48 | 1.00 | |||
| 14-high | 0.21 | 0.16 | 0.49 | 0.49 | 0.92 | 1.00 | ||
| 7-ultra high | 0.23 | 0.21 | 0.23 | 0.23 | 0.41 | 0.56 | 1.00 | |
| 7-high | 0.18 | 0.17 | 0.17 | 0.17 | 0.37 | 0.53 | 0.93 | 1 |
| Dry/Wet Days | Model | (mm) | Abs (mm) | Std (mm) |
|---|---|---|---|---|
| Dry | 49-ultra high | −195.49 | 1.39 | 1.77 |
| 49-high | −194.48 | 1.59 | 2.02 | |
| 28-ultra high | −195.96 | 1.64 | 2.36 | |
| 28-high | −194.81 | 1.94 | 2.76 | |
| 14-ultra high | −195.06 | 3.43 | 4.89 | |
| 14-high | −193.17 | 3.80 | 5.23 | |
| 7-ultra high | −191.19 | 5.15 | 6.09 | |
| 7-high | −190.13 | 6.45 | 7.49 | |
| Wet | 49-ultra high | −195.52 | 1.31 | 1.72 |
| 49-high | −194.86 | 1.48 | 1.93 | |
| 28-ultra high | −193.79 | 2.54 | 2.80 | |
| 28-high | −192.56 | 2.44 | 2.79 | |
| 14-ultra high | −194.54 | 2.77 | 3.51 | |
| 14-high | −193.49 | 3.08 | 3.97 | |
| 7-ultra high | −194.27 | 4.71 | 5.54 | |
| 7-high | −193.66 | 5.46 | 6.58 |
| Model | Mean Error (mm) | Absolute Error (mm) | RMSE (mm) |
|---|---|---|---|
| 49-ultra high | −0.56 | 1.57 | 2.01 |
| 49-high | −1.55 | 2.45 | 3.14 |
| 28-ultra high | −0.80 | 1.77 | 2.41 |
| 28-high | −2.21 | 2.89 | 3.80 |
| 14-ultra high | −1.14 | 1.93 | 2.52 |
| 14-high | −1.89 | 3.03 | 4.03 |
| 7-ultra high | −1.24 | 2.16 | 2.94 |
| 7-high | −2.44 | 3.51 | 4.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Ma, S.; Chen, R. Exploring the Optimal 4D-SfM Photogrammetric Models at Plot Scale. Remote Sens. 2023, 15, 2269. https://doi.org/10.3390/rs15092269
Liu J, Ma S, Chen R. Exploring the Optimal 4D-SfM Photogrammetric Models at Plot Scale. Remote Sensing. 2023; 15(9):2269. https://doi.org/10.3390/rs15092269
Chicago/Turabian StyleLiu, Junfeng, Shaoxiu Ma, and Rensheng Chen. 2023. "Exploring the Optimal 4D-SfM Photogrammetric Models at Plot Scale" Remote Sensing 15, no. 9: 2269. https://doi.org/10.3390/rs15092269
APA StyleLiu, J., Ma, S., & Chen, R. (2023). Exploring the Optimal 4D-SfM Photogrammetric Models at Plot Scale. Remote Sensing, 15(9), 2269. https://doi.org/10.3390/rs15092269







