Analysis of Characteristics for Inter-System Bias on Multi-GNSS Undifferenced and Uncombined Precise Point Positioning
Abstract
1. Introduction
2. Methods
2.1. Undifferenced and Uncombined Observation Equations
2.2. ISB Definition
2.3. ISB Parameter Stochastic Model
3. Data Sets and Processing Strategies
4. Experimental Validation
4.1. Analysis of Short- and Long-Term Time Characteristics of ISB
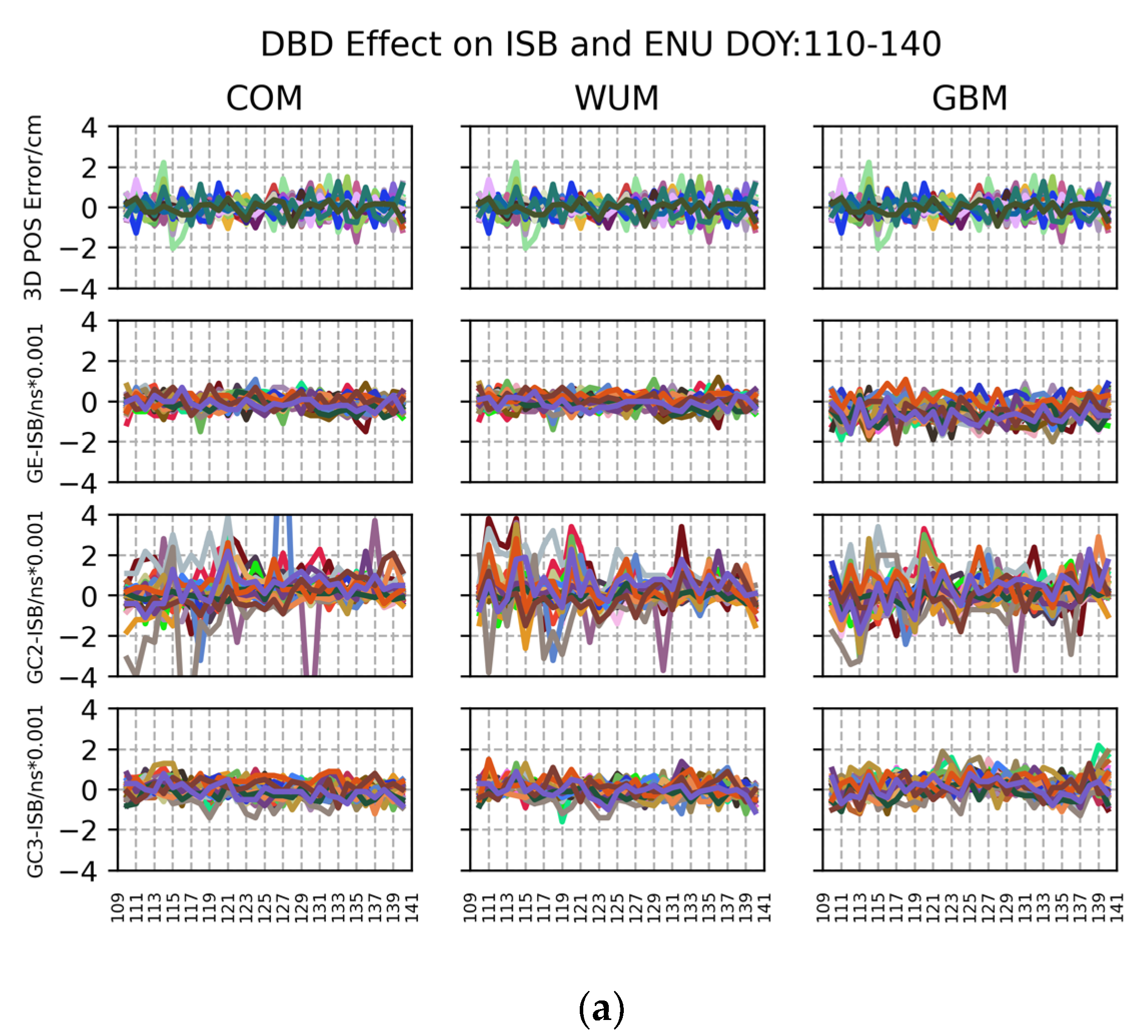
4.1.1. Analysis of DBD Effect on Time Characteristics of the ISB
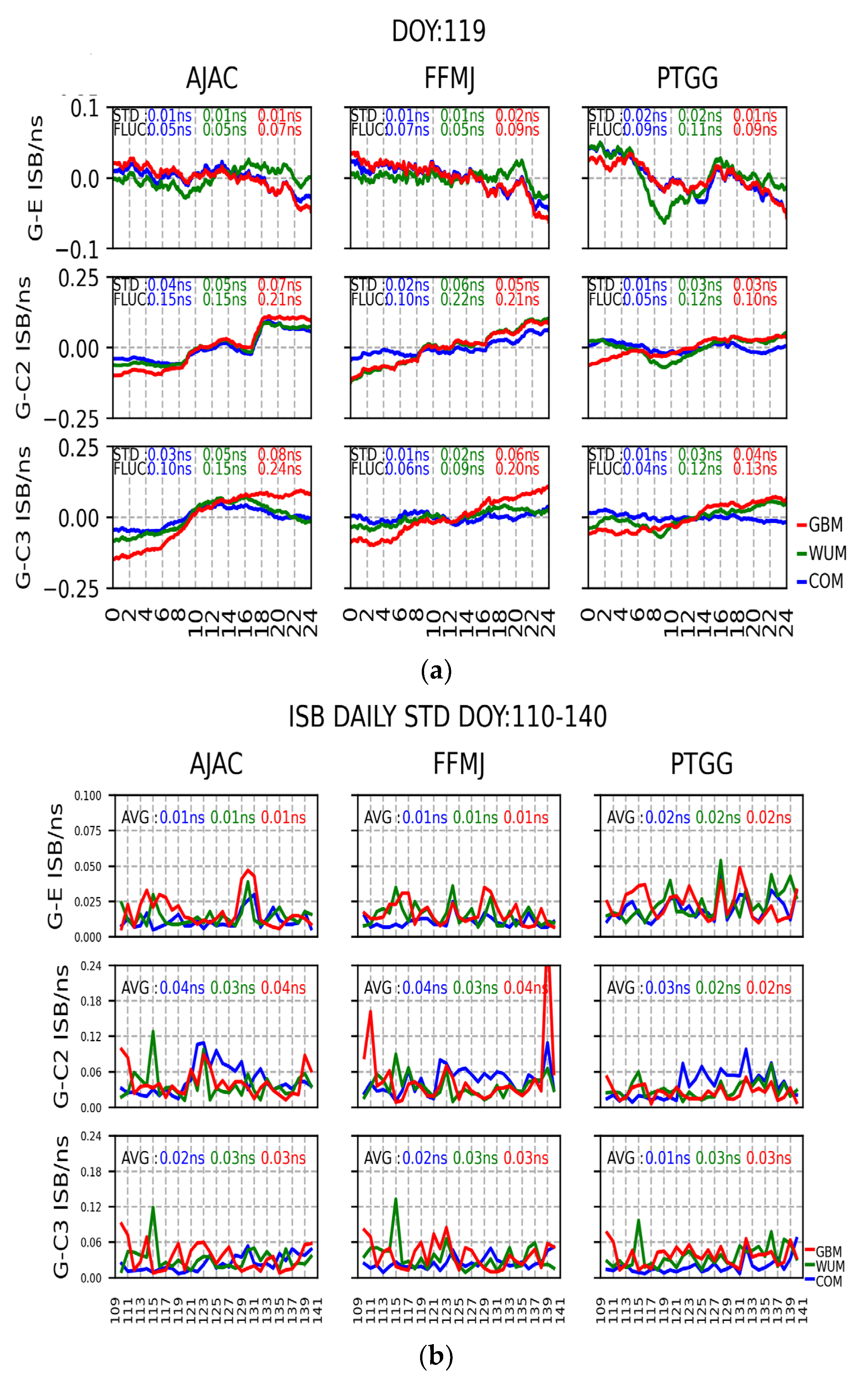
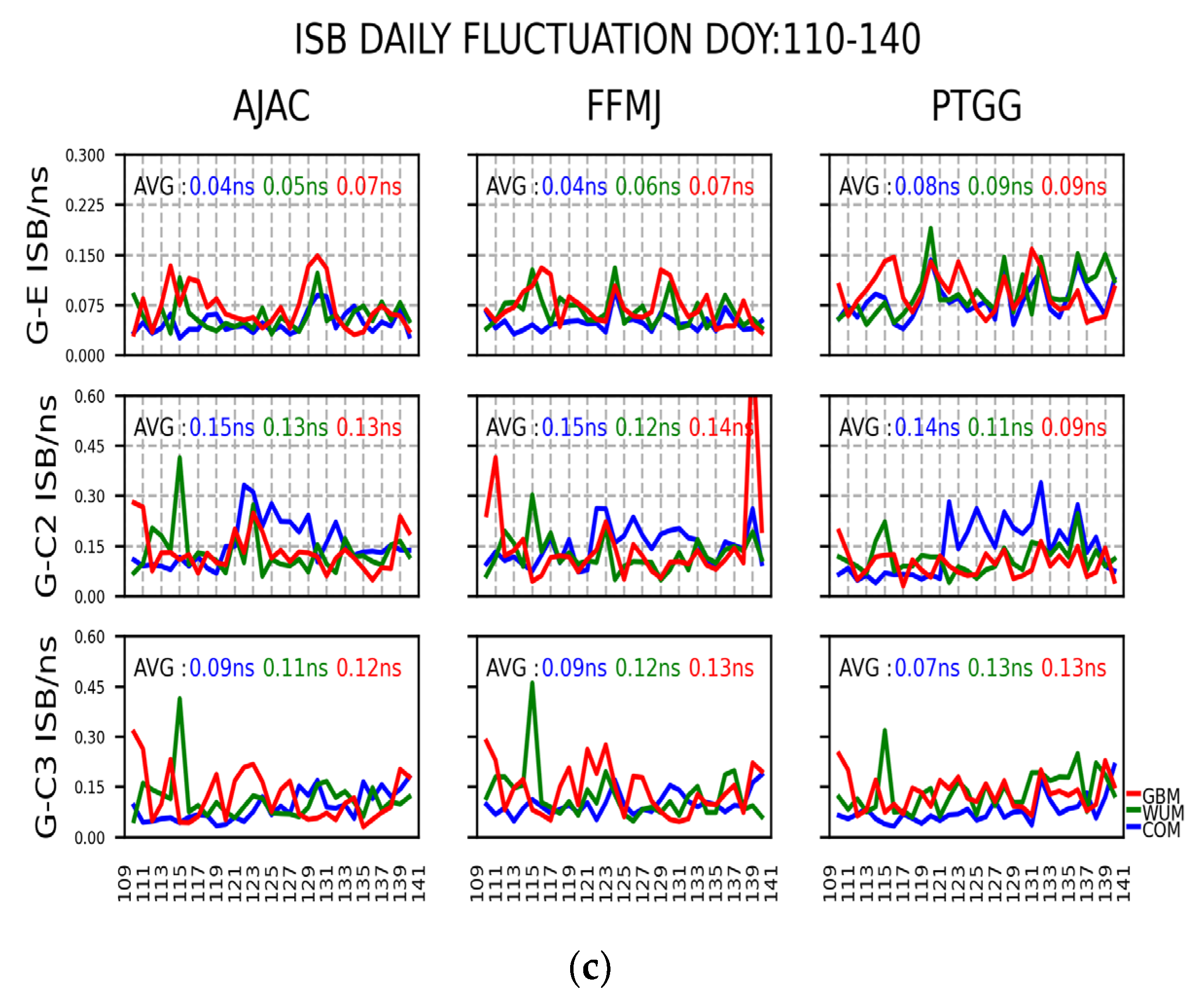
4.1.2. Analysis of Short-Term Time Characteristics of the ISB
- (1)
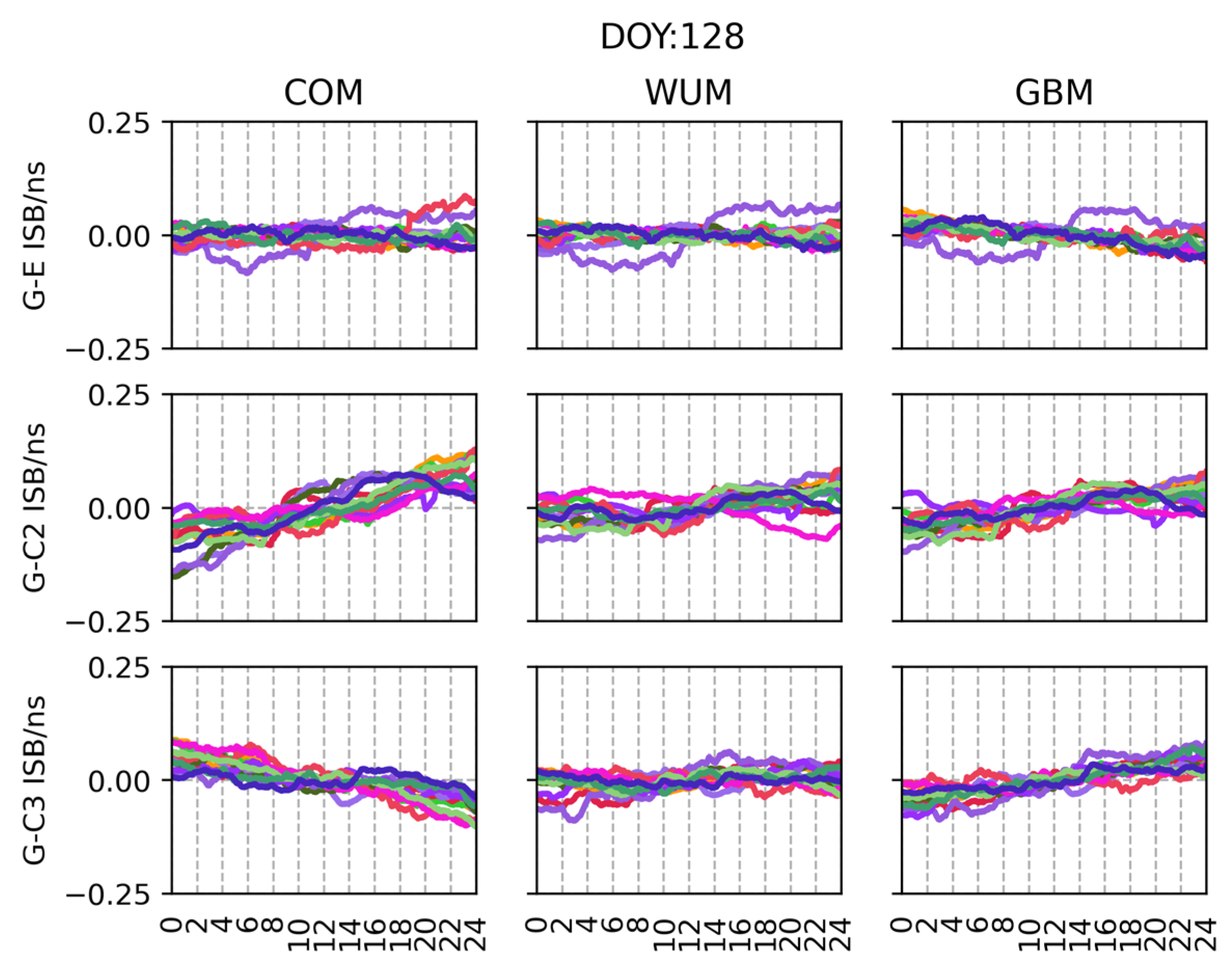
- The , and values estimated are not the same because of the differences in data processing strategies used by different analysis centers. , , and values are different due to time system differences between GNSS systems and receiver hardware delays. Thus, in the short term, the ISB values are correlated with the receiver, GNSS system, the adoption of analysis center products.
- (2)
- For the , , and results, where FLUC was ±0.25 ns, the monthly average short-term FLUC was ±0.20 ns, even was ±0.10 ns, which can be related to Galileo’s good signal quality. The , , and short-term TC show similarity in variation for the same stations. Moreover, it is evident that the ISB TC values of the same GNSS system fall within the same magnitude range. Among the three analysis center products, which use GBM product stability as the worst, COM and WUM are comparable.
- (3)
- The short-term FLUC of , , and are not the same, but the TC values in the same magnitude. The , with monthly average short-term ISB STD less than 0.02 ns and FLUC within ±0.07 ns, shows the best performance. performs slightly worse than , STD less than 0.03 ns and the FLUC is within ±0.10 ns. The is the worst.
4.1.3. Analysis of the Long-Term Time Characteristics of ISB
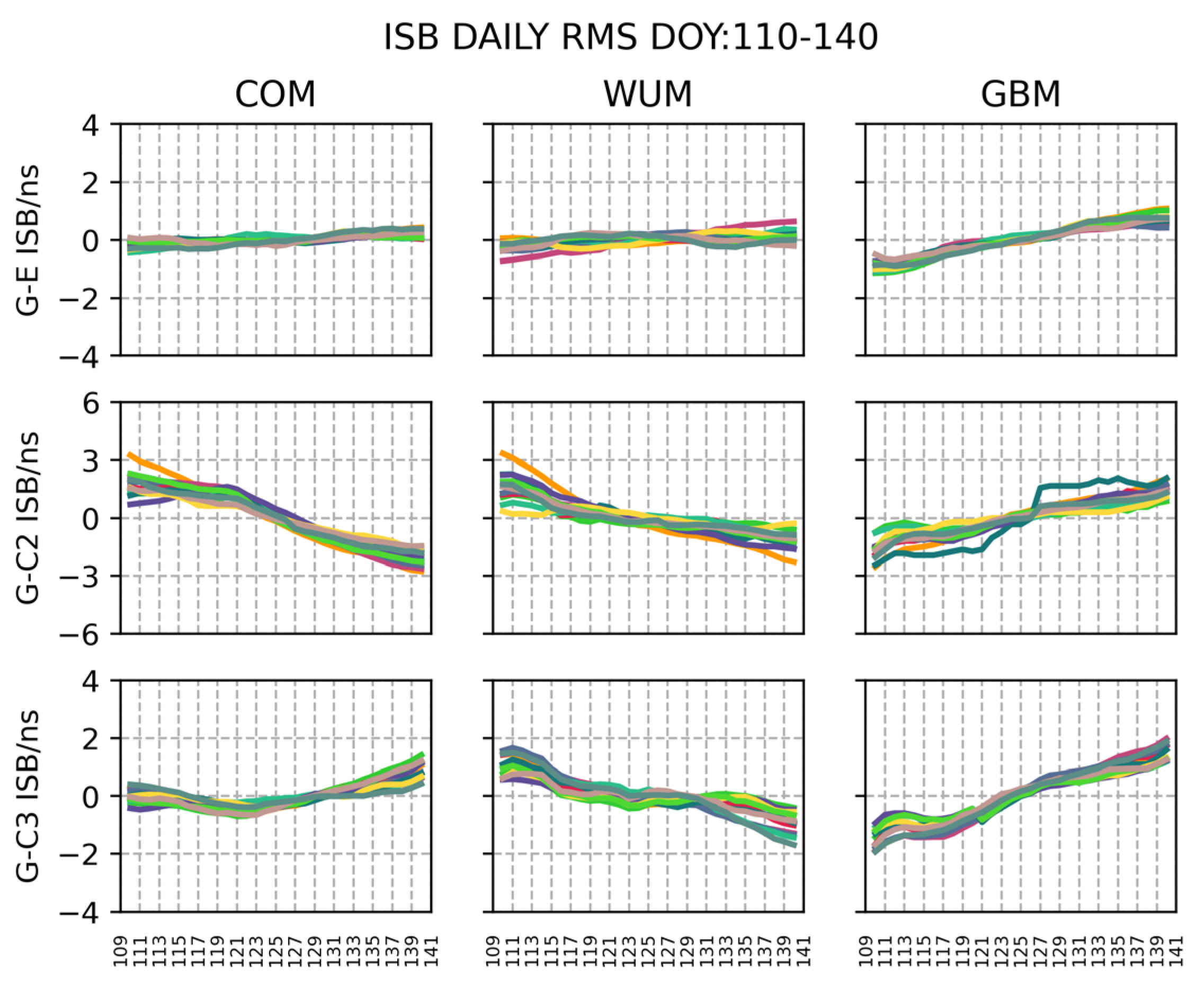
- (1)
- The RMS values of , , and are different, as well as the RMS values of , , and . Thus, the RMS of the ISBs on different stations, such as , , and , indicates that the ISBs are correlated with receivers, GNSS systems, and adoption of analysis center products in the long term.
- (2)
- It is clear that the FLUC of , , and are not the same, but the TC values between the three are in the same magnitude. The monthly average FLUCs of , , and were 1.82 ns, 1.69 ns, and 2.58 ns, corresponding to average STDs of 0.59 ns, 0.47 ns, and 0.76 ns, respectively, where performed the best, and were comparable.
- (3)
- , , and long-term TC are not the same. Within 31 days, their monthly average FLUCs were 0.88 ns, 2.86 ns, and 2.06 ns, respectively. The overall ISB monthly average FLUC was 2.03 ns, and the corresponding monthly average STDs were 0.28 ns, 0.88 ns, and 0.59 ns, with an overall monthly average STD < 0.61 ns, fluctuating the smallest, the second, and performed the worst.
4.2. Receiver and ISB Relationship Analysis
5. Conclusions
- (1)
- ISB is associated with the station receiver type, receiver antenna type, various analysis center products, and GNSS systems.
- (2)
- Variations in the short- and long-term TC of , , and are not the same. The short-term TC of , , and are similar, while not for the long-term. The short-term ISB time series performed better than the long-term time series.
- (3)
- The results of the ISB TC show little correlation between receiver type and receiver antenna. DBD effect on ISB can be ignored for the concussive day’s process.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- China Satellite Navigation Office BDS System Constellation Status. Available online: http://www.csno-tarc.cn/system/constellation (accessed on 20 February 2023).
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Earth Sci. 2014, 57, 144–152. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, J. GNSS receiver autonomous integrity monitoring (RAIM) algorithm based on robust estimation. Geod. Geodyn. 2016, 7, 117–123. [Google Scholar] [CrossRef]
- Wang, J.; Knight, N.L.; Lu, X. Impact of the GNSS Time Offsets on Positioning Reliability. J. Glob. Position. Syst. 2011, 10, 165–172. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Xu, J.; Tang, J. Generalised DOPs with consideration of the influence function of signal-in-space errors. J. Navig. 2011, 64 (Suppl. S1), S3–S18. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, J. New Characteristics of Geometric Dilution of Precision (GDOP) for Multi-GNSS Constellations. J. Navig. 2014, 67, 1018–1028. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, P.; Li, X.; Schuh, H. Influence of stochastic modeling for inter-system biases on multi-GNSS undifferenced and uncombined precise point positioning. GPS Solut. 2019, 23, 59. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wang, J.; Yang, S.; Dong, D.; Wang, J.; Qu, W.; Wu, B. A simplified and unified model of multi-GNSS precise point positioning. Adv. Space Res. 2015, 55, 125–134. [Google Scholar] [CrossRef]
- Jiang, N.; Xu, Y.; Xu, T.; Xu, G.; Sun, Z.; Schuh, H. GPS/BDS short-term ISB modeling and prediction. GPS Solut. 2017, 21, 163–175. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solut. 2014, 18, 461–471. [Google Scholar] [CrossRef]
- Bakker, P.; Christian, T. Real-Time Multi-GNSS Single-Frequency Precise Point Positioning. GPS Solut. 2017, 4, 1791–1803. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Cheng, J.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Real-time tropospheric delay retrieval from multi-GNSS PPP ambiguity resolution: Validation with final troposphere products and a numerical weather model. Remote Sens. 2018, 10, 481. [Google Scholar] [CrossRef]
- Mi, X.; Zhang, B.; Yuan, Y. Multi-GNSS inter-system biases: Estimability analysis and impact on RTK positioning. GPS Solut. 2019, 23, 81. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Shi, C.; Yi, W.; Song, W.; Lou, Y.; Yao, Y.; Zhang, R. GLONASS pseudorange inter-channel biases and their effects on combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 439–451. [Google Scholar]
- Nadarajah, N.; Teunissen, P.J.G.; Raziq, N. Beidou inter-satellite-type bias evaluation and calibration for mixed receiver attitude determination. Sensors 2013, 13, 9435–9463. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zhang, Y.; Yang, S.; Chen, Q.; Gong, X. Modeling and Assessment of GPS/BDS Combined Precise Point Positioning. Sensors 2016, 16, 1151. [Google Scholar] [CrossRef]
- El-Mowafy, A.; Deo, M.; Rizos, C. On biases in precise point positioning with multi-constellation and multi-frequency GNSS data. Meas. Sci. Technol. 2016, 27, 035102. [Google Scholar] [CrossRef]
- Torre, A.D.; Caporali, A. An analysis of inter-system biases for multi-GNSS positioning. GPS Solut. 2015, 19, 297–307. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, P.; Zhang, Y.; Wu, B. GPS/GLONASS System Bias Estimation and Application in GPS/GLONASS Combined Positioning. In China Satellite Navigation Conference (CSNC) 2013 Proceedings; Sun, J., Jiao, W., Wu, H., Shi, C., Eds.; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2013; pp. 323–333. ISBN 978-3-642-37403-6. [Google Scholar]
- Dach, R.; Schaer, S.; Hugentobler, U. Combined multi-system GNSS analysis for time and frequency transfer. In Proceedings of the European Frequency Time Forum, Braunschweig, Germany, 27–30 March 2006. [Google Scholar]
- Gioia, C.; Gaglione, S.; Borio, D. Inter-system Bias: Stability and impact on multi-constellation positioning. In Proceedings of the 2015 IEEE Metrology for Aerospace, Benevento, Italy, 4–5 June 2015. [Google Scholar]
- Zeng, A.; Yang, Y.; Ming, F.; Jing, Y. BDS–GPS inter-system bias of code observation and its preliminary analysis. GPS Solut. 2017, 21, 1573–1581. [Google Scholar] [CrossRef]
- Jiao, G.; Song, S.; Chen, Q.; Huang, C.; Su, K.; Wang, Z.; Cheng, N. Modeling and Analysis of BDS-2 and BDS-3 Combined Precise Time and Frequency Transfer Considering Stochastic Models of Inter-System Bias. Remote Sens. 2021, 13, 793. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International Gnss Service (IGS) Products; Geodetic Survey Division, Natural Resources Canada: Ottawa, ON, Canada, 2015. [Google Scholar]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, Z.; Wang, N. Multi-GNSS triple-frequency differential code bias (DCB) determination with precise point positioning (PPP). J. Geod. 2018, 93, 765–784. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.; Yuan, Y. On the short-term temporal variations of GNSS receiver differential phase biases. J. Geod. 2017, 91, 563–572. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Li, B.; Mi, J.; Zhu, H.; Gu, S.; Xu, Y.; Wang, H.; Yang, L.; Chen, Y.; Pang, Y. BDS-3/GPS/Galileo OSB Estimation and PPP-AR Positioning Analysis of Different Positioning Models. Remote Sens. 2022, 14, 4207. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, W.; Chen, H.; Zhao, W.; Huo, L.; Huang, L.; Chen, Q. An analysis of inter-system biases in BDS/GPS precise point positioning. GPS Solut. 2019, 23, 116. [Google Scholar] [CrossRef]
- Tu, R.; Hong, J.; Zhang, P.; Zhang, R.; Fan, L.; Liu, J.; Lu, X. Multiple GNSS inter-system biases in precise time transfer. Meas. Sci. Technol. 2019, 30, 115003. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Tao, L.; Wang, B.; Gao, Y.; Lu, X. Preliminary Analysis of Intersystem Biases in BDS-2/BDS-3 Precise Time and Frequency Transfer. Remote Sens. 2022, 14, 4594. [Google Scholar] [CrossRef]
- Blewitt, G. An Automatic Editing Algorithm for GPS data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Yang, H.; Tang, L.; Zhu, H.; Xu, A.; Li, B. A Concise Method for Calibrating the Offset of GPS Precise Satellite Orbit. Remote Sens. 2023, 15, 8. [Google Scholar] [CrossRef]
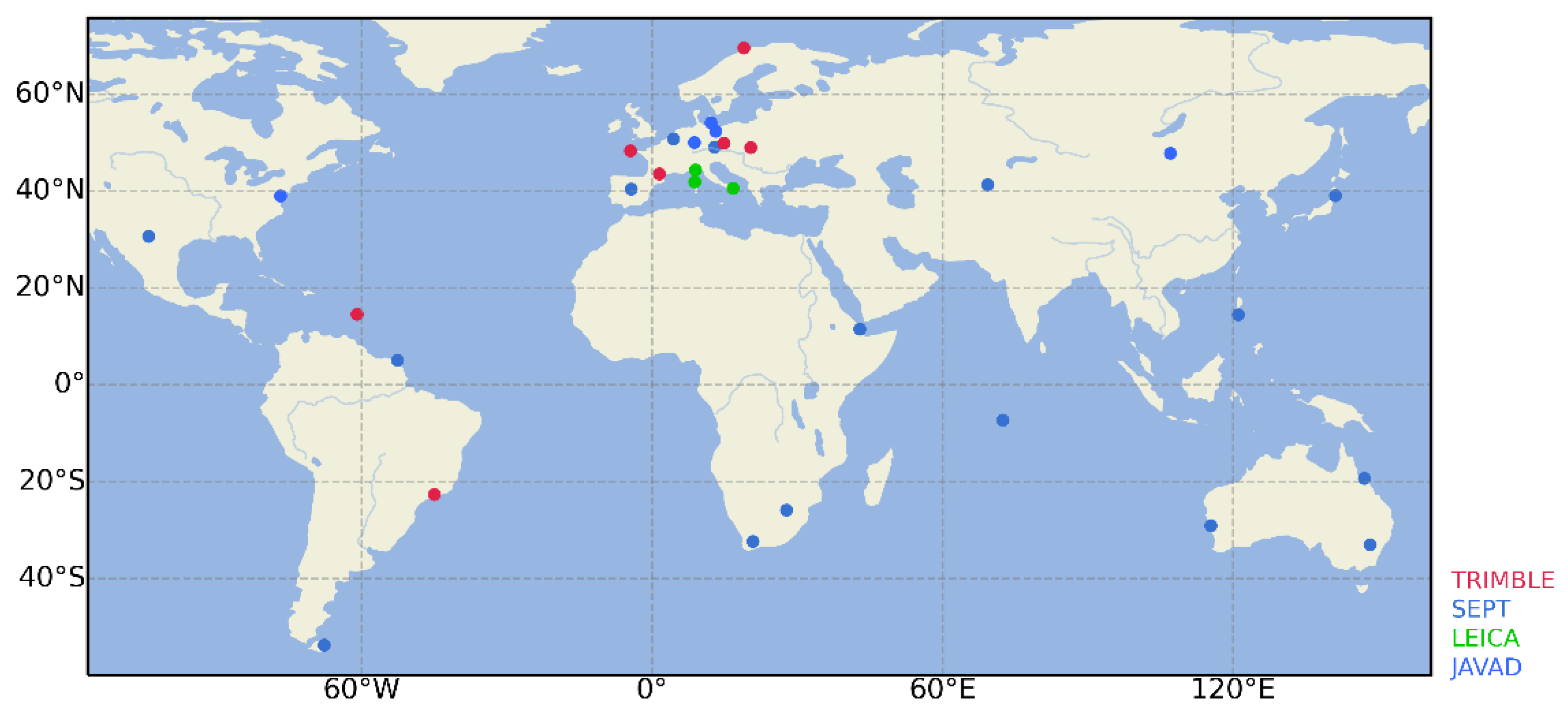

| Manufacturer | Number of Stations (Site Name) | |
|---|---|---|
| JAVAD | TRE_3 | 2 (POTS, ULAB) |
| TRE_3 DELTA | 3 (FFMJ, GODN, WARN) | |
| LEICA | GR30 | 2 (GENO, MATE) |
| GR50 | 1 (AJAC) | |
| TRIMBLE | NTR9 | 2 (TRO1, TLSE) |
| ALLOY | 4 (BRST, CHPG, GANP, LMMF) | |
| NTR10 | 1 (GOPE) | |
| SEPTENTRIO | ASTERX4 | 2 (RIO2, TASH) |
| POLARX5 | 8 (DGAR, DJIG, MDO1, MIZU, PTGG, SUTH, TOW2, YAR3) | |
| POLARX5TR | 6 (BRUX, CEBR, HARB, KOUG, PARK, WTZS) | |
| sum | 31 | |
| Options | Processing Strategies |
|---|---|
| Observation | UC observation |
| Signal | BDS: B1, B3; GPS: L1, L2; GAL: E1, E5a |
| Parameter estimation | EKF |
| Observation interval | 30 s |
| Weight distribution of observed values | Height angle model |
| Elevation | 7° |
| Satellite orbit | CODE, WHU, GFZ precise ephemeris |
| Satellite clock | CODE, WHU, GFZ precise clock offset |
| Phase center correction | IGS14.ATX |
| PCV | GPS/Galileo |
| Phase windup | Model correction |
| Solid earth tide | |
| Ocean load | |
| Polar motion | |
| Relativistic effect | |
| Tropospheric delay | Model correction + random walk |
| Ionospheric delay | Random walk |
| ISB | White noise |
| Receiver coordinates | Static, estimated as constants |
| Receiver clock | White noise estimation |
| Ambiguity | Estimated as float constants for each arc |
| RMS/ns | ||||
|---|---|---|---|---|
| AC | SITE | |||
| COM | AJAC | 13.54 | 37.43 | 38.75 |
| FFMJ | 6.38 | 16.65 | 7.95 | |
| PTGG | 14.70 | 43.12 | 45.71 | |
| WUM | AJAC | 15.50 | 42.06 | 45.69 |
| FFMJ | 8.39 | 21.50 | 14.22 | |
| PTGG | 16.31 | 46.60 | 52.23 | |
| GBM | AJAC | 8.22 | 24.74 | 21.17 |
| FFMJ | 1.05 | 44.69 | 52.18 | |
| PTGG | 9.57 | 18.95 | 13.74 | |
| ISB STD/ns | ISB FLUC/ns | |||||||
|---|---|---|---|---|---|---|---|---|
| AC | COM | WUM | GBM | AVG | COM | WUM | GBM | AVG |
| 0.01 | 0.02 | 0.02 | 0.02 | 0.06 | 0.07 | 0.08 | 0.07 | |
| 0.04 | 0.03 | 0.04 | 0.04 | 0.15 | 0.12 | 0.13 | 0.13 | |
| 0.02 | 0.03 | 0.04 | 0.03 | 0.09 | 0.10 | 0.10 | 0.10 | |
| AVG | 0.03 | 0.03 | 0.04 | 0.03 | 0.11 | 0.11 | 0.13 | 0.11 |
| ISB STD/ns | ISB FLUC/ns | |||||||
|---|---|---|---|---|---|---|---|---|
| AC | COM | WUM | GBM | AVG | COM | WUM | GBM | AVG |
| 0.14 | 0.12 | 0.57 | 0.28 | 0.45 | 0.45 | 1.74 | 0.88 | |
| 1.32 | 0.64 | 0.69 | 0.88 | 3.78 | 2.33 | 2.46 | 2.86 | |
| 0.40 | 0.56 | 0.80 | 0.59 | 1.45 | 2.08 | 2.64 | 2.06 | |
| AVG | 0.59 | 0.47 | 0.76 | 0.61 | 1.82 | 1.69 | 2.58 | 2.03 |
| ISB STD/ns | ISB FLUC/ns | |||||||
|---|---|---|---|---|---|---|---|---|
| AC | COM | WUM | GBM | AVG | COM | WUM | GBM | AVG |
| 0.0208 | 0.0205 | 0.0205 | 0.0206 | 0.1100 | 0.1220 | 0.1260 | 0.1193 | |
| 0.0351 | 0.0247 | 0.0256 | 0.0285 | 0.1250 | 0.1710 | 0.1840 | 0.1600 | |
| 0.0241 | 0.0224 | 0.0253 | 0.0239 | 0.0900 | 0.0919 | 0.0939 | 0.0919 | |
| AVG | 0.0267 | 0.0225 | 0.0238 | 0.0243 | 0.1083 | 0.1283 | 0.1346 | 0.1238 |
| ISB STD/ns | ISB FLUC/ns | |||||||
|---|---|---|---|---|---|---|---|---|
| AC | COM | WUM | GBM | AVG | COM | WUM | GBM | AVG |
| 0.1383 | 0.2122 | 0.2879 | 0.2128 | 0.5400 | 0.7680 | 0.7310 | 0.6797 | |
| 0.661 | 0.8643 | 0.9217 | 0.8157 | 1.9260 | 2.2100 | 2.2960 | 2.1440 | |
| 0.2035 | 0.208 | 0.2913 | 0.2343 | 0.6830 | 0.7610 | 0.8600 | 0.7680 | |
| AVG | 0.3343 | 0.4282 | 0.5003 | 0.4209 | 1.0497 | 1.2463 | 1.2957 | 1.1972 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Yang, H.; Li, B.; Li, J.; Xu, A.; Zhang, M. Analysis of Characteristics for Inter-System Bias on Multi-GNSS Undifferenced and Uncombined Precise Point Positioning. Remote Sens. 2023, 15, 2252. https://doi.org/10.3390/rs15092252
Lu Y, Yang H, Li B, Li J, Xu A, Zhang M. Analysis of Characteristics for Inter-System Bias on Multi-GNSS Undifferenced and Uncombined Precise Point Positioning. Remote Sensing. 2023; 15(9):2252. https://doi.org/10.3390/rs15092252
Chicago/Turabian StyleLu, Yangyang, Hu Yang, Bo Li, Jun Li, Aigong Xu, and Mingze Zhang. 2023. "Analysis of Characteristics for Inter-System Bias on Multi-GNSS Undifferenced and Uncombined Precise Point Positioning" Remote Sensing 15, no. 9: 2252. https://doi.org/10.3390/rs15092252
APA StyleLu, Y., Yang, H., Li, B., Li, J., Xu, A., & Zhang, M. (2023). Analysis of Characteristics for Inter-System Bias on Multi-GNSS Undifferenced and Uncombined Precise Point Positioning. Remote Sensing, 15(9), 2252. https://doi.org/10.3390/rs15092252








