The Development of Dark Hyperspectral Absolute Calibration Model Using Extended Pseudo Invariant Calibration Sites at a Global Scale: Dark EPICS-Global

Abstract

This research aimed to develop a novel dark hyperspectral absolute calibration (DAHAC) model using stable dark targets of “Global Cluster-36” (GC-36), one of the clusters from the “300 Class Global Classification”. The stable dark sites were identified from GC-36 called “Dark EPICS-Global” covering the surface types viz. dark rock, volcanic area, and dark sand. The Dark EPICS-Global shows a temporal variation of 0.02 unit reflectance. This work used the Landsat-8 (L8) Operational Land Imager (OLI), Sentinel-2A (S2A) Multispectral Instrument (MSI), and Earth Observing One (EO-1) Hyperion data for the DAHAC model development, where well-calibrated L8 and S2A were used as the reference sensors, while EO-1 Hyperion with a 10 nm spectral resolution was used as a hyperspectral library. The dark hyperspectral dataset (DaHD) was generated by combining the normalized hyperspectral profile of L8 and S2A for the DAHAC model development. The DAHAC model developed in this study takes into account the solar zenith and azimuth angles, as well as the view zenith and azimuth angles in Cartesian coordinates form. This model is capable of predicting TOA reflectance in all existing spectral bands of any sensor. The DAHAC model was then validated with the Landsat-7 (L7), Landsat-9 (L9), and Sentinel-2B (S2B) satellites from their launch dates to March 2022. These satellite sensors vary in terms of their spectral resolution, equatorial crossing time, spatial resolution, etc. The comparison between the DAHAC model and satellite measurements showed an accuracy within 0.01 unit reflectance across the overall spectral band. The proposed DAHAC model uncertainty level was determined using Monte Carlo simulation and found to be 0.04 and 0.05 unit reflectance for the VNIR and SWIR channels, respectively. The DAHAC model double ratio was used as a tool to perform the inter-comparison between two satellites. The sensor inter-comparison results for L8 and L9 showed a 2% difference and 1% for S2A and S2B across all spectral bands.

1. Introduction

Satellite imagery is a means to uncover the Earth’s changes; however, it is critical to have credible data for scientific study, which are obtained by optical satellite sensors. A wide range of applications, including atmospheric physics and geoscience, make use of physical quantities converted from the digital data recorded from satellite images. The reflection or emission of radiation by the Earth’s surface or atmosphere is being used by satellites, allowing the retrieval of the corresponding physical quantities. Although voltage or recorded digital data serve as the sensors’ primary measuring quantity, calibration must be carried out to compare the sensor-derived digital data with incoming radiance in their physical interest. At present, satellite instruments are typically well-designed and calibrated before launch. Though the satellite equipment is advanced and robust, they eventually deteriorate in space owing to factors including temperature, mechanical, electrical, or UV radiation exposure [1]. In order to ensure the quality of the derived variables and products, reliable remote sensing relies on a sensor re-calibration, commonly called radiometric calibration [2].

1.1. Absolute Radiometric Calibration

Data evaluation and the quality of satellite data highly depend on the absolute radiometric calibration of the sensor. During the absolute calibration process, the satellite images are processed and converted into digital numbers or the measured voltage in the form of physical quantities such as at-sensor spectral radiance or the top of atmosphere (TOA) reflectance [3,4]. The absolute calibration approach helps in characterizing and measuring the sensor’s performance from the early pre-launch stage to its on-orbit operation. Calibration can also be performed using different methods, for example pre-launch, onboard, and vicarious calibration. The results of post-launch calibration are compared with pre-launch calibration using several different methods in the lab [5]. After the satellite is placed in its orbit, the sensor characterization and its accuracy measurement are needed throughout its lifetime. Onboard calibrators, such as solar diffuser panels, lamps, etc., can be used to perform radiometric calibration [6,7]. However, onboard calibrators require routine operation and maintenance. They are expensive and also prone to the effects of harsh conditions in the space environment. For these reasons, many satellite sensors do not include onboard calibration. In order to overcome these limitations, pseudo invariant calibration sites (PICSs) were discovered for satellite calibration. The satellite imagery over the PICSs across the Earth’s surface is spatially, temporally, and spectrally stable [8].

1.2. Stable Calibration Sites

Several studies on PICS-based assessment have been performed to identify the stable pixels for sensor radiometric stability for more than 20 years [3]. Spatially uniform PICSs exhibit stable spectral features over time, higher reflectance, and no atmospheric influence on upward radiation [9]. A spatial uniformity of at least 3% and a temporal variability of 1–2% was found by Cosnefroy et al. over twenty desert locations [10]. There are six PICSs for North Africa that the Committee on Earth Observation Satellites (CEOS) recommended showing temporal variability in all bands of 3% or less [11]. According to Helder et al., Libya 4, Libya 1, Algeria 3, Arabia 2, Egypt 2, and Egypt 1 had variabilities of less than 3% and were capable of monitoring long-term trends [8]. Research studies on identifying stable pixels were then conducted by the South Dakota State University Image Processing Laboratory (SDSU IP Lab) to identify the best locations with 3% or less of temporal, spatial, and spectral variability. Less temporal uncertainty was considered in Libya 4, Niger 1, Sudan 1, Niger 2, Egypt 1, and Libya 1. With a temporal variation of less than 3%, Libya 4 stood out as the most-consistently stable site among them and could be widely employed in radiometric calibration work [3,12,13,14]. Shrestha et al. [6] applied the K-means unsupervised classification method, which resulted in identifying 19 clusters representing distinct land surface types in North Africa with pixels having 5% or less of both the spatial and temporal uncertainty. Fajardo et al. expanded the unsupervised classification to 160 clusters at a global scale and identified a cluster with stable bright sites named “global EPICS” [5]. The global EPICS showed a temporal variation of less than 4% for all bands, with some as low as 2.7%. The global classification with 160 clusters was further improved by the author to develop the “300 Class Global Classification” with its 300 clusters around the globe [15]. Past studies, including the research at SDSU IP Lab, focused on absolute calibration using stable bright sites, i.e., PICSs. However, the absolute calibration model developed in the past works neither covers the dynamic range of reflectance measurements nor developed the calibration model using stable dark targets at a global scale. This work proposes an algorithm to build an absolute calibration model using low reflectance dark targets capable of performing satellite calibration in addition to a bright target absolute calibration model. In this study, low reflectance measurements were identified from the stable dark targets of “Global Cluster-36” (GC-36), one of the clusters from the “300 Class Global Classification”. This study used the identified stable dark targets of the GC-36, named “Dark EPICS-Global”.

1.3. Evolution on Development of Absolute Calibration Model

Govaerts et al. [16] developed an absolute calibration model using the PICSs for geostationary satellite sensors. To characterize the atmospheric effects more accurately, an advanced radiative transfer model was developed for the Libya 4 site in 2012. The expanded model included the polarization effects and non-spherical aerosol models and showed accuracy within 3% [17]. In 2010, Helder et al. developed the concept of an empirical absolute calibration model using PICSs and the Terra Moderate Resolution Imaging Spectroradiometer (MODIS) as a reference sensor. The model was validated with Landsat-7 (L7) with an accuracy of 3% and 6% for the visible and short-wave infrared (SWIR) channels, respectively [12]. Based on daily radiance observations over Libya 4 using a geostationary Earth orbit (GEO) sensor, Bhatt et al. developed a desert daily exoatmospheric radiance model (DERM) [18]. The model accuracy remained consistent within 0.4% and 1.9% for Meteosat-8 and Meteosat-7 with the reference Meteosat-9 DERM. Likewise, GOES-11 DERM showed an accuracy of 1% and 3% while calibrating GOES-10 and GOES-15, respectively [19]. In order to minimize the bidirectional reflectance distribution function (BRDF) impact generated by the sensor’s off-nadir observations and seasonal fluctuations owing to solar position shift, Mishra et al. [4] considered a view zenith angle (VZA) for the absolute calibration model. Using Terra MODIS as a reference sensor, this model achieved 3% accuracy and uncertainty within 2% for six spectral bands [4]. In 2017, the coastal aerosol band was included as part of an improvement to the existing absolute calibration model using data from Landsat-8 (L8) images named the refined absolute calibration model. The accuracy of the refined absolute calibration model was within 3% for all spectral bands [20]. Raut et al. [3] expanded the absolute calibration model considering five additional Saharan Desert PICSs and found the model performance within 3% accuracy with 2% precision for three sites viz. Egypt 1, Libya 1, and Sudan 1. However, due to a lack of insufficient reliable Hyperion data, the model performance showed less accuracy for Niger 1 and Niger 2 [3].

In the previous studies, the scene-center-specific spherical angle was used to develop a BRDF model to finalize the absolute calibration model [3,4,12]. The reprocessing of the Landsat archive was performed in 2017, including the geometric error of the 12 m root-mean-squared error and 3% radiometric uncertainty [21]. All Landsat Collection-1 data produced by this method contain files including the Sun illumination and sensor viewing angle coefficients, as well as details about the quality assessment (QA) bands. Using the existing information in the Level-1 product of Landsat-8, Farhad et al. developed a novel four-angle BRDF model using the solar and view geometry angles in the form of Cartesian coordinates. This four-angle BRDF model preserves the data nature to achieve a robust fit. The estimated temporal variation across all the spectral bands was within 1.8% over Libya 4 PICSs [22]. In 2019, the Extended PICS Absolute Calibration (ExPAC) model with solar and view angles was developed using extended pseudo invariant calibration site in North African desert sites (EPICS-NA) as a target and L8 as a reference sensor. The ExPAC model showed a prediction accuracy of 2% after validation with the L7, L8, Sentinel-2A (S2A), and Sentinel-2B (S2B) sensors [23]. Chaity et al. developed an empirical hyperspectral absolute calibration model for the Libya 4 PICS (hyperspectral APICS) using the L8 Operational Land Imager (OLI) and Earth Observing-1 (EO-1) Hyperion sensors [1]. To better represent the angles, the hyperspectral APICS model used pixelwise four-angle BRDF information in Cartesian coordinates. This model had the potential to perform absolute calibration in 1 nm spectral resolution and showed an accuracy and precision of 6% and 4%, respectively, for the off-nadir viewing sensor. Similarly, the model showed an accuracy and precision of 3% for the nadir viewing sensor, respectively [1]. However, the hyperspectral APICS model was constrained for the Libya-4 PICS and showed poor performance for non-Landsat bands, although this could be improved.

1.4. Objectives of the Study

The main objective of this study was to develop a novel dark hyperspectral absolute calibration (DAHAC) model using the L8, S2A, and EO-1 Hyperion measurements over the identified stable dark sites (Dark EPICS-Global) of “Global Cluster-36” (GC-36). L8 OLI and S2A MSI were used as reference sensors and EO-1 Hyperion as the hyperspectral library to convert the multispectral profile of L8 and S2A in the hyperspectral domain. The dark hyperspectral data and their angular information in the Cartesian coordinate form were used to build the four-angle hyperspectral BRDF model, which was further simplified to develop the DAHAC model. Unlike Chaity’s development, the proposed model is unique with its novel algorithm to develop a more accurate model using the “low reflectance measurements” at a global scale. The DAHAC model is capable of predicting the top of atmosphere (TOA) reflectance in all existing hyperspectral bands for any sensors. The DAHAC model’s validation was performed with respect to L7, S2B, and Landsat-9 OLI (L9). Furthermore, the DAHAC model double ratio was estimated to perform sensor inter-comparison between L8 and L9 for Landsats and S2A and S2B for Sentinel-2.

This paper is organized into the following sections: Section 1 illustrates the background and literature review on radiometric calibration along with the absolute calibration model development techniques based on PICSs and its evolution towards EPICS Global. Section 2 outlines the sensor characteristics used in this study, the selection of dark targets for the study area and its validation, the dark hyperspectral dataset generation, and the DAHAC model development process. Section 3 discusses the DAHAC model validation results with respect to several sensors. Section 4 presents the DAHAC model uncertainty estimation process. Section 5 describes the sensor inter-comparison based on the DAHAC model double ratio estimation. Finally, Section 6 summarizes and concludes the paper.

2. Methodology

This section explains the development of the dark hyperspectral absolute calibration (DAHAC) model using reflectance measurements of L8, S2A, and EO-1 over Dark EPICS-Global. Figure 1 shows the overall architecture of the study area selection and sensor data pre-processing for generating the dark hyperspectral dataset required for the DAHAC model’s development. This work started with a thorough analysis of different satellite sensors viz. L7, L8, L9, S2A, S2B, and EO-1 Hyperion. The multispectral sensors (L8 and S2A) were utilized as the reference sensors, and EO-1 was used as a hyperspectral library source. The preliminary selection and identification of many dark targets around the globe from 300 global clusters was the first major step. GC-36 was selected as the most-suitable dark target as its spectral response is closely similar to the volcanic site used for the cross-calibration of S2A and L8 [22]. In this study, the selected dark sites from GC-36 were validated by comparing their TOA reflectance with the overall GC-36 TOA reflectance measurements to provide Dark EPICS-Global. Furthermore, this section also explains the detailed process to generate the normalized hyperspectral profile for two multispectral sensors, L8 and S2A, using EO-1 Hyperion as a hyperspectral library. The procedures to generate the dark hyperspectral dataset for creating the 4-angle BRDF model are also presented in detail. Finally, the process of developing the DAHAC model from the 4-angle BRDF model is also discussed in the sections below.

2.1. Satellite Data

2.1.1. Landsat-7, -8, -9

Since 1972, Landsat missions have continuously collected multispectral data covering the entire planet with a temporal resolution of 16 days. L7, which was launched on 15 April 1999, has eight spectral bands and operates at a mean altitude of 705 km in a Sun-synchronous orbit. Prior to the launch of L8, L7 had a satellite calibration of 5%, making it the most-stable sensor within the Landsat family [7]. However, Scan Line Corrector (SLC) issues with L7 have existed since May 2003 and have resulted in scenes with wedge-shaped data gaps [24]. The radiometric stability of the ETM+ satellite has been evaluated with the help of on-orbit calibration and vicarious measurements. The partial- and full-aperture solar calibration is continuously performed by taking the source as the Sun for onboard calibrators [25]. The official science mission of L7 ended on 6 April 2022. L7 started its extended science mission on 5 May 2022, from a lower orbit of 697 km [26].

L8 is part of the Landsat series, which was launched on 11 February 2013. It has two different instruments: an OLI sensor and the Thermal Infrared Sensor (TIRS). L8 has been producing high-quality image information for Earth observation with spatial resolutions of 30 m for eight separate spectral bands and 15 m for the panchromatic band. The uncertainty associated with the L8 post-launch reflectance calibration is within 2% [7]. The improvement in the Landsat image product was performed in 2018, which provided a Level-1 product with angle information and the quality assessment band. The radiometric calibration was updated in the coastal aerosol and blue band for the Level-1 Collection-2 product [27].

The most recent satellite in the Landsat constellation is Landsat 9, which was launched on 27 September 2021. Landsat 9 is an identical instrument to Landsat 8 with better radiometric resolution. The increased quantization from 12 to 14 bits in L9 enables the sensor to acquire more small variations, resulting in better image quality. The Sun-synchronous orbit of L9 is at an altitude of 705 km and takes 16 days to complete one orbit cycle [28].

Equation (1) shows the conversion of Landsat imagery digital number (DN) values to TOA reflectance [29].

$${\rho }_{observed}=\frac{M_{\rho }\times Q_{Cal}+A_{\rho }}{cos\alpha }$$

(1)

where $M_{\rho }$ and $A_{\rho }$ are the multiplicative and additive factors in metadata format, $Q_{Cal}$ represents the calibrated DN value, and $\alpha$ is the solar zenith angle.

2.1.2. Sentinel-2A, -2B

The European Space Agency (ESA) launched S2A on 23 June 2015 and S2B on 7 March 2017 under the Copernicus program. S2A and S2B are positioned in a Sun-synchronous orbit at an altitude of 786 km, phased at 180° relative to one another. These sensors are equipped with push-broom sensor multi-spectral instruments (MSIs) that measure the solar reflectance for 13 different spectral bands with 10m, 20m, and 60m spatial resolutions. The orbital period and combined orbital period for these two satellites are ten days and five days, respectively. The MSI focal plane detectors are divided into 12 different modules to allow these sensors to provide an image with a 290 km swath width at a 20.6° field of view [30,31]. In 2017, the study on the Sentinel-2 satellite showed that the absolute calibration was better than 5% for the overall sensor spectral band [32]. The European Space Agency reported that Sentinel-2 products would soon be upgraded. Sentinel-2A and -2B have undergone multiple processing systems during the course of their lifetimes. The processed data with a baseline of 2.0 or above, from the launch time to October 2022, were used in this study. The TOA reflectance is calculated using Equations (2) and (3).

$${\rho }_{\lambda }=\frac{D{N}_{cal}}{Q}$$

(2)

where $D{N}_{cal}$ represents the calibrated DN value and Q is a scale factor that is equal to 10,000. This scaling factor accounts for the Earth–Sun distance, exoatmospheric irradiation, and cosine correction. The Sentinel-2 Processing System Version 4.0 has been installed since 25 January 2022. Thus, the TOA reflectance conversion equation is updated as shown in Equation (3).

$${\rho }_{\lambda }=\frac{D{N}_{cal}+Offset}{Q}$$

(3)

where offset = −1000 is reported in the metadata image information. The estimated TOA reflectance for S2A is illustrated in Section 2.2.4.

2.1.3. Earth Observing-1 Hyperion

EO-1 Hyperion was a hyperspectral satellite that was part of NASA’s New Millennium Program. This satellite was launched on 21 November 2000 and was discontinued on 20 March 2017 [33]. There were two instruments on board: the Advanced Land Imager (ALI), a hyperspectral imaging spectrometer, and the Linear Etalon Imaging Spectral Array (LEISA) Atmospheric Corrector (LAC). The push-broom hyperspectral sensor covers the 400–2500 nm spectral range and 242 band images (including 196 onboard calibrated bands [34]) with a 10 nm spectral resolution and a 30 m spatial resolution over a 7.7 km swath width. The EO-1 stability analysis for 16 years of operation with varying orbital precession revealed calibration uncertainty for all spectral bands within 5 and 10% [35]. The following Equation (4) is used to convert the EO-1 Hyperion DN values to TOA reflectance.

$${\rho }_{\lambda }=\frac{\frac{D{N}_{cal}}{h}\times \pi \times d^2}{E_{Sun}\times sin\varphi \times cos\theta }$$

(4)

where $D{N}_{cal}$ represents the calibrated digital number value, h defines the scale factor, d indicates Earth–Sun distance in A.U., $E_{Sun}$ demonstrates the conversion of calibrated radiance to reflectance derived from the ChKur solar spectrum (ESUN(ChKur)) [36], and $\varphi$ and $\theta$ are the Sun elevation and sensor look angle, respectively. The summarized information for the sensors used in this study is shown in

Table 1. Different sensor information used in the DAHAC model’s development.

Information	Sensors
	Landsat-7	Landsat-8	Landsat-9	Sentinel-2A	Sentinel-2B	EO-1 Hyperion
No. of Images	764	1150	84	775	456	64
Image Dates	2000–2022	2013–2022	2021–2022	2015–2022	2017–2022	2001–2017
SZA Range (°)	20–58	20–60	20–60	15–51	15–54	23–77
SAA Range (°)	36–160	35–160	35–158	31–164	31–165	70–145
VZA Range (°)	0.10–8	0.03–5	0.17–8	0.04–10	0.09–10	0.04–25
VAA Range (°)	−94–136	−178–180	−80–118	−89–130	−162–135	−82–98
No. of Sites	8 WRS-2 paths/rows	8 WRS-2 paths/rows	8 WRS-2 paths/rows	12 Tiles	12 Tiles	3 paths/rows

.

2.2. Dark Target Selection

This section explains the steps for identifying dark targets by choosing the stable pixels from the dark target clusters under the “300 Class Global Classification” using the L8 imagery information. This section also describes the zonal mask creation process and filtering technique.

2.2.1. Identifying Stable Dark Target Using Landsat-8

Three different global clusters, Global Cluster-6 (GC-6), Global Cluster-26 (GC-26), and Global Cluster-36 (GC-36), were discovered to be the dark clusters among the 300 clusters from the “300 Class Global Classification”. These clusters include surface types viz. dark rock, dark sand, volcanic area, dark pond, etc. GC-36 was selected as the dark cluster for this study based on the higher pixel counts and pixel density. Since GC-36 is a GeoTIFF format, the Geospatial Data Abstraction Library (GDAL) is used to generate Keyhole Markup Language (KML) files for GC-36. Using a kmL file, L8 WRS-2 system, Google Earth Pro, and Earth Explorer program, an initial visual inspection was performed to choose the WRS-2 paths/rows with the surface type: dark rock, dark sand, volcanic area, and vegetation area on each continent. Initially, 13 distinct WRS-2 paths/rows from the Middle East, South Africa, and North Africa were chosen. However, the surface types viz. dark rock, dark sand, and volcanic area showed a similar spectral response as the Libyan volcanic site that was used for cross-calibration purposes between the L8 and S2A sensors [22].

Based on the spectral characteristics, eight different WRS-2 paths/row were chosen as dark sites for this study. The eight selected WRS-2 paths/rows have pixel counts within the range of 21,726–2,359,755. The 8 WRS-2 paths/rows in the three continents with surface type description are illustrated in

Table 2. Showing WRS-2 paths/rows, surface types, and pixel count across different continents.

Continents	Paths/Rows	Surface Description	Pixel Count
Middle East	159/40	dark rock	73,544
	163/37	dark rock	36,070
	168/51	dark rock, dark sand	2,359,755
	170/42	volcanic area	710,696
South Africa	180/75	volcanic area, dark rock	40,626
	181/73	dark rock, dark sand	21,726
North Africa	183/46	volcanic area	30,009
	184/43	volcanic area	133,950

. The selected WRS-2 paths/rows for L8, along with the global map are shown in Figure 2. They are further used to perform temporal stability analysis in Section 2.2.4.

2.2.2. Creation of Zonal Mask for Satellites

Following the selected dark pixels’ location information in Section 2.2.1, a zonal dark pixel mask was generated using the “gdalwarp” function from the GDAL library based on the spatial resolutions of 10 m, 20 m, 30 m, and 60 m and the Universal Transverse Mercator (UTM) zone. To accommodate images positioned in two distinct UTM zones, the zonal mask was extended by 100 km in the east–west direction.

2.2.3. Filtering and Dark Pixel Validation

The primary goal of applying filters is to obtain a clear pixel by removing the clouds from images. The Landsat products with Level 1 Collection 2 (L1C2) are provided with a pixel quality assessment band (BQA) [37]. Based on the BQA information, a binary cloud mask is built, including fill values, dilated cloud, cirrus, cloud, cloud shadow, cloud confidence, and cloud shadow confidence, which is then applied for each L7, L8, and L9 satellite image. In the case of the Sentinel-2 sensor, the provided binary cloud mask is applied for each Sentinel-2 image. Similarly, to remove the cloudy pixels from Hyperion images, Band-123 (1376 nm) image information with almost a 100% absorption feature is used as a binary cloud mask.

Although these cloud binary masks can be employed at the pixel level, we chose to use them first at the scene level to eliminate dates where the region of interest (GC-36 pixels) is substantially obscured by clouds. This is because cloud filters are not perfect and can miss cloud pixels on days that are extremely cloudy. To remove the cloudy image, a potential threshold containing a clear pixel for each image was determined at 40%. In other words, if the number of clear pixels in the cloud binary mask is larger than 40% of the number of pixels in the satellite images, the image is selected for applying the pixel-by-pixel cloud mask; otherwise, the entire scene is discarded.

Even after filtering the cloud in the sensor images, there could be a chance that the cloud shadow pixel has the same pixel values as the clear dark pixel. The clear dark pixels in the sensor images were validated using reference L8 image information. First, the BQA filter with cloud shadow and cloud shadow confidence was employed on the L8 images. The L8 images were also applied to the BQA filter without cloud shadow and cloud shadow confidence. Further, the convolution theory was applied to the resulting two sets of images in order to distinguish the real dark pixels in the images. This process clarified that the pixels associated with each image were clear dark pixels.

2.2.4. Dark Target Data for Absolute Calibration

The cloud-free images were used to estimate the TOA reflectance for each sensor. The estimated TOA reflectance for L8 (1150 images) for dark sites ranges from 0.043 to 0.17, as shown in Figure 3. It can be observed that the selected dark sites were temporally stable with a standard deviation of 0.02 across all the spectral bands. The selected sites (paths/rows) for L8 were validated with respect to GC-36 by comparing the estimated TOA reflectance. GC-36 itself is defined in a way that the pixels included within this class represent identical attributes based on unsupervised K-means clustering. The mean and standard deviation of TOA reflectance for each of the selected sites for each band was compared against the mean and 3$\sigma$ standard deviation of GC-36, as shown in Figure 4. The minimum and maximum 3$\sigma$ values for GC-36 are shown by red-colored dotted lines. In Figure 4, it can be observed that, for all spectral bands, the estimated mean TOA reflectance for each site is within the boundary line, except for the SWIR-2 band crossing the boundary line within an acceptable range. Therefore, the selected dark sites under GC-36 for the L8 sensor were validated and represented as “Dark EPICS-Global” for this study.

After identifying Dark EPICS-Global using L8 as a reference sensor, the locations of these selected dark sites were further used to investigate the availability of data for the S2A and EO-1 sensors. There are 12 tiles representing the dark sites selected for the S2A sensor. Figure 5 shows the estimated TOA reflectance using 775 images obtained from the 12 stable dark tiles. The TOA reflectance for each tile was within the range of 0.04–0.18, with a standard deviation of 0.02 for all spectral bands. Likewise, among the selected dark sites, three distinct WRS paths/rows, i.e., 168/50, 183/46, and 184/43 were available for the EO-1 sensor. A total of 64 Hyperion images were obtained from the selected stable sites, and their estimated hyperspectral TOA reflectance for the 196 calibrated bands are shown in Figure 6. The average TOA reflectance of all 64 EO-1 Hyperion images with their standard deviation is shown in Figure A1 presented in Appendix B. The estimated TOA reflectance using Dark EPICS-Global for L8, S2A, and EO-1 is called dark target data. The estimated dark target data were further used to generate the dark hyperspectral dataset (DaHD).

2.3. Dark Hyperspectral Dataset

This section explains the dark hyperspectral data generation process to develop the hyperspectral absolute calibration model. L8 and S2A were used as reference sensors since they are well-calibrated and their combination covers a wide range of angular information, as well as non-Landsat spectral bands. L8 and S2A have their TOA reflectance measurements in the multispectral domain, which were converted into the hyperspectral domain. The multispectral to hyperspectral profile conversion was performed using EO-1 Hyperion as a hyperspectral library.

The hyperspectral profile of L8 and S2A was achieved in two steps requiring two inputs, “Input 1” and “Input 2”, as shown in Figure 7. Input 1 consisted of the processed image (${\rho }_{L8}$), S2A (${\rho }_{S2A}$), and EO-1 Hyperion (${\rho }_h$). After going through the process of converting the multispectral domain to the hyperspectral domain as described in Figure 8, the output was the L8 and S2A hyperspectral profile. This hyperspectral profile was validated with L8 and S2A data to see if they represent the measured TOA reflectance. It was found that there was some discrepancy between the hyperspectral profile and the satellite measurements of approximately 1 unit TOA reflectance in the CA, green, and SWIR2 bands, as shown in Figure 9. Therefore, the EO-1 hyperspectral profile (${\rho }_{h}cal$) was modified by applying the relative gain to the Hyperion data as described in Section 2.3.2. “Input 2” consisted of ${\rho }_{L8}$, ${\rho }_{S2A}$, and ${\rho }_{h}cal$, used to obtain the final hyperspectral profile for L8 and S2A. The detailed procedures to convert the multispectral to hyperspectral profile are explained in the sections below.

2.3.1. Estimation of Satellite Hyperspectral Profile

Figure 8 shows the detailed conversion process of the multispectral profile into its hyperspectral profile. There were three satellite data: L8 (M = 1150 images), S2A (P = 775 images), and EO-1 (N = 64 images), represented by (${\rho }_{{L8}_{i=1\dots M}}$), S2A (${\rho }_{S2A_{k=1\dots P}}$), and (${\rho }_{h_{j=1\dots N}}$), respectively. Using Equation (5), the band-integrated TOA reflectance (${\rho }_{h_{sat}}$) for the satellites viz. L8 (${\rho }_{h_{L{8}_{j=1\dots N}}}$) and S2A (${\rho }_{h_{S2A_{j=1\dots N}}}$) was estimated by integrating the relative spectral response (RSR) of the reference sensors ($RS{R}_{sat}$) with the Hyperion profile (${\rho }_h$) at each sampled wavelength (dλ), weighted by the corresponding RSR of the reference sensor.

$${\rho }_{h_{sat}}\left(\lambda \right)=\frac{{\int }_{{\lambda }_1}^{{\lambda }_2}{\rho }_h\times RS{R}_{sat}d\lambda }{{\int }_{{\lambda }_1}^{{\lambda }_2}RS{R}_{sat}d\lambda }$$

(5)

The TOA reflectance ratio ($R_{L{8}_{i=1,j}}$) was estimated between L8 TOA reflectance (${\rho }_{L{8}_{i=1}}$) for the first image with respect to the N number of EO-1 to L8-integrated TOA reflectance (${\rho }_{h_{L{8}_{j=1\dots N}}}$) across all the bands (b1…b7). The average TOA reflectance ratio ($A_{L{8}_{i=1,j=1\dots N}}$) was taken across the bands for the N number of $R_{L{8}_{i=1,j=1\dots N}}$. EO-1 to L8-normalized TOA reflectance ${\rho }_{nor{m}_{L{8}_{i=1,j=1\dots N}}}$ was then computed by multiplying ${\rho }_{h_{{L8}_{j=1\dots N}}}$ with $A_{L{8}_{i=1,j=1\dots N}}$. Further, the mean-squared errors ($MS{E}_{i=1,j=1\dots N}$) were calculated among ${\rho }_{nor{m}_{L{8}_{j=1\dots N}}}$ with respect to ${\rho }_{L{8}_{i=1}}$ using Equation (6) given below:

$$MS{E}_{ij}=\frac{\sum {({\rho }_{sa{t}_i}-{\rho }_{{norm}_{sa{t}_{ij}}})}^2}{\mathrm{No}.\mathrm{of}\mathrm{Bands}}$$

(6)

where ${\rho }_{sat}$ and ${\rho }_{{norm}_{sat}}$ are the TOA reflectance and normalized TOA reflectance of satellites (“sat” refers to either L8 or S2A). For ${\rho }_{L{8}_{i=1}}$, the minimum MSE value was observed from the N number of MSEs at instant $j=a$ (say). The final hyperspectral spectrum (${\rho }_{L{8}_{hype{r}_{i=1}}}$) was then picked from the Hyperion library (${\rho }_{h_{j=1\dots N}}$) at $j=a$. Finally, the L8-normalized hyperspectral TOA reflectance (${\rho }_{L{8}_{hy{p}_{i=1}}}$) was obtained by further multiplying ${\rho }_{L{8}_{hype{r}_{i=1}}}$ with the average TOA reflectance ratio ($A_{L{8}_{i=1,j=a}}$) for the first ${\rho }_{L{8}_{i=1}}$. This process was repeated for $M=1150$ L8-processed images to achieve the M number of L8 normalized hyperspectral TOA reflectance profiles. The same process was applied to the Sentinel-2A data to obtain $P=775$ S2A-normalized hyperspectral profiles (${\rho }_{S2A_{hy{p}_{k=1\dots P}}}$).

The normalized hyperspectral TOA reflectance for both L8 (${\rho }_{{L8}_{hy{p}_i}}$) and S2A (${\rho }_{S2A_{hy{p}_k}}$) was further integrated into the multispectral bands (${\rho }_{L{8}_{hy{p}_{mult}}}$) and compared with their observed TOA reflectance (${\rho }_{{L8}_{i=1}}$) measurements to check the accuracy of their hyperspectral profile. Figure 9 shows the ${\rho }_{L{8}_{i=1}}$ (orange color), ${\rho }_{L{8}_{hy{p}_{i=1}}}$ (grey color), ${\rho }_{L{8}_{hy{p}_{mult}}}$ (purple color), and absolute difference between ${\rho }_{L{8}_{i=1}}$ and ${\rho }_{L{8}_{hy{p}_{mult}}}$ (red colored). It can be observed that there was a discrepancy of 0.0106 TOA reflectance between ${\rho }_{L{8}_{i=1}}$ and ${\rho }_{L{8}_{hy{p}_{mult}}}$. This might be because of EO-1 Hyperion’s different band-to-band attributes in their relative domain. This small offset can further be minimized by finding the relative gain and performing relative calibration on the Hyperion sensor, which brought the satellite (L8 and S2A) hyperspectral profile to match its multispectral domain.

2.3.2. Relative Calibration on EO-1 Sensor

In the relative calibration process, the ratios between satellite measurements (${\rho }_{L{8}_i}$ and ${\rho }_{S2A_k}$) and the band-integrated TOA reflectance (${\rho }_{L{8}_{hy{p}_{mult}}}$ and ${\rho }_{S2A_{hy{p}_{mult}}}$) were first calculated. Then, the mean ratio across the central wavelengths was taken for L8 and S2A, called the “relative gain” values.

Figure 10 shows the relative gain for L8 (orange color) and S2A (blue color) versus the central wavelength. The relative gain values for L8 and S2A were combined to be the “superspectral relative gain” values (orange color), as shown in Figure 11. In order to obtain the “hyperspectral relative gain” values, the modified Akima cubic Hermite (makima) interpolation was applied to the superspectral relative gains. The interpolated values can be obtained based on a piecewise function of polynomials with at most three degrees, which is the advantage of using the “makima” approach [38]. The interpolation was employed separately for the VNIR and SWIR channels due to the two sensors onboard Hyperion. Before employing the interpolation on the VNIR channel, the average relative gain between L8 and S2A was taken for the “green”, “red”, and “NIR” bands because they are very close to each other. Then, the interpolation was performed to obtain interpolated relative gain values with a 1 nm spectral resolution for the VNIR channels. Similarly, for the SWIR channels, the average relative gain of L8 and S2A was computed and taken as a relative gain with a 1 nm spectral resolution. The interpolated relative gain for VNIR and SWIR channels was further extrapolated and combined in order to cover the entire hyperspectral wavelength region. The EO-1 sensor used in this study has a hyperspectral TOA reflectance profile with a 10 nm spectral resolution. In order to match the EO-1 sensor’s resolution, the combined interpolated relative gain values were integrated to obtain a 10 nm resolution of the hyperspectral relative gain values.

Figure 11 shows the hyperspectral (grey color) and superspectral (orange-color) relative gain plot. Finally, the hyperspectral relative gain was multiplied with the TOA reflectance of the 64 Hyperion processed images (${\rho }_{h_{j=1\dots N}}$), which completed the relative calibration on the EO-1 sensor, as shown in Figure 12. The output of the relative calibration process, which is the relative calibrated EO-1 Hyperion processed image (${\rho }_{h_{cal}}$), was used as an input parameter for “Input 2” in Figure 7.

2.3.3. Normalized Hyperspectral Profile after Relative Calibration

The processed image information for L8 (${\rho }_{L8}$), S2A (${\rho }_{S2A}$) and relative calibrated EO-1 Hyperion-processed image information (${\rho }_{h_{cal}}$) formed a new input data called “Input 2”. Input 2, shown in Figure 7, was now used in the multispectral to hyperspectral profile conversion for L8 and S2A following the same procedures illustrated in Figure 8 and explained in Section 2.3.1. The normalized hyperspectral profile obtained from the conversion process using “Input 2” was then compared with their satellite measurements. Figure 13 shows the L8-normalized hyperspectral profile, ${\rho }_{L{8}_{hyp}}$ (grey color), along with its band-integrated multispectral form, ${\rho }_{L{8}_{hy{p}_{mult}}}$ (purple circle). The orange circle represents the observed TOA reflectance (${\rho }_{{L8}_{i=1}}$). The absolute difference (red bar) was calculated between ${\rho }_{L{8}_{i=1}}$ and band-integrated multispectral TOA reflectance (${\rho }_{L{8}_{hy{p}_{mult}}}$), as shown in Figure 13. It can be concluded that performing the relative calibration on the EO-1 sensor reduced the offset and the hyperspectral profile highly matched its observed multispectral domain.

There are M and N numbers of hyperspectral profile for L8 (${\rho }_{L{8}_{hyp}}$) and S2A (${\rho }_{S2A_{hyp}}$), respectively. Figure 14 shows the L8- normalized hyperspectral profile (gray color), the L8 measurements (orange circle), and the relative calibrated Hyperion profile (blue color). The S2A-normalized hyperspectral profile (grey color), the S2A measurements (orange circle), and the relative calibrated Hyperion profile (blue color) are shown in Figure 15. It can be observed that ${\rho }_{L8}$ and ${\rho }_{S2A}$ aligned within the range of normalized hyperspectral profile for both the L8 and S2A sensors. It can also be justified that the normalized hyperspectral profile obtained in this process truly represents satellite data in the multispectral domain.

The DaHD consists of a combination of L8- and S2A-normalized hyperspectral profiles, a total of 1925 (M = 1150, N = 775) profiles. The DaHD, consisting of reflectance measurements in the range of 0.04–0.2, was then used to develop the DAHAC model.

2.4. Dark Hyperspectral Absolute Calibration Model Development

2.4.1. Four-Angle Hyperspectral BRDF Model

Since the Earth’s surface is the non-Lambertian target, solar illumination and sensor viewing geometry can significantly impact the TOA reflectance of a given target. Most often, the BRDF can be used to model this effect [1]. In this study, the DaHD was used to develop the four-angle hyperspectral BRDF model. During this process, the spherical angles associated with the DaHD viz. a solar zenith angle (SZA) ranging from 15–60°, a solar azimuth angle (SAA) from 31–163°, a view zenith angle (VZA) from 0.03–10°, and a view azimuth angle (VAA) from −177–180° were converted into the Cartesian coordinates form using Equations (7)–(10), respectively.

$$Y_1=sin\left(SZA\right)\times cos\left(SAA\right)$$

(7)

$$X_1=sin\left(SZA\right)\times sin\left(SAA\right)$$

(8)

$$Y_2=sin\left(VZA\right)\times cos\left(VAA\right)$$

(9)

$$X_2=sin\left(VZA\right)\times sin\left(VAA\right)$$

(10)

where $X_1$ and $Y_1$ represent the Cartesian coordinates obtained using SZA and SAA, while $X_2$ and $Y_2$ represent the Cartesian coordinates obtained using VZA and VAA.

In order to achieve symmetry with regard to the scattering plane and to provide a robust fit to the four-angle hyperspectral BRDF model, the DaHD along with the angular information in the converted Cartesian coordinates were then mirrored to each quadrant. Consequently, the TOA reflectance became a continuous function of independent variables [22]. Using the new set of the independent variables in the Cartesian coordinates form ($X_1,Y_1,X_2,Y_2$) and the mirrored DaHD, the four-angle multi-quadratic least-squares regression model was derived as shown in Equation (11). It is important to note that the four-angle hyperspectral BRDF model developed in this study utilizes all the DaHD imagery data to cover all the angular information.

$$\begin{array}{cc}\hfill \rho (\lambda ,X_1,Y_1,X_2,Y_2)=& {\beta }_0+{\beta }_1{X}_1\left(\lambda \right)+{\beta }_2{Y}_1\left(\lambda \right)+{\beta }_3{X}_2\left(\lambda \right)+{\beta }_4{Y}_2\left(\lambda \right)+{\beta }_5{X}_1{Y}_1\left(\lambda \right)\hfill \\ & +{\beta }_6{X}_1{X}_2\left(\lambda \right)+{\beta }_7{X}_1{Y}_2\left(\lambda \right)+{\beta }_8{Y}_1{X}_2\left(\lambda \right)+{\beta }_9{Y}_1{Y}_2\left(\lambda \right)+{\beta }_{10}{X}_2{Y}_2\left(\lambda \right)\hfill \\ & +{\beta }_{11}{X}_1^2\left(\lambda \right)+{\beta }_{12}{Y}_1^2\left(\lambda \right)+{\beta }_{13}{X}_2^2\left(\lambda \right)+{\beta }_{14}{Y}_2^2\left(\lambda \right)\hfill \end{array}$$

(11)

where $\rho$ is the predicted TOA reflectance with respect to the wavelength ($\lambda$) and four-angle Cartesian coordinates ($X_1,Y_1,X_2,Y_2$). ${\beta }_0$ represents the BRDF intercept, and the 14 BRDF model coefficients ${\beta }_1$, ${\beta }_2$, ${\beta }_3$, ${\beta }_4$, ${\beta }_5$, ${\beta }_6$, ${\beta }_7$, ${\beta }_8$, ${\beta }_9$, ${\beta }_{10}$, ${\beta }_{11}$, ${\beta }_{12}$, ${\beta }_{13}$, and ${\beta }_{14}$ represent quadratic and linear coefficients.

Once the four-angle BRDF model had been developed, the predicted TOA reflectance was compared against the DaHD, as shown in Figure 16. The TOA reflectance difference was calculated between the DaHD profile and the predicted four-angle BRDF model to determine the level of agreement between them. The distribution of the TOA reflectance differences for all 196 bands is shown in the histogram in Figure 17. It can be observed that the TOA reflectance difference was normally distributed and the majority of the difference lied within a 0.02 TOA reflectance for all 196 hyperspectral bands.

2.4.2. Dark Hyperspectral Absolute Calibration Model

In order to develop the DAHAC model, a hypothesis test was applied to all 15 BRDF model coefficients at the 95% significance level for all 196 hyperspectral bands. The hypothesis test results (model coefficients, estimate, standard error, t-statistics values, p-values, and each coefficient statistical significance) for the band with a 864 nm wavelength are summarized in

Table 3. Showing 4-angle hyperspectral BRDF model coefficients for 864 nm wavelength.

Coefficient	Estimate	Standard Error	t-Statistic	p-Value	Statistical Response
Intercept	0.14	6e-04	226.20	0	Significant
$X_1$	−7.59e-18	3.30e-04	−2.3e-14	1.0	Insignificant
$Y_1$	−2.71e-17	3.88e-04	−6.98e-14	1.0	Insignificant
$X_2$	7.33e-18	0.006	1.18e-15	1.0	Insignificant
$Y_2$	1.50e-18	0.002	7.64e-16	1.0	Insignificant
$X_1$$Y_1$	3.24e-18	9.59e-04	3.38e-15	1.0	Insignificant
$X_1$$X_2$	0.16	0.02	9.08	1.27e-19	Significant
$X_1$$Y_2$	−4.67e-17	0.005	−8.7e-15	1.0	Insignificant
$Y_1$$X_2$	2.79e-17	0.02	1.27e-15	1.0	Insignificant
$Y_1$$Y_2$	0.16	0.007	22.32	5.42e-107	Significant
$X_2$$Y_2$	2.45e-18	0.05	4.58e-17	1.0	Insignificant
$X_1^2$	−0.08	8.13e-04	−107.41	0	Significant
$Y_1^2$	−0.06	0.003	−19.69	2.75e-84	Significant
$X_2^2$	16.97	0.48	−35.29	4.32e-253	Significant
$Y_2^2$	1.62	0.04	36.63	5.69e-271	Significant

.

All of the Hyperion bands were validated by this statistical analysis, excluding a few bands at 942 nm and 1386 nm, which represent water vapor and cirrus with high absorption features. The p-value for the t-statistic hypothesis evaluated whether or not the BRDF coefficients were equal to zero. When the p-value exceeds 0.05, the corresponding BRDF coefficient becomes insignificant and vice versa. There were only seven significant coefficients viz. $X_1{X}_2$, $Y_1{Y}_2$, $X_1^2$, $Y_1^2$, $X_2^2$, $Y_2^2$, and the intercept, as shown in Table 3. They were used to represent the DAHAC model. It is important to note that the atmospheric parameters were not considered when developing the model in this study since they had a negligible effect on the atmospheric model and the absolute calibration model [39]. The DAHAC model with seven coefficients was derived using the solar zenith and azimuth angles and sensor zenith and azimuth angles, as shown in Equation (12) below:

$$\begin{array}{c}\hfill \rho {(\lambda ,X_1,Y_1,X_2,Y_2)}_{DAHAC}=B_0\left(\lambda \right)+B_1\left(\lambda \right)X_1{X}_2+B_2\left(\lambda \right)Y_1{Y}_2+B_3\left(\lambda \right)X_1^2+\\ \hfill B_4\left(\lambda \right)Y_1^2+B_5\left(\lambda \right)X_2^2+B_6\left(\lambda \right)Y_2^2\end{array}$$

(12)

where ${\rho }_{{(\lambda ,X_1,Y_1,X_2,Y_2)}_{DAHAC}}$ is the model-predicted TOA reflectance with respect to the wavelength ($\lambda$) and the Cartesian coordinates ($X_1,Y_1,X_2,Y_2$). The predicted TOA reflectance had a spectral resolution of 10 nm. $B_0$ represents the intercept, and $B_1$, $B_2$, $B_3$, $B_4$, $B_5$, and $B_6$ are the model coefficients corresponding to $X_1{X}_2$, $Y_1{Y}_2$, $X_1^2$, $Y_1^2$, $X_2^2$, and $Y_2^2$, respectively.

Unlike the hyperspectral model developed by Chaity et al. [1], it should be noted that the DAHAC model does not require any adjustment factor in the model equation to scale the Hyperion spectrum due to low reflectance in all bands. The DAHAC model coefficient values for 196 hyperspectral bands are shown in Figure 18.

The validation of the DAHAC model (7 coefficients) with the four-angle hyperspectral BRDF model (15 coefficients) for all hyperspectral bands is shown in Figure 19a. It can be observed that the plot shows a linear behavior, which means the DAHAC model statistically agrees with the four-angle hyperspectral BRDF model with a slope equal to one and a bias close to zero. Figure 19b shows the TOA reflectance differences between the two models, and the mean absolute error (MAE) calculated using Equation (13) was found to be close to zero.

$$\begin{array}{c}\hfill MAE=\frac{{\sum }_{j=1}^n|y_j-{\widehat{y}}_j|}{n}\end{array}$$

(13)

where $y_j$: four-angle hyperspectral BRDF Model predicted TOA reflectance, ${\widehat{y}}_j$: DAHAC model-predicted TOA reflectance, and n: number of hyperspectral bands.

This provided significant evidence that the DAHAC model is capable of predicting the DaHD. The DAHAC model is further validated with Landsat missions and Sentinel-2 missions in Section 3. The model performance was evaluated using two metrics: accuracy and precision in unit reflectance due to the low-reflectance target. The accuracy and precision were measured by calculating the mean and standard deviation of the differences between the satellite-observed and model-predicted TOA reflectance using Equations (14) and (15), respectively.

$$\mathrm{Accuracy}=mean({\rho }_{sat}-{\rho }_{model})$$

(14)

$$\mathrm{Precision}=std({\rho }_{sat}-{\rho }_{model})$$

(15)

where ${\rho }_{sat}$ refers to the satellite-observed TOA reflectance and ${\rho }_{model}$ represents the DAHAC-model-predicted TOA reflectance, i.e., $\rho {(\lambda ,X_1,Y_1,X_2,Y_2)}_{DAHAC}$.

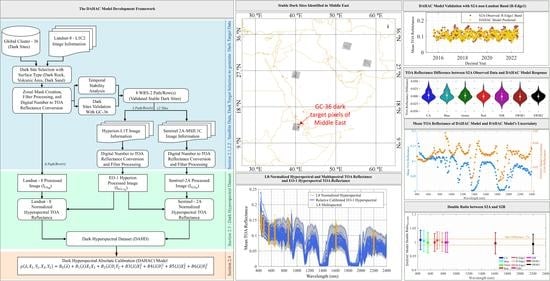
3. Results and Discussion

In this section, the results of the model validation to determine the model accuracy with respect to different sensors are presented and analyzed.

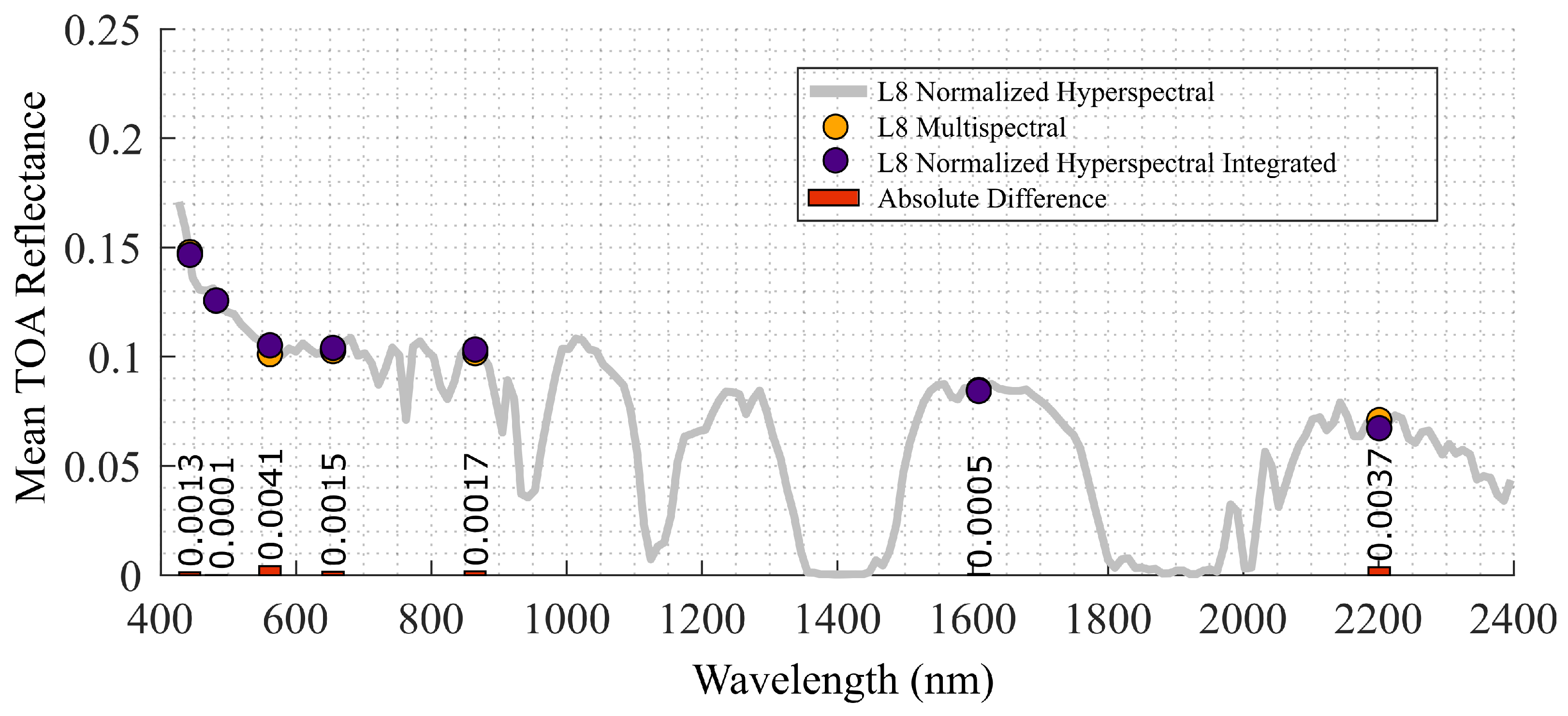
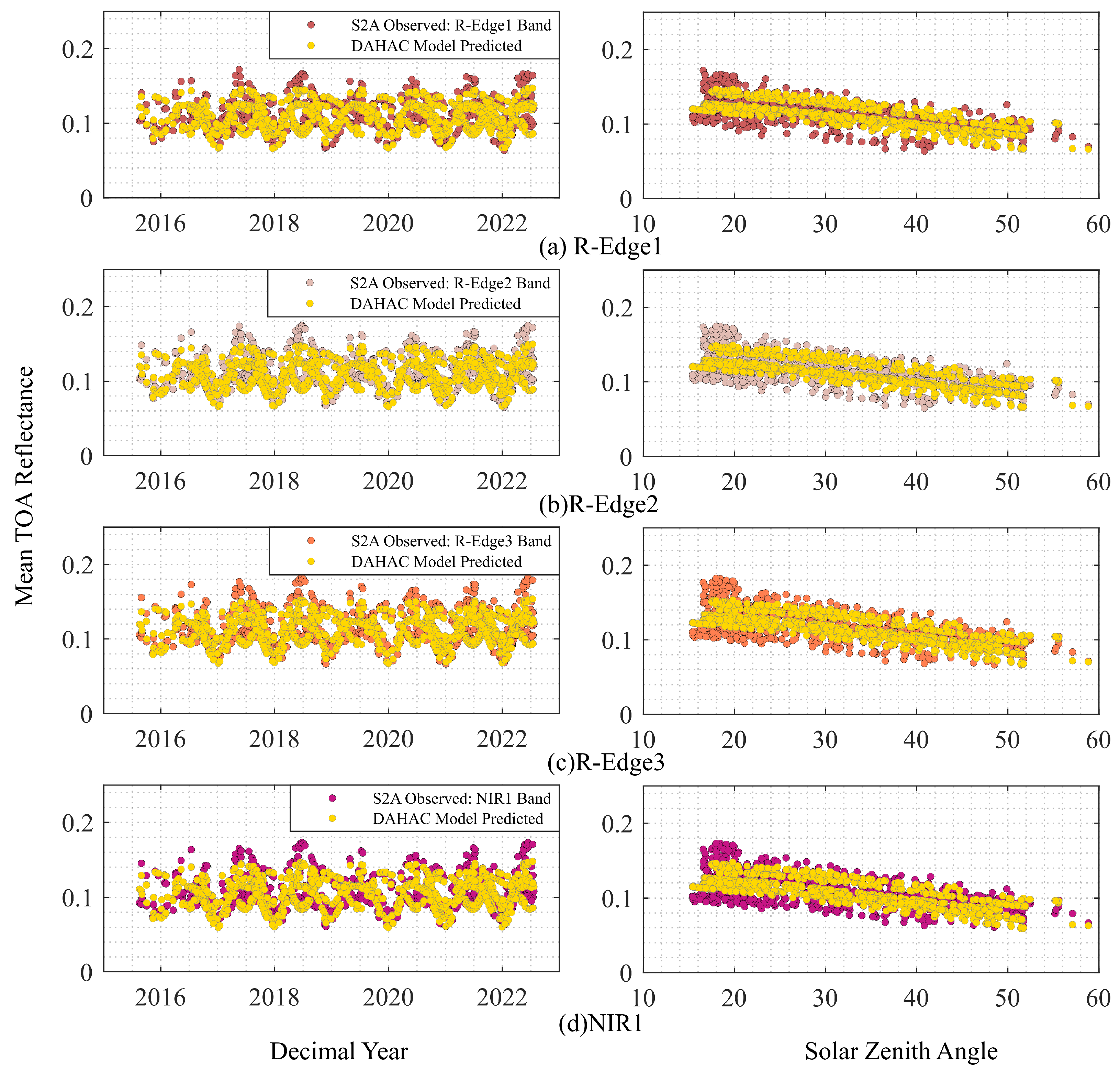
3.1. DAHAC Model Validation Process

In order to evaluate the DAHAC model performance and its accuracy, it was validated with five different sensors viz. L7, L8, L9, S2A, and S2B. During the validation process, the spherical angular information (SZA, SAA, VZA, and VAA) was first transformed into the Cartesian coordinates form for each sensor (L7, L8, L9, S2A, and S2B). Using the converted Cartesian coordinates and the DAHAC model coefficients shown in Figure 18 as the input parameters for the DAHAC model, the hyperspectral TOA reflectance was predicted for each sensor. The hyperspectral TOA reflectance response from the model had a 10 nm resolution, which was then subjected to cubic interpolation to obtain a finer 1 nm spectral resolution. Since multispectral sensors were used for validation in this study, the RSR of each sensor was then used to integrate the interpolated hyperspectral TOA reflectance into the multispectral TOA reflectance. Finally, the model response in the form of multispectral TOA reflectance was compared with the observed TOA reflectance of each sensor used for validation purposes. The results from the DAHAC model validation for L7, L8, L9, S2A, and S2B are presented in the following subsections.

3.1.1. DAHAC Model Validation with Landsat Missions

The DAHAC model-predicted and the observed L8 TOA reflectance for seven bands were compared with respect to the decimal year and SZA, as shown in Figure 20a–g.

The left-hand side plots with respect to the decimal year show the seasonal variation and were well-captured by the model for every band. The right-hand side plots show the decreasing linear trend of the observed TOA reflectance with respect to the SZA, and the DAHAC model-predicted TOA reflectance agreed well with L8 measurements for all spectral bands.

The performance of the DAHAC model on the Landsat sensors (L7, L8, and L9) was evaluated by measuring the difference between the observed TOA reflectance of the Landsat sensors with the DAHAC model’s response. The error distribution for L7, L8, and L9 across the bands are further shown in the violin plot in Figure 21a–c, respectively. The error bar in each violin plot shows the mean and $1\sigma$ standard deviation of the TOA reflectance difference. It is clearly seen from the violin distribution in Figure 21a–c that, for all three Landsat sensors (L7, L8, L9), the majority of TOA reflectance difference fell within ±0.02 for all spectral bands. The average mean difference ranged between 0 and 0.012 for all bands.

3.1.2. DAHAC Model Validation with Sentinel-2 Missions

The DAHAC model validation process for Sentinel-2 missions was the same as for the Landsat missions. Figure 22 shows the comparison between the predicted TOA reflectance and observed S2A measurements for non-Landsat bands (Red-Edge1, Red-Edge2, Red-Edge3, NIR1) with respect to the decimal year and SZA. It can be observed that the seasonal variation in the Sentinel measurements matched very well with the DAHAC-model-predicted TOA reflectance for all non-Landsat bands. Figure 23a,b show that the majority of the TOA reflectance difference fell within ±0.02 TOA reflectance for Sentinel-2 missions (S2A, S2B). The average mean difference ranged within 0 and 0.004 TOA reflectance for all spectral bands.

The hyperspectral BRDF model developed in [1] depends on the hyperspectral cross-scale factor to normalize the Hyperion intercept spectral profile for different spectral bands. The advantage of using the DAHAC model is that it will be independent of calculating and estimating the adjustment factors for scaling the Hyperion spectrum. The dark target data were obtained from all three sensors (L8, S2A, and EO-1) in the range of 0.04–0.2 TOA reflectance for all spectral bands used for the DAHAC model development. Following the DAHAC model specifications for the solar zenith angle (15–60°), solar azimuth angle (31–163°), view zenith angle (0.03–10°), and view azimuth angle (−177–180°), the predicted results showed that the model was able to estimate the TOA reflectance measurements with the highest accuracy of ±0.012 and a precision within 0.02 unit reflectance for all Landsat satellites spectral bands. The model performance for the Sentinel sensors (S2A and S2B) showed an accuracy and precision within ±0.004 and ±0.02 unit reflectance. Additionally, the TOA reflectance predicted using the DAHAC model had a 10 nm spectral resolution, and a finer 1 nm resolution was then obtained by further subjecting the model to cubic interpolation. This implies that the DAHAC model can perform the absolute calibration of any sensor over Dark EPICS-Global with a 1 nm spectral resolution.

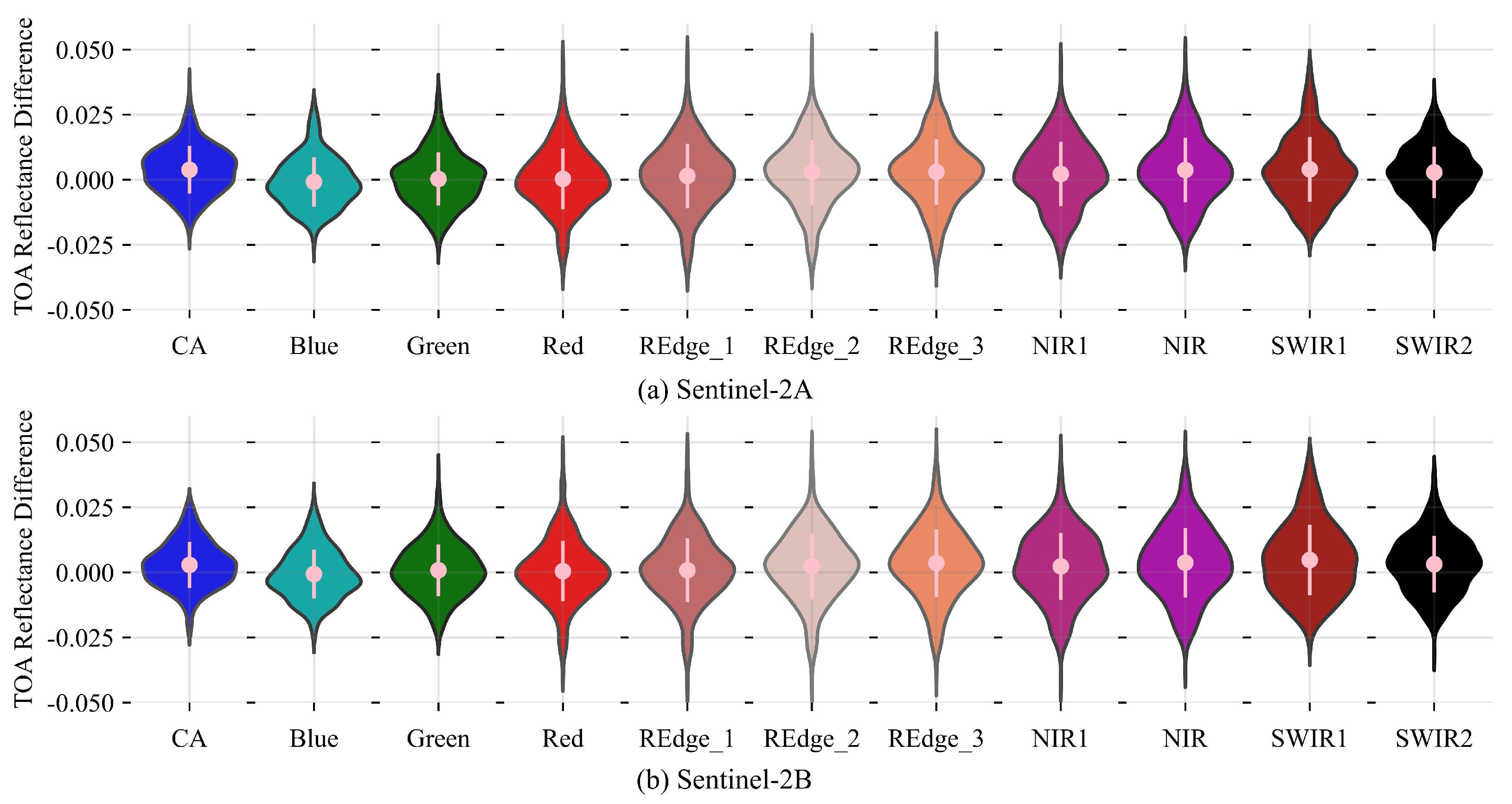
4. Uncertainty Analysis

In this section, the uncertainty analysis for the DAHAC model is performed. The sensors viz. L8, S2A, and EO-1 Hyperion used for the DAHAC model’s development have currently been determined to have uncertainties at 2% [7], 4% [39], and 5–10% [35], respectively. It was initially assumed that the DAHAC model’s uncertainty is related to the uncertainty on the relative calibration of the EO-1 sensor, all the steps involved in the model development, the DaHD generation process, and the development of the BRDF model, as described in Section 2.3 and Section 2.4.

The flowchart shown in Figure 24 illustrates the steps followed in the DAHAC model’s uncertainty calculation.

The standard deviation for coefficient estimates of the DAHAC model was calculated using the formula: $Coef{f}_{std}=\frac{C{I}_U-C{I}_L}{2\times t-value}$, where $C{I}_U$ and $C{I}_L$ represent the upper bound and lower bound of the confidence interval (CI), respectively, and the t-value corresponds to the 95% CI and the degrees of freedom. The initial distribution of the mean and standard deviation of the seven DAHAC model coefficients for 196 bands are tabulated in

Table A1. Showing the initial distribution of the mean and standard deviation of the DAHAC model’s coefficients for 196 bands.

Wavelength (nm)	$\mathit{B}{0}_{\mathit{mean}}$	$\mathit{B}{0}_{\mathit{SD}}$	$\mathit{B}{1}_{\mathit{mean}}$	$\mathit{B}{1}_{\mathit{SD}}$	$\mathit{B}{2}_{\mathit{mean}}$	$\mathit{B}{2}_{\mathit{SD}}$	$\mathit{B}{3}_{\mathit{mean}}$	$\mathit{B}{3}_{\mathit{SD}}$	$\mathit{B}{4}_{\mathit{mean}}$	$\mathit{B}{4}_{\mathit{SD}}$	$\mathit{B}{5}_{\mathit{mean}}$	$\mathit{B}{5}_{\mathit{SD}}$	$\mathit{B}{6}_{\mathit{mean}}$	$\mathit{B}{6}_{\mathit{SD}}$
426.8	0.168	5.90E-04	0.308	1.70E-02	0.2	6.90E-03	−0.037	8.00E-04	−0.029	3.20E-03	17.243	4.70E-01	−1.666	4.30E-02
437	0.155	5.50E-04	0.314	1.60E-02	0.175	6.40E-03	−0.034	7.40E-04	−0.023	3.00E-03	16.453	4.40E-01	−1.542	4.00E-02
447.2	0.134	4.90E-04	0.272	1.40E-02	0.152	5.70E-03	−0.029	6.60E-04	−0.021	2.70E-03	15.8	3.90E-01	−1.463	3.60E-02
457.3	0.13	4.70E-04	0.274	1.40E-02	0.145	5.50E-03	−0.029	6.40E-04	−0.022	2.60E-03	15.326	3.80E-01	−1.391	3.50E-02
467.5	0.131	4.80E-04	0.281	1.40E-02	0.149	5.60E-03	−0.03	6.50E-04	−0.025	2.60E-03	16.189	3.90E-01	−1.455	3.50E-02
477.7	0.133	4.90E-04	0.282	1.40E-02	0.155	5.70E-03	−0.033	6.60E-04	−0.028	2.70E-03	16.335	3.90E-01	−1.449	3.60E-02
487.9	0.127	4.60E-04	0.275	1.30E-02	0.149	5.40E-03	−0.034	6.20E-04	−0.029	2.50E-03	15.26	3.70E-01	−1.335	3.40E-02
498	0.125	4.60E-04	0.272	1.30E-02	0.148	5.30E-03	−0.035	6.20E-04	−0.03	2.50E-03	14.998	3.60E-01	−1.299	3.40E-02
508.2	0.126	4.50E-04	0.27	1.30E-02	0.154	5.30E-03	−0.037	6.10E-04	−0.034	2.50E-03	14.561	3.60E-01	−1.247	3.40E-02
518.4	0.122	4.40E-04	0.26	1.30E-02	0.15	5.10E-03	−0.038	5.90E-04	−0.035	2.40E-03	13.24	3.50E-01	−1.12	3.20E-02
528.6	0.121	4.20E-04	0.252	1.20E-02	0.15	4.90E-03	−0.041	5.70E-04	−0.037	2.30E-03	11.479	3.40E-01	−0.953	3.10E-02
538.7	0.12	4.10E-04	0.241	1.20E-02	0.151	4.80E-03	−0.043	5.50E-04	−0.04	2.20E-03	9.941	3.30E-01	−0.812	3.00E-02
548.9	0.119	4.00E-04	0.232	1.20E-02	0.153	4.70E-03	−0.046	5.50E-04	−0.043	2.20E-03	8.645	3.20E-01	−0.69	3.00E-02
559.1	0.121	4.10E-04	0.225	1.20E-02	0.158	4.80E-03	−0.049	5.50E-04	−0.046	2.20E-03	7.054	3.30E-01	−0.546	3.00E-02
569.3	0.12	4.00E-04	0.206	1.20E-02	0.16	4.70E-03	−0.052	5.40E-04	−0.051	2.20E-03	5.003	3.20E-01	−0.367	2.90E-02
579.5	0.12	4.00E-04	0.189	1.20E-02	0.164	4.70E-03	−0.056	5.40E-04	−0.055	2.20E-03	2.653	3.20E-01	−0.161	3.00E-02
589.6	0.126	4.30E-04	0.191	1.30E-02	0.179	5.10E-03	−0.062	5.90E-04	−0.063	2.40E-03	2.091	3.50E-01	−0.103	3.20E-02
599.8	0.128	4.60E-04	0.181	1.30E-02	0.193	5.40E-03	−0.066	6.20E-04	−0.072	2.50E-03	1.091	3.70E-01	−0.012	3.40E-02
610	0.13	4.60E-04	0.182	1.30E-02	0.183	5.30E-03	−0.067	6.20E-04	−0.067	2.50E-03	−0.664	3.70E-01	0.144	3.40E-02
620.1	0.128	4.50E-04	0.175	1.30E-02	0.181	5.30E-03	−0.067	6.10E-04	−0.067	2.50E-03	−1.025	3.60E-01	0.175	3.30E-02
630.3	0.127	4.60E-04	0.168	1.30E-02	0.182	5.40E-03	−0.068	6.20E-04	−0.069	2.50E-03	−2.241	3.70E-01	0.284	3.40E-02
640.5	0.129	4.70E-04	0.168	1.40E-02	0.186	5.50E-03	−0.07	6.40E-04	−0.071	2.60E-03	−2.911	3.80E-01	0.346	3.50E-02
650.7	0.135	5.10E-04	0.169	1.50E-02	0.207	6.00E-03	−0.076	6.90E-04	−0.081	2.80E-03	−2.889	4.10E-01	0.35	3.80E-02
660.9	0.131	5.00E-04	0.162	1.50E-02	0.2	5.90E-03	−0.075	6.80E-04	−0.078	2.70E-03	−3.382	4.00E-01	0.391	3.70E-02
671	0.136	5.10E-04	0.169	1.50E-02	0.197	6.00E-03	−0.077	6.90E-04	−0.077	2.80E-03	−4.42	4.10E-01	0.485	3.80E-02
681.2	0.139	5.20E-04	0.171	1.50E-02	0.201	6.10E-03	−0.079	7.10E-04	−0.079	2.90E-03	−4.967	4.20E-01	0.537	3.90E-02
691.4	0.132	5.20E-04	0.155	1.50E-02	0.197	6.10E-03	−0.078	7.00E-04	−0.079	2.90E-03	−6.192	4.20E-01	0.65	3.80E-02
701.6	0.138	5.90E-04	0.152	1.70E-02	0.229	6.90E-03	−0.086	8.00E-04	−0.094	3.20E-03	−6.858	4.70E-01	0.72	4.40E-02
711.7	0.135	5.90E-04	0.148	1.70E-02	0.225	7.00E-03	−0.086	8.00E-04	−0.095	3.30E-03	−7.72	4.80E-01	0.801	4.40E-02
721.9	0.136	7.40E-04	0.132	2.20E-02	0.276	8.70E-03	−0.097	1.00E-03	−0.122	4.10E-03	−9.343	5.90E-01	0.976	5.50E-02
732.1	0.138	6.70E-04	0.139	2.00E-02	0.248	7.80E-03	−0.093	9.00E-04	−0.107	3.70E-03	−9.926	5.30E-01	1.01	4.90E-02
742.2	0.138	5.70E-04	0.16	1.70E-02	0.193	6.60E-03	−0.085	7.70E-04	−0.078	3.10E-03	−10.728	4.50E-01	1.057	4.20E-02
752.4	0.132	5.50E-04	0.156	1.60E-02	0.171	6.40E-03	−0.082	7.40E-04	−0.07	3.00E-03	−12.114	4.40E-01	1.18	4.00E-02
762.6	0.1	4.70E-04	0.103	1.40E-02	0.139	5.50E-03	−0.068	6.30E-04	−0.059	2.60E-03	−12.521	3.70E-01	1.206	3.50E-02
772.8	0.137	5.80E-04	0.156	1.70E-02	0.175	6.80E-03	−0.087	7.90E-04	−0.072	3.20E-03	−14.417	4.70E-01	1.384	4.30E-02
783	0.141	5.90E-04	0.162	1.70E-02	0.182	6.90E-03	−0.088	8.00E-04	−0.075	3.20E-03	−13.813	4.70E-01	1.338	4.40E-02
793.1	0.139	6.10E-04	0.153	1.80E-02	0.196	7.10E-03	−0.09	8.20E-04	−0.082	3.30E-03	−13.809	4.90E-01	1.342	4.50E-02
803.3	0.137	6.10E-04	0.147	1.80E-02	0.197	7.10E-03	−0.09	8.30E-04	−0.084	3.30E-03	−14.017	4.90E-01	1.361	4.50E-02
813.5	0.13	6.70E-04	0.121	2.00E-02	0.231	7.90E-03	−0.093	9.10E-04	−0.103	3.70E-03	−13.661	5.40E-01	1.354	5.00E-02
823.6	0.126	6.90E-04	0.111	2.00E-02	0.235	8.10E-03	−0.093	9.30E-04	−0.107	3.80E-03	−13.857	5.50E-01	1.372	5.10E-02
833.8	0.129	6.30E-04	0.124	1.90E-02	0.211	7.40E-03	−0.09	8.50E-04	−0.093	3.50E-03	−14.159	5.10E-01	1.384	4.70E-02
844	0.136	6.00E-04	0.151	1.80E-02	0.179	7.10E-03	−0.089	8.10E-04	−0.076	3.30E-03	−15.524	4.80E-01	1.494	4.40E-02
854.2	0.139	6.10E-04	0.161	1.80E-02	0.169	7.10E-03	−0.089	8.20E-04	−0.07	3.30E-03	−16.403	4.90E-01	1.574	4.50E-02
864.4	0.136	6.00E-04	0.16	1.80E-02	0.157	7.00E-03	−0.087	8.10E-04	−0.065	3.30E-03	−16.983	4.80E-01	1.624	4.40E-02
874.5	0.132	6.00E-04	0.157	1.70E-02	0.149	7.00E-03	−0.086	8.10E-04	−0.062	3.30E-03	−17.69	4.80E-01	1.688	4.40E-02
884.7	0.127	6.00E-04	0.152	1.70E-02	0.145	7.00E-03	−0.085	8.10E-04	−0.061	3.30E-03	−18.731	4.80E-01	1.784	4.40E-02
894.9	0.119	6.30E-04	0.119	1.80E-02	0.181	7.40E-03	−0.087	8.50E-04	−0.082	3.50E-03	−17.835	5.10E-01	1.712	4.70E-02
905	0.108	6.90E-04	0.088	2.00E-02	0.205	8.10E-03	−0.088	9.40E-04	−0.096	3.80E-03	−17.935	5.50E-01	1.737	5.10E-02
912.5	0.164	1.30E-03	0.009	3.80E-02	0.487	1.50E-02	−0.133	1.70E-03	−0.204	7.00E-03	−7.523	1.00E+00	0.656	9.50E-02
922.5	0.146	1.20E-03	−0.013	3.40E-02	0.428	1.40E-02	−0.119	1.60E-03	−0.188	6.30E-03	−10.073	9.30E-01	0.938	8.50E-02
932.6	0.102	1.10E-03	0.017	3.30E-02	0.349	1.30E-02	−0.101	1.50E-03	−0.172	6.20E-03	−13.369	9.00E-01	1.268	8.30E-02
942.7	0.105	1.20E-03	0.034	3.40E-02	0.363	1.40E-02	−0.107	1.60E-03	−0.179	6.50E-03	−13.796	9.40E-01	1.323	8.70E-02
952.8	0.108	1.10E-03	0.055	3.30E-02	0.352	1.30E-02	−0.106	1.50E-03	−0.175	6.20E-03	−12.392	9.10E-01	1.24	8.40E-02
962.9	0.124	9.90E-04	0.098	2.90E-02	0.336	1.20E-02	−0.108	1.30E-03	−0.157	5.40E-03	−11.545	7.90E-01	1.154	7.30E-02
973	0.131	8.10E-04	0.135	2.40E-02	0.274	9.50E-03	−0.103	1.10E-03	−0.126	4.50E-03	−13.709	6.50E-01	1.373	6.00E-02
983.1	0.137	6.80E-04	0.172	2.00E-02	0.218	8.00E-03	−0.097	9.20E-04	−0.095	3.70E-03	−13.958	5.50E-01	1.365	5.00E-02
993.2	0.141	6.10E-04	0.157	1.80E-02	0.196	7.10E-03	−0.091	8.20E-04	−0.079	3.30E-03	−13.799	4.90E-01	1.304	4.50E-02
1003.3	0.139	5.90E-04	0.154	1.70E-02	0.186	7.00E-03	−0.089	8.00E-04	−0.074	3.30E-03	−13.922	4.80E-01	1.31	4.40E-02
1013.3	0.14	5.70E-04	0.16	1.70E-02	0.177	6.70E-03	−0.087	7.70E-04	−0.065	3.10E-03	−13.366	4.60E-01	1.246	4.20E-02
1023.4	0.14	5.70E-04	0.154	1.70E-02	0.175	6.70E-03	−0.086	7.70E-04	−0.064	3.10E-03	−13.416	4.60E-01	1.252	4.20E-02
1033.4	0.132	5.40E-04	0.158	1.60E-02	0.154	6.30E-03	−0.081	7.30E-04	−0.057	3.00E-03	−12.981	4.30E-01	1.228	4.00E-02
1043.5	0.131	5.30E-04	0.155	1.60E-02	0.152	6.20E-03	−0.079	7.20E-04	−0.056	2.90E-03	−12.661	4.30E-01	1.197	3.90E-02
1053.6	0.126	5.50E-04	0.143	1.60E-02	0.145	6.40E-03	−0.079	7.40E-04	−0.061	3.00E-03	−14.396	4.40E-01	1.376	4.00E-02
1063.7	0.123	5.40E-04	0.137	1.60E-02	0.147	6.40E-03	−0.079	7.30E-04	−0.063	3.00E-03	−14.361	4.30E-01	1.373	4.00E-02
1073.8	0.126	5.70E-04	0.136	1.70E-02	0.169	6.70E-03	−0.085	7.80E-04	−0.074	3.10E-03	−15.261	4.60E-01	1.457	4.20E-02
1083.9	0.125	5.90E-04	0.122	1.70E-02	0.188	6.90E-03	−0.087	8.00E-04	−0.083	3.20E-03	−14.719	4.70E-01	1.415	4.40E-02
1094	0.12	6.70E-04	0.094	2.00E-02	0.221	7.90E-03	−0.092	9.10E-04	−0.102	3.70E-03	−15.105	5.40E-01	1.49	5.00E-02
1104.1	0.108	8.20E-04	0.047	2.40E-02	0.267	9.60E-03	−0.094	1.10E-03	−0.13	4.50E-03	−14.596	6.60E-01	1.472	6.00E-02
1114.1	0.073	8.20E-04	0.007	2.40E-02	0.237	9.70E-03	−0.077	1.10E-03	−0.128	4.50E-03	−12.411	6.60E-01	1.286	6.10E-02
1124.2	0.058	8.40E-04	0.023	2.50E-02	0.22	9.80E-03	−0.073	1.10E-03	−0.125	4.60E-03	−12.566	6.70E-01	1.29	6.20E-02
1134.3	0.069	9.00E-04	0.037	2.60E-02	0.247	1.10E-02	−0.082	1.20E-03	−0.134	4.90E-03	−13.375	7.20E-01	1.365	6.60E-02
1144	0.073	9.40E-04	0.032	2.70E-02	0.261	1.10E-02	−0.086	1.30E-03	−0.14	5.10E-03	−13.705	7.50E-01	1.402	6.90E-02
1154	0.092	9.70E-04	0.055	2.90E-02	0.291	1.10E-02	−0.099	1.30E-03	−0.147	5.30E-03	−14.373	7.80E-01	1.452	7.20E-02
1164	0.11	8.30E-04	0.077	2.40E-02	0.272	9.80E-03	−0.099	1.10E-03	−0.13	4.60E-03	−14.213	6.70E-01	1.424	6.10E-02
1174	0.114	7.50E-04	0.086	2.20E-02	0.24	8.70E-03	−0.096	1.00E-03	−0.112	4.10E-03	−15.784	6.00E-01	1.552	5.50E-02
1184	0.114	7.30E-04	0.094	2.10E-02	0.231	8.50E-03	−0.095	9.80E-04	−0.108	4.00E-03	−15.922	5.80E-01	1.566	5.40E-02
1194	0.111	6.60E-04	0.116	1.90E-02	0.197	7.80E-03	−0.09	9.00E-04	−0.095	3.60E-03	−15.691	5.30E-01	1.567	4.90E-02
1205	0.111	6.40E-04	0.127	1.90E-02	0.187	7.50E-03	−0.089	8.70E-04	−0.09	3.50E-03	−15.877	5.20E-01	1.578	4.80E-02
1215	0.116	6.10E-04	0.147	1.80E-02	0.169	7.20E-03	−0.089	8.30E-04	−0.078	3.40E-03	−15.827	4.90E-01	1.551	4.50E-02
1225	0.117	5.90E-04	0.161	1.70E-02	0.145	6.90E-03	−0.086	8.00E-04	−0.065	3.20E-03	−16.195	4.70E-01	1.577	4.40E-02
1235	0.117	5.70E-04	0.148	1.70E-02	0.128	6.70E-03	−0.081	7.70E-04	−0.058	3.10E-03	−16.386	4.60E-01	1.59	4.20E-02
1245	0.115	5.70E-04	0.144	1.70E-02	0.12	6.70E-03	−0.08	7.70E-04	−0.054	3.10E-03	−16.973	4.50E-01	1.643	4.20E-02
1255	0.114	5.40E-04	0.121	1.60E-02	0.138	6.40E-03	−0.08	7.30E-04	−0.055	3.00E-03	−16.82	4.30E-01	1.596	4.00E-02
1265	0.107	5.40E-04	0.11	1.60E-02	0.141	6.30E-03	−0.079	7.30E-04	−0.057	3.00E-03	−16.877	4.30E-01	1.59	4.00E-02
1275	0.114	5.60E-04	0.115	1.60E-02	0.143	6.50E-03	−0.083	7.60E-04	−0.058	3.10E-03	−17.627	4.50E-01	1.658	4.10E-02
1285	0.12	5.70E-04	0.113	1.70E-02	0.162	6.70E-03	−0.086	7.70E-04	−0.067	3.10E-03	−16.777	4.60E-01	1.593	4.20E-02
1295	0.113	5.60E-04	0.096	1.60E-02	0.179	6.60E-03	−0.083	7.60E-04	−0.077	3.10E-03	−14.127	4.50E-01	1.371	4.10E-02
1305	0.106	6.30E-04	0.065	1.90E-02	0.215	7.40E-03	−0.085	8.60E-04	−0.097	3.50E-03	−13.101	5.10E-01	1.296	4.70E-02
1316	0.1	7.00E-04	0.048	2.10E-02	0.244	8.20E-03	−0.086	9.50E-04	−0.113	3.90E-03	−11.74	5.60E-01	1.174	5.20E-02
1326	0.089	8.00E-04	0.017	2.30E-02	0.259	9.30E-03	−0.084	1.10E-03	−0.127	4.40E-03	−11.857	6.40E-01	1.2	5.90E-02
1336	0.079	8.70E-04	0.02	2.60E-02	0.245	1.00E-02	−0.084	1.20E-03	−0.131	4.80E-03	−14.88	7.00E-01	1.494	6.40E-02
1346	0.039	5.30E-04	−0.004	1.50E-02	0.119	6.20E-03	−0.046	7.10E-04	−0.073	2.90E-03	−10.89	4.20E-01	1.088	3.90E-02
1356	0.004	9.30E-05	0.021	2.70E-03	−0.005	1.10E-03	−0.005	1.30E-04	−0.002	5.10E-04	−2.067	7.40E-02	0.227	6.90E-03
1366	0.002	3.80E-05	0.004	1.10E-03	0	4.50E-04	−0.002	5.20E-05	−0.003	2.10E-04	−0.603	3.10E-02	0.08	2.80E-03
1376	0.003	1.00E-04	0.019	2.90E-03	−0.001	1.20E-03	−0.005	1.30E-04	−0.002	5.50E-04	−2.058	8.00E-02	0.215	7.30E-03
1386	0.005	1.20E-04	0.019	3.70E-03	0.003	1.50E-03	−0.008	1.70E-04	−0.006	6.80E-04	−3.102	1.00E-01	0.319	9.20E-03
1396	0.008	1.70E-04	0.021	5.10E-03	0.016	2.00E-03	−0.014	2.30E-04	−0.013	9.50E-04	−5.006	1.40E-01	0.496	1.30E-02
1406	0.013	2.60E-04	0.018	7.50E-03	0.035	3.00E-03	−0.022	3.50E-04	−0.026	1.40E-03	−7.397	2.10E-01	0.724	1.90E-02
1416	0.024	4.30E-04	0.016	1.30E-02	0.077	5.00E-03	−0.037	5.80E-04	−0.052	2.40E-03	−10.549	3.40E-01	1.038	3.20E-02
1426	0.031	5.50E-04	0.02	1.60E-02	0.11	6.40E-03	−0.048	7.40E-04	−0.07	3.00E-03	−12.412	4.40E-01	1.232	4.00E-02
1437	0.036	6.30E-04	0.017	1.80E-02	0.127	7.40E-03	−0.055	8.50E-04	−0.08	3.50E-03	−14.749	5.00E-01	1.445	4.60E-02
1447	0.048	7.80E-04	0.037	2.30E-02	0.176	9.10E-03	−0.07	1.10E-03	−0.104	4.30E-03	−15.968	6.20E-01	1.591	5.80E-02
1457	0.066	9.70E-04	0.023	2.80E-02	0.246	1.10E-02	−0.09	1.30E-03	−0.133	5.30E-03	−18.262	7.80E-01	1.805	7.20E-02
1467	0.057	8.90E-04	0.012	2.60E-02	0.215	1.00E-02	−0.081	1.20E-03	−0.119	4.90E-03	−17.937	7.10E-01	1.758	6.60E-02
1477	0.07	9.90E-04	0.003	2.90E-02	0.262	1.20E-02	−0.091	1.30E-03	−0.137	5.40E-03	−18.477	7.90E-01	1.753	7.30E-02
1487	0.087	1.00E-03	0.029	3.00E-02	0.296	1.20E-02	−0.102	1.40E-03	−0.147	5.60E-03	−17.638	8.20E-01	1.675	7.50E-02
1497	0.102	8.20E-04	0.063	2.40E-02	0.279	9.60E-03	−0.094	1.10E-03	−0.13	4.50E-03	−12.237	6.60E-01	1.175	6.10E-02
1507	0.111	7.20E-04	0.09	2.10E-02	0.258	8.50E-03	−0.093	9.80E-04	−0.115	4.00E-03	−11.727	5.80E-01	1.117	5.30E-02
1517	0.115	6.70E-04	0.095	2.00E-02	0.232	7.80E-03	−0.092	9.00E-04	−0.1	3.70E-03	−14.36	5.30E-01	1.325	4.90E-02
1527	0.118	6.10E-04	0.109	1.80E-02	0.205	7.20E-03	−0.089	8.30E-04	−0.085	3.40E-03	−15.082	4.90E-01	1.373	4.50E-02
1537	0.12	5.70E-04	0.133	1.70E-02	0.186	6.70E-03	−0.085	7.70E-04	−0.076	3.10E-03	−13.871	4.50E-01	1.26	4.20E-02
1548	0.122	5.70E-04	0.14	1.70E-02	0.178	6.60E-03	−0.084	7.70E-04	−0.071	3.10E-03	−14.171	4.50E-01	1.281	4.20E-02
1558	0.122	5.70E-04	0.144	1.70E-02	0.171	6.70E-03	−0.084	7.70E-04	−0.068	3.10E-03	−14.859	4.60E-01	1.346	4.20E-02
1568	0.115	5.50E-04	0.129	1.60E-02	0.163	6.50E-03	−0.081	7.50E-04	−0.065	3.00E-03	−15.455	4.40E-01	1.397	4.10E-02
1578	0.115	5.50E-04	0.153	1.60E-02	0.159	6.40E-03	−0.081	7.40E-04	−0.064	3.00E-03	−13.645	4.40E-01	1.25	4.00E-02
1588	0.119	5.50E-04	0.155	1.60E-02	0.163	6.40E-03	−0.081	7.40E-04	−0.064	3.00E-03	−12.981	4.40E-01	1.193	4.00E-02
1598	0.114	5.40E-04	0.133	1.60E-02	0.155	6.40E-03	−0.079	7.30E-04	−0.061	3.00E-03	−15.101	4.30E-01	1.359	4.00E-02
1608	0.115	5.50E-04	0.145	1.60E-02	0.158	6.50E-03	−0.081	7.50E-04	−0.061	3.00E-03	−14.818	4.40E-01	1.33	4.10E-02
1618	0.12	5.50E-04	0.159	1.60E-02	0.157	6.40E-03	−0.081	7.40E-04	−0.06	3.00E-03	−12.724	4.40E-01	1.181	4.00E-02
1628	0.119	5.40E-04	0.153	1.60E-02	0.156	6.30E-03	−0.08	7.30E-04	−0.06	3.00E-03	−12.681	4.30E-01	1.179	4.00E-02
1638	0.118	5.40E-04	0.15	1.60E-02	0.159	6.30E-03	−0.08	7.20E-04	−0.061	2.90E-03	−12.4	4.30E-01	1.145	4.00E-02
1648	0.119	5.40E-04	0.154	1.60E-02	0.165	6.40E-03	−0.081	7.40E-04	−0.064	3.00E-03	−12.243	4.40E-01	1.129	4.00E-02
1659	0.118	5.30E-04	0.15	1.60E-02	0.166	6.20E-03	−0.08	7.20E-04	−0.064	2.90E-03	−11.219	4.30E-01	1.05	3.90E-02
1669	0.119	5.40E-04	0.152	1.60E-02	0.168	6.30E-03	−0.081	7.30E-04	−0.065	2.90E-03	−10.966	4.30E-01	1.025	4.00E-02
1679	0.119	5.30E-04	0.146	1.60E-02	0.167	6.20E-03	−0.081	7.20E-04	−0.064	2.90E-03	−11.124	4.30E-01	1.048	3.90E-02
1689	0.118	5.40E-04	0.134	1.60E-02	0.174	6.30E-03	−0.082	7.20E-04	−0.069	2.90E-03	−11.091	4.30E-01	1.048	3.90E-02
1699	0.116	5.50E-04	0.13	1.60E-02	0.173	6.40E-03	−0.083	7.40E-04	−0.069	3.00E-03	−12.244	4.40E-01	1.165	4.00E-02
1709	0.116	5.60E-04	0.128	1.60E-02	0.181	6.60E-03	−0.085	7.60E-04	−0.074	3.10E-03	−12.175	4.50E-01	1.162	4.10E-02
1719	0.113	5.60E-04	0.119	1.60E-02	0.189	6.50E-03	−0.083	7.60E-04	−0.08	3.10E-03	−11.097	4.50E-01	1.066	4.10E-02
1729	0.111	5.70E-04	0.111	1.70E-02	0.197	6.70E-03	−0.083	7.70E-04	−0.084	3.10E-03	−10.892	4.60E-01	1.051	4.20E-02
1739	0.111	6.10E-04	0.1	1.80E-02	0.218	7.20E-03	−0.087	8.30E-04	−0.094	3.40E-03	−10.597	4.90E-01	1.027	4.50E-02
1749	0.108	6.20E-04	0.09	1.80E-02	0.224	7.30E-03	−0.086	8.40E-04	−0.097	3.40E-03	−10.345	5.00E-01	1.003	4.60E-02
1759	0.103	6.50E-04	0.068	1.90E-02	0.238	7.70E-03	−0.085	8.80E-04	−0.105	3.60E-03	−9.324	5.20E-01	0.92	4.80E-02
1769	0.096	7.60E-04	0.04	2.20E-02	0.265	9.00E-03	−0.087	1.00E-03	−0.122	4.20E-03	−9.948	6.10E-01	0.987	5.60E-02
1780	0.086	8.60E-04	0.018	2.50E-02	0.271	1.00E-02	−0.088	1.20E-03	−0.131	4.70E-03	−11.474	6.90E-01	1.135	6.30E-02
1790	0.072	8.70E-04	−0.009	2.50E-02	0.254	1.00E-02	−0.082	1.20E-03	−0.128	4.80E-03	−12.535	7.00E-01	1.231	6.40E-02
1800	0.045	6.60E-04	−0.017	1.90E-02	0.172	7.70E-03	−0.058	8.90E-04	−0.092	3.60E-03	−11.209	5.30E-01	1.074	4.90E-02
1810	0.029	4.70E-04	−0.013	1.40E-02	0.109	5.50E-03	−0.04	6.40E-04	−0.062	2.60E-03	−9.576	3.80E-01	0.901	3.50E-02
1820	0.019	2.40E-04	−0.005	6.90E-03	0.061	2.80E-03	−0.021	3.20E-04	−0.033	1.30E-03	−4.567	1.90E-01	0.402	1.70E-02
1830	0.007	5.40E-05	0.009	1.60E-03	0.011	6.30E-04	−0.002	7.30E-05	−0.003	3.00E-04	−0.292	4.30E-02	−0.008	4.00E-03
1840	0.002	7.10E-05	0.024	2.10E-03	−0.006	8.40E-04	0.001	9.60E-05	0.005	3.90E-04	1.261	5.70E-02	−0.099	5.30E-03
1850	0.002	6.80E-05	0.023	2.00E-03	−0.005	7.90E-04	0.001	9.20E-05	0.004	3.70E-04	1.229	5.40E-02	−0.098	5.00E-03
1860	0.007	1.10E-04	0.002	3.10E-03	0.015	1.20E-03	−0.008	1.40E-04	−0.009	5.80E-04	−2.43	8.50E-02	0.229	7.80E-03
1870	0.005	7.20E-05	0.004	2.10E-03	0.008	8.40E-04	−0.005	9.70E-05	−0.005	3.90E-04	−1.476	5.70E-02	0.138	5.30E-03
1880	0.01	1.80E-04	0.002	5.30E-03	0.03	2.10E-03	−0.015	2.50E-04	−0.02	1.00E-03	−5.062	1.50E-01	0.467	1.30E-02
1891	0.009	1.60E-04	0.001	4.80E-03	0.028	1.90E-03	−0.014	2.20E-04	−0.017	9.00E-04	−4.536	1.30E-01	0.417	1.20E-02
1901	0.006	8.90E-05	0.02	2.60E-03	0.006	1.00E-03	−0.007	1.20E-04	−0.005	4.90E-04	−1.539	7.20E-02	0.164	6.60E-03
1911	0.009	1.30E-04	0.016	3.80E-03	0.018	1.50E-03	−0.011	1.80E-04	−0.013	7.10E-04	−2.656	1.00E-01	0.272	9.60E-03
1921	0.01	2.00E-04	0.006	5.90E-03	0.031	2.40E-03	−0.016	2.70E-04	−0.022	1.10E-03	−5.467	1.60E-01	0.537	1.50E-02
1931	0.015	2.90E-04	0.002	8.50E-03	0.049	3.40E-03	−0.023	3.90E-04	−0.035	1.60E-03	−7.681	2.30E-01	0.748	2.10E-02
1941	0.031	5.60E-04	−0.016	1.60E-02	0.121	6.60E-03	−0.046	7.60E-04	−0.07	3.10E-03	−13.169	4.50E-01	1.2	4.10E-02
1951	0.031	5.30E-04	−0.017	1.60E-02	0.121	6.20E-03	−0.045	7.20E-04	−0.067	2.90E-03	−12.295	4.20E-01	1.116	3.90E-02
1961	0.037	6.30E-04	0.03	1.80E-02	0.121	7.30E-03	−0.055	8.50E-04	−0.073	3.40E-03	−14.932	5.00E-01	1.469	4.60E-02
1971	0.064	8.00E-04	0.069	2.30E-02	0.199	9.40E-03	−0.08	1.10E-03	−0.105	4.40E-03	−15.314	6.40E-01	1.547	5.90E-02
1981	0.089	8.60E-04	0.06	2.50E-02	0.267	1.00E-02	−0.095	1.20E-03	−0.127	4.70E-03	−15.061	6.90E-01	1.426	6.30E-02
1991	0.072	7.10E-04	0.012	2.10E-02	0.207	8.30E-03	−0.077	9.60E-04	−0.1	3.90E-03	−16.013	5.70E-01	1.498	5.20E-02
2002	0.023	3.90E-04	0.007	1.10E-02	0.061	4.50E-03	−0.035	5.20E-04	−0.034	2.10E-03	−13.108	3.10E-01	1.219	2.90E-02
2012	0.03	4.90E-04	0.019	1.40E-02	0.077	5.70E-03	−0.046	6.60E-04	−0.043	2.70E-03	−16.364	3.90E-01	1.518	3.60E-02
2022	0.074	7.00E-04	0.064	2.10E-02	0.192	8.20E-03	−0.08	9.50E-04	−0.086	3.80E-03	−17.896	5.60E-01	1.585	5.20E-02
2032	0.102	6.80E-04	0.095	2.00E-02	0.221	7.90E-03	−0.09	9.20E-04	−0.093	3.70E-03	−16.173	5.40E-01	1.427	5.00E-02
2042	0.09	6.40E-04	0.074	1.90E-02	0.179	7.50E-03	−0.084	8.70E-04	−0.08	3.50E-03	−18.753	5.10E-01	1.734	4.70E-02
2052	0.068	6.30E-04	0.044	1.90E-02	0.142	7.40E-03	−0.074	8.60E-04	−0.066	3.50E-03	-21.492	5.10E-01	1.974	4.70E-02
2062	0.079	5.90E-04	0.051	1.70E-02	0.177	6.90E-03	−0.073	8.00E-04	−0.076	3.20E-03	−16.355	4.70E-01	1.442	4.30E-02
2072	0.094	6.30E-04	0.09	1.80E-02	0.201	7.40E-03	−0.083	8.50E-04	−0.083	3.50E-03	−15.682	5.00E-01	1.368	4.60E-02
2082	0.101	6.30E-04	0.108	1.80E-02	0.181	7.40E-03	−0.088	8.50E-04	−0.075	3.40E-03	−17.125	5.00E-01	1.587	4.60E-02
2092	0.107	6.40E-04	0.118	1.90E-02	0.191	7.50E-03	−0.091	8.60E-04	−0.079	3.50E-03	−16.11	5.10E-01	1.508	4.70E-02
2102	0.111	5.60E-04	0.133	1.60E-02	0.197	6.50E-03	−0.084	7.50E-04	−0.077	3.00E-03	−10.081	4.50E-01	0.927	4.10E-02
2113	0.112	5.60E-04	0.131	1.60E-02	0.199	6.60E-03	−0.085	7.60E-04	−0.078	3.10E-03	−10.225	4.50E-01	0.935	4.10E-02
2123	0.109	6.30E-04	0.151	1.80E-02	0.176	7.40E-03	−0.091	8.50E-04	−0.07	3.40E-03	−15.05	5.00E-01	1.416	4.60E-02
2133	0.11	6.20E-04	0.154	1.80E-02	0.164	7.30E-03	−0.09	8.40E-04	−0.062	3.40E-03	−15.332	5.00E-01	1.439	4.60E-02
2143	0.116	5.60E-04	0.132	1.60E-02	0.201	6.50E-03	−0.084	7.50E-04	−0.074	3.00E-03	−10.712	4.40E-01	0.929	4.10E-02
2153	0.113	5.80E-04	0.123	1.70E-02	0.214	6.70E-03	−0.086	7.80E-04	−0.082	3.20E-03	−10.691	4.60E-01	0.924	4.20E-02
2163	0.105	6.40E-04	0.135	1.90E-02	0.176	7.50E-03	−0.09	8.60E-04	−0.068	3.50E-03	−16.148	5.10E-01	1.498	4.70E-02
2173	0.105	6.40E-04	0.132	1.90E-02	0.177	7.50E-03	−0.09	8.70E-04	−0.069	3.50E-03	−16.258	5.10E-01	1.508	4.70E-02
2183	0.109	5.30E-04	0.135	1.50E-02	0.209	6.20E-03	−0.078	7.10E-04	−0.082	2.90E-03	−5.235	4.20E-01	0.453	3.90E-02
2193	0.105	5.00E-04	0.126	1.50E-02	0.196	5.90E-03	−0.074	6.80E-04	−0.077	2.70E-03	−5.702	4.00E-01	0.493	3.70E-02
2203	0.101	5.50E-04	0.126	1.60E-02	0.182	6.40E-03	−0.08	7.40E-04	−0.067	3.00E-03	−11.499	4.40E-01	1.014	4.00E-02
2213	0.106	5.50E-04	0.126	1.60E-02	0.186	6.50E-03	−0.081	7.50E-04	−0.067	3.00E-03	−11.337	4.40E-01	0.994	4.10E-02
2224	0.106	4.70E-04	0.134	1.40E-02	0.185	5.50E-03	−0.071	6.30E-04	−0.067	2.60E-03	−4.707	3.80E-01	0.389	3.50E-02
2234	0.103	4.60E-04	0.129	1.30E-02	0.179	5.40E-03	−0.07	6.20E-04	−0.065	2.50E-03	−4.9	3.70E-01	0.407	3.40E-02
2244	0.097	5.20E-04	0.112	1.50E-02	0.151	6.10E-03	−0.075	7.00E-04	−0.057	2.90E-03	−11.624	4.20E-01	1.1	3.80E-02
2254	0.094	5.20E-04	0.099	1.50E-02	0.15	6.10E-03	−0.075	7.10E-04	−0.057	2.90E-03	−12.622	4.20E-01	1.187	3.90E-02
2264	0.099	4.80E-04	0.088	1.40E-02	0.189	5.60E-03	−0.072	6.50E-04	−0.069	2.60E-03	−7.969	3.80E-01	0.674	3.50E-02
2274	0.099	4.70E-04	0.088	1.40E-02	0.188	5.50E-03	−0.071	6.40E-04	−0.068	2.60E-03	−7.625	3.80E-01	0.636	3.50E-02
2284	0.092	4.40E-04	0.102	1.30E-02	0.154	5.10E-03	−0.066	5.90E-04	−0.061	2.40E-03	−6.184	3.50E-01	0.619	3.20E-02
2294	0.089	4.60E-04	0.094	1.30E-02	0.159	5.40E-03	−0.068	6.20E-04	−0.066	2.50E-03	−7.235	3.70E-01	0.728	3.40E-02
2304	0.096	4.80E-04	0.103	1.40E-02	0.179	5.60E-03	−0.072	6.40E-04	−0.072	2.60E-03	−6.05	3.80E-01	0.6	3.50E-02
2314	0.091	4.90E-04	0.07	1.40E-02	0.184	5.70E-03	−0.069	6.60E-04	−0.077	2.70E-03	−6.443	3.90E-01	0.65	3.60E-02
2324	0.096	5.00E-04	0.099	1.50E-02	0.204	5.90E-03	−0.072	6.80E-04	−0.083	2.70E-03	−3.781	4.00E-01	0.377	3.70E-02
2335	0.091	4.90E-04	0.073	1.40E-02	0.2	5.80E-03	−0.068	6.70E-04	−0.084	2.70E-03	−4.101	3.90E-01	0.416	3.60E-02
2345	0.086	5.80E-04	0.051	1.70E-02	0.22	6.80E-03	−0.072	7.90E-04	−0.096	3.20E-03	−5.935	4.70E-01	0.592	4.30E-02
2355	0.09	6.00E-04	0.072	1.70E-02	0.229	7.00E-03	−0.075	8.10E-04	−0.099	3.30E-03	−4.63	4.80E-01	0.472	4.40E-02
2365	0.086	5.90E-04	0.037	1.70E-02	0.232	6.90E-03	−0.071	8.00E-04	−0.101	3.20E-03	−4.453	4.70E-01	0.446	4.40E-02
2375	0.084	6.80E-04	0.03	2.00E-02	0.253	7.90E-03	−0.076	9.20E-04	−0.114	3.70E-03	−5.112	5.40E-01	0.499	5.00E-02
2385	0.088	8.30E-04	0.04	2.40E-02	0.275	9.70E-03	−0.081	1.10E-03	−0.128	4.50E-03	−5.591	6.60E-01	0.603	6.10E-02
2395	0.095	8.10E-04	0.052	2.40E-02	0.287	9.50E-03	−0.077	1.10E-03	−0.129	4.40E-03	0.097	6.50E-01	0.085	6.00E-02

presented in Appendix A. Monte Carlo simulation was then employed to generate multivariate normal random numbers for the model coefficients using the model coefficients and their standard deviation information with the number of iterations set to 100. Using the randomized model coefficients obtained from this simulation and the angular information (SZA, SAA, VZA, VAA) from the DaHD in Cartesian coordinates, the DAHAC model predicted the TOA reflectance at each iteration level. The standard deviation of the predicted TOA reflectance of the DAHAC model was then estimated for all 196 bands. The simulation was performed by increasing the number of iterations at different levels (100, 500, 1000, 1500, 2000, 2500) until the standard deviation of the predicted TOA reflectance of the DAHAC model converged. Once the standard deviation converged to a stationary point, the simulation stopped, and the standard deviation at that point represented the DAHAC model’s uncertainty.

Figure 25 shows the results of the standard deviation of the DAHAC-model-predicted TOA reflectance using the Monte Carlo simulation. The three plots in Figure 25a–c represent different wavelength ranges: (426–905) nm, (912–1507) nm, and (1517–2395) nm, respectively. It can be observed that the standard deviation nearly converged between 1500 and 2500 iterations; the range was stable for all 196 bands. The uncertainty of the DAHAC model was then selected to be the model standard deviation at the 1500 iterations level. Figure 26 shows the DAHAC-model-predicted TOA reflectance and the DAHAC model’s uncertainty associated with each hyperspectral band. This analysis showed that the model uncertainty for the VNIR and SWIR channels was within 0.04 and 0.05 unit reflectance, respectively.

5. The DAHAC Model’s Double Ratio for Sensors Inter-Comparison

The ratio between the DAHAC model’s TOA reflectance and satellite measurements was used to determine the DAHAC model’s double ratio. The DAHAC model’s double ratio was used as a metric to perform the inter-comparison between two satellites across each spectral band. The double ratio approach eliminated any possible bias or error that could be embedded in the DAHAC model. Thus, it can be used as a transfer mechanism to directly compare two satellites, for instance L8 and L9 or S2A and S2B. During this process, the ratio between the model-predicted TOA reflectance and observed TOA reflectance measurements was calculated using Equation (16), called the “reflectance ratio”. Further, the DAHAC model’s double ratio was calculated using Equation (17).

$$\mathrm{Reflectance}{\mathrm{Ratio}}_{sat}=\frac{\mathrm{DAHAC} \mathrm{Model} \mathrm{TOA} \mathrm{Reflectance}}{\mathrm{Observed} \mathrm{TOA} \mathrm{Reflectance}}$$

(16)

$$\mathrm{DAHAC} \mathrm{Model} \mathrm{Double} \mathrm{Ratio}=\frac{\mathrm{Reflectance} {\mathrm{Ratio}}_{sat}}{\mathrm{Reflectance} {\mathrm{Ratio}}_{ref}}$$

(17)

where “sat” refers to the L8, L9, S2A, and S2B satellite sensors. “ref” represents the reference sensors viz. L8 and S2A.

The image information from November 2021 to October 2022 was used to perform the inter-comparison between L8 and L9. For S2A and S2B, the data for the inter-comparison analysis were taken from July 2017 to July 2022 over the dark target. In order to prevent the study from being influenced by site variation resulting from various atmospheric conditions, the image information was assumed to be stable within seven days. According to Gross et al., a smaller difference in the view zenith angle between two sensors leads to a reduced impact of several aspects of the BRDF [40]. Using nearby coincident pairs within seven days with a view zenith angle (VZA) difference less than 2°, 46 and 617 pairs were obtained for L8 and L9 and S2A and S2B, respectively. The DAHAC model’s double ratio result showed that L8 and L9 were comparable within 1% for all bands except for the red band within 2%, as shown in Figure 27. The Sentinel-2A and 2-B inter-comparison result showed the agreement within 1% for eleven spectral bands, as shown in Figure 28. In this way, the DAHAC model’s double ratio helped to evaluate the measurement differences across each spectral band for different sensors.

Being a part of the Landsat Cal/Val team, the SDSU IP Lab performed the cross-calibration between L8 and L9, showing the agreement within 0.5–1% [41]. The cross-calibration result between S2A and S2B was within ±2% over the Libya 4 site [42]. The DAHAC model’s double ratio gave similar results as reported in previous studies [15,23,41]. It proved that the DAHAC model’s double ratio can be a complementary tool to be used for satellite calibration.

6. Conclusions

This paper presented the development of the novel DAHAC model using the normalized hyperspectral profile of L8 and S2A over Dark EPICS-Global. Dark EPICS-Global includes different surface types viz. dark rock, volcanic area, and dark sand with a temporal variation of 0.02 unit reflectance, as illustrated in Table 2. The measurements of the L8, S2A, and EO-1 Hyperion sensors were used to generate the dark hyperspectral data for the DAHAC model’s development. L8 and S2A are well-calibrated and were used as reference sensors and the EO-1 Hyperion sensor as the hyperspectral library source. This study proposed an algorithm to obtain the normalized hyperspectral profile for L8 and S2A using the multispectral (L8, S2A) and hyperspectral (EO-1 Hyperion) domain data. The relative calibration of the EO-1 sensor significantly improved the agreement between the hyperspectral profile of L8 and S2A with its multispectral domain. The DaHD was generated by aggregating the normalized hyperspectral profile of L8 and S2A.

The DaHD with TOA reflectance in the range of 0.04–0.2 across all spectral bands was used to develop the four-angle hyperspectral BRDF model. The four-angle hyperspectral BRDF model was further simplified to develop the DAHAC model by considering the significant coefficients in the model parameters. The simplified DAHAC model was leveraged to predict the TOA reflectance with a 10 nm spectral resolution and further subjected to cubic interpolation to achieve a finer 1 nm resolution. Thus, the DAHAC model can perform the absolute calibration of any sensor with a 1 nm spectral resolution over Dark EPICS-Global.

The DAHAC model was validated with several multispectral sensors viz. L7 ETM+, L8, L9, S2A, and S2B. The validation results showed that the model was able to predict the TOA reflectance measurements with the highest accuracy of ±0.012 and a precision within 0.02 unit reflectance for all spectral bands of the Landsat missions (L7, L8, and L9). The model performance for the Sentinel-2 missions (S2A and S2B) showed an accuracy and precision within ±0.004 and ±0.02 unit reflectance. In contrast to the hyperspectral APICS model estimation accuracy within limited bands [1], the DAHAC model can predict the satellite measurements across all the spectral bands, especially for non-Landsat equivalent bands with higher accuracy. This result proved the DAHAC model is a robust tool for performing absolute calibration of any sensors on multispectral and hyperspectral instruments.

A thorough analysis was performed to determine the model’s overall uncertainty. Using the Monte Carlo simulation on the DAHAC model, the DAHAC-model-predicted TOA reflectance and the standard deviation were estimated at different iteration levels. The DAHAC model’s uncertainty was found to be within 0.04 and 0.05 unit reflectance for the VNIR and SWIR channels, respectively.

The sensor inter-comparison for the Landsat and Sentinel-2 missions was performed using the DAHAC model’s double ratio. The agreement between L8 and L9 was within 0.06–2% and 1% for S2A and S2B. These results match closely the results from the L8–L9 cross-calibration (0.5–1%) [41] and the S2A-S2B inter-comparison over Libya 4 (2%) [42].

The DAHAC model is capable of a nadir look angle of up to 10° and a solar zenith angle of up to 60°, however, it would be more challenging for larger viewing angles. When the view zenith angle increases, the RSR shifts towards a shorter wavelength, leading to changes in the sensor’s received radiance information [43]. However, the RSR shift effect was not considered in this study. In addition, the DAHAC model does not consider factors such as atmospheric scatterings, Rayleigh scattering, aerosol optical load, and gas absorption properties before developing the model.

However, increasing the DAHAC model’s accuracy, decreasing its uncertainty, and improving the TOA reflectance consistency are still possible. The calibration variations between L8 and S2A with other sensors and random anomalies at the time of the sensor overpass due to atmospheric conditions were most likely the cause of the reduced accuracy. In general, the model accuracy can be improved by using more data samples with high-quality hyperspectral images for absolute calibration and sensor inter-comparison applications.

In the future, the proposed model’s development algorithm will be applied over stable bright sites to check its reliability and performance accuracy. The ability of the proposed algorithm to perform satellite absolute calibration will be tested for the dynamic range of TOA reflectance measurement. The RSR shift effect will also be considered during the absolute calibration model’s development with larger viewing angles of satellite data.