Abstract
A new technique for reconstructing the magnetic image of Mercury from satellite observation data is proposed. The technique is based on extracting from the general observational data only the part that is associated with magnetic field sources concentrated in Mercury’s crust. The extracted data are used to solve the inverse problem of reconstructing the near-surface magnetic image of Mercury. The results of processing real experimental data obtained via the MESSENGER interplanetary mission are presented.
Keywords:
magnetic parameters reconstruction; magnetic image; Mercury; MESSENGER; inverse problem; regularization MSC:
45Q05; 65Rxx; 85A99; 86A22
1. Introduction
Over the past 10–20 years, the volume of information about the physical fields of Mercury has increased greatly. With various automatic satellite missions (such as Mariner and MESSENGER [1,2,3,4,5,6,7,8,9,10,11]), researchers were able to obtain high-quality satellite observational data. The quality of the data was due primarily to the fact that the specificity of the orbits of the spacecraft ensured the acquisition of experimental data distributed in three-dimensional space. This made it possible to solve rather complex problems of determining various physical parameters of the planet.
As noted in our previous work [12], the results of processing data from remote sensing of celestial bodies are used to specify models of the internal structure of the planets of the Solar System. Launched as part of a joint Japanese–European program, the BepiColombo spacecraft should reach Mercury in 2025, and then knowledge about the planet closest to the Sun will be supplemented with qualitatively new information [13]. Nowadays, researchers believe that the internal structure of Mercury is “arranged” approximately as described, for example, in the works [14,15]. However, new space missions may prompt scientists to rethink established models regarding the internal structure of this enigmatic planet. This is due to the fact that the models of physical fields are corrected when new data arrays appear after the launch of each next interplanetary mission. At the moment, the main emphasis in research is on different approaches to the interpretation of the main components of the fields and their high-frequency components. It must be emphasized that we are interpreting real, satellite data on the magnetic field of Mercury. There are no other experimental data yet, and our goal is to construct efficient algorithms for finding a stable approximate solution to the inverse problem of determining the magnetic masses in the planet’s crust.
Mercury’s magnetic field is not stationary. The presence of a magnetic dynamo on the planet (as established by MESSENGER’s data [16]) determines a very complex nature of the interaction of the internal magnetic field with the solar wind, which is a stream of charged particles. When constructing analytical models of the magnetic field of planets, including Mercury, both “isolated” expansions of signals in a series in terms of spherical harmonics [17,18] and combined representations of the magnetic field components in the form sums of poloidal and toroidal components (the so-called Mie representation [16]) are used. To build specified models of the planetary magnetic field, it is necessary to isolate the “crustal” component, which is due to the presence of the magnetic inhomogeneities close to the surface [17,19,20,21,22,23,24,25,26,27,28]. Thus, the restoration of the near-surface magnetic image of Mercury is an urgent task. At the same time, the importance of separating the fields created by sources occurring at different depths should be noted separately. Away from the surface of the planet, the “crustal” component of the magnetic field looks like a noise having a small amplitude compared to the time-dependent trend component. Therefore, new effective regularizing algorithms seem to be relevant, because they allow obtaining an approximate solution of the inverse problem of geomagnetic that is resistant to random noise in the input data [29,30,31,32,33,34].
The structure of the work is as follows. Section 2 contains a general statement of the problem and its division into two sub-problems. The first sub-problem is to extract from the observed data only that component of the magnetic field that is directly related to the sources of the magnetic field concentrated in the crust of Mercury. The second sub-problem is to find the local sources of the magnetic field themselves from the selected data. Further, in Section 3, a method for extracting the magnetic field component we need is described. Section 5 contains the results of processing real experimental data obtained by the MESSENGER interplanetary mission.
2. Problem Statement
The purpose of this work is to determine the magnetic moment density , , only in the near-surface layer V of Mercury according to measurements of the magnetic field at the points , , located at a significant distance from the planet. In the explanatory Figure 1, the green dots mark the points of the experimental observation of the magnetic field by satellite mission MESSENGER.

Figure 1.
(a) The location relative to Mercury of the magnetic field measurement points by the MESSENGER mission; (b) location of points in a thin spherical layer where the magnetic field was recalculated. is the average radius of Mercury, = 2,439,700 (m).
In our previous paper [35], we used similar data to directly reconstruct the magnetization parameters in the narrow “crustal” layer V of Mercury without any preprocessing. As a result, the problem of recovering the magnetic image of Mercury in the “zero” approximation was solved. In fact, one of the distributions of magnetic field sources equivalent in terms of the measured external field was found. In this work, we will try to recover the true distribution of “fine structures” in Mercury’s crust, by which we mean only the local near-surface distribution of magnetic masses.
To do this, it is necessary to isolate the internal magnetic field from the data of experimental observations, and from it to isolate that part of the field that is generated by magnetic masses in the crust of Mercury. To solve this problem, one could use experimental observations of the magnetic field by the MESSENGER satellite mission (see Figure 1) and extract the internal field from them. However, in the current work we do a preliminary conversion of these experimental data. First, we solve the forward (direct) problem based on the results of the article [35], and as a result we find the values of the magnetic field in some spherical layer surrounding Mercury. In fact, we continue the experimentally observed magnetic field at relatively arbitrary points (see Figure 1) into a region convenient for further processing (a thin spherical layer at some distance from the surface of Mercury). This preprocessing of the data helps to significantly simplify the solution of the first sub-problem of extracting the magnetic field component of interest to us (details will be given in Section 3). After that, using our achievements from the works [12,35], we will be able to solve the second sub-problem of recovering the near-surface magnetic image of Mercury.
Below, we formally describe the statements of these two sub-problems, to the solution of which our main problem is reduced.
2.1. Separation of the High-Frequency Component of the Internal Field
Consider the spherical layer surrounding Mercury. The inner radius of this spherical layer is equal to a, the outer one is c. The Gauss–Mie expansion of the experimentally observed field inside this spherical layer, according to the principle of superposition, has the form [16,36]
Here, is Mie expansion into the toroidal and poloidal component (T—toroidal; P—poloidal; —shell)); —internal field (—internal) generated by currents in ; —external field (—external) generated by currents in ; —field in the region generated by poloidal currents; —field in the region generated by toroidal currents; (—unit vector in spherical coordinates; see Figure 2); functions , , , —scalar potentials.
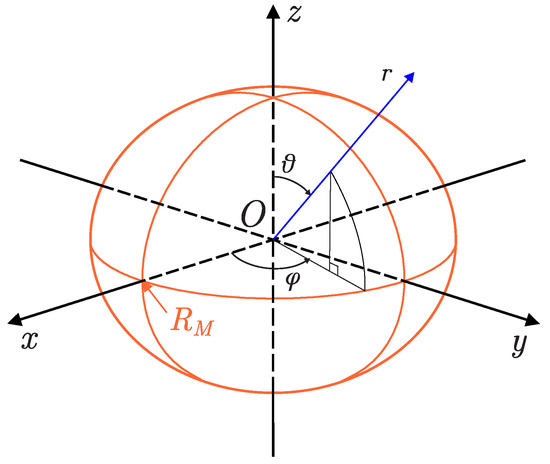
Figure 2.
The planetary coordinate system used in solving the problem.
To extract “fine structures”, it is necessary to extract the high-frequency component from the internal magnetic field . How to do this will be detailed in Section 3. The next subsection sets out the sub-problem of determining the magnetic image in Mercury’s crust from the field .
2.2. Reconstruction of the Near-Surface Magnetic Image of Mercury
The equation describing the magnetic field induction induced by an object with a magnetization distribution and a localization in a domain V has the form
where is a distance between the point , at which the triaxial sensor s measuring magnetic field induction is located, and the point of the domain V, at which a magnetic source with a total magnetic moment per unit volume is placed, and is a permeability in vacuum.
As a result, to restore the vector function , which determines the near-surface magnetic image of Mercury, it is necessary to solve the following inverse problem.
The inverse problem is to define the magnetic moment density , , according to measurements of magnetic field at the points , .
The found magnetization will make it possible to localize “fine structures” in the form of local maxima of the magnetization modulus.
3. Separation of the High-Frequency Component of Mercury’s Internal Magnetic Field
To isolate the high-frequency component of Mercury’s internal magnetic field, it is necessary to parametrize field (1) in terms of expansion coefficients in terms of spherical harmonics of the potentials of the corresponding fields in the Gauss–Mie expansion. We will use the body-fixed, planetary-centered spherical coordinates (see Figure 2) with , and . Here, is the average radius of Mercury. In this coordinate system, scalar potentials can be represented as follows [16,36]:
and —desired coefficients; and are the coefficients for a poloidal field (having a thin shell approximation, so this field is not taken into account in our work); —associated Legendre polynomials (with Schmidt normalization) of degree l, and order m (the Schmidt-normalized associated Legendre polynomials).
Let us write Equation (1) in terms of potentials. For this, we immediately note that in the problem under consideration, the thickness of the spherical layer is assumed to be small enough to use the thin shell approximation; that is, ignore [16,36]. The “thin shell” approximation allows us to exclude the dipole and quadrupole components from satellite data, since the values of these components within a thin spherical layer remain practically unchanged, while the conditionally “high-frequency” part of the signal can vary depending on the geometry of the sources located in the crust. Therefore, Equation (1) takes the form
To calculate gradients and vector products, we introduce the following generalizations.
- .
- .
- .
Using the introduced notation, we rewrite the expressions for the potentials:
In the problem under consideration, for the potentials of the internal and external fields ; for the potential of the toroidal field, .
The toroidal magnetic field in the spherical layer can be rewritten as follows [16,36]:
Thus, in a spherical coordinate system, at each fixed point inside the spherical layer , the field will have the following form:
The total field is parametrized by the coefficients of the internal Gaussian dipole , coefficients of the internal Gaussian quadrupole , coefficients of the internal Gaussian octupole , coefficients of the external Gaussian dipole , coefficients of the outer Gaussian quadrupole , coefficients of the outer Gaussian octupole and toroidal coefficients .
We write all these parameters into one vector of coefficients of the Gauss–Mie expansion:
Note that we assume that all magnetic field measurement points are located on a sphere of radius b, so in the system Equations (4)–(6) in the expressions for and the last group of terms can be ignored. Recall that we assume that the magnetic fields at S measurement points are obtained in the course of solving the direct problem based on the results of the article [35].
To pass from Equations (4)–(6) to a complete system of linear algebraic equations, we introduce grids , and and write finite-difference approximations of the equations of the system Equations (4)–(6). Thus, to isolate the internal component of the magnetic induction , we obtain a system consisting of linear algebraic equations:
Here, the right-hand side vector B contains the magnetic field components measured at the grid nodes (the left-hand sides of the system Equations (4)–(6)), and the matrix A consists of elements determined by the finite-difference approximation of the right-hand sides of the system Equations (4)–(6).
To find the coefficients of the Gauss–Mie expansion , it is necessary to numerically solve the system of linear algebraic Equation (8). This can be done using the least squares method. Thus, the solution of the system can be found by the formula
The vector that corresponds to the internal magnetic field is
Then, from the field, it is necessary to extract the high-frequency component , which is responsible for the magnetic masses in the surface layer of Mercury and allows us to localize “fine structures”.
To obtain the high-frequency component from the vector , it is necessary to take the expansion components, starting from the sixth one. Thus, we “discard” the dipole part of the internal magnetic field, which can drown out all other components of the field, and we are able to localize “fine structures”. Therefore, the Gaussian coefficients of the high-frequency component of the magnetic field are determined as follows:
Remark 1.
Here, in order to restore higher frequencies in the signal, we exclude the dipole component of the magnetic field and take into account the general principles of expanding magnetic fields into a series in terms of spherical harmonics. The dipole component is characterized by the vanishing of the degree 1 component, and the component describing the so-called “eccentric dipole’’ is characterized by the vanishing of the order 2 component (quadrupole).
These coefficients are used to calculate the high frequency component , whose components are determined by the following formulas:
The transition to Cartesian coordinates is carried out by a standard rotation transformation. The resulting magnetic field is used to solve the inverse problem for “fine structure” localization in the next section.
4. Recovering of the Near-Surface Magnetic Image of Mercury
Concerning the numerical algorithm for solving problem (2), search for , , from known values of , exactly repeating the algorithm described in detail in [12]. We limit ourselves to a reference to the specified work, so as not to repeat several pages of identical text. However, we highlight this section, because it is a very important step in solving the problem under consideration.
Taking into account the fact that the method of recovering the near-surface magnetic image of Mercury described above in the article is rather complicated, we will formulate the corresponding actions in the form of a simplified algorithm.
Our aim is to restore the distribution of magnetic masses in some spherical layer chosen by us in advance from the known values of magnetic induction on some sphere or inside a spherical shell. To do this, the following sequence of actions need to be performed.
- The parameters of the spherical layer are set, in which, according to our assumption, there are magnetic masses that create the same external magnetic field with respect to them as real (unknown) sources.
- The inverse problem of finding the indicated magnetic masses is solved. The integral Equation (2) is discretized, and a system of linear algebraic equations is obtained with an approximately given right side (the right side contains the values of the components of the magnetic induction vector measured via the satellite during orbits near Mercury).
- The field is recalculated to another spherical shell.
- Again, the inverse problem of finding fictitious sources (magnetic masses) is solved.
- The results of the decisions of items 2 and 4 are compared qualitatively, according to the geometric properties of the distributions of magnetic masses. Quantitative comparison is expected to be carried out in the future. Those values of the regularization parameters for which the geometric characteristics are similar are considered admissible by us.
5. Results of Experimental Data Processing
To isolate the high-frequency component of the internal magnetic field, the method from Section 3 was applied to three spherical layers surrounding Mercury (see Figure 1). For this, the direct problem (2) was previously solved based on the results of the article [35]. When solving the direct problem, grids with the number of intervals , , and were used. Thus, .
We chose three thin spherical layers sufficiently distant from each other in order to restore the geometry of the “crusta” sources of Mercury’s magnetic field with the highest possible degree of reliability. The solution of the inverse problem is considered admissible (regardless of the regularization parameter, which plays only an auxiliary role in our calculations) if the magnetic field, recalculated into three different levels, is generated by almost identical (in terms of their geometric properties) sources: the magnetic masses lie on approximately the same depth, sources have almost equal power, etc. The study of the properties of the magnetic field for is important even despite the fact that only magnetic carriers in the subpolar region are determined from the field of this layer. From this, we can conclude that powerful sources of the “crustal” field are located near the poles. It should also be emphasized that we are solving inverse problems under the conditions of a non-working generalized residual principle, so quantitative information about the regularization parameter is of no fundamental importance (recall that a detailed algorithm, which uses the regularizing parameter , is described in [35]).
Parameters of spherical layers for which the values of the magnetic field were recalculated:
- The magnetic field measurement points are located at an altitude of 10 (km) relative to the surface of Mercury. , where , , (m), = 10,001 (m). The value of the parameter + 10,000 (m).
- The magnetic field measurement points are located at an altitude of 50 (km) relative to the surface of Mercury. , where , , = 49,999 (m), = 50,001 (m). The value of the parameter + 50,000 (m).
- The magnetic field measurement points are located at an altitude of 100 (km) relative to the surface of Mercury. , where , , = 99,999 (m), = 100,001 (m). The value of the parameter + 100,000 (m).
It should be noted that in all three cases we took a spherical layer two meters thick. Such a thin spherical layer was taken in order to satisfy the condition of the thin shell approximation, which makes it possible to significantly simplify the problem of extracting the internal field (see Section 3).
To localize “fine structures” in Mercury’s crust, we use the approach we tested in our works [12,35]. We assume that the magnetic masses are located in a spherical layer completely immersed in the planet’s crust. The thickness of the spherical layer, in which, by assumption, there are magnetic masses, was chosen by us based on the physical conditions of the problem: if the field sources are located in the crust, then the outer radius of the layer should be close to the average radius of Mercury, and the inner one should be 10–15 km less than external. However, this approach does not limit the generality: it is possible to set the sources of the magnetic field on various surfaces that limit volumetric formations inside Mercury. At the same time, the requirements for such volumetric sources of the magnetic field should be made on the basis of a priori information about the geological structure of the planet. It is hoped that after 2025 (when the BepiColombo spacecraft enters a stationary orbit around Mercury [13]), the amount of real-time data on the planet closest to the Sun will increase significantly.
In all three cases, to solve the inverse problem (recall that a detailed algorithm is described in [35]), grids with the number of intervals and were used. For calculations, the values for the average radius of Mercury = 2,439,700 (m) and the thickness of the surface layer h = 15,000 (m) were taken.
The first series of calculations was carried out for points with recalculated values of magnetic fields located in the spherical layer for several different values of the regularization parameters (see the description of the algorithm in [35]). Below, in Figure 3 and Figure 4 the two most characteristic results are presented for and .
Figure 3.
The normalized value of the magnitude of the retrieved magnetic mass carrier density . The calculations were carried out for data localized in the spherical layer . Regularization parameter: .
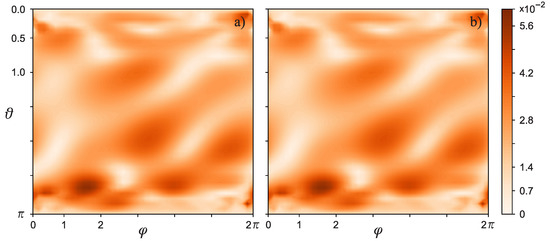
Figure 4.
The normalized value of the magnitude of the retrieved magnetic mass carrier density . The calculations were carried out for data localized in the spherical layer . Regularization parameter: (a) , (b) .
Since we are solving the problem in the absence of knowledge about the input data specification error, we cannot apply the generalized discrepancy principle [37] to justify the choice of the regularization parameter . Therefore, to find a solution, we carried out two more series of calculations for spherical layers and for different values of the regularization parameter. The results of these calculations are shown in Figure 5 and Figure 6.

Figure 5.
The normalized value of the magnitude of the retrieved magnetic mass carrier density . The calculations were carried out for data localized in the spherical layer: (a) , (b) . Regularization parameter: .
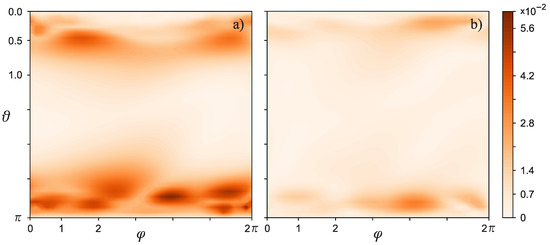
Figure 6.
The normalized value of the magnitude of the retrieved magnetic mass carrier density . The calculations were carried out for data localized in the spherical layer: (a) , (b) . Regularization parameter: .
It can be seen from Figure 4 and Figure 5 that the morphological features of the magnetic mass carrier density distribution do not change for the regularization parameter and . With the value of the regularization parameter , the morphology of the magnetic image in Mercury’s crust undergoes significant changes: magnetic field sources located at high latitudes are restored (in areas close to the geographic poles of Mercury; see Figure 4). The magnetic masses distributed in the rest of the planet are difficult to identify. It should be noted that all three images contain sources in the sub-polar regions. From this, we can conclude that there is some invariance of the external field-equivalent distributions of “crustal” magnetic masses with respect to transformations carried out with the help of regularizing operators. Or, in other words, we find an approximate solution of the inverse problem of reconstructing the sources of the magnetic field that is resistant to noise in the observed signal.
When comparing the obtained results, we noticed that for three different data distribution heights, a similar configuration of the maxima of the normalized magnetization values was restored. Moreover, the configurations of the maxima of the normalized values of the magnetization in Figure 3 and Figure 4 are not reproduced for the spherical layer for any regularization parameters. Thus, the most likely candidates for the solution are the images in Figure 4 and Figure 6. As a solution, we chose the image for the spherical layer with (see Figure 6a), due to its closer location to Mercury’s crust, but not close enough to cause strong instability. Comparison with Figure 4 and Figure 6 gives grounds to consider as the optimal value of the regularization parameter. In order to be more illustrative, we have redrawn Figure 6a, which corresponds to the desired near-surface magnetic image of Mercury, in the Mollweide projection—see Figure 7.
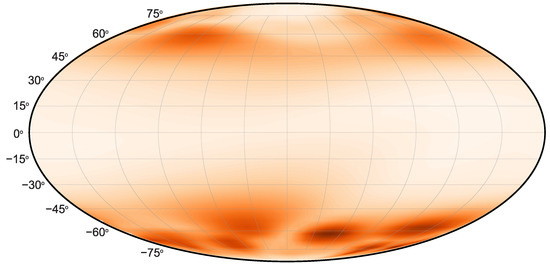
Figure 7.
Recovered near-surface magnetic image of Mercury (redrawing of Figure 6a in the Mollweide projection).
6. Discussion
- It should be emphasized that outside the field sources (i.e., outside the outer liquid core of Mercury and other space objects with an internal magnetic field generator), the method of expanding signals into a series in terms of spherical harmonics, representations in the form of Fourier integrals, wavelets, etc. [38,39], is quite acceptable and can give good results when solving problems of analysis and synthesis. However, modeling of Mercury’s magnetic field adequate to reality cannot be obtained without taking into account magneto-hydrodynamic relations [40,41]. All mathematical models of physical fields must be properly tested: they must guarantee high accuracy in constructing linear field transforms, which include analytic continuation towards sources, higher derivatives of the potential, etc. As is known, the analytical continuation of the signal down, in the direction of singularities, is an ill posed problem and requires the development of efficient regularization algorithms. Otherwise, we get models that do not meet the requirement of adequacy to real physical data. When modeling the magnetic field of the planets of the Solar System, various methods of solving inverse problems were used (see, for example, [42,43]). In the latest work, a model of a continuously magnetized Mars was constructed. However, as we pointed out above, the reconstruction of the sources of physical fields from remote sensing data is an ill posed problem, so a variety of interpretations of satellite information are acceptable. The choice of the most adequate of the existing analytical models of the magnetic field can only be made with a comprehensive analysis of data from various geophysical surveys. Separately, the importance of separating the fields created by carriers occurring at different depths should be noted. Away from the surface of the planet, the “crustal” component of the magnetic field looks like a noise having a small amplitude compared to the time-dependent trend component. Therefore, new effective regularizing algorithms seem to be quite relevant, which allows one to obtain an approximate solution of the inverse problem of magnetic prospecting that is resistant to random noise in the input data.
- It can be noted that the spherical harmonic coefficients describing the distribution of the magnetization within a thin spherical layer can be obtained directly from the coefficients of the lithospheric magnetic field [44]. Of course, the expansion coefficients of the “core” magnetic field in a series of spherical harmonics can be useful for calculating the field values inside a thin spherical shell. We propose an alternative way of finding these coefficients to ensure the stability of the approximate solution of the inverse problem. With the method described in the article for finding the Gaussian coefficients inside a thin shell, more accurate values of the magnetic field in it are obtained: we do not need to look for the field expansion coefficients throughout the entire thickness of the crust. It can be expressed differently: the more “local” the inverse problem is (in our case, the search for expansion coefficients), the better the quality of the regularized solution.
- There are alternative models such as a possible remanent magnetization [45,46] of the crust and non-dipole component of Mercury’s magnetic field generated in the liquid core. These models are able to interpret the results in the context of Mercury’s crustal structure. However, detailed analyses of the structure of the crust and the distributions of magnetic masses found by us in the crust have not yet been carried out—this requires more accurate information about the magnetic field from orbits close to the surface.
7. Conclusions
The original method of recovering the near-surface magnetic image of Mercury from satellite data, proposed in the article, makes it possible to extract the high-frequency component from a huge array of “raw” experimental data on the magnetic field of the planets of the Solar System. In the future, it is planned to study the question of the influence of the geometry of magnetic mass carriers on the accuracy of solving the problem of magnetic field inversion. It is important to emphasize that the filtering algorithm developed by the authors for the “dipole” component of the global magnetic field of Mercury can be useful in the study of other physical fields of the planets of the Solar System, in particular, the gravitational field (detection of the so-called “shallows”). As a rule, in practice, it is very difficult to separate weak signals from low-power and deep-seated sources from random noise. Our regularization algorithms allow us to “fine tune” the regularization parameter to produce physically meaningful solutions to ill posed problems. By themselves, mathematical procedures for filtering heterogeneous data based on algorithms for suppressing interference or a useful signal (depending on the context) cannot be considered fully implemented until the results of solving specific problems of processing large and super-large data arrays are presented. about physical, chemical, thermal, etc., properties of natural objects. In particular, this concerns the methodology for interpreting satellite data on the physical fields and topography of the Earth and planets. We offer not only reliable computational algorithms for solving problems of magnetic data inversion, but also a highly efficient adaptive regularization mechanism for finding the analytical continuation of the field measured in satellite orbit down towards the magnetized rock.
Author Contributions
Conceptualization, I.S. and D.L.; methodology, I.S., Y.W., D.L., I.K. and A.Y.; software, I.K. and D.L.; validation, I.S. and D.L.; formal analysis, D.L. and I.K.; investigation, I.K., D.L. and I.S.; writing—original draft preparation, D.L., I.S. and I.K.; writing—review and editing, D.L.; visualization, D.L. and I.K.; supervision, D.L.; project administration, D.L. All authors have read and agreed to the published version of the manuscript.
Funding
Russian Science Foundation (project 23-41-00002).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The research is carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University [47]. We also acknowledge support by Schmidt Institute of Physics of the Earth, Moscow, Russia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alexeev, I.; Belenkaya, E.; Slavin, J.; Korth, H.; Anderson, B.; Baker, D.; Boardsen, S.; Johnson, C.; Purucker, M.; Sarantos, M.; et al. Mercury’s magnetospheric magnetic field after the first two MESSENGER flybys. Icarus 2010, 209, 23–39. [Google Scholar] [CrossRef]
- Anderson, B.; Acuna, M.; Korth, H.; Purucker, M.; Johnson, C.; Slavin, J.; Solomon, S.; McNutt, R. The structure of Mercury’s magnetic field from MESSENGER’s first flyby. Science 2008, 321, 82–85. [Google Scholar] [CrossRef]
- Anderson, B.; Acuna, M.; Korth, H.; Slavin, J.; Uno, H.; Johnson, C.; Purucker, M.; Solomon, S.; Raines, J.; Zurbuchen, T.; et al. The Magnetic Field of Mercury. Space Sci. Rev. 2010, 152, 307–339. [Google Scholar] [CrossRef]
- Anderson, B.; Johnson, C.; Korth, H.; Purucker, M.; Winslow, R.; Slavin, J.; Solomon, S.; McNutt, R.; Raines, J.; Zurbuchen, T. The Global Magnetic Field of Mercury from MESSENGER Orbital Observations. Science 2011, 333, 1859–1862. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.; Johnson, C.; Korth, H.; Winslow, R.; Borovsky, J.; Purucker, M.; Slavin, J.; Solomon, S.; Zuber, M.; McNutt, R. Low-degree structure in Mercury’s planetary magnetic field. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Mayhew, M. Inversion of satellite magnetic anomaly data. J. Geophys. 1979, 45, 119–128. [Google Scholar]
- Ness, N.; Behannon, K.; Lepping, R.; Whang, Y.; Schatten, K. Magnetic Field Observations near Mercury: Preliminary Results from Mariner 10. Science 1974, 185, 151–160. [Google Scholar] [CrossRef]
- Ness, N.; Behannon, K.; Lepping, R.; Whang, Y. The magnetic field of Mercury, 1. J. Geophys. Res. 1975, 80, 2708–2716. [Google Scholar] [CrossRef]
- Solomon, S.; McNutt, R.; Gold, R.; Acuna, M.; Baker, D.; Boynton, W.; Chapman, C.; Cheng, A.; Andrew, F.; Gloeckler, G.; et al. The MESSENGER mission to Mercury: Scientific objectives and implementation. Planet. Space Sci. 2001, 49, 1445–1465. [Google Scholar] [CrossRef]
- Philpott, L.; Johnson, C.; Winslow, R.; Anderson, B.; Korth, H.; Purucker, M.; Solomon, S. Constraints on the secular variation of Mercury’s magnetic field from the combined analysis of MESSENGER and Mariner 10 data. Geophys. Res. Lett. 2014, 41, 6627–6634. [Google Scholar] [CrossRef]
- Wicht, J.; Heyner, D. Planetary Geodesy and Remote Sensing; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Kolotov, I.; Lukyanenko, D.; Stepanova, I.; Wang, Y.; Yagola, A. Recovering the magnetic image of Mars from satellite observations. J. Imaging 2021, 7, 234. [Google Scholar] [CrossRef]
- Milillo, A.; Fujimoto, M.; Murakami, G.; Benkhoff, J.; Zender, J.; Aizawa, S.; Dosa, M.; Griton, L.; Heyner, D.; Ho, G.; et al. Investigating Mercury’s Environment with the Two-Spacecraft BepiColombo Mission. Earth Planet. Sci. Lett. 2020, 216, 93. [Google Scholar] [CrossRef]
- Plagemann, S. Model of the internal constitution and temperature of the planet Mercury. J. Geophys. Res. 1965, 70, 985–993. [Google Scholar] [CrossRef]
- Smith, D.; Zuber, M.; Phillips, R.; Solomon, S.; Hauck, S.; Lemoine, F.; Mazarico, E.; Neumann, G.; Peale, S.; Margot, J.; et al. Gravity Field and Internal Structure of Mercury from MESSENGER. Science 2012, 336, 214–217. [Google Scholar] [CrossRef] [PubMed]
- Toepfer, S.; Narita, Y.; Glassmeier, K.H.; Heyner, D.; Kolhey, P.; Motschmann, U.; Langlais, B. The Mie representation for Mercury’s magnetic field. Earth Planets Space 2021, 73, 65. [Google Scholar] [CrossRef]
- Langlais, B.; Purucker, M.; Mandea, M. Crustal magnetic field of Mars. J. Geophys. Res. Planets 2004, 109, E02008. [Google Scholar] [CrossRef]
- Oliveira, J.; Langlais, B.; Pais, M.; Amit, H. A modified equivalent source dipole method to model partially distributed magnetic field measurements, with application to Mercury. J. Geophys. Res. Planets 2015, 120, 1075–1094. [Google Scholar] [CrossRef]
- Gudkova, T.; Stepanova, I.; Batov, A. Density anomalies in subsurface layers of Mars: Model estimates for the site of the InSight mission seismometer. Sol. Syst. Res. Vol. 2020, 54, 15–19. [Google Scholar] [CrossRef]
- Pan, L.; Quantin, C.; Tauzin, B.; Michaut, C.; Golombek, M.; Lognonne, P.; Grindrod, P.; Langlais, B.; Gudkova, T.; Stepanova, I.; et al. Crust heterogeneities and structure at the dichotomy boundary in western Elysium Planitia and Implications for InSight lander. Icarus 2020, 338, 113511. [Google Scholar] [CrossRef]
- Johnson, C.; Mittelholz, A.; Langlais, B.; Russell, C.; Ansan, V.; Banfield, D.; Chi, P.; Fillingim, M.; Forget, F.; Haviland, H.; et al. Crustal and time-varying magnetic fields at the InSight landing site on Mars. Nat. Geosci. 2020, 13, 199–204. [Google Scholar] [CrossRef]
- Stepanova, I. On the S-approximation of the Earth’s gravity field. Regional version. Inverse Probl. Sci. Eng. 2009, 16, 1095–1111. [Google Scholar] [CrossRef]
- Stepanova, I.; Shchepetilov, A.; Mikhailov, P. Analytical Models of the Physical Fields of the Earth in Regional Version with Ellipticity. Izv. Phys. Solid Earth 2022, 58, 406–419. [Google Scholar] [CrossRef]
- Stepanova, I.; Kerimov, I.; Raevskiy, D.; Shchepetilov, A. Improving the methods for processing large data in geophysics and geomorphology based on the modified S- and F-approximations. Izv. Phys. Solid Earth 2020, 16, 1095–1111. [Google Scholar] [CrossRef]
- Salnikov, A.; Batov, A.; Gudkova, T.; Stepanova, I. Analysis of the Magnetic Field Data of Mars. 2020. Available online: https://www.elibrary.ru/item.asp?id=45672757 (accessed on 15 February 2023).
- Salnikov, A.; Stepanova, I.; Gudkova, T.; Batov, A. Analytical modeling of the magnetic field of Mars from satellite data using modified S-approximations. Dokl. Earth Sci. 2021, 499, 575–579. [Google Scholar] [CrossRef]
- Lowes, F.; Duka, B. Magnetic multipole moments (Gauss coefficients) and vector potential given by an arbitrary current distribution. Earth Planets Space 2011, 63, i–vi. [Google Scholar] [CrossRef]
- Hood, L.; Oliveira, J.; Galluzzi, V.; Rothery, D. Investigating sources of Mercury’s crustal magnetic field: Further mapping of Messenger magnetometer data. JGR Planets 2018, 123, 2647–2666. [Google Scholar] [CrossRef]
- Lukyanenko, D.; Yagola, A.; Evdokimova, N. Application of inversion methods in solving ill-posed problems for magnetic parameter identification of steel hull vessel. J. Inverse-Ill-Posed Probl. 2011, 18, 1013–1029. [Google Scholar] [CrossRef]
- Lukyanenko, D.; Yagola, A. Some methods for solving of 3d inverse problem of magnetometry. Eurasian J. Math. Comput. Appl. 2016, 4, 4–14. [Google Scholar] [CrossRef]
- Wang, Y.; Lukyanenko, D.; Yagola, A. Magnetic parameters inversion method with full tensor gradient data. Inverse Probl. Imaging 2019, 13, 745–754. [Google Scholar] [CrossRef]
- Wang, Y.; Rong, L.; Qiu, L.; Lukyanenko, D.; Yagola, A. Magnetic susceptibility inversion method with full tensor gradient data using low temperature SQUIDs. Pet. Sci. 2019, 16, 794–807. [Google Scholar] [CrossRef]
- Wang, Y.; Kolotov, I.; Lukyanenko, D.; Yagola, A. Reconstruction of magnetic susceptibility using full magnetic gradient data. Comput. Math. Math. Phys. 2020, 60, 1000–1007. [Google Scholar] [CrossRef]
- Wang, Y.; Leonov, A.; Lukyanenko, D.; Yagola, A. General Tikhonov regularization with applications in geoscience. CSIAM Trans. Appl. Math. 2020, 1, 53–85. [Google Scholar] [CrossRef]
- Kolotov, I.; Lukyanenko, D.; Stepanova, I.; Wang, Y.; Yagola, A. Recovering the magnetic properties of Mercury from satellite observations. Eurasian J. Math. Comput. Appl. 2022, 10, 26–41. [Google Scholar] [CrossRef]
- Toepfer, S.; Oertel, I.; Schiron, V.; Narita, Y.; Glassmeier, K.H.; Heyner, D.; Kolhey, P.; Motschmann, U. Reconstruction of Mercury’s internal magnetic field beyond the octupole. Ann. Geophys. 2022, 40, 91–105. [Google Scholar] [CrossRef]
- Tikhonov, A.; Goncharsky, A.; Stepanov, V.; Yagola, A. Numerical Methods for the Solution of Ill-Posed Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Frick, P.; Sokoloff, D.; Stepanov, R. Wavelets for the space-time structure analysis of physical fields. Phys. Uspekhi 2020, 65, 62. [Google Scholar] [CrossRef]
- Kazantsev, S.; Kardakov, V. Poloidal-Toroidal Decomposition of Solenoidal Vector Fields in the Ball. J. Appl. Ind. Math. 2019, 13, 480–499. [Google Scholar] [CrossRef]
- Reshetnyak, M. Spatial Spectra of the geomagnetic Field in the Observations and Geodynamo Models. Izv. Phys. Solid Earth 2015, 51, 354–361. [Google Scholar] [CrossRef]
- Reshetnyak, M. Inverse problem in Parker’s dynamo. Russ. J. Earth Sci. 2015, 15, ES4001. [Google Scholar] [CrossRef]
- Uno, H.; Anderson, B.; Korth, H.; Johnson, C.; Solomon, S. Modeling Mercury’s internal magnetic field with smooth inversions. Earth Planet. Sci. Lett. 2009, 285, 328–339. [Google Scholar] [CrossRef]
- Whaler, K.; Purucker, M. A spatially continuous magnetization model for Mars. Earth Planet. Sci. Lett. 2005, 110. [Google Scholar] [CrossRef]
- Gubbins, D.; Ivers, D.; Masterton, S.M.; Winch, D.E. Analysis of lithospheric magnetization in vector spherical harmonics. Geophys. J. Int. 2011, 187, 99–117. [Google Scholar] [CrossRef]
- Johnson, C.L.; Purucker, M.E.; Korth, H.; Anderson, B.J.; Winslow, R.M.; Al Asad, M.M.H.; Slavin, J.A.; Alexeev, I.I.; Phillips, R.J.; Zuber, M.T.; et al. MESSENGER observations of Mercury’s magnetic field structure. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Winslow, R.M.; Anderson, B.J.; Johnson, C.L.; Slavin, J.A.; Korth, H.; Purucker, M.E.; Baker, D.N.; Solomon, S.C. Mercury’s magnetopause and bow shock from MESSENGER Magnetometer observations. J. Geophys. Res. Space Phys. 2013, 118, 2213–2227. [Google Scholar] [CrossRef]
- Voevodin, V.; Antonov, A.; Nikitenko, D.; Shvets, P.; Sobolev, S.; Sidorov, I.; Stefanov, K.; Voevodin, V.; Zhumatiy, S. Supercomputer Lomonosov-2: Large Scale, Deep Monitoring and Fine Analytics for the User Community. Supercomput. Front. Innov. 2019, 6, 4–11. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).