Range-Doppler Based Moving Target Image Trace Analysis Method in Circular SAR
Abstract
:1. Introduction
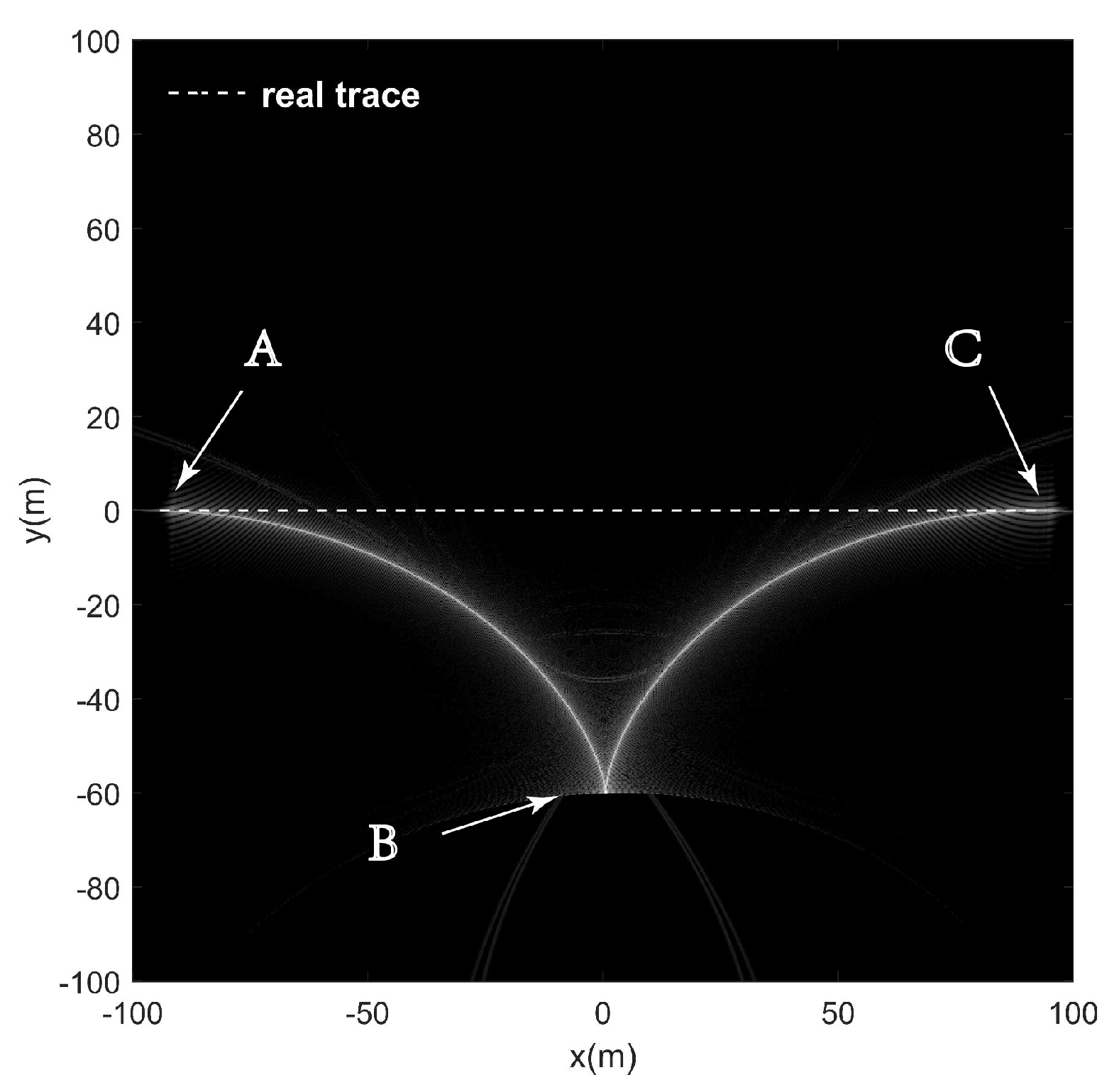
- Type A:
- constant speed
- Type B:
- constant acceleration
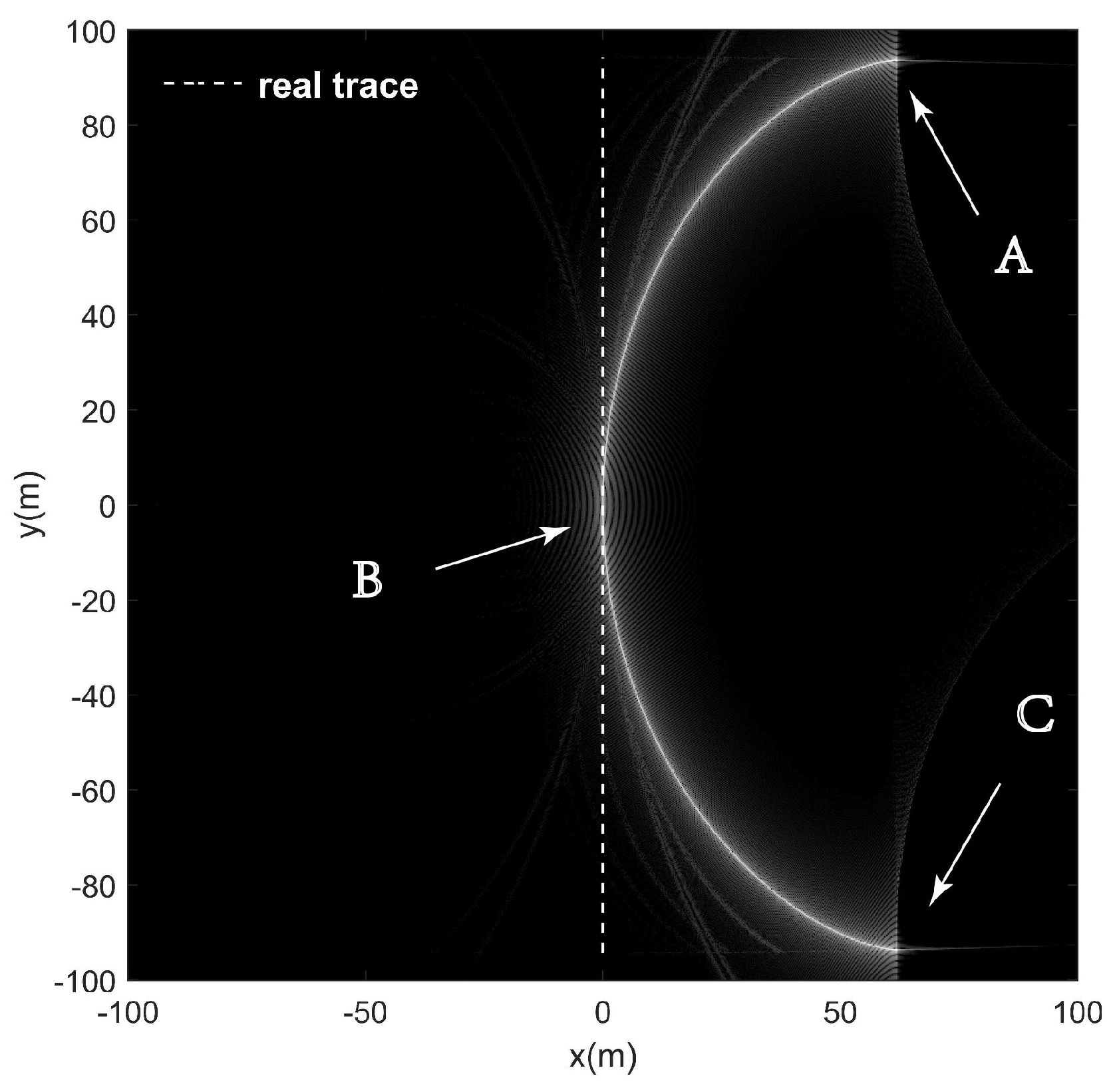
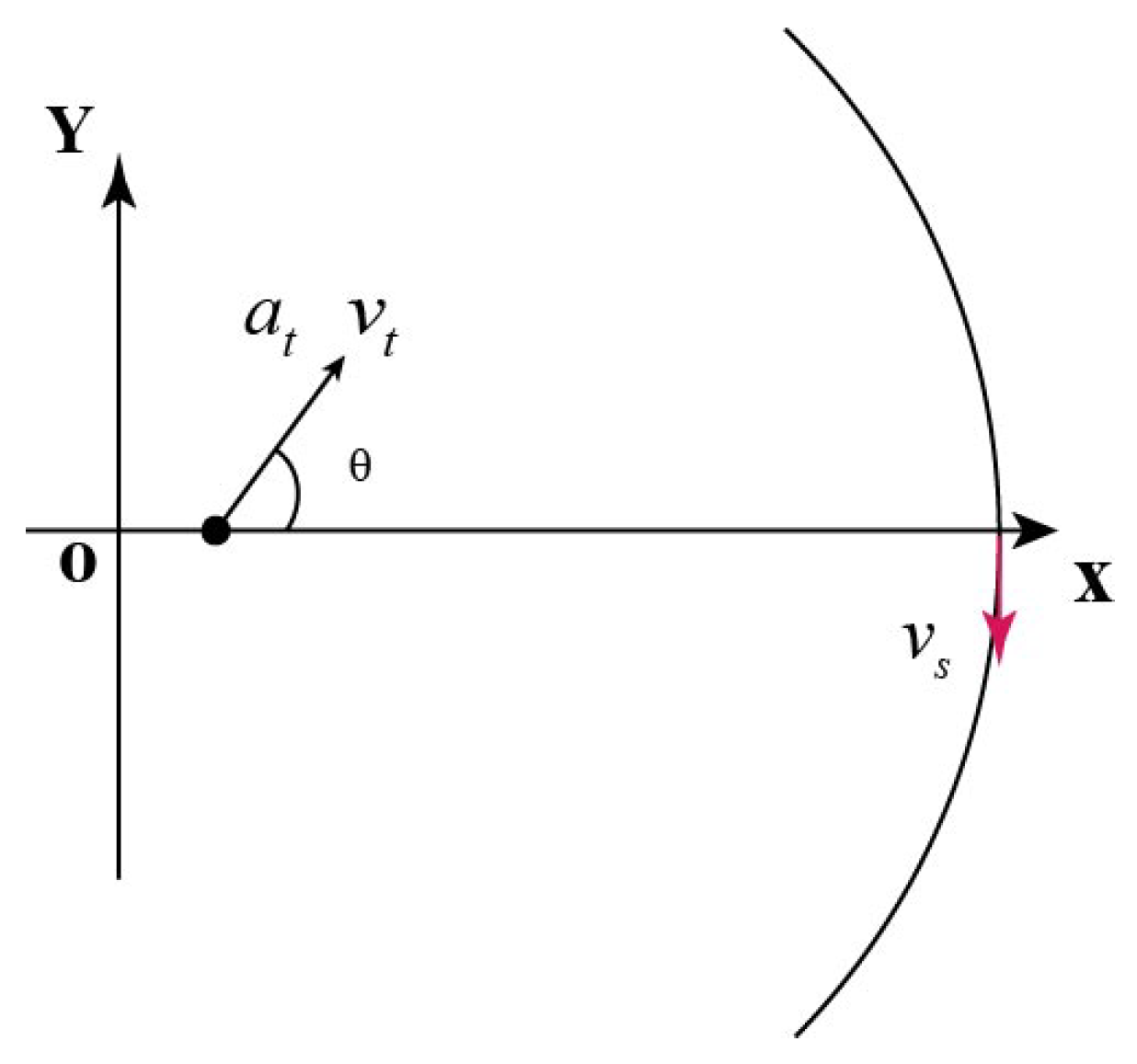
- Type C:
- rotating around a scene center with a constant speed
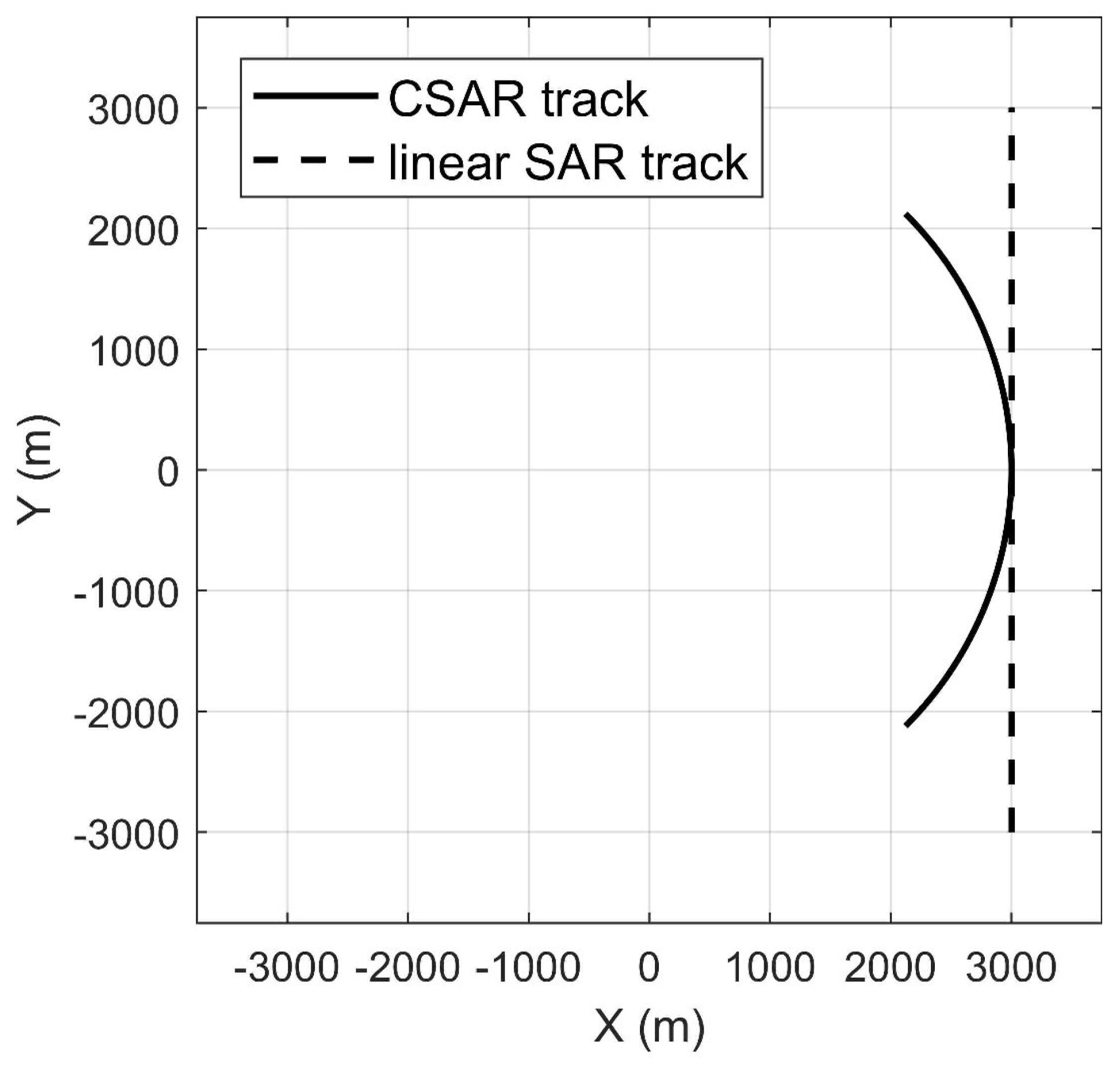
2. Material and Dataset
2.1. Simulated Data
2.2. Real Data
3. Image Trace Formulation Method
3.1. Step 1: Transformation
3.2. Step 2: Solution of Range-Doppler Equation
3.3. Step 3: Inverse Transformation
4. Specific Examples Analysis and Simulated Data Experiment
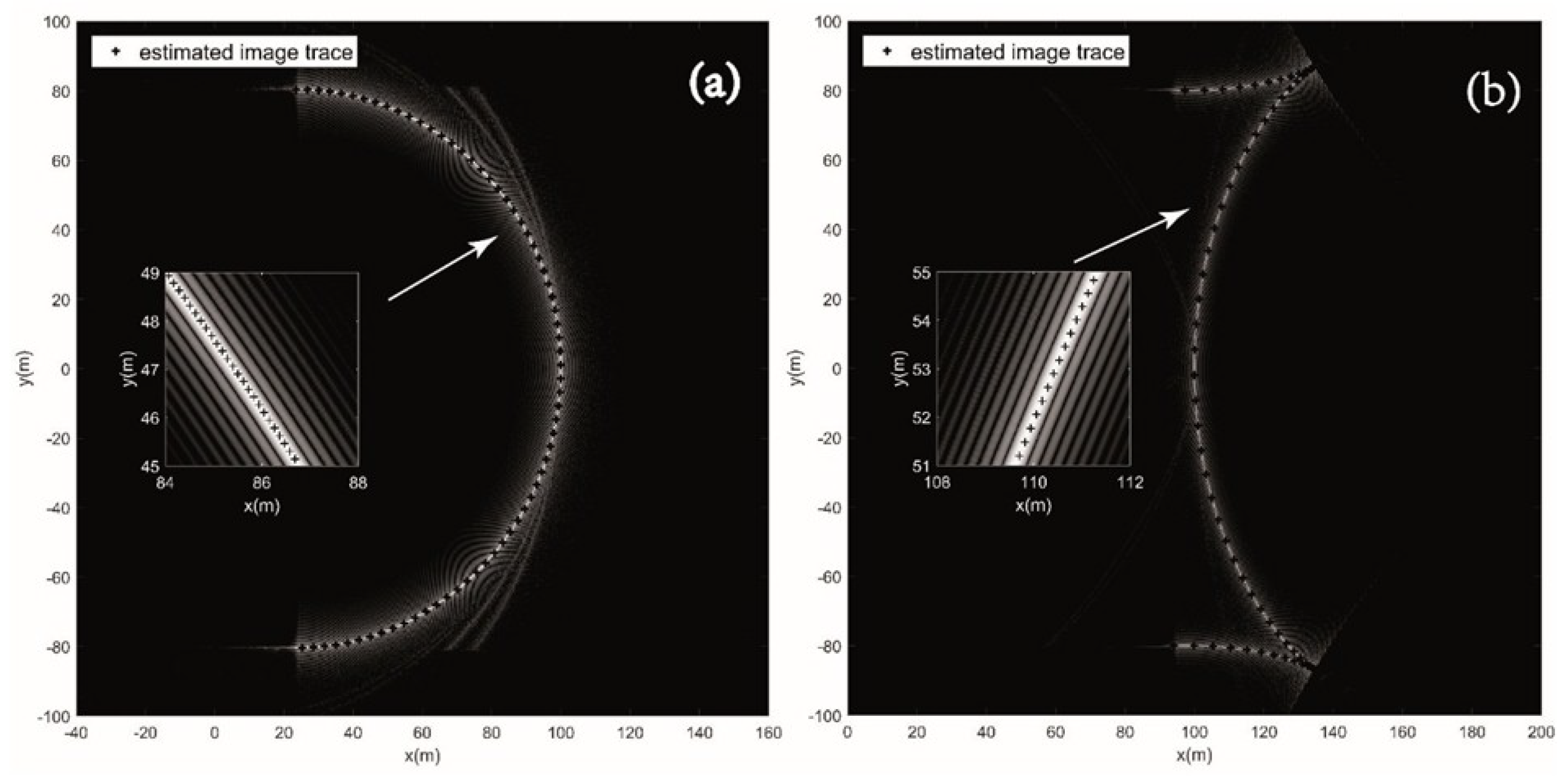
4.1. Constant Speed Target (Type A)
4.1.1. Case 1
4.1.2. Case 2
4.1.3. Case 3
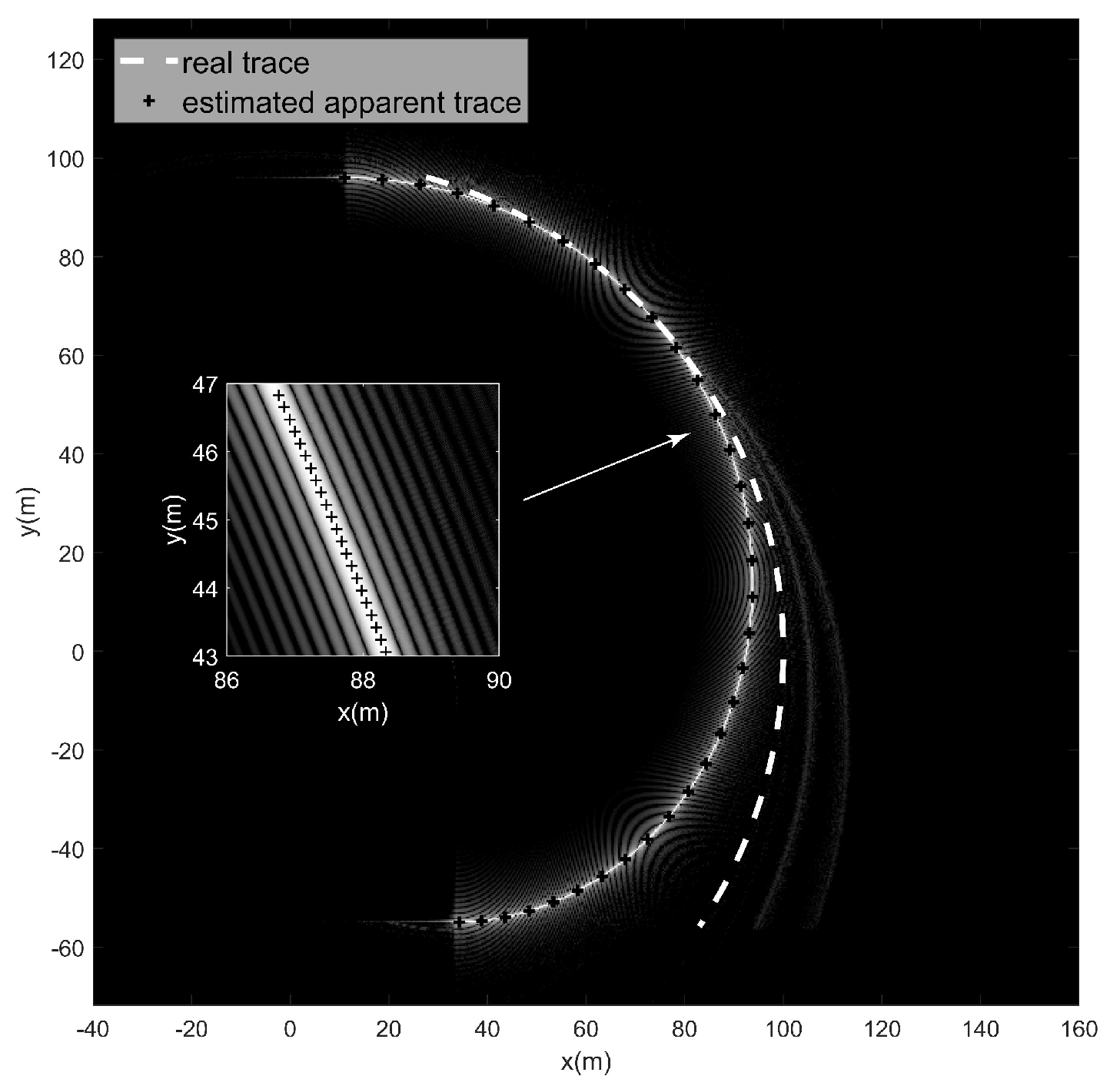
4.2. Constant Acceleration Target (Type B)
4.3. Constant Rotating Speed Target (Type C)
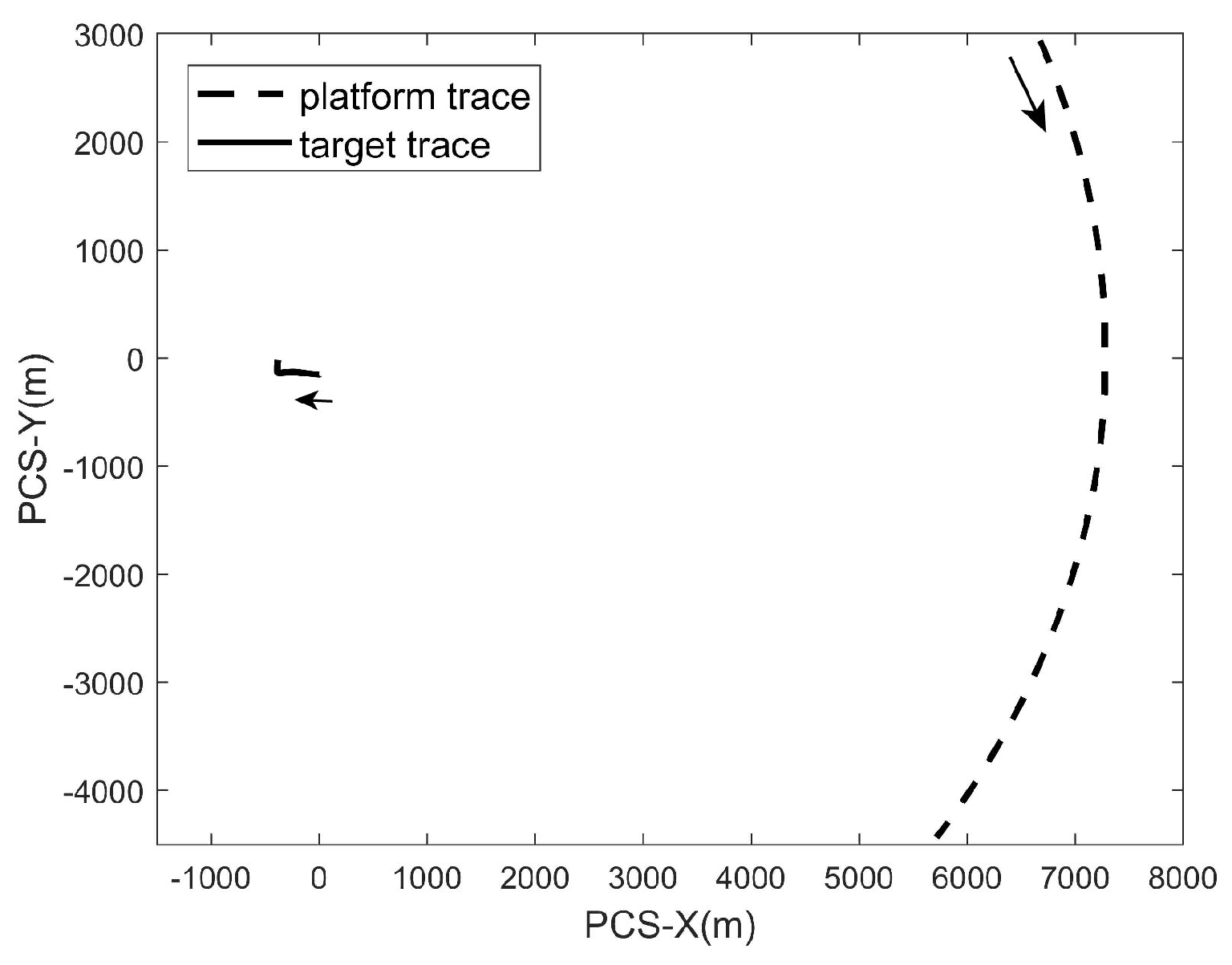
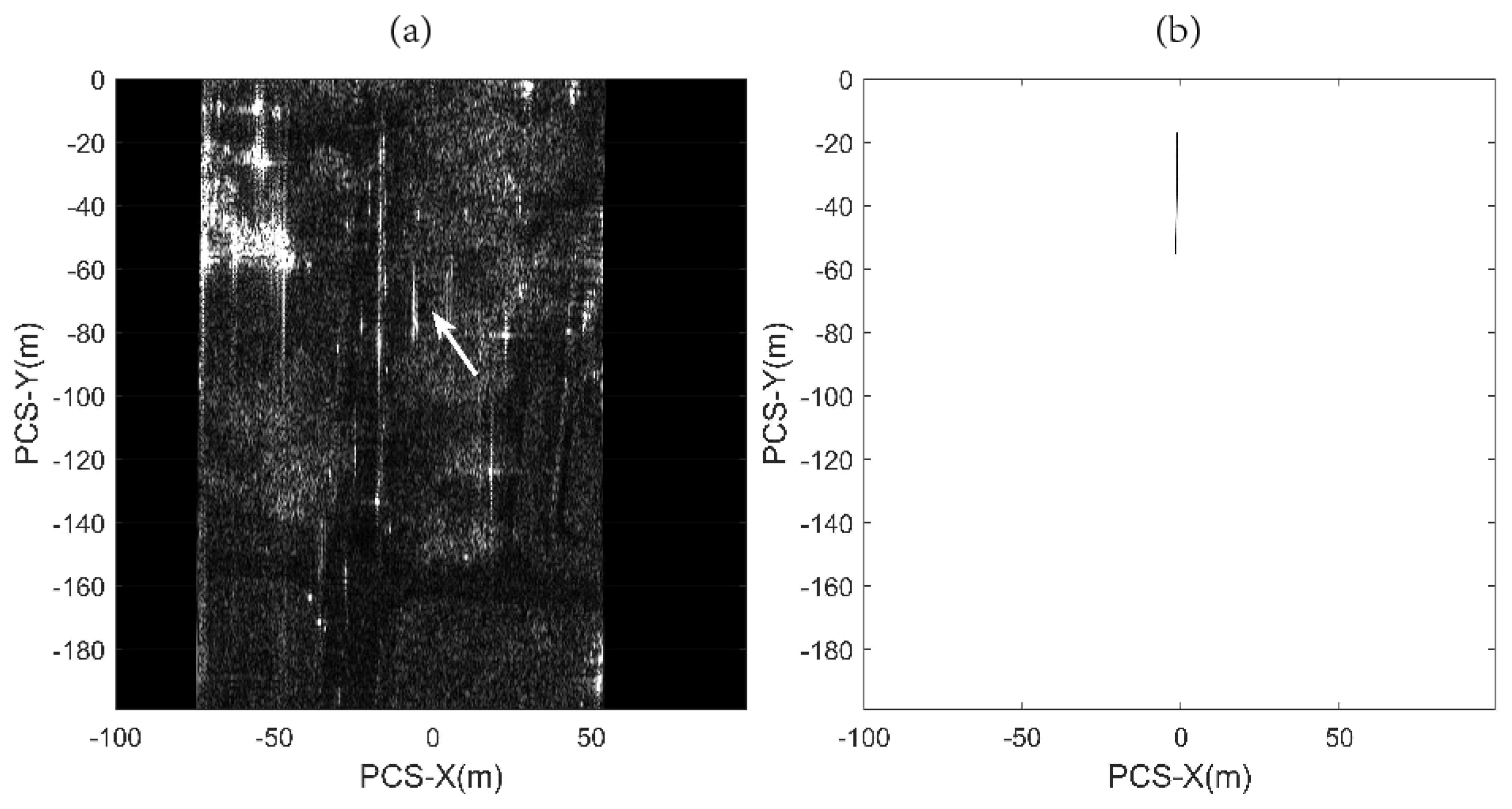
5. Real Data Experiment
6. Discussion
6.1. Example 1
6.2. Example 2
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Raney, R.K. Synthetic Aperture Imaging Radar and Moving Targets. IEEE Trans. Aerosp. Electron. Syst. 1971, AES-7, 499–505. [Google Scholar] [CrossRef]
- Ender, J.H.G. Space-time processing for multichannel synthetic aperture radar. Electron. Commun. Eng. J. 1999, 11, 29–38. [Google Scholar] [CrossRef]
- Makhoul, E.; Baumgartner, S.V.; Jager, M.; Broquetas, A. Multichannel SAR-GMTI in Maritime Scenarios With F-SAR and TerraSAR-X Sensors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5052–5067. [Google Scholar] [CrossRef]
- Chapin, E.; Chen, C.W. Airborne along-track interferometry for GMTI. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 13–18. [Google Scholar] [CrossRef]
- Vu, V.T.; Sjogren, T.K.; Pettersson, M.I.; Gustavsson, A.; Ulander, L.M. Detection of moving targets by focusing in UWB SAR Theory and experimental results. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3799–3815. [Google Scholar] [CrossRef]
- Fienup, J.R. Detecting moving targets in SAR imagery by focusing. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 794–809. [Google Scholar] [CrossRef]
- Lin, Y.; Hong, W.; Tan, W.; Wang, Y.; Xiang, M. Airborne circular SAR imaging: Results at P-band. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5594–5597. [Google Scholar] [CrossRef]
- Frolind, P.O.; Gustavsson, A.; Lundberg, M.; Ulander, L.M.H. Circular-Aperture VHF-Band Synthetic Aperture Radar for Detection of Vehicles in Forest Concealment. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1329–1339. [Google Scholar] [CrossRef]
- Cantalloube, H.M.J.; Koeniguer, E.C.; Oriot, H. High resolution SAR imaging along circular trajectories. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 850–853. [Google Scholar] [CrossRef]
- Hong, W.; Li, Y.; Tan, W.; Wang, Y.; Xiang, M. Study on geosynchronous circular SAR. J. Radars 2015, 4, 241–253. [Google Scholar]
- Zeng, T.; Yin, W.; Ding, Z.; Long, T. Motion and Doppler Characteristics Analysis Based on Circular Motion Model in Geosynchronous SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1132–1142. [Google Scholar] [CrossRef]
- Shen, W.; Lin, Y.; Yu, L.; Xue, F.; Hong, W. Single Channel Circular SAR Moving Target Detection Based on Logarithm Background Subtraction Algorithm. Remote Sens. 2018, 10, 742. [Google Scholar] [CrossRef] [Green Version]
- Poisson, J.B.; Oriot, H.M.; Tupin, F. Ground Moving Target Trajectory Reconstruction in Single-Channel Circular SAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1976–1984. [Google Scholar] [CrossRef] [Green Version]
- Jao, J.K. Theory of synthetic aperture radar imaging of a moving target. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1984–1992. [Google Scholar] [CrossRef] [Green Version]
- Moyer, L.R.; Govoni, M.A. Moving target trajectories in low-frequency SAR imagery. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2354–2360. [Google Scholar] [CrossRef]
- Garren, D.A. Smear signature morphology of surface targets with arbitrary motion in spotlight synthetic aperture radar imagery. IET Radar Sonar Navig. 2014, 8, 435–448. [Google Scholar] [CrossRef]
- Garren, D.A. Theory of Two-Dimensional Signature Morphology for Arbitrarily Moving Surface Targets in Squinted Spotlight Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4997–5008. [Google Scholar] [CrossRef]
- Garren, D.A. Signature Morphology Effects of Squint Angle for Arbitrarily Moving Surface Targets in Spotlight Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6241–6251. [Google Scholar] [CrossRef]
- Chapman, R.D.; Hawes, C.M.; Nord, M.E. Target Motion Ambiguities in Single-Aperture Synthetic Aperture Radar. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 459–468. [Google Scholar] [CrossRef]
- Gorham, L.A.; Moore, L.G. SAR image formation toolbox for MATLAB. SPIE 2010, 7699, 769906. [Google Scholar] [CrossRef]
- Scarborough, S.M.; Casteel, C.H., Jr.; Gorham, L.; Minardi, M.J.; Majumder, U.K.; Judge, M.G.; Zelnio, E.; Bryant, M.; Nichols, H.; Page, D. A challenge problem for SAR-based GMTI in urban environments. SPIE 2009, 7337, 73370G. [Google Scholar] [CrossRef]
- Deming, R.W. Along-track interferometry for simultaneous SAR and GMTI: Application to Gotcha challenge data. In Algorithms for Synthetic Aperture Radar Imagery XVIII; Zelnio, E.G., Garber, F.D., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 8051, p. 80510P. [Google Scholar] [CrossRef]
- Barber, B. Indication of slowly moving ground targets in non-Gaussian clutter using multi- channel synthetic aperture radar. IET Signal Process. 2012, 6, 424–434. [Google Scholar] [CrossRef]
- Deming, R.; Best, M.; Farrell, S. Simultaneous SAR and GMTI using ATI/DPCA. In Algorithms for Synthetic Aperture Radar Imagery XXI; Zelnio, E., Garber, F.D., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9093, p. 90930U. [Google Scholar] [CrossRef]
- Riedl, M.; Potter, L.; Bryant, C.; Ertin, E. Joint synthetic aperture radar and space-time adaptive processing on a single receive channel. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 331–341. [Google Scholar] [CrossRef]
- Greenewald, K.; Zelnio, E.; Hero, A.H. Robust SAR STAP via Kronecker decomposition. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2612–2625. [Google Scholar] [CrossRef] [Green Version]
- An, D.; Wang, W.; Zhou, Z. Refocusing of Ground Moving Target in Circular Synthetic Aperture Radar. IEEE Sens. J. 2019, 19, 8668–8674. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, W.; Lin, Y.; Hong, W. Single-Channel Circular SAR Ground Moving Target Detection Based on LRSD and Adaptive Threshold Detector. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4505505. [Google Scholar] [CrossRef]
- Ponce, O.; Prats-Iraola, P.; Pinheiro, M.; Rodriguez-Cassola, M.; Scheiber, R.; Reigber, A.; Moreira, A. Fully Polarimetric High-Resolution 3-D Imaging with Circular SAR at L-Band. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3074–3090. [Google Scholar] [CrossRef]






















| Symbol | SAR Parameters | Value |
|---|---|---|
| Center frequency | 9.6 GHz | |
| Bandwidth | 640 MHz | |
| Pulse repetition frequency | 1.32 kHz | |
| Ground range to scene center | 3000 m | |
| Incidence angle | ||
| Radar speed | 200 m/s | |
| Azimuth integration angle | (90°~−90°) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, W.; Wang, Y.; Lin, Y.; Li, Y.; Jiang, W.; Hong, W. Range-Doppler Based Moving Target Image Trace Analysis Method in Circular SAR. Remote Sens. 2023, 15, 2073. https://doi.org/10.3390/rs15082073
Shen W, Wang Y, Lin Y, Li Y, Jiang W, Hong W. Range-Doppler Based Moving Target Image Trace Analysis Method in Circular SAR. Remote Sensing. 2023; 15(8):2073. https://doi.org/10.3390/rs15082073
Chicago/Turabian StyleShen, Wenjie, Yanping Wang, Yun Lin, Yang Li, Wen Jiang, and Wen Hong. 2023. "Range-Doppler Based Moving Target Image Trace Analysis Method in Circular SAR" Remote Sensing 15, no. 8: 2073. https://doi.org/10.3390/rs15082073
APA StyleShen, W., Wang, Y., Lin, Y., Li, Y., Jiang, W., & Hong, W. (2023). Range-Doppler Based Moving Target Image Trace Analysis Method in Circular SAR. Remote Sensing, 15(8), 2073. https://doi.org/10.3390/rs15082073







