Next Article in Journal
KeyShip: Towards High-Precision Oriented SAR Ship Detection Using Key Points
Next Article in Special Issue
Blind Adaptive Beamforming for a Global Navigation Satellite System Array Receiver Based on Direction Lock Loop
Previous Article in Journal
Evaluation of Radar Precipitation Products and Assessment of the Gauge-Radar Merging Methods in Southeast Texas for Extreme Precipitation Events
Previous Article in Special Issue
Carrier Characteristic Bias Estimation between GNSS Signals and Its Calibration in High-Precision Joint Positioning
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 15
Issue 8
10.3390/rs15082034
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluation and Analysis of the Accuracy of Open-Source Software and Online Services for PPP Processing in Static Mode

by
Jesus René Vázquez-Ontiveros
1,
Jorge Padilla-Velazco
1,
J. Ramon Gaxiola-Camacho
2 and
Guadalupe Esteban Vázquez-Becerra
1,*
1
Department of Earth and Space Sciences, Autonomous University of Sinaloa, Culiacan 80040, Mexico
2
Department of Civil Engineering, Autonomous University of Sinaloa, Culiacan 80040, Mexico
*
Author to whom correspondence should be addressed.
Remote Sens. 2023, 15(8), 2034; https://doi.org/10.3390/rs15082034
Submission received: 7 March 2023 / Revised: 4 April 2023 / Accepted: 10 April 2023 / Published: 12 April 2023
(This article belongs to the Special Issue Advancement of GNSS Signal Processing and Navigation)
Browse Figures
Review Reports Versions Notes

Abstract

:
It has been proven that precise point positioning (PPP) is a well-established technique to obtain high-precision positioning in the order between centimeters and millimeters. In this context, different studies have been carried out to evaluate the performance of PPP in static mode as a possible alternative to the relative method. However, only a few studies have evaluated the performance of a large number of different open-source software programs and have focused extensively on online free PPP services. Therefore, in this paper, a comprehensive comparison of processing in static mode between different open-source software and the online free PPP services is developed. For the evaluation, different GNSS observation files collected at 45 International GNSS Service (IGS) stations distributed worldwide were processed in static PPP mode. Within this frame of reference, ten open-source PPP software and five online free PPP services were studied. The results from the processing strategy demonstrate that it is possible to obtain precision in the order of millimeters with both open-source software and online PPP services. In addition, online PPP services experienced better performance than some other specialized PPP software. In summary, the results show that the daily solutions for the E (East), N (North), and U (Up) components estimated by the ten open-source software and by the five online free PPP services can reach millimeter precision for some stations. Among the open-source software, the PRIDE-PPPAR presented the best performance with a Root Mean Square Error (RMSE) of 5.52, 5.40, and 6.79 mm in the E, N, and U components, respectively. Alternatively, in the case of the online free PPP services, the APPS and CSRS-PPP produced the most accurate results, with RMSE values less than 12 mm for the three components. Finally, the open-source software and online free PPP services experienced similar positioning performance in the horizontal and vertical components, demonstrating that both can be implemented in static mode without compromising the accuracy of the measurement.

1. Introduction

The Precise Point Positioning (PPP) technique was first implemented in the research work developed by [1]. However, it was not until the late 90s that the PPP approach was improved based on studies documented by Zumbergue et al. (1997) [2] and Kouba and Heroux (2001) [3]. In nature, the PPP technique requires three important aspects: (1) carrier phase and pseudorange observations from a single Global Navigation Satellite System (GNSS) receiver; (2) precise satellite orbit and clock products; and (3) model corrections to achieve high-precision three-dimensional positioning [4,5]. It is also known that PPP does not require a reference station and determines the coordinates of a station on the International Terrestrial Reference Frame (ITRF) [6]. Unfortunately, a limiting factor in PPP is the long convergence time (<30 min in static PPP) required for ambiguity resolution and obtaining stable results [7,8]. Nevertheless, it is now possible to achieve integer ambiguity resolutions in about 10 min, considering combinations of GNSS constellations, through the ambiguity resolution (AR) method [9]. In this sense, AR is a method that helps to speed up the convergence while increasing the positioning accuracy [10,11,12]. One can find in the literature that the performance of PPP-AR is based on the accuracy of the ambiguity resolution products [9,13]. In recent years, the PPP technique has been used in different applications such as tropospheric delay determination [14], cartography [5], structural health monitoring of infrastructure [15], water vapor determination/study [16], and photogrammetry georeferencing [17]. Therefore, it has been widely demonstrated, for several applications, the beneficial effect of using the PPP technique as an alternative to relative positioning.
Alternatively, to perform the post-processing step with the PPP-AR technique, it is necessary to use compatible software with products that enable AR. Usually, this type of product is the Bias SINEX file, the precise sp3, the clk file, and the erp file, including the error models that may affect the traditional PPP. Such a problem will depend on the required precision selected by the user. Within this context, many research institutes and universities have created PPP software packages, including online PPP processing platforms as well. Online PPP services are free and available 24/7. The user only needs to send the GNSS observation data files in RINEX or compressed format. Then, once the online processing is performed, the results are immediately sent back to the user. Thus, online PPP services represent a feasible option for non-expert GNSS users. Alternatively, the PPP software packages require knowledge about the processing because it is necessary to download the precise products to perform the PPP processing. There are different open-source software and online free PPP services for GNSS data processing with the PPP technique with/without ambiguity resolution in static and kinematic modes. Some of the most well-known GNSS software packages are: RTKLIB, PPPH, gLAB, PRIDE-PPPAR, Net_Diff, goGPS, GAMP, GPS Tools, PPPLib, MG-APP, and GIPSY X. Conversely, in the case of online PPP services, the most popular are: CSRS-PPP, APPS, GAPS, TRIMBLE Center-Point RTK, and MagicGNSS.
Based on the above discussion, the PPP technique has been evolving and getting very popular in recent years, mainly due to its high precision for obtaining 3D coordinates. This is the reason why the performance of both open-source software and online free PPP services has been evaluated in different studies. For example, Ghoddousi-Fard and Dara (2006) [18] used five online GNSS data processing services in relative (AUSPOS, SCOUT, OPUS) and absolute (Auto-GIPSY, CSRS-PPP) modes to compare and analyze the coordinates in static mode of different GNSS stations distributed around the world. Additionally, in Guo 2015 [19], four online free PPP services were evaluated, namely APPS, GAPS, CSRS-PPP, and Magic-PPP, to obtain static positioning and estimate tropospheric delay. They concluded that the four online free PPP services can provide centimeter- to millimeter-level accuracy in positioning and 1–2 cm in Zenith Total Delay (ZTD) estimation. In this context, other studies have been conducted to evaluate the accuracy of online PPP services with different approaches [20,21,22,23]. Very recently, Alkan et al. 2020 [24] evaluated the performance precision of the Trimble Center Point RTX real-time PPP positioning service and the Canadian Spatial Reference System Precise Point Positioning (CSRS-PPP) post-processing online PPP service. In such an investigation, [24] obtained coordinates from Center Point RTX and compared them with previously determined coordinates. They concluded that the real-time 3D positioning achieved a precision of one centimeter and a convergence time of a few minutes. In addition, it was reported that the CSRS-PPP had centimeter-level precision. Alternatively, the number of studies conducted to evaluate a set of open-source software used in GNSS data processing with the PPP technique in static mode has been minimal. This represents one of the main motivations for the scientific community to conduct experiments to evaluate open-source software. Within this frame of reference, Bahadur and Nohutcu 2019 [25] used the open-source PPPH software to process multi-GNSS data with different MGEX products. Furthermore, Grinter et al. 2020 [26] implemented the modified RTKLIB software to determine real-time simulated ambiguity solutions in PPP. Malik, 2020 [27] evaluated the performance of GAMP open-source software in static PPP mode using the combinations GPS only, GLONASS only, and GPS + GLONASS. They used ten days of ten IGS stations for the analysis. Standard deviations of the horizontal component of 3.83, 13.8, and 3.3 cm were obtained for GPS only, GLONASS only, and GPS + GLONASS, respectively. Other studies have been carried out where they evaluated the performance mainly of online PPP services and some open-source software [28,29,30,31]. However, an evaluation study of a set of open-source software and online services that process the PPP technique in static mode under the same measurement conditions has not been carried out.
In summary, there is no doubt that the PPP technique has been well-established and implemented in GNSS applications. However, there is a knowledge gap about detailed research on open-source software and online services for PPP processing. This represents a challenge because the selection of open-source or online software plays an important role in the accuracy of positioning. Therefore, the main objective of this research is to evaluate the precision of the PPP technique with/without ambiguity resolution in static mode, considering different open-source PPP software and online free PPP services. The open-source software was evaluated in its original version, that is, as such, they were published by their authors without modifying the source code; this is because the users who use these software only import input files and change the processing parameters. Then, a comparison is developed based on the results and reference values published on the Scripps Orbit and Permanent Array Center (SOPAC) website. Briefly, this paper is organized as follows: Section 2 provides a summary of the open-source software and online PPP services used in the study. Section 3 documents the methodology and data processing strategy. Section 4 summarizes the results. Finally, Section 5 and Section 6 contain the discussion and conclusions, respectively.

2. Summary of Open-Source PPP Software and Online Free PPP Services

This section briefly describes the open-source software and online PPP services evaluated. The authors selected the software packages and online services because of their free access and popularity. For example, GIPSY X scientific software was selected due to its availability from the Jet Propulsion Laboratory (JPL) for academic and scientific purposes.

2.1. Open-Source PPP Software

PPPH is an open-source GNSS analysis software based on MATLAB. PPPH supports processing data from GPS, GLONASS, Galileo, and Beidou constellations [32]. PPPH offers users the advantage of setting different options and processing parameters. In addition, the output file contains the coordinates and parameters for each epoch. As a complement, PPPH gives the user the option of analyzing and graphing the results to visualize them more clearly. The MATLAB open-source, manual, and sample data for PPPH are available on the GPS Toolbox website: https://geodesy.noaa.gov/gps-toolbox/PPPH.htm (accessed on 20 November 2022).
gLAB (GNSS-Lab) is an open-source educational software for GNSS data processing and analysis [33,34]. It is important to mention that gLAB was developed in 2009 as an educational program for the European Space Agency (ESA). Currently, gLAB only processes GPS. However, it is being updated to allow the processing of multiple constellations. The window installer, user manual, and detailed information about gLAB can be found on the website https://gage.upc.edu/en/learning-materials/software-tools/glab (accessed on 20 November 2022).
One more open-source piece of software is Net_Diff, which is used to download GNSS data for positioning and analysis. This software was developed by the GNSS Analysis Center at the Shanghai Astronomical Observatory (SHAO) [35,36]. In general, Net_Diff is software that processes SPP/PPP/PPP-AR/DSPP/DPPP/RTK/PPP-RTK. In addition, Net_Diff is compatible with all current signals from GPS/GLONASS/BeiDou/Galileo/QZSS/IRNSS systems, from single frequency to triple frequency. It also supports PPP-AR. For more information about Net_Diff, readers are referred to the website http://center.shao.ac.cn/shao_gnss_ac/Net_diff/Net_diff.html (accessed on 20 November 2022). Finally, Net_Diff has an online service for PPP and PPPAR data at processing (http://129.211.69.159:8090/ (accessed on 20 November 2022)).
RTKLib is an open-source toolkit for GNSS positioning developed by Dr. T. Takasu [37]. RTKLib currently supports positioning algorithms with GPS, GLONASS, Galileo, BeiDou, QZSS, and SBAS constellations [38]. Furthermore, RTKLib supports different positioning modes such as single-point positioning (absolute technique), DGNSS (relative technique), kinematic, static, moving baseline, PPP-kinematic, PPP-static, and PPP-fixed. Processing results can be found in files with different output options, such as geodetic coordinates (lat., lon., h), geocentric coordinates (X, Y, Z), baselines (E, N, h), and message NMEA0183. RTKLIB allows for the automated processing of a large number of IGS stations through a batch process in Linux. For more information about RTKLIB input and output files, visit the official page at https://rtklib.com/ (accessed on 20 November 2022).
Another alternative for GNSS Precise Point Positioning Ambiguity Resolution (PPP-AR) is the PRIDE-PPPAR open-source software. It was developed by the Pride Lab at the GNSS Research Center of Wuhan University [39]. Within this context, PRIDE-PPPAR was designed following the principles of readability, modularity, extensibility, and maintainability. These elements represent the basis for using this software in an easy and flexible way. In general, PRIDE-PPPAR is mainly composed of two modules: (1) undifferentiated GPS data processing, and (2) integer ambiguity resolution. It is important to note as well that the PRIDE-PPPAR software generates output files containing the coordinates of the solution in ECEF coordinates (X, Y, and Z). PRIDE-PPPAR is capable of processing RINEX files sampled at 50 Hz. The software, user manuals, and more detailed information such as compatibility of GNSS constellations and signals can be downloaded from the PRIDE official website, http://pride.whu.edu.cn/indexone.shtml (accessed on 20 November 2022).
In addition to the above-reported software, the Multi-GNSS Automatic Precise Positioning (MG-APP) is an open-source software that can be run on Windows/Linux/Unix. In this sense, MG-APP can process GPS, GLONASS, BDS, and Galileo observations using the Kalman filter or the square root information filter (SRIF) [40]. One of the innovative tools of MG-APP is that it is possible to perform real-time data processing in a mode where it uses two adjacent epochs to detect data quality and filter calculation. MG-APP can be downloaded from the website, https://github.com/XiaoGongWei/MG_APP (accessed on 20 November 2022). Additionally, manuals and detailed features of the software can be found.
The goGPS software is also an important option for processing position data. This is open-source software that aims to process GNSS raw data. It was first reported in the literature in 2007 [41]. Initially, goGPS was designed to work with low-cost, single-frequency GPS receivers. However, now it can work with multiple constellations and multiple frequencies. Over and above that, goGPS contains multiple least-squares data analysis algorithms that work with combinations of observables using all frequencies and tracks. The goGPS software uses the LAMBDA method to resolve ambiguities. More information about goGPS can be found at https://gogps-project.github.io/ (accessed on 20 November 2022).
In accordance with the literature, GAMP is an open-source software derived from the RTK library of RTKLIB, written in the ANSI C language [42]. It can be compiled and run on Windows, UNIX/Linux, and Macintosh operating systems. The source code can be accessed through the GPS Toolbox website at https://www.ngs.noaa.gov/gps-toolbox/GAMP/ (accessed on 20 November 2022). The GAMP improvements over RTKLIB were cycle slip detection, GLONASS pseudorange inter-frequency bias handling, and receiver clock jump repair. The GAMP output file contains the positioning, number of satellites, pseudorange and carrier phase residuals, satellite elevation angles, and slant total electron content.
The Precise Point Positioning Library (PPPLib) is another open-source software written in the C/C++ programming language for multi-GNSS data processing and is capable of processing GPS, BeiDou, GLONASS, Galileo, and QZSS multi-frequency data [43]. The PPPLib can be compiled and run on Windows and Linux operating systems. Using such capabilities, the PPPLib software resolves various parameters such as positioning, ionospheric delay, tropospheric delay, and ambiguity information. It is powerful software for calculating PPP solutions using different GNSS constellations or combinations between them, and for processing, it is capable of automatically downloading necessary files such as precise orbit and clock, EOP, DCB, and ATX. For more information, visit the official website of the software: https://github.com/yxw027/PPPLib (accessed on 20 November 2022).
As an alternative, the GIPSY X/RTGx software is expected to be a solid option for processing position measurements. It is a software package developed and maintained by the Jet Propulsion Laboratory (JPL) for positioning, navigation, timing, and Earth sciences. The GIPSY X software uses different measurement geodetic techniques: Global Navigation Satellite Systems (GNSS), Satellite Laser Ranging (SLR), and Doppler Orbitography and Radioposition Integrated by Satellite (DORIS), with very long baseline interferometry (VLBI) under development. The software provides combined estimates of geodetic and geophysical parameters by applying a Kalman filter approach to real or simulated data [44]. Estimated parameters include coordinates and velocities of stations of interest, satellite orbits and clocks, Earth’s orientation, and ionospheric and tropospheric delays. For more information, visit the website at https://gipsy-oasis.jpl.nasa.gov/ (accessed on 20 November 2022).

2.2. Online PPP Services

Compared with open-source software that must be installed on a computer, online platforms for processing GNSS observation files are easier to use. The user only uploads the file of interest, and in some online services, it is possible to configure the elevation angle and the PPP solution mode. In the case of CSRS-PPP, it uses an elevation angle of 7.5° and is not editable. The output files for these services’ results usually contain the processing summary, geodetic or cartesian coordinates, tropospheric delays, clock parameters, and graphs representing the results.
The CSRS-PPP is a service developed by the Canadian government and has been operated by Natural Resource Canada since 2003 [45,46]. This service supports single and dual-frequency data from the GPS and GLONASS constellations. It uses the precise products of the International GNSS Service (IGS) and NRCan. If correctly used, the CSRS-PPP online service reaches an accuracy of 1 and 2 cm for the horizontal and vertical components, respectively. The CSRS-PPP service includes PPP with ambiguity resolution (PPP-AR) for data collected on or after 1 January 2018. CSRS-PPP supports RINEX files with a maximum size of 300 MB; more information about this online service can be found in Table 1.
Between several options of online PPP services, the APPS (Automatic Precise Positioning Service) is a service operated by NASA’s Jet Propulsion Laboratory (JPL) and the California Institute of Technology and was originally named the Auto-GIPSY service (now superseded by APPS) (http://apps.gdgps.net/apps_howtouse.php (accessed on 20 November 2022)) [30]. The APPS service requires precise products (GPS orbit and clock) from JPL and uses JPL’s GIPSY 6.4 software to process submitted observation files. This service can process single- and dual-frequency data from the GPS constellation. For more information, visit Table 1.
The GAPS (GNSS Analysis and Positioning Software) service was developed and is currently operated by the Department of Geodesy and Geomatics Engineering at the University of New Brunswick [47]. This service, compared with APPS, accepts different types of GNSS data, as shown in Table 1. GAPS uses precise orbit and clock products provided by the IGS and NRCan [21]. More information about the GAPS online service is found in Table 1.
The Trimble Center Point RTX (Real Time Extended) is a dual-frequency GNSS measurement processing service for static sessions [48,49]. This service is limited to minimum measurements of 1 h and up to 24 h. The TCP-RTX service uses TRIMBLE’s global network of reference stations to compute precise satellite orbits and clocks. It can achieve an accuracy ranging from 2 to 6 cm for horizontal and vertical positioning coordinates, respectively. It is important to mention as well that the above accuracy may be reached for one-hour measurements. It can be found on a website provided by TRIMBLE (https://www.trimblertx.com/UploadForm.aspx (accessed on 20 November 2022)). The Trimble online service does not consider antenas that are not in its database.
Another option for online PPP service is MagicGNSS. This is an online GNSS data processing service operated by the company GMV Aerospace and Defense [50]. The MagicGNSS service contains two processing methods: (1) using an interactive web interface, and (2) via email. The IGS and GMV issue the precise products (orbit and clock) used by MagicGNSS (https://magicgnss.gmv.com/user/ppp (accessed on 20 November 2022)).
To summarize the main features of the online PPP services and open-source software described above, Table 1 and Table 2 are introduced, respectively. The mathematical model of PPP-GNSS can be consulted in [15,39].

3. Methodology

A comprehensive comparative analysis of coordinates was carried out to evaluate the positioning performance of open-source software and online services, respectively, using the PPP technique in static mode. The coordinates resulting from the static PPP processing of 45 IGS stations were transformed to ENU topocentric coordinates considering such factors as the origin of the topocentric system and the reference values published on the SOPAC website (http://sopac-old.ucsd.edu/sector.shtml (accessed on 20 November 2022)) to analyze the precision in long observation periods for each open-source software and online service, respectively. SOPAC is a global data center and global analysis center for the International GNSS Service (IGS) that maintains data from thousands of regional and global GNSS stations and generates data products, such as precise coordinates, which are considered a reference for other studies [19]. The coordinates published by SOPAC are obtained through relative processing with the scientific software GAMIT/GLOBK. The 45 IGS stations selected for this study are shown in Figure 1. For each station, 24 h observation files were downloaded at 30 s intervals for the year 2020 (1–7 January) from the IGS web server (https://cddis.nasa.gov/archive/gps/data/daily/ (accessed on 20 November 2022)). This sampling rate was selected because, in static mode, observations at rates higher than 30 s do not improve the precision of the solution [51]. Since not all the online PPP services and open-source software studied in this document are compatible with multi-constellations and multi-frequency GNSS, it was decided to standardize on only GPS (L1, L2). Thus, GLONASS, Galileo, BeiDou, QZSS, and IRSS constellations were removed using the software GFZRNX [45,52].

Processing Strategies

For the processing of the GPS observation files through the PPP technique in static mode, it is necessary to utilize precise products [3]. Each software requires a different number of input files; therefore, for this study, the same exact products were considered for all the used open-source software (see Table 3). In this way, it is ruled out that the differences in the results are due to the precise input products and not to the performance of the different algorithms and PPP processing strategies of each software. Alternatively, it is important to mention that not all the analyzed software has an integer ambiguity resolution strategy. Particularly precise products are required for integer ambiguity resolution. In the case of online PPP services, default settings are used for PPP-static processing. Meanwhile, Table 3 summarizes the general configuration used in the software processing. Some online PPP services have an elevation angle of 7.5° in their processing settings, and it is not possible to change it; consequently, it was decided to set an elevation angle of 8° for all the studied open-source software and most online PPP services.
The GPS double-frequency observation files of each IGS station were processed in the different software and online services by the PPP method in static mode. The results were assessed considering the reference coordinates of each IGS station described in Figure 1 at the same epoch as ITRF2014. This evaluation consisted in calculating the Root Mean Square Error (RMSE) of the ENU coordinates since each component (East, North, and Up) represents the distance between the reference coordinate (origin) and the one obtained with PPP. The use of RMSE is very common, and it is considered an excellent precision metric to evaluate errors [53]. The RMSE is expressed as follows [54]:
R M S E = 1 n ∑ i = 1 n ( x i − μ ) 2
where x i − μ represents the ENU coordinates in each component (East, North, Up); n is the number of IGS stations.

4. Results

In this section, a precision analysis of ENU topocentric coordinates is presented. The first part describes the results of open-source software, followed by the results of online PPP services.

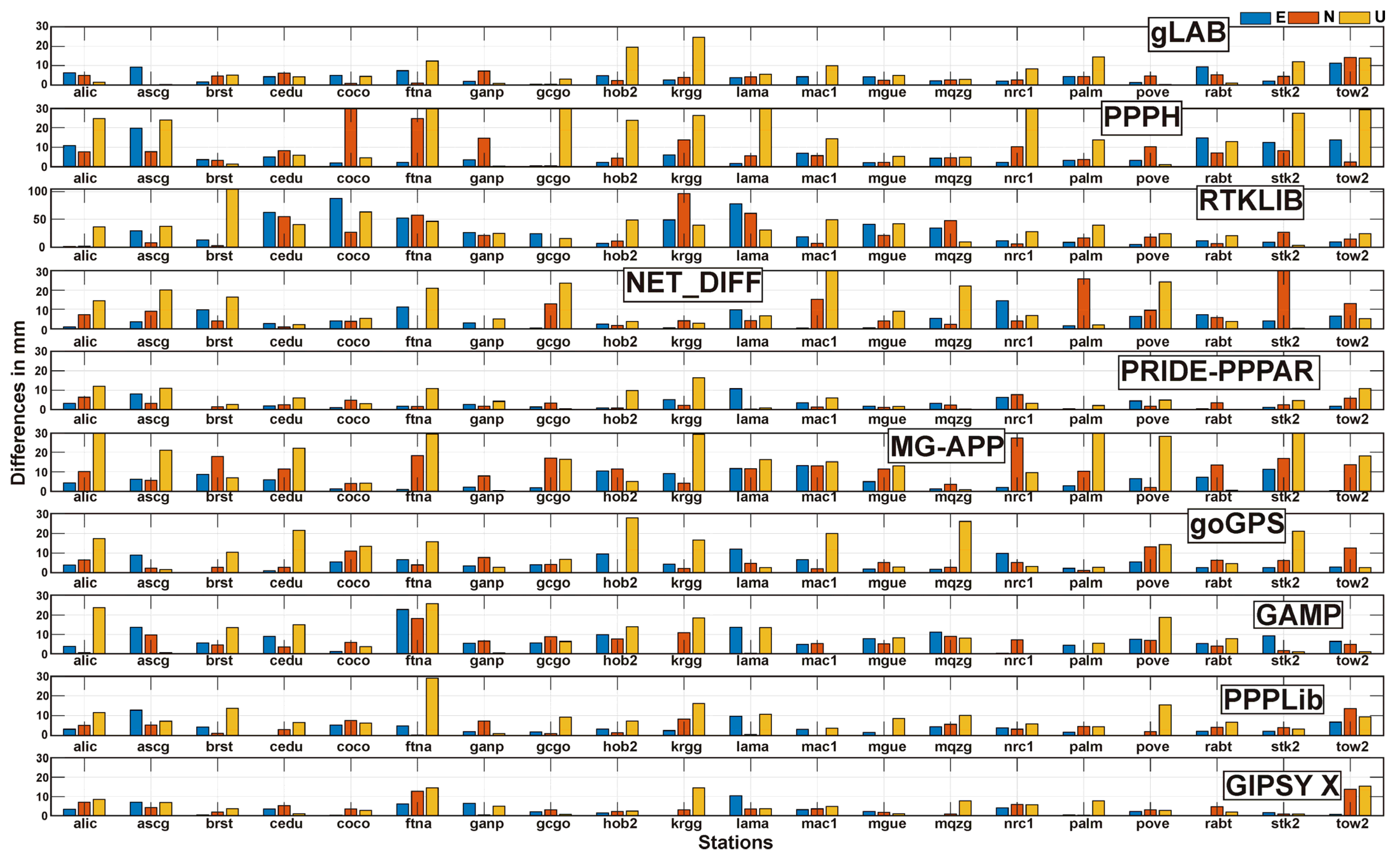
4.1. Results of Open-Source Software

The coordinates resulting from the processing with the ten open-source software programs and five online services referenced in ITRF2014 for the 45 IGS stations are transformed into ENU absolute coordinates for each day. The ENU coordinates from 1–7 January were averaged and can be seen in Figure 2. Figure 2 shows only 20 IGS stations because readability decreases when all 45 are displayed. Most of the software experienced differences of less than 5 cm; however, in RTKLIB, the discrepancies were very large (close to 10 cm). These differences can be derived from the internal processing algorithms and strategies of each software and not from the precise products used, since they are the same in all software.
Alternatively, some stations IGS presented large differences in every software. This might be due to the environment and monument where the GNSS antenna was installed. Additionally, maximum discrepancies of 5 mm were found in the daily solutions published by the IGS for these stations; therefore, they were not taken into account for the statistical analysis and the calculation of the RMSE because they are atypical values and skew the results of reality. Another important factor that correlates with these differences is the availability of some software for integer ambiguity resolution (AR). The software with AR evaluated in this paper presents better precision, generally in the order of millimeters. Table 4 summarizes the standard deviation, the mean, and the maximum and minimum values of the ENU coordinates of all IGS stations (for each software). Table 4 contains the maximum differences for E, N, and U of 94 mm, 96 mm, and 121 mm, respectively, corresponding to the RTKLIB software, which showed the lowest performance. GIPSY X, GAMP, goGPS, PPPLIB, and PRIDE-PPPAR presented the maximum differences below 3 cm for the three components. However, 90.38%, 73.3%, 72%, 81.4%, and 87.4% of the differences were less than 10 mm for GIPSY X, GAMP, goGPS, PPPLIB, and PRIDE-PPPAR, respectively. In the minimal differences, only RTKLIB presented results greater than 0 mm; for the rest of the software, at least one station presented differences of 0 and 1 mm.
The RMSE was calculated to assess the performance of the evaluated software in static-PPP positioning. Figure 3 illustrates the calculated RMSE of each software product. The worst performance was obtained by having RTKLIB present RMSE values of up to 4.7 cm for the U component. Alternatively, the three softwares with the best performance in the three components were GIPSY X, PRIDE-PPPAR, and gLAB, with RMSE values less than 12 mm. Two of the last three software packages have the availability of an integer ambiguity solution, which results in higher precision. In this same sense, the group composed of PPPH, Net_Diff, MG-APP, goGPS, GAMP, and PPPLib software was the second to present an outstanding performance with RMSE values less than 30 mm and greater than 12 mm. Consequently, RTKLIB belongs to Group 3, which presents RMSE less than 5 cm and greater than 3.5 cm. RTKLIB constitutes the group with the worst performance.
Also, an analysis corresponding to the standard deviation obtained in calculating the coordinates by the different software was performed. Unfortunately, not all software offers this information. For our case study, only RTKLIB, PPPLib, and GIPSY X have the standard deviations available in their output files. The E, N, and U components of the 45 IGS stations of each software were averaged to establish a value that represents the performance of the software. Alternatively, the mean of the standard deviations (software precision) for each E, N, and U component was calculated and taken as the mean value for the proposed analysis. Figure 4 illustrates the average E/N/U components of each software, and at the top of the bars is the average standard deviation with which they were calculated.
In the first place, it is observed that the U component had the greatest magnitude. However, it is the one that presents the best precision in the case of RTKLIB, with a standard deviation of 8.4 mm. For PPPLib, the E, N, and U components are small, and the average standard deviations are less than 2 mm. In the case of GIPSY X, the average magnitude of the E, N, and U components is less than 6 mm, and they have an average precision of 6, 8, and 19 mm, respectively. Alternatively, the standard deviation of the deviations in the E, N, and U components with respect to the real coordinates of the IGS stations and the standard deviations reported by the software are analyzed. Table 4 shows the values of the standard deviations of the deviations of the E, N, and U components of 4.4, 3.7, and 8 mm, respectively, for the PPPLib software. These standard deviations are up to eight times larger than those reported by the software. For RTKLIB and GIPSY X, the behavior is similar. The ENU components are determined with high precision in all software but with lower accuracy.

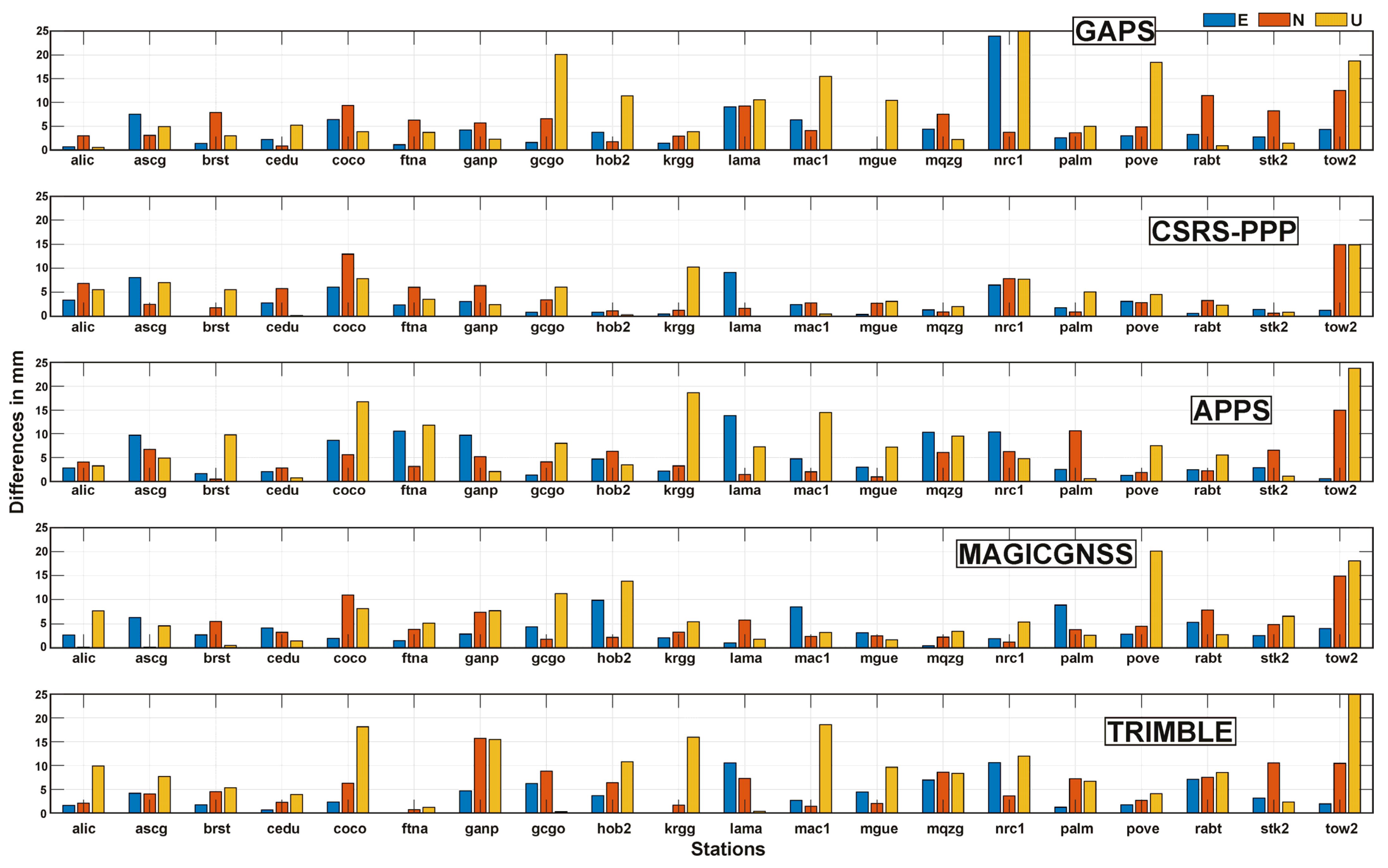
4.2. Results of Online Free PPP Services

The E, N, and U components of the seven days obtained with online free PPP services were averaged and can be seen in Figure 5. Only 20 of the 45 IGS stations are illustrated in Figure 5 for better readability; for the statistical analysis of online services, all 45 stations were used. In general, the E, N, and U components for the five online services are close to 10 mm. The performance of the online PPP services evaluated is similar, obtaining differences of less than 15 mm compared with the reference coordinates obtained through the relative positioning technique. Online services have internal processing software, such as APPS, that uses GIPSY-OASIS v5 for processing and sending results to the user’s email. An important factor in online PPP services is the availability of ambiguity resolution to achieve high accuracy.
Alternatively, the standard deviation, the mean, and the maximum and minimum values of the absolute E, N, and U components for each online PPP service are found in Table 5. It is observed that the APPS service presented the highest difference in the N and U components, while the CSRS-PPP service had the lowest in the U. However, for CSRS-PPP and MagicGNSS, 91% and 88.14% of the E, N, and U components were below 15 mm, respectively. For APPS, Trimble, and GAPS, 89.62%, 88.14%, and 89.62% of the E, N, and U components were also below 15 mm, respectively. The maximum E, N, and U components in online services were less than those obtained with open-source software. The U component presented the highest magnitudes in the five online free PPP services.
Finally, to evaluate the performance of each online PPP service, the RMSE of the E, N, and U components was calculated. The RMSE for each online free PPP service is displayed in Figure 6.
It is observed that for the five online free PPP services, the RMSE for the three components is below 13 mm. The CSRS-PPP service showed the best performance with RMSE less than 9 mm in the three components; however, the differences between the RMSE obtained by it and the remaining four online services were only about 3 mm for the horizontal (E and N) and 4 mm for the vertical (U). Hence, for these online services, since the user only sends or uploads the observation files to any of the five online PPP services, it represents one of the best options to obtain precise coordinates. This fact may demonstrate the feasibility of using online PPP services when high accuracy is required to solve the problem.
Alternatively, to analyze the precision of the E, N, and U components obtained by the different online PPP services, it was necessary to extract the standard deviations offered by these services. The standard deviations were averaged and taken as final values to analyze the E, N, and U components. Additionally, the average of the coordinates, or components E, N, and U, of the 45 stations for the seven days processed was calculated. Only the GAPS, CSRS-PPP, and TRIMBLE services provide the standard deviations of coordinate processing. The results can be seen in Figure 7.
The average of the E, N, and U components for the CSRS-PPP online service is less than 6 mm, and the precision with which they were obtained was around 6 mm. Alternatively, for GAPS and TRIMBLE, the average of the E, N, and U components was higher, mainly in the vertical component; however, the precision of these components presented standard deviations of up to 10 mm. In general, the standard deviations for the horizontal and vertical components were similar, even though the magnitude of the components was different. Based on the above, the ability of online services to achieve millimeter-level precision in calculating coordinates is demonstrated.

5. Discussion

In nature, the PPP measurement technique does not require a reference station or network to achieve centimeter-level precision. The precisions presented in previous sections of the paper have demonstrated the potential benefit of using PPP in static mode in comparison with relative positioning. The low consumption of processing and low costs of PPP make it one of the most used techniques in geosciences. The novel processing algorithms and new precise devices are the main reasons why PPP can minimize the convergence time and resolve integer ambiguities, helping in the process to obtain high performance in positioning. However, the authors of this paper believe that the processing algorithm of each piece of software is a fundamental factor in the accuracy of the PPP technique. In this context, few studies have been conducted on the performance of a large number of software under the same conditions that process static PPP; consequently, the scientific community does not have a benchmark study to identify the best-performing software for their experiments, and commonly reported studies evaluate only one software. This fact justifies the study presented in this paper.
In addition, every piece of PPP open-source software contains different processing strategies, algorithms, and filtering techniques. Thus, different files and input formats are required. This means that each piece of software must work differently. It is important to mention that not all the evaluated open-source software has the AR option, which is one of the most important parameters in PPP for achieving high precision. Alternatively, the availability of multi-constellation and multi-frequency processing is not enabled by many open-source software projects and online free PPP services. The above-mentioned are some of the most common questions that researchers have when selecting PPP processing software. In this study, the authors conducted a precision evaluation and analysis of all open-source software and online free PPP services available for static mode PPP processing. The reference coordinates (of each station) obtained with GAMIT/GLOBK scientific software and published by SOPAC (Scripps Orbit and Permanent Array Center) were used as such in the local topocentric system to transform the X, Y, and Z coordinates estimated with open-source software and online free PPP services to E (East), N (North), and U (Up) coordinates. The components E, N, and U represented the evaluation strategy to determine positioning performance. The RMSE value is the main metric used to evaluate the performance of the ten open-source software products and five online free PPP services studied. The resulted RMSE value of six of the studied software was below 20 mm, while the PRIDE-PPPAR and GIPSY X software were the ones that presented the best performance with RMSE values of less than 8 mm. The difference between the best-performing software and the next four below it was only 8 mm, demonstrating the high performance of available open-source software for static PPP processing. Alternatively, RTKLIB is not highly recommended software for precise positioning of less than 5 cm in measurement conditions such as those exposed in this study. In the case of online PPP services, APPS, MAGICGNSS, and CSRS-PPP are the services that obtained the best performance with an RMSE of less than 12 mm, and for the remaining services, it was below 13 mm. Hence, online PPP services represent an easy option for users who want to obtain only precise positioning in a straightforward format since only basic knowledge about GNSS is required.
However, online PPP services do not allow processing large observation files, as some open-source software does. CSRS-PPP is the service that allows the user to upload observation files up to 300 MB. Nevertheless, in research areas such as Structural Health Monitoring, it is required to measure at high sampling frequencies and for long periods of time, generating observation files larger than 1 GB. Therefore, online free PPP services are not an option for processing such large files. For the open-source software evaluated in this study, only PRIDE-PPPAR and RTKLIB were tested to process an observation file of 4 GB, with PRIDE-PPPAR obtaining more accurate results.
Alternatively, the results achieved in this study were like those found in other works. For example, Bahadur and Nohutcu (2019) [25] evaluated the PPPH software considering different GNSS combinations, and in the case of GPS alone, a 3D positioning precision of 18.1 mm was reported, which is similar to those illustrated in Figure 3. Additionally, Xiao et al. (2020) [40] reported precisions in the North and East components of less than 10 mm and close to 20 mm in the Up component of the MG-APP software. The precisions reported in our study for MG-APP were 9, 13, and 24 mm for the N, E, and U components, respectively. For online services, Guo (2014) [19] evaluated the CSRS-PPP, APPS, GAPS, and MAGICGNSS services and concluded that these online services are capable of reaching precisions in the order of millimeters, just as those achieved in this study, where all online services had accuracies less than 15 mm. In general, the results achieved in our study are similar to those reported in other works [18,20,21,22,23,24,43]. Additionally, the geographical location of the IGS stations and the ENU coordinates were analyzed, and it was found that there is no correlation between these two variables, that is, the stations with higher latitudes are not less precise with respect to latitudes near the Equator. These results reflect that the accuracy of an IGS station does not depend on its geographic location but rather on the software or online service used for static PPP processing.
Finally, to classify the performance of the online PPP services and open-source software evaluated in this study, the total uncertainty [55,56] of the RMSE was determined considering the three components.
T o t a l   U n c e r t a i n t y = R M S E E 2 + R M S E N 2 + R M S E U 2
where R M S E E , R M S E N and R M S E U represent the root mean square errors for the East, North, and Up components, respectively. Total uncertainty represents the quality of a measurement considering all the variables involved in a process. The total uncertainty for our case study represents the total precision of each software and online service, considering the square root of the sum of the RMSE of each component squared [55]. The results, ordered from lowest to highest, are shown in Table 6.
Based on the results of Table 6, it is observed that the PRIDE-PPPAR software achieved the best performance. However, the difference between PRIDE-PPPAR and GIPSY X was only 0.34 mm, which is a negligible value for many applications. Alternatively, the results achieved with online PPP services reveal the efficiency required to obtain high-precision positioning. Additionally, the online services CSRS-PPP, APPS, MagicGNSS, and TRIMBLE obtained accuracy similar to that obtained by scientific software such as GIPSY X.

6. Conclusions

The precision of different open-source software and online free PPP services with the PPP technique in static mode was evaluated and comprehensively analyzed in this paper. The XYZ geocentric coordinates were estimated with software and online services. Seven days of observations at 45 IGS stations distributed worldwide were transformed to ENU local topocentric coordinates. The reference coordinates were used as the origin of the ENU local system. The Root Mean Square Error (RMSE) of the mean ENU coordinates was determined as a metric for the evaluation of positioning performance. Based on the results, the following conclusions were reached:
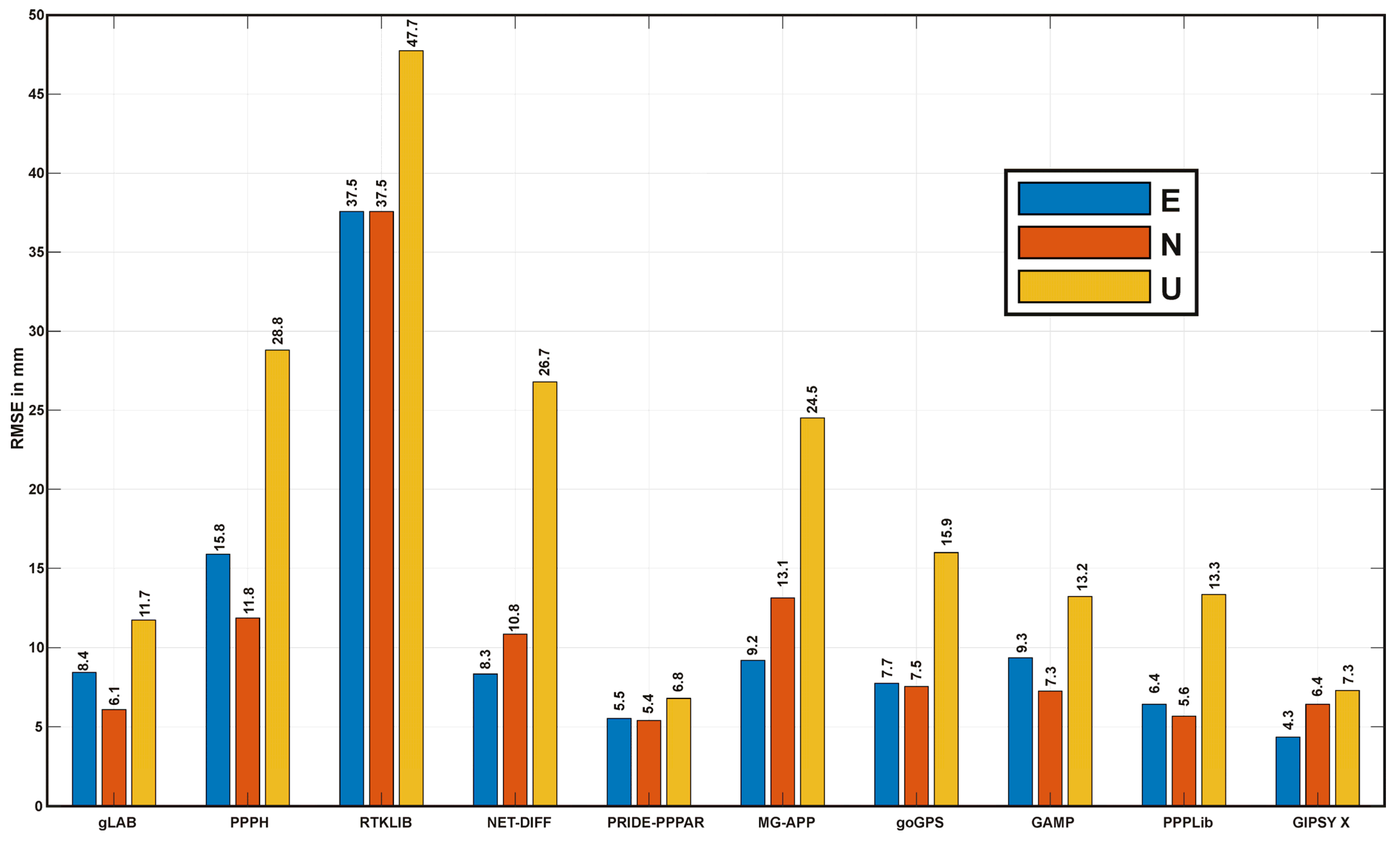
  • PRIDE-PPPAR software represents the most precise option for positioning via static PPP of all open-source software and online PPP services evaluated in this research, achieving RMSEs in the E, N, and U components of 5.52, 5.4, and 6.79 mm, respectively.
  • gLAB, PPPH, Net_Diff, MG-APP goGPS, PPPLib, and GAMP obtained similar RMSE values with respect to GIPSY X, with small differences of up to 5 mm.
  • The authors classify the open-source software evaluated based on their RMSE values into three groups: the first group contains the software with RMSE estimates less than 12 mm in its three components, that is, PRIDE-PPPAR, gLAB, and GIPSY X; the second group contains Net_Diff, MG-APP, goGPS, GAMP, PPPLib, and PPPH, which have RMSE rates between 12 and 30 mm. Finally, Group 3 comprises only RTKLIB, which has the lowest performance, with RMSE amounts between 37 and 48 mm.
  • CSRS-PPP was the best-performing online free PPP service, with RMSEs below 9 mm for all three components. The difference in RMSE of TRIMBLE, MagicGNSS, APPS, and GAPS compared with CSRS-PPP was only 4 mm, concluding that online free PPP services generally perform similarly.
  • The difference between the RMSE obtained by the online free PPP services and GIPSY X demonstrated that they are viable options for scientific work due to the high precision achieved.
  • Ambiguity resolution in open-source software and online free PPP services plays an important role in achieving precisions in the order of millimeters through the static mode PPP positioning technique.
  • Results from open-source software and free online PPP services reflect the potential of static PPP as an alternative to relative positioning due to the high precision achieved.
The authors recommend using the PRIDE-PPPAR software for scientific works related to high-precision GNSS positioning; however, software that makes up Group 1 can be used as a second option after PRIDE-PPPAR. In geosciences scientific works where users do not need a deep knowledge of GNSS, it is recommended to them the online PPP services APPS and CSRS-PPP for their ease of use, considering the size of the file to be processed. The total uncertainties of the online free PPP services were higher than those obtained from the six open-source software products evaluated, including Net_Diff.
More evaluation work on open-source software and online free PPP services that process PPP in static mode is needed. For example, the authors recently evaluated the performance of high-rate GNSS observations and the impact of combining multi-constellations and multi-frequency in PRIDE-PPPAR. Additionally, the authors seek to select open-source software that allows processing high-rate multi-frequency and multi-constellation observation files in PPP in static and kinematic modes with ambiguity resolution for signal spectral analysis.

Author Contributions

Conceptualization, J.R.V.-O.; methodology, J.R.V.-O.; software, J.R.V.-O. and J.P.-V.; validation, J.R.V.-O.; formal analysis, J.R.V.-O., J.P.-V., J.R.G.-C. and G.E.V.-B.; investigation, J.R.V.-O. and J.P.-V.; data curation, J.R.V.-O.; writing—original draft preparation, J.R.V.-O.; writing—review and editing, J.R.V.-O., J.P.-V., J.R.G.-C. and G.E.V.-B.; supervision, J.R.G.-C. and G.E.V.-B.; project administration, J.R.G.-C. and G.E.V.-B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

This work was financially supported by several agencies of the government of Mexico. The authors would like to thank the Consejo Nacional de Ciencia y Tecnología (CONACYT) and Universidad Autónoma de Sinaloa (UAS). The results, observations, and conclusions presented in this paper are those of the authors and do not reflect the point of view of the sponsors.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Anderle, R.J. Point positioning concept using precise ephemeris. Satell. Doppler Position. 1976, 1, 47–75. [Google Scholar]
  2. Zumbergue, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
  3. Kouba, J.; Heroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
  4. Xi, R.; Chen, Q.; Meng, X.; Psimoulis, P.; Jiang, W.; Xu, C. Pass-by-Pass Ambiguity Resolution in Single GPS Receiver PPP Using Observations for Two Sequential Days: An Exploratory Study. Remote Sens. 2021, 13, 3728. [Google Scholar] [CrossRef]
  5. Liu, T.; Wang, J.; Yu, H.; Cao, X.; Ge, Y. A new weighting approach with application to ionospheric delay constraint for GPS/GALILEO real-time precise point positioning. Appl. Sci. 2018, 8, 2537. [Google Scholar] [CrossRef] [Green Version]
  6. Yan, C.; Wang, Q.; Zhang, Y.; Ke, F.; Gao, W.; Yang, Y. Analysis of GNSS clock prediction performance with different interrupt intervals and application to real-time kinematic precise point positioning. Adv. Space Res. 2020, 65, 978–996. [Google Scholar] [CrossRef]
  7. Yigit, C.O.; Gurlek, E. Experimental testing of high-rate GNSS precise point positioning (PPP) method for detecting dynamic vertical displacement response of engineering structures. Geomat. Nat. Hazards Risk 2017, 8, 893–904. [Google Scholar] [CrossRef] [Green Version]
  8. Romero-Andrade, R.; Trejo-Soto, M.E.; Vázquez-Ontiveros, J.R.; Hernández-Andrade, D.; Cabanillas-Zavala, J.L. Sampling rate impact on Precise Point Positioning with a Low-Cost GNSS receiver. Appl. Sci. 2021, 11, 7669. [Google Scholar] [CrossRef]
  9. Du, S.; Shu, B.; Xie, W.; Huang, G.; Ge, Y.; Li, P. Evaluation of Real-time Precise Point Positioning with Ambiguity Resolution Based on Multi-GNSS OSB Products from CNES. Remote Sens. 2022, 14, 4970. [Google Scholar] [CrossRef]
  10. Ge, M.; Gendt, G.; Rothacher, M.A.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
  11. Collins, P.; Lahaye, F.; Heroux, P.; Bisnath, S. Precise point positioning with ambiguity resolution using the decoupled clock model. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation, Savannah, GA, USA, 16–19 September 2008; pp. 1315–1322. [Google Scholar]
  12. Laurichesse, D.; Mercier, F.; Berthias, J.P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
  13. Chen, C.; Xiao, G.; Chang, G.; Xu, T.; Yang, L. Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution Using Products from Different Analysis Centers. Remote Sens. 2021, 13, 3266. [Google Scholar] [CrossRef]
  14. Bahadur, B. An improved weighting strategy for tropospheric delay estimation with real-time single-frequency precise positioning. Earth Sci. Inform. 2022, 15, 1267–1284. [Google Scholar] [CrossRef]
  15. Vazquez-Ontiveros, J.R.; Vazquez-Becerra, G.E.; Quintana, J.A.; Carrion, F.J.; Guzman-Acevedo, G.M.; Gaxiola-Camacho, J.R. Implementation of PPP-GNSS measurement technology in the probabilistic SHM of bridge structures. Measurement 2021, 173, 108677. [Google Scholar] [CrossRef]
  16. Lu, C.; Feng, G.; Zheng, Y.; Zhang, K.; Tan, H.; Dick, G.; Wickert, J. Real-time retrieval of precipitable water vapor from Galileo observations by using the MGEX network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4743–4753. [Google Scholar] [CrossRef]
  17. Ocalan, T.; Turk, T.; Tunalioglu, N.; Gurturk, M. Investigation of accuracy of PPP and PPP-AR methods for direct georeferencing in UAV photogrammetry. Earth Sci. Inform. 2020, 15, 2231–2238. [Google Scholar] [CrossRef]
  18. Ghoddousi-Fard, R.; Dare, P. Online GPS processing services: An initial study. GPS Solut. 2006, 10, 12–20. [Google Scholar] [CrossRef]
  19. Guo, Q. Precision comparison and analysis of four online free PPP services in static positioning and tropospheric delay estimation. GPS Solut. 2015, 19, 537–544. [Google Scholar] [CrossRef]
  20. El Shouny, A.; Miky, Y. Accuracy assessment of relative and precise point positioning online GPS processing services. J. Appl. Geod. 2019, 13, 215–227. [Google Scholar] [CrossRef]
  21. Leandro, R.F.; Santos, M.C.; Langley, R.B. Analyzing GNSS data in precise point positioning software. GPS Solut. 2010, 15, 1–13. [Google Scholar] [CrossRef]
  22. Wanas, S.K.; Alhamadani, O.Y.M.Z. Evaluation of the Performance of Online GPS/GNSS Data Processing Services for Monitoring the Land Deformations and Movements. J. Eng. 2019, 25, 108–119. [Google Scholar] [CrossRef] [Green Version]
  23. El-Mowafy, A. Analysis of web-based GNSS post-processing services for static and kinematic positioning using short data spans. Surv. Rev. 2011, 43, 535–549. [Google Scholar] [CrossRef] [Green Version]
  24. Alkan, R.M.; Erol, S.; Ozulu, I.M.; Ilci, V. Accuracy comparison of post-processed PPP and real-time absolute positioning techniques. Geomat. Nat. Hazards Risk 2020, 11, 178–190. [Google Scholar] [CrossRef]
  25. Bahadur, B.; Nohutcu, M. Comparative analysis of MGEX products for post-processing multi-GNSS PPP. Measurement 2019, 145, 361–369. [Google Scholar] [CrossRef]
  26. Grinter, T.; Roberts, C.; Janssen, V. Ambiguity-resolved real-time precise point positioning as a potential fill-in service for sparse CORS networks. J. Surv. Eng. 2020, 146, 04020007. [Google Scholar] [CrossRef]
  27. Malik, J.S. Performance analysis of static precise point positioning using open-source GAMP. Artif. Satell. 2020, 55, 5–19. [Google Scholar] [CrossRef]
  28. Yigit, C.O.; Gikas, V.; Alcay, S.; Ceylan, A. Performance evaluation of short to long term GPS, GLONASS and GPS/GLONASS post-processed PPP. Surv. Rev. 2014, 46, 155–166. [Google Scholar] [CrossRef]
  29. Alkan, R.M.; IIci, V.; Ozulu, I.M.; Saka, M.H. A comparative study for accuracy assessment of PPP technique using GPS and GLONASS in urban areas. Measurement 2015, 69, 1–8. [Google Scholar] [CrossRef]
  30. Mohammed, I.H.; Ataiwe, T.N.; Al Sharaa, H. Accuracy Assessment of a Variety of GPS Data Processing, Online Services and Software. Geomat. Environ. Eng. 2021, 15, 5–19. [Google Scholar] [CrossRef]
  31. Dawidowicz, K.; Bakula, M. Impact of BeiDou Observations on the Accuracy of Multi-GNSS PPP in a Function of Observing Session Duration within Europe-Analysis Based on Open-Source Software GAMP. Remote Sens. 2023, 15, 158. [Google Scholar] [CrossRef]
  32. Bahadur, B.; Nohutcu, M. PPPH: A MATLAB-based software for multi-GNSS precise point positioning analysis. GPS Solut. 2018, 22, 1–10. [Google Scholar] [CrossRef]
  33. Ibáñez, D.; Rovira-Garcia, A.; Sanz, J.; Juan, J.M.; González-Casado, G.; Jimenez-Baños, D.; Lapin, I. The GNSS laboratory tool suite (gLAB) updates: SBAS, DGNSS and global monitoring system. In Proceedings of the 2018 9th ESA Workshop on Satellite NavigationTechnologies and European Workshop on GNSS Signals and Signal Processing, Noordwijk, The Netherlands, 5–7 December 2018. [Google Scholar] [CrossRef]
  34. Hernandez-Pajares, M.; Juan, J.M.; Sanz, J.; Ramos-Bosch, P.; Rovira-Garcia, A.; Salazar, D.; Hein, G. The ESA/UPC GNSS-Lab tool (gLAB): An advanced multipurpose package for GNSS data processing. In Proceedings of the 2010 5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 8–10 December 2018. [Google Scholar] [CrossRef]
  35. Zhang, Y.; Kubo, N.; Chen, J.; Wang, J.; Wang, H. Initial positioning assessment of BDS new satellites and new signals. Remote Sens. 2019, 11, 1320. [Google Scholar] [CrossRef] [Green Version]
  36. Zhang, Y.; Chen, J.; Gong, X.; Chen, Q. The update of BDS-2 TGD and its impact on positioning. Adv. Space Res. 2020, 65, 2645–2661. [Google Scholar] [CrossRef]
  37. Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open-source program package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, Jeju, Republic of Korea, 4–6 November 2009. [Google Scholar]
  38. Angrisano, A.; Dardanelli, G.; Innac, A.; Pisciotta, A.; Pipitone, C.; Gaglione, S. Performance Assessment of PPP Surveys with Open-Source Software Using the GNSS GPS–GLONASS–Galileo Constellations. Appl. Sci. 2020, 10, 5420. [Google Scholar] [CrossRef]
  39. Geng, J.; Chen, X.; Pan, Y.; Mao, S.; Li, C.; Zhou, J.; Zhang, K. PRIDE PPP-AR: An open-source software for GPS PPP ambiguity resolution. GPS Solut. 2019, 23, 1–10. [Google Scholar] [CrossRef]
  40. Xiao, G.; Liu, G.; Ou, J.; Liu, G.; Wang, S.; Guo, A. MG-APP: An open-source software for multi-GNSS precise point positioning and application analysis. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
  41. Herrera, A.M.; Suhandri, H.F.; Realini, E.; Reguzzoni, M.; de Lacy, M.C. goGPS: Open-source MATLAB software. GPS Solut. 2016, 20, 595–603. [Google Scholar] [CrossRef]
  42. Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 1–10. [Google Scholar] [CrossRef]
  43. Chen, C.; Chang, G. PPPLib: An open-source software for precise point positioning using GPS, BeiDou, Galileo, GLONASS, and QZSS with multi-frequency observations. GPS Solut. 2021, 25, 1–7. [Google Scholar] [CrossRef]
  44. Bertiger, W.; Bar-Sever, Y.; Dorsey, A.; Haines, B.; Harvey, N.; Hemberger, D.; Willis, P. GipsyX/RTGx, a new tool set for space geodetic operations and research. Adv. Space Res. 2020, 66, 469–489. [Google Scholar] [CrossRef]
  45. Héroux, P.; Kouba, J.; Beck, N.; Lahaye, F.; Mireault, Y.; Tétreault, P.; Caissy, M. Space geodetic techniques and the Canadian spatial reference system evolution, status and possibilities. Geomatica 2006, 60, 137–150. [Google Scholar] [CrossRef]
  46. Tétreault, P.; Kouba, J.; Héroux, P.; Legree, P. CSRS-PPP: An internet service for GPS user access to the Canadian Spatial Reference Frame. Geomatica 2005, 59, 17–28. [Google Scholar] [CrossRef]
  47. Leandro, R.F. Precise Point Positioning with GPS: A New Approach for Positioning, Atmospheric Studies, and Signal Analysis. Ph.D. Dissertation, University of New Brunswick, Frederiction, NB, Canada, 2009. [Google Scholar]
  48. Doucet, K.; Herwing, M.; Kipka, A.; Kreikenbohm, P.; Landau, H.; Leandro, R.; Pagels, C. Introducing ambiguity resolution in web-hosted global multi-GNSS Precise Point Positioning with trimble RTK-PP. In Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 1115–1125. [Google Scholar]
  49. Nardo, A.; Drescher, R.; Brandl, M.; Chen, X.; Landau, H.; Rodriguez-Solano, C.; Weinbach, U. Experiences with trimble center point RTX with fast convergence. In Proceedings of the ESA European Navigation Conference (ENC2015), Bordeaux, France, 7–10 April 2015. [Google Scholar]
  50. García, A.M.; Píriz, R.; Samper, M.D.L.; Merino, M.M.R. Multisystem Real Time Precise-Point-Positioning, today with GPS+ GLONASS in the near future also with QZSS, Galileo, Compass, IRNSS. In Proceedings of the International Symposium on GPS/GNSS, Taipei, Taiwan, 26–28 October 2010. [Google Scholar]
  51. CSRS-PPP. Canadian Spatial Reference System Precise Point Positioning, Natural Resources Canada. Available online: https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/ppp-info.php?locale=en (accessed on 20 November 2022).
  52. Nischan, T. GFZRNX-RINEX GNSS Data Conversion and Manipulation Toolbox, version 1.05; GFZ Data Services: Potsdam, Germany, 2016. [Google Scholar]
  53. Dadras Eslamlou, A.; Huang, S. Artificial-Neural-Network-Based Surrogate Models for Structural Health Monitoring of Civil Structures: A Literature Review. Buildings 2022, 12, 2067. [Google Scholar] [CrossRef]
  54. Wang, H.; Wang, Y.; Fang, J.; Chai, H.; Zheng, H. Simulation research on a minimum root-mean-square error rotation-fitting algorithm for gravity matching navigation. Sci. China Earth Sci. 2012, 55, 90–97. [Google Scholar] [CrossRef]
  55. Rizos, C. Principles and Practice of GPS Surveying, 1st ed.; School of Geomatic Engineering, University of New South Wales: Kensington, NSW, Australia, 1997. [Google Scholar]
  56. Ghilani, C.D. Adjustment Computations: Spatial Data Analysis, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
Remotesensing 15 02034 g001 550
Figure 1. Geographic distribution of the 45 IGS stations used in this study.
Figure 1. Geographic distribution of the 45 IGS stations used in this study.
Remotesensing 15 02034 g001
Remotesensing 15 02034 g002 550
Figure 2. Bar diagrams of the means of the E, N, and U components obtained for the 20 IGS stations with the open-source software.
Figure 2. Bar diagrams of the means of the E, N, and U components obtained for the 20 IGS stations with the open-source software.
Remotesensing 15 02034 g002
Remotesensing 15 02034 g003 550
Figure 3. RMSE of the E, N, and U components obtained with open-source software.
Figure 3. RMSE of the E, N, and U components obtained with open-source software.
Remotesensing 15 02034 g003
Remotesensing 15 02034 g004 550
Figure 4. Bar diagram of the means of the E, N, and U components and their corresponding standard deviations for the different software.
Figure 4. Bar diagram of the means of the E, N, and U components and their corresponding standard deviations for the different software.
Remotesensing 15 02034 g004
Remotesensing 15 02034 g005 550
Figure 5. Bar diagrams of the means of the components E, N, and U for the 20 IGS stations obtained in the different online free PPP services.
Figure 5. Bar diagrams of the means of the components E, N, and U for the 20 IGS stations obtained in the different online free PPP services.
Remotesensing 15 02034 g005
Remotesensing 15 02034 g006 550
Figure 6. RMSE of online free PPP services.
Figure 6. RMSE of online free PPP services.
Remotesensing 15 02034 g006
Remotesensing 15 02034 g007 550
Figure 7. Bar diagram of the mean of the E, N, and U components and their corresponding standard deviation for the different online free PPP services.
Figure 7. Bar diagram of the mean of the E, N, and U components and their corresponding standard deviation for the different online free PPP services.
Remotesensing 15 02034 g007
Table
Table 1. Main feature of online PPP services.
Table 1. Main feature of online PPP services.
General InformationGAPSCSRS-PPPAPPSMagicGNSSTrimble Center Point RTX
Web sitehttp://gaps.gge.unb.ca/ (accessed on 20 November 2022)https://webapp.csrs-scrs.nrcan-rncan.gc.ca/geod/tools-outils/ppp.php?locale=en (accessed on 20 November 2022)https://pppx.gdgps.net// (accessed on 20 November 2022)https://magicgnss.gmv.com/user/ppp (accessed on 20 November 2022)https://trimblertx.com/ (accessed on 20 November 2022)
DeveloperUniversity of New Brunswick (UNB)Natural Resources Canada (NRCan)NASA-Jet Propulsion Laboratory (JPL)Spain GMV CompanyTrimble Navigation
Latest versionGAPS v6.0.0 r587 (2016)SPARK v3.54.2 (2022)GIPSY-OASIS v5Magic PPP (2016)8.5.1.20196
Supported process modeStatic, kinematicStatic, kinematicStatic, kinematicStatic, kinematicStatic
Observation dataDual-frequencySingle- or Dual-frequencyDual-frequencyDual-frequencyDual-frequency
ConstellationGPS + Galileo + BeiDouGPS + GLONASSGPSGNSSGNSS
Orbit and of satelliteIGS and NRCanIGS and NRCanJPL finalIGS finalTrimble
Limitations of uploaded file≤10 Mb≤300 MbUnregistered: ≤5 Mb
Registered: ≤100 Mb		≤10 Mb≤10 Mb
Coordinate frameITRF2014IGb2014/NAD83/IGS20ITRF2014ITRF2014ITRF2014
Tropospheric delay model and mapping functionUNB-VMF1; UNB3
MF: VMF1-gridded		Dry delay: Davis
Wet delay: Hopf
MF: GMF 		GMF: troposphere mapping functionMF: GPT2-
Angle of cut-off horizon10°7.5°7.5°8°N/A
Ambiguity resolutionNoYesYesNoNo
Table
Table 2. Main characteristics of the evaluated open-source software.
Table 2. Main characteristics of the evaluated open-source software.
General InformationgLABPPPHRTKLIBNET_DIFFPRIDE-PPPARMG-APPgoGPSGAMPPPPLibGIPSY X
DeveloperEuropean Space AgencyBahadur and Nohutcu [32]Takasu and Yasuda [37]GNSS Analysis Center at Shanghai Astronomical Observatory (SHA)Geng et al. [39]Xiao et al. [40] Herrera et al. [41] Zhou et al. [42]Chen et al. [43]Jet Propulsion Laboratory (JPL)
Latest versionV5.5.1 (2020)PPPH (2018)2.4.2 b34b (2020)V1.16 (2020)V2.2 (2023)V1.0 (2019)V1.0 (2021)GAMP (2018)PPPLib (2020)GIPSY X-1.7 (2021)
Supported process modeStatic, kinematicStatic, kinematicStatic, kinematicStatic, kinematicStatic, kinematicStatic, kinematicStaticStatic, kinematicStatic, kinematicStatic, kinematic
Observation dataDual-frequencyDual-frequencyMulti-frequencyMulti-frequencyDual-frequencyDual-frequencyMulti-frequencyDual-frequencyDual-frequencyMulti-frequency
ConstellationGPSGNSSGNSSGNSSGNSSGNSSGNSSGNSSGNSSGNSS
Tropospheric delay model and mapping functionNiell mapping
UNB3-3		Saastamoinen (GPT2)
GMF		SaastamoinenSaastamoinen (GPT2-5W), UNB3, VMF1 GPT3
VMF3		Saastamoinen (GPT2), Hopfield (GPT2)VMFVMFSaastamoinen
Rando walk		GPT2
VMF
Coordinate frameITRF2014ITRF2014ITRF2014INTRF2014ITRF2014ITRF2014ITRF2014ITRF2014ITRF2014ITRF2014
Ambiguity resolutionNoNoNoYesYesNoNoNoNoYes
Operating systemWindows, Linux, MacWindows, Linux, MacWindows, LinuxWindowsWindows, LinuxWindows, LinuxWindows, LinuxWindows, LinuxWindows, LinuxLinux
Table
Table 3. The summary of general data processing strategies.
Table 3. The summary of general data processing strategies.
ModeStatic
Sampling rate30 s
GNSS typeGPS
Elevation mask8°
Observation processedCode and phase
Frequency observedL1, L2
Troposphere correctionSaastamoinen
Ionosphere correctionIonosphere-free linear combination
Satellite orbitsPrecise (IGS Final)
Differential code biases P1C1.DCB (CODE)
Clock productsIGS final (clk_30)
Earth Rotation ParameterIGS final (ERP)
Ocean loadingFES2014b *
Phase center offsets/variationsIgs14.atx
* http://holt.oso.chalmers.se/loading/ (accessed on 20 November 2022).
Table
Table 4. Standard deviation, maximum, and minimum values of the ENU absolute coordinates in the ITRF2014 reference frame (unit: mm).
Table 4. Standard deviation, maximum, and minimum values of the ENU absolute coordinates in the ITRF2014 reference frame (unit: mm).
SoftwareE N U
MaxMinStandard DeviationMeanMaxMinStandard DeviationMeanMaxMinStandard DeviationMean
gLAB3005.961803.84.733088.6
PPPH45011.610.94408.8864117.423
RTKLIB94 125289602429.14121326.939.6
NET_DIFF21.705.46.332.706.98.450.560.315.721.8
PRIDE-PPPAR19.2704.23.622043.616045.4
MG-APP3206.36.727.407.310.948.3013.120.7
goGPS22055.91904.95.7301.68.213.74
GAMP27.8067.2418.24046280810.5
PPPLib22.3504.44.61803.74.28290810.65
GIPSY X12.202.93.182004.154.921804.85.52
Table
Table 5. Standard deviation, mean, maximum, and minimum values of the absolute E, N, and U components (unit: mm).
Table 5. Standard deviation, mean, maximum, and minimum values of the absolute E, N, and U components (unit: mm).
Online PPP ServiceE N U
MaxMinStandard
Deviation		MeanMaxMinStandard
Deviation		MeanMaxMinStandard
Deviation		Mean
CSRS-PPP2304.663.520.804.374.931.705.875.9
APPS1904.215.823.220.334.224.733.790.586.899.14
TRIMBLE20.1304.324.521.8045.427.707.110.13
MAGICGNSS29.2805.484.918.5204.264.730.240.467.78.8
GAPS23.905.06518.480.123.75.731.60.488.239.9
Table
Table 6. Total uncertainty of the root mean square errors.
Table 6. Total uncertainty of the root mean square errors.
Software/Online PPP ServiceTotal Uncertainty/mm
PRIDE-PPPAR10.29
GIPSY X10.63
CSRS-PPP12.07
APPS14.87
MagicGNSS15.18
TRIMBLE15.41
gLAB15.69
PPPLib15.87
GAPS16.19
GAMP17.75
goGPS19.31
MG-APP29.29
Net_Diff30.07
PPPH34.98
RTKLIB71.43
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Vázquez-Ontiveros, J.R.; Padilla-Velazco, J.; Gaxiola-Camacho, J.R.; Vázquez-Becerra, G.E. Evaluation and Analysis of the Accuracy of Open-Source Software and Online Services for PPP Processing in Static Mode. Remote Sens. 2023, 15, 2034. https://doi.org/10.3390/rs15082034

AMA Style

Vázquez-Ontiveros JR, Padilla-Velazco J, Gaxiola-Camacho JR, Vázquez-Becerra GE. Evaluation and Analysis of the Accuracy of Open-Source Software and Online Services for PPP Processing in Static Mode. Remote Sensing. 2023; 15(8):2034. https://doi.org/10.3390/rs15082034

Chicago/Turabian Style

Vázquez-Ontiveros, Jesus René, Jorge Padilla-Velazco, J. Ramon Gaxiola-Camacho, and Guadalupe Esteban Vázquez-Becerra. 2023. "Evaluation and Analysis of the Accuracy of Open-Source Software and Online Services for PPP Processing in Static Mode" Remote Sensing 15, no. 8: 2034. https://doi.org/10.3390/rs15082034

APA Style

Vázquez-Ontiveros, J. R., Padilla-Velazco, J., Gaxiola-Camacho, J. R., & Vázquez-Becerra, G. E. (2023). Evaluation and Analysis of the Accuracy of Open-Source Software and Online Services for PPP Processing in Static Mode. Remote Sensing, 15(8), 2034. https://doi.org/10.3390/rs15082034

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop