1. Introduction
Weather radar not only plays an essential role in meteorology, but it is also used in a variety of fields, such as biology [
1,
2], urban hydrology [
3], geophysical [
4], and vocanology [
5]. Its all-weather, all-day capability makes it an indispensable tool for detecting precipitation systems and providing early warnings for severe weather events, such as heavy rain, squall lines, hail, and tornadoes. The China New Generation of Weather Radar (CINRAD) uses system echoes to quantify precipitation and monitor extreme weather conditions. The higher the radar resolution, the more detailed the structures of the detected weather targets become, enabling earlier warnings for potential catastrophic weather events.
In weather radar applications, certain regions may not be monitored due to factors, such as the scanning strategy of a radar, the curvature of the earth, and obstructions from terrain. This leads to a lack of comprehensive and objective data for studying various atmospheric patterns. The current CINRAD radar is limited by its spatial and temporal resolution, making it challenging to effectively monitor the rapidly changing severe weather conditions. CINRAD, based on a mechanical scanning system, also faces several challenges in detecting the fine structures of weather processes [
6]. These challenges include (1) low spatial resolution with a distance resolution of 1 km, making it difficult to refine the observation weather processes; (2) a volume scan time of 5–6 min, with limited ability to track the evolution of strong weather systems; and (3) a volume coverage pattern of 9 or 14 elevation angles results in limited vertical detail. The medium- and small-scale weather processes, which can span only a few kilometers, are typically represented as a dozen valid range bins in the CINRAD radar echoes, making it challenging to observe the evolution of weather processes.
The Center for Collaborative Adaptive Sensing of the Atmosphere (CASA) in Dallas–Fort Worth (DFW) has established a state-of-the-art urban demonstration network to address weather-related problems. The network consists of eight X-band radar and a National Weather Service S-band radar system [
7]. The DFW network observation experiments have shown that radar co-observation technology has better spatial–temporal resolution than a single radar product, and can provide refined observation of the target, which is conducive to the identification of weather systems [
8]. In recent years, China has commenced collaborative network observation studies. In 2015, the Foshan Meteorological Bureau built four X-band dual-polarization radars to monitor and warn against strong convection and tornadoes in the Foshan area [
9]. The Beijing Meteorological Bureau also deployed five X-band dual-polarization weather radars to overcome blind spots in low-altitude radar detection and enhance weather prediction and warning accuracy [
10]. The S-band radar system operates differently from the X-band radar. The S-band radar updates every 5 to 6 min, whereas the X-band radar produces a volume every minute. The X-band radar has a 30∼150 m radial resolution and a detection distance of 60 km. The S-band radar has a 1 km radial resolution and a detection distance of 460 km. The X-band radar has a high resolution but a short detection distance, while the S-band radar has a low resolution but a long detection distance, as shown in
Table 1. To address these differences, the S-band radar distance is mapped onto a 250 m × 250 m grid (original distance resolution of 1 km) by using super-resolution algorithms. Therefore, the X-band radar and the S-band radar can be used in combination to effectively make up for their respective shortcomings for refined detection of severe weather events, such as strong convective storms.
The current research on improving radar resolution can be divided into two categories: modifying the radar system hardware and using radar signal processing. The first category involves modifying the radar system hardware. For example, Shinriki et al. [
11] used the least-error shaping filters by compressing the outputs to the desired pulse width (the elapsed time between two points with
of the pulse peak value) to reduce the size of the range side-lobes (the lobes (local maxima) of the far field radiation pattern of an antenna or other radiation source) after compression, and the schemes effectively improved the range resolution for the targets. Mar et al. [
12] applied the pulse compression technique of the linear frequency modulation (LFM) pulse modulation to improve the range resolution. Zhang et al. [
13] verified that Angular Interferometry (AI) can improve the azimuthal resolution of radar and Range Interferometry (RI) can improve the distance resolution of radar using interferometric techniques and demonstrated the feasibility of this method in practical applications. However, the hardware-based approach implies the improving and updating of the radar transmitter, antenna, and receiver, an impractical approach for the new generation of Doppler weather radars currently in operation. The second category uses radar signal processing to analyze radar echoes of redundant information or correlations resulting in the reconstruction of radar data with higher resolution. Wood and Brown et al. [
14,
15] proposed a super-resolution algorithm of increasing the radial sampling interval to reduce the effective width of the radar antenna beam, and, based on this research result, the U.S. added a 0.5° elevation scan and a data scan mode with a distance resolution of 250 m to the WSR-88D radar in the observation mode. Ruzanski et al. [
16] used an improved interpolation method applied to weather radar data to perform windowing and preserved the important echo structure features. Yuan et al. [
17] applied different regularization constraints to the sparse representation algorithm to improve the resolution of radar echo data. Zhang et al. [
18] proposed the Total Variation-Sparse (TV-Sparse) algorithm, which effectively improves the angular resolution and preserves the contour features of important targets. However, super-resolution algorithms based on these methods may be influenced by the statistical characteristics of radar data and their performance may be impacted by parameters. The deep learning algorithm can effectively overcome these limitations and their performance can be further improved with more observation data samples.
With the advancement of convolutional neural networks (CNNs), super-resolution algorithms have gained significant attention in various fields, including remote sensing [
19,
20], medical [
21,
22], agriculture [
23,
24], and video surveillance [
25]. Researchers began to apply super-resolution algorithms based on neural networks to the field of meteorology. Geiss et al. [
26] used U-net combined with several densely connected blocks to learn precipitation features, and the reconstructed image results were better than conventional interpolation schemes in terms of objective evaluation metrics and visual quality. Chen et al. [
27] applied a generative adversarial network to sub-images of 500 radar images and obtained improved perceptual quality and better peak signal-to-noise ratio (PSNR)/structural similarity index (SSIM) results compared to non-local self-similarity sparse representation. Yuan et al. [
28] proposed a non-local residual network that uses radar reflectivity images as a dataset to recover more information about the edge details of the precipitation echo structure.
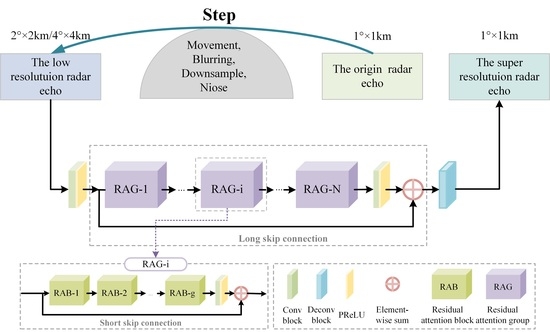
The current approach to enhance radar resolution with CNNs involves super-resolution reconstruction of radar data represented as PPI images. However, the radar data have been quantified when converted into images, resulting in the loss of important information. To address this, the proposed method in this paper aims to reconstruct high-resolution radar echoes directly from radar data, retaining more of the original information and improving the quality of the super-resolution reconstruction. To achieve this, firstly, the paper introduces a residual attention back-projection network (RABPN) which can recover detailed radar echo features and retain more of the original echo information. Additionally, a residual attention block (RAB) is proposed by introducing a channel attention mechanism into the deep attention back-projection network (DBPN). The network structure of [
29] network structure uses iterative up- and down-sampling to leverage the interdependence between low- and high-resolution radar echoes compared with the predefined up-sampling [
30,
31,
32] and single up-sampling [
33,
34] network structures, and the channel attention mechanism [
35] can selectively extract relevant information to refine the structure of the radar echoes. To further improve the network’s effectiveness, long and short skip connections [
36] are added to the network to prevent the network becoming too deep and avoiding issues with gradient disappearance or gradient explosion.
The rest of the paper is structured as follows. In
Section 2, we provide a comprehensive overview of the weather radar super-resolution reconstruction model. In
Section 3, we delve into the technical details of the residual attention back-projection network (RABPN). In
Section 4, we present a thorough evaluation of the experimental results, including both qualitative and quantitative analyses. Finally, in
Section 5, we provide a conclusion and outline potential avenues for future research.
2. Weather Radar Super-Resolution Reconstruction Model
The impact of factors, such as radar beam width (the angular distance between the half power points), the offset produced by the radar elevation angle lifting, and noise, leads to a decrease in radar resolution during weather radar detection. As the detection distance increases, the radar beam tension angle widens and the resolution worsens. Taking CINRAD-SA’s 1° beamwidth as an example, when the weather radar detection distance is 400 km, the azimuth resolution has increased to 6.89 km, which reduces the measurement accuracy of weather targets, as is depicted in
Figure 1 and
Table 2.
The acquisition of weather radar echo is distinct from that of videos and images captured by cameras, and the degradation model for radar echo is not the same as that used in optical imaging models. The accuracy of the degradation model approximation can determine the proximity of the super-resolution reconstructed echoes to the actual situation. By establishing a low-resolution observation model for radar echo resolution, the degradation process during the acquisition of radar echo is simulated, as is shown in
Figure 2.
The degradation model of weather radar, also known as the low-resolution observation model, is generated by simulating the operations of movement, blurring, down-sampling, and noise addition. Movement is a shifting operator; blurring represents a point spread function to simulate the radar echo of blurring; down sampling is achieved through neighborhood averaging of high-resolution echoes; noise is zero-mean Gaussian white noise to simulate system noise introduced during the acquisition, transmission, and storage of weather radar echoes. The degradation process can be equated to the convolution of a point spread function and the radar high-resolution echo, as is shown in Equation (
1):
where
x represents the original radar high-resolution echo,
y represents the observed low-resolution radar echo,
n is the zero-mean Gaussian additive noise, and
A is the degenerate matrix, which encompasses the point-based diffusion function and downsampling.
The process of super-resolution reconstruction for weather radar echoes involves solving an underdetermined, inversed problem [
37]. The slight modification in input echo data, such as noise, receiver offset, and atmospheric perturbation, might have a significant impact on the reconstructed echoes. Over the years, various regularization methods [
38,
39,
40] have been proposed to solve the ill-posed problem, but these methods require manual modeling, and the accuracy of modeling affects the the quality of reconstruction results. To overcome these challenges, this paper utilizes deep convolutional neural networks (DCNNs) based on a data-driven approach for end-to-end radar data reconstruction. By learning the non-linear mapping relationship between low-resolution (LR) and high-resolution (HR) radar echoes from radar data without manual modeling, the super-resolution reconstruction has excellent generalization performance. The details of the network structure are described in
Section 3.
5. Results
To evaluate the accuracy of the reconstruction results of the RABPN model and validate its performance, two representative examples were selected for testing and were analyzed through visual and quantitative evaluations. Considering that catastrophic weather can be of great help to us in monitoring and providing early warning about medium- and small-scale extreme weather if early warnings can be carried out, this paper reconstructs the one-hour echo data, and the specific visualization results are shown in the
Appendix A and
Appendix B. To validate the performance of RABPN network, the visual results and the quantitative results by peak signal-to-noise ratio (PSNR)/structural similarity index (SSIM) were analyzed. LR radar echoes are generated by down-sampling HR radar echoes with specific scaling factors, PSF functions, and noise addition. The LR echoes were used as an input for the super-resolution reconstruction and the high-resolution echoes were obtained through the interpolation reconstruction learning method.
The selected case of the medium-scale weather system took place at 9:30 on 15 May 2016 in Heyuan, Guangdong, China and was characterized by intense precipitation with strong precipitation activity indicated in red (≥40 dBZ) in
Figure 9. On the other hand, the selected case of the small-scale weather system took place at 14:08 on 23 June 2016 in Yancheng, Jiangsu, China and involved a tornado event. This event is shown in the black box of
Figure 9, which displays a tornado vortex feature located at the end of the hook echo. The PPI map displays a strong reflectivity feature with an intensity of about 55 dBZ.
Visual Comparison. Visual comparisons on the scale factor ×2 and the scale factor ×4 is shown in
Figure 10 and
Figure 11. The scale factor ×2 represents a two-times increase in range and radial resolution of reflectivity, and the LR echoes’ resolution increased from algorithms increased from
to
; the scale factor ×4 represents 4 times increase in range and radial resolution of reflectivity, and the LR echoes’ resolution increased from
to
). As is shown in
Figure 10, the RABPN model outperforms interpolation-based methods in terms of recovering more detailed echo features in the precipitation process. The interpolation-based method tends to lose some important information in the strong echoes, leading to too smooth radar echoes. In comparison to other deep learning-based models, such as SRCNN (Super Resolution Convolutional Network) [
30], FSRCNN (Fast Super-Resolution Convolutional Neural Network) [
33], ESPCN (Efficient Sub-pixel Convolutional Neural Network) [
34], EDSR (Enhanced Deep Super-resolution Network) [
41], VDSR (Very Deep Convolutional Network) [
31], and DBPN (Deep Back-Projection Network) [
29], RABPN effectively captures the interrelationship between the low-resolution radar echoes and the original echoes, resulting in better recovery of detailed radar echo features and retention of more information from the original echoes. Although there may still be differences between the reconstructed echoes using RABPN and the original echoes, RABPN effectively recovers the texture features of the strong echo regions and highlights the locations of the strong echoes. This makes RABPN a valuable tool for researching and forecasting heavy precipitation weather.
Tornadoes are small-scale convective vortexes produced under unstable weather conditions, with short lifespans and high catastrophic potential. Most tornadoes, especially those above EF-2, occur mainly in supercell storms, and the hook echo is the region where tornadoes can occur in supercell thunderstorms [
54]. The tornado vortex feature can serve as an early warning signal, characterized by a strong reflectivity feature on the PPI map (approximately 55 dBZ), as shown in the black box in
Figure 11, which exhibits a strong reflectivity feature on the PPI map with an intensity of about 55 dBZ. However, the limited resolution of the CINRAD-SA radar often hinders the effective observation of the tornado formation and termination process. By reconstructing the hook echo and vortex features as accurately as possible, we can improve the monitoring and providing early warnings for tornado weather conditions.
For a scale factor ×2, the neural network-based method can recover a portion of the hook echoes and can restore information on the edge details of the echo structure compared to the interpolation-based method. For scale factor ×4, most comparison methods produce blurred results; however, RABPN can recover more echo details and hook features. Despite being unable to recover the detailed structure of the hook echo compared to the original radar echo at both scale factors, RABPN is still able to accurately recover the hook echo and highlight the location of strong echoes. This makes it great helpful for our monitoring and providing early warning of small-scale extreme disaster weather, such as tornadoes.
Quantitative results by PSNR/SSIM. PSNR and SSIM [
55] were selected to verify the reconstruction quality of radar echo and the similarity with the original echo resolution, respectively. The radar echo size is
,
denotes the original high-resolution echo, and
denotes the reconstructed echo, then the PSNR has the following definition:
PSNR measures the reconstruction quality by quantifying the difference between the original and reconstructed radar echoes, with higher values indicating better performance. Considering the correlation between adjacent distance library values and the perceptual properties of the human visual system, the paper uses the SSIM metric to evaluate the structural characteristics of the echoes, as is shown in Equation (
18).
where
and
denote the mean values of the original high-resolution echo and the reconstructed echo, respectively.
and
denote the standard deviation of the original high-resolution and reconstructed echoes, respectively.
denotes the covariance between the two.
and
denote two constants to avoid the denominator being zero and maintain the stability of the results. SSIM values range from 0 to 1, where a higher value indicates closer similarity between the original and reconstructed radar echoes in terms of structure. The results of the comparison for scale factors ×2 and ×4 is presented in
Table 4.
To further validate the effectiveness of RABPN, we compared the proposed RABPN with various SR methods under different weather conditions, such as medium- and small-scale weather systems, and the results showed that RABPN achieved the highest PSNR and SSIM values, indicating that RABPN has better performance. When considering the scale factor ×2, the PSNR values of RABPN are up to 0.14 dB and 0.31 dB higher than DBPN on precipitation and tornado data, respectively; for the scale factor ×4, the PSNR values of RABPN are up to 0.68 dB and 0.72 dB higher than DBPN on precipitation and tornado data, respectively. The comparisons indicates that CAM and the network depth improve the performance. Moreover, since tornadoes have obvious echo characteristics, our network achieves better results in the tornado case than in the precipitation case by utilizing CAM to emphasize the information characteristics of the strong radar echo region. This result demonstrate that networks with more representational ability can extract more sophisticated features from the LR radar echoes. When the scaling factor is large, LR radar echoes contain minimal information for SR radar echoes. Losing most high-frequency information makes reconstructing informative results difficult for SR methods.
6. Conclusions
The purpose of this paper was to enhance the spatial resolution of weather radar data. To achieve this goal, CINRAD-SA reflectivity data were used as the training set for a network model, and using RABPN for super-resolution reconstruction of individual cases of small- and medium-scale weather. Through constant parameter tuning, network structure optimization, and continuous debugging, the following main conclusions were drawn:
(1) For precipitation cases, RABPN can recover fine echo edges and details in the scaling factor ×2 and the scale factor ×4, achieving fine reconstruction of the structure of weak and strong echo regions. The results of the quantitative analysis showed that RABPN outperformed other compared super-resolution reconstruction methods in terms of PSNR and SSIM values, demonstrating that the algorithm had superior reconstruction performance and a closer similarity to the original echo structure. This is of great significance for monitoring and providing early warning about catastrophic weather processes.
(2) For the tornado case, RABPN can effectively recover the hook echo characteristics of the tornado, enabling the reconstructed hook echoes to be closer to the real radar echoes. Additionally, RABPN can reasonably recover the strong echo information with echo intensity values above 55 dBZ. Compared with other networks, RABPN has better performance in highlighting strong echoes.
RABPN is composed of multiple residual attention groups (RAG) and residual attention blocks (RAB), which utilize long and short skip connections, respectively, to enable the network to reach a significant depth. Furthermore, by adding the channel attention mechanism to the network means that the concerns between the different channels change for the low- and high-frequency information. Unlike previous CNN algorithms for weather radar that rely on radar image reconstruction, this paper adopts raw radar data in order to preserve crucial information in the weather radar echoes.
Extensive results illustrated that our proposed network provides a more nuanced view of the internal structure of the echoes and clearer edge details compared with the previous CNN radar image reconstruction, particularly in the scaling factor. It is worth noting that the vertical structure of radar is essential for the in-depth study of the generation and elimination process of disastrous weather. Currently, the majority of focus in this research area is on reconstructing the horizontal structure, and the application of vertical structure in the weathering process leaves much to be desired. In the future, deep learning algorithms have the potential to enhance the resolution of vertical structure data, enable multi-radar super-resolution data fusion, and generate high spatial and temporal resolution vertical structure data.