Accuracy Assessment of the Positioning of a Swarm of Underwater Vehicles in Relation to Four Surface Vehicles Using the TDOA Method

Abstract

This paper presents the results of research on the accuracy assessment of the positioning of a swarm of underwater vehicles based on hydroacoustic measurements made with respect to four surface vehicles under the time difference of arrival (TDOA) method. The assessment consisted of the estimation of accuracy parameters for determining the position of an underwater vehicle in relation to surface vehicles forming a so-called moving geometrical measurement structure (MGMS) in the following shapes: square, rectilinear, triangular, and three-pointed. This demonstrated that MGMS makes it possible to estimate the relative position of underwater vehicles in a swarm with an accuracy of 2.1 m (RMS) over an area of approx. 1000 m² and approx. 3.0 m (RMS) over an area of approx. 1600 m². The most favourable MGMS shapes include three-pointedwhile maximising the size of the positioning area, where the positioning accuracy should not exceed 3.0 m (RMS)—and rectilinear—while maximising the size of the positioning area, where the positioning accuracy should not exceed 10.0 m (RMS).

1. Introduction

Modern underwater vehicles require precise positioning in the wide range of their operations [1,2]. Most often, they use an external hydroacoustic system of the long baseline (LBL) type for this purpose [3,4,5,6]. LBL operation is based on measuring the distance between the transceiver node and the vehicle to be located. Hence, the location of vehicles based on distance measurement depends on the accuracy of the distance measurement and the calibration of the transceiver node position. Currently, there are three most commonly used distance measurement methods: time of arrival (TOA), time difference of arrival (TDOA), received signal strength indicator (RSSI) and angle of arrival of the received signal (angle of arrival—AOA) [7,8,9,10,11]. Due to the high variability of acoustic signal propagation conditions in aquatic environments, it is difficult to obtain an accurate RSSI value [11,12]. On the other hand, the measurement of AOA requires the use of very expensive directional antennas of large sizes [13,14]. TOA and TDOA measurements are currently the most widely used, primarily due to the fact that the speed of sound propagation in water is low (about 1500 m/s) and there is no need to receive signals with high time resolutions. Nevertheless, the measurement of TOA requires the time synchronization of the LBL transmitting system and the receiving system mounted on an underwater vehicle, which is difficult to implement in an aquatic environment.

LBL based on TDOA measurements in operation can ensure the accurate positioning of an underwater vehicle in a given area without cumulative time function errors [15,16,17,18,19].

Regretfully, its classical form is not necessarily a good solution for submersible vehicles operating in a swarm over a large sea area for several main reasons. First, this is due to the very high cost of hydroacoustic system infrastructures that consist of a network of transceiver nodes (so-called transceivers deployed on the seabed) that must cover the entire area. Second, only one vehicle at a time may use the exposed network of infrastructure nodes. Third, this is due to the nature of vehicle positioning in a swarm, wherein it is more important to maintain an accurate position relative to the leader rather than relative to the Earth. Therefore, it seems fully reasonable to use so-called mobile hydroacoustic systems, the nodes of which are deployed on floating surface vehicles, for the positioning of underwater vehicles in a swarm. These vehicles, then acting as nodes of such a positioning system, have the following tasks: maintaining a fixed position relative to one another and transmitting acoustic impulses at fixed synchronised moments, e.g., pulse per second (PPS) global navigation satellite system (GNSS) signals [20]. The underwater vehicles determine their position relative to each other based on time difference of arrival (TDOA) measurements of the received acoustic pulses. The positioning accuracy of a swarm of underwater vehicles then depends primarily on the following:

• The way the surface vehicles are positioned in relation to one another (the shape of the so-called geometrical measurement structure formed by the nodes);
• The ability to keep the surface vehicles in motion in a constant position in relation to one another (not distorting the shape of the measurement structure while all its nodes are moving in parallel).

Given that surface vehicles can be equipped with very accurate navigation systems (using, e.g., GNSS real-time kinematic (RTK) receivers for positioning) and very precise propulsion and steering systems, only the geometric shape of the measurement structure—determined according to the size, shape, and relative position of the swarm of underwater vehicles—remains as the main determinant of the positioning accuracy.

Thus, it is reasonable to evaluate the proposed methodology for positioning underwater vehicles relative to surface vehicles in terms of accuracy in the context of the possibility of its future implementation for use.

The innovativeness of the assessed methodology consists primarily of the use of various shapes of a movable geometric measurement structure based on surface vehicles for the passive positioning of a swarm of underwater vehicles. The underwater vehicles determined their positions solely on the basis of time differences of sequentially received acoustic pulses sent by surface vehicles. The time synchronization of the underwater vehicles with the surface vehicles was not needed for positioning. Maintaining the expected level of the positioning accuracy of the underwater vehicles in a given area was achieved by selecting the appropriate shape of the mobile geometric measurement structure.

Due to the excessive number of measurements of time differences (position lines in the form of hyperboloids), the determination (estimation) of position coordinates in this study was carried out using the geodetic least-squares adjustment (GLSA) method. This method eliminates the limitations of the methods proposed, e.g., by Y.T. Chan [21], B.T. Fang [22], and W.H. Foy [23], i.e., the ambiguity of the solution—in the case of Y.T. Chan—and the possibility of using only three transmitting systems—in the case of B.T. Fang and W.H. Foy.

The GLSA method allows for relative positioning in a local area [24]. However, it should be borne in mind that its convergence and computational accuracy are strongly related to the geometrical shape of the measuring system [25,26].

This paper presents a study on the accuracy analysis of the positioning of a swarm of underwater vehicles in accordance with the TDOA method relative to four surface vehicles.

In the first part, the idea of positioning a swarm of underwater vehicles relative to surface vehicles in accordance with TDOA is presented. Against this background, a method for estimating the position and its accuracy based on hydroacoustic measurements of distance differences made between the underwater vehicle and the surface vehicles is proposed.

In the second part, research is described that consisted of estimating the accuracy parameters of the estimated position of a submersible vehicle on the basis of simulated results of distance difference measurements performed in relation to four surface vehicles. As a result, four tests were carried out for the most representative, in terms of measurement, shapes of the so-called moving geometrical measurement structure formed by the surface vehicles, i.e., square, rectilinear, triangular, and three-pointed.

The third part is a detailed analysis of the obtained test results conducted in terms of the accuracy assessment of the position estimation based on maps with accuracy areas, charts with mean error distributions, and a summary of test area percentages for the selected accuracy levels.

Based on this, the final section draws generalised conclusions regarding the selection of the shape of the mobile geometric survey structure created by the surface vehicles, taking into account the size and shape of the swarm of underwater vehicles and the expected level of the positioning accuracy in the relevant area. It also presents directions for further developmental research related to the issues discussed in this article.

2. Materials and Methods

It was assumed that the autonomous underwater vehicles (AUVs) were to swim in a swarm whilst maintaining a fixed position relative to autonomous surface vehicles (ASVs). Relative positioning was carried out using a hyperbolic hydroacoustic positioning system (HHPS) with transmitting systems (transceivers) placed, for example, on four ASVs, and receiving systems (transponders) placed on all AUVs in the swarm (Figure 1).

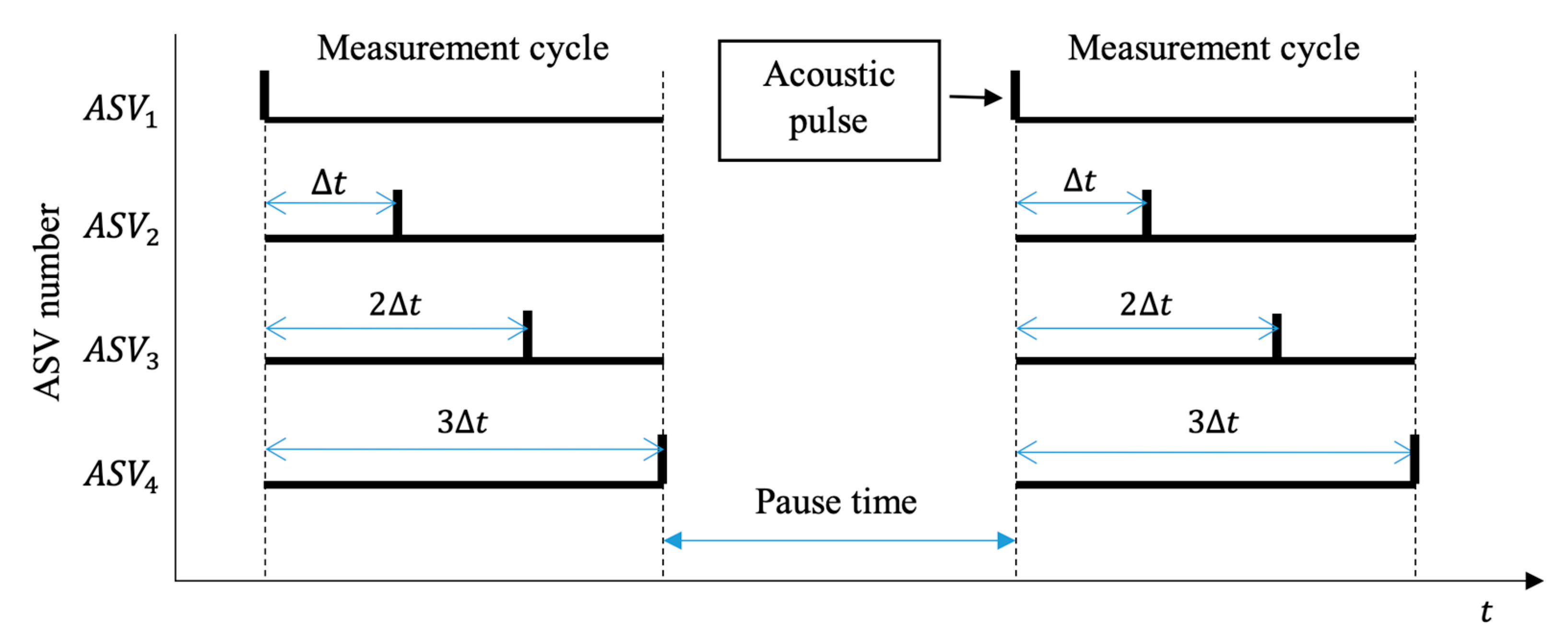
The transmitting systems operated at the same frequency in so-called measurement cycles (Figure 2). Each measurement cycle was preceded by a time pause identifiable to the receiving systems. Each transmitting system transmitted an acoustic signal (acoustic pulse) only once in a measurement cycle at a synchronised time moment fixed for it, for instance, pulse per second—PPS signal GNSS [20]—or chip-scale atomic clock—CSAC [27].

The receiving systems determined the time differences between the matched acoustic signals (acoustic pulses) sent by the transmitting systems in one measurement cycle, taking into account their known time offset Δt. From this, the following was calculated:

$$n_{\Delta d}=\frac{n!}{2!·\left(n-2\right)!}$$

(1)

Differences in distances $\Delta d^m$ to the paired n transmitting systems (in the considered case, four) in all possible combinations (without repetitions) were calculated according to the relation:

$$\Delta d_i^m=d_{\left(1,i\right)}^m-d_{\left(2,i\right)}^m=c·\left(t_{\left(1,i\right)}-t_{\left(2,i\right)}\right) \mathrm{for} i=1, 2, \dots , n_{\Delta d},$$

(2)

where:

• $c$—the speed of sound propagation in water, most often modelled by three parameters: temperature, salinity, and pressure [28,29,30,31,32];
• $\left(t_{\left(1,i\right)}-t_{\left(2,i\right)}\right)$—the measured difference in transit time of the acoustic signal in water from the $i$th pair of transmitting systems to the receiving system.

Let us now assume that $AS{V}_2$, $AS{V}_3$ and $AS{V}_4$ flowed while maintaining as accurately as possible the predetermined navigational parameters of the bearings (B₂₁, B₃₁ and B₄₁) and distances (D₂₁, D₃₁ and D₄₁) to $AS{V}_1$ as accurately as possible and that the so-called “moving” geometric measuring structure (MGMS) composed of transmitting systems maintained a constant shape and an unchanging angular orientation with respect to north (Figure 3).

The AUVs flowing in the swarm were positioned relative to the MGMS. Each AUV was tasked with maintaining the fixed coordinates of its position in the local coordinate system (LCS). In accomplishing this task, it used the HHPS to take time-difference measurements and then, based on these, determined the coordinates of its position.

At this point, two scientifically relevant questions can be asked regarding the positioning accuracy of the swarm of underwater vehicles relative to the four surface vehicles according to the proposed concept, namely:

1.

With what accuracy can the position coordinates of the AUVs be determined?

2.

How does a change in the geometrical shape of the survey structure affect the accuracy of determining the position coordinates of the AUVs?

In order to obtain a meaningful answer to the questions posed in this way, it was first necessary to select the most appropriate mathematical method for calculating (estimating) the position coordinates and assessing their accuracy.

Taking into account the so-called redundant number of time-difference measurements (of position lines in the form of hyperboloids) and the limitations of the methods proposed, it was reasonable to determine (estimate) the position coordinates by relying on the geodetic adjustment method GLSA.

Once the position coordinates, $AS{V}_1$ $\left(0, 0, 0\right)$, bearings (B₂₁, B₃₁ and B₄₁), and distances (D₂₁, D₃₁, and D₄₁) were known, the “fixed” position coordinates, $AS{V}_2$, $AS{V}_3$, and $AS{V}_4$, could be calculated, which, in combination with the approximate coordinates $\left(x_{AUV},y_{AUV},z_{AUV}\right)$ of the position of any AUV, allowed the formation of the following system of non-linear distance difference equations:

$$\begin{array}{c}\Delta d_1=d_{\left(1,1\right)}-d_{\left(2,1\right)}=\sqrt{{\left(x_{AUV}-x_{\left(1,1\right)}\right)}^2+{\left(y_{AUV}-y_{\left(1,1\right)}\right)}^2+{\left(z_{AUV}-z_{\left(1,1\right)}\right)}^2}-\\ -\sqrt{{\left(x_{AUV}-x_{\left(2,1\right)}\right)}^2+{\left(y_{AUV}-y_{\left(2,1\right)}\right)}^2+{\left(z_{AUV}-z_{\left(2,1\right)}\right)}^2}\\ \Delta d_2=d_{\left(1,2\right)}-d_{\left(2,2\right)}=\sqrt{{\left(x_{AUV}-x_{\left(1,2\right)}\right)}^2+{\left(y_{AUV}-y_{\left(1,2\right)}\right)}^2+{\left(z_{AUV}-z_{\left(1,2\right)}\right)}^2}-\\ -\sqrt{{\left(x_{AUV}-x_{\left(2,2\right)}\right)}^2+{\left(y_{AUV}-y_{\left(2,2\right)}\right)}^2+{\left(z_{AUV}-z_{\left(2,2\right)}\right)}^2}\\ \\ \Delta d_{n_k}=d_{\left(1,n_k\right)}-d_{\left(2,n_k\right)}=\sqrt{{\left(x_{AUV}-x_{\left(1,n_k\right)}\right)}^2+{\left(y_{AUV}-y_{\left(1,n_k\right)}\right)}^2+{\left(z_{AUV}-z_{\left(1,n_k\right)}\right)}^2}-\\ -\sqrt{{\left(x_{AUV}-x_{\left(2,n_k\right)}\right)}^2+{\left(y_{AUV}-y_{\left(2,n_k\right)}\right)}^2+{\left(z_{AUV}-z_{\left(2,n_k\right)}\right)}^2}\end{array}\}.$$

(3)

Linearising the equations by their expansions into Taylor series restricted to the first words, a matrix of coefficients could be formed:

$$\begin{array}{l}\mathbf{A}=\left[\begin{array}{ccc}\frac{\partial \Delta d_1}{\partial x_{AUV}}& \frac{\partial \Delta d_1}{\partial y_{AUV}}& \frac{\partial \Delta d_{1,}}{\partial z_{AUV}}\\ \frac{\partial \Delta d_2}{\partial x_{AUV}}& \frac{\partial \Delta d_2}{\partial y_{AUV}}& \frac{\partial \Delta d_2}{\partial z_{AUV}}\\ ⋮& ⋮& ⋮\\ \frac{\partial \Delta d_{n_k}}{\partial x_{AUV}}& \frac{\partial \Delta d_{n_k}}{\partial y_{AUV}}& \frac{\partial \Delta d_{n_k}}{\partial z_{AUV}}\end{array}\right]=\\ =\left[\begin{array}{ccc}\frac{x_{AUV}-x_{\left(1,1\right)}}{d_{\left(1,1\right)}}-\frac{x_{AUV}-x_{\left(2,1\right)}}{d_{\left(2,1\right)}}& \frac{y_{AUV}-y_{\left(1,1\right)}}{d_{\left(1,1\right)}}-\frac{y_{AUV}-y_{\left(2,1\right)}}{d_{\left(2,1\right)}}& \frac{z_{AUV}-z_{\left(1,1\right)}}{d_{\left(1,1\right)}}-\frac{z_{AUV}-z_{\left(2,1\right)}}{d_{\left(2,1\right)}}\\ \frac{x_{AUV}-x_{\left(1,2\right)}}{d_{\left(1,2\right)}}-\frac{x_{AUV}-x_{\left(2,2\right)}}{d_{\left(2,2\right)}}& \frac{y_{AUV}-y_{\left(1,2\right)}}{d_{\left(1,2\right)}}-\frac{y_{AUV}-y_{\left(2,2\right)}}{d_{\left(2,2\right)}}& \frac{z_{AUV}-z_{\left(1,2\right)}}{d_{\left(1,2\right)}}-\frac{z_{AUV}-z_{\left(2,2\right)}}{d_{\left(2,2\right)}}\\ ⋮& ⋮& ⋮\\ \frac{x_{AUV}-x_{\left(1,n_k\right)}}{d_{\left(1,n_k\right)}}-\frac{x_{AUV}-x_{\left(2,n_k\right)}}{d_{\left(2,n_k\right)}}& \frac{y_{AUV}-y_{\left(1,n_k\right)}}{d_{\left(1,n_k\right)}}-\frac{y_{AUV}-y_{\left(2,n_k\right)}}{d_{\left(2,n_k\right)}}& \frac{z_{AUV}-z_{\left(1,n_k\right)}}{d_{\left(1,n_k\right)}}-\frac{z_{AUV}-z_{\left(2,n_k\right)}}{d_{\left(2,n_k\right)}}\end{array}\right]\end{array}$$

(4)

Based on this, the estimator of the AUV coordinate increment vector could be easily calculated by taking recourse to the geodesic least-squares adjustment method (assuming a redundant number of distance difference measurements, i.e., $n_k>3$):

$${\hat{\Delta }}_{AUV}=\left[\begin{array}{c}{\widehat{\Delta x}}_{AUV}\\ {\widehat{\Delta y}}_{AUV}\\ {\widehat{\Delta z}}_{AUV}\end{array}\right]=-{\left(A^{\mathrm{T}}·P·A\right)}^{-1}{A}^{\mathrm{T}}·P·L$$

(5)

where:

• $L=\left[\begin{array}{c}\Delta d_1-\Delta d_1^m\\ \Delta d_2-\Delta d_2^m\\ ⋮\\ \mathsf{\Delta }{d}_{n_k}-\Delta d_{n_k}^m\end{array}\right]$—residual vector;
• $P=\left[\begin{array}{cccc}\frac{1}{{\left(m_1\right)}^2}& 0& 0& 0\\ 0& \frac{1}{{\left(m_2\right)}^2}& 0& 0\\ 0& 0& \ddots & 0\\ 0& 0& 0& \frac{1}{{\left(m_{n_k}\right)}^2}\end{array}\right]$—weight matrix;
• $d_i^m$—ith distance difference calculated from the time difference $\left(t_{\left(1,i\right)}-t_{\left(2,i\right)}\right)$ taking into account the time offset $\Delta t$ via formula (2);
• $m_i$—mean error of the distance difference measurement $d_i^m$.

The vector of increments ${\hat{\Delta }}_{AUV}$ calculated in this way could then be used to estimate the AUV position coordinates according to the formula:

$$\left[\begin{array}{c}{\widehat{x}}_{AUV}\\ {\widehat{y}}_{AUV}\\ {\widehat{z}}_{AUV}\end{array}\right]=\left[\begin{array}{c}{x}_{AUV}\\ y_{AUV}\\ z_{AUV}\end{array}\right]+\left[\begin{array}{c}{\widehat{\Delta x}}_{AUV}\\ {\widehat{\Delta y}}_{AUV}\\ {\widehat{\Delta z}}_{AUV}\end{array}\right].$$

(6)

In order to assess the accuracy of their determination, the distance difference correction vector ${\widehat{\Delta }}_d$ must be estimated according to the formula:

$${\widehat{\Delta }}_d=\left[\begin{array}{c}{\widehat{\Delta d}}_1\\ {\widehat{\Delta d}}_2\\ ⋮\\ {\widehat{\Delta d}}_{n_k}\end{array}\right]=A·{\widehat{\Delta }}_{AUV}+L,$$

(7)

which helps one, in turn, to determine the variance ratio estimator:

$${\hat{m}}_0^2=\frac{{\hat{\Delta }}_d^{\mathrm{T}}P{\hat{\Delta }}_d}{n_k-k},$$

(8)

where:

• $k$—the number of unknowns (equal to 3 for 3D positioning).

By using ${\hat{m}}_0^2$, the covariance matrix estimator could be calculated according to the relation:

$${\hat{C}}_{AUV}={\hat{m}}_0^2·{\left(A^{\mathrm{T}}·P·A\right)}^{-1}.$$

(9)

Given the values of the elements located on the diagonal ${\hat{C}}_{AUV}$ (the trace of the matrix), the mean error of the estimated coordinates of the position of the AUV receiving system could be easily calculated with the following relation:

$$M_{AUV}=\sqrt{\mathrm{Tr}\left({\hat{C}}_{AUV}\right)}.$$

(10)

In turn, the calculated values of the matrix elements $E_{AUV}$ were determined as follows:

$$E_{AUV}=A^{\mathrm{T}}·P·A=\left[\begin{array}{cc}{E}_{AUV}^x& E_{AUV}^{xy}\\ E_{AUV}^{xy}& E_{AUV}^y\end{array}\right],$$

(11)

The above formula made it possible to determine the parameters of the confidence ellipse of the estimated 2D position coordinates (in the XY plane) of the AUV. The formulae for calculating the lengths of the half-axes, $a$, $b$, and the rotation angle, $\theta$, of the half-axis, a, can then be presented in the following form:

$$a={\hat{m}}_0\sqrt{2·{\alpha }_1{}^{-1}·F_{\gamma }},$$

(12)

$$b={\hat{m}}_0\sqrt{2·{\alpha }_2{}^{-1}·F_{\gamma }},$$

(13)

$$\theta =atan\left(\frac{2·E_{AUV}^{xy}}{E_{AUV}^x-E_{AUV}^y}\right)/2$$

(14)

where:

• ${\alpha }_1=\frac{E_{AUV}^x+E_{AUV}^y-\sqrt{{\left(E_{AUV}^x-E_{AUV}^y\right)}^2+4·E_{AUV}^{xy}{}^2}}{2}$,
• ${\alpha }_2=\frac{E_{AUV}^x+E_{AUV}^y+\sqrt{{\left(E_{AUV}^x-E_{AUV}^y\right)}^2+4·E_{AUV}^{xy}{}^2}}{2}$,
• $F_{\gamma }$—the value for which $P\left(F_{2,n_k-k}\le F_{\gamma }\right)$ equals the expected probability $\gamma$ in an F-Snedecor distribution [33].

Based on the mathematical relationships presented (3)–(14), simulation studies were carried out to assess the positioning accuracy of a swarm of underwater vehicles relative to four surface vehicles. A description of these studies and an analysis of their results is presented in the following section.

3. Results

An in-house software application prepared in the integrated development environment C++ Builder [34] with the template library package for linear algebra Eigen [35] installed was used to carry out the simulation studies. It was designed to perform simulation calculations taking into account the following assumed principles of HHPS operation in the transmitter–receiver system relationship:

• The acoustic signal must be received from the four transmitting systems for the position to be calculated;
• The receiving system knew the local coordinates of the position of the transmitting systems ($AS{V}_1$ determined the origin of the local coordinate system);
• The receiving system did not change its position during the measurement cycle;
• The acoustic signal emitted with the omni-directional antenna by the transmitting system was propagated in all directions in the same way;
• There were no obstacles in the path of the acoustic signal (acoustic beam), i.e., the transmitting antenna could “see” the receiving antenna (line of sight (LOS) communication);
• The transmitting systems generated the acoustic signal cyclically with a fixed time offset (this offset was known for the receiving system);
• The receiving system determined the difference in the time of reception of the acoustic signals transmitted by the individual transmitters in one cycle;
• The receiving system did not know the transmission time of the acoustic signal.

The study consisted of estimating the accuracy parameters of the AUV position based on simulated results of distance difference measurements performed with respect to the four ASVs forming the MGMS in the selected most representative geometrical shapes, i.e., square, rectilinear, triangular, and three-pointed. In the calculations, it was arbitrarily assumed that the mean error of the measurement of the $i$th distance difference $m_i=3 \mathrm{m}$. Thus, it was assumed that the ASVs were able to maintain their position relative to each other with an mean error of no more than 1.5 m (e.g., they used a dynamic positioning system [36] equipped with a GNSS RTK receiver coupled via an autopilot to a precision drive and control system for this purpose). The calculations also arbitrarily assumed that the estimator of the variance coefficient ${\hat{m}}_0^2=1$, i.e., the value of $m_i$, was estimated “perfectly”.

The test area was a square with sides equal to 3000 m. At its geometric centre was the MGMS. The distance between each node of the MGMS was 1000 m. The transmitting and receiving systems were located at the same depth, i.e., $z_{\left(1,i\right)}=z_{\left(2,i\right)}=z_{AUV}$. Thus, on the one hand, it was assumed that the AUV would determine its draught with a much higher accuracy (even centimetres) with the hydrostatic pressure sensor [37] than with the HHPS, and, on the other hand, it was assumed that the test results could be presented on a plane—this would undoubtedly simplify both their presentation and facilitate their interpretation.

The result of a single simulation test conducted for a specific geometric shape of the MGMS (adjustment of surface vehicles with respect to each other) was a set of groups of values representing the mean position error, $M_{AUV}$, and the confidence ellipse parameters: $a$, $b$, and $\theta$. These values were determined according to relations (3)–(14) separately for each node of the regular grid of squares “GRID” representing the test area in a discrete manner with a resolution of one metre (in this area, there may be a swarm of underwater vehicles).

On the basis of the GRIDs thus obtained, the following were prepared:

• Maps with accuracy areas determined by the inverse distance weighting interpolation method [38] (power = 2, number of points (nodes) taken for interpolation = 12) with error ellipses superimposed on them at selected locations (p = 0.68);
• Graphs with interval distributions of the frequency of occurrence of the mean error (not exceeding the 20 m value);
• A table describing the percentage of the test area in which the mean error in the determination of position coordinates did not exceed 3 m and 10 m.

These were ultimately used to evaluate the comparative positioning accuracy of the AUVs against MGMS in the shapes selected for testing.

It should be noted that these studies omitted special cases (which cannot be excluded), e.g., when the dynamic positioning systems [39] of the ASVs would not have been able to counteract external forces such as wind, waves, or sea currents. The inevitable consequences of such a situation would certainly be, firstly, a sharp increase in the value of the average error of measuring the distance difference, and secondly, a significant decrease in the accuracy of determining the position of the AUVs.

One of the solutions to this problem may be the identification, suppression, or elimination of measurements of distance differences with gross error on the AUVs side. However, this task may be difficult to perform due to the need to have redundant measurements ($n_k>3$) used in calculating the coordinates of the AUVs. Thus, it may be reasonable to create a MGMS composed of more than four ASVs in this solution.

Another solution to this problem (only on the transmitting side) may be to use a time shift of the moment of transmitting the acoustic impulse corresponding to the ASV path vector to the assumed reference position. This solution seems to be better considering the fact that it does not require increasing the number of ASVs that make up the MGMS.

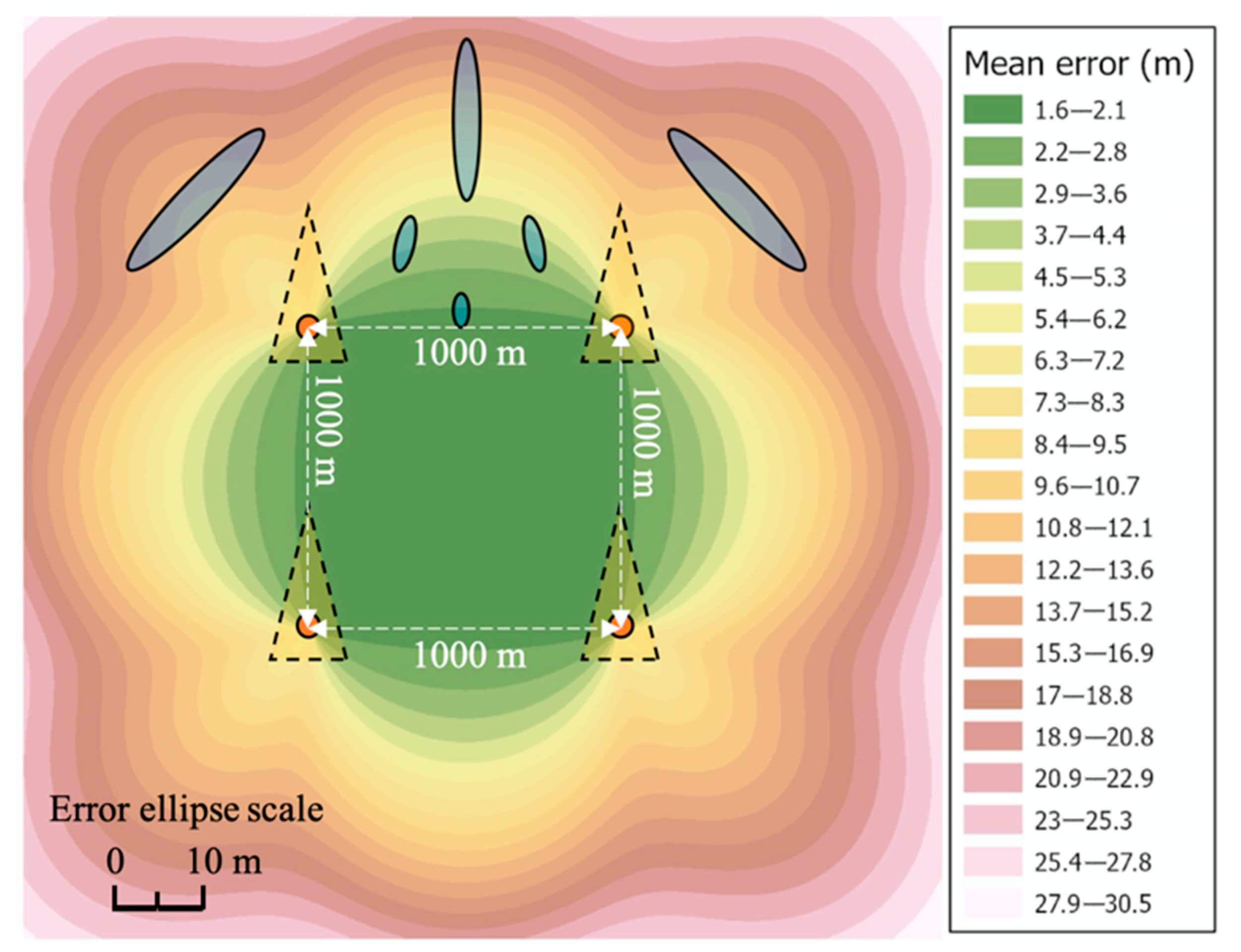
3.1. Test No. 1

Figure 4 shows a map with accuracy areas and error ellipses for the MGMS in a square shape.

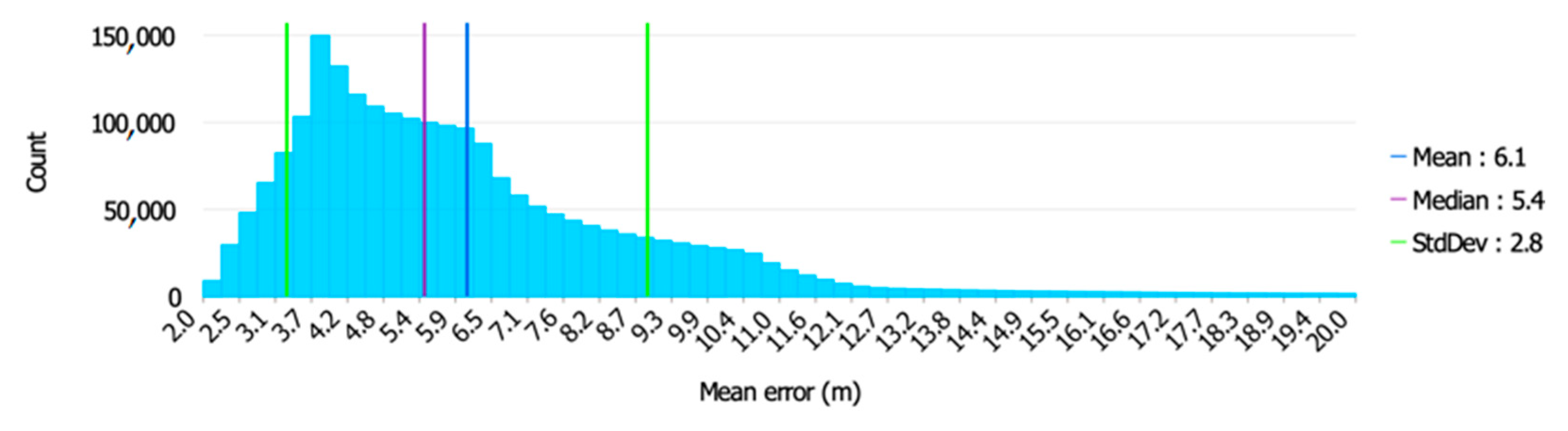
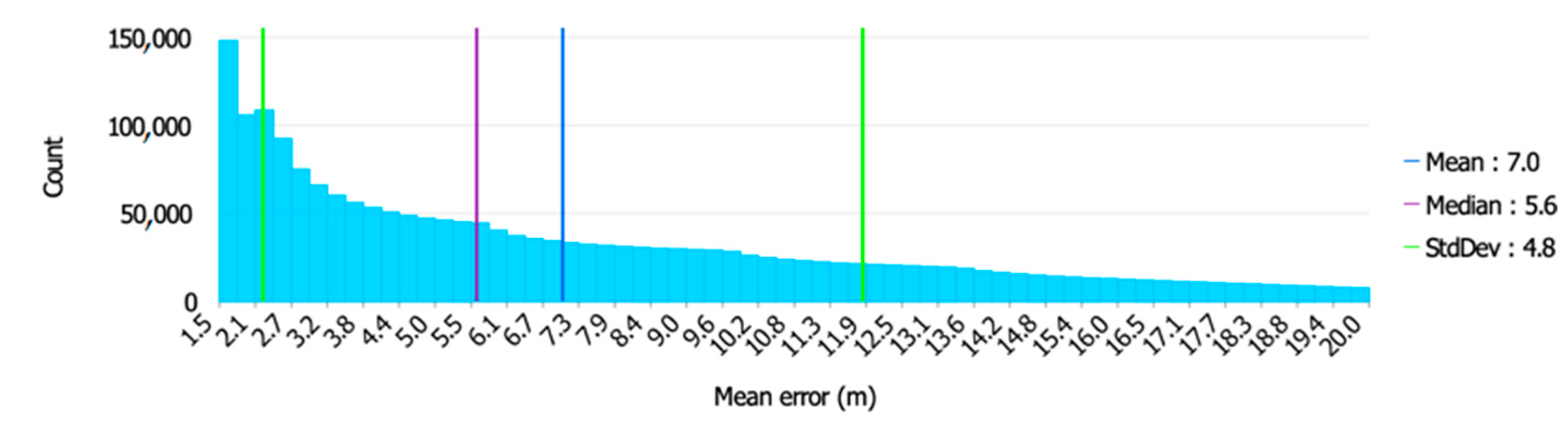
Figure 5 shows the accuracy distribution for the square-shaped MGMS.

3.2. Test No. 2

Figure 6 shows a map with accuracy areas and error ellipses for a rectilinear-shaped MGMS.

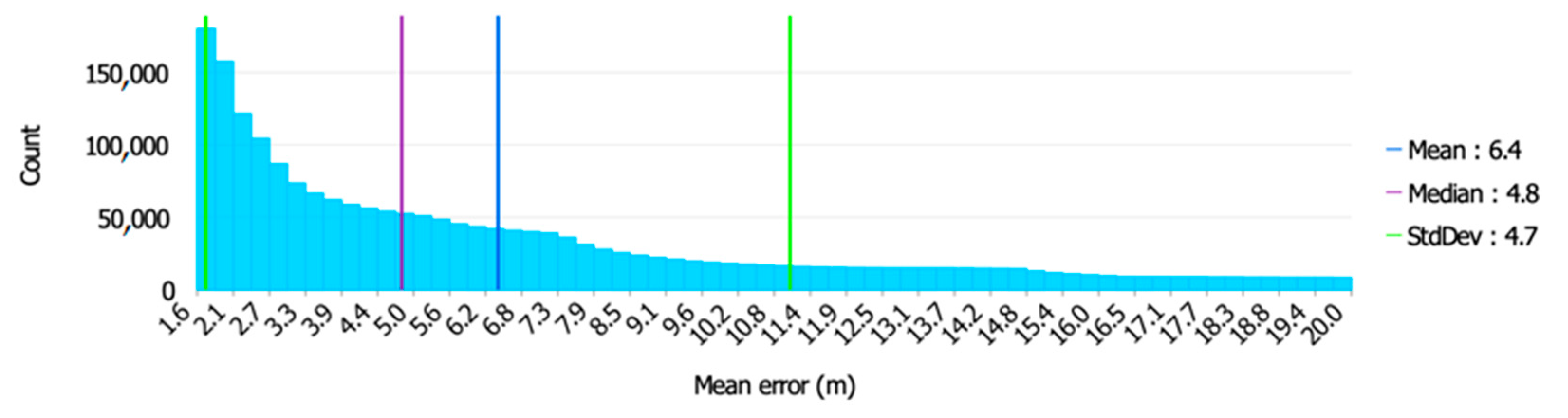
Figure 7 shows the accuracy distribution for the rectilinear-shaped MGMS.

3.3. Test No. 3

Figure 8 shows a map with accuracy areas and error ellipses for a triangular-shaped MGMS.

Figure 9 shows the accuracy distribution for the triangular-shaped MGMS.

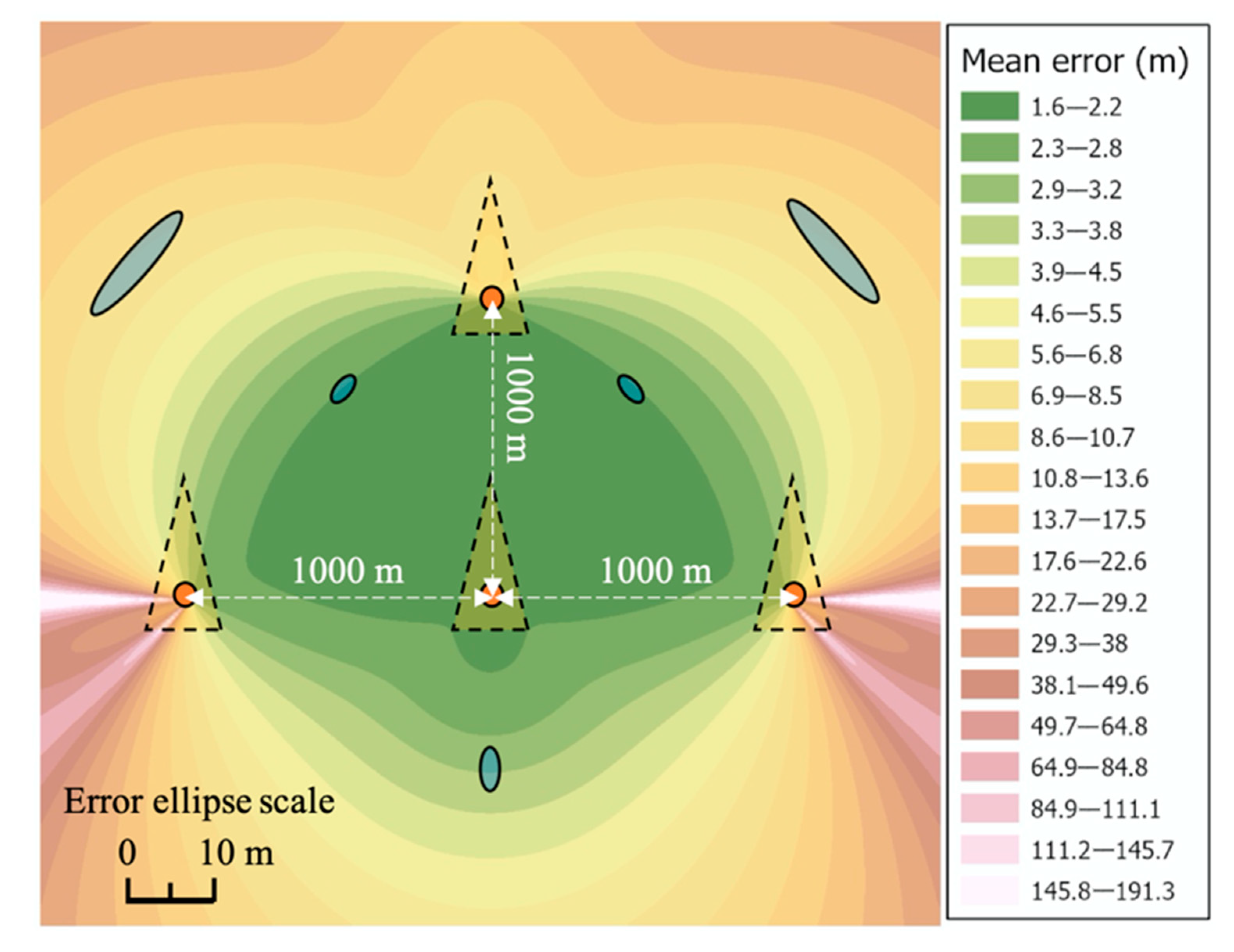
3.4. Test No. 4

Figure 10 shows a map with accuracy areas and error ellipses for a three-pointed MGMS.

Figure 11 shows the accuracy distribution for the three-pointed MGMS.

Table 1. Percentage of the test area where $M_{AUV}<3 \mathrm{m}$ and $M_{AUV}<10 \mathrm{m}$.

Shape of MGMS	Part of the Test Area Where ${\mathit{M}}_{\mathit{A}\mathit{U}\mathit{V}}<3 \mathbf{m}$ (%)	Part of the Test Area Where ${\mathit{M}}_{\mathit{A}\mathit{U}\mathit{V}}<10 \mathbf{m}$ (%)
Square	17.6	41.9
Rectilinear	5.5	86.9
Triangular	24.1	67.0
Three-pointed	28.8	73.5

shows the percentage of the test area in which the mean error of position coordinate determination with $M_{AUV}$ did not exceed 3 m and 10 m.

4. Discussion

Analysing the maps with the accuracy areas shown in Figure 4, Figure 6, Figure 8, and Figure 10 more broadly, it should be noted that the square and triangular-shaped MGMS guaranteed a high positioning accuracy ($M_{AUV}<2.8 \mathrm{m}$) inside them. On the other hand, directing attention to the entire test area, it should be noted that the $M_{AUV}$ values with the smallest amplitude, falling within the ranges $\langle 1.6 \mathrm{m};30.5 \mathrm{m}\rangle$ and $\langle 1.7 \mathrm{m};42.9 \mathrm{m}\rangle$, were characteristic of the square-shaped MGMS and the three-pointed MGMS. For the outer area of the square-shaped MGMS, it is also important to note the very flat shapes of the error ellipses. This spread of positions will result in submersibles at cardinal heading angles moving away from or closer to the MGMS and a large difference in the angular position of submersibles at intercardinal heading angles relative to the MGMS. It should also be emphasised that for both rectilinear and triangular-shaped MGMS, there were locations in the test area where $M_{AUV}>190 \mathrm{m}$. These sites extended along the line where three and four ASVs were located.

However, when comparing the accuracy distributions shown in Figure 5, Figure 7, Figure 9, and Figure 11 with each other, it should be noted that the three-pointed MGMS stood out with a numerical predominance of $M_{AUV}$ with small values, while the square-shaped MGMS stood out with a numerical predominance of $M_{AUV}$ with large values. The mean value of $M_{AUV}$ was most favourable for the rectilinear-shaped MGMS and least favourable for the square-shaped MGMS. For the standard deviation of the $M_{AUV}$, the rectilinear-shaped MGMS was also the most favourable with a value of only 2.8 m (indicating a high clustering around the value of the mean of $M_{AUV}=6.1 \mathrm{m}$). In contrast, the median $M_{AUV}$ was least favourable for the square-shaped MGMS, with a value of as much as 9.8 m, and most favourable for the three-pointed MGMS, with a value of 4.8 m.

On the other hand, comparing the sizes of the areas summarised in Table 1, where $M_{AUV}<3 \mathrm{m}$ and $M_{AUV}<10 \mathrm{m}$, two MGMS shapes, three-pointed and rectilinear, were identified as the most favourable. For the three-pointed MGMS, this applied to 28% of the central part of the test area (the single area located between the lower arms), where $M_{AUV}<3 \mathrm{m}$. In contrast, the rectilinear-shaped MGMS affected as much as 86.9% of the part of the test area (two areas separated by the adjustment line of the ASVs), where $M_{AUV}<10 \mathrm{m}$. The least favourable for $M_{AUV}<10 \mathrm{m}$ was the square-shaped MGMS, with only 41.9% of the part of the test area.

Although in the calculations of $M_{AUV}$ the value of the mean error of measuring the distance difference $m_i$ was adopted arbitrarily, all the presented analyses of the accuracy distributions can be treated as representative, taking into account the characteristics of changes. Thus, a change in the $m_i$ value will only result in a change in the value of the isolines limiting the accuracy areas. It should be mentioned here that estimating the value of $m_i$ is a very difficult task that requires taking into account:

• The accuracy of the position determination of the ASVs, which can be very high when using a GNSS RTK receiver;
• The ability of the ASVs to stay in position, which depends on the applied propulsion and rudder system and hydro-meteorological conditions;
• The shape of the path covered by the acoustic impulse (the so-called acoustic ray), which depends on the conditions of sound propagation in water.

5. Conclusions

The test results obtained confirmed that the coordinates of the position of a swarm of underwater vehicles could be estimated via the TDOA method in relation to four surface vehicles with an accuracy of 2.1 m (RMS)—over an area of approx. 1000 m²—and approx. 3.0 m (RMS)—over an area of approximately 1600 m². They also highlighted the fact that the accuracy of the position coordinate estimation depended very much on the shape of the MGMS. The following shapes proved to be the most favourable out of the most representative MGMS shapes covered by the research:

• Three-pointed—for maximising the size of the positioning area, where the mean error of the estimated position coordinates $M_{AUV}<3 \mathrm{m}$;
• Rectilinear—for maximising the size of the positioning area, where the mean error of the estimated position coordinates $M_{AUV}<10 \mathrm{m}$.

However, it should be noted that the shape of the MGMS should be optimised primarily by taking into account the size, shape, and relative position of the swarm of vehicles. At the same time, an optimal result does not necessarily mean that there are no areas where the accuracy of the position estimation decreases extremely. Therefore, in order to prevent such situations, the possible selection of MGMS in shapes close to rectilinear and triangular should be eliminated.

When making the final choice of MGMS shape, error ellipses can also be helpful. From these, the error values of the polar mean coordinates (direction and distance) describing the position of the swarm of underwater vehicles relative to the MGMS can be easily estimated. As demonstrated in the study, this problem particularly affected the outer square-shaped area of the MGMS.

Further developmental research on the issues addressed in the paper will be directed towards accuracy analyses of more complex MGMS shapes (consisting of more than four surface vehicles) in combination with the application of free and robust geodetic adjustment methods. Their results will certainly be reflected in the subsequent scientific publication.