Proposed Machine Learning Techniques for Bridge Structural Health Monitoring: A Laboratory Study
Abstract
1. Introduction
- Suggesting four SVM-based algorithms to detect damages in SHM;
- Analyzing and comparing our proposed algorithms with other algorithms using statistical tools;
- Verifying the proposed algorithms’ effectiveness in detecting and monitoring flexural cracks in simple concrete beams using mounted smart aggregate transducers;
- Verifying the proposed algorithms in detecting and monitoring flexural cracks in reinforced concrete (RC) beams using mounted smart aggregate transducers.
2. Literature Review
3. Learning Algorithms
3.1. Support Vector Machine (SVM)
3.2. Kernels
3.3. Proposed Algorithms
3.3.1. SVM Based on Misclassified Data (SVM-MD)
- In training phase, perform the SVM training;
- Use Equation (9) to find the misclassified data (MD);
- Investigate the existence of misclassified data maintaining in a MD structure. If the MD includes the data, the CL is computed through Equation (10) for each member of MD; otherwise, the normal procedure of SVM is continued;
- In the testing phase, compute the self-advised weights of each xk in the test set;
- For each xk in the test set, the absolute values of SVM decision values are computed and scaled to [0, 1];
- The SVM labelling is followed based on the conditions in Equation (15). The normal SVM labelling is performed if SW (xk) < decision value (xk).
3.3.2. SVM Based on Hybrid Kernels
| Algorithm 1 SVM-S2 and SVM-SP |
Set the kernel function to Equation (21). If SVM-SP: Set the kernel function to Equation (23).
|
3.3.3. SVM Based on Ensemble Classifiers (SVM-EN)
| Algorithm 2 SVM-EN |
| Input: X: training data, Y: class labels of X, K: number of nearest neighbors. Output: Class of a test sample x. Start 1. Implement algorithm 1, Section 3.3.1. 2. Compute the accuracy (Acc1) and F-score (F1-S). 3. Specify class/label. 4. Implement algorithm 2, Section 3.3.2. 5. Compute the accuracy (Acc2) and F-score (F2-S) 6. Specify class/label. 7. Classify (X, Y, x) by implementing KNN. 7.1. For each sample x do. Calculate the distance: d (x, X) = . End for. Classify x in the majority class: . 7.2. Compute the accuracy (Acc3) and F-score (F1-S3). 7.3. Specify class/label. 8. Use majority voting to specify final output based on steps 3, 6, 7.4. End. |
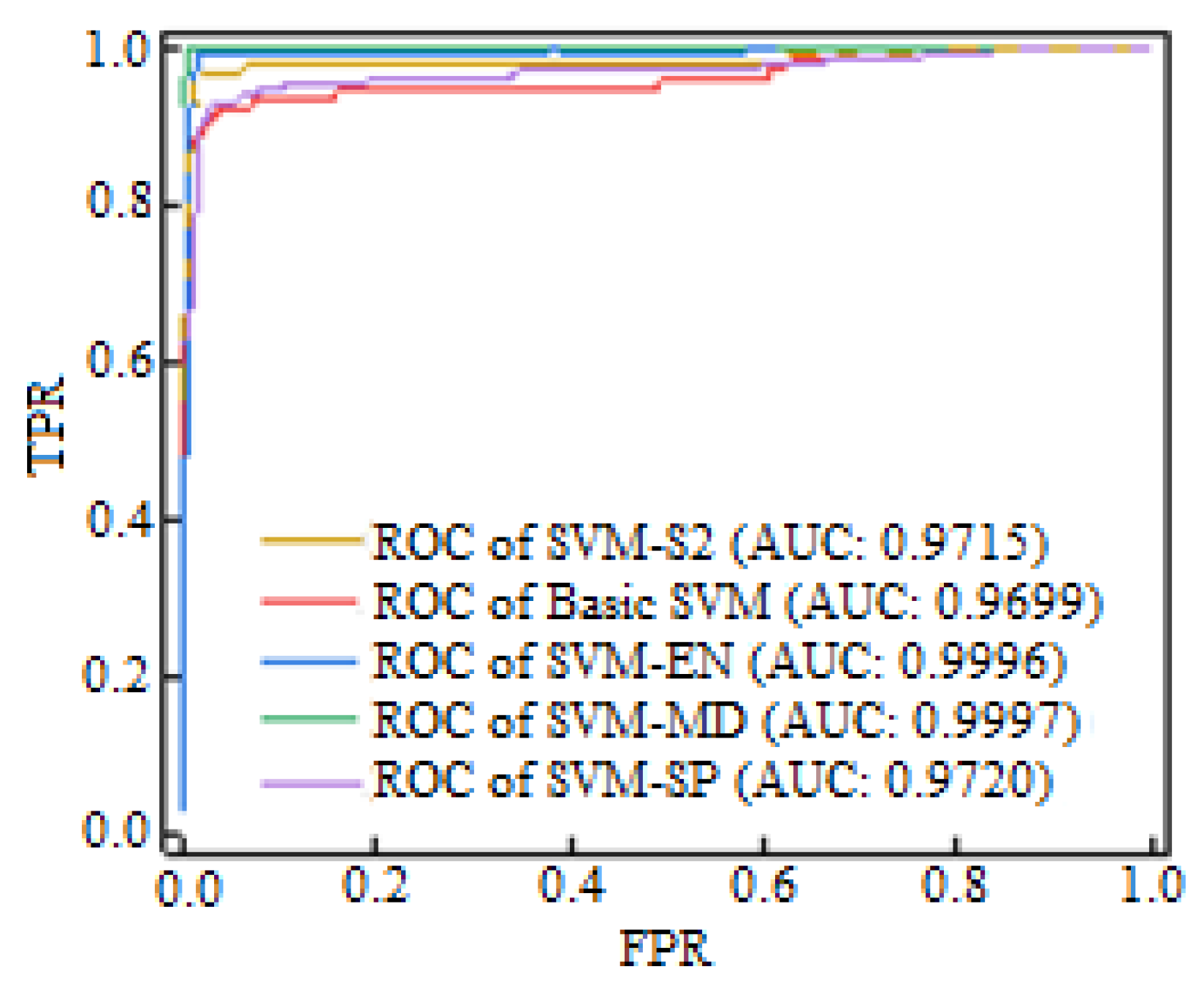
4. Performance Indications
5. Experimental Analysis
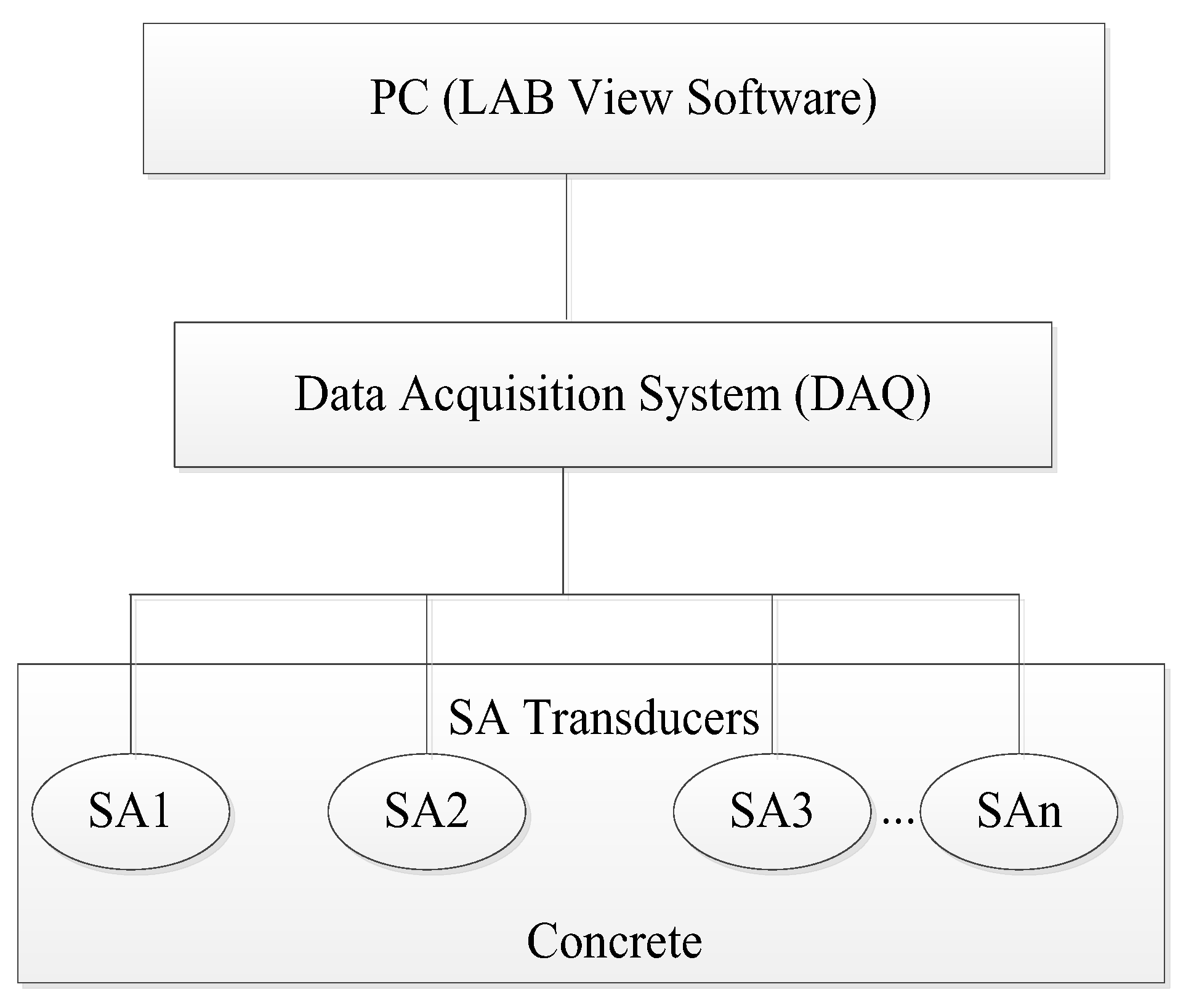
5.1. Concrete Beam Preparation
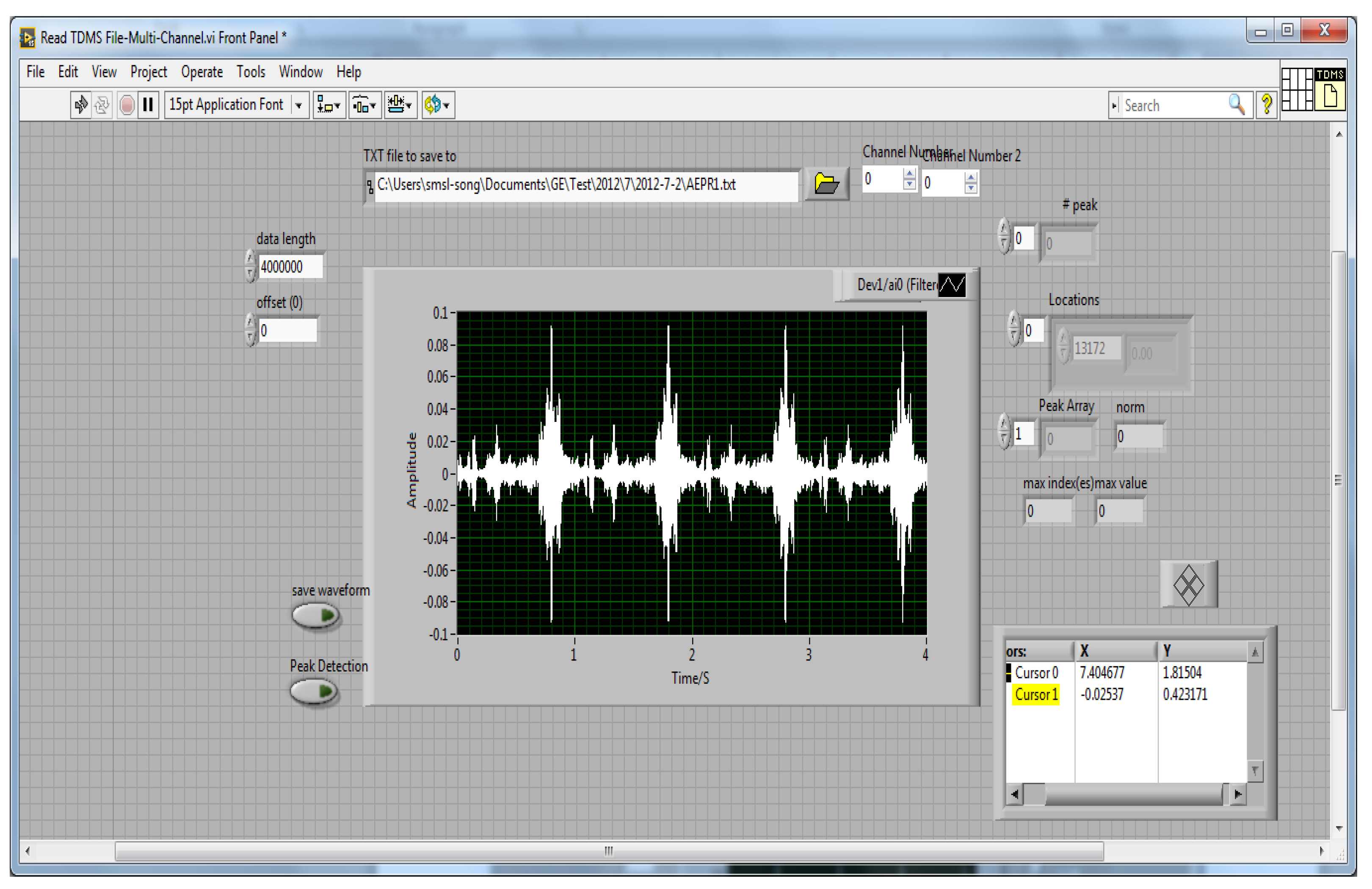
5.2. Data Collection and Measurement Setup
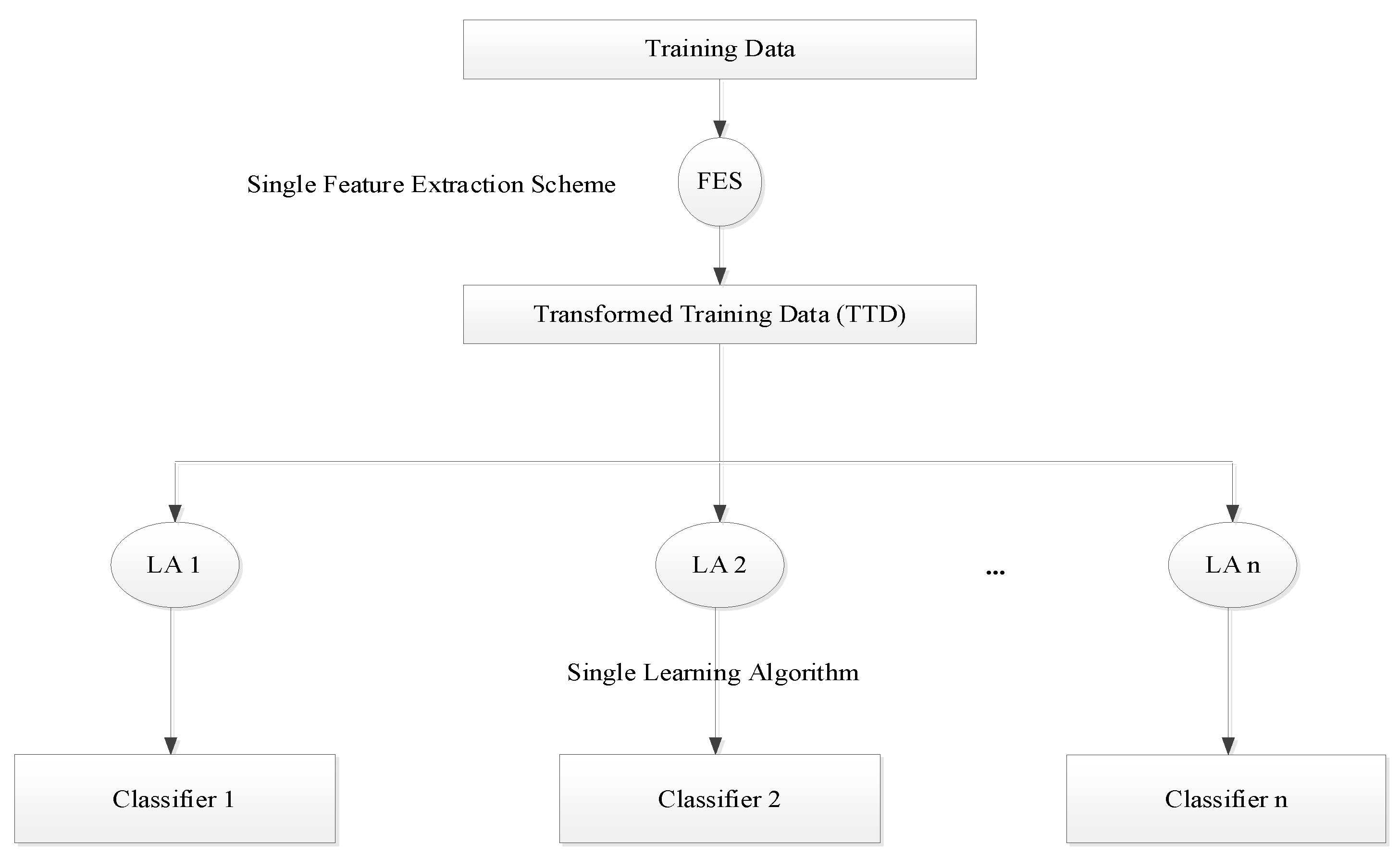
5.3. Feature Extraction
5.4. Classification
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Basic SVM | SVM-MD | |
|---|---|---|
| Standard deviation | 0.13 | 0.03 |
| Observations | 29 | 29 |
| Hypothesized mean difference | 0 | |
| df | 34 | |
| t Stat | −97.32 | |
| P(T ≤ t) one-tail | 1.75 × 10−3 | |
| t Critical one-tail | 1.69 | |
| P(T ≤ t) two-tail | 3.50 × 10−3 | |
| t critical two-tail | 2.03 |
| Basic SVM | SVM-S2 | |
|---|---|---|
| Standard deviation | 0.13 | 0.08 |
| Observations | 29 | 29 |
| Hypothesized mean difference | 0 | |
| df | 45 | |
| t Stat | −73.63 | |
| P(T ≤ t) one-tail | 7.45 × 10−3 | |
| t Critical one-tail | 1.68 | |
| P(T ≤ t) two-tail | 1.49 × 10−3 | |
| t critical two-tail | 2.01 |
| Basic SVM | SVM-SP | |
|---|---|---|
| Standard deviation | 0.13 | 0.08 |
| Observations | 29 | 29 |
| Hypothesized mean difference | 0 | |
| df | 49 | |
| t Stat | −58.70 | |
| P(T ≤ t) one-tail | 2.25 × 10−3 | |
| t Critical one-tail | 1.68 | |
| P(T ≤ t) two-tail | 4.51 × 10−3 | |
| t critical two-tail | 2.01 |
| Basic SVM | SVM-EN | |
|---|---|---|
| Standard deviation | 0.13 | 0.11 |
| Observations | 29 | 29 |
| Hypothesized mean difference | 0 | |
| df | 55 | |
| t Stat | −75.20 | |
| P(T ≤ t) one-tail | 1.92 × 10−3 | |
| t Critical one-tail | 1.67 | |
| P(T ≤ t) two-tail | 3.85 × 10−3 | |
| t critical two-tail | 2.00 |
| Basic SVM | SVM-MD | |
|---|---|---|
| Standard deviation | 0.24 | 0.22 |
| Observations | 29 | 29 |
| Hypothesized mean difference | 0 | |
| df | 35 | |
| t Stat | −20.37 | |
| P(T ≤ t) one-tail | 2.72 × 10−3 | |
| t Critical one-tail | 1.69 | |
| P(T ≤ t) two-tail | 5.44 × 10−3 | |
| t critical two-tail | 2.03 |
| Basic SVM | SVM-S2 | |
|---|---|---|
| Standard deviation | 0.24 | 0.07 |
| Observations | 29 | 29 |
| Hypothesized mean difference | 0 | |
| df | 35 | |
| t Stat | −13.75 | |
| P(T ≤ t) one-tail | 5.57 × 10−3 | |
| t Critical one-tail | 1.69 | |
| P(T ≤ t) two-tail | 1.11 × 10−3 | |
| t critical two-tail | 2.03 |
| Basic SVM | SVM-SP | |
|---|---|---|
| Standard deviation | 0.24 | 0.08 |
| Observations | 29 | 29 |
| Hypothesized mean difference | 0 | |
| df | 56 | |
| t Stat | −7.65 | |
| P(T ≤ t) one-tail | 1.44 × 10−3 | |
| t Critical one-tail | 1.67 | |
| P(T ≤ t) two-tail | 2.87 × 10−3 | |
| t critical two-tail | 2.00 |
| Basic SVM | SVM-EN | |
|---|---|---|
| Standard deviation | 0.24 | 0.15 |
| Observations | 29 | 29 |
| Hypothesized mean difference | 0 | |
| df | 42 | |
| t Stat | −21.78 | |
| P(T ≤ t) one-tail | 8.35 × 10−3 | |
| t Critical one-tail | 1.68 | |
| P(T ≤ t) two-tail | 1.67 × 10−3 | |
| t critical two-tail | 2.01 |
References
- Pines, D.; Aktan, A.E. Status of structural health monitoring of long-span bridges in the United States. Prog. Struct. Eng. Mater. 2002, 4, 372–380. [Google Scholar] [CrossRef]
- Islam, A.K.M.; Li, F.; Hamid, H.; Jaroo, A. Bridge Condition Assessment and Load Rating using Dynamic Response; Youngstown State University: Youngstown, OH, USA, 2014. [Google Scholar]
- Heasler, P.G.; Taylor, T.T.; Spanner, J.C.; Doctor, S.R.; Deffenbaugh, J.D. Ultrasonic Inspection Reliability for Intergranular Stress Corrosion Cracks; Nuclear Regulatory Commission: Washington, DC, USA, 1990. [Google Scholar]
- Zhu, Z.; Paal, S.; Brilakis, I. Detection of large-scale concrete columns for automated bridge inspection. Autom. Constr. 2010, 19, 1047–1055. [Google Scholar] [CrossRef]
- Bourgeois, A. I-35W Highway Bridge Collapse; University of Iowa College of Engineering: Minneapolis, MN, USA, 2007. [Google Scholar]
- Alavi, A.H.; Hasni, H.; Lajnef, N.; Chatti, K.; Faridazar, F. An intelligent structural damage detection approach based on self-powered wireless sensor data. Autom. Constr. 2016, 62, 24–44. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Guven, A.; Demir, Y.K. Linear genetic programming to scour below submerged pipeline. Ocean Eng. 2011, 38, 995–1000. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pham, A.-D. Hybrid computational model for predicting bridge scour depth near piers and abutments. Autom. Constr. 2014, 48, 88–96. [Google Scholar] [CrossRef]
- Das, S.K.; Samui, P.; Sabat, A.K. Application of Artificial Intelligence to Maximum Dry Density and Unconfined Compressive Strength of Cement Stabilized Soil. Geotech. Geol. Eng. 2011, 29, 329–342. [Google Scholar] [CrossRef]
- Flood, I.; Christophilos, P. Modeling construction processes using artificial neural networks. Autom. Constr. 1996, 4, 307–320. [Google Scholar] [CrossRef]
- Salehi, H.; Das, S.; Chakrabartty, S.; Biswas, S.; Burgueño, R. Structural Assessment and Damage Identification Algorithms Using Binary Data. In Proceedings of the ASME 2015 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Volume 2: Integrated System Design and Implementation; Structural Health Monitoring; Bioinspired Smart Materials and Systems; Energy Harvesting., Colorado Springs, CO, USA, 21–23 September 2015; p. 57304. [Google Scholar]
- Tran, H. A hybrid fuzzy inference model based on RBFNN and artificial bee colony for predicting the uplift capacity of suction caissons. Autom. Constr. 2014, 41, 60–69. [Google Scholar]
- Yuvaraj, P.; Murthy, A.R.; Iyer, N.R.; Samui, P.; Sekar, S.K. Prediction of fracture characteristics of high strength and ultra high strength concrete beams based on relevance vector machine. Int. J. Damage Mech. 2014, 23, 979–1004. [Google Scholar] [CrossRef]
- Bornn, L.; Farrar, C.R.; Park, G.; Farinholt, K. Structural Health Monitoring With Autoregressive Support Vector Machines. J. Vib. Acoust. 2009, 131, 021004–021009. [Google Scholar] [CrossRef]
- Worden, K.; Lane, A.J. Damage identification using support vector machines. Smart Mater. Struct. 2001, 10, 540. [Google Scholar] [CrossRef]
- Yeesock, K.; Jo Woon, C.; Ki, H.C.; JungMi, K. Wavelet-based AR–SVM for health monitoring of smart structures. Smart Mater. Struct. 2013, 22, 015003. [Google Scholar]
- Radhika, S.; Tamura, Y.; Matsui, M. Cyclone damage detection on building structures from pre- and post-satellite images using wavelet based pattern recognition. J. Wind Eng. Ind. Aerodyn. 2015, 136, 23–33. [Google Scholar] [CrossRef]
- Alves, V.; Cury, A.; Roitman, N.; Magluta, C.; Cremona, C. Structural modification assessment using supervised learning methods applied to vibration data. Eng. Struct. 2015, 99, 439–448. [Google Scholar] [CrossRef]
- Bo, Y.; Cui, Y.; Zhang, L.; Zhang, C.; Yang, Y.; Bao, Z.; Ning, G. Beam Structure Damage Identification Based on BP Neural Network and Support Vector Machine. Math. Probl. Eng. 2014, 2014, 850141 . [Google Scholar] [CrossRef]
- Liu, C.C.; Liu, J. Damage identification of a long-span arch bridge based on support vector machine. Zhendong Yu Chongji/J. Vib. Shock 2010, 29, 174–178. [Google Scholar]
- Hirokane, M.; Nomura, Y.; Kusunose, Y. Damage detection using support vector machine for integrity assessment of concrete structures. Doboku Gakkai Ronbunshuu A 2008, 64, 739–749. [Google Scholar] [CrossRef]
- Satpal, S.B.; Khandare, Y.; Guha, A.; Banerjee, S. Structural health monitoring of a cantilever beam using support vector machine. Int. J. Adv. Struct. Eng. 2013, 5, 2. [Google Scholar] [CrossRef]
- Cao, Y.F.; Wu, W.; Zhang, H.L.; Pan, J.M. Prediction of the Elastic Modulus of Self-Compacting Concrete Based on SVM. Appl. Mech. Mater. 2013, 357–360, 1023–1026. [Google Scholar] [CrossRef]
- Cha, Y.-J.; Buyukozturk, O. Modal Strain Energy Based Damage Detection Using Multi-Objective Optimization. In Structural Health Monitoring; Springer: Cham, Switzerland, 2014; Volume 5, pp. 125–133. [Google Scholar]
- Chen, B.-T.; Chang, T.-P.; Shih, J.-Y.; Wang, J.-J. Estimation of exposed temperature for fire-damaged concrete using support vector machine. Comput. Mater. Sci. 2009, 44, 913–920. [Google Scholar] [CrossRef]
- Gong, L.; Wang, C.; Wu, F.; Zhang, J.; Zhang, H.; Li, Q. Earthquake-Induced Building Damage Detection with Post-Event Sub-Meter VHR TerraSAR-X Staring Spotlight Imagery. Remote Sens. 2016, 8, 887. [Google Scholar] [CrossRef]
- Huanrui, H. New Mixed Kernel Functions of SVM Used in Pattern Recognition. Appl. Adv. Comput. Simul. Inf. Syst. 2016, 16, 5–14. [Google Scholar] [CrossRef]
- Li, Z.; Burgueño, R. Using Soft Computing to Analyze Inspection Results for Bridge Evaluation and Management. J. Bridge Eng. 2010, 15, 430–438. [Google Scholar] [CrossRef]
- Shuai, Y.; Fang, C.Q.; Yuan, Z.J. Study on Mechanical Properties of Corroded Reinforced Concrete Using Support Vector Machines. Appl. Mech. Mater. 2014, 578–579, 1556–1561. [Google Scholar] [CrossRef]
- Ying, Y.; Garrett James, H.; Oppenheim Irving, J.; Soibelman, L.; Harley Joel, B.; Shi, J.; Jin, Y. Toward Data-Driven Structural Health Monitoring: Application of Machine Learning and Signal Processing to Damage Detection. J. Comput. Civ. Eng. 2013, 27, 667–680. [Google Scholar] [CrossRef]
- Yan, K.; Xu, H.; Shen, G.; Liu, P. Prediction of Splitting Tensile Strength from Cylinder Compressive Strength of Concrete by Support Vector Machine. Adv. Mater. Sci. Eng. 2013, 2013, 597257. [Google Scholar] [CrossRef]
- Ghiasi, R.; Torkzadeh, P.; Noori, M. A machine-learning approach for structural damage detection using least square support vector machine based on a new combinational kernel function. Struct. Health Monit. 2016, 15, 302–316. [Google Scholar] [CrossRef]
- Jianhong, X. Kernel optimization of LS-SVM based on damage detection for smart structures. In Proceedings of the 2009 2nd IEEE International Conference on Computer Science and Information Technology, Beijing, China, 8–11 August 2009; pp. 406–409. [Google Scholar]
- Kasnavi, S.A.; Aminafshar, M.; Shariati, M.M.; Emam Jomeh Kashan, N.; Honarvar, M. The effect of kernel selection on genome wide prediction of discrete traits by Support Vector Machine. Gene Rep. 2018, 11, 279–282. [Google Scholar] [CrossRef]
- Raghavendra, N.S.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Otchere, D.A.; Arbi Ganat, T.O.; Gholami, R.; Ridha, S. Application of supervised machine learning paradigms in the prediction of petroleum reservoir properties: Comparative analysis of ANN and SVM models. J. Pet. Sci. Eng. 2021, 200, 108182. [Google Scholar] [CrossRef]
- Kandola, J.; Shawe-Taylor, J.; Cristianini, N. On the Extensions of Kernel Alignment; Project Report; University of Southampton: Southampton, UK, 2002. [Google Scholar]
- Seni, G.; Elder, J. Ensemble Methods in Data Mining: Improving Accuracy through Combining Predictions; Morgan & Claypool Publishers: San Rafael, CA, USA, 2010. [Google Scholar]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Lauer, F.; Bloch, G. Incorporating prior knowledge in support vector machines for classification: A review. Neurocomputing 2008, 71, 1578–1594. [Google Scholar] [CrossRef]
- Zhan, Y.; Shen, D. An adaptive error penalization method for training an efficient and generalized SVM. Pattern Recogn. 2006, 39, 342–350. [Google Scholar] [CrossRef]
- Campbell, C. An introduction to kernel methods. In Radial Basis Function Networks 1; Physica Verlag Rudolf Liebing KG: Heidelberg, Germany, 2001; pp. 155–192. [Google Scholar]
- Moghaddam, V.H.; Hamidzadeh, J. New Hermite orthogonal polynomial kernel and combined kernels in Support Vector Machine classifier. Pattern Recogn. 2016, 60, 921–935. [Google Scholar] [CrossRef]
- Maali, Y.; Al-Jumaily, A. Self-advising support vector machine. Knowl.-Based Syst. 2013, 52, 214–222. [Google Scholar] [CrossRef]
- Huang, F.; Yan, L. Combined Kernel-Based BDT-SMO Classification of Hyperspectral Fused Images. Sci. World J. 2014, 2014, 738250. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Lu, X.; Wang, X.; Lu, S.; Zhong, N. Biomedical classification application and parameters optimization of mixed kernel SVM based on the information entropy particle swarm optimization. Comput. Assist. Surg. 2016, 21, 132–141. [Google Scholar] [CrossRef]
- Dasarathy, B.V.; Sheela, B.V. A composite classifier system design: Concepts and methodology. Proc. IEEE 1979, 67, 708–713. [Google Scholar] [CrossRef]
- Dietterich, T.G. Machine-Learning Research—Four Current Directions. AI Mag. 1997, 18, 97–136. [Google Scholar]
- Ho, T. Multiple classifier combination: Lessons and next steps. In Hybrid Methods in Pattern Recognition; World Scientific: Singapore, 2002. [Google Scholar] [CrossRef]
- Duin, R.P.W. The combining classifier: To train or not to train? In Proceedings of the Object Recognition Supported by User Interaction for Service Robots, Quebec City, QC, Canada, 11–15 August 2002; Volume 762, pp. 765–770. [Google Scholar]
- Valentini, G.; Masulli, F. Ensembles of Learning Machines. In Proceedings of the Neural Nets: 13th Italian Workshop on Neural Nets, WIRN VIETRI 2002, Vietri sul Mare, Italy, 30 May–1 June 2002; Volume 2486, pp. 3–22. [Google Scholar]
- Bahler, D.; Navarro, L. Methods for Combining Heterogeneous Sets of Classiers. Artif. Intell. 2000. [Google Scholar]
- Briem, G.J.; Benediktsson, J.A.; Sveinsson, J.R. Boosting, Bagging, and Consensus Based Classification of Multisource Remote Sensing Data. In Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2001; pp. 279–288. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Aleksandra, P.; Michael, A.; Galina, M. Heterogeneous versus Homogeneous Machine Learning Ensembles. Inf. Technol. Manag. Sci. 2015, 18, 135–140. [Google Scholar] [CrossRef]
- Samworth, R.J. Optimal weighted nearest neighbour classifiers. Ann. Statist. 2012, 40, 2733–2763. [Google Scholar] [CrossRef]
- Sattar, A.; Kang, B.H. AI 2006: Advances in Artificial Intelligence; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Taghavipour, S.; Kharkovsky, S.; Kang, W.H.; Samali, B.; Mirza, O. Detection and monitoring of flexural cracks in reinforced concrete beams using mounted smart aggregate transducers. Smart Mater. Struct. 2017, 26, 104009. [Google Scholar] [CrossRef]
- Sohn, H.; Farrar, C.; Hemez, F.; Shunk, D.; Stinemates, D.W.; Nadler, B. A Review of Structural Health Monitoring Literature: 1996–2001; Los Alamos National Laboratory: Los Alamos, NM, USA, 2004. [Google Scholar]
- Scott, S.; Landis, E.N.; Peterson, M.L.; Shah, S.P.; Achenbach, J.D. Ultrasonic investigation of concrete with distributed damage. ACI Mater. J. 1998, 95, 27–36. [Google Scholar]
- Dorfman, L.S.; Trubelja, M. Structural Integrity Associates San Jose, CA. Torsional monitoring of turbine-generators for incipient failure detection. In Proceedings of the 6th EPRI Steam Turbine/Generator Workshop, St. Louis, MI, USA, 17–20 August 1999. [Google Scholar]
- Aggelis, D.G. Classification of cracking mode in concrete by acoustic emission parameters. Mech. Res. Commun. 2011, 38, 153–157. [Google Scholar] [CrossRef]
- Tayfur, S.; Alver, N.; Abdi, S.; Saatcı, S.; Ghiami, A. Characterization of concrete matrix/steel fiber de-bonding in an SFRC beam: Principal component analysis and k-mean algorithm for clustering AE data. Eng. Fract. Mech. 2018, 194, 73–85. [Google Scholar] [CrossRef]
- Nahm, F.S. Receiver operating characteristic curve: Overview and practical use for clinicians. Korean J. Anesthesiol. 2022, 75, 25–36. [Google Scholar] [CrossRef]





| Ref No. | Algorithm | Domain and Outcome |
|---|---|---|
| [31] | SVM |
|
| [32] | SVM-combination of kernels (spline and wavelet) |
|
| [33] | Combination of kernels (Gaussian RBF and Polynomial) |
|
| [34] | Linear, radial, polynomial and sigmoid kernel-based Support vector machine (SVM) |
|
| RBF | |
| Sigmoid | |
| Polynomial | |
| Wavelet | |
| Chebyshev | |
| Gaussian radial basis | |
| Exponential radial basis | |
| Multi-layer Fourier series | |
| Fourier series | |
| Splines | |
| B splines |
| Predicted Positive | Predicted Negative | |
|---|---|---|
| Label positive | tp: true positive | fn: false negative |
| Label negative | fp: false positive | tn: true negative |
| Materials | Characteristics | Values |
|---|---|---|
| Portland cement type GB | Specific gravity | 3.15 |
| Natural river sand (Fine aggregate) | Specific gravity | 2.55 |
| Size | 0.15 to 4.75 mm | |
| Natural river gravel (Coarse aggregate) | Specific gravity | 2.60 |
| Maximum size | 10 mm | |
| Tap water | Density | 998–1000 kg/m3 |
| Crest factor: The L infinity norm and RMS values are computed throughout the specified dimension. | |
| Root-mean-square level: where x is a vector, y indicates that the y is a real-valued scalar. | , |
| is the jth feature value for the ith column. | |
| Average frequency: n = number of frequency bins in the spectrum; fi = frequency of spectrum at bin i of n; Ii = Intensity (dB scale) of spectrum at bin i of n. | |
| Energy: Z is the magnitude; Es is signal energy. | |
| Maximum-to-minimum difference: | |
| Rise level: | RL = value (Rwave) − value (Qwave) |
| Fall time: | tf = Time lasts for the amplitude of a pulse to fall from a specified value to another specified value. |
| Fall level | FL = value (Rwave) − value (Swave) |
| Models | 1 S. Beam | RC Beam | ||
|---|---|---|---|---|
| Acc (%) | F1-S | Acc (%) | F1-S | |
| Basic SVM | 84.72 | 0.58 | 85.38 | 0.63 |
| SVM-MD | 87.22 | 0.80 | 86.29 | 0.73 |
| SVM-S2 | 86.82 | 0.77 | 86 | 0.70 |
| SVM-SP | 86.46 | 0.73 | 85.54 | 0.68 |
| SVM-EN | 87.2 | 0.79 | 86.08 | 0.71 |
| Models | P(T ≤ t) One-Tail | P(T ≤ t) Two-Tail |
|---|---|---|
| SVM-MD | 1.75 × 10−3 | 3.50 × 10−3 |
| SVM-S2 | 7.45 × 10−3 | 1.49 × 10−3 |
| SVM-SP | 2.25 × 10−3 | 4.51 × 10−3 |
| SVM-EN | 1.92 × 10−3 | 3.85 × 10−3 |
| Models | P(T ≤ t) One-Tail | P(T ≤ t) Two-Tail |
|---|---|---|
| SVM-MD | 2.72 × 10−3 | 5.44 × 10−3 |
| SVM-S2 | 5.57 × 10−3 | 1.11 × 10−3 |
| SVM-SP | 1.44 × 10−3 | 2.87 × 10−3 |
| SVM-EN | 8.35 × 10−3 | 1.67 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noori Hoshyar, A.; Rashidi, M.; Yu, Y.; Samali, B. Proposed Machine Learning Techniques for Bridge Structural Health Monitoring: A Laboratory Study. Remote Sens. 2023, 15, 1984. https://doi.org/10.3390/rs15081984
Noori Hoshyar A, Rashidi M, Yu Y, Samali B. Proposed Machine Learning Techniques for Bridge Structural Health Monitoring: A Laboratory Study. Remote Sensing. 2023; 15(8):1984. https://doi.org/10.3390/rs15081984
Chicago/Turabian StyleNoori Hoshyar, Azadeh, Maria Rashidi, Yang Yu, and Bijan Samali. 2023. "Proposed Machine Learning Techniques for Bridge Structural Health Monitoring: A Laboratory Study" Remote Sensing 15, no. 8: 1984. https://doi.org/10.3390/rs15081984
APA StyleNoori Hoshyar, A., Rashidi, M., Yu, Y., & Samali, B. (2023). Proposed Machine Learning Techniques for Bridge Structural Health Monitoring: A Laboratory Study. Remote Sensing, 15(8), 1984. https://doi.org/10.3390/rs15081984









