Abstract
Poplar plantations in high-density and short-rotation coppices (SRC) are a suitable way for the fast production of wood that can be transformed into bioproducts or bioenergy. Optimal management of these coppices requires accurate assessment of the total standing biomass. However, traditional field inventory is a challenging task, given the existence of multiple shoots, the difficulty of identifying terminal shoots, and the extreme high density. As an alternative, in this work, we propose to develop individual stool and plot biomass models using metrics derived from terrestrial laser scanning (TLS) as predictors. To this aim, we used data from a SRC poplar plantation, including nine plots and 154 individual stools. Every plot was scanned from different positions, and individual stools were felled, weighed, and dried to compute aboveground biomass (AGB). Individual stools were segmented from the cloud point, and different TLS metrics at stool and plot level were derived following processes of bounding box, slicing, and voxelization. These metrics were then used, either alone or combined with field-measured metrics, to fit biomass models. Our results indicate that at individual-stool level, the biomass models combining TLS metrics and easy to measure in field metrics (stool diameter) perform similarly to the traditional allometric models based on field inventories, while at plot scales, TLS-derived models show superiority over traditional models. Our proposed methodology permits accurate and non-destructive estimates of the biomass fixed in SRC plantations.
1. Introduction
Poplar plantations in high-density and short-rotation coppice (SRC) provide a viable option for short-term wood production. This important raw material for the bioeconomy can be transformed into bioproducts or bioenergy within the context of biorefineries [1]. In addition, these plantations play a role in carbon capture and, therefore, in the mitigation of climate change [2,3]. Hence, the implementation of such plantations is widespread in many parts of Europe [2] and worldwide [4,5,6].
Both of the abovementioned aspects, wood production, and carbon sequestration, are closely linked to biomass productivity, so rapid, reliable biomass predictions are key to appropriate decision-making. Biomass quantification using non-destructive methods necessarily requires the use of predictive calculations based on the direct non-destructive collection of growth-related data. In this regard, there have been many advances in modeling across all fields of forest science, including SRC plantations [4,7]. Allometric models, which relate diameter at breast height (or other easily measurable variables) to biomass, are those most commonly used in forest inventories and have also been employed in the case of SRC plantations to estimate available biomass [8,9]. There are several examples in which the power function (W = aDb) has been applied in poplar SRC plantations [10,11]. The accuracy of such allometric equations is generally sufficient [12]. However, other predictive variables have also been included, such as height, the number of shoots per stool, or age, among others, which can improve the accuracy of the estimations [13,14,15].
One of the main problems when predicting biomass in SRC plantations is the large variability present due to the genotype-environment interaction [16,17]. Most of the biomass models for these plantations are site and genotype-specific models [18,19], and therefore their applicability is limited [20]. However, there are also examples of models developed for higher hierarchical levels [21,22,23]. In fact, the use of statistical models based on a wide range of empirical data has become more frequent due to the difficulty involved in extrapolating specific values to greater scales, given the wide variability in production [24,25,26].
Despite the high predictive capacity of the existing biomass models based on field measurements, the practical application of these models has certain limitations. The coppice system stimulates the production of multiple shoots from the same stool, the individual diameter of which should be measured to obtain accurate information. This is a highly time-consuming task, which adds considerable difficulty not only to the data collection but also to model fitting and even the further application of the models. In addition, due to the extremely high density of SRC systems, measuring the individual height of each stool can be a challenging task, given the occlusion between the crowns of the stools and the difficulty in identifying the terminal apex of each stool, thus leading to imprecise estimates. Finally, the short spacing between individual stools and the profusion of shoots prevents accurate assessment of individual crown attributes, such as crown diameter or maximum projection. As an alternative, the direct collection of individual tree-size attributes by means of a traditional field inventory is increasingly replaced by the use of new technologies capable of estimating these parameters.
Aboveground biomass has traditionally been estimated through allometric equations using tree attributes recorded in the field as predictors [27,28,29,30,31]. Development of these equations, based on destructive sampling, is both highly time-consuming and very expensive. Plantations with fast-growing species require frequent evaluations over time in order to adopt the best felling strategy without having to resort to destructive methods [32]. Many recent studies have focused on biomass estimation techniques that are not based on destructive sampling, using new technologies such as terrestrial (TLS) or aerial laser scanning data (Airborne LiDAR) [33,34,35,36]. These alternatives to destructive allometric approaches open possibilities for a wide array of purposes [37].
Terrestrial laser scanning (TLS) is an active remote sensing technique that allows accurate measurement of distances by transmitting laser pulses and analyzing the returned energy as a function of time. TLS, therefore, can provide detailed three-dimensional information to precisely describe forest structure [38,39], allowing unprecedented forest-attribute measurement capability at both stand and tree scale [40]. TLS allows the characterization of the vertical distribution of vegetation structure [41] and the reconstruction of individual tree structure [42,43] or vegetation profiles [44]. In addition, thanks to the precise measurement potential of TLS, it is possible to obtain crown variables such as height, width, crown projection area, and volume [45,46,47]. It is also possible to estimate tree volume or biomass (e.g., [38,40,48,49,50]), to reconstruct the stem and branching system using quantitative structural models (QSM) in order to study the whole-tree topology [51,52,53] or to estimate leaf indices such as leaf area index (LAI) and leaf area density (LAD) [47,54]. While the QSM method has shown its potentiality for large, well-individualized trees, its application to small trees, coppices, or shrubs may be problematic, given the difficulty of defining a dominant stem and the problems of shadowing and occlusion [55,56].
To the best of our knowledge, TLS has not been widely used in studies aimed at estimating biomass from short-rotation crops such as the poplar plantations on which our work is focused. For example, [48] estimated merchantable volume in a 20–24-year-old hybrid poplar (Populus x Canadensis Moench cv. ‘I-72/58’) plantation in China, while [49] and [39,43] studied three neighboring stands of hybrid poplar (Populus x euramericana) plantations of differing ages, developing non-destructive tree stem and crown allometry, evaluating of eccentricities of stem profiles and studying the influence of voxel size and point cloud density on crown cover estimation, respectively. The study [49] was carried out in a plantation with ages ranging from four to ten years. Another study [39] focused their study on plots with three different ages: six, eight, and ten years old. The study carried out by [43] dealt with a ten-year-old plantation along with a row of other valuable (although slower growth rate) species and different distances depending on the part of the plantation. All the previous works are focused on timber-oriented low-dense plantations. The main exception is the work by [57], where TLS was used for defining the basal area in a high-dense poplar plantation, though no estimates on individual stool or plot-level biomass were provided.
The main aim of this study is to evaluate the potential of TLS to facilitate biomass estimation in short-rotation poplar crops. This main objective is broken down into the following more specific objectives: (1) to identify TLS metrics and their possible correlation to traditional field-inventory metrics at tree and plot level, including biomass; and (2) to evaluate the efficiency of using TLS metrics as predictors in biomass models at tree and plot level.
We hypothesized that: (i) TLS metrics can provide an initial accurate approach for estimating the amount of biomass at plot level; (ii) TLS metrics combined with variables easily measured in the field can be used to predict biomass as accurately as traditional allometric models.
2. Materials and Methods
2.1. Experimental Sites
In 2014, a multi-clonal poplar short-rotation coppice (SRC) plantation was established at a density of 4000 trees ha−1 (spacing 1 m × 2.5 m), applying two rotations of four years each. The experimental site is located in the center of the Iberian Peninsula (40°28′N, 3°22′W) at an elevation of 595 m with an average mean temperature of 15.3 °C. The soil at the site has a silty loam texture with a pH of 8.1 and 0.80 organic matter content.
The plantation was established manually using unrooted cuttings (30 cm long) of seventeen different genotypes of Populus x Canadensis (Dode) Guinier and P. x generosa Henry. The main aim of the plantation was to evaluate the different clones with regard to site adaptation. Different cultural management techniques were applied in order to enhance establishment and growth, including drip irrigation, which is necessary for Mediterranean conditions (for more details, see [5]). The experimental design consisted of three blocks with the genotypes randomized in each of them. The number of stems per genotype included in each of the blocks was 40, although only the central 16 stems were measured to exclude edge effects. These 16 central stools from a given genotype and block form an experimental 40 m2 rectangular subplot (Figure 1).
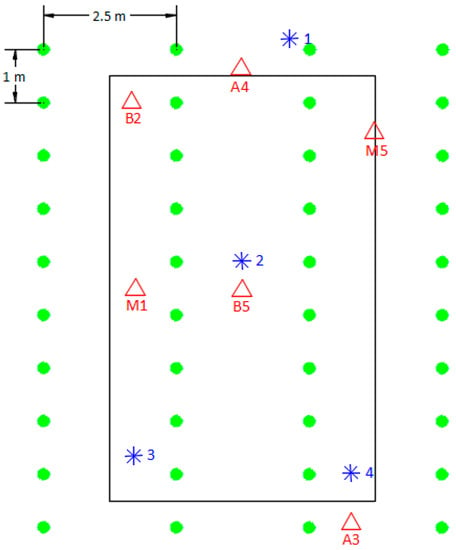
Figure 1.
Diagram of TLS data acquired from the FARO Focus3D M70 scanner in one of the study plots. Stools represented by green circles; scan positions represented by blue asterisks; spheres represented by red triangles.
For the purposes of this research, subplots of three of the most productive clones under Mediterranean conditions were considered. These were ‘AF2’ and ‘AF34’ (both from P. x canadensis) and ‘AF8’ (P. x generosa x P. trichocarpa). Therefore, nine subplots in the plantation, one for each selected genotype and block (144 trees in total), were evaluated. The age of the plantation (root and shoots) at that moment was R8S4 (Root eight years—Shoots four years).
2.2. Laser Scanning
In each of the nine analyzed plots, several scans were performed from different sides in order to perform a complete digitalization. The scans were carried out in November 2021 using a phase-based FARO Focus3D M70 scanner. The scanner uses phase-shift technology to measure the distance to objects intercepted by the laser beam. We used the following settings when scanning the plots: 360° horizontal angle, 120° vertical angle, color pictures, Resolution: ¼, and Quality: 2x. These settings resulted in a resolution of about 6.1 mm at a distance of 10 m and a scanning time of about five minutes per scan. Previous studies in solid wood volume [40] or biomass [34,58] tested the use of TLS with similar resolutions in the scanning process of their trees.
Given the size of the plots, four or five positions per plot were needed to provide complete coverage for the plot. Scan positions were chosen such that there was sufficient distance from stools and good tree-crown visibility in all directions. After marking the scan positions with plastic pegs, six spheres were set up on wooden poles at different heights in the plot so that at least four spheres were visible from all four or five scan positions. These spheres would serve as target points to merge the different point clouds taken from the different stations. Visibility of spheres was checked from all the scan positions, and the positions were moved where necessary to ensure full visibility. Understory vegetation obstructing the visibility of the spheres was removed. Figure 1 shows the diagram of one of the scanned plots to clarify the location of all the necessary equipment for the scanning process. The laser scanner was mounted on a leveled tripod at a height of 1.5 m and positioned so that there was a clear line between the scanner and the target stools. All data was obtained under calm conditions to limit movement errors caused by the wind moving the leaves and branches of the sample trees. Figure 2 shows one of the study plots (left) and some of the target spheres during the scanning process (right).

Figure 2.
Detail of one of the study plots (left), and the target spheres and the FARO Focus3D M70 scanner during the scanning process (right).
2.3. Field Measurements, Destructive Measurements, and Biomass Estimation
Once the TLS scans had been performed in the plot, the following data were recorded for each of the 16 stools within the plot: number of shoots per stool (n), breast height diameter of the dominant shoot (d_st, mm) using a digital caliper, and the total height of the dominant shoot (h_st, cm) to the nearest 0.1 cm using a digital hypsometer.
Immediately after recording field measurements, the stools were destructively felled, and the fresh weight of each individual stool was measured in the field using a digital scale (kg). The moisture content was determined from a subsample of the tree with the most common diameter class in each plot, drying it in an oven in the lab at 105 °C to constant weight. Individual aboveground dry biomass of the stool (w_st, kg dry matter) was then computed for each stool. Total aboveground dry biomass per hectare (W_tot, t dry matter) was computed by summing the total biomass of all the individual trees and expanding such value based on plot size.
2.4. Point Cloud Processing
The main steps in this study comprise initial point cloud processing, stool segmentation, volume estimation, and statistical analysis at both stool and plot levels.
The FARO Scene 2021 5.0 software was used for the processing of raw data and registration of individual scans into plot point clouds, resulting in a single file per plot to facilitate processing operations. Sphere targets were automatically detected by the software in individual scans, but the information had to be manually corrected to include missing spheres or remove false detections. The number of visible spheres was four for most of the scans. Manual co-registration of the four or five scans into a plot point cloud was target-based. The registration accuracy was described by a target error range of 7.9–16.7 mm (median 12.8 mm) for all nine plots, which is within the range of tolerance commonly accepted for this type of work [34,58]. In order to accurately clip and individualize the stools from each plot and favor the further process of stool individualization, we manually removed points clearly corresponding to the ground, stones, and shrubs, as well as those points clearly belonging to stools located beyond the plot. Through this scanning protocol, it was possible to obtain an accurate 3D representation of each plot and of the individual stools (Figure 3).

Figure 3.
Example of TLS data acquired from the FARO Focus3D M70 scanner in one of the study plots: overhead view (left) and side view (right) showing detail from the studied stools.
2.5. Analysis at Stool Level
2.5.1. Stool Segmentation
Once the scans were registered, the resulting point cloud for the plot was imported to CloudCompare (CloudCompare v2.1) (an open-source point cloud editing software) for further analysis. Each plot was clipped using the cloud subsampling tool, cleaned using the interactive segmentation tool, and identified for future analysis. The aim of the segmentation steps was to extract an individual point cloud for each target stool from the global point cloud for the plot. Each stool was manually clipped from the plot point cloud using the interactive segmentation tool, which resulted in as many standard boxes as stools in the plot.
2.5.2. Stool Volume Computation
Different approaches to calculating stool volume were used. Three processing algorithms were tested using CloudCompare (CloudCompare v2.1), CompuTree software (Version 5.0, Computree Group, 2017), and R statistical software (4.1.3): bounding box assignment, calculation by slicing and rasterization in voxels (Figure 4).
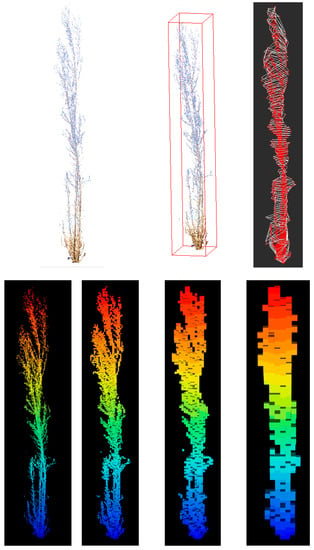
Figure 4.
Representation of the three algorithms used to derive stool volume from TLS data. From left to right and top to bottom: picture of the scanned stool; bounding vox; slices; and voxels (2 cm, 5 cm, 10 cm, and 25 cm).
- Bounding box assignment. Bounding box volume was estimated as the volume of the smallest box that encompassed the entire tree point cloud. The dimensions of the bounding box can be found by calculating the difference between the maximum and minimum coordinates on each axis. This is performed automatically in CloudCompare (CloudCompare v2.1), so we used the box dimensions reported for the individual stool point cloud. This is an application of the study by [59], who developed methods to use bounding box volume as a predictor for peatland shrub aboveground biomass.
- Individual stool slicing. The stool was divided into slices of 10 cm in height using CompuTree software (Version 5.0, Computree Group, 2017). In a first step, we defined a horizontal plane with this algorithm by selecting the lowest point of the stool. From this value, all points within a slice of 2 cm in height were selected and considered to be in the same plane by ignoring their Z coordinate. The Delaunay triangulation was then applied to the points considered in the same horizontal plane, and the area of the section was calculated. This step was repeated for every 10 cm of stool height. The volume of each slice from consecutive sections was calculated by:where S1 and S2 are the areas of the consecutive sections, and h is the separation between sections (10 cm). The total volume of the stool is the sum of all the single volumes between two sections. Stool height is computed as the difference between the height of the upper slice and the height of the stool slice. We also considered the area of the maximum section generated, the areas of both the stump (0.10 cm) and breast height (1.30 m) sections, the volume of these sections, and combinations among them as relevant variables.
- Rasterization in voxels (voxelization). According to [60], a volumetric pixel, also known as a voxel, is the minimum discrete volume that can be processed in a tridimensional object. The basis of this method is the organization of the point cloud on a tridimensional regular grid where each cell with at least one point inside is a voxel. We tested four different grids depending on the size of the voxels (2 cm, 5 cm, 10 cm, and 25 cm) using the R package “lidR” (Version 4.0.1, available online at: https://cran.r-project.org/web/packages/lidR/index.html, accessed on 13 January 2023). Once the stool had been voxelized, we needed to approximate the occupancy of the space by classifying each voxel as empty/not empty based on the number of returns within each voxel. In order to consider the potential impact of the distance from the stool to the TLS, or the different number of return points within each voxel due to occlusions or shadowing [61,62,63,64], we proposed two alternatives. In the first, we estimated the median number of returns per voxel for each stool, and for occupations equal to or greater than that value, the voxel was considered full, otherwise it was considered empty. This approach was compared with an alternative that considers as full those voxels including at least one return. For either approach, if the voxel was considered full, then its volume was also considered in the quantification. The total volume was obtained by multiplying the number of full voxels by the volume of a voxel (8 cm3, 125 cm3, 1000 cm3, or 15,625 cm3).
These three methods enable the estimation of 20 different metrics for each individual stool (Table 1). In addition, 18 plot-level metrics were obtained by either summing or averaging the different individual metrics from the 16 stools within each plot (Table 2). Plot-level metrics obtained by summing were subsequently upscaled to the hectare.

Table 1.
Definition of the individual stool metrics derived from the different TLS methods.

Table 2.
Definition of the plot-level metrics derived from the different TLS methods.
Mean values and standard deviations for each of the variables evaluated are presented in Table 3.

Table 3.
Mean values and standard deviations for the different dendrometric and TLS covariables.
2.6. Exploratory Analysis
The TLS-derived metrics at stool and plot scales allow us to establish relationships with the real dendrometric and biomass values obtained from standing inventory and destructive measurements carried out in the field. To this aim, in the first step, we checked for statistically significant relationships between stool-scale variables of interest measured in the field and stool TLS-derived metrics (Table 1) by means of a Pearson’s correlation. The field-measured variables selected were:
- Individual stool dry biomass (w_st);
- Stool_height (h_st);
- Diameter at breast height of the largest shoot within the stool (d_st);
- Number of shoots in the stool with breast height diameter > 2 cm (N_shoot).
In a similar process, we analyzed the correlation between the plot-level TLS-derived metrics and four plot-level variables derived from field measurements:
- Total plot dry biomass (W_tot)—computed as the sum of the biomass of each individual stool;
- Mean height (hm)—the mean height of the different stools in the plot;
- Basal area (BA)—defined as the sum of the sections measured at breast height diameter in the largest shoot of the stool;
- Total number of shoots in the plot (N_shoot_tot)—the sum of N_shoot for all the stools in the plot.
W_tot, BA, and N_shoot_tot were upscaled from the plot to the hectare. Mean values and standard deviations for each of the field-inventory variables are presented in Table 3.
2.7. Modeling Approach
The second main objective of this study was to evaluate the suitability of constructing models based on TLS-derived metrics (Table 1) at individual-stool level in order to forecast individual stool dry biomass (w_st). To achieve this, we fitted three different basic linear models. In this sense, we want to stress that our main objective was not to construct new, improved allometric biomass models using TLS metrics but to explore the potential of incorporating these metrics (either alone or combined with traditional inventory metrics) into future models. Due to this, we have only evaluated linear mixed models and have skipped out the comparison of the results with other modeling approaches, as could be fitting random forests or generalized additive models. In the first step, we fitted a model for w_st only, using TLS variables (from now TLS model) as predictors. The second model (field-inventory model) was constructed using only field-observed metrics (h_st, d_st, and N_shoot, and the products [d_st]2.h_st and [d_st]2. N_shoot. Finally, we developed a third model (combined model), in which we evaluated the inclusion of both individual TLS shoot metrics along with that most easily measured in the field, which is the diameter at breast of the largest shoot in the stool (d_st). In addition, in this third model, we evaluated the inclusion of the products [d_st]2.h_slice, [d_st]2.h_vox, and [d_st]2. z_bound.
The three models were fitted following a similar procedure. In order to identify the variables entering each model, we first fitted a multiple linear regression by means of OLS techniques using the stepwise selection method. Multicollinearity among the potential covariates entering the model was controlled by avoiding Variance Inflation Factor (VIF) values over 10. Given the hierarchical structure of the data (individual stools from different plots and clones), we evaluated the inclusion of random effects acting at plot and clone level in the model by fitting a multilevel linear mixed model. The final expression for the model is given in Equation (2):
where Xi represents the potential explanatory covariates; βi unknown but estimable parameters; u and v are plot and clone random effects, with mean zero and variances and ; e is a random error term.
The three models were compared in terms of different goodness-of-fit statistics, such as adjusted coefficient of determination (R2adj), root mean square error (RMSE), relative root mean square error (RRMSE), and Akaike’s Information Criterion (AIC).
For the total dry biomass at plot level (W_tot), we carried out a similar procedure, fitting three different models and evaluating the inclusion as predictors of only plot-scale TLS-derived metrics (Table 2), only field-inventory plot-level metrics (BA, hm, N_shoots:plot, BA.hm), or a combination of both TLS and field-inventory. For this third model, we only kept the most easily recorded traits in the analysis, which are basal area (BA), together with the product BA.Hm_slice and BA.Plot_Z_bound. Inclusion of clone random effects was also considered when fitting the model.
3. Results
3.1. Correlation Analysis
The analysis of the correlation between individual stool attributes measured using field and TLS-derived metrics (Table 4) revealed the existence of some significant, though not very high, relationships. The TLS-derived covariate showing the highest correlation (r: 0.4829) with the individual stool biomass (w_st) was H-slice, which is stool height computed as the difference between the height of the upper section and the stool sections after the slicing process (H_slice). Z_bound, defined as the length of the bounding box over the Z axis, was the covariate that had the second highest correlation (r: 0.4150). Other TLS-derived covariates displaying significant correlation with the individual stool biomass were those metrics representing volumes, either of the bounding box (Vol_bound) or following slicing (Vol_slice, Box_proj, and Box_BH). Voxelization-derived covariates did not reach the levels of correlation with w_st obtained from the metrics obtained by bounding or slicing. Among these voxelization metrics, the highest correlation with stool biomass was obtained using a voxel side of 25 cm. There was little difference between the criteria for considering a voxel as full, using either the median value as the threshold or the approach using all the voxels with a minimum of one return point.

Table 4.
Correlation analysis between the main dendrometric attributes and TLS-derived metrics.
H_slice and Z_bound were also the TLS-derived metrics that showed the highest correlation (Table 4) with both the individual height observed in the field (h_st) and the diameter of the largest shoot within the stool (d_st). The rest of the TLS-derived metrics presented a significant correlation with h_st or d_st as with those observed for w_st, except for the metrics obtained from voxelization. As regards the number of shoots within the stool (N_shoot), we observed a different pattern of correlation since the highest correlations were identified with Box_BH (product of the section at breast height BH_sec and H_slice), the stool volume Vol_stool and BH_Sec, all metrics derived from slicing. Voxelization-derived metrics were significantly correlated with N_shoot; the greater the size of the voxel, the higher the correlation.
At the plot scale, the small number of plots involved (n = 9) resulted in a large number of non-significant correlations (Table 4). We identified a significant correlation between the total biomass at the plot scale and the mean height of the stools derived by either slicing (Hm_slice, r: 0.9327, p-value < 0.001) or box bounding (Plot_Z_bound, r: 0.9624, p-value < 0.001). Less significant relationships were observed between the total biomass of the plot and the sum of the volumes of the bounding boxes of every stool within the plot (Plot_vol_bound, r: 0.8277, p-value < 0.01) and between total biomass and the sum of the volumes of the individual boxes obtained by slicing (Plot_Box_BH, r: 0.6021, p-value < 0.1). The mean height of the plot (Hm_plot) and plot basal area was only significantly correlated with both Hm_slice and Plot_Z_bound, while no significant correlations were detected for the total number of shoots within the plot.
3.2. Modeling Approach
3.2.1. Models for Individual Stool Biomass
We fitted three different models for the biomass of the individual stool (w_st) using only TLS-derived metrics, only field-inventory metrics, or a combination of both (Table 5). Our results revealed that the TLS model performed worse than the other two approaches. The TLS model included the height computed as the difference between the height of the upper section and stool slices (H_slice) and the volume of the stool (Vol_stool) as predictors, both variables being derived from the slicing process. Both variables entered the model with a positive sign, indicating that the larger the values, the larger the predicted individual biomass. The model showed low predictive capacity (R2adj = 0.2490, RMSE = 8.7527 kg, RRMSE = 46.1%) and low agreement between observed vs. predicted analysis (Figure 5a), indicating that the model tends to overestimate biomass for the smaller stools and underestimate the larger ones.

Table 5.
Parameter estimates and goodness-of-fit statistics for the three fitted models (Equation (2)) for individual stool biomass.
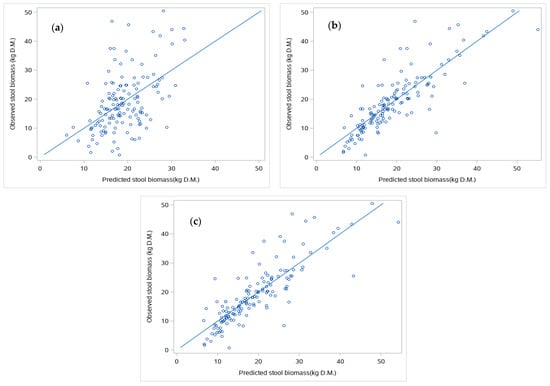
Figure 5.
Concordance between observed and predicted values of individual stool biomass for the TLS model (a), Field-inventory model (b), and combined model (c). Straight lines indicate the 1:1.
The best model only using field-inventory covariates included the product between the squared diameter of the largest shoot within the stool and the height of the stool (d_st2.h_st) and the number of shoots within the stool as predictors, both entering with a positive sign. Using this model resulted in higher predictive capacity (R2adj = 0.7070, RMSE = 5.4675 kg, RRMSE = 28.8%) and greater agreement between observed vs. predicted values (Figure 5b) than the TLS model. Finally, the best model combining TLS-derived metrics and the easily measured field-inventory covariate included the product between the squared diameter of the largest shoot within the stool and the height derived from the slicing process (d_st2.H_slice) and the volume of the 10 cm-sided voxels filled with return point over the median value (Vox10_med) as predictors. This combined model performed quite similarly to the field-inventory model, resulting in similar values for R2adj (0.7018), RMSE (5.5152 kg), and RRMSE (29.1%) and agreement between observed and predicted values (Figure 5c).
In all three fitted models, the inclusion of plot and/or clone random effects did not lead to an increase in AIC; thus, we omitted these terms from Equation (2). This result points to a non-significant effect of the clone over the relationship between biomass and different metrics. In this regard, Figure 6 shows the individual behavior of each clone in terms of the relationship between w_st and h_slices, revealing non-significant differences between clones.
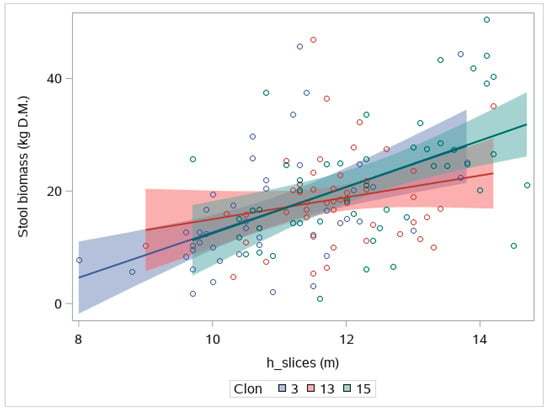
Figure 6.
Effect of clone over the relation between individual stool biomass and the height derived from TLS slicing (H_slice). Shaded indicate 95% confidence intervals.
3.2.2. Models for Total Biomass
Table 6 shows the results after fitting the three different models to total biomass. In this case, the TLS model was that which performed best, displaying high predictive capacity (R2adj = 0.9756, RMSE = 2.2082 t·ha−1, RRMSE = 2.9%) and almost 1:1 agreement between observed and predicted values (Figure 7a). The TLS model included the mean value of the Z-bounds from the bounding box of the stools within the plot (Plot-Z_bound) and the total volume of the stool sections (Plot-stool-vol) as predictors. For both the field inventory and the combined models, only one predictor significantly entered the model, this being the product between basal area (BA) and the mean height Hm (field-inventory model) or the product between BA and the mean height obtained from the bounding approach (Plot_Z_bound). Both models performed worse than the TLS model, with the combined model showing little superiority with respect to the field-inventory model (Table 6, Figure 7a,b). As in the case of the models for the individual stool, the inclusion of a random clone effect did not lead to an improvement in terms of AIC; thus, this term was removed from the models.

Table 6.
Parameter estimates and goodness-of-fit statistics for the three fitted models (Equation (2)) for total biomass.
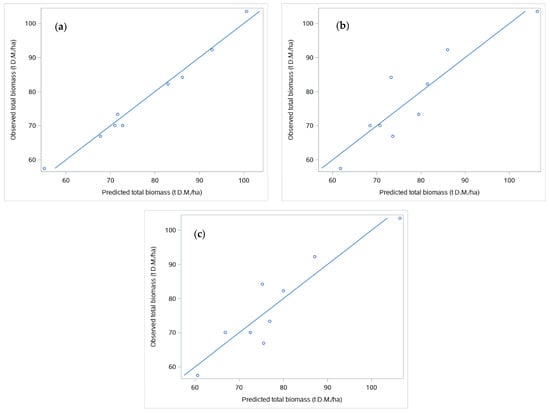
Figure 7.
Concordance between observed and predicted values of total biomass for the TLS model (a), Field-inventory model (b), and combined model (c). Straight lines indicate the 1:1.
4. Discussion
Our study reveals that using TLS metrics can provide a reliable, non-destructive approach for estimating aboveground biomass and other tree and plot metrics in poplar short-rotation coppices. Our results showed that TLS metrics presented significant correlations with field observations of the most relevant tree and plot attributes. Direct estimate of tree biomass from the TLS cloud can be assessed by means of estimating tree volume through QSM (quantitative structural modeling) assuming geometrical shapes (commonly cylinders) for both the stem and branches of the tree [34,65]. While this method seems optimal for estimating the biomass of adult or even extra mature trees [34,66,67], its application to short-rotation coppices is quite difficult since a single stool may share different small-sized shoots, and the dominant one is occluded by the lateral shoots, which makes difficult the correct definition of the main stem volume, where a large amount of biomass is accumulated. As an alternative, and conforming to the main innovation of our work, we do not aim to directly obtain estimates of stool biomass from TLS measurements, but we focus on obtaining easy-to-measure TLS-derived metrics to be included in the models for individual stool and plot biomass.
4.1. Individual Correlations
The TLS-derived heights, obtained using different procedures (bounding, voxelization, or slicing), were the TLS-derived metrics which presented the highest correlation not only with the stool height (as expected) but also with the diameter at breast height of the dominant shoot within the stool, and the total biomass of the stool. Surprisingly, at the plot level, we obtained a similar result, the mean value of the TLS-derived heights being the covariate highly correlated with plot attributes.
TLS has the potential to more accurately estimate tree height than traditional field measurements, although in dense forest environments, this assertion needs further testing [35]. Studies such as [58,68,69,70] have previously investigated the accuracy of tree height estimation using terrestrial laser scanning. They concluded that this methodology leads to an underestimation of 1–3 m caused by occlusions in the highest parts of the canopy. In addition, other studies have found that TLS-derived heights are strongly affected by the visibility of the tree, especially in denser stand conditions [69,71,72]. However, such limitations are likely to be less relevant in tree plantations such as that of our study, due to the greater homogeneity of the trees and lower complexity, compared with natural forest conditions. Moreover, these studies suggest that reliable tree heights can be expected when trees are below 20 m in height, as in this study (mean tree height 11.48 m), whereas the height of taller trees is likely to be underestimated by TLS [71]. Our results also agree with those of [34], who concluded that TLS-derived height correlates better with the reference tree height than field-measured height when evaluating height as a predictor for aboveground biomass. Moreover, our approach, based on scanning the individual stool from different positions, also reduces the problems associated with occlusion and inefficient identification of the terminal shoot of the stool.
The only tree-level metric measured in the field that is not highly correlated with TLS-derived heights is the number of shoots per stool (N_shoot), which showed a significant correlation with TLS metrics such as the area of the breast height slice (BH_sec), the maximum area of the slices included in the stool (Stool_sec) or the box at 1.3 m (Box_BH). This aspect reveals the importance of the number of shoots per stool in coppice species. In addition, the number of shoots per stool is directly related to variables such as diameter at breast height of the shoots—this variable generally being higher the lower the number of shoots in the stool- [16], or the profile of the stems—the latter generally being more sinuous the higher the number of shoots in the stool [73]. Furthermore, the average number of shoots per stool is often highly correlated to total biomass [23] and, therefore, is considered an explanatory variable when fitting biomass models for coppice species [15,23,29].
With regard to individual stool biomass, we identified significant correlations with the volumes computed after bounding box, slicing, or voxelization of the TLS-derived cloud point, although the observed correlations were lower than those obtained between stool biomass and the TLS-derived heights. Our results also provide evidence that, among the three different evaluated methods for processing the TLS cloud point (bounding box, slicing, and voxelization), the simplest method (bounding box) performs similarly or even more efficiently than the most complex ones (slicing or voxelization). This pattern is also observed when evaluating the correlation between the plot-level biomass and the TLS-derived metrics aggregated at the plot level. This result agrees with previous findings by [74] that compared the ability of Quantitative Structure Models (QSMs) and bounding boxing to estimate aboveground biomass in small Picea mariana (L.) trees, with a higher accuracy (R2adj = 0.89) for the bounding box in comparison to the QSM (R2adj = 0.82). In contrast, other studies such as [50,65] have demonstrated the superiority of slicing or voxelization over simpler methods in computing crown volume, crown structure, or aboveground biomass. In our case, the superiority of the bounding box may be related to the small distance between stools within the same row (1 m), which results in severe overlapping between the crowns of adjacent stools and complicates the individual segmentation of the trees. Moreover, this narrow spacing prevents crown expansion, thus constraining the shape of the stool. A similar finding was observed in [55], where the volume of a simple geometric box was identified as the best predictor for shrub volume. In this regard, shrubs and coppices may share similar properties, such as the existence of multiple stems, structural heterogeneity, and difficulty in differentiating between the main stem and crown.
Our finding that the simpler methods perform better is emphasized by the fact that in the case of voxelization methods, the most efficient one was that of a large voxel grid of 25 cm (low number of voxels) when compared with finer resolutions of voxelization. With regard to the use of virtual laser scanning in forestry applications, the findings of a study by [56] contradict those of our research in that these authors concluded that using regular fixed-sized voxel models with notably finer resolution (2 cm) presented high accuracy in the derived metrics. However, in their comparison of four voxel sizes (as in our study), it was concluded that the scaled voxels better represent gaps in the canopy, allowing for higher and more realistic crown penetration. Due to the structure of the stools in the evaluated plots, our results revealed that the effort involved in voxelization and subsequent quantification of full vs. empty voxels is not rewarded by an improvement in stool biomass prediction. In addition, the structure of SRC plantations makes it more difficult to scale the size of voxels depending on the section of the stool in the study.
4.2. Modeling Approach
The model with the best fit for individual stool biomass using only TLS metrics was based on the combination of H_slice and Stump_vol. As previously mentioned, TLS-derived heights, such as H-slice, are the TLS metrics that are strongly correlated with individual biomass (Table 4); thus, their inclusion in the model seems logical. In [66], TLS-derived height was successfully used as the main predictor of tree AGB, performing even better than crown-related covariates, as in our case. The other variable entering the model, the stump volume (Stump_vol), showed the strongest significant correlation (p-value < 0.0004) with the number of shoots. The number and size of the shoots in the stool were identified in this case as important variables for estimating aboveground biomass, which is supported by the findings of previous studies carried out in similar poplar plantations [15,23]. In particular, in a study by [23] of a three-year-old SRC, the authors reported that the average number of shoots per stool might have a major impact on models developed for subsequent rotations, as in our case, where the stools have one more rotation. These findings are also supported by the fact that both h_st and N_shoot are the covariates included in the model, which only considers field-inventory metrics.
However, none of the models based only on TLS metrics allowed the individual stool biomass to be predicted as efficiently (R2adj = 0.2490, RMSE = 8.7527 kg) as the models constructed using metrics recorded in traditional field inventories (R2adj = 0.7070, RMSE = 5.4675 kg). This may be due to the difficulty associated with the individual segmentation of the stools, given the dense overlap between the crowns of adjacent trees, which makes it difficult to correctly assign each shoot and branch to their corresponding stool. A potential improvement in the TLS-derived AGB models may be achieved if cloud point data were used to determine the diameter at breast height of the dominant shoot by means of algorithms such as least-square circle or cylinder fitting [75].
Furthermore, the combination of variables easily measured in the field and TLS metrics allowed more accurate predictions of stool biomass (R2adj = 0.7018, RMSE = 5.5152 kg), almost equaling the precision obtained by the model which only uses inventory metrics (R2adj = 0.7070, RMSE = 5.4675 kg). In our case, the best model was that which combined the product of the squared diameter at breast height of the largest shoot within the stool (measured in the field), with the height of the stool measured using TLS (d_st2. H_slice) together with the volume of the 10 cm-sided voxels with the number of returns > median (Vox10_med). This finding once more demonstrates the ability of TLS metrics to accurately estimate the height of the stool, avoiding the difficulties associated with directly measuring the height in the field from the ground [34]. The combined use of TLS and field-inventory metrics in models has previously been proposed by [76], who successfully modeled cone production in Pinus pinea L. using accurate crown metrics obtained from TLS and classical inventory metrics, such as mean quadratic diameter, as predictors. In this regard, TLS-derived metrics must be seen as a potential tool for obtaining accurate and unbiased measurements of tree parameters not easily accessible from the ground or whose measurement is highly laborious and time-consuming.
In the case of the total biomass per ha, TLS metrics entering the model are, as in the individual biomass models, the mean value of the heights derived from box bounding (Plot_Z_bound) and the plot-level sum of the stump volumes (Plot_Stump_volume), highlighting the importance of these metrics in determining aboveground biomass in poplar SRC. The most surprising finding was that, in this case, models which only depend on TLS metrics performed much better (R2adj = 0.9756, RMSE = 2.2082 t·ha−1) than those based only on field-inventory variables (R2adj = 0.8052, RMSE = 6.2447 t·ha−1). A potential explanation for this behavior may be the fact that, at the plot level, the errors arising when assigning individual branches or terminal shoots to their corresponding stool may be compensated. In addition, the low number of plots we were able to use in this study could also influence this behavior. Therefore, the inclusion of more plots would be advisable to improve these models in further studies.
4.3. Final Remarks
The results obtained in this work highlight the great potential of TLS to replace traditional SRC measurements. On the one hand, it allows biomass to be estimated in a similar way to field inventories without the need to measure individual stool heights from the ground. On the other hand, TLS permits the quantification and inclusion in the models of certain metrics that cannot easily be assessed through traditional inventories, such as stool volume or the volume of the 10 cm-sided voxels with the number of returns > median. These variables improve the model fit statistics and help us to better understand biomass development in poplar SRC.
In addition, stand-level biomass can be estimated more quickly and easily without the need for destructive sampling. In short, the method allows us to conduct a non-destructive, short-frequency, low-cost assessment of standing biomass and biomass increment in poplar SRC. Focusing on the potential for lowering costs, TLS inventories permit the reduction of working time in the field but require a large investment of deskwork for post-processing data, together with an initial investment in the acquisition of the scanning device. However, as new techniques for automatic stool segmentation are developed, new models relating easy-to-obtain TLS-derived metrics with biomass (as the one presented in this work) are constructed, and new and cheaper scanning equipment enters the market, costs for a TLS-based assessment of biomass will be reduced. In this sense, comparing costs between traditional field inventories and TLS surveys is a topic requiring further research.
TLS metrics permit a significant improvement in estimates obtained through allometric biomass models since these models predict population averages for individuals with the same characteristics [77]. Furthermore, TLS approaches allow us to account for regional and/or local variations in trees associated with different clones or possible abiotic/biotic effects, as could be the case with poplars in SRC. Future research initiatives should focus on testing the results obtained in this study, comparing a larger number of clones with more widely differing characteristics as well as different stand densities. In addition, a detailed analysis comparing the cost of TLS, traditional field, and mixed TLS-field inventories should be carried out. The development of new point cloud metrics should also be addressed, and new methodologies such as convex hulls should be included, along with the building of more efficient algorithms for automatic stool segmentation.
Author Contributions
Conceptualization, M.M.-M. and R.C.; methodology, M.M.-M. and R.C.; software, M.M.-M. and G.M.; formal analysis, M.M.-M. and R.C.; data acquisition, M.M.-M., G.M., H.S., N.O. and R.C.; writing—original draft preparation, M.M.-M., R.C., H.S. and N.O.; project administration, H.S. and R.C.; funding acquisition, R.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the MITECO (Spanish Ministry of Ecological Transition, EG-17-042-C2.2 and 20234TE005 agreements) and INIA (project IMP-2018-0042-C2.2).
Data Availability Statement
The data presented in this study are available on request from the leading author.
Acknowledgments
We thank Adam Collins for revision and editing the English grammar. We thank José Pablo de la Iglesia for his valuable help in the field. We also thank the reviewers and the academic editor, who provided useful comments to improve the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Bioplat Manual Sobre Biorrefinerías En España; Ministerio de Economía Industria y Competividad: Madrid, Spain, 2017; pp. 1–92.
- Bastin, J.-F.; Finegold, Y.; Garcia, C.; Mollicone, D.; Rezende, M.; Routh, D.; Zohner, C.M.; Crowther, T.W. Comment on “The Global Tree Restoration Potential. Science 2019, 365, 76–79. [Google Scholar] [CrossRef]
- Djomo, S.N.; El Kasmioui, O.; Ceulemans, R.J. Energy and greenhouse gas balance of bioenergy production from poplar and willow: A review. GCB Bioenergy 2011, 3, 181–197. [Google Scholar] [CrossRef]
- Corona, P.; Chianucci, F.; Marcelli, A.; Gianelle, D.; Fattorini, L.; Grotti, M.; Puletti, N.; Mattioli, W. Probabilistic sampling and estimation for large-scale assessment of poplar plantations in Northern Italy. Eur. J. For. Res. 2020, 139, 981–988. [Google Scholar] [CrossRef]
- Oliveira, N.; Pérez-Cruzado, C.; Cañellas, I.; Rodríguez-Soalleiro, R.; Sixto, H. Poplar Short Rotation Coppice Plantations under Mediterranean Conditions: The Case of Spain. Forests 2020, 11, 1352. [Google Scholar] [CrossRef]
- Stanturf, J.A.; Perdue, J.H.; Young, T.M.; Huang, X.; Guo, Z.; Dougherty, D.; Pigott, M. A spatially explicit approach to modeling biological productivity and economic attractiveness of short-rotation woody crops in the eastern USA. Energy Sustain. Soc. 2019, 9, 28. [Google Scholar] [CrossRef]
- Ruiz-Peinado, R.; Montero, G.; Cañellas, I. Growth and Yield Models for Pinus Halepensis Mill. Investig. For. Syst. 2001, 10, 179–201. [Google Scholar] [CrossRef]
- Verwijst, T.; Lndkvist, A.; Edelfeldt, S.; Albertsson, J. Development of Sustainable Willow Short Rotation Forestry in Northern Europe. In Biomass NOw-Sustainable Growth and Use; Matovic, D.M.D., Ed.; IntechOpen: London, UK, 2013; pp. 479–502. ISBN 0000957720. [Google Scholar]
- Verlinden, M.S.; Broeckx, L.S.; Ceulemans, R. First vs. second rotation of a poplar short rotation coppice: Above-ground biomass productivity and shoot dynamics. Biomass Bioenergy 2015, 73, 174–185. [Google Scholar] [CrossRef]
- Al Afas, N.; Marron, N.; Van Dongen, S.; Laureysens, I.; Ceulemans, R. Dynamics of biomass production in a poplar coppice culture over three rotations (11 years). For. Ecol. Manag. 2008, 255, 1883–1891. [Google Scholar] [CrossRef]
- Vanbeveren, S.P.; Ceulemans, R. Genotypic differences in biomass production during three rotations of short-rotation coppice. Biomass Bioenergy 2018, 119, 198–205. [Google Scholar] [CrossRef]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe; Finnish Society of Forest Science, Finnish Forest Research Institute: Helsinki, Finland, 2005; Volume 4, ISBN 9514019830. [Google Scholar]
- Zabek, L.M.; Prescott, C.E. Biomass equations and carbon content of aboveground leafless biomass of hybrid poplar in Coastal British Columbia. For. Ecol. Manag. 2006, 223, 291–302. [Google Scholar] [CrossRef]
- Huber, J.A.; May, K.; Hülsbergen, K.-J. Allometric tree biomass models of various species grown in short-rotation agroforestry systems. Eur. J. For. Res. 2017, 136, 75–89. [Google Scholar] [CrossRef]
- Oliveira, N.; Rodríguez-Soalleiro, R.; Hernández, M.J.; Cañellas, I.; Sixto, H.; Pérez-Cruzado, C. Improving biomass estimation in a Populus short rotation coppice plantation. For. Ecol. Manag. 2017, 391, 194–206. [Google Scholar] [CrossRef]
- Benetka, V.; Novotná, K.; Štochlová, P. Biomass production of Populus nigra L. clones grown in short rotation coppice systems in three different environments over four rotations. iForest-Biogeosci. For. 2014, 7, 233–239. [Google Scholar] [CrossRef]
- Sixto, H.; Cañellas, I.; van Arendonk, J.; Ciria, P.; Camps, F.; Sánchez, M.; Sánchez-González, M. Growth potential of different species and genotypes for biomass production in short rotation in Mediterranean environments. For. Ecol. Manag. 2015, 354, 291–299. [Google Scholar] [CrossRef]
- Verwijst, T.; Telenius, B. Biomass estimation procedures in short rotation forestry. For. Ecol. Manag. 1999, 121, 137–146. [Google Scholar] [CrossRef]
- Mosseler, A.; Major, J.E.; Labrecque, M.; Larocque, G.R. Allometric relationships in coppice biomass production for two North American willows (Salix spp.) across three different sites. For. Ecol. Manag. 2014, 320, 190–196. [Google Scholar] [CrossRef]
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Ambagau’, Y.; Palm, C.A. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Ben Brahim, M.; Gavaland, A.; Cabanettes, A. Generalized Allometric Regression to Estimate Biomass of Populus in Short-rotation Coppice. Scand. J. For. Res. 2000, 15, 171–176. [Google Scholar] [CrossRef]
- Dillen, S.Y.; Marron, N.; Bastien, C.; Ricciotti, L.; Salani, F.; Sabatti, M.; Pinel, M.P.C.; Rae, A.M.; Taylor, G.; Ceulemans, R. Effects of environment and progeny on biomass estimations of five hybrid poplar families grown at three contrasting sites across Europe. For. Ecol. Manag. 2007, 252, 12–23. [Google Scholar] [CrossRef]
- Oliveira, N.; Sixto, H.; Cañellas, I.; Rodríguez-Soalleiro, R.; Pérez-Cruzado, C. Productivity model and reference diagram for short rotation biomass crops of poplar grown in Mediterranean environments. Biomass Bioenergy 2015, 72, 309–320. [Google Scholar] [CrossRef]
- Oliveira, N.; Rodríguez-Soalleiro, R.; Pérez-Cruzado, C.; Cañellas, I.; Sixto, H. On the Genetic Affinity of Individual Tree Biomass Allometry in Poplar Short Rotation Coppice. BioEnergy Res. 2017, 10, 525–535. [Google Scholar] [CrossRef]
- Dickmann, D.I. Silviculture and biology of short-rotation woody crops in temperate regions: Then and now. Biomass Bioenergy 2006, 30, 696–705. [Google Scholar] [CrossRef]
- Tallis, M.J.; Casella, E.; Henshall, P.A.; Aylott, M.J.; Randle, T.J.; Morison, J.I.L.; Taylor, G. Development and evaluation of ForestGrowth-SRC a process-based model for short rotation coppice yield and spatial supply reveals poplar uses water more efficiently than willow. GCB Bioenergy 2013, 5, 53–66. [Google Scholar] [CrossRef]
- Ruiz-Peinado, R.; Del Rio, M.; Montero, G. New models for estimating the carbon sink capacity of Spanish softwood species. For. Syst. 2011, 20, 176–188. [Google Scholar] [CrossRef]
- Gertrudix, R.R.-P.; Montero, G.; del Rio, M. Biomass models to estimate carbon stocks for hardwood tree species. For. Syst. 2012, 21, 42–52. [Google Scholar] [CrossRef]
- Menéndez-Miguélez, M.; Canga, E.; Barrio-Anta, M.; Majada, J.; Álvarez-Álvarez, P. A three level system for estimating the biomass of Castanea sativa Mill. coppice stands in north-west Spain. For. Ecol. Manag. 2013, 291, 417–426. [Google Scholar] [CrossRef]
- Menéndez-Miguélez, M.; Ruiz-Peinado, R.; Del Río, M.; Calama, R. Improving tree biomass models through crown ratio patterns and incomplete data sources. Eur. J. For. Res. 2021, 140, 675–689. [Google Scholar] [CrossRef]
- Menéndez-Miguélez, M.; Calama, R.; Del Río, M.; Madrigal, G.; López-Senespleda, E.; Pardos, M.; Ruiz-Peinado, R. Species-specific and generalized biomass models for estimating carbon stocks of young reforestations. Biomass Bioenergy 2022, 161, 106453. [Google Scholar] [CrossRef]
- Picard, N.; Saint-André, L.; Henry, M. Manual for Building Tree Volume and Biomass Allometric Equations: From Field Measurement to Prediction; Food and Agricultural Organization of the United Nations: Rome, Italy; Centre de Coopération Internationale En Recherche Agronomique Pour Le Développement: Paris, France, 2012; ISBN 9789251073476. [Google Scholar]
- Metz, J.Ô.; Seidel, D.; Schall, P.; Scheffer, D.; Schulze, E.-D.; Ammer, C. Crown modeling by terrestrial laser scanning as an approach to assess the effect of aboveground intra- and interspecific competition on tree growth. For. Ecol. Manag. 2013, 310, 275–288. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.S.; Avitabile, V.; Disney, M.; Armston, J.D.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Disney, M.I.; Vicari, M.B.; Burt, A.; Calders, K.; Lewis, S.L.; Raumonen, P.; Wilkes, P. Weighing trees with lasers: Advances, challenges and opportunities. Interface Focus 2018, 8, 20170048. [Google Scholar] [CrossRef] [PubMed]
- Stovall, A.E.L.; Shugart, H.H. Improved Biomass Calibration and Validation With Terrestrial LiDAR: Implications for Future LiDAR and SAR Missions. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3527–3537. [Google Scholar] [CrossRef]
- Taeroe, A.; Nord-Larsen, T.; Stupak, I.; Raulund-Rasmussen, K. Allometric Biomass, Biomass Expansion Factor and Wood Density Models for the OP42 Hybrid Poplar in Southern Scandinavia. BioEnergy Res. 2015, 8, 1332–1343. [Google Scholar] [CrossRef]
- Calders, K.; Armston, J.; Newnham, G.; Herold, M.; Goodwin, N. Implications of sensor configuration and topography on vertical plant profiles derived from terrestrial LiDAR. Agric. For. Meteorol. 2014, 194, 104–117. [Google Scholar] [CrossRef]
- Puletti, N.; Grotti, M.; Ferrara, C.; Chianucci, F. Influence of voxel size and point cloud density on crown cover estimation in poplar plantations using terrestrial laser scanning. Ann. Silvic. Res. 2021, 46, 148–154. [Google Scholar] [CrossRef]
- Dassot, M.; Colin, A.; Santenoise, P.; Fournier, M.; Constant, T. Terrestrial laser scanning for measuring the solid wood volume, including branches, of adult standing trees in the forest environment. Comput. Electron. Agric. 2012, 89, 86–93. [Google Scholar] [CrossRef]
- Radtke, P.J.; Bolstad, P.V. Laser point-quadrat sampling for estimating foliage-height profiles in broad-leaved forests. Can. J. For. Res. 2001, 31, 410–418. [Google Scholar] [CrossRef]
- Côté, J.-F.; Widlowski, J.-L.; Fournier, R.A.; Verstraete, M.M. The structural and radiative consistency of three-dimensional tree reconstructions from terrestrial lidar. Remote Sens. Environ. 2009, 113, 1067–1081. [Google Scholar] [CrossRef]
- Puletti, N.; Grotti, M.; Scotti, R. Evaluating the Eccentricities of Poplar Stem Profiles with Terrestrial Laser Scanning. Forests 2019, 10, 239. [Google Scholar] [CrossRef]
- Ashcroft, M.B.; Gollan, J.R.; Ramp, D. Creating vegetation density profiles for a diverse range of ecological habitats using terrestrial laser scanning. Methods Ecol. Evol. 2014, 5, 263–272. [Google Scholar] [CrossRef]
- Tumbo, S.D.; Salyani, M.; Whitney, J.D.; Wheaton, T.A.; Miller, W.M. Investigation of laser and ultrasonic ranging sensors for measurements of citrus canopy volume. Appl. Eng. Agric. 2002, 18, 367. [Google Scholar] [CrossRef]
- Lee, K.H.; Ehsani, R. A Laser Scanner Based Measurement System for Quantification of Citrus Tree Geomtric Characteristics. Am. Soc. Agric. Biol. 2009, 25, 777–788. [Google Scholar]
- Moorthy, I.; Miller, J.R.; Berni, J.A.J.; Zarco-Tejada, P.; Hu, B.; Chen, J. Field characterization of olive (Olea europaea L.) tree crown architecture using terrestrial laser scanning data. Agric. For. Meteorol. 2011, 151, 204–214. [Google Scholar] [CrossRef]
- Sun, Y.; Liang, X.; Liang, Z.; Welham, C.; Li, W. Deriving Merchantable Volume in Poplar through a Localized Tapering Function from Non-Destructive Terrestrial Laser Scanning. Forests 2016, 7, 87. [Google Scholar] [CrossRef]
- Chianucci, F.; Puletti, N.; Grotti, M.; Ferrara, C.; Giorcelli, A.; Coaloa, D.; Tattoni, C. Nondestructive Tree Stem and Crown Volume Allometry in Hybrid Poplar Plantations Derived from Terrestrial Laser Scanning. For. Sci. 2020, 66, 737–746. [Google Scholar] [CrossRef]
- Fernández-Sarría, A.; Martínez, L.; Velázquez-Martí, B.; Sajdak, M.; Estornell, J.; Recio, J.A. Different methodologies for calculating crown volumes of Platanus hispanica trees using terrestrial laser scanner and a comparison with classical dendrometric measurements. Comput. Electron. Agric. 2013, 90, 176–185. [Google Scholar] [CrossRef]
- Côté, J.-F.; Fournier, R.A.; Frazer, G.W.; Niemann, K.O. A fine-scale architectural model of trees to enhance LiDAR-derived measurements of forest canopy structure. Agric. For. Meteorol. 2012, 166–167, 72–85. [Google Scholar] [CrossRef]
- Hackenberg, J.; Spiecker, H.; Calders, K.; Disney, M.; Raumonen, P. Simple Tree—An Efficient Open Source Tool to Build Tree Models from TLS Clouds. Forests 2015, 6, 4245–4294. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Rosell, J.R.; Llorens, J.; Sanz, R.; Arnó, J.; Ribes-Dasi, M.; Masip, J.; Escolà, A.; Camp, F.; Solanelles, F.; Gràcia, F.; et al. Obtaining the three-dimensional structure of tree orchards from remote 2D terrestrial LIDAR scanning. Agric. For. Meteorol. 2009, 149, 1505–1515. [Google Scholar] [CrossRef]
- Li, L.; Mu, X.; Soma, M.; Wan, P.; Qi, J.; Hu, R.; Zhang, W.; Tong, Y.; Yan, G. An Iterative-Mode Scan Design of Terrestrial Laser Scanning in Forests for Minimizing Occlusion Effects. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3547–3566. [Google Scholar] [CrossRef]
- Weiser, H.; Winiwarter, L.; Anders, K.; Fassnacht, F.E.; Höfle, B. Opaque voxel-based tree models for virtual laser scanning in forestry applications. Remote Sens. Environ. 2021, 265, 112641. [Google Scholar] [CrossRef]
- Seidel, D.; Ammer, C. Efficient measurements of basal area in short rotation forests based on terrestrial laser scanning under special consideration of shadowing. iForest-Biogeosci. For. 2014, 7, 227–232. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Flade, L.; Hopkinson, C.; Chasmer, L. Allometric Equations for Shrub and Short-Stature Tree Aboveground Biomass within Boreal Ecosystems of Northwestern Canada. Forests 2020, 11, 1207. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. Voxel-Based 3-D Modeling of Individual Trees for Estimating Leaf Area Density Using High-Resolution Portable Scanning Lidar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3610–3618. [Google Scholar] [CrossRef]
- Hyyppä, E.; Hyyppä, J.; Hakala, T.; Kukko, A.; Wulder, M.A.; White, J.C.; Pyörälä, J.; Yu, X.; Wang, Y.; Virtanen, J.-P.; et al. Under-canopy UAV laser scanning for accurate forest field measurements. ISPRS J. Photogramm. Remote Sens. 2020, 164, 41–60. [Google Scholar] [CrossRef]
- Béland, M.; Baldocchi, D.D.; Widlowski, J.-L.; Fournier, R.A.; Verstraete, M.M. On seeing the wood from the leaves and the role of voxel size in determining leaf area distribution of forests with terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
- Hilker, T.; van Leeuwen, M.; Coops, N.C.; Wulder, M.A.; Newnham, G.J.; Jupp, D.L.B.; Culvenor, D.S. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a Douglas-fir dominated forest stand. Trees-Struct. Funct. 2010, 24, 819–832. [Google Scholar] [CrossRef]
- Hosoi, F.; Omasa, K. Estimation of Leaf Area Density Profiles of Japanese Maple and Camellia Woody Canopies Using Portable Scanning Lidars. Eco-Engineering 2011, 23, 105–109. [Google Scholar] [CrossRef]
- Calders, K.; Verbeeck, H.; Burt, A.; Origo, N.; Nightingale, J.; Malhi, Y.; Wilkes, P.; Raumonen, P.; Bunce, R.G.H.; Disney, M. Laser scanning reveals potential underestimation of biomass carbon in temperate forest. Ecol. Solut. Evid. 2022, 3, e12197. [Google Scholar] [CrossRef]
- Burt, A.; Vicari, M.B.; da Costa, A.C.L.; Coughlin, I.; Meir, P.; Rowland, L.; Disney, M. New insights into large tropical tree mass and structure from direct harvest and terrestrial lidar. R. Soc. Open Sci. 2021, 8, 201458. [Google Scholar] [CrossRef]
- Dong, Y.; Fan, G.; Zhou, Z.; Liu, J.; Wang, Y.; Chen, F. Low Cost Automatic Reconstruction of Tree Structure by AdQSM with Terrestrial Close-Range Photogrammetry. Forests 2021, 12, 1020. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing forest metrics with a ground-based scanning lidar. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef]
- Maas, H.-G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic Stem Mapping Using Single-Scan Terrestrial Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is field-measured tree height as reliable as believed—A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests 2018, 9, 398. [Google Scholar] [CrossRef]
- Menéndez-Miguélez, M.; Canga, E.; Álvarez-Álvarez, P.; Majada, J. Stem taper function for sweet chestnut (Castanea sativa Mill.) coppice stands in northwest Spain. Ann. For. Sci. 2014, 71, 761–770. [Google Scholar] [CrossRef]
- Wagers, S.; Castilla, G.; Filiatrault, M.; Sanchez-Azofeifa, G.A. Using TLS-Measured Tree Attributes to Estimate Aboveground Biomass in Small Black Spruce Trees. Forests 2021, 12, 1521. [Google Scholar] [CrossRef]
- Terryn, L.; Calders, K.; Åkerblom, M.; Bartholomeus, H.; Disney, M.; Levick, S.; Origo, N.; Raumonen, P.; Verbeeck, H. Analysing individual 3D tree structure using the R package ITSMe. Methods Ecol. Evol. 2022, 14, 231–241. [Google Scholar] [CrossRef]
- Schneider, R.; Calama, R.; Martin-Ducup, O. Understanding Tree-to-Tree Variations in Stone Pine (Pinus pinea L.) Cone Production Using Terrestrial Laser Scanner. Remote Sens. 2020, 12, 173. [Google Scholar] [CrossRef]
- Olivier, M.-D.; Robert, S.; Richard, A.F. A method to quantify canopy changes using multi-temporal terrestrial lidar data: Tree response to surrounding gaps. Agric. For. Meteorol. 2017, 237–238, 184–195. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).