Centimeter-Level Orbit Determination of GRACE-C Using IGS-RTS Data
Abstract
1. Introduction
2. Methods
2.1. Real-Time Orbit and Clock Recovery
2.1.1. Real-Time Orbit Recovery
2.1.2. Real-Time Clock Recovery
2.2. Clock Evaluation
2.2.1. Coordinate Frame Unification
2.2.2. Time Frame Unification
- 1.
- Trend Error Correction
- 2.
- Systematic Bias Correction
3. Accuracy Evaluation of SSR Products
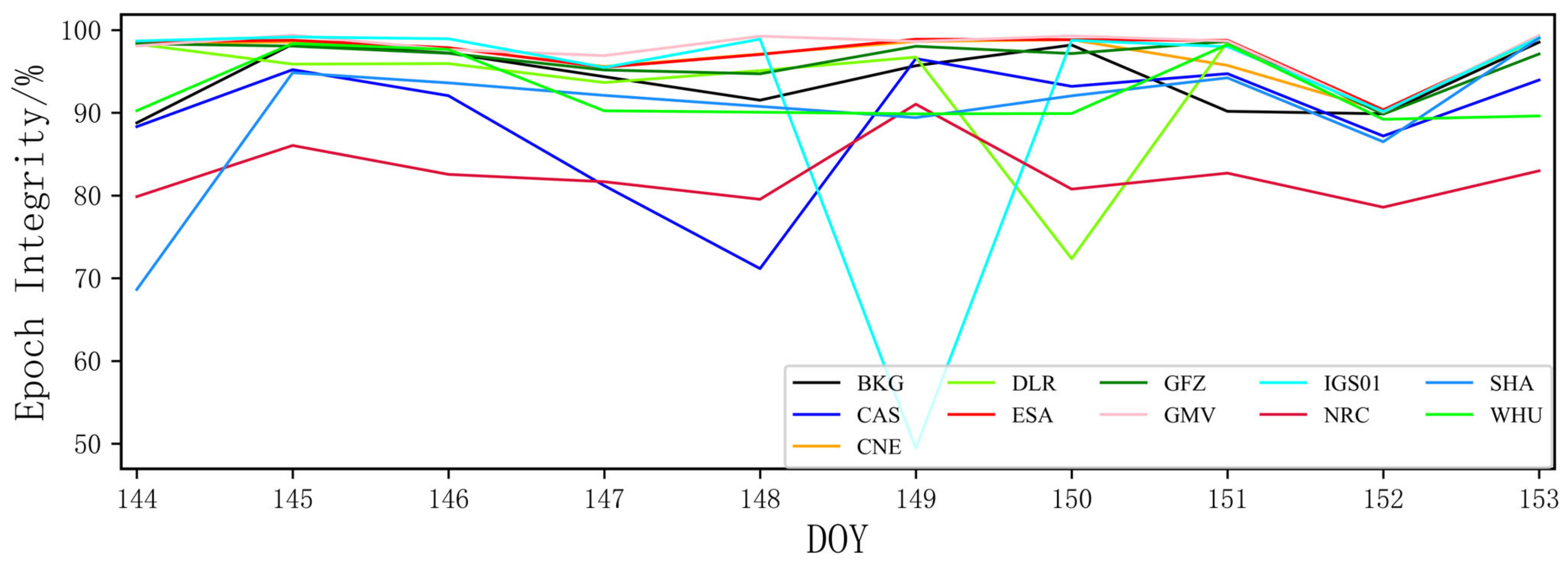
3.1. Integrity
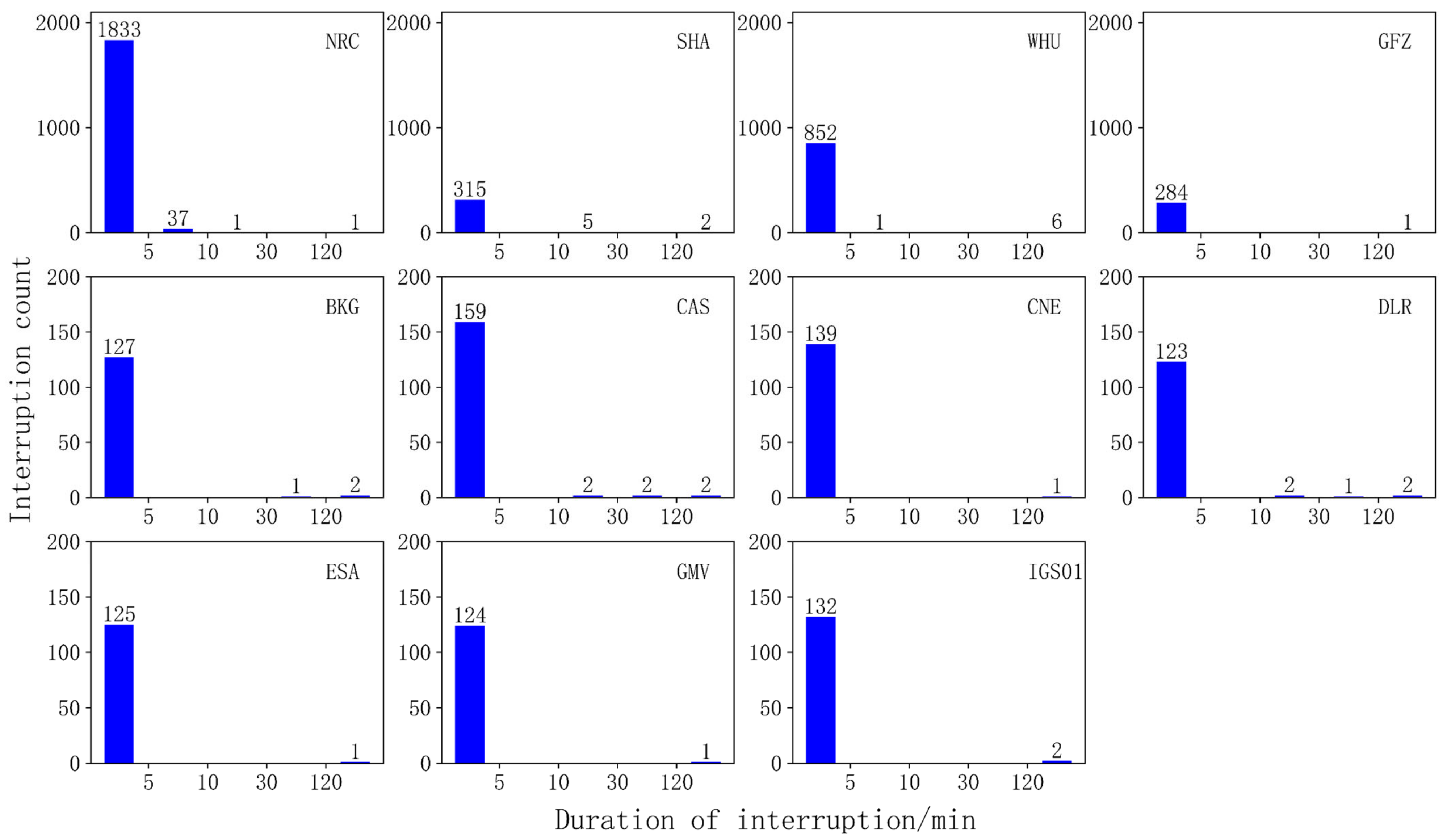
3.2. Continuity
3.3. Accuracy
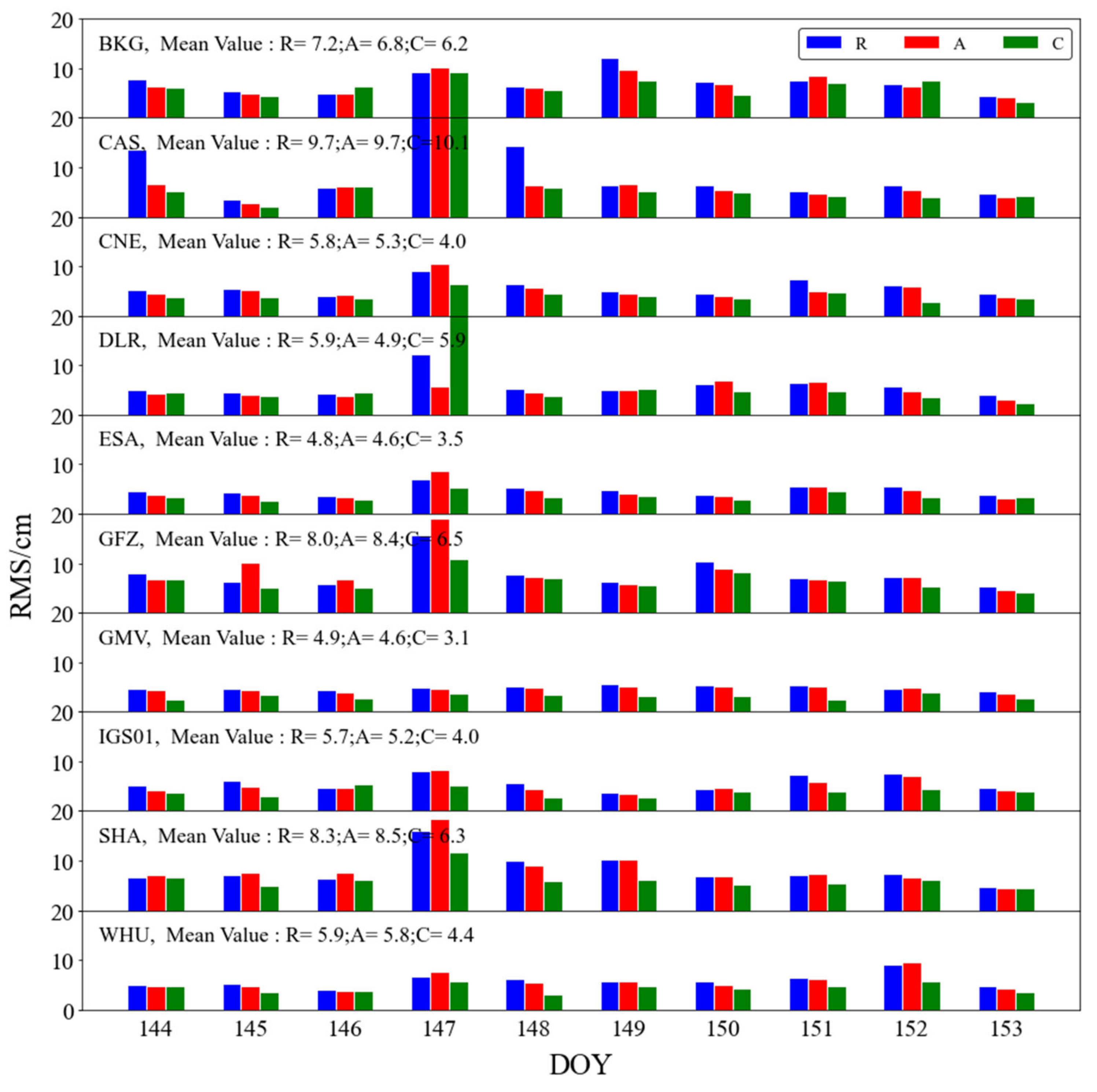
3.3.1. Orbit Accuracy
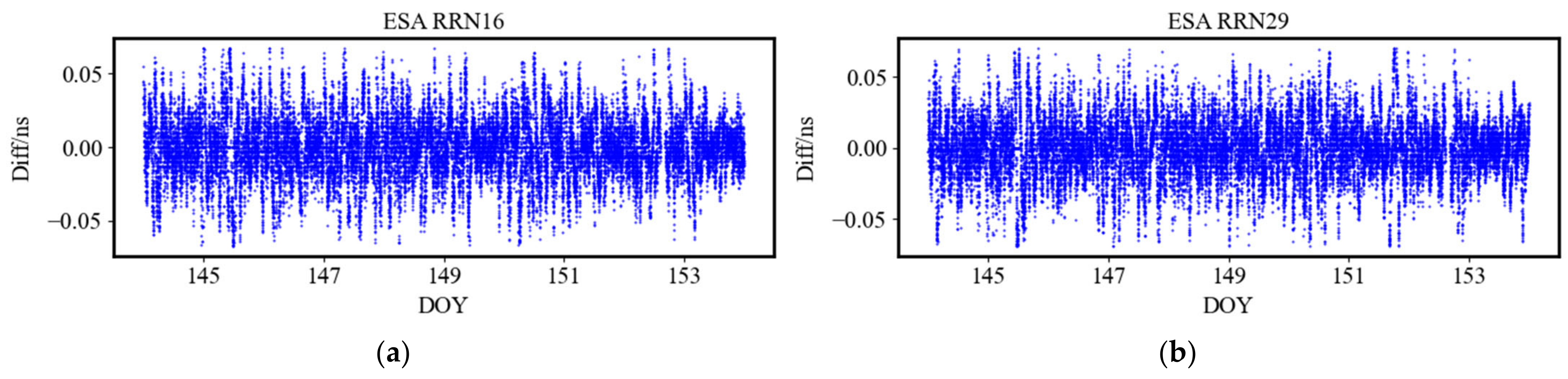
3.3.2. Clock Error Accuracy
4. Space-Borne POD Experiment and Accuracy Analysis
4.1. Reduced-Dynamic Precise Orbit Determination
4.2. Kinematic Precise Orbit Determination
5. Conclusions
- (1)
- By studying the real-time orbit and clock correction products provided by 11 research institutions, including BKG, CAS, CNES, DLR, ESA, GFZ, GMV, IGS, NRC, SHA, and WHU, we concluded that the product integrity of BKG, CAS, and NRC needs to be improved, and the product continuity of NRC and WHU needs to be strengthened.
- (2)
- Compared with IGS final precise products, the numerical results showed that the RTS orbit accuracy of all ACs reached the centimeter level and the RMS in the radial direction was better than 0.02 m. Among the ACs, the orbit accuracy of IGS, SHA, and WHU was relatively high. The real-time clock error STD was 30 ps overall; WHU and CNES performed best, with STDs of 15.65 ps and 16.98 ps, respectively. In addition, the clock error accuracy was related to the Block. It was verified that the accuracy of Block IIR and Block IIR-M was slightly worse than that of Block IIF and Block IIIA.
- (3)
- Using RTS orbit and clock products, the radial accuracy of the GRACE-C space-borne GPS orbit determination based on the reduced-dynamic and kinematic methods reached the centimeter level and the average three-dimensional position accuracy values were 3.8 cm and 10.6 cm, respectively. As expected, the reduced-dynamic orbit was more robust and less affected by product integrity and continuity. It is advised that RTS products are used to carry out large-scale ultra-rapid orbit determinations for LEO satellites in the future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tapley, B.; Ries, J.C.; Davis, G.; Eanes, R.; Schultz, B.; Shum, C.K.; Watkins, M.; Marshall, J.; Nerem, R.; Putney, B. Precision Orbit Determination for TOPEX/Poseidon. J. Geophys. Res. Atmos. 1995, 99, 24383–24404. [Google Scholar] [CrossRef]
- Kuang, D.; Bar-Sever, Y.; Bertiger, W.; Desai, S.; Haines, B.; Iijima, B.; Kruizinga, G.; Meehan, T.; Romans, L. Precise Orbit Determination for CHAMP Using GPS Data from BlackJack Receiver. In Proceedings of the 2001 National Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 24 January 2001; pp. 762–770. [Google Scholar]
- Cerri, L.; Berthias, J.P.; Bertiger, W.I.; Haines, B.J.; Lemoine, F.G.; Mercier, F.; Ries, J.C.; Willis, P.; Zelensky, N.P.; Ziebart, M. Precision Orbit Determination Standards for the Jason Series of Altimeter Missions. Mar. Geod. 2010, 33, 379–418. [Google Scholar] [CrossRef]
- Jäggi, A.; Hugentobler, U.; Bock, H.; Beutler, G. Precise Orbit Determination for GRACE Using Undifferenced or Doubly Differenced GPS Data. Adv. Space Res. 2007, 39, 1612–1619. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Jäggi, A. Precise Orbit Determination of the Sentinel-3A Altimetry Satellite Using Ambiguity-Fixed GPS Carrier Phase Observations. J. Geod. 2018, 92, 711–726. [Google Scholar] [CrossRef]
- Darugna, F.; Casotto, S.; Bardella, M.; Sciarratta, M.; Zoccarato, P. Sub-Decimeter Onboard Orbit Determination of LEO Satellites Using SSR Corrections: A Galileo-Based Case Study for the Sentinel-6A Satellite. Remote Sens. 2022, 14, 6121. [Google Scholar] [CrossRef]
- Li, K.; Zhou, X.; Wang, W.; Gao, Y.; Zhao, G.; Tao, E.; Xu, K. Centimeter-Level Orbit Determination for TG02 Spacelab Using Onboard GNSS Data. Sensors 2018, 18, 2671. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Arnold, D.; Girardin, V.; Villiger, A.; Jggi, A. Dynamic GPS-Based LEO Orbit Determination with 1 Cm Precision Using the Bernese GNSS Software. Adv. Space Res. 2020, 67, 788–805. [Google Scholar] [CrossRef]
- Van den IJssel, J.; Encarnação, J.; Doornbos, E.; Visser, P. Precise Science Orbits for the Swarm Satellite Constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Allahvirdi-Zadeh, A.; El-Mowafy, A. Precise Orbit Determination of CubeSats Using a Proposed Observations Weighting Model. In Proceedings of the Scientific Assembly of the International Association of Geodesy (IAG), Beijing, China, 28 June 2021. [Google Scholar]
- Caissy, M.; Agrotis, L.; Weber, G.; Fisher, S. The IGS Real-Time Service. In Proceedings of the EGU General Assembly Conference Abstracts 2013, Vienna, Austria, 7–12 April 2013. [Google Scholar]
- Agrotis, L.; Caissy, M.; Ruelke, A.; Fisher, S. Real-Time Service Technical Report 2014. In IGS Technical Report 2014; IGS Central Bureau: Pasadena, CA, USA, 2014. [Google Scholar]
- Rülke, A.; Agrotis, L. IGS Realtime Service Technical Report 2016. In IGS Technical Report 2016; IGS Central Bureau: Pasadena, CA, USA, 2016. [Google Scholar]
- Weber, G.; Mervart, L.; Stürze, A.; Rülke, A.; Stcker, D. BKG Ntrip Client (BNC); Version 2.12; Mitteilungen des Bundesamtes für Kartographie und Geodäsie: Frankfurt, Germany, 2016. [Google Scholar]
- Takasu, T. An Open Source Program Package for Gnss Positioning; RTKLIB: Hokuto, Japan, 2013. [Google Scholar]
- Zhang, Y. Research on Real-Time High Precision BeiDou Positioning Service System. Acta Geod. Cartogr. Sin. 2018, 47, 1293. [Google Scholar]
- Tegedor, J.; Lapucha, D.; Melgrd, T.E.; Vigen, E.; Strandli, R. The New G4: Multi-Constellation Precise Point Positioning Using GPS, Glonass, Galileo and BeiDou. In Proceedings of the ION GNSS+ 2015, Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Jokinen, A.; Ellum, C.; Neumann, J.; Chan, D.; Morley, T. Kinematic Performance of NovAtel CORRECT with Terrastar-D Precise Point Positioning (PPP) Service. In Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2014), Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- Dixon, K. StarFire: A Global SBAS for Sub-Decimeter Precise Point Positioning. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation 2006, Fort Worth, TX, USA, 26–29 September 2006. [Google Scholar]
- Miya, M.; Fujita, S.; Sato, Y.; Ota, K.; Takiguchi, J. Centimeter Level Augmentation Service (CLAS) in Japanese Quasi-Zenith Satellite System, Its User Interface, Detailed Design, and Plan. In Proceedings of the 29th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016. [Google Scholar]
- Pintor, P.; González, E.; Senado, A.; Bohlig, P.; Sperl, A.; Henkel, P.; Simón, J.; Hernández, C.; de Blas, J.; Vázquez, J. Galileo High Accuracy Service (HAS) Algorithm and Receiver Development and Testing. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022. [Google Scholar]
- Xu, Y.; Yang, Y.; Li, J. Performance Evaluation of BDS-3 PPP-B2b Precise Point Positioning Service. GPS Solut. 2021, 25, 142. [Google Scholar] [CrossRef]
- Barrios, J.; Caro, J.; Calle, J.D.; Carbonell, E.; Pericacho, J.G.; Fernández, G.; Esteban, V.M.; Fernández, M.A.; Bravo, F.; Torres, B.; et al. Update on Australia and New Zealand DFMC SBAS and PPP System Results. In Proceedings of the 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018. [Google Scholar]
- Li, B.; Ge, H.; Bu, Y.; Zheng, Y.; Yuan, L. Comprehensive Assessment of Real-Time Precise Products from IGS Analysis Centers. Satell. Navig. 2022, 3, 12. [Google Scholar] [CrossRef]
- Alcay, S.; Turgut, M. Evaluation of the Positioning Performance of Multi-GNSS RT-PPP Method. Arab. J. Geosci. 2021, 14, 155. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, Y.; Chen, J.; Chen, Q.; Xu, K.; Wang, B. Performance Assessment of Multi-GNSS Real-Time Products from Various Analysis Centers. Remote Sens. 2022, 15, 140. [Google Scholar] [CrossRef]
- Kazmierski, K.; Sośnica, K.; Hadas, T. Quality Assessment of Multi-GNSS Orbits and Clocks for Real-Time Precise Point Positioning. GPS Solut. 2017, 22, 11. [Google Scholar]
- Elsobeiey, M.; Al-Harbi, S. Performance of Real-Time Precise Point Positioning Using IGS Real-Time Service. GPS Solut. 2016, 20, 565–571. [Google Scholar] [CrossRef]
- Zhiyu, W.; Zishen, L.; Liang, W.; Xiaoming, W.; Hong, Y. Assessment of Multiple GNSS Real-Time SSR Products from Different Analysis Centers. ISPRS Int. J. Geo-Inf. 2018, 7, 85. [Google Scholar]
- Wang, Z.; Li, Z.; Wang, L.; Wang, N.; Yang, Y.; Li, R.; Zhang, Y.; Liu, A.; Yuan, H.; Hoque, M. Comparison of the Real-Time Precise Orbit Determination for LEO between Kinematic and Reduced-Dynamic Modes. Measurement 2022, 187, 110224. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Wang, N.; Hoque, M.; Wang, L.; Li, R.; Zhang, Y.; Yuan, H. Real-Time Precise Orbit Determination for LEO between Kinematic and Reduced-Dynamic with Ambiguity Resolution. Aerospace 2022, 9, 25. [Google Scholar] [CrossRef]
- Giordano, P.; Zoccarato, P.; Otten, M.; Crisci, M. P2OD: Real-Time Precise Onboard Orbit Determination for LEO Satellites. In Proceedings of the 30th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017. [Google Scholar]
- El-Mowafy, A.; Deo, M.; Kubo, N. Maintaining Real-Time Precise Point Positioning during Outages of Orbit and Clock Corrections. GPS Solut. 2017, 21, 937–947. [Google Scholar] [CrossRef]
- Hauschild, A.; Tegedor, J.; Montenbruck, O.; Visser, H.; Markgraf, M. Precise Onboard Orbit Determination for LEO Satellites with Real-Time Orbit and Clock Corrections. In Proceedings of the 29th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016. [Google Scholar]
- El-Mowafy; Ahmed Real-Time Precise Point Positioning Using Orbit and Clock Corrections as Quasi-Observations for Improved Detection of Faults. J. Navig. 2018, 71, 769–787. [CrossRef]
- Svehla, D.; Rothacher, M. Kinematic and Reduced-Dynamic Precise Orbit Determination of Low Earth Orbiters. Adv. Geosci. 2003, 1, 47–56. [Google Scholar] [CrossRef]
- Wu, S.C.; Yunck, T.P.; Thornton, C.L. Reduced-Dynamic Technique for Precise Orbit Determination of Low Earth Satellites. J. Guid. Control Dyn. 2012, 14, 24–30. [Google Scholar] [CrossRef]
- Kouba, J.; Springer, T. New IGS Station and Satellite Clock Combination. GPS Solut. 2001, 4, 31–36. [Google Scholar] [CrossRef]
- Dai, X.; Gong, X.; Li, C.; Qing, Y.; Gu, S.; Lou, Y. Real-Time Precise Orbit and Clock Estimation of Multi-GNSS Satellites with Undifferenced Ambiguity Resolution. J. Geod. 2022, 96, 73. [Google Scholar] [CrossRef]
- Tan, B.; Yuan, Y.; Ai, Q.; Zha, J. Real-Time Multi-GNSS Precise Orbit Determination Based on the Hourly Updated Ultra-Rapid Orbit Prediction Method. Remote Sens. 2022, 14, 4412. [Google Scholar] [CrossRef]





| AC | Mount Point | Supported System | Interval for Orbit and Clock Corrections (s) |
|---|---|---|---|
| BKG | SSRA00BKG0 | G | 60, 5 |
| CAS | SSRA00CAS0 | GREC | 5, 5 |
| CNE | SSRA00CNE0 | GREC | 5, 5 |
| DLR | SSRA00DLR0 | GREC | 30, 5 |
| ESA | SSRA00ESA0 | G | 5, 5 |
| GFZ | SSRA00GFZ0 | GREC | 5, 5 |
| GMV | SSRA00GMV0 | GRE | 5, 5 |
| IGS 1 | SSRA01IGS0 | G | 5, 5 |
| SSRA02IGS0 | GR | 60, 10 | |
| SSRA03IGS0 | GREC | 60, 10 | |
| NRC | SSRA00NRC0 | G | 5, 5 |
| SHA | SSRA00SHA0 | GREC | 5, 5 |
| WHU | SSRA00WHU0 | GREC | 5, 5 |
| ACs | Block IIR | Block IIR-M | Block IIF | Block IIIA |
|---|---|---|---|---|
| BKG | 25.02 | 23.88 | 21.67 | 22.96 |
| CAS | 31.89 | 30.08 | 22.26 | 22.77 |
| CNE | 17.86 | 17.66 | 16.03 | 17.05 |
| DLR | 19.34 | 20.93 | 21.09 | 18.65 |
| ESA | 19.8 | 19.89 | 17.79 | 19.03 |
| GFZ | 26.95 | 24.86 | 21.51 | 21.41 |
| GMV | 35.83 | 37.38 | 24.23 | 24.17 |
| IGS01 | 36.94 | 43.16 | 23.9 | 22.19 |
| NRC | 21.13 | 20.93 | 18.22 | 19.70 |
| SHA | 20.88 | 22.19 | 17.42 | 18.47 |
| WHU | 16.75 | 16.59 | 14.36 | 15.91 |
| Mean | 24.76 | 25.23 | 19.86 | 20.21 |
| Reference Frame | Description |
|---|---|
| Protocol inertial reference system | Geocenter inertial reference system in J2000 |
| Precession and nutation model | IAU2000 R06 |
| Earth orientation parameter | IERS C04 |
| Dynamic model | Description |
| N-body gravity | JPL DE421 |
| Gravity field of the earth | GOCO06S |
| Relativity effect | IERS 2010 Conventions |
| Solid tide | IERS 2010 Conventions |
| Ocean tide | FES2004 |
| Radiation pressure | Empirical force model |
| Observation model | Description |
| Measurements | L3 P3 undifferenced ionosphere-free |
| Arc length and interval | 24 h, 30 s |
| Cut-off elevation (°) | 5 |
| GPS satellite orbits and clocks | RTS-recovered products |
| Receiver antenna PCO/PCV | Pre-calibrated values |
| Parameter estimation | Description |
| Initial state | Initial position and velocity |
| Receiver clock error | Estimated as white noise, one bias per epoch |
| Ambiguity | Float solution |
| Pseudo-stochastic pulses | One group in the R, A, and C directions every 6 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Zhou, X.; Li, K. Centimeter-Level Orbit Determination of GRACE-C Using IGS-RTS Data. Remote Sens. 2023, 15, 1832. https://doi.org/10.3390/rs15071832
Li D, Zhou X, Li K. Centimeter-Level Orbit Determination of GRACE-C Using IGS-RTS Data. Remote Sensing. 2023; 15(7):1832. https://doi.org/10.3390/rs15071832
Chicago/Turabian StyleLi, Duoduo, Xuhua Zhou, and Kai Li. 2023. "Centimeter-Level Orbit Determination of GRACE-C Using IGS-RTS Data" Remote Sensing 15, no. 7: 1832. https://doi.org/10.3390/rs15071832
APA StyleLi, D., Zhou, X., & Li, K. (2023). Centimeter-Level Orbit Determination of GRACE-C Using IGS-RTS Data. Remote Sensing, 15(7), 1832. https://doi.org/10.3390/rs15071832






