A Comprehensive Correction Method for Radiation Distortion of Multi-Strip Airborne Hyperspectral Images
Abstract
1. Introduction
2. Study Area and Data Overview
2.1. Study Area
2.2. Remote Sensing Data
3. Methodology
3.1. Radiation Attenuation Difference Correction
3.2. Topographic Correction
3.2.1. Model Construction and Kernel Selection
3.2.2. Kernel Coefficients Determination
3.2.3. Angle Normalization
3.3. Consistency Adjustment between Multi-Strip Images
3.4. Correction Effect Evaluation
4. Results
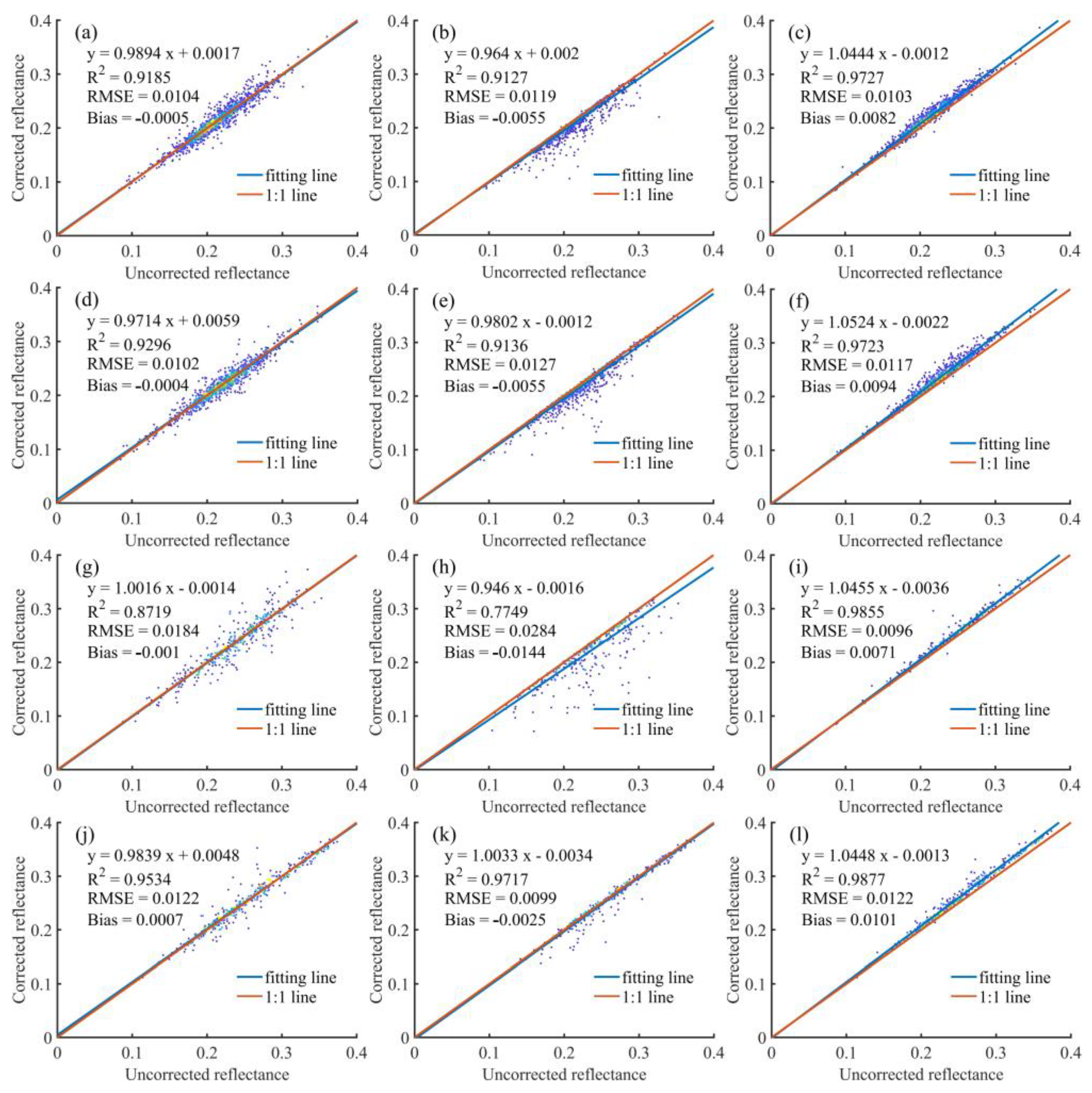
4.1. Effects of Radiation Attenuation Difference Correction
4.2. Visual Inspection of Radiation Distortion Correction
4.3. Effects of Topographic Correction
4.3.1. Correlation Analysis of Reflectance and Cosine of the Local Solar Incidence Angle
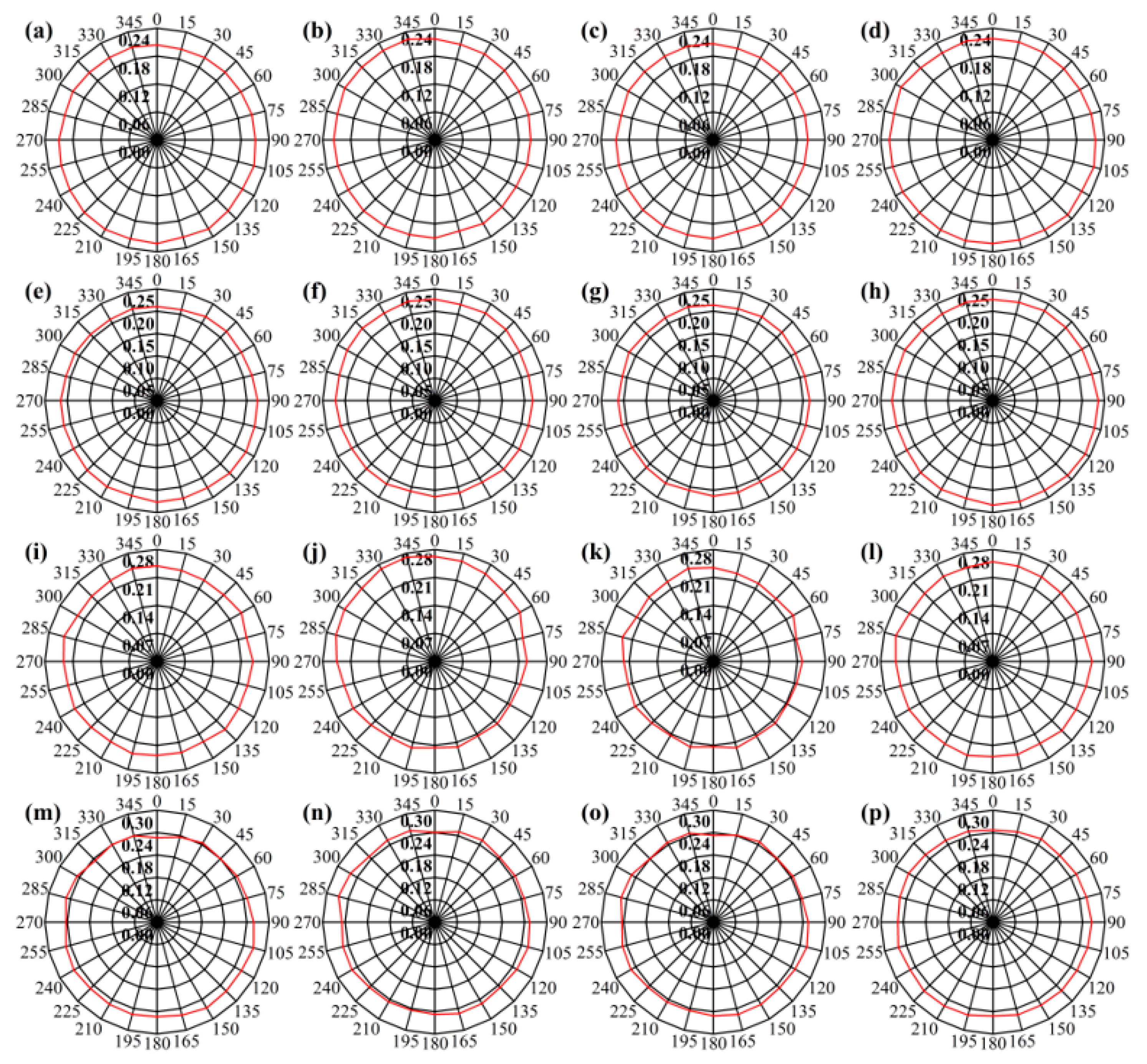
4.3.2. Reflectance of Different Aspects
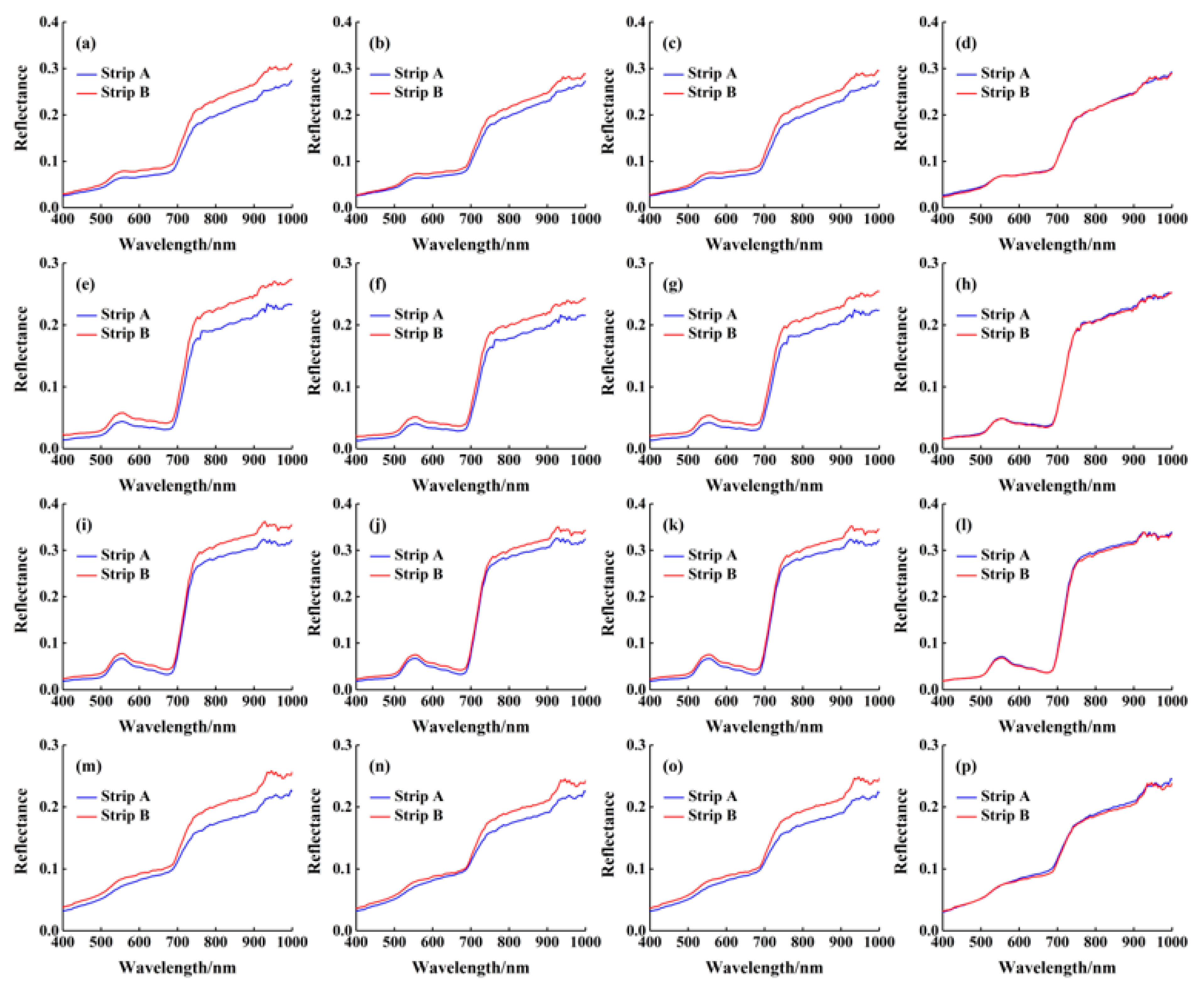
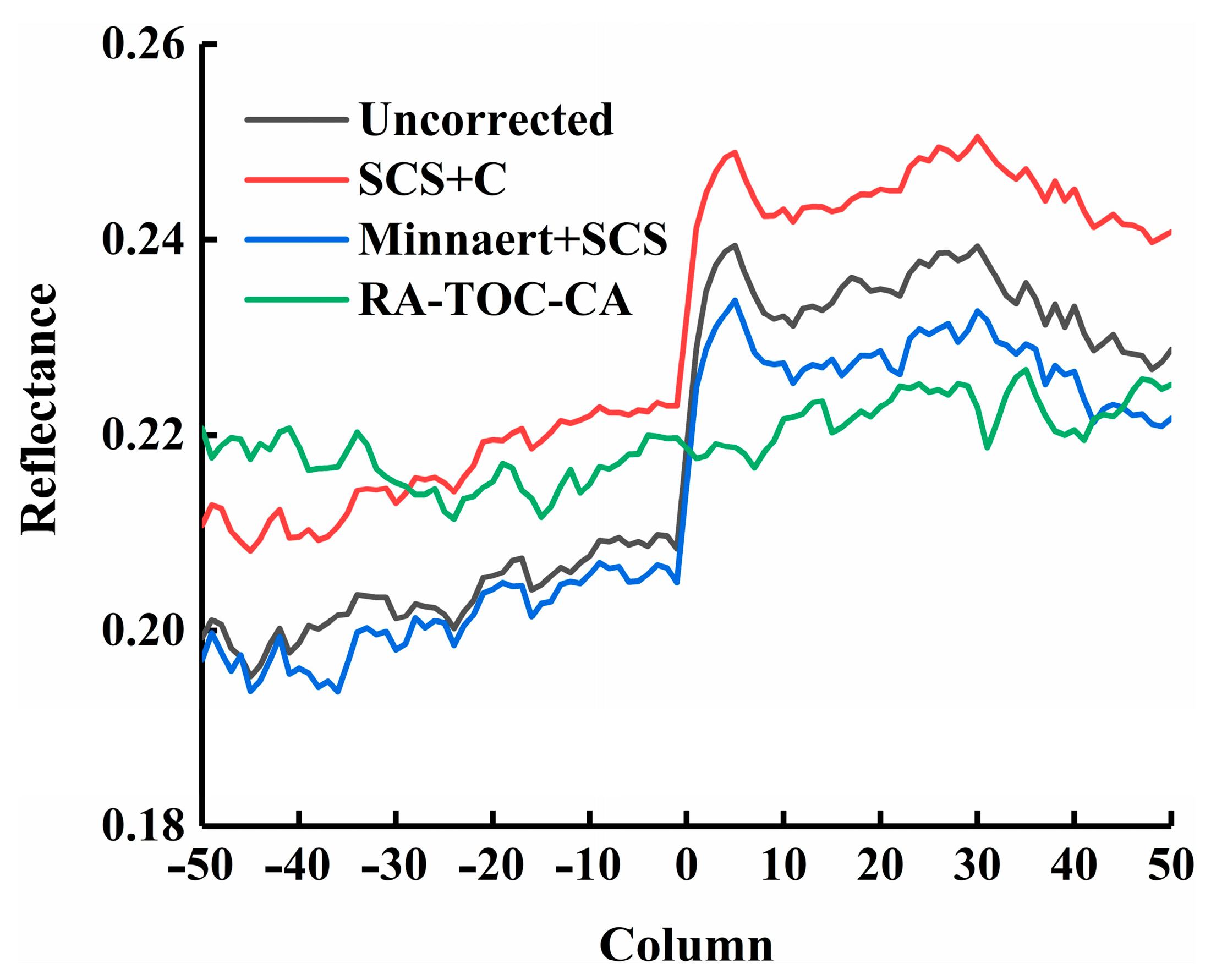
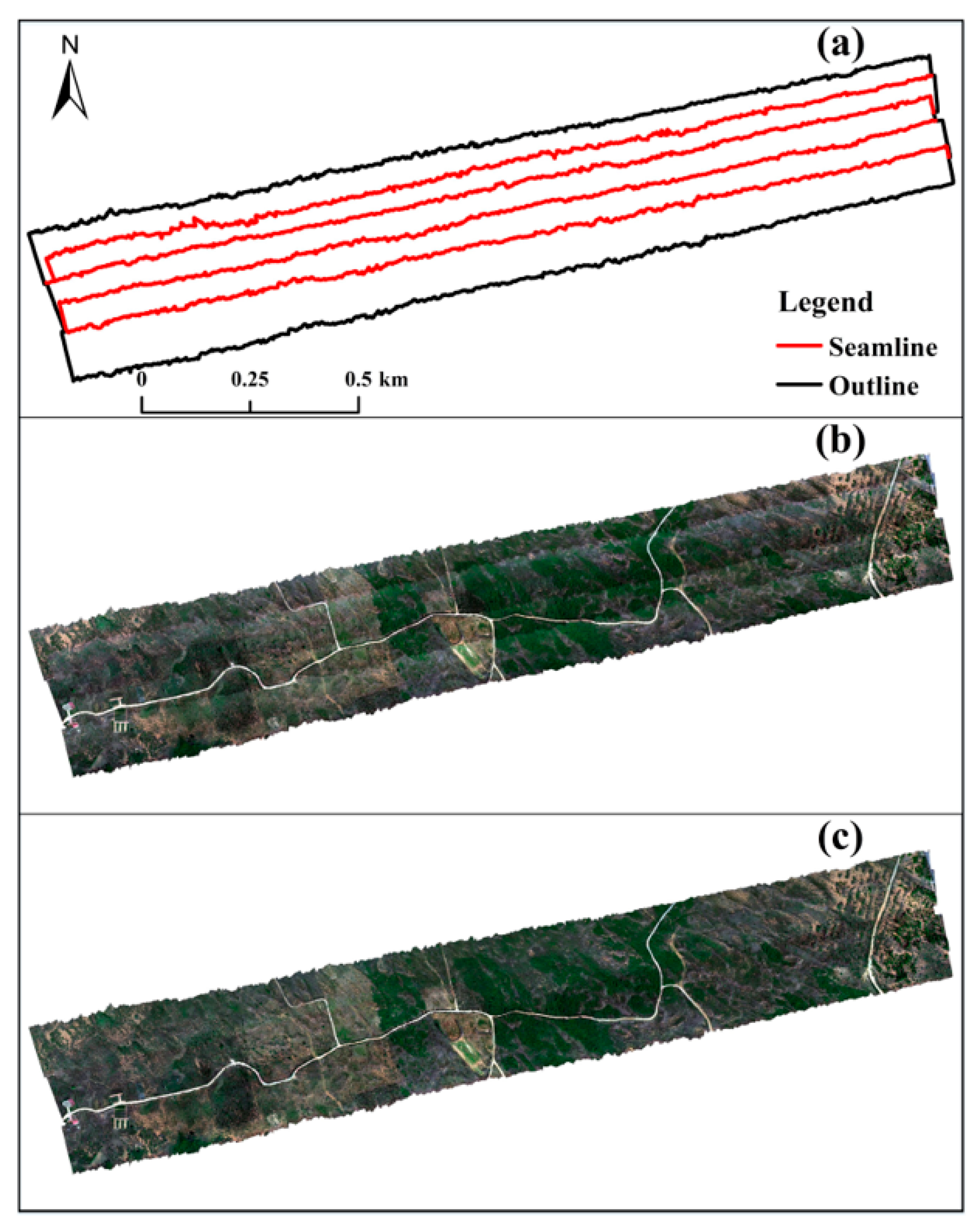
4.4. Analysis of Overlapping Areas of Adjacent Flight Strips
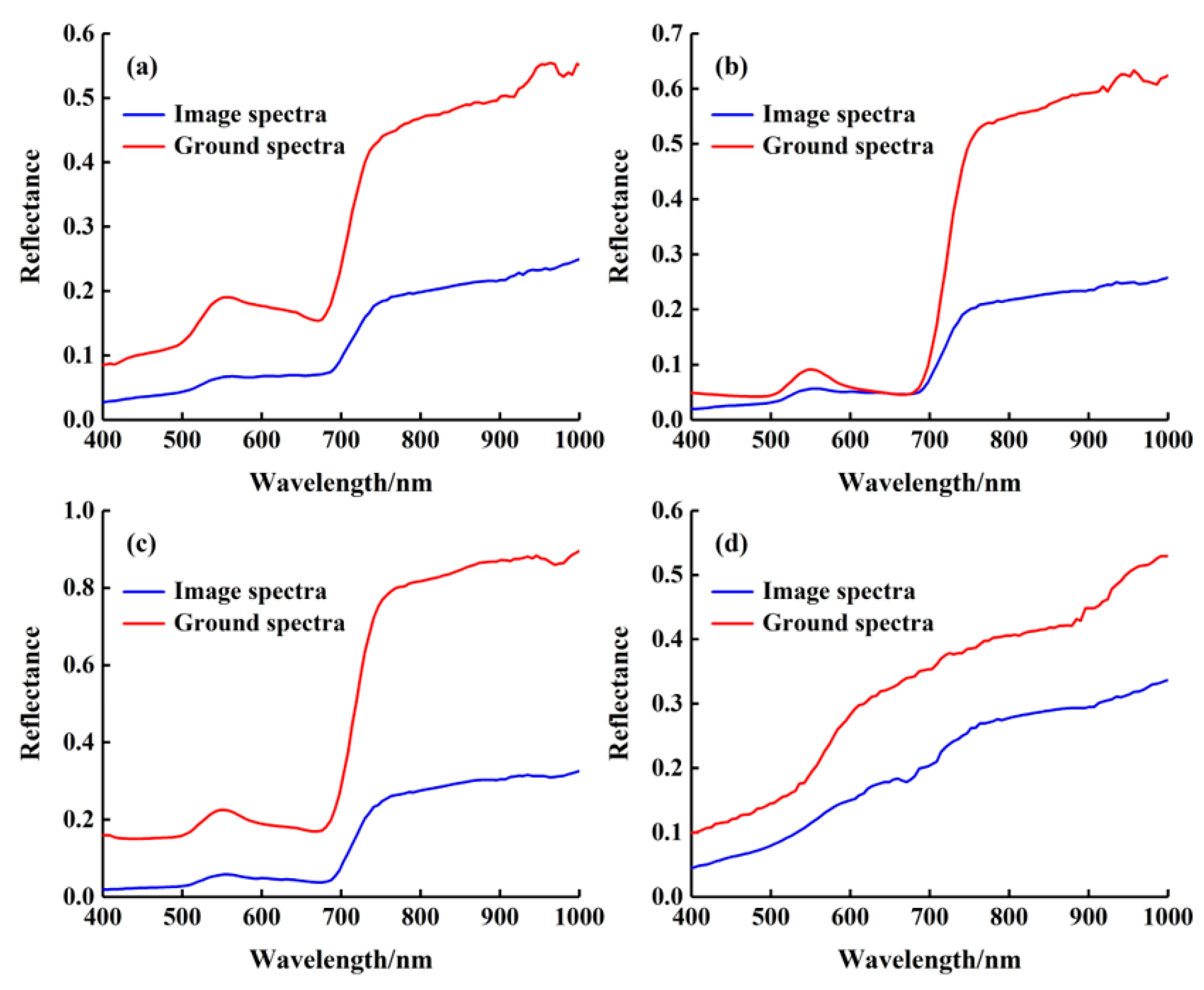
4.5. Reflectance Comparison between the Image and the Ground Spectra
4.6. The Generalizability of RA-TOC-CA
5. Discussion
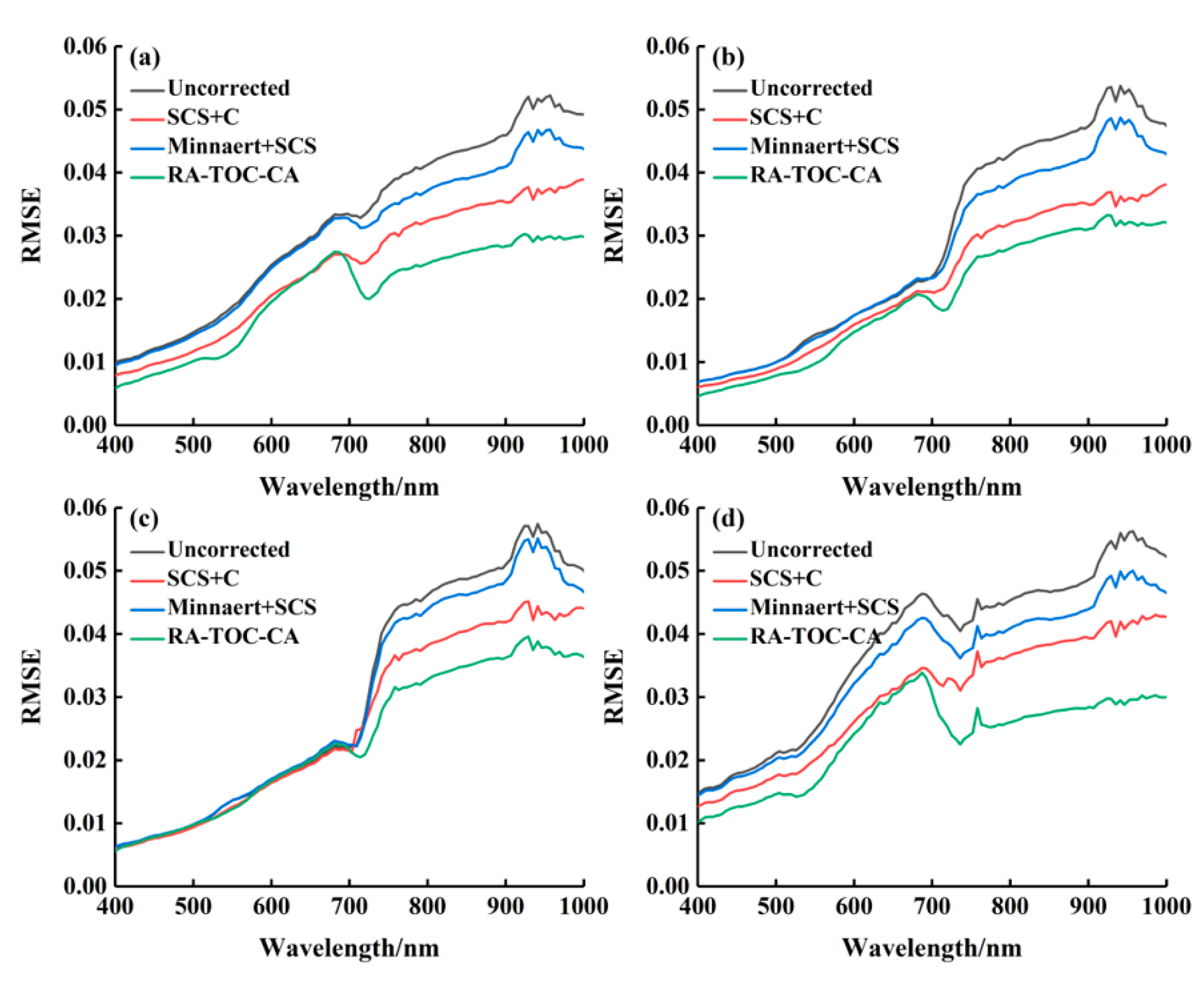
5.1. Comparison of Different Methods
5.2. Physical Soundness Analysis
5.3. Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Tan, K.; Du, Q.; Chen, Y.; Du, P. Caps-TripleGAN: GAN-Assisted CapsNet for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7232–7245. [Google Scholar] [CrossRef]
- Zhang, C.; Han, M. Multi-feature hyperspectral image classification with L 2,1 norm constrained joint sparse representation. Int. J. Remote Sens. 2021, 42, 4785–4804. [Google Scholar] [CrossRef]
- Myr, J.; Keski-Saari, S.; Kivinen, S.; Tanh Ua Np, T.; Vihervaara, P. Tree species classification from airborne hyperspectral and LiDAR data using 3D convolutional neural networks. Remote Sens. Environ. 2021, 256, 112322. [Google Scholar] [CrossRef]
- Shi, T.; Chen, Y.; Liu, Y.; Wu, G. Visible and near-infrared reflectance spectroscopy-An alternative for monitoring soil contamination by heavy metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef]
- Liu, P.; Liu, Z.; Hu, Y.; Shi, Z.; Pan, Y.; Wang, L.; Wang, G. Integrating a Hybrid Back Propagation Neural Network and Particle Swarm Optimization for Estimating Soil Heavy Metal Contents Using Hyperspectral Data. Sustainability 2019, 11, 419. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, Y.; Peng, Y.; Zhao, L.; Hu, Y. Estimation of Soil Heavy Metal Content Using Hyperspectral Data. Remote Sens. 2019, 11, 1464. [Google Scholar] [CrossRef]
- Tan, K.; Wang, H.; Chen, L.; Du, Q.; Du, P.; Pan, C. Estimation of the spatial distribution of heavy metal in agricultural soils using airborne hyperspectral imaging and random forest. J. Hazard. Mater. 2020, 382, 120987. [Google Scholar] [CrossRef]
- Landmann, T.; Piiroinen, R.; Makori, D.M.; Abdel-Rahman, E.M.; Makau, S.; Pellikka, P.; Raina, S.K. Application of hyperspectral remote sensing for flower mapping in African savannas. Remote Sens. Environ. 2015, 166, 50–60. [Google Scholar] [CrossRef]
- Roth, K.L.; Roberts, D.A.; Dennison, P.E.; Alonzo, M.; Beland, M. Differentiating plant species within and across diverse ecosystems with imaging spectroscopy. Remote Sens. Environ. 2015, 167, 135–151. [Google Scholar] [CrossRef]
- Hakkenberg, C.; Peet, R.; Urban, D.; Song, C. Modeling plant composition as community continua in a forest landscape with LiDAR and hyperspectral remote sensing. Ecol. Appl. 2017, 28, 177–190. [Google Scholar] [CrossRef]
- Schiefer, S.; Hostert, P.; Damm, A. Correcting brightness gradients in hyperspectral data from urban areas. Remote Sens. Environ. 2006, 101, 25–37. [Google Scholar] [CrossRef]
- Köppl, C.J.; Malureanu, R.; Dam-Hansen, C.; Wang, S.; Jin, H.; Barchiesi, S.; Sandí, J.M.S.; Munoz-Carpena, R.; Johnson, M.; Durán-Quesada, A.M. Hyperspectral reflectance measurements from UAS under intermittent clouds: Correcting irradiance measurements for sensor tilt. Remote Sens. Environ. 2021, 267, 112719. [Google Scholar] [CrossRef]
- Jensen, D.J.; Simard, M.; Cavanaugh, K.C.; Thompson, D.R. Imaging spectroscopy BRDF correction for mapping Louisiana’s coastal ecosystems. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1739–1748. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R.; Feingersh, T. Operational BRDF effects correction for wide-field-of-view optical scanners (BREFCOR). IEEE Trans. Geosci. Remote Sens. 2014, 53, 1855–1864. [Google Scholar] [CrossRef]
- Guo, X.; Wang, R. Radiometric Correction of Airborne Imaging Spectrometer Data. J. Image Graph. 2000, 5, 19–23. [Google Scholar]
- Tian, Y.; Wu, W.; Yang, G. Edge radiation distortion correction of whiskbroom airborne hyperspectral image by considering BRDF effect and atmospheric attenuation. J. Infrared Millim. Waves. 2016, 35, 701–707. [Google Scholar]
- Horvath, R.; Braithwaite, J.G.; Polcyn, F.C. Effects of atmospheric path on airborne multispectral sensors. Remote Sens. Environ. 1970, 1, 203–215. [Google Scholar] [CrossRef]
- Stokkom, H.V.; Guzzi, R. Atmospheric spectral attenuation of airborne remote-sensing data Comparison between experimental and theoretical approach. Int. J. Remote Sens. 1984, 5, 925–938. [Google Scholar] [CrossRef]
- Li, F.; Jupp, D.; Thankappan, M.; Lymburner, L.; Mueller, N.; Lewis, A.; Held, A. A physics-based atmospheric and BRDF correction for Landsat data over mountainous terrain. Remote Sens. Environ. 2012, 124, 756–770. [Google Scholar] [CrossRef]
- Li, A.; Wang, Q.; Bian, J.; Lei, G. An Improved Physics-Based Model for Topographic Correction of Landsat TM Images. Remote Sens. 2015, 7, 6296–6319. [Google Scholar] [CrossRef]
- Flood, N.; Danaher, T.; Gill, T.; Gillingham, S. An Operational Scheme for Deriving Standardised Surface Reflectance from Landsat TM/ETM+ and SPOT HRG Imagery for Eastern Australia. Remote Sens. 2013, 5, 83–109. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Li, X.; Strahler, A.H. Topographic effects on bidirectional and hemispherical reflectances calculated with a geometric-optical canopy model. IEEE Trans. Geosci. Remote Sens. 2002, 32, 1186–1193. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, W. A simple empirical topographic correction method for ETM+ imagery. Int. J. Remote Sens. 2009, 30, 2259–2275. [Google Scholar] [CrossRef]
- Jiang, K.; Hu, C.; Yu, K.; Zhao, Y. Landsat TM/ETM + topographic correction method based on smoothed terrain and semi-empirical model. J. Remote Sens. 2014, 18, 287–306. [Google Scholar]
- Lin, Q.; Huang, H.; Chen, L.; Chen, E. Topographic correction method for steep mountain terrain images. J. Remote Sens. 2017, 21, 776–784. [Google Scholar]
- Zhang, Y.; Li, X.; Wen, J.; Liu, Q.; Yan, G. Improved Topographic Normalization for Landsat TM Images by Introducing the MODIS Surface BRDF. Remote Sens. 2015, 7, 6558–6575. [Google Scholar] [CrossRef]
- Sandmeier, S.; Itten, K.I. A physically-based model to correct atmospheric and illumination effects in optical satellite data of rugged terrain. IEEE Trans. Geosci. Remote Sens. 1997, 35, 708–717. [Google Scholar] [CrossRef]
- Zhang, Z.; He, G.; Liu, D.; Wang, X.; Jiang, H. An Improved Physical Model to Correct Topographic Effects in Remotely Sensed Imagery. Spectrosc. Spectr. Anal. 2010, 30, 1839–1842. [Google Scholar]
- Collings, S.; Caccetta, P.; Campbell, N.; Wu, X. Techniques for BRDF Correction of Hyperspectral Mosaics. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3733–3746. [Google Scholar] [CrossRef]
- Jiao, Z.; Dong, Y.; Schaaf, C.B.; Chen, J.M.; Román, M.; Wang, Z.; Zhang, H.; Ding, A.; Erb, A.; Hill, M.J.; et al. An algorithm for the retrieval of the clumping index (CI) from the MODIS BRDF product using an adjusted version of the kernel-driven BRDF model. Remote Sens. Environ. 2018, 209, 594–611. [Google Scholar] [CrossRef]
- Roujean, J.L.; Leroy, M.; Deschamps, P.Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L. Correcting Bidirectional Effect for Multiple-Flightline Aerial Images Using a Semiempirical Kernel-Based Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4450–4463. [Google Scholar] [CrossRef]
- Jia, W.; Pang, Y.; Tortini, R.; Schläpfer, D.; Li, Z.; Roujean, J.-L. A Kernel-Driven BRDF Approach to Correct Airborne Hyperspectral Imagery over Forested Areas with Rugged Topography. Remote Sens. 2020, 12, 432. [Google Scholar] [CrossRef]
- Queally, N.; Ye, Z.; Zheng, T.; Chlus, A.; Schneider, F.; Pavlick, R.P.; Townsend, P.A. FlexBRDF: A flexible BRDF correction for grouped processing of airborne imaging spectroscopy flightlines. J. Geophys. Res. 2022, 127, e2021JG006622. [Google Scholar] [CrossRef] [PubMed]
- Kizel, F.; Benediktsson, J.A.; Bruzzone, L.; Pedersen, G.B.; Vilmundardóttir, O.K.; Falco, N. Simultaneous and constrained calibration of multiple hyperspectral images through a new generalized empirical line model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2047–2058. [Google Scholar] [CrossRef]
- Li, D.; Wang, M.; Pan, J. Auto-dodging Processing and Its Application for Optical RS Images. Geomat. Inf. Sci. Wuhan Univ. 2006, 31, 753–756. [Google Scholar]
- Patterson, E.M.; Gillette, D.A.; Stockton, B.H. Complex index of refraction between 300 and 700 nm for Saharan aerosols. J. Geophys. Res. 1977, 82, 3153–3160. [Google Scholar] [CrossRef]
- Weyermann, J.; Kneubuhler, M.; Schlapfer, D.; Schaepman, M.E. Minimizing Reflectance Anisotropy Effects in Airborne Spectroscopy Data Using Ross–Li Model Inversion with Continuous Field Land Cover Stratification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5814–5823. [Google Scholar] [CrossRef]
- Guo, Y.; Jia, X.; Paull, D. Superpixel-based adaptive kernel selection for angular effect normalization of remote sensing images with kernel learning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4262–4271. [Google Scholar] [CrossRef]
- Li, X.; Gao, F.; Chen, L.; Strahler, A.H. Derivation and validation of a new kernel for kernel-driven BRDF models. Remote. Sens. Earth Sci. Ocean. Sea Ice Appl. 1999, 3868, 368–379. [Google Scholar]
- Zhang, X.; Jiao, Z.; Dong, Y.; Zhang, H.; Li, Y.; He, D.; Ding, A.; Yin, S.; Cui, L.; Chang, Y. Potential Investigation of Linking PROSAIL with the Ross-Li BRDF Model for Vegetation Characterization. Remote Sens. 2018, 10, 437. [Google Scholar] [CrossRef]
- Maignan, F.; Bréon, F.M.; Lacaze, R. Bidirectional reflectance of Earth targets: Evaluation of analytical models using a large set of spaceborne measurements with emphasis on the Hot Spot. Remote Sens. Environ. 2004, 90, 210–220. [Google Scholar] [CrossRef]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A general method to normalize Landsat reflectance data to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef]
- Gatebe, C.K.; King, M.D. Airborne spectral BRDF of various surface types (ocean, vegetation, snow, desert, wetlands, cloud decks, smoke layers) for remote sensing applications. Remote Sens. Environ. 2016, 179, 131–148. [Google Scholar] [CrossRef]
- Mira, M.; Weiss, M.; Baret, F.; Courault, D.; Hagolle, O.; Gallego-Elvira, B.; Olioso, A. The MODIS (collection V006) BRDF/albedo product MCD43D: Temporal course evaluated over agricultural landscape. Remote Sens. Environ. 2015, 170, 216–228. [Google Scholar] [CrossRef]
- Luo, Y. Surface bidirectional reflectance and albedo properties derived using a landcover based approach with MODIS observations. J. Geophys. Res. 2005, 110, D1106. [Google Scholar] [CrossRef]
- Colgan, M.S.; Baldeck, C.A.; Féret, J.; Asner, G.P. Mapping savanna tree species at ecosystem scales using support vector machine classification and BRDF correction on airborne hyperspectral and LiDAR data. Remote Sens. 2012, 4, 3462–3480. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Zhao, W.; Jin, H.; Bian, J. Modeling Canopy Reflectance Over Sloping Terrain Based on Path Length Correction. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4597–4609. [Google Scholar] [CrossRef]
- Balthazar, V.; Vanacker, V.; Lambin, E.F. Evaluation and parameterization of ATCOR3 topographic correction method for forest cover mapping in mountain areas. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 436–450. [Google Scholar] [CrossRef]
- Tan, K.; Niu, C.; Jia, X.; Ou, D.; Lei, S. Complete and accurate data correction for seamless mosaicking of airborne hyperspectral images: A case study at a mining site in Inner Mongolia, China. ISPRS J. Photogramm. Remote Sens. 2020, 165, 1–15. [Google Scholar] [CrossRef]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+ C: A modified sun-canopy-sensor topographic correction in forested terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Reeder, D.H. Topographic Correction of Satellite Images: Theory and Application; Dartmouth College: Hanover, NH, USA, 2002. [Google Scholar]
- Yin, G.; Li, A.; Wu, S.; Fan, W.; Zeng, Y.; Yan, K.; Xu, B.; Li, J.; Liu, Q. PLC: A simple and semi-physical topographic correction method for vegetation canopies based on path length correction. Remote Sens. Environ. 2018, 215, 184–198. [Google Scholar] [CrossRef]
- Ediriweera, S.; Pathirana, S.; Danaher, T.; Nichols, D.; Moffiet, T. Evaluation of different topographic corrections for Landsat TM data by prediction of foliage projective cover (FPC) in topographically complex landscapes. Remote Sens. 2013, 5, 6767–6789. [Google Scholar] [CrossRef]
- Sola, I.; González-Audícana, M.; Álvarez-Mozos, J. The added value of stratified topographic correction of multispectral images. Remote Sens. 2016, 8, 131. [Google Scholar] [CrossRef]
- Teillet, P.M.; Guindon, B.; Goo De Nough, D.G. On the Slope-Aspect Correction of Multispectral Scanner Data. Can. J. Remote Sens. 1981, 8, 84–106. [Google Scholar] [CrossRef]
- Reese, H.; Olsson, H. C-correction of optical satellite data over alpine vegetation areas: A comparison of sampling strategies for determining the empirical c-parameter. Remote Sens. Environ. 2011, 115, 1387–1400. [Google Scholar] [CrossRef]
- Park, S.; Jung, H.; Choi, J.; Jeon, S. A quantitative method to evaluate the performance of topographic correction models used to improve land cover identification. Adv. Space Res. 2017, 60, 1488–1503. [Google Scholar] [CrossRef]
- Wu, Q.; Jin, Y.; Fan, H. Evaluating and comparing performances of topographic correction methods based on multi-source DEMs and Landsat-8 OLI data. Int. J. Remote Sens. 2016, 37, 4712–4730. [Google Scholar] [CrossRef]
- Dong, C.; Zhao, G.; Meng, Y.; Li, B.; Peng, B. The effect of topographic correction on forest tree species classification accuracy. Remote Sens. 2020, 12, 787. [Google Scholar] [CrossRef]
- Gao, M.; Zhao, W.; Gong, Z.; Gong, H.; Chen, Z.; Tang, X. Topographic correction of ZY-3 satellite images and its effects on estimation of shrub leaf biomass in mountainous areas. Remote Sens. 2014, 6, 2745–2764. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, G.; Liu, C. Terrain Correction and Evaluation Methods of Hyperspectral Remote Sensing Image. Mt. Res. 2016, 34, 632–636. [Google Scholar]
- Lin, X.; Wen, J.; Wu, S.; Hao, D.; Xiao, Q.; Liu, Q. Advances in topographic correction methods for optical remote sensing imageries. J. Remote Sens. 2020, 24, 958–974. [Google Scholar]
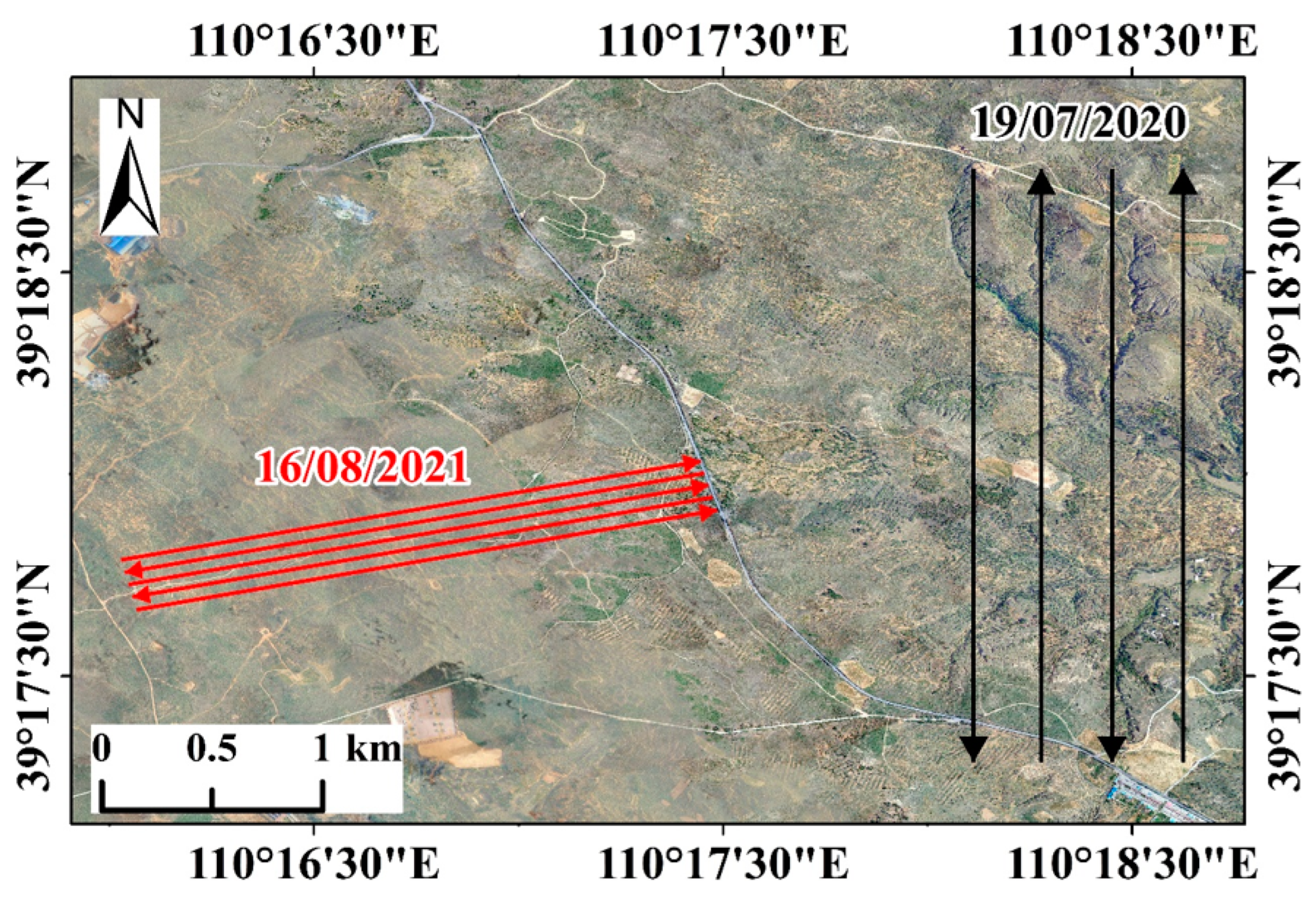
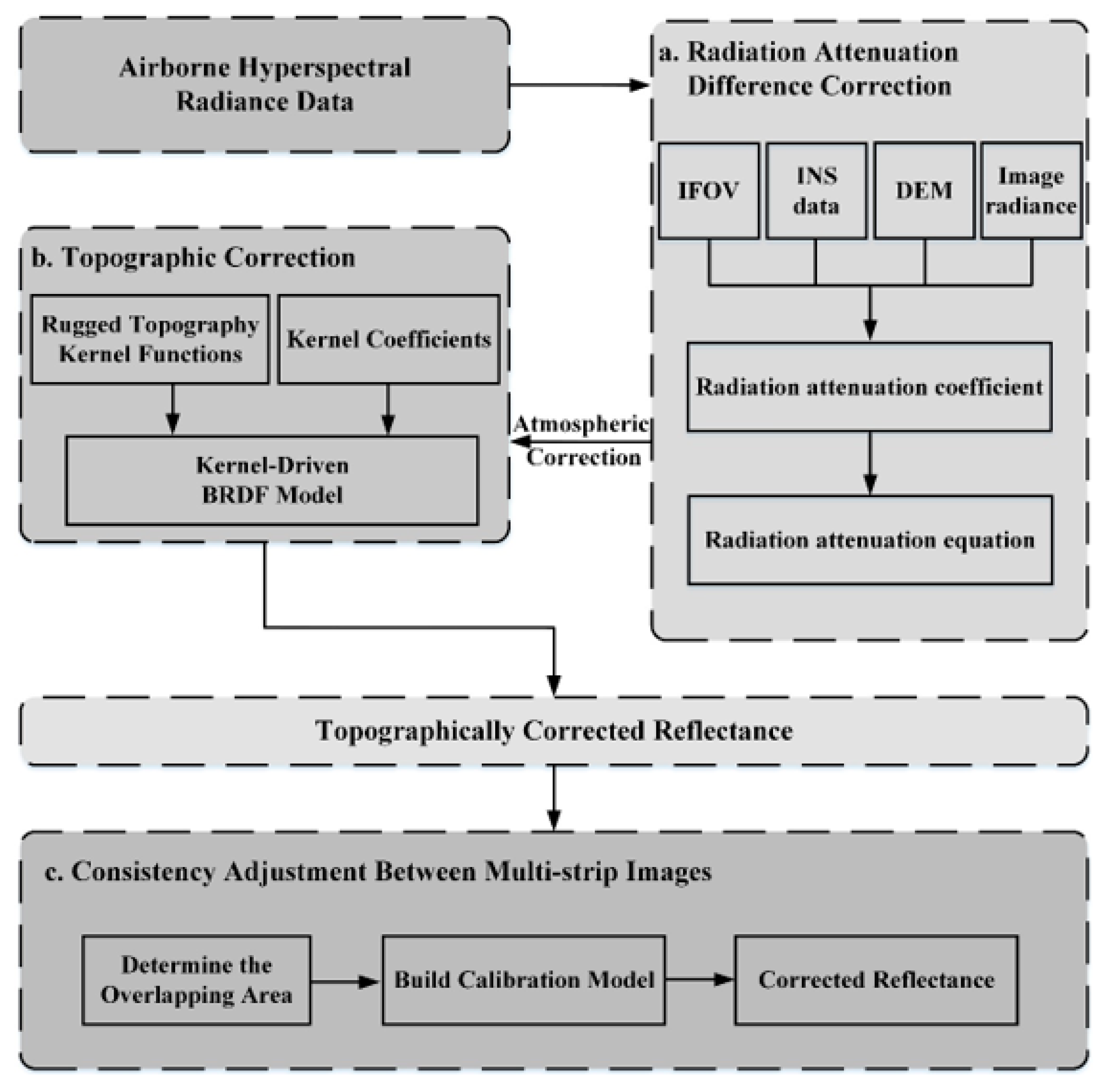

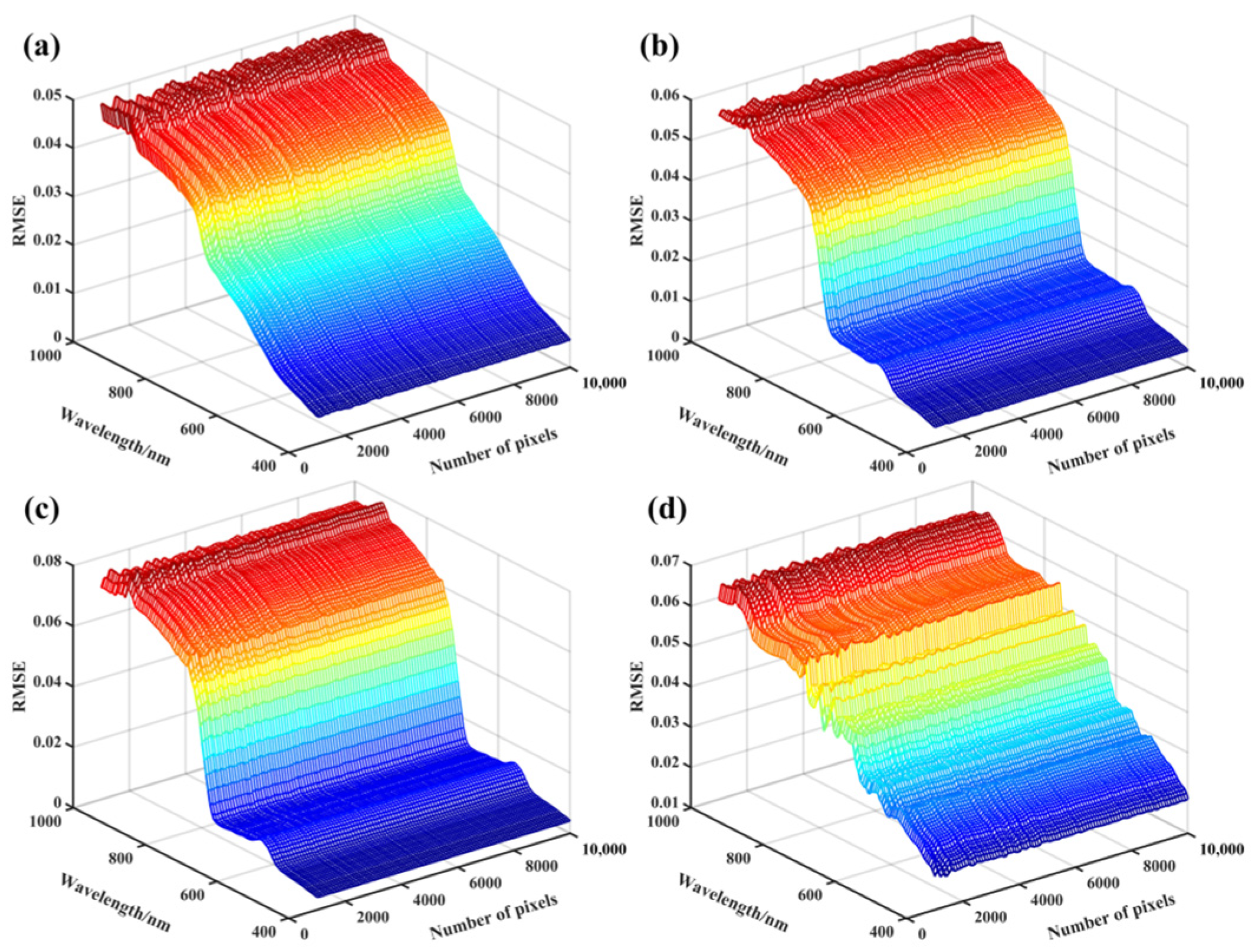


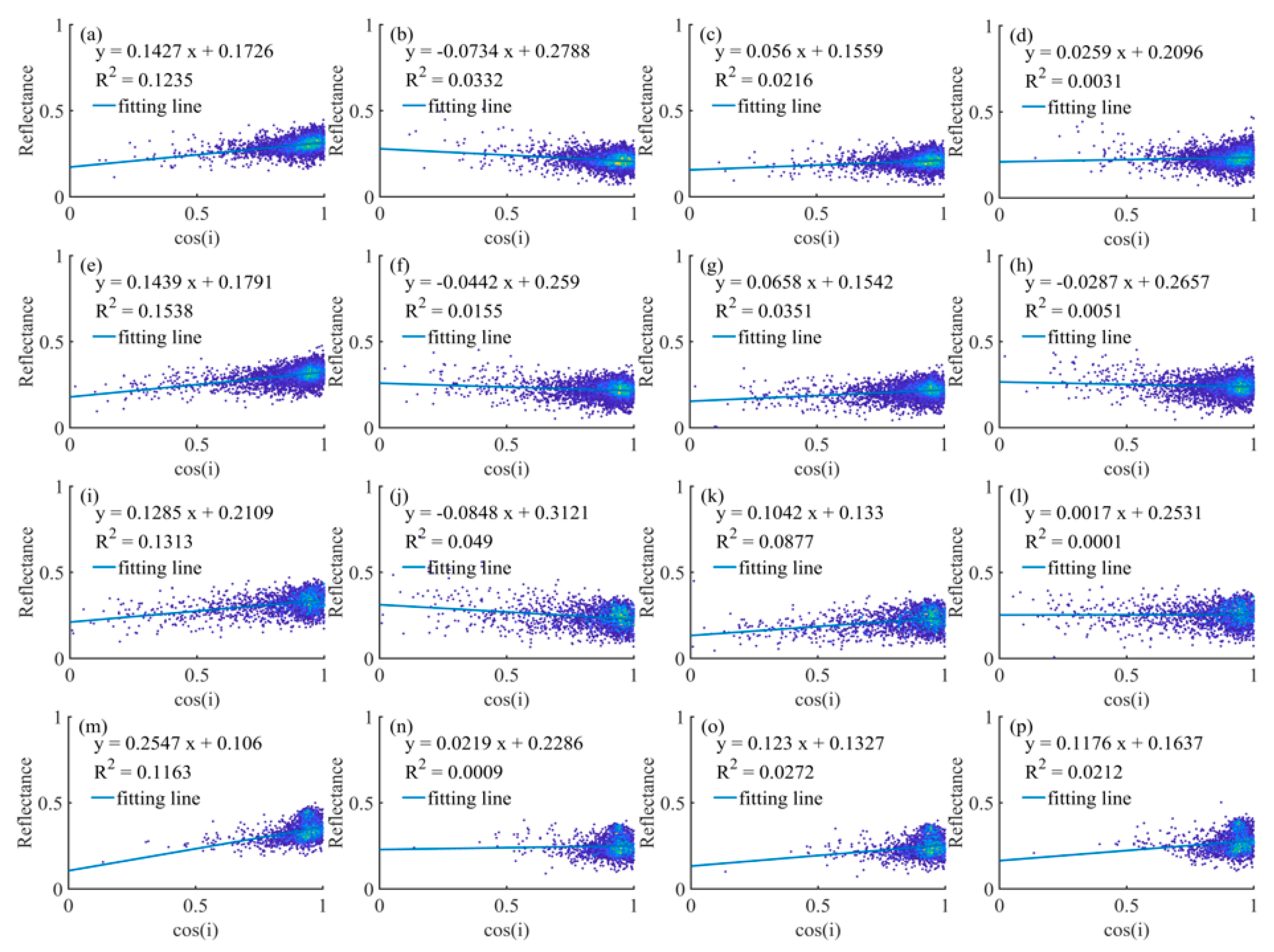

| Flight Date | Strip Name | Time Interval | Solar Zenith Angle (°) | Solar Azimuth Angle (°) |
|---|---|---|---|---|
| 19 July 2020 | a1 | 9:46–9:51 AM | 41.61–42.52 | 102.64–103.64 |
| a2 | 9:51–9:57 AM | 40.54–41.44 | 103.82–104.85 | |
| a3 | 12:17–12:23 PM | 19.28–19.57 | 160.57–163.79 | |
| a4 | 12:23–12:29 PM | 19.01–19.24 | 164.39–167.74 | |
| 16 August 2021 | b1 | 10:09–10:14 AM | 41.51–42.26 | 116.52–117.64 |
| b2 | 10:14–10:19 AM | 40.68–41.42 | 117.78–118.92 | |
| b3 | 11:04–11:09 AM | 32.91–33.52 | 133.04–134.62 | |
| b4 | 12:28–12:33 PM | 25.71–25.82 | 172.07–174.49 | |
| b5 | 12:33–12:38 PM | 25.64–25.71 | 174.78–177.22 |
| Main Technical Details | Data |
|---|---|
| Spectral range (nm) | 400–1000 |
| Spectral resolution (nm) | 2.7 |
| Bands | 224 |
| Samples | 1024 |
| Frame frequency (Hz) | <300 |
| FOV (°) | 38 |
| Correction Method | Expression | Reference |
|---|---|---|
| SCS+C | [51] | |
| Minnaert+SCS | [52] |
| Correction Method | Herb | Shrub | Tree | Bare Soil |
|---|---|---|---|---|
| Uncorrected | 2.98 | 2.91 | 1.63 | 4.06 |
| SCS+C | 2.99 | 2.57 | 7.56 | 2.22 |
| Minnaert+SCS | 1.69 | 1.24 | 3.29 | 2.39 |
| RA-TOC-CA | 1.44 | 2.13 | 1.54 | 1.57 |
| Correction Method | Equation | R2 |
|---|---|---|
| Uncorrected | y = 0.3584x + 0.0486 | 0.8356 |
| SCS+C | y = 0.3404x + 0.0546 | 0.7899 |
| Minnaert+SCS | y = 0.3438x + 0.0504 | 0.7937 |
| RA-TOC-CA | y = 0.3679x + 0.0548 | 0.8534 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Tian, Y.; Lei, S.; Li, Y.; Hua, X.; Guo, D.; Ji, C. A Comprehensive Correction Method for Radiation Distortion of Multi-Strip Airborne Hyperspectral Images. Remote Sens. 2023, 15, 1828. https://doi.org/10.3390/rs15071828
Zhao Y, Tian Y, Lei S, Li Y, Hua X, Guo D, Ji C. A Comprehensive Correction Method for Radiation Distortion of Multi-Strip Airborne Hyperspectral Images. Remote Sensing. 2023; 15(7):1828. https://doi.org/10.3390/rs15071828
Chicago/Turabian StyleZhao, Yibo, Yu Tian, Shaogang Lei, Yuanyuan Li, Xia Hua, Dong Guo, and Chuning Ji. 2023. "A Comprehensive Correction Method for Radiation Distortion of Multi-Strip Airborne Hyperspectral Images" Remote Sensing 15, no. 7: 1828. https://doi.org/10.3390/rs15071828
APA StyleZhao, Y., Tian, Y., Lei, S., Li, Y., Hua, X., Guo, D., & Ji, C. (2023). A Comprehensive Correction Method for Radiation Distortion of Multi-Strip Airborne Hyperspectral Images. Remote Sensing, 15(7), 1828. https://doi.org/10.3390/rs15071828





