Improving Consistency of GNSS-IR Reflector Height Estimates between Different Frequencies Using Multichannel Singular Spectrum Analysis
Abstract
1. Introduction
2. Methods and Data
2.1. Basic Principle of GNSS-IR Inversion Model
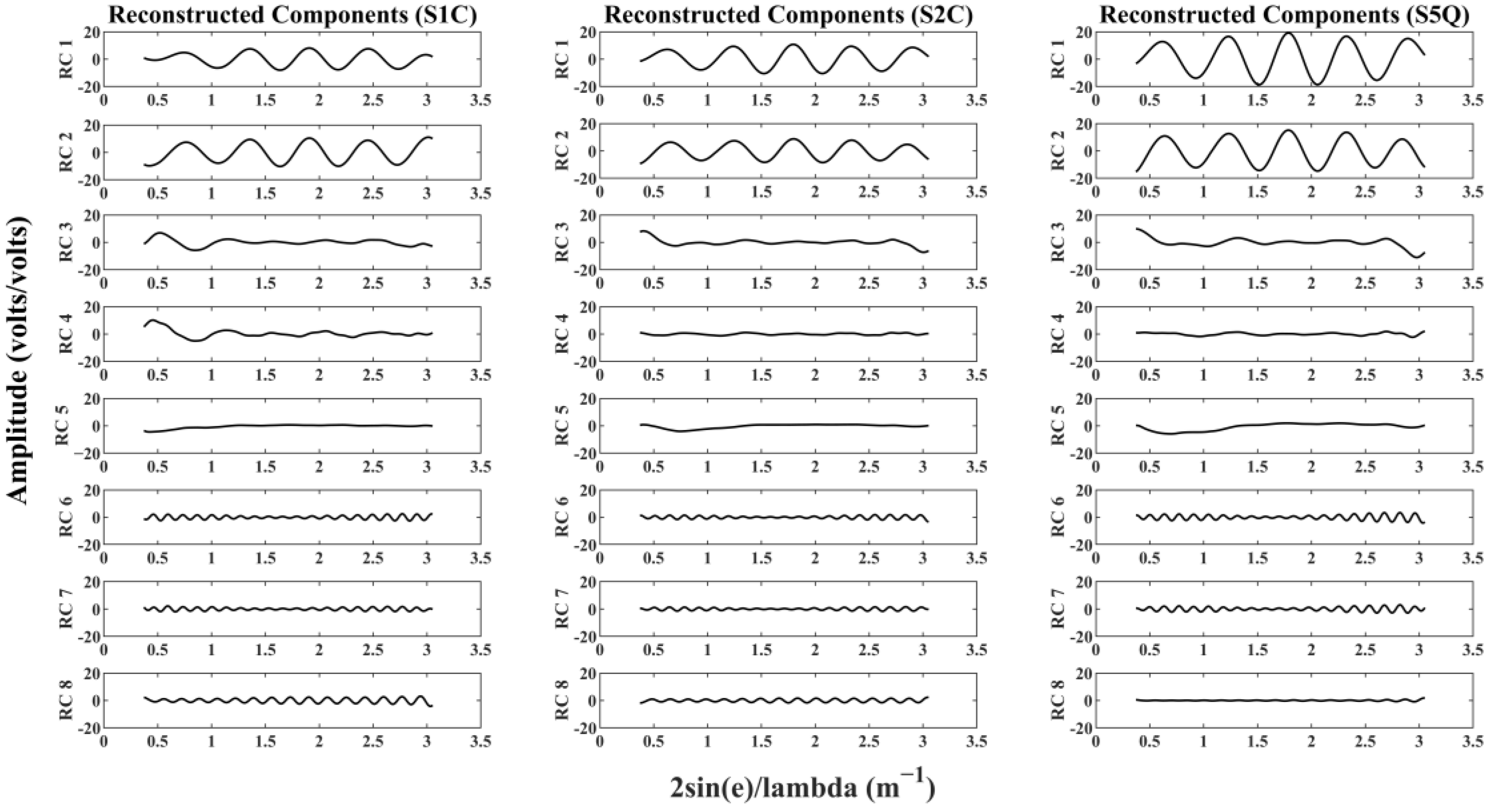
2.2. Mathematical Framework of M-SSA
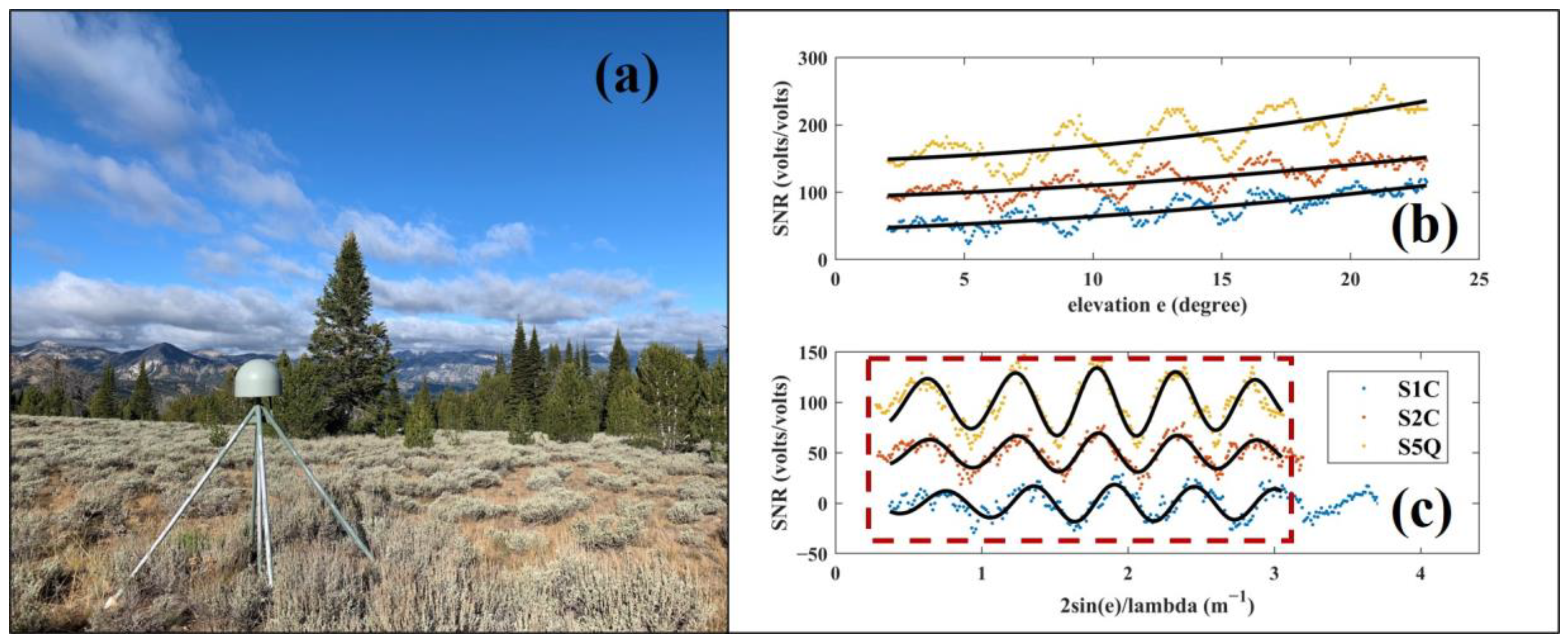
2.3. SNR Measurements
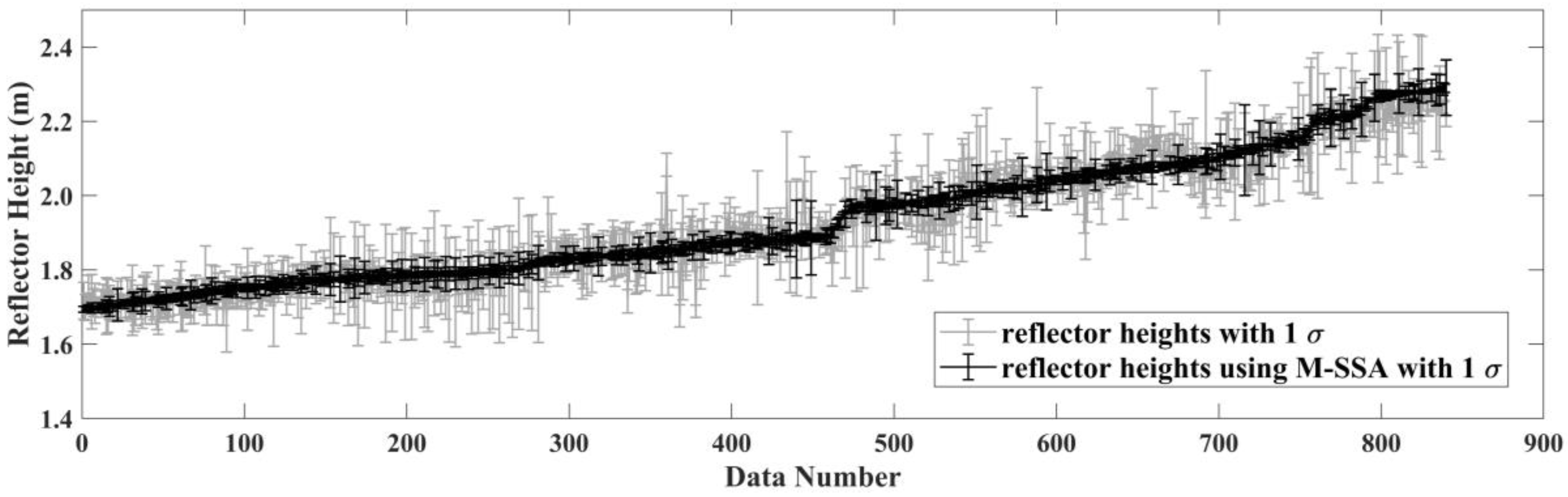
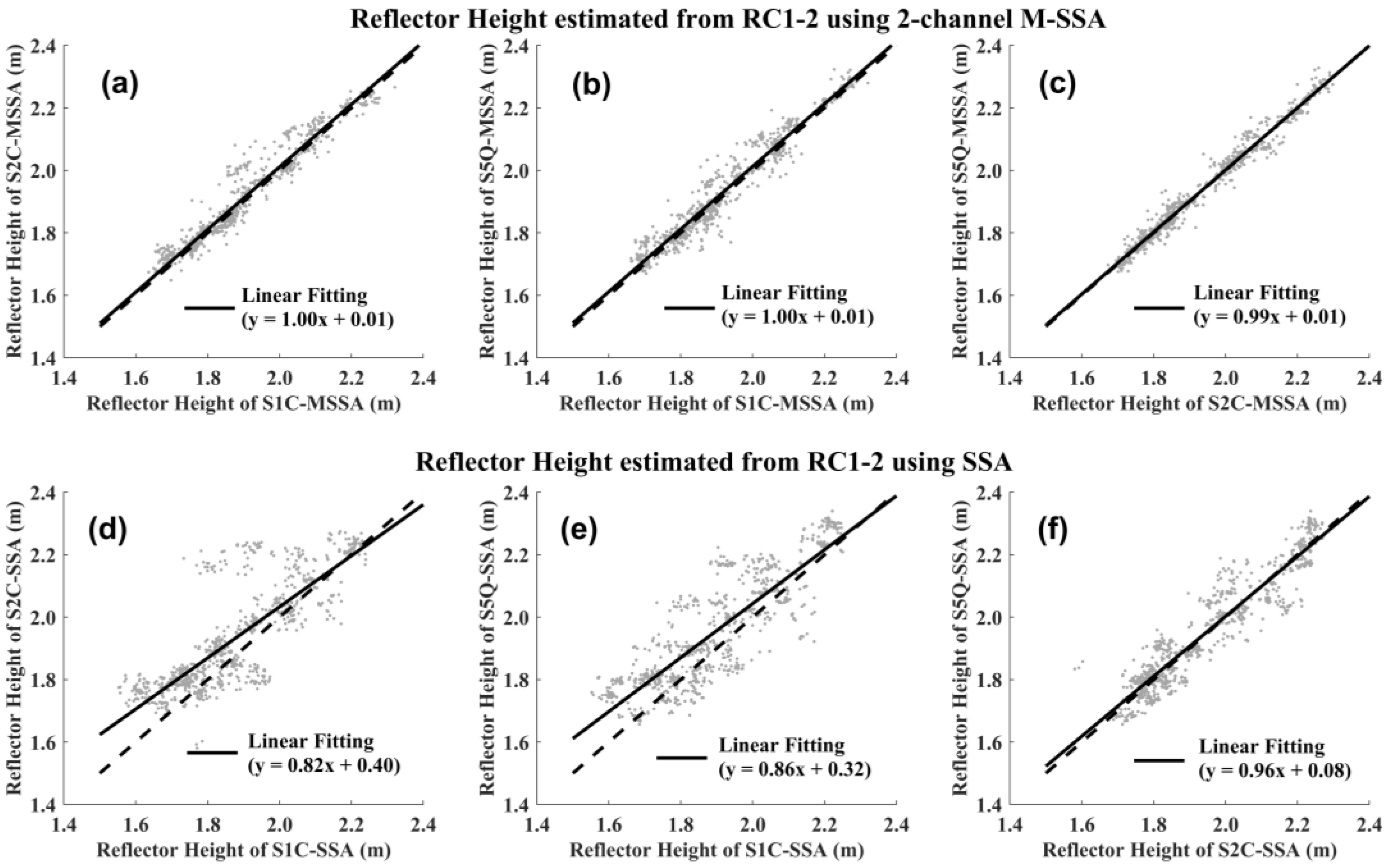
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nievinski, F.G.; Larson, K.M. An open source GPS multipath simulator in Matlab/Octave. GPS Solut. 2014, 18, 473–481. [Google Scholar] [CrossRef]
- Nievinski, F.G.; Larson, K.M. Forward modeling of GPS multipath for near-surface reflectometry and positioning applications. GPS Solut. 2013, 18, 309–322. [Google Scholar] [CrossRef]
- Roesler, C.; Larson, K.M. Software tools for GNSS interferometric reflectometry (GNSS-IR). GPS Solut. 2018, 22, 80. [Google Scholar] [CrossRef]
- Ran, Q.; Zhang, B.; Yao, Y.; Yan, X.; Li, J. Editing arcs to improve the capacity of GNSS-IR for soil moisture retrieval in undulating terrains. GPS Solut. 2022, 26, 19. [Google Scholar] [CrossRef]
- Nievinski, F.G.; Larson, K.M. Inverse Modeling of GPS Multipath for Snow Depth Estimation—Part I: Formulation and Simulations. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6555–6563. [Google Scholar] [CrossRef]
- Nievinski, F.G.; Larson, K.M. Inverse Modeling of GPS Multipath for Snow Depth Estimation—Part II: Application and Validation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6564–6573. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J.; Li, Z.; Peng, J. Ground surface elevation changes over permafrost areas revealed by multiple GNSS interferometric reflectometry. J. Geod. 2022, 96, 56. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Zhang, S. Sea level estimation from SNR data of geodetic receivers using wavelet analysis. GPS Solut. 2019, 23, 6. [Google Scholar] [CrossRef]
- Tabibi, S.; Nievinski, F.G.; van Dam, T.; Monico, J.F.G. Assessment of modernized GPS L5 SNR for ground-based multipath reflectometry applications. Adv. Space Res. 2015, 55, 1104–1116. [Google Scholar] [CrossRef]
- Larson, K.M.; Nievinski, F.G. GPS snow sensing: Results from the EarthScope Plate Boundary Observatory. GPS Solut. 2012, 17, 41–52. [Google Scholar] [CrossRef]
- Fontana, R.; Latterman, D. GPS Modernization and the Future. In Proceedings of the IAIN World Congress and the 56th Annual Meeting of The Institute of Navigation, San Diego, CA, USA, 28 June 2000. [Google Scholar]
- Steigenberger, P.; Thölert, S.; Montenbruck, O. Flex power on GPS Block IIR-M and IIF. GPS Solut. 2019, 23, 8. [Google Scholar] [CrossRef]
- Navstar, G.P.S. Space Segment/Navigation User Segment Interfaces. In Interface Specification; (IS-GPS-200E); National Coordination Office for Space-Based Positioning, Navigation, and Timing: Washington, DC, USA, 2013. [Google Scholar]
- Wang, X.; He, X.; Zhang, Q. Evaluation and combination of quad-constellation multi-GNSS multipath reflectometry applied to sea level retrieval. Remote Sens. Environ. 2019, 231, 111229. [Google Scholar] [CrossRef]
- Strode, P.R.R.; Groves, P.D. GNSS multipath detection using three-frequency signal-to-noise measurements. GPS Solut. 2015, 20, 399–412. [Google Scholar] [CrossRef]
- Martín, A.; Luján, R.; Anquela, A.B. Python software tools for GNSS interferometric reflectometry (GNSS-IR). GPS Solut. 2020, 24, 94. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, K.; Liu, Q.; Zhang, C.; Zhang, Q.; Nan, Y. Tide variation monitoring based improved GNSS-MR by empirical mode decomposition. Adv. Space Res. 2019, 63, 3333–3345. [Google Scholar] [CrossRef]
- Li, Z.; Chen, P.; Zheng, N.; Liu, H. Accuracy analysis of GNSS-IR snow depth inversion algorithms. Adv. Space Res. 2021, 67, 1317–1332. [Google Scholar] [CrossRef]
- Hu, Y.; Yuan, X.; Liu, W.; Hu, Q.; Wickert, J.; Jiang, Z. Snow depth estimation from GNSS SNR data using variational mode decomposition. GPS Solut. 2022, 27, 33. [Google Scholar] [CrossRef]
- Hu, Y.; Yuan, X.; Liu, W.; Wickert, J.; Jiang, Z. GNSS-R Snow Depth Inversion Based on Variational Mode Decomposition With Multi-GNSS Constellations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Ansari, K.; Seok, H.W.; Jamjareegulgarn, P. Quasi zenith satellite system-reflectometry for sea-level measurement and implication of machine learning methodology. Sci. Rep. 2022, 12, 21445. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Yue, J.; Chu, Z.; Zhu, S.; Liu, Z.; Wu, J. An improved snow depth retrieval method with adaptive noise reduction for GPS/GLONASS/Galileo/BDS multi-frequency signals. Meas. Sci. Technol. 2022, 33, 085011. [Google Scholar] [CrossRef]
- Dettinger, M.D.; Ghil, M.; Strong, C.M.; Weibel, W.; Yiou, P. Software expedites singular-spectrum analysis of noisy time series. EOS Trans. Am. Geophys. Union 2012, 76, 12–21. [Google Scholar] [CrossRef]
- Ansari, K.; Panda, S.K.; Jamjareegulgarn, P. Singular spectrum analysis of GPS derived ionospheric TEC variations over Nepal during the low solar activity period. Acta Astronaut. 2020, 169, 216–223. [Google Scholar] [CrossRef]
- Dabbakuti, J.K.; Peesapati, R.; Panda, S.K.; Thummala, S. Modeling and analysis of ionospheric TEC variability from GPS–TEC measurements using SSA model during 24th solar cycle. Acta Astronaut. 2021, 178, 24–35. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced Spectral Methods for Climatic Time Series. Rev. Geophys. 2002, 40, 3-1–3-41. [Google Scholar] [CrossRef]
- Groth, A.; Ghil, M. Multivariate singular spectrum analysis and the road to phase synchronization. Phys. Rev. 2011, 84, 036206. [Google Scholar] [CrossRef] [PubMed]
- Škare, M.; Porada-Rochoń, M. Multi-channel singular-spectrum analysis of financial cycles in ten developed economies for 1970–2018. J. Bus. Res. 2020, 112, 567–575. [Google Scholar] [CrossRef]
- Groth, A.; Ghil, M. Monte Carlo Singular Spectrum Analysis (SSA) Revisited: Detecting Oscillator Clusters in Multivariate Datasets. J. Clim. 2015, 28, 7873–7893. [Google Scholar] [CrossRef]
- Walwer, D.; Calais, E.; Ghil, M. Data-adaptive detection of transient deformation in geodetic networks. J. Geophys. Res. Solid Earth 2016, 121, 2129–2152. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Xiao, R.; Song, M.; Jia, D. Millimeter to centimeter scale precision water-level monitoring using GNSS reflectometry: Application to the South-to-North Water Diversion Project, China. Remote Sens. Environ. 2021, 265, 112645. [Google Scholar] [CrossRef]



| Original | 3-Channel M-SSA | 2-Channel M-SSA | SSA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1–S2 | S1–S5 | S2–S5 | S1–S2 | S1–S5 | S2–S5 | S1–S2 | S1–S5 | S2–S5 | S1–S2 | S1–S5 | S2–S5 | |
| a | 0.77 | 0.76 | 0.94 | 0.97 | 0.99 | 1.01 | 1.00 | 1.00 | 0.99 | 0.82 | 0.86 | 0.96 |
| b | 0.49 | 0.51 | 0.13 | 0.07 | 0.03 | −0.01 | 0.01 | 0.01 | 0.01 | 0.40 | 0.32 | 0.08 |
| 0.69 | 0.67 | 0.89 | 0.95 | 0.96 | 0.98 | 0.88 | 0.94 | 0.98 | 0.67 | 0.73 | 0.88 | |
| RMSE (m) | 0.10 | 0.10 | 0.06 | 0.04 | 0.04 | 0.02 | 0.06 | 0.04 | 0.02 | 0.09 | 0.09 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, J.; Li, W.; Zhang, S. Improving Consistency of GNSS-IR Reflector Height Estimates between Different Frequencies Using Multichannel Singular Spectrum Analysis. Remote Sens. 2023, 15, 1779. https://doi.org/10.3390/rs15071779
Lei J, Li W, Zhang S. Improving Consistency of GNSS-IR Reflector Height Estimates between Different Frequencies Using Multichannel Singular Spectrum Analysis. Remote Sensing. 2023; 15(7):1779. https://doi.org/10.3390/rs15071779
Chicago/Turabian StyleLei, Jintao, Wenhao Li, and Shengkai Zhang. 2023. "Improving Consistency of GNSS-IR Reflector Height Estimates between Different Frequencies Using Multichannel Singular Spectrum Analysis" Remote Sensing 15, no. 7: 1779. https://doi.org/10.3390/rs15071779
APA StyleLei, J., Li, W., & Zhang, S. (2023). Improving Consistency of GNSS-IR Reflector Height Estimates between Different Frequencies Using Multichannel Singular Spectrum Analysis. Remote Sensing, 15(7), 1779. https://doi.org/10.3390/rs15071779








