Joint Estimation of Ground Displacement and Atmospheric Model Parameters in Ground-Based Radar
Abstract
1. Introduction
2. Method Development for Joint Estimation of Ground Displacement and Atmospheric Model Parameters
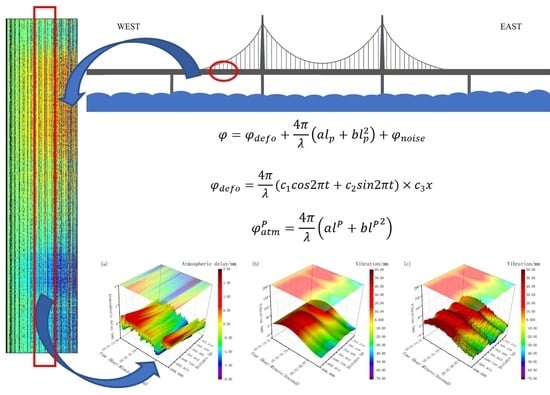
2.1. Phase Model of Ground-Based Radar
2.2. Atmospheric Phase Modeling for Ground-Based Radar
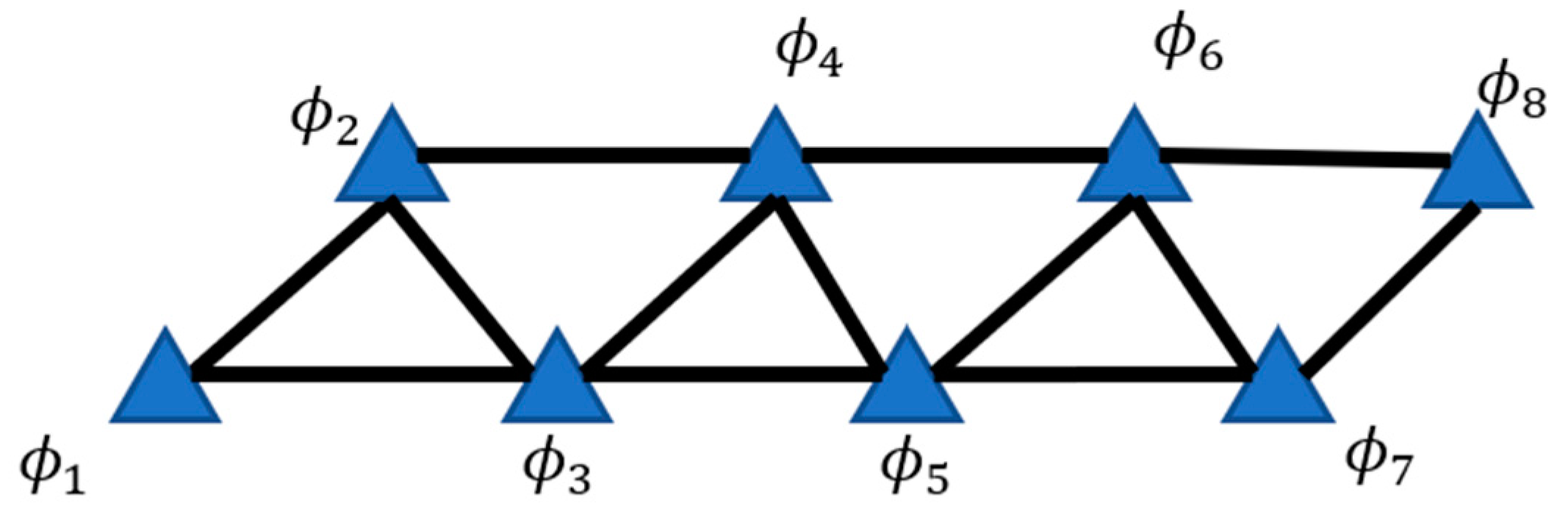
2.3. Function and Stochastic Model for Joint Estimation of Displacement and Atmosphere
2.4. Joint Estimation of Ground Displacement and Atmospheric Model Parameters
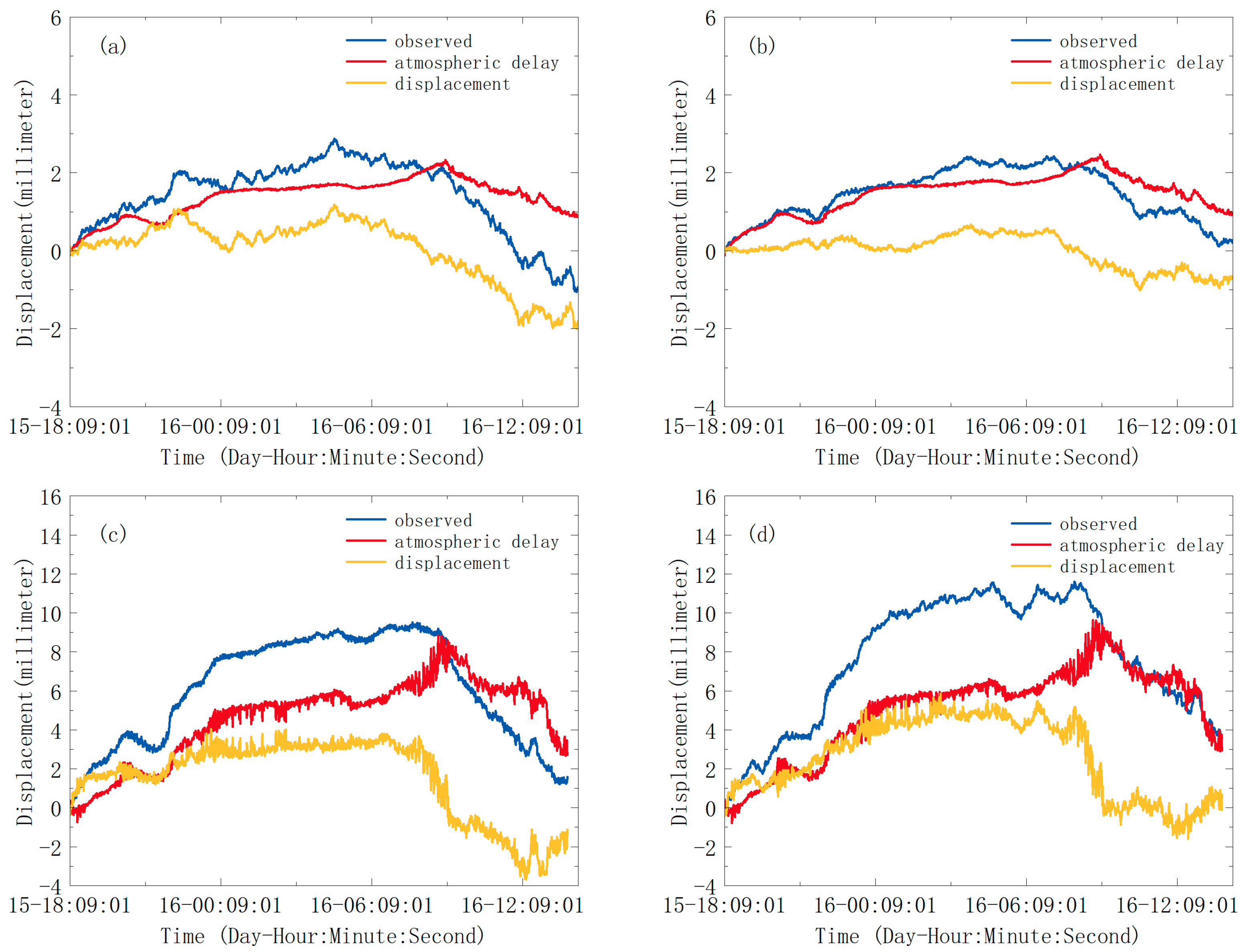
3. Validation of the Developed Method
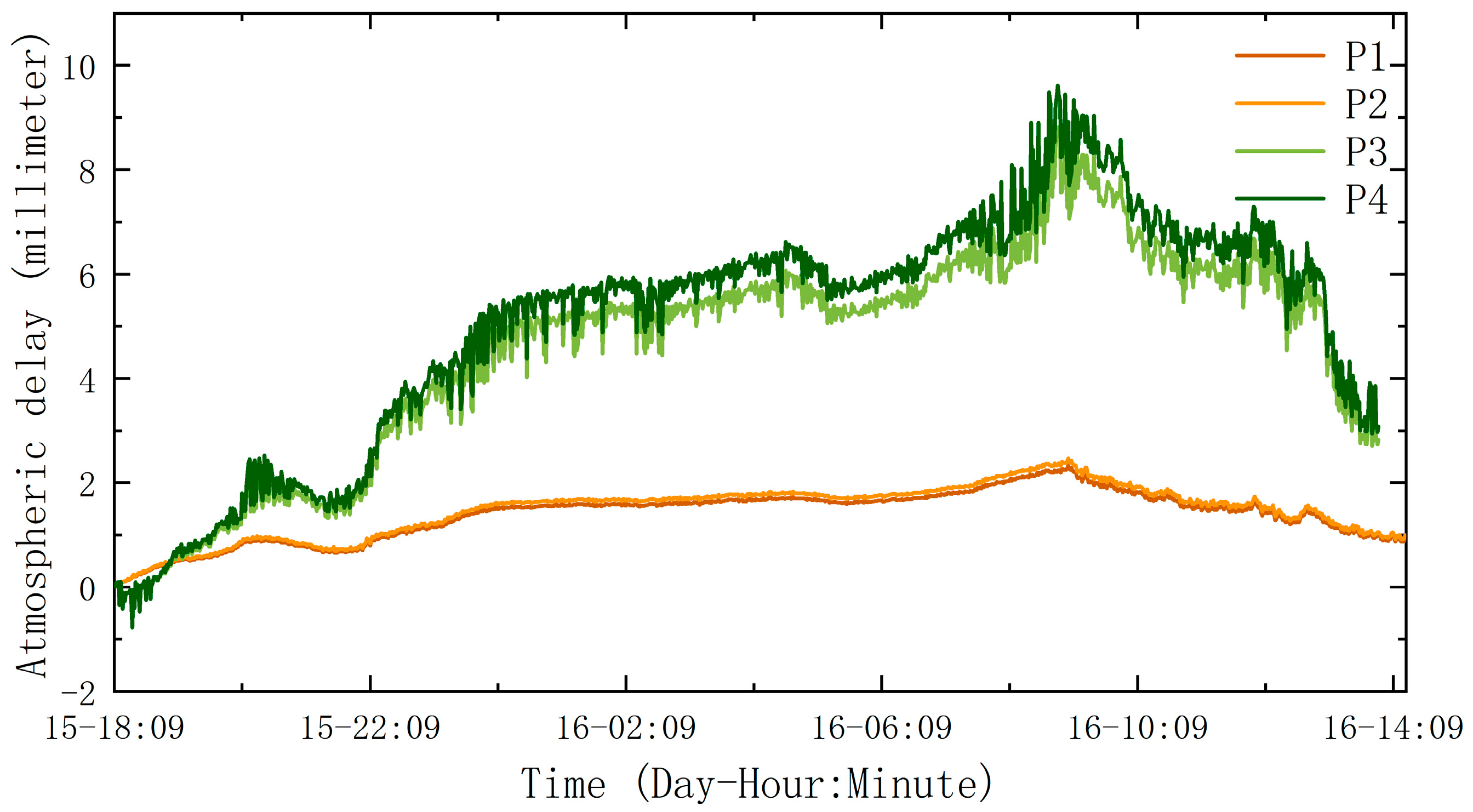
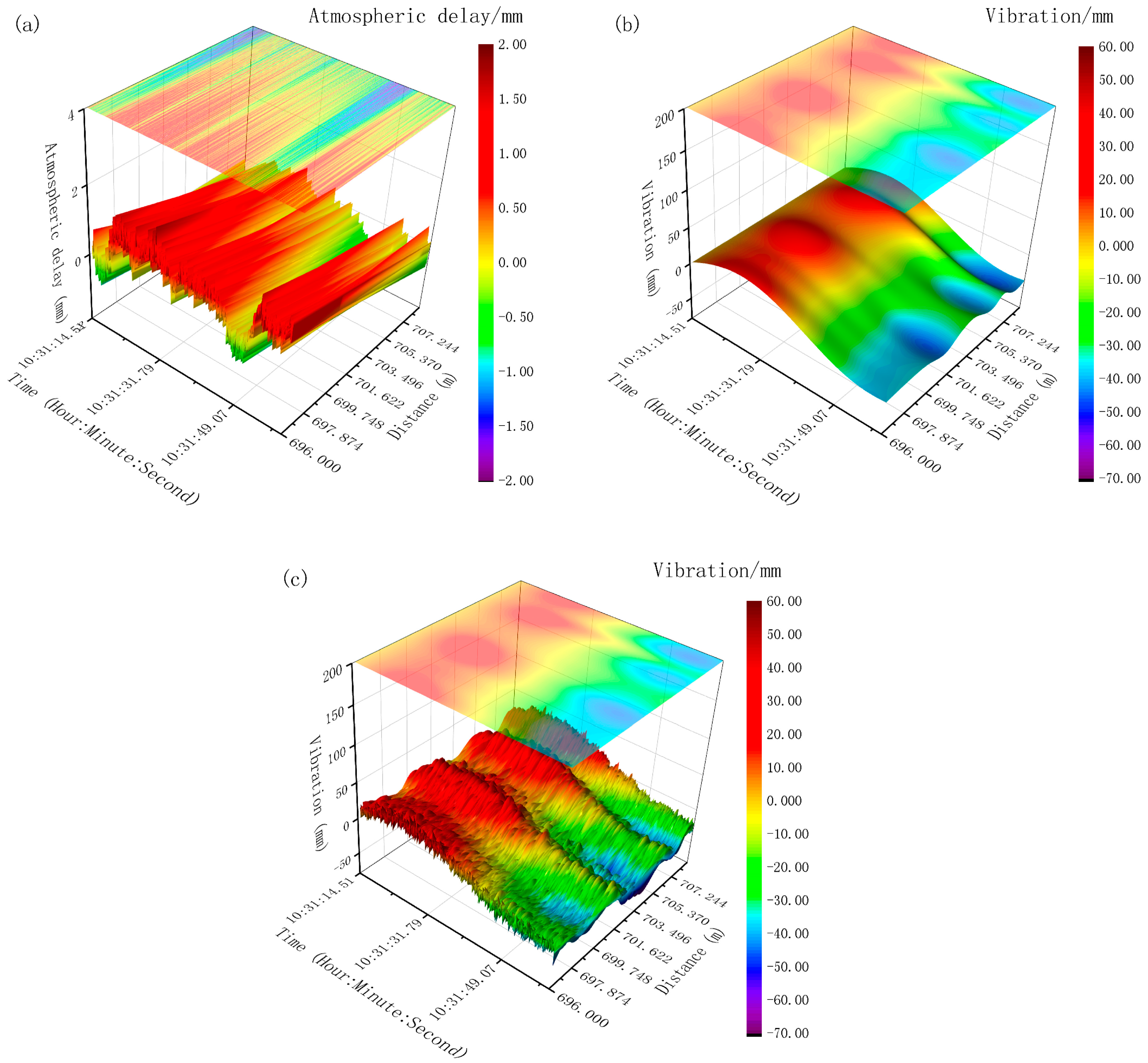
4. Application of the Developed Method for Monitoring Bridge Displacement
5. Discussion
5.1. Significance of Incorporating the System Parameters
5.2. Comparisons of Atmospheric Delay Calculated by Different Methods
5.3. Comparisons between the Vibration Time Series Acquired by the GPS and GBSAR
6. Conclusions
- (1)
- Additional systematic parameters are necessary for the functional model according to the hypothesis testing and the practical test. It is indicated that the original function model which only contains the unknown deformation parameters is inappropriate.
- (2)
- The proposed method is a significant improvement compared to the external meteorological data correction method and the polynomial fitting method. The external meteorological data correction method is the worst among the three methods.
- (3)
- The proposed method can split the atmospheric delay and displacement, and enhance the capacity of the monitoring bridge with the GBSAR device. It is suggested that reflectors are recommended when the device is employed to monitor the vibration of structures. An appropriate displacement model should be selected based on the displacement features of the structures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tarchi, D.; Rudolf, H.; Luzi, G.; Chiarantini, L.; Coppo, P.; Sieber, A.J. SAR Interferometry for Structural Changes Detect ion a Demonstration Test on a Dam. In Proceedings of the IGARSS, Hamburg, Germany, 28 June–2 July 1999; pp. 1522–1524. [Google Scholar]
- Zhang, B.; Ding, X.; Werner, C.; Tan, K.; Zhang, B.; Jiang, M.; Zhao, J.; Xu, Y. Dynamic displacement monitoring of long-span bridges with a microwave radar interferometer. ISPRS J. Photogramm. Remote Sens. 2018, 138, 252–264. [Google Scholar] [CrossRef]
- Tarchi, D.; Casagli, N.; Fanti, R.; Leva, D.D.; Luzi, G.; Pasuto, A.; Pieraccini, M.; Silvano, S. Landslide monitoring by using ground-based SAR interferometry: An example of application to the Tessina landslide in Italy. Eng. Geol. 2003, 68, 15–30. [Google Scholar] [CrossRef]
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Macaluso, G.; Galgaro, A.; Atzeni, C. Advances in ground-based microwave interferometry for landslide survey: A case study. Int. J. Remote Sens. 2006, 27, 2331–2350. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Y.; Wei, J.; Duan, M.; Wu, L.; Hou, J.; Zhu, J. Time-series InSAR ground deformation monitoring: Atmospheric delay modeling and estimating. Earth-Sci. Rev. 2019, 192, 258–284. [Google Scholar] [CrossRef]
- Monserrat, O.; Crosetto, M.; Luzi, G. A review of ground-based SAR interferometry for deformation measurement. ISPRS J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef]
- Owerko, T.; Kuras, P.; Ortyl, Ł. Atmospheric Correction Thresholds for Ground-Based Radar Interferometry Deformation Monitoring Estimated Using Time Series Analyses. Remote Sens. 2020, 12, 2236. [Google Scholar] [CrossRef]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tamburini, A.; Broccolato, M. Permanent scatterers analysis for atmospheric correction in ground-based SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1471. [Google Scholar] [CrossRef]
- Iglesias, R.; Fabregas, X.; Aguasca, A.; Mallorqui, J.J.; Lopez-Martinez, C.; Gili, J.A.; Corominas, J. Atmospheric Phase Screen Compensation in Ground-Based SAR With a Multiple-Regression Model Over Mountainous Regions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2436–2449. [Google Scholar] [CrossRef]
- Pipia, L.; Fabregas, X.; Aguasca, A.; Lopez-Martinez, C. Atmospheric Artifact Compensation in Ground-Based DInSAR Applications. IEEE Geosci. Remote Sens. Lett. 2008, 5, 88–92. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, Y.; Guo, X. Atmospheric phase screen correction in ground-based SAR with PS technique. SpringerPlus 2016, 5, 1594. [Google Scholar] [CrossRef] [PubMed]
- Jianping, Y.; Zhiwei, Q.; Xueqin, W.; Shun, Y. Atmospheric phase correction using permanent scatterers in ground-based radar interferometry. J. Appl. Remote Sens. 2016, 10, 046013. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar system theory and interferometric processing. In Radar Interferometry: Data Interpretation and Error Analysis; Hanssen, R.F., Ed.; Springer: Dordrecht, The Netherlands, 2001; pp. 9–60. [Google Scholar]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Liebe, H.J. Modeling attenuation and phase of radio waves in air at frequencies below 1000 GHz. Radio Sci. 1981, 16, 1183–1199. [Google Scholar] [CrossRef]
- Murray, J. On the computation of saturated vapour pressure. J. Appl. Meteorol. 1967, 6, 203–204. [Google Scholar] [CrossRef]
- Blaunstein, N.; Christodoulou, C.G. (Eds.) Effects of the Troposphere on Radio Propagation. In Radio Propagation and Adaptive Antennas for Wireless Communication Networks; Wiley: Hoboken, NJ, USA, 2014; pp. 536–590. [Google Scholar]
- Radiocommunication Study Group 3. Effects of Tropospheric Refraction on Radiowave Propagation, 9th ed.; International Telecommunication Union: Genevam Switzerland, 2017; pp. 1–15. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]










| P1 | P2 | P3 | P4 | |
|---|---|---|---|---|
| Mean | −0.07 | −0.11 | −0.61 | 0.42 |
| SD | 0.32 | 0.21 | 0.40 | 0.34 |
| RMSE | 0.33 | 0.24 | 0.73 | 0.54 |
| Parameter | Value |
|---|---|
| Radar type | Frequency-modulated continuous wave (FMCW) |
| Antenna type | Slotted waveguide |
| Frequency range | 17.1–17.3 GHz (Ku-band) |
| Bandwidth | 200 MHz |
| Frequency accuracy | <100 Hz |
| Maximum sampling frequency | 4000 Hz |
| Measurement range | 50–10,000 m |
| Azimuth beamwidth | 0.385 deg (−3 dB) |
| Elevation beamwidth | 35 deg (−3 dB) |
| Range sample spacing | 0.75 m |
| Range resolution | 0.95 m (−3 dB) |
| Azimuth resolution | 6.8 m at 1 km (−3 dB) |
| Displacement accuracy | <1 mm at 1 km |
| Time reference | UTC |
| P1 1 | P2 | P3 | P4 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M1 3 | M2 4 | M3 5 | M1 | M2 | M3 | M1 | M2 | M3 | M1 | M2 | M3 | |
| Mean | 0.03 | 0.00 | −0.07 | 0.00 | −0.03 | −0.11 | 1.53 | −0.89 | −0.61 | 2.61 | 0.00 | 0.42 |
| SD | 0.80 | 0.00 | 0.32 | 0.42 | 0.49 | 0.21 | 2.00 | 0.60 | 0.40 | 1.99 | 0.00 | 0.34 |
| RMSE | 0.80 | 0.00 | 0.33 | 0.42 | 0.49 | 0.24 | 2.52 | 1.08 | 0.73 | 3.28 | 0.00 | 0.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Xu, B.; Li, Z.; Li, J.; Hou, J.; Mao, W. Joint Estimation of Ground Displacement and Atmospheric Model Parameters in Ground-Based Radar. Remote Sens. 2023, 15, 1765. https://doi.org/10.3390/rs15071765
Zhu Y, Xu B, Li Z, Li J, Hou J, Mao W. Joint Estimation of Ground Displacement and Atmospheric Model Parameters in Ground-Based Radar. Remote Sensing. 2023; 15(7):1765. https://doi.org/10.3390/rs15071765
Chicago/Turabian StyleZhu, Yan, Bing Xu, Zhiwei Li, Jie Li, Jingxin Hou, and Wenxiang Mao. 2023. "Joint Estimation of Ground Displacement and Atmospheric Model Parameters in Ground-Based Radar" Remote Sensing 15, no. 7: 1765. https://doi.org/10.3390/rs15071765
APA StyleZhu, Y., Xu, B., Li, Z., Li, J., Hou, J., & Mao, W. (2023). Joint Estimation of Ground Displacement and Atmospheric Model Parameters in Ground-Based Radar. Remote Sensing, 15(7), 1765. https://doi.org/10.3390/rs15071765