Development and Testing of Octree-Based Intra-Voxel Statistical Inference to Enable Real-Time Geotechnical Monitoring of Large-Scale Underground Spaces with Mobile Laser Scanning Data
Abstract
1. Introduction
- Design of a purpose-built voxel-based octree data structure for efficient processing of MLS point clouds and geotechnical metadata.
- Development of a novel change detection algorithm that utilizes MLS-sensor-specific parameters to derive intra-voxel inference statistics to determine geotechnical risk and handle the low signal-to-noise ratio of MLS.
- Comparison of our new framework using mine-wide MLS data collected with state-of-the-art SLAM-MLS against traditional change-detection methods, showing significantly improved computational performance for convergence and rockfall detection.
1.1. Traditional Deformation Analysis and Change Detection
1.2. Challenges in Large-Scale MLS Data Analysis
1.3. Octree-Based Deformation Analysis and Change Detection
2. Materials and Methods
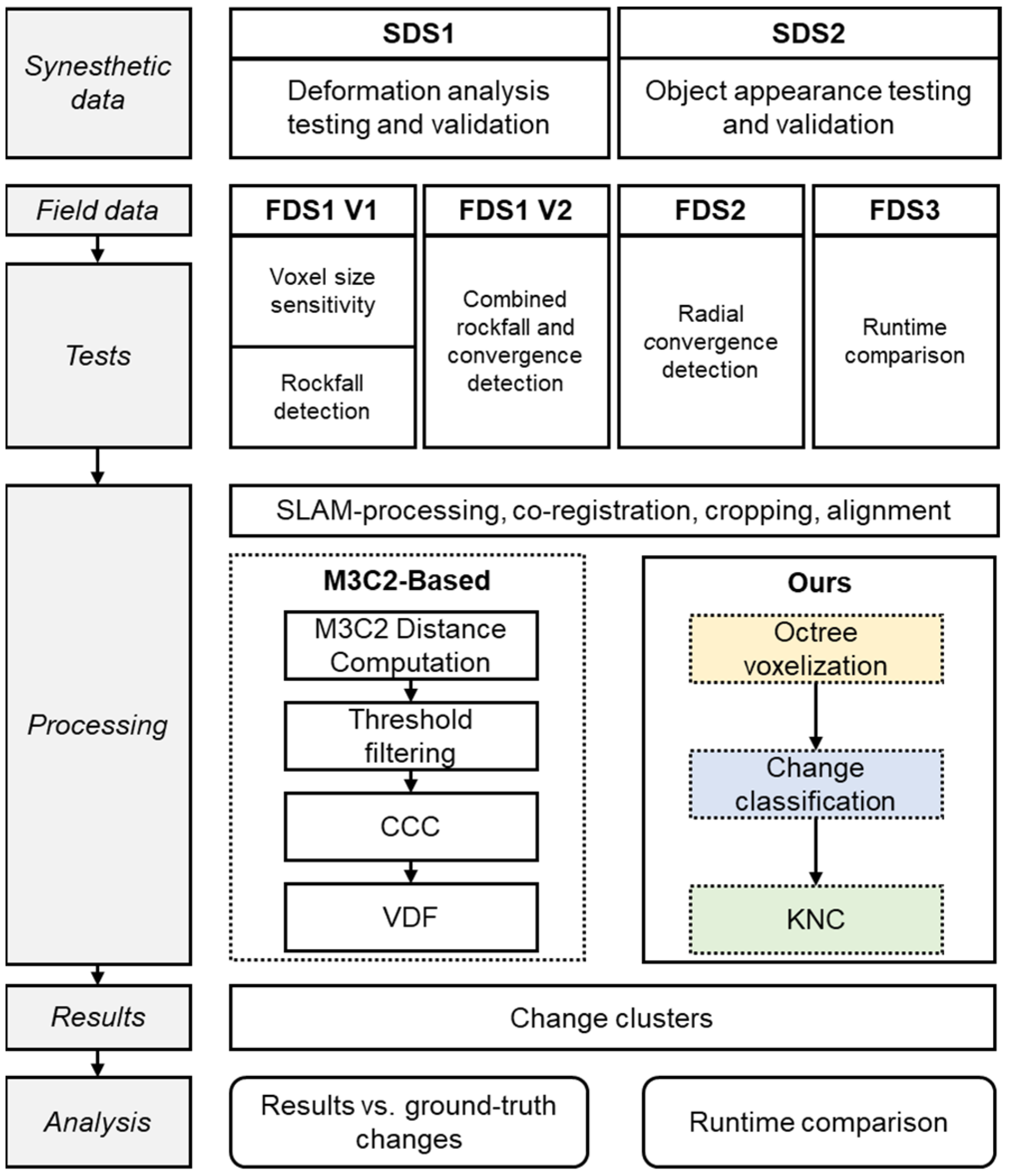
2.1. Octree and Statistical Inference-Based Change Detection Framework
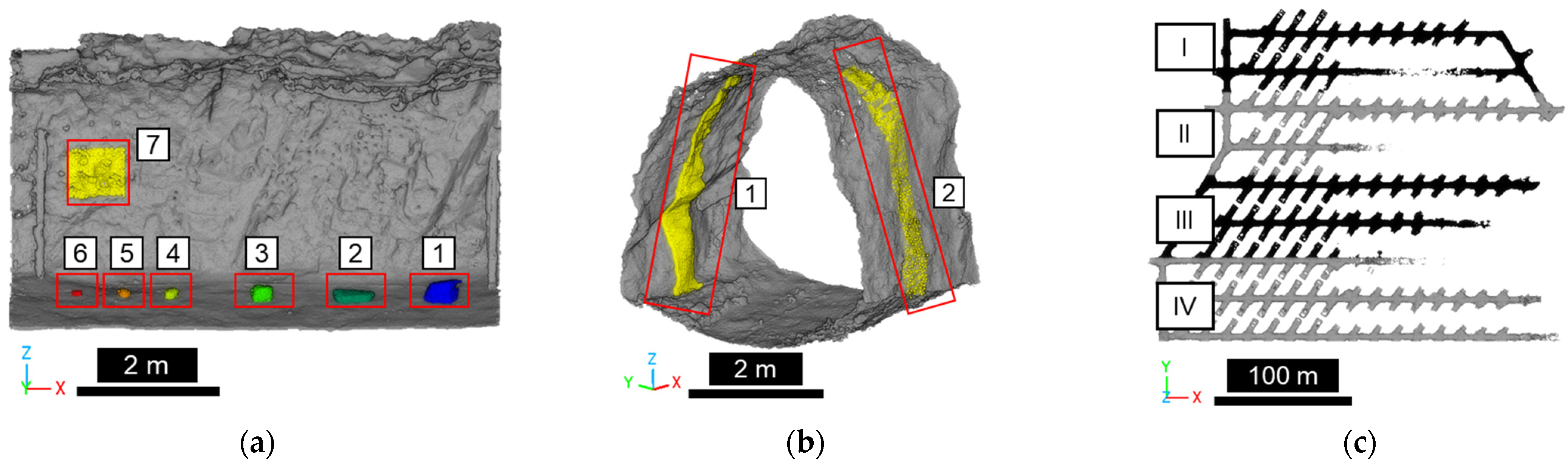
2.2. Synthetic Datasets Generation
2.3. Field Data Acquisition
2.4. Workflow and Parameter Selection
3. Results and Discussion
3.1. Proof of Concept
3.2. Voxel Size Sensitivity Tests
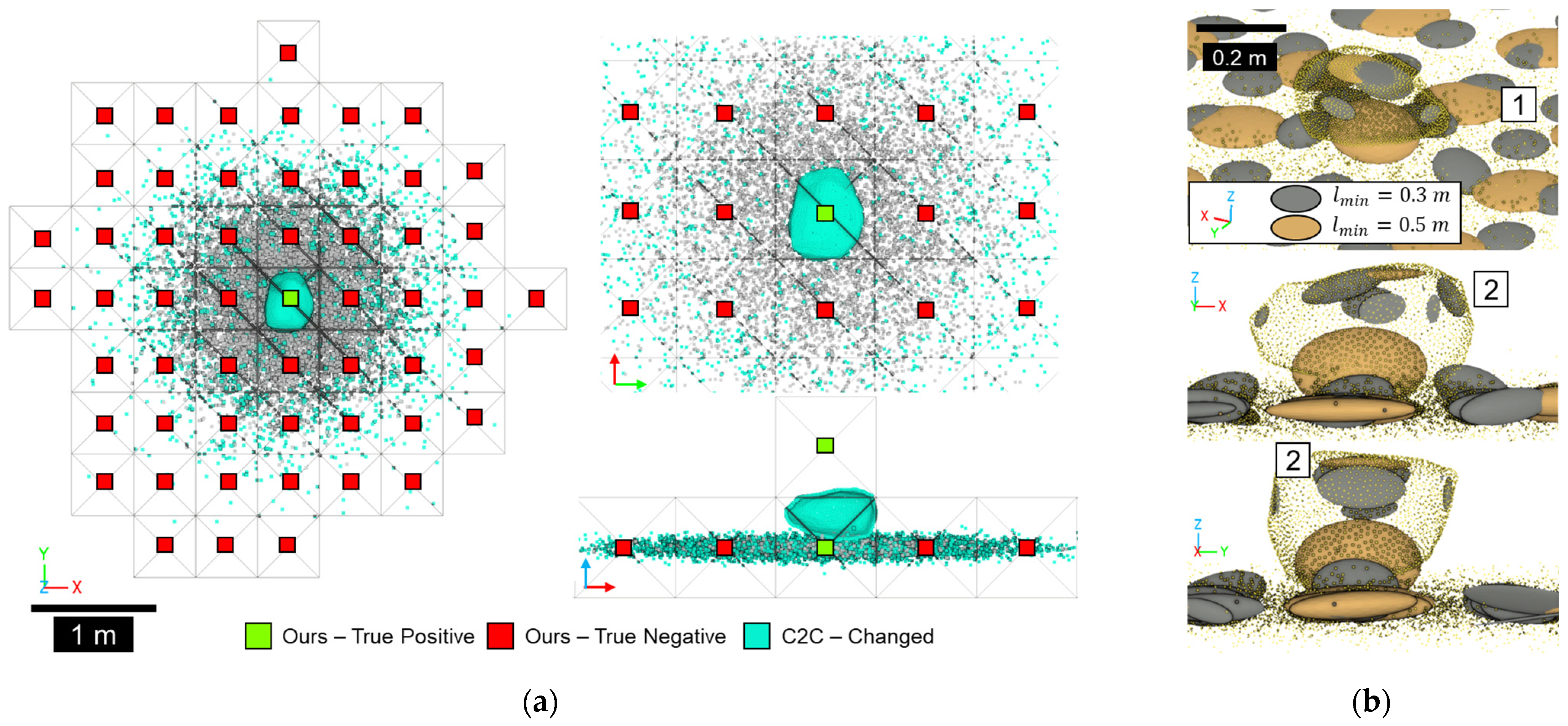
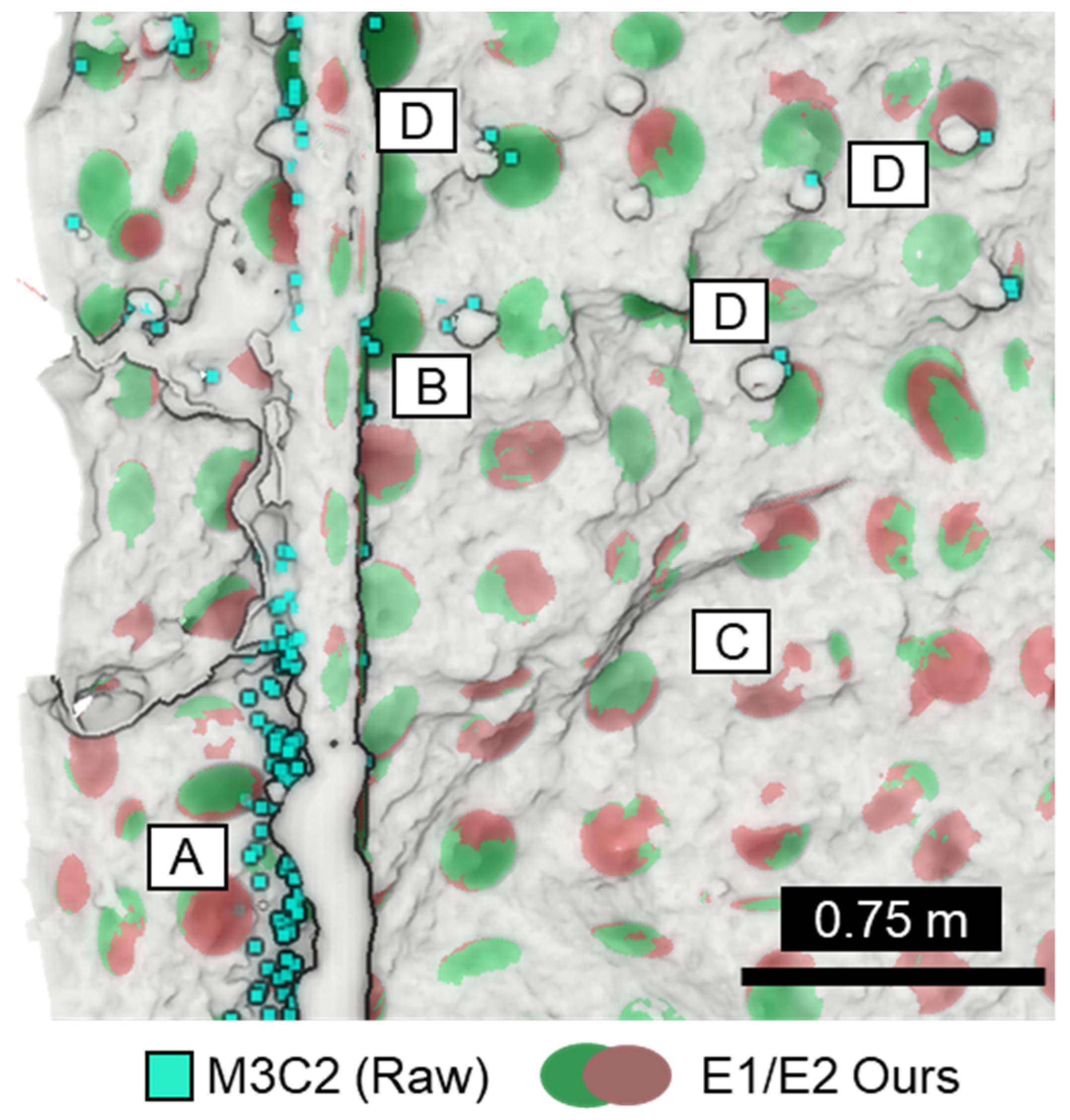
3.3. Change Detection Accuracy Tests
3.4. Runtime Comparison
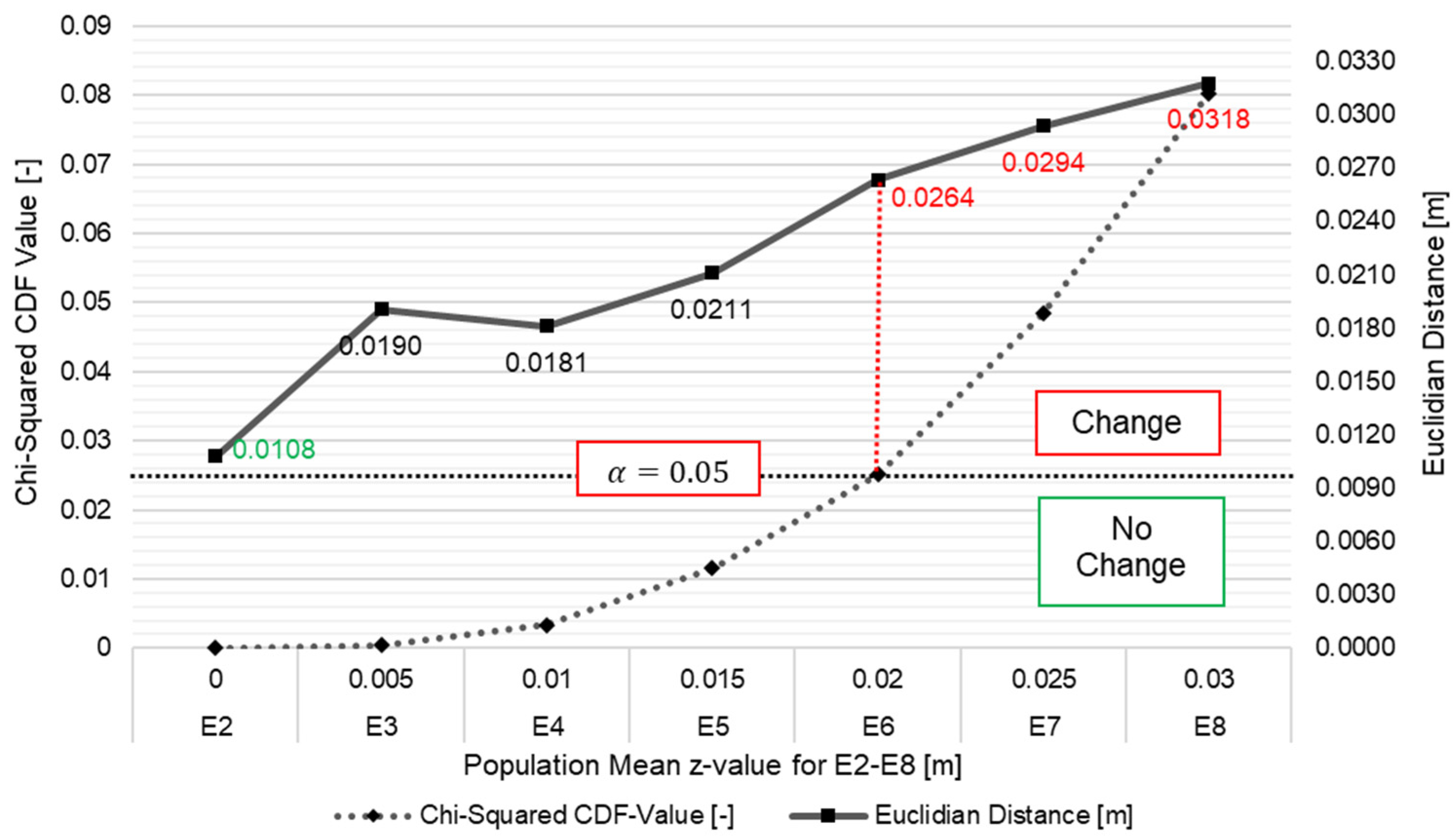
3.5. Discussion of p-Value-Based Decision-Making
3.6. Additional Benefits of an Octree-Based Framework
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Unit | FDS1 V1 | FDS1 V2 | FDS2 | FDS3 | |
|---|---|---|---|---|---|
| Dataset Properties | |||||
| Test Focus | - | Rockfall | Rockfall & Convergence | Radial Convergence | Runtime |
| Instrument | - | Hovermap | Hovermap | Hovermap | Stencil 2 |
| Points per Epoch | M | 3.3 | 3.3 | 2.2 | 5–27 |
| Raw Data Point Spacing | m | 0.005 | 0.005 | 0.005 | 0.05 |
| Mean Roughness | - | 0.04 | 0.04 | 0.04 | 0.13 |
| M3C2-Based Method | |||||
| M3C2 Distance Computations | |||||
| Normal Calculation Method | m | Fixed | Multi-Scale | Multi-Scale | Both |
| Core Point Spacing | m | 0.01 | 0.01 | 0.01 | 0.1 |
| Fixed Normal Diameter | m | 1.0 | - | - | 3.25 |
| Minimum Normal Diameter | m | - | 0.125 | 0.125 | 0.125 |
| Step Normal Diameter | m | - | 0.2 | 0.2 | 0.2 |
| Max Normal Diameter | m | - | 6.125 | 6.125 | 6.125 |
| Projection Diameter | m | 0.03 | 0.03 | 0.03 | 0.3 |
| Maximum Projection Depth | m | 0.5 | 0.5 | 0.5 | 0.5 |
| Threshold Filtering | |||||
| Limit of Detection | m | 0.05 | 0.01 | 0.01 | - |
| Clustering | |||||
| CCC Octree Depth | - | 8 | 8 | 8 | - |
| CCC Minimum Points | - | 30 | 30 | 30 | - |
| Volume Density Filtering | |||||
| Points per Cubic Meter | pts/m3 | 50k | 35k | 35k | - |
| Ours | |||||
| Octree Voxelization | |||||
| Voxel Size | m | 0.1 | 0.1 | 0.25 | 0.25 |
| Change Classification | |||||
| Min Points per Voxel | - | 50 | 50 | 50 | 50 |
| Significance Level | - | 0.05 | 0.05 | 0.05 | 0.05 |
| KNC | |||||
| Minimum Cluster Size | - | 2 | 2 | 2 | 2 |
References
- Terzaghi, K. Shield tunnels of the Chicago Subway. J. Boston Soc. Civ. Eng. 1942, 29, 163–210. [Google Scholar]
- Ma, K.; Zhang, J.; Zhou, Z.; Xu, N. Comprehensive analysis of the surrounding rock mass stability in the underground caverns of Jinping I hydropower station in Southwest China. Tunn. Undergr. Space Technol. 2020, 104, 103525. [Google Scholar] [CrossRef]
- Hu, Z.; Wu, B.; Xu, N.; Wang, K. Effects of discontinuities on stress redistribution and rock failure: A case of underground caverns. Tunn. Undergr. Space Technol. 2022, 127, 104583. [Google Scholar] [CrossRef]
- Li, S.; Yu, H.; Liu, Y.; Wu, F. Results from in-situ monitoring of displacement, bolt load, and disturbed zone of a powerhouse cavern during excavation process. Int. J. Rock Mech. Min. Sci. 2008, 45, 1519–1525. [Google Scholar] [CrossRef]
- Zhao, J.S.; Jiang, Q.; Lu, J.F.; Chen, B.R.; Pei, S.F.; Wang, Z.L. Rock fracturing observation based on microseismic monitoring and borehole imaging: In situ investigation in a large underground cavern under high geostress. Tunn. Undergr. Space Technol. 2022, 126, 104549. [Google Scholar] [CrossRef]
- Wittke, W.; Pierau, B.; Erichsen, C. New Austrian Tunneling Method (NATM)—Stability Analysis and Design; WBI: Essen, Germany, 2006. [Google Scholar]
- Walton, G.; Delaloye, D.; Diederichs, M.S. Development of an elliptical fitting algorithm to improve change detection capabilities with applications for deformation monitoring in circular tunnels and shafts. Tunn. Undergr. Space Technol. 2014, 43, 336–349. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Cai, M. Design of rock support system under rockburst condition. J. Rock Mech. Geotech. Eng. 2012, 4, 215–227. [Google Scholar] [CrossRef]
- Mark, C.; Molinda, G.M. Preventing falls of ground in coal mines with exceptionally low-strength roof: Two case studies. In Proceedings of the 23rd International Conference on Ground Control in Mining, Morgantown, WV, USA, 3–5 August 2004. [Google Scholar]
- Nordlund, E. Deep hard rock mining and rock mechanics challenges. In Proceedings of the Ground Support 2013: The Seventh International Symposium on Ground Support in Mining and Underground Construction, Perth, Australia, 13 May 2013; pp. 39–56. [Google Scholar] [CrossRef]
- Oraee, K.; Oraee, N.; Goodarzi, A.; Khajehpour, P. Effect of discontinuities characteristics on coal mine stability and sustainability: A rock fall prediction approach. Int. J. Min. Sci. Technol. 2016, 26, 65–70. [Google Scholar] [CrossRef]
- Palei, S.K.; Das, S.K. Sensitivity analysis of support safety factor for predicting the effects of contributing parameters on roof falls in underground coal mines. Int. J. Coal Geol. 2008, 75, 241–247. [Google Scholar] [CrossRef]
- Sandbak, L.A.; Rai, A.R. Ground Support Strategies at the Turquoise Ridge Joint Venture, Nevada. Rock Mech. Rock Eng. 2013, 46, 437–454. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. NIOSH Mine and Mine Worker Charts. 2021. Available online: https://wwwn.cdc.gov/niosh-mining/MMWC (accessed on 2 September 2021).
- Williams, K.; Olsen, M.J.; Roe, G.; Glennie, C. Synthesis of transportation applications of mobile LiDAR. Remote Sens. 2013, 5, 4652–4692. [Google Scholar] [CrossRef]
- Luo, X.; Ren, X.T.; Li, Y.; Wang, J.J. Mobile surveying system for road assets monitoring and management. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 1688–1693. [Google Scholar]
- Puente, I.; Akinci, B.; González-Jorge, H.; Díaz-Vilariño, L.; Arias, P. A semi-automated method for extracting vertical clearance and cross sections in tunnels using mobile LiDAR data. Tunn. Undergr. Space Technol. 2016, 59, 48–54. [Google Scholar] [CrossRef]
- Raval, S.; Banerjee, B.P.; Singh, S.K.; Canbulat, I. A Preliminary Investigation of Mobile Mapping Technology for Underground Mining. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 6071–6074. [Google Scholar]
- Lynch, B.K.; Marr, J.; Marshall, J.A.; Greenspan, M. Mobile LiDAR-Based Convergence Detection in Underground Tunnel Environments. 2017. Available online: http://hdl.handle.net/1974/15638 (accessed on 17 May 2022).
- Singh, S.K.; Banerjee, B.P.; Raval, S. A review of laser scanning for geological and geotechnical applications in underground mining. Int. J. Min. Sci. Technol. 2023, 33, 133–154. [Google Scholar] [CrossRef]
- Fahle, L.; Holley, E.; Walton, G. Toward a mine-wide, real-time, and autonomous geotechnical change detection, monitoring, and prediction framework for underground mines. In Proceedings of the 39th International Conference on Ground Control in Mining, ICGCM 2020, Canonsburg, PA, USA, 28–30 July 2020. [Google Scholar]
- Fahle, L.; Holley, E.A.; Walton, G.; Petruska, A.J.; Brune, J.F. Analysis of SLAM-Based Lidar Data Quality Metrics for Geotechnical Underground Monitoring. Min. Metall. Explor. 2022, 39, 1939–1960. [Google Scholar] [CrossRef]
- Gallwey, J.; Eyre, M.; Coggan, J. A machine learning approach for the detection of supporting rock bolts from laser scan data in an underground mine. Tunn. Undergr. Space Technol. 2021, 107, 103656. [Google Scholar] [CrossRef]
- Watson, C.; Marshall, J. Estimating underground mine ventilation friction factors from low density 3D data acquired by a moving LiDAR. Int. J. Min. Sci. Technol. 2018, 28, 657–662. [Google Scholar] [CrossRef]
- Engin, I.C.; Maerz, N.H.; Boyko, K.J.; Reals, R. Practical Measurement of Size Distribution of Blasted Rocks Using LiDAR Scan Data. Rock Mech. Rock Eng. 2020, 53, 4653–4671. [Google Scholar] [CrossRef]
- Marshall, J.; Barfoot, T.; Larsson, J. Autonomous underground tramming for center-articulated vehicles. J. Field Robot. 2008, 25, 400–421. [Google Scholar] [CrossRef]
- Jones, E.; Ghabraie, B.; Beck, D. A method for determining field accuracy of mobile scanning devices for geomechanics applications. In Proceedings of the ISRM International Symposium—10th Asian Rock Mechanics Symposium, ARMS 2018, Singapore, 29 October–3 November 2018; pp. 978–981. [Google Scholar]
- Lindenbergh, R.; Pietrzyk, P. Change detection and deformation analysis using static and mobile laser scanning. Appl. Geomat. 2015, 7, 65–74. [Google Scholar] [CrossRef]
- Wannenmacher, H.; Krenn, H.; Komma, N.; Tunnel, A.S. Improved pressure tunnel lining methods, a case study of the Niagara Tunnel Facility Project. In World Tunnel Congress 2013, Geneva; Anagnostou, G., Ehrbar, H., Eds.; CRC Press: London, UK, 2013. [Google Scholar]
- Nuttens, T.; Stal, C.; de Backer, H.; Schotte, K.; van Bogaert, P.; de Wulf, A. Methodology for the ovalization monitoring of newly built circular train tunnels based on laser scanning: Liefkenshoek Rail Link (Belgium). Autom. Constr. 2014, 43, 1–9. [Google Scholar] [CrossRef]
- Walton, G.; Diederichs, M.S.; Weinhardt, K.; Delaloye, D.; Lato, M.J.; Punkkinen, A. Change detection in drill and blast tunnels from point cloud data. Int. J. Rock Mech. Min. Sci. 2018, 105, 172–181. [Google Scholar] [CrossRef]
- Han, J.Y.; Guo, J.; Jiang, Y.S. Monitoring tunnel deformations by means of multi-epoch dispersed 3D LiDAR point clouds: An improved approach. Tunn. Undergr. Space Technol. 2013, 38, 385–389. [Google Scholar] [CrossRef]
- Fekete, S.; Diederichs, M.; Lato, M. Geotechnical and operational applications for 3-dimensional laser scanning in drill and blast tunnels. Tunn. Undergr. Space Technol. 2010, 25, 614–628. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change Detection on Points Cloud Data Acquired with A Ground Laser Scanner. In Proceedings of the ISPRS WG III/3, III/4, V/3 Workshop “Laser Scanning 2005”, Enschede, The Netherlands, 12–14 September 2005. [Google Scholar]
- Barnhart, T.B.; Crosby, B.T. Comparing two methods of surface change detection on an evolving thermokarst using high-temporal-frequency terrestrial laser scanning, Selawik River, Alaska. Remote Sens. 2013, 5, 2813–2837. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J.; Afana, A.A. Optimising 4-D surface change detection: An approach for capturing rockfall magnitude-frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef]
- van Veen, M.; Hutchinson, D.J.; Kromer, R.; Lato, M.; Edwards, T. Effects of sampling interval on the frequency—magnitude relationship of rockfalls detected from terrestrial laser scanning using semi-automated methods. Landslides 2017, 14, 1579–1592. [Google Scholar] [CrossRef]
- Kromer, R.A.; Abellán, A.; Hutchinson, D.J.; Lato, M.; Edwards, T.; Jaboyedoff, M. A 4D filtering and calibration technique for small-scale point cloud change detection with a terrestrial laser scanner. Remote Sens. 2015, 7, 13029–13058. [Google Scholar] [CrossRef]
- Bonneau, D.A.; Hutchinson, D.J. The use of terrestrial laser scanning for the characterization of a cliff-talus system in the Thompson River Valley, British Columbia, Canada. Geomorphology 2019, 327, 598–609. [Google Scholar] [CrossRef]
- Winiwarter, L.; Anders, K.; Höfle, B. M3C2-EP: Pushing the limits of 3D topographic point cloud change detection by error propagation. ISPRS J. Photogramm. Remote Sens. 2021, 178, 240–258. [Google Scholar] [CrossRef]
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J.M. Detection of millimetric deformation using a terrestrial laser scanner: Experiment and application to a rockfall event. Nat. Hazards Earth Syst. Sci. 2009, 9, 365–372. [Google Scholar] [CrossRef]
- Abellán, A.; Oppikofer, T.; Jaboyedoff, M.; Rosser, N.J.; Lim, M.; Lato, M.J. Terrestrial laser scanning of rock slope instabilities. Earth Surf. Process. Landf. 2014, 39, 80–97. [Google Scholar] [CrossRef]
- DiFrancesco, P.M.; Bonneau, D.; Hutchinson, D.J. The implications of M3C2 projection diameter on 3D semi-automated rockfall extraction from sequential terrestrial laser scanning point clouds. Remote Sens. 2020, 12, 1885. [Google Scholar] [CrossRef]
- Kromer, R.A.; Hutchinson, D.J.; Lato, M.J.; Gauthier, D.; Edwards, T. Identifying rock slope failure precursors using LiDAR for transportation corridor hazard management. Eng. Geol. 2015, 195, 93–103. [Google Scholar] [CrossRef]
- Lato, M.J.; Diederichs, M.S.; Hutchinson, D.J.; Harrap, R. Evaluating roadside rockmasses for rockfall hazards using LiDAR data: Optimizing data collection and processing protocols. Nat. Hazards 2012, 60, 831–864. [Google Scholar] [CrossRef]
- Evans, P. Improving Convergence Monitoring Using Lidar Data At Rio Tinto’S Argyle Diamond Mine Improving Convergence Monitoring Using Lidar Data at Rio Tinto’S Argyle Diamond Mine. 2021, pp. 1–12. Available online: https://www.emesent.io/2021/05/26/improving-convergence-monitoring-using-lidar-data-at-rio-tintos-argyle-diamond-mine/ (accessed on 21 March 2023).
- Vanneschi, C.; Mastrorocco, G.; Salvini, R. Assessment of a rock pillar failure by using change detection analysis and FEM modelling. ISPRS Int. J. Geo-Inf. 2021, 10, 774. [Google Scholar] [CrossRef]
- Benjamin, J.; Rosser, N.; Brain, M. Rockfall detection and volumetric characterisation using LiDAR. In Landslides and Engineered Slopes. Experience, Theory and Practice; CRC Press: Boca Raton, FL, USA, 2016; Volume 2, pp. 389–395. [Google Scholar] [CrossRef]
- Ozdogan, M.V.; Deliormanli, A.H. Landslide detection and characterization using terrestrial 3D laser scanning (LIDAR). Acta Geodyn. Geomater. 2019, 16, 379–392. [Google Scholar] [CrossRef]
- Gandomi, A.; Haider, M. Beyond the hype: Big data concepts, methods, and analytics. Int. J. Inf. Manag. 2015, 35, 137–144. [Google Scholar] [CrossRef]
- Tonini, M.; Abellan, A. Rockfall detection from terrestrial lidar point clouds: A clustering approach using R. J. Spat. Inf. Sci. 2014, 8, 95–110. [Google Scholar] [CrossRef]
- Sharon, R.; Eberhardt, E. Guidelines for Slope Performance Monitoring; CSIRO Publishing: Collingwood, Australia, 2020. [Google Scholar] [CrossRef]
- Mercier-Langevin, F.; Hadjigeorgiou, J. Towards a better understanding of squeezing potential in hard rock mines. Min. Technol. 2011, 120, 36–44. [Google Scholar] [CrossRef]
- Mark, C.; Iannacchione, A.T. Best Practices to mitigate injuries and fatalities from rock falls. In Proceedings of the 31st Annual Institute on Mining Health, Safety and Research, Roanoke, Virginia, 27–30 August 2000; pp. 115–129. Available online: https://stacks.cdc.gov/view/cdc/8586 (accessed on 14 August 2022).
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robot. 2017, 41, 401–416. [Google Scholar] [CrossRef]
- Wilhelms, J.; van Gelder, A. Octrees for faster isosurface generation. ACM Trans. Graph. 1992, 11, 201–227. [Google Scholar] [CrossRef]
- Meagher, D. Geometric modeling using octree encoding. Comput. Graph. Image Process. 1982, 19, 129–147. [Google Scholar] [CrossRef]
- Berrio, J.S.; Zhou, W.; Ward, J.; Worrall, S.; Nebot, E. Octree map based on sparse point cloud and heuristic probability distribution for labeled images. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar] [CrossRef]
- Park, C.; Moghadam, P.; Kim, S.; Elfes, A.; Fookes, C.; Sridharan, S. Elastic LiDAR Fusion: Dense Map-Centric Continuous-Time SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018. [Google Scholar] [CrossRef]
- Whelan, T.; Leutenegger, S.; Salas-Moreno, R.F.; Glocker, B.; Davison, A.J. ElasticFusion: Dense SLAM without a pose graph. Robot. Sci. Syst. 2015, 11, 1–9. [Google Scholar] [CrossRef]
- Behley, J.; Stachniss, C. Efficient Surfel-Based SLAM using 3D Laser Range Data in Urban Environments. Robot. Sci. Syst. XIV 2018, 2018, 59. [Google Scholar] [CrossRef]
- Droeschel, D.; Behnke, S. Efficient continuous-time SLAM for 3D lidar-based online mapping. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 5000–5007. [Google Scholar] [CrossRef]
- Zlot, R.; Bosse, M. Efficient Large-Scale 3D Mobile Mapping and Surface Reconstruction of an Underground Mine; Springer Tracts in Advanced Robotics: Heidelberg, Germany, 2014; Volume 92, pp. 479–494. [Google Scholar] [CrossRef]
- Gehrung, J.; Hebel, M.; Arens, M.; Stilla, U. A Voxel-Based Metadata Structure for Change Detection in Point Clouds of Large-Scale Urban Areas. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 97–104. [Google Scholar] [CrossRef]
- Xu, Y.; Tong, X.; Stilla, U. Voxel-based representation of 3D point clouds: Methods, applications, and its potential use in the construction industry. In Automation in Construction; Elsevier B.V.: Amsterdam, The Netherlands, 2021; Volume 126. [Google Scholar] [CrossRef]
- Gehrung, J.; Hebel, M.; Arens, M.; Stilla, U. A fast voxel-based indicator for change detection using low resolution octrees. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4, 357–364. [Google Scholar] [CrossRef]
- Gehrung, J.; Hebel, M.; Arens, M.; Stilla, U. Change Detection and Deformation Analysis Based on Mobile Laser Scanning Data of Urban Areas. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 703–710. [Google Scholar] [CrossRef]
- Wellhausen, L.; Dube, R.; Gawel, A.; Siegwart, R.; Cadena, C. Reliable real-time change detection and mapping for 3D LiDARs. In Proceedings of the SSRR 2017—15th IEEE International Symposium on Safety, Security and Rescue Robotics, Shanghai, China, 11–13 October 2017; pp. 81–87. [Google Scholar] [CrossRef]
- Schiefer, H.; Schiefer, F. Statistics for Engineers; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021. [Google Scholar] [CrossRef]
- Pearson, K. X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Emesent. Hovermap. 2022. Available online: https://www.emesent.com/hovermap/ (accessed on 15 August 2022).
- Kaarta. Kaarta Products. 2022. Available online: https://www.kaarta.com/products/stencil-2-for-rapid-long-range-mobile-mapping/ (accessed on 21 March 2023).
- Velodyne LiDAR. Velodyne LiDAR ‘Puck’ LITE Light Weight Real-Time 3D LiDAR Sensor: Product Specification. 2022. Available online: https://velodynelidar.com/products/puck-lite/ (accessed on 21 March 2023).
- CloudCompare. CloudCompare. 2021. Available online: https://www.danielgm.net/cc/ (accessed on 21 March 2023).
- Park, C.; Kim, S.; Moghadam, P.; Fookes, C.; Sridharan, S. Probabilistic Surfel Fusion for Dense LiDAR Mapping. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops, ICCVW 2017, Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef]
- Trăsnea, B.; Ginerică, C.; Zaha, M.; Măceşanu, G.; Pozna, C.; Grigorescu, S. Octopath: An octree-based self-supervised learning approach to local trajectory planning for mobile robots. Sensors 2021, 21, 3606. [Google Scholar] [CrossRef] [PubMed]
- Nuzzo, R. Statistical Errors. Nature 2014, 506, 150–152. [Google Scholar] [CrossRef] [PubMed]
- Baker, M. Statisticians issue warning on P values. Nature 2016, 531, 151. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Lazar, N.A. The ASA’s Statement on p-Values: Context, Process, and Purpose. In American Statistician; American Statistical Association: Boston, MA, USA, 2016; Volume 70, pp. 129–133. [Google Scholar] [CrossRef]
- Siegfried, T. Odds Are, It’s Wrong. Available online: https://www.sciencenews.org/article/odds-are-its-wrong (accessed on 12 March 2010).
- Ouster. ULTRA-WIDE VIEW LIDAR SENSOR OS0. 2021. Available online: https://ouster.com/products/os0-lidar-sensor/ (accessed on 21 March 2023).
- Hoetzlein, R.K. GVDB: Raytracing sparse voxel database structures on the GPU. In Proceedings of the High-Performance Graphics—ACM SIGGRAPH/Eurographics Symposium Proceedings, HPG, Dublin, Ireland, 20–22 June 2016; Volume 2016. [Google Scholar] [CrossRef]
- Min, H.; Han, K.M.; Kim, Y.J. Accelerating Probabilistic Volumetric Mapping using Ray-Tracing Graphics Hardware. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar] [CrossRef]
- Underwood, J.P.; Gillsjo, D.; Bailey, T.; Vlaskine, V. Explicit 3D change detection using ray-tracing in spherical coordinates. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4735–4741. [Google Scholar] [CrossRef]
- Wang, P.S.; Liu, Y.; Guo, Y.X.; Sun, C.Y.; Tong, X. O-CNN: Octree-based convolutional neural networks for 3D shape analysis. ACM Trans. Graph. 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Sennersten, C.; Davie, A.; Lindley, C. Voxelnet—An Agent Based System for Spatial Data Analytics. In Proceedings of the COGNITIVE: The Eigth International Conference on Advanced Cognitive Technologies and Applications, Rome, Italy, 20–24 March 2016; pp. 133–136. [Google Scholar]
- Sennersten, C.; Lindley, C.; Evans, B. VoxelNET’s Geo-Located Spatio Temporal Softbots. In Proceedings of the COGNITIVE: The Eigth International Conference on Advanced Cognitive Technologies and Applications, Venice, Italy, 5–9 May 2019; pp. 20–27. [Google Scholar]
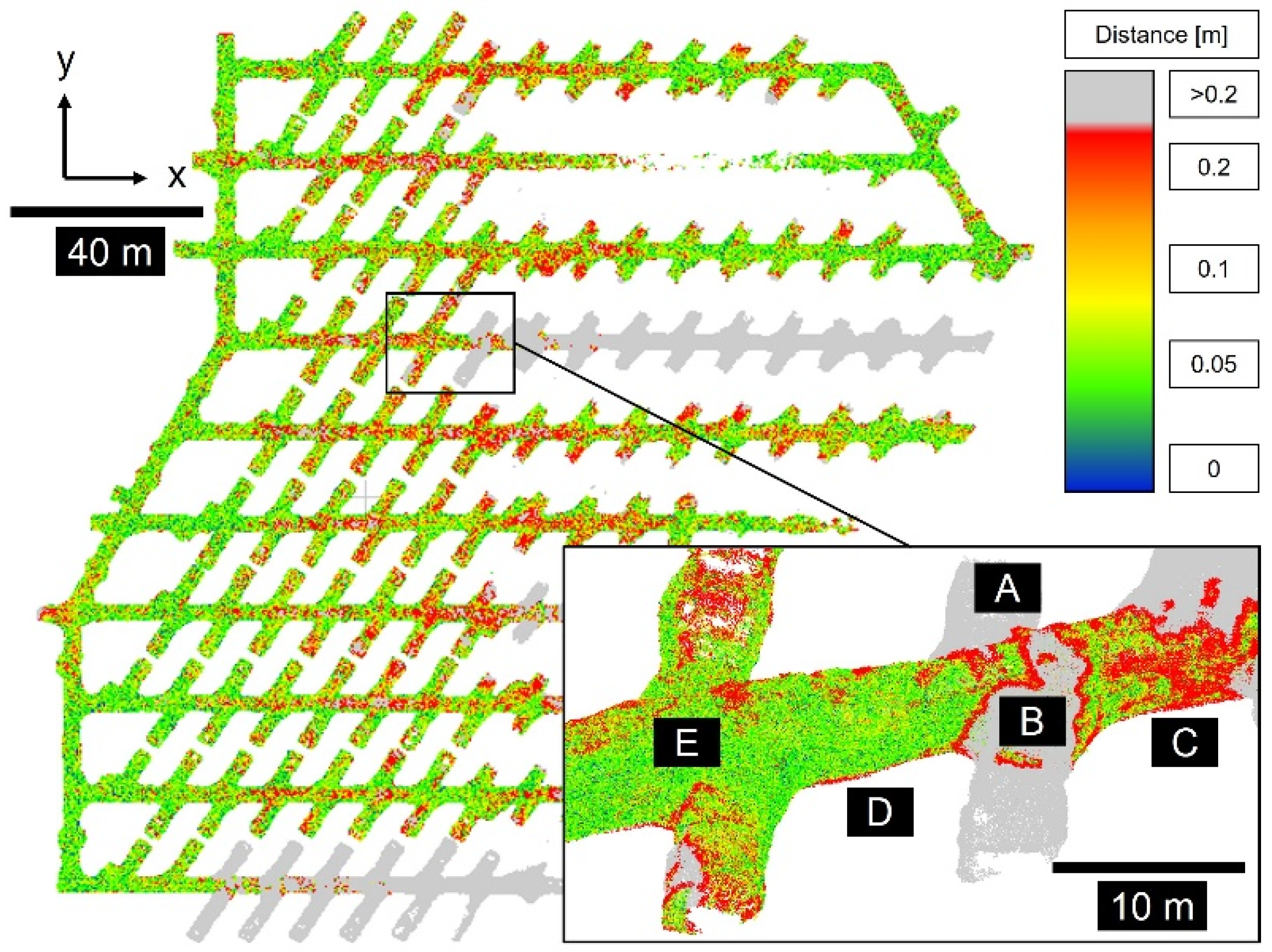
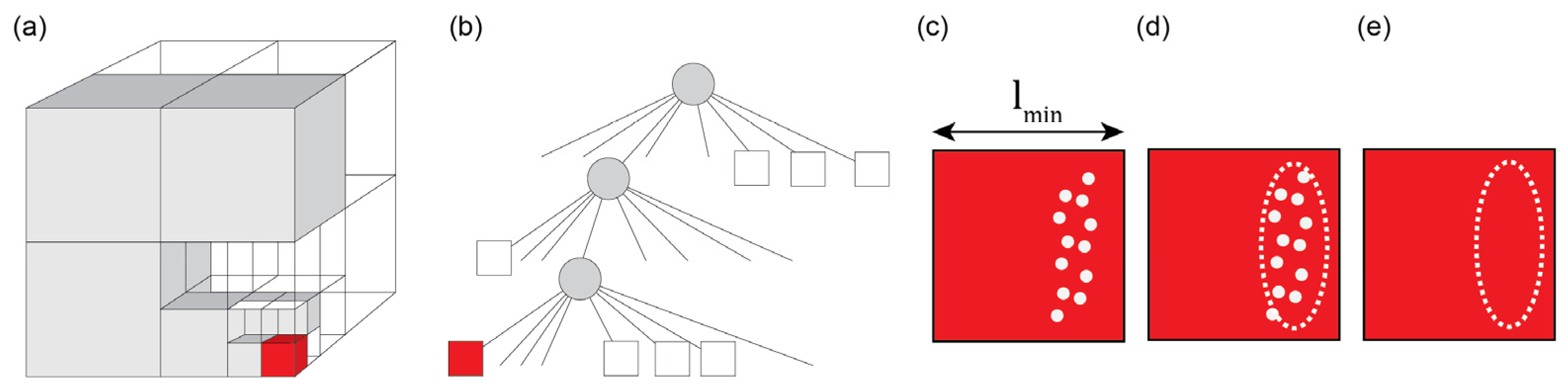
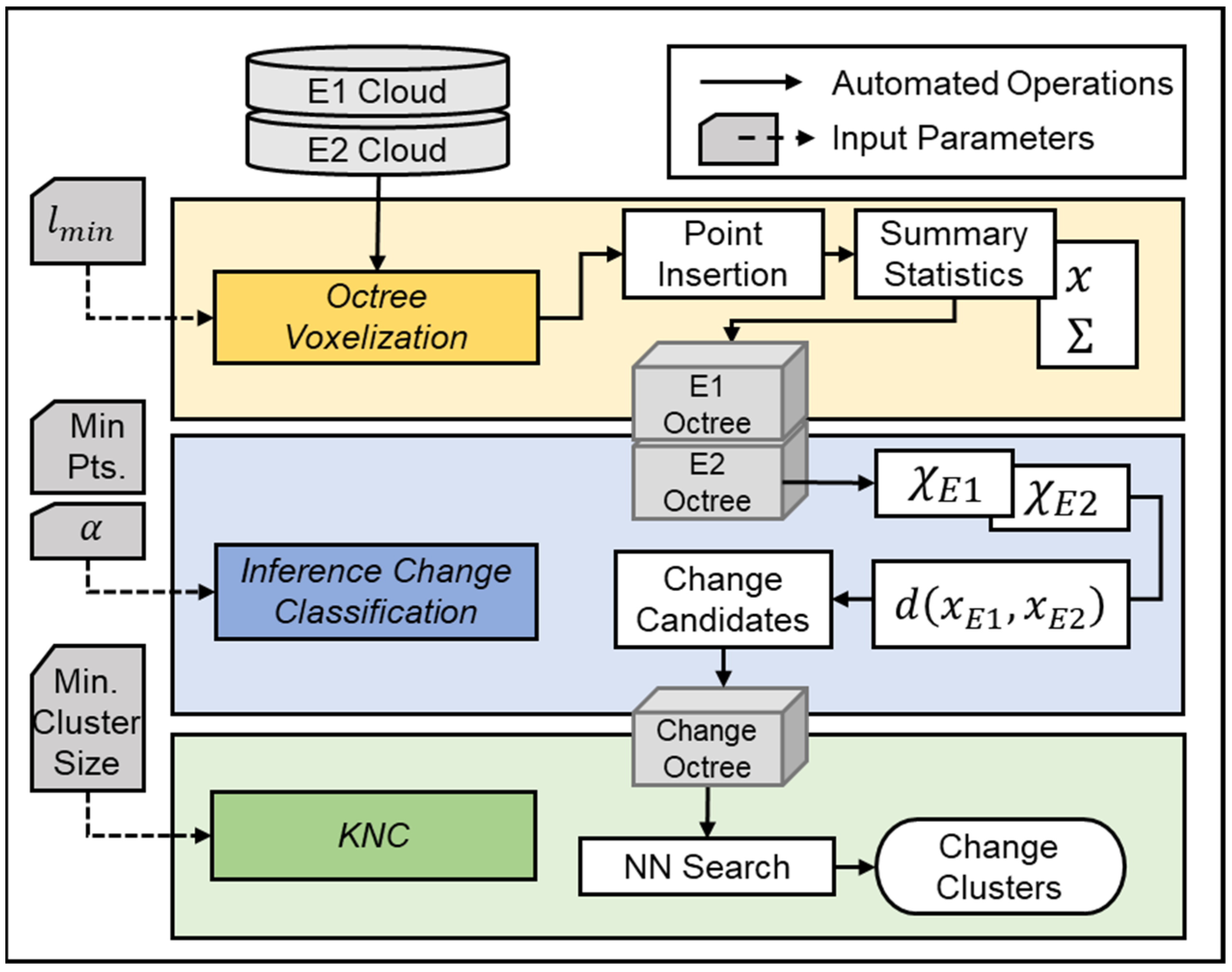
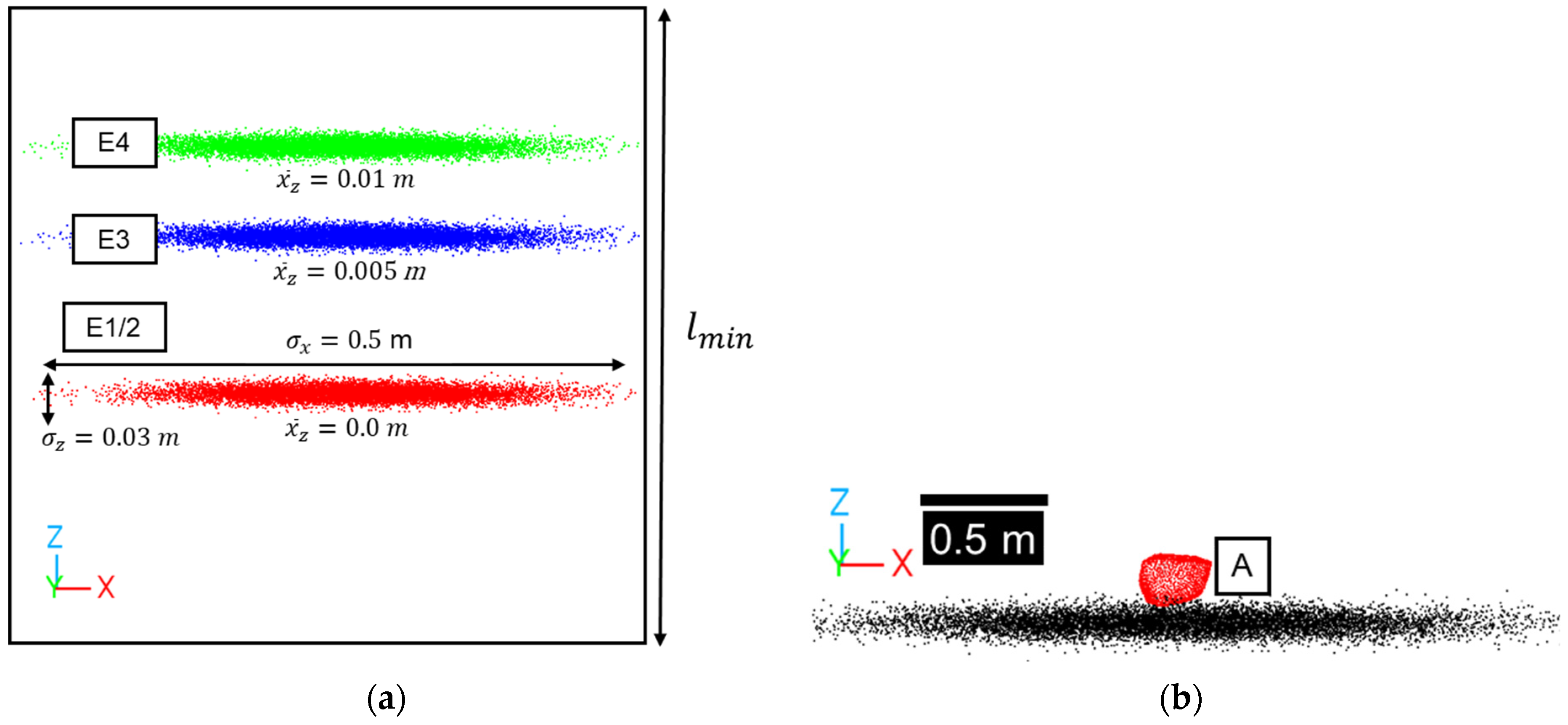

| Method | Robust to Noise | Computationally Efficient | Topological Structure | Classification-Based | References |
|---|---|---|---|---|---|
| Shape Fitting | Yes | No | No | No | [7,29,30,31] |
| C2C | No | Yes | No | No | [34,35] |
| C2M | No | No | No | No | [34] |
| M3C2 | Yes | No | No | No | [36] |
| ID | Voxel Size [m] | Detected Targets | Comment | |
|---|---|---|---|---|
| KNC | No Filter | |||
| A | 0.10 | 6/6 | 6/6 | - |
| B | 0.15 | 5/6 | 6/6 | KNC removes target cluster (No. 6) with <2 voxels |
| C | 0.25 | 2/6 | 6/6 | KNC removes target clusters No. 3–6 with <2 voxels |
| D | 0.50 | 2/6 | 4/6 | KNC removes target clusters No. 4–6 and No. 2 with <2 voxels |
| E | 1.00 | 0/6 | 1/6 | Only target No. 1 is correctly classified in unfiltered data |
| Dataset | M3C2 (CCC) | Ours (KNC) | M3C2 Comment |
|---|---|---|---|
| FDS1 V1 | 5/6 | 6/6 | One false negative (Target No. 6) caused by threshold filtering Fifteen false positive noise clusters remain after CCC |
| FDS1 V2 | 7/7 | 7/7 | Twenty-eight false positive clusters caused by 0.01 m threshold filter VDF not applicable |
| FDS2 | 2/2 | 2/2 | One hundred sixty-three false positive clusters remain after CCC |
| Setting | Core Points | Multi-Scale Normals | Threads |
|---|---|---|---|
| S1 | False | False | 8 |
| S2 | False | True | 8 |
| S3 | True | False | 8 |
| S4 | True | True | 8 |
| S5 | True | False | 1 |
| S6 | True | True | 1 |
| FDS3 Section | |||||
|---|---|---|---|---|---|
| M3C2 Setting | I 5.4 M Pts/Epoch | II 10.9 M Pts/Epoch | III 18.7 M Pts/Epoch | IV 27.7 Pts/Epoch | Change from I to IV |
| S1 | 25.32 | DNC | DNC | DNC | - |
| S2 | 1.22 | DNC | DNC | DNC | |
| S3 | 318.67 | 321.46 | 297.20 | 297.97 | −6% |
| S4 | 33.24 | 30.03 | 28.81 | 29.48 | −11% |
| S5 | 137.85 | 139.95 | 120.80 | 114.75 | −17% |
| S6 | 10.75 | DNC | DNC | DNC | - |
| Ours | 546.39 | 546.13 | 534.29 | 524.88 | −4% |
| Real-Time Margin | 82% | 82% | 78% | 75% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fahle, L.; Petruska, A.J.; Walton, G.; Brune, J.F.; Holley, E.A. Development and Testing of Octree-Based Intra-Voxel Statistical Inference to Enable Real-Time Geotechnical Monitoring of Large-Scale Underground Spaces with Mobile Laser Scanning Data. Remote Sens. 2023, 15, 1764. https://doi.org/10.3390/rs15071764
Fahle L, Petruska AJ, Walton G, Brune JF, Holley EA. Development and Testing of Octree-Based Intra-Voxel Statistical Inference to Enable Real-Time Geotechnical Monitoring of Large-Scale Underground Spaces with Mobile Laser Scanning Data. Remote Sensing. 2023; 15(7):1764. https://doi.org/10.3390/rs15071764
Chicago/Turabian StyleFahle, Lukas, Andrew J. Petruska, Gabriel Walton, Jurgen F. Brune, and Elizabeth A. Holley. 2023. "Development and Testing of Octree-Based Intra-Voxel Statistical Inference to Enable Real-Time Geotechnical Monitoring of Large-Scale Underground Spaces with Mobile Laser Scanning Data" Remote Sensing 15, no. 7: 1764. https://doi.org/10.3390/rs15071764
APA StyleFahle, L., Petruska, A. J., Walton, G., Brune, J. F., & Holley, E. A. (2023). Development and Testing of Octree-Based Intra-Voxel Statistical Inference to Enable Real-Time Geotechnical Monitoring of Large-Scale Underground Spaces with Mobile Laser Scanning Data. Remote Sensing, 15(7), 1764. https://doi.org/10.3390/rs15071764








