An Atmospheric Phase Correction Method Based on Normal Vector Clustering Partition in Complicated Conditions for GB-SAR
Abstract
1. Introduction
2. Related Works
2.1. Methods Based on Meteorological Data
2.2. Methods Based on Permanent Scatterers
2.2.1. Permanent Scatterers
2.2.2. Conventional Model-Based Methods
2.2.3. Some Novel Data-Driven Methods
3. Data Acquisition and Analysis
3.1. Data Acquisition
3.2. Data Analysis
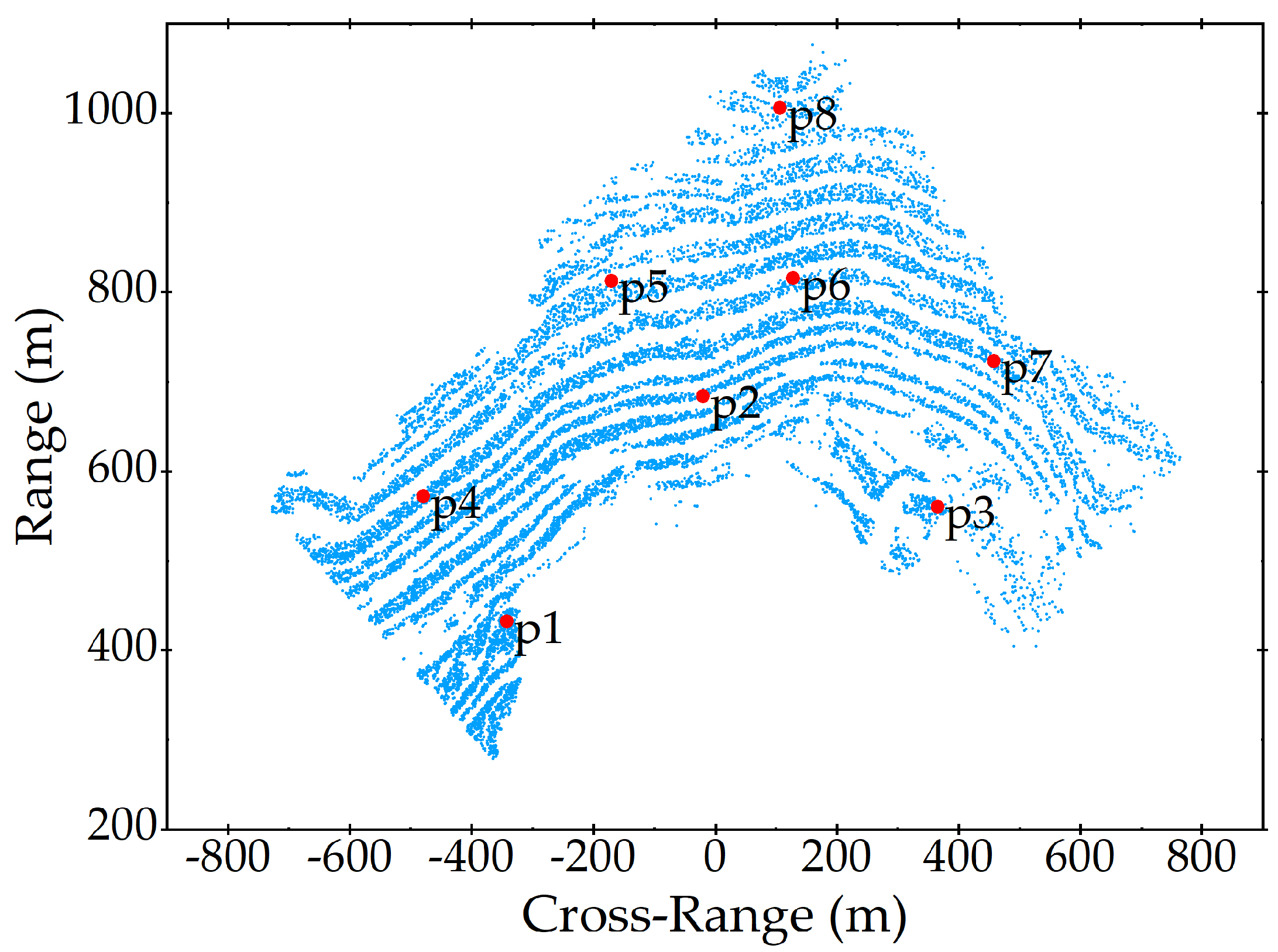
3.2.1. PSs Selection
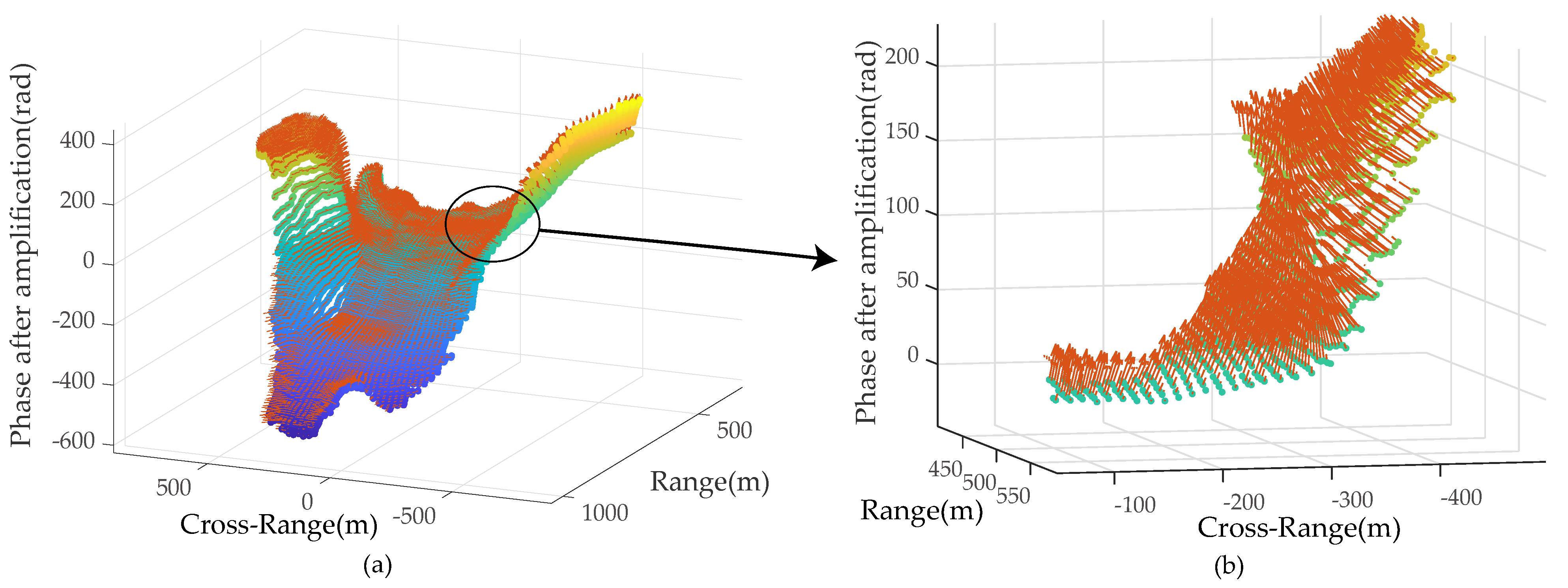
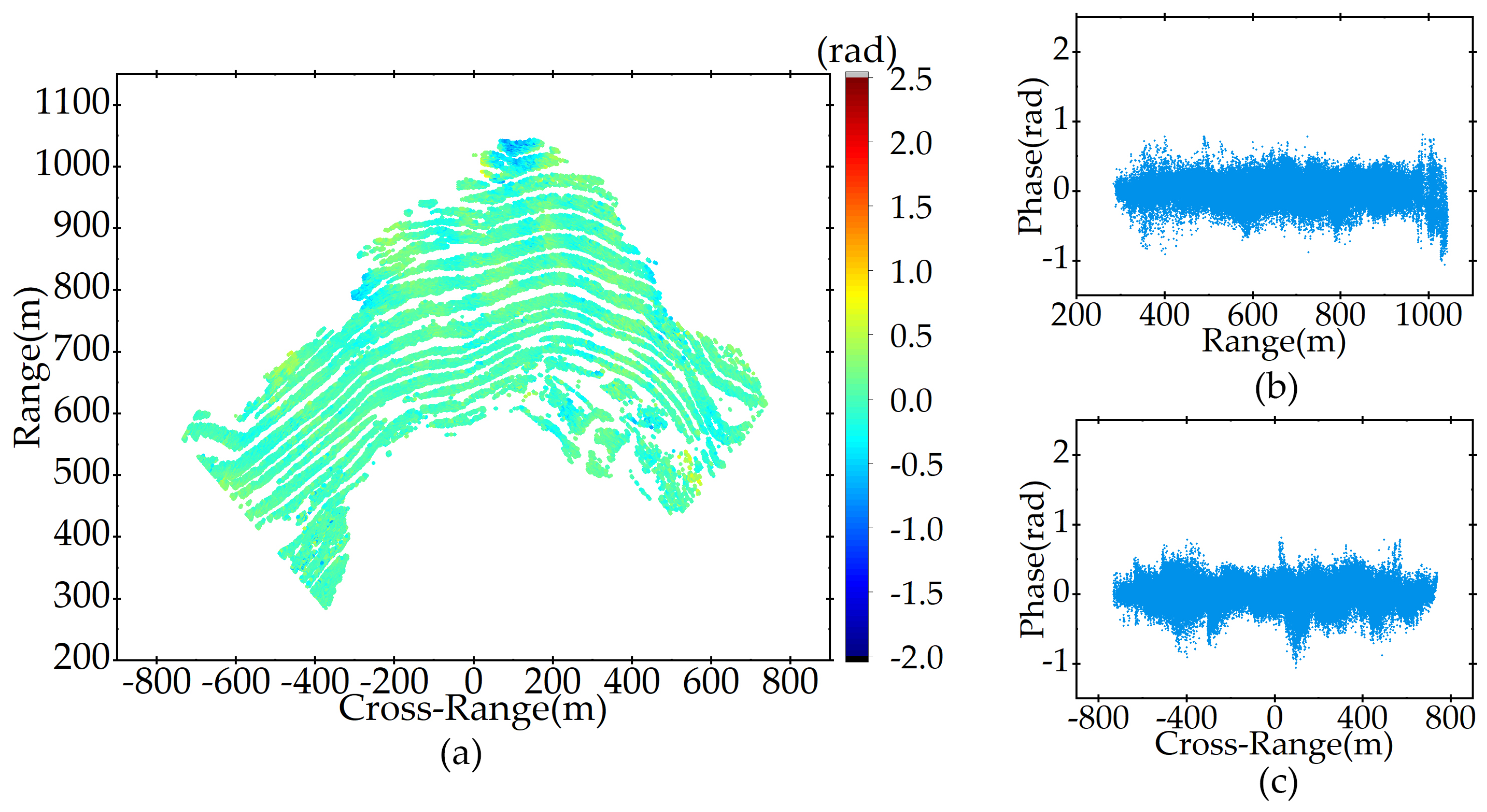
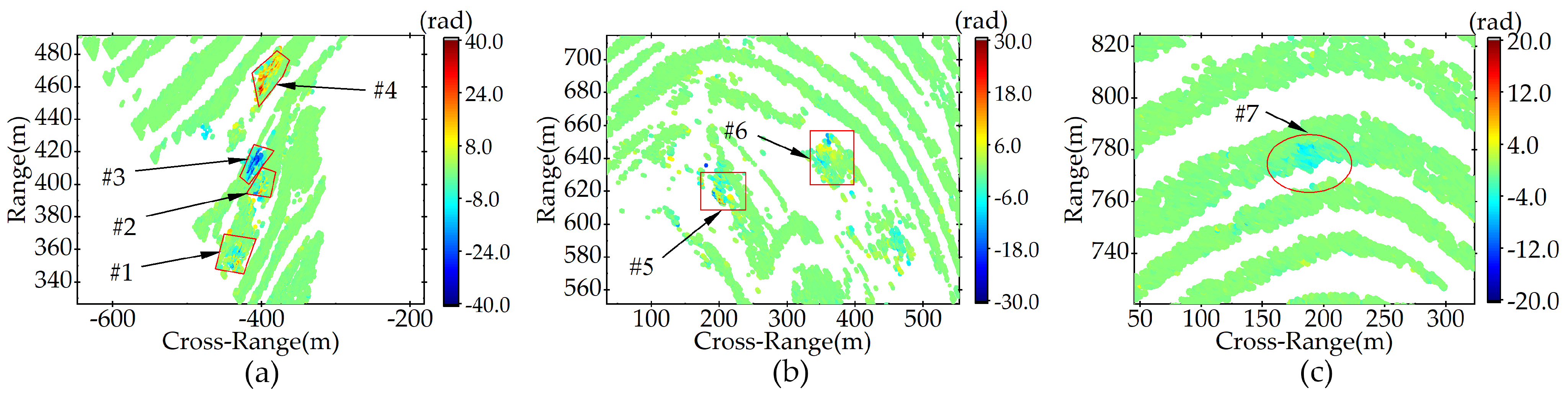
3.2.2. Spatial Phase Wrapping in the Dataset
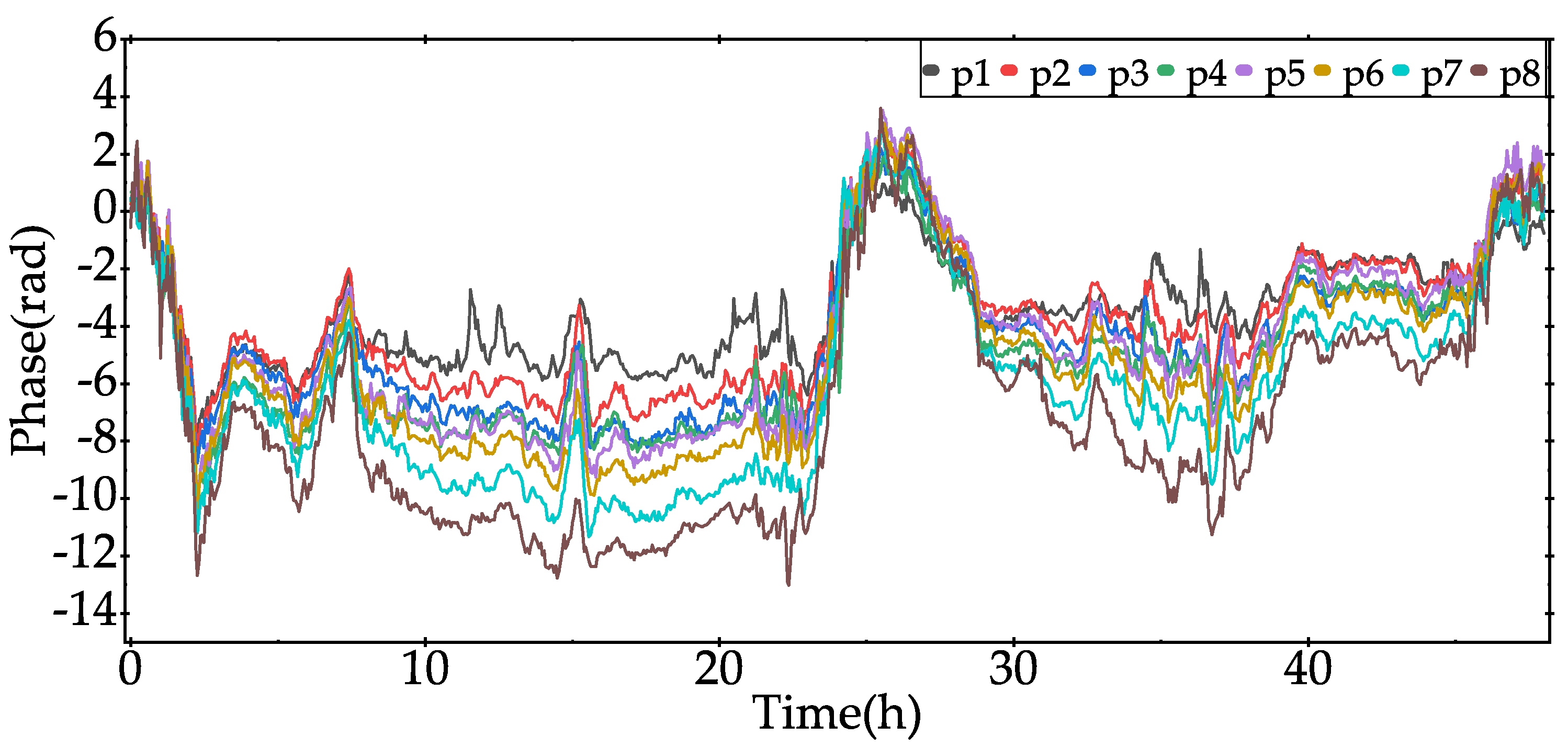
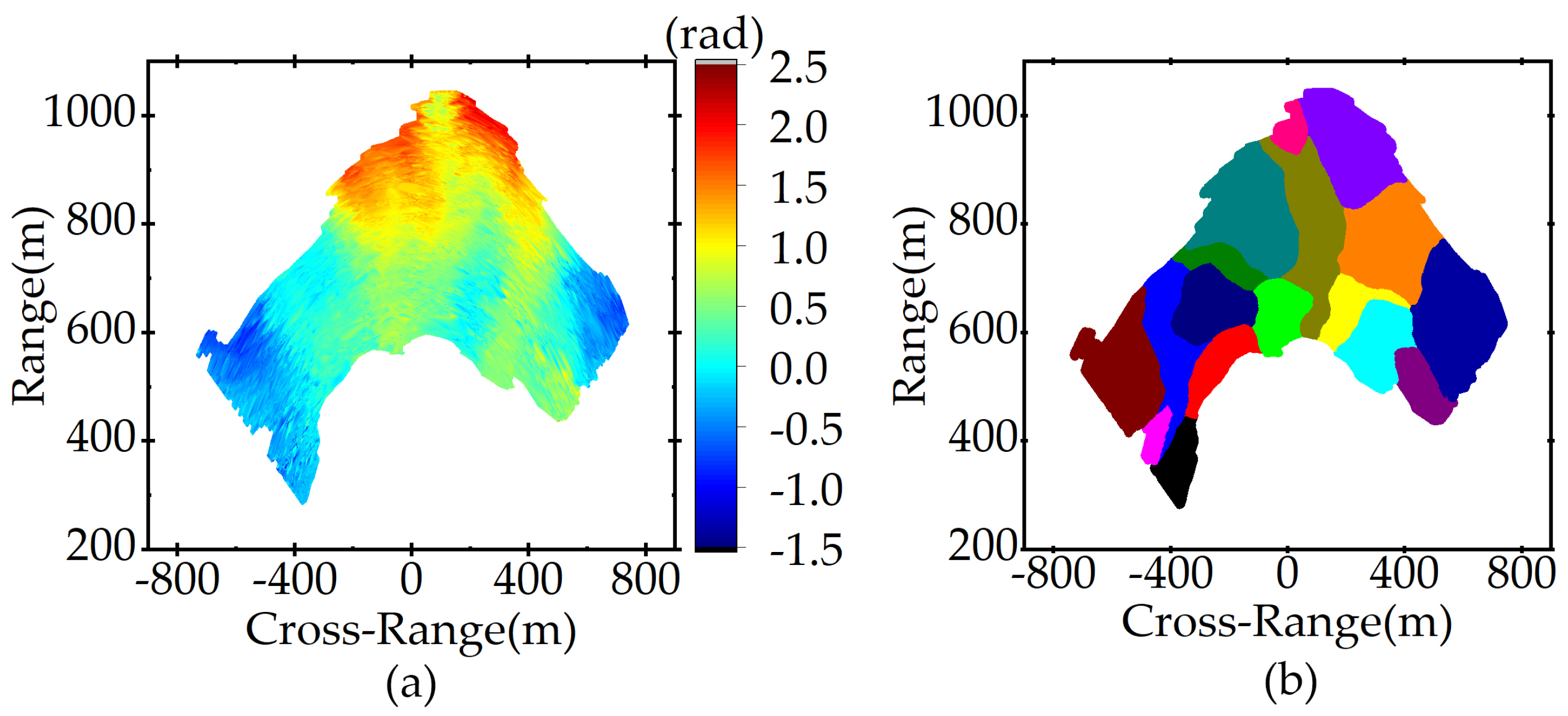
3.2.3. Cumulative Phase Analysis
4. Methodology
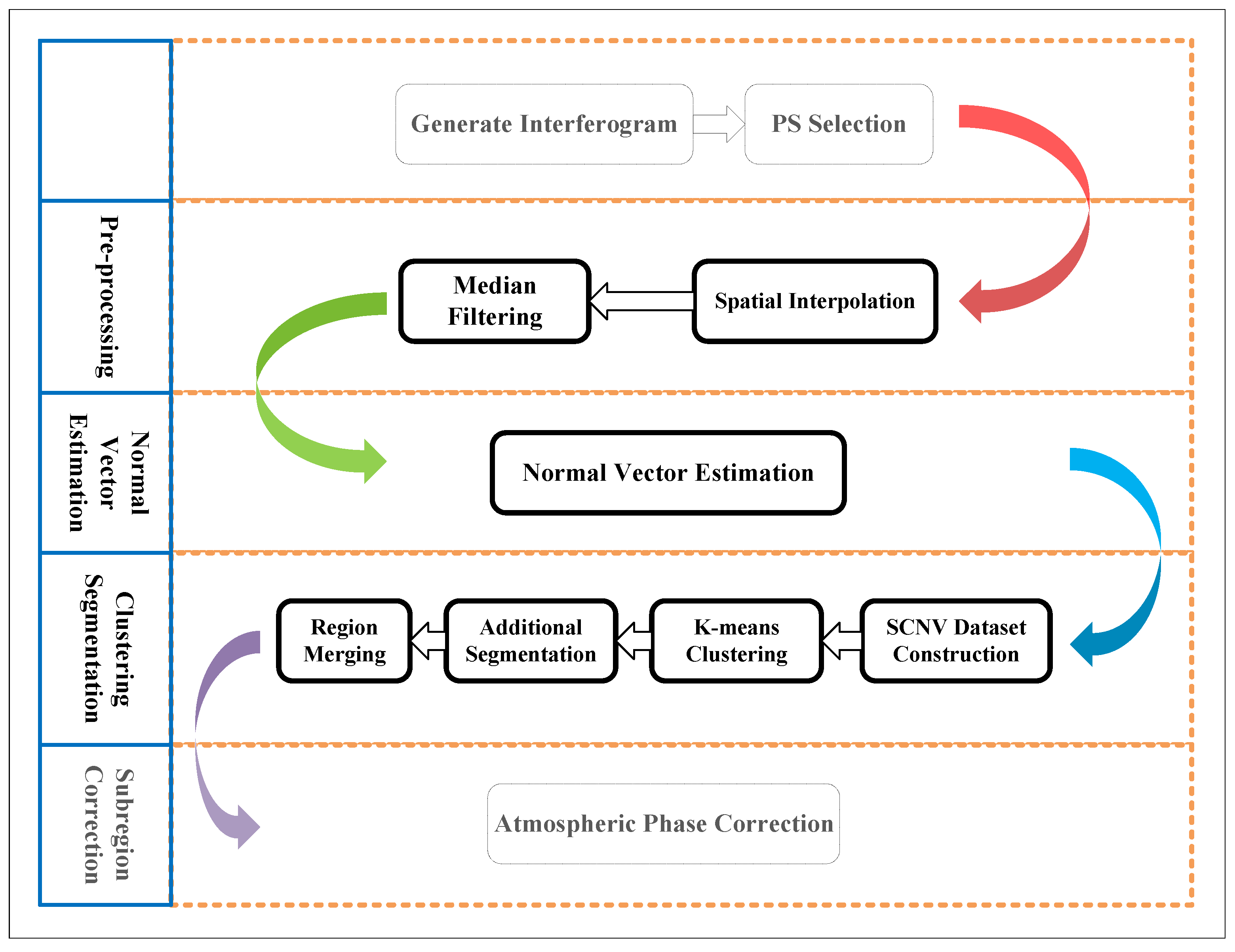
4.1. Algorithm Flowchart
4.2. Data Pre-Processing
- (1)
- Construct a Delaunay triangulation network, which is denoted T, to connect all PS points. The IDWI is performed only within the convex packet of PSs. Delaunay triangulation is an optimized spatial structure and can make the interpolation result automatically approach the regular triangle, improving the interpolation precision [28,29];
- (2)
- For a pending interpolation point p, in the convex package, it must be inside a triangle T, and three vertices of this triangle , , and are selected as reference points for interpolation;
- (3)
- The estimated phase of p, which is denoted , is calculated by
4.3. Spatial Normal Vector Estimation
- (1)
- Perform a k-nearest neighbor search, to find the nearest k CPSs to p, the points set is denoted N:wherewhere , , and are slant distance, azimuth angle, and amplified phase of the ith CPSs in N, respectively.The general form of the plane to be fitted is:
- (2)
- Construct the covariance matrix for N:where , , and so on.
- (3)
- Solve the normalized eigenvectors corresponding to the minimum eigenvalue of , to obtain the normal vector:
- (4)
- Adjust the direction of so that , to ensure that all normal vectors point to the same side.
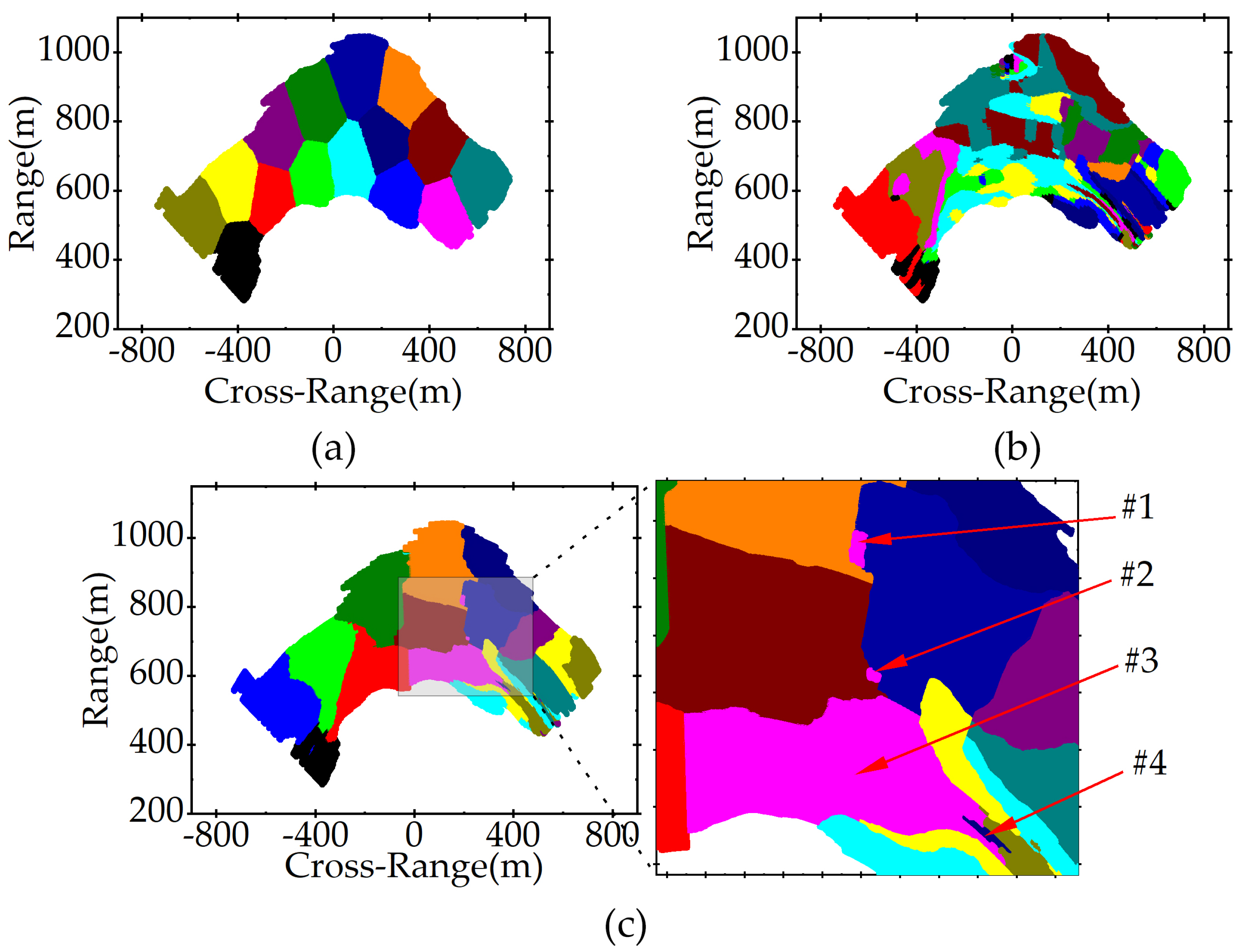
4.4. Clustering Partition
- (1)
- Construct the SCNV set , where m is the number of all CPS points;
- (2)
- Set the number of clusters to and initialize the clustering center ;
- (3)
- Calculate the Euclidean distance from to each cluster center and assign to the cluster with the closest Euclidean distance;
- (4)
- Calculate the center of mass of each cluster and update the cluster center with the center of mass;
- (5)
- The above steps are iteratively processed until the clustering centers no longer change, or a predetermined number of iterations is reached.
- (1)
- Calculate the average normal vector of each too-small sub-block;
- (2)
- Search the sub-blocks adjacent to the too-small sub-block, calculate their average normal vectors, and then calculate the spatial distance between these average normal vectors and the normal vector of the too-small sub-block;
- (3)
- Merge the too-small sub-block into the block corresponding to the minimum spatial distance in step 2.
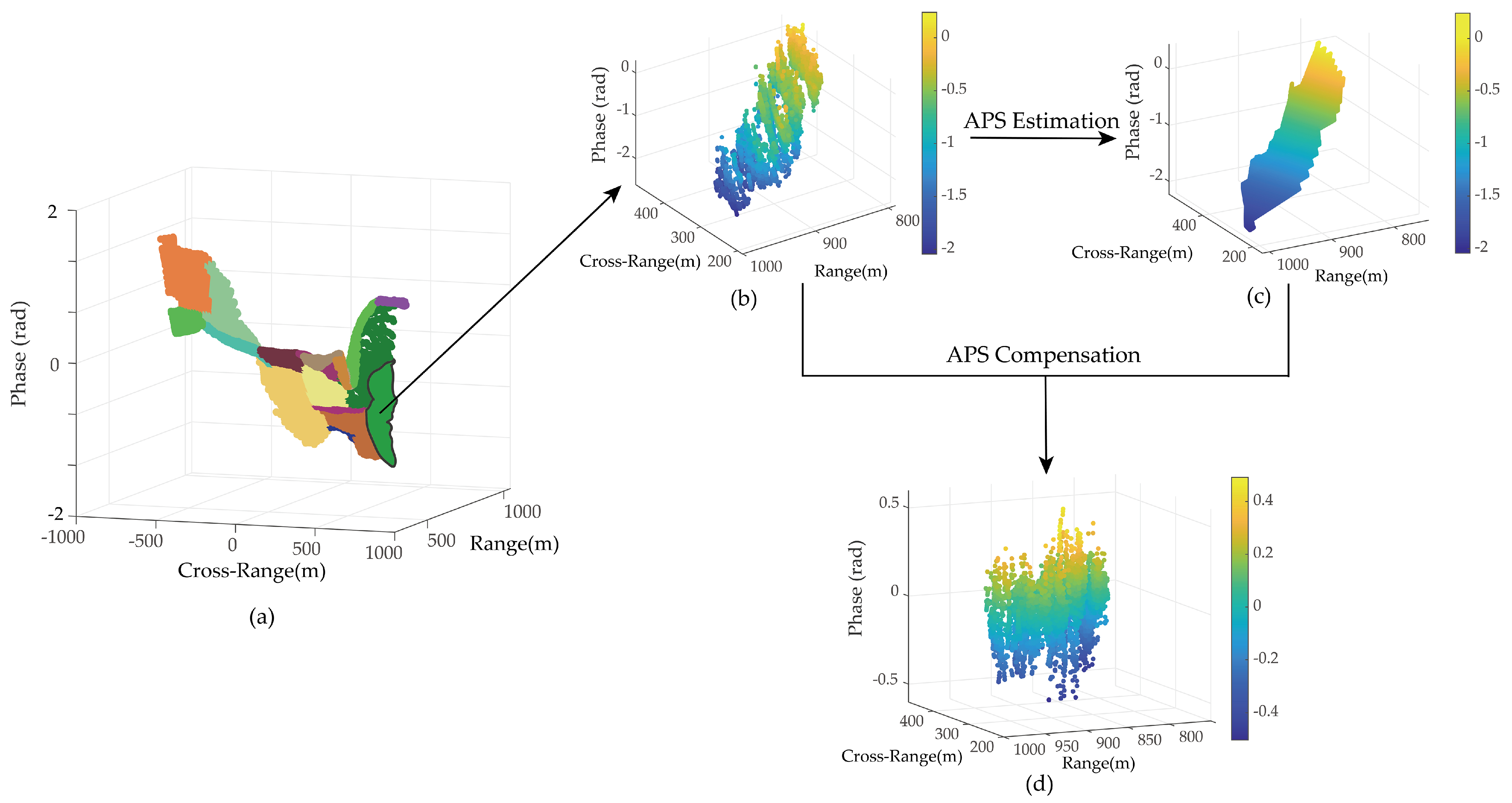
4.5. Atmospheric Phase Correction
5. Results and Analysis
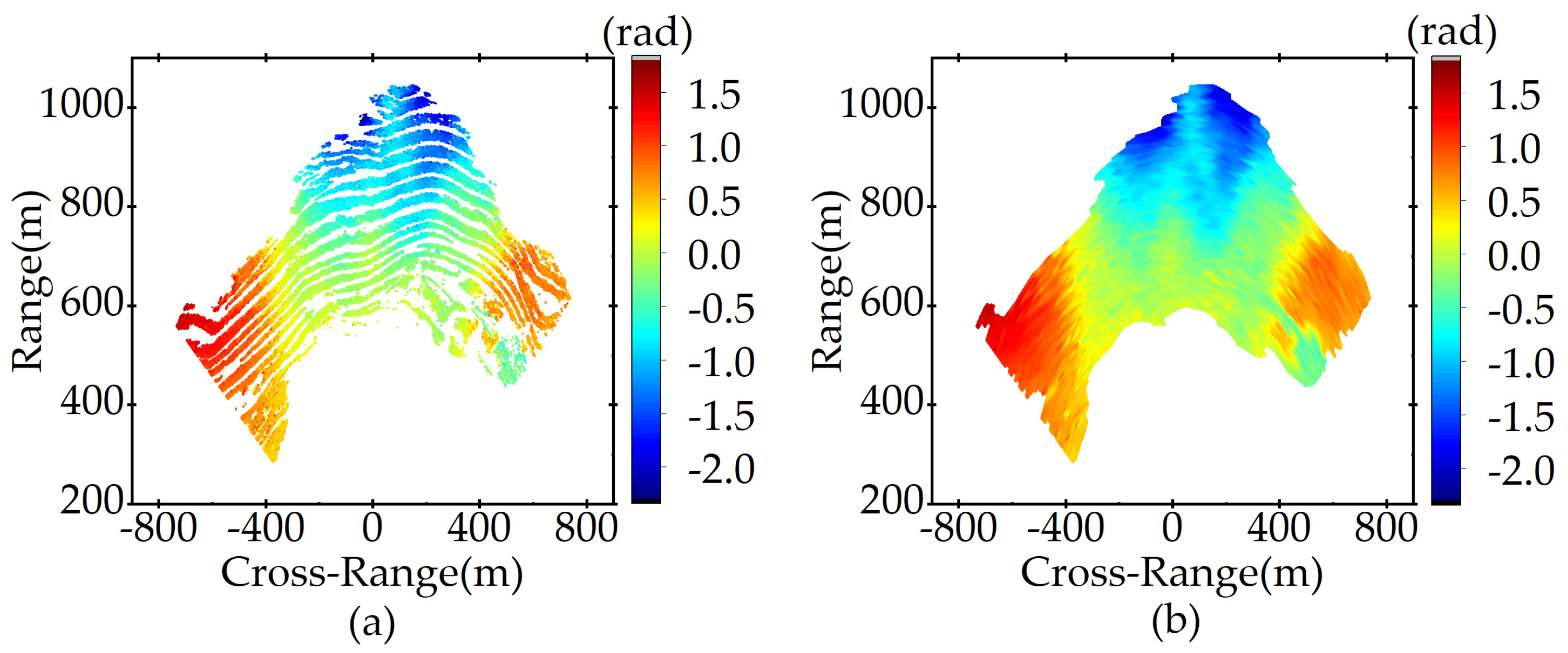
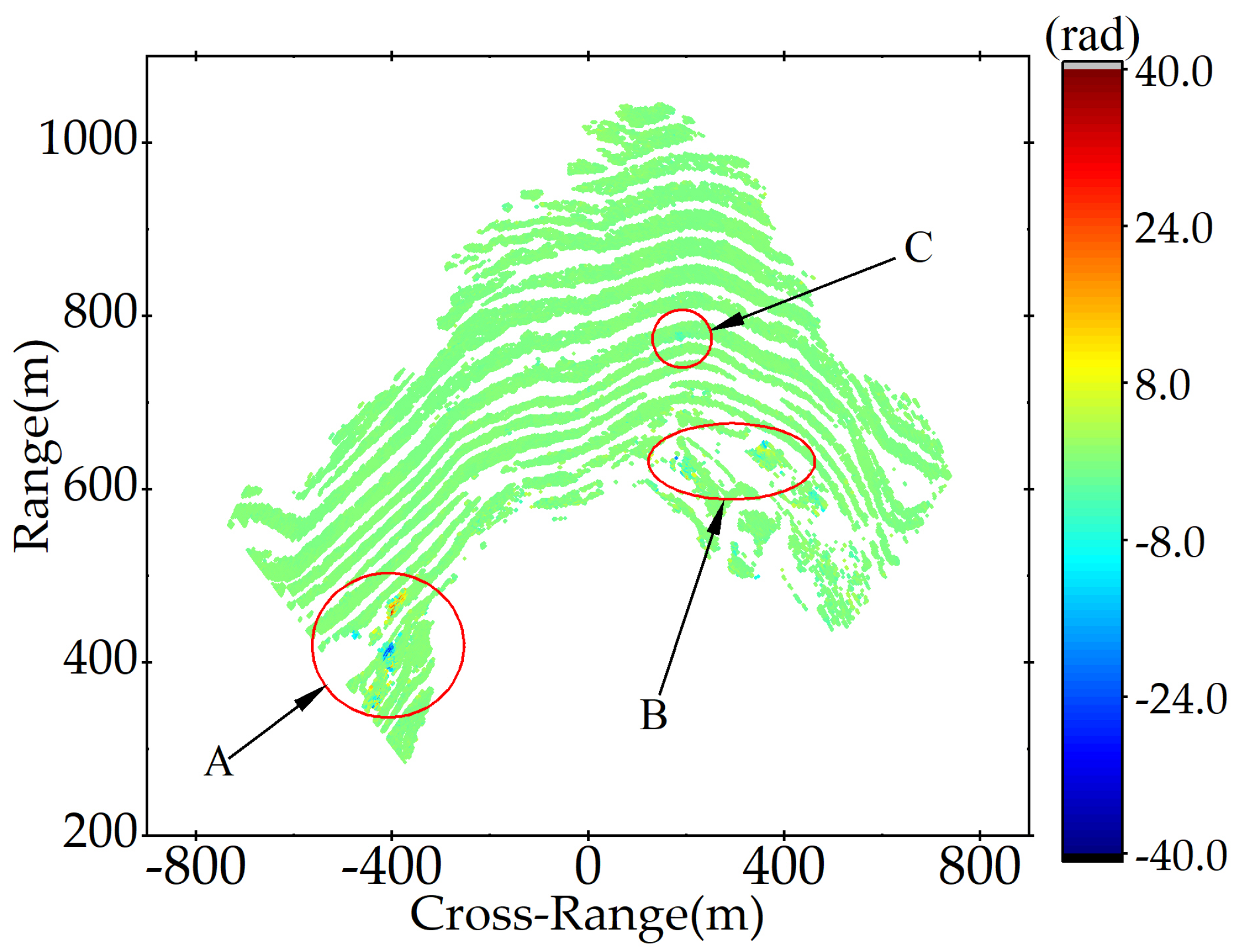
5.1. APS Estimation on Interferograms
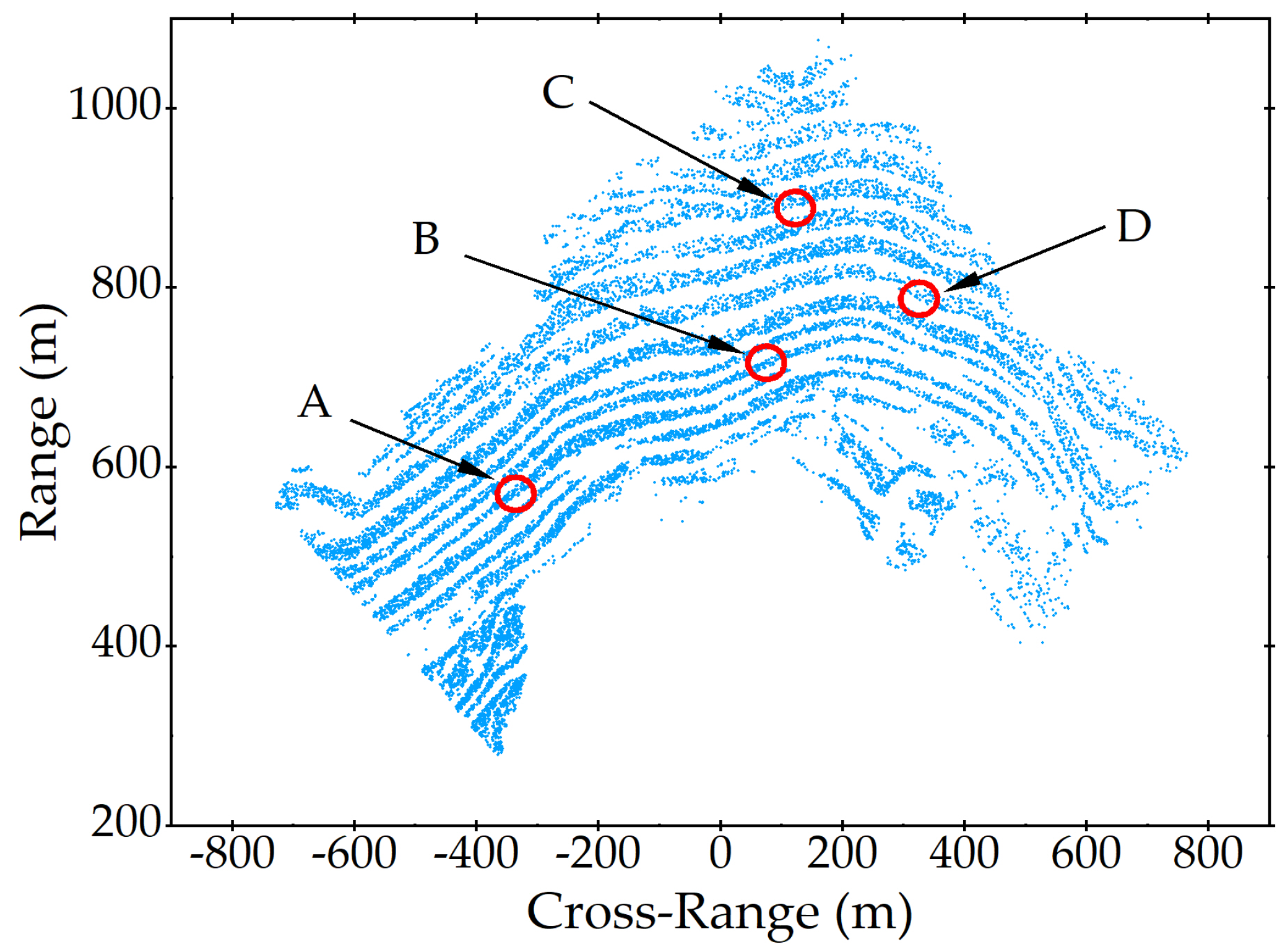
5.2. Simulation Experiment of Deformation Monitoring
5.3. Parameter Settings Analysis
5.3.1. Effect of and on Atmospheric Phase Correction Accuracy
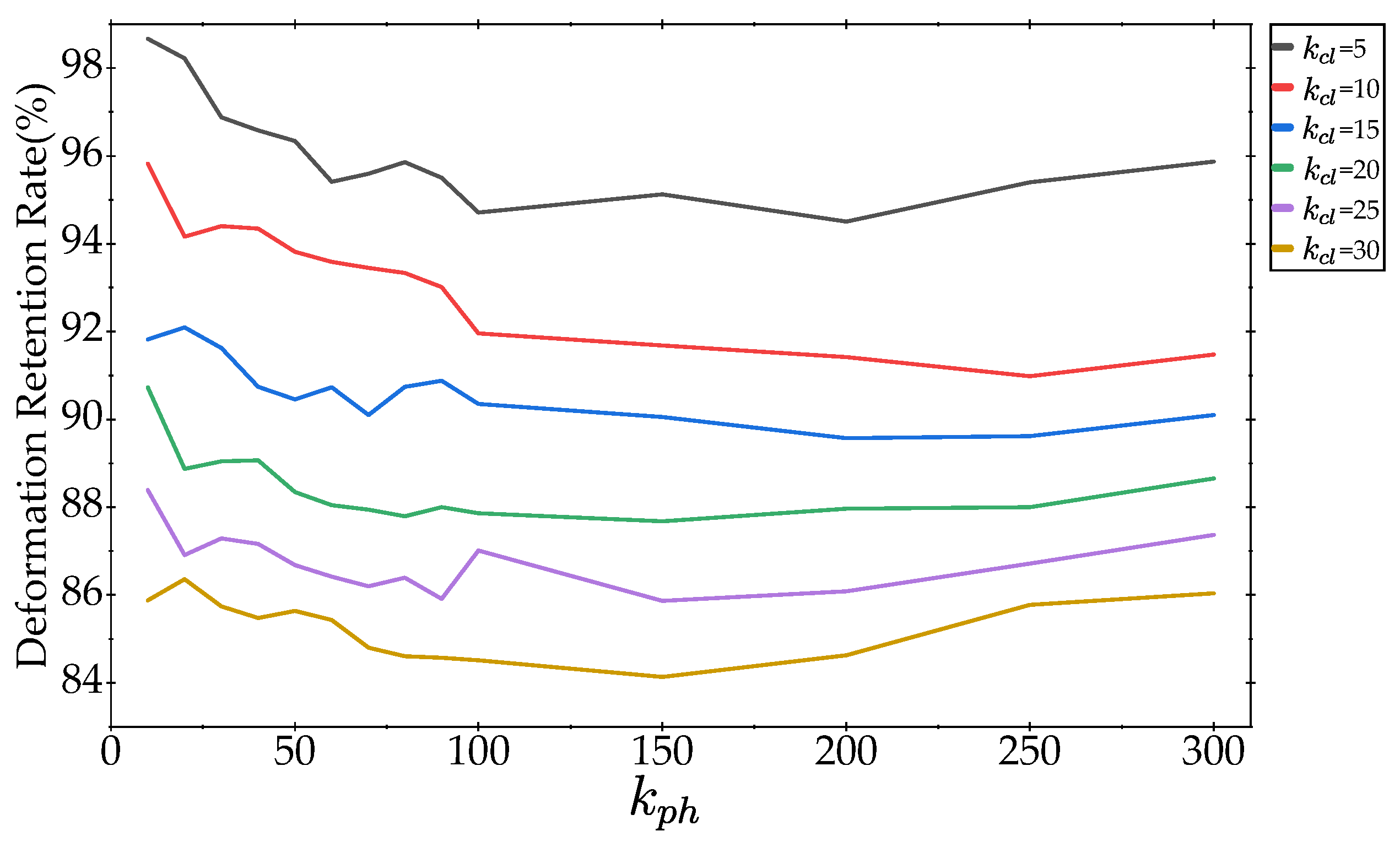
5.3.2. Effect of and on Deformation Retention Rate
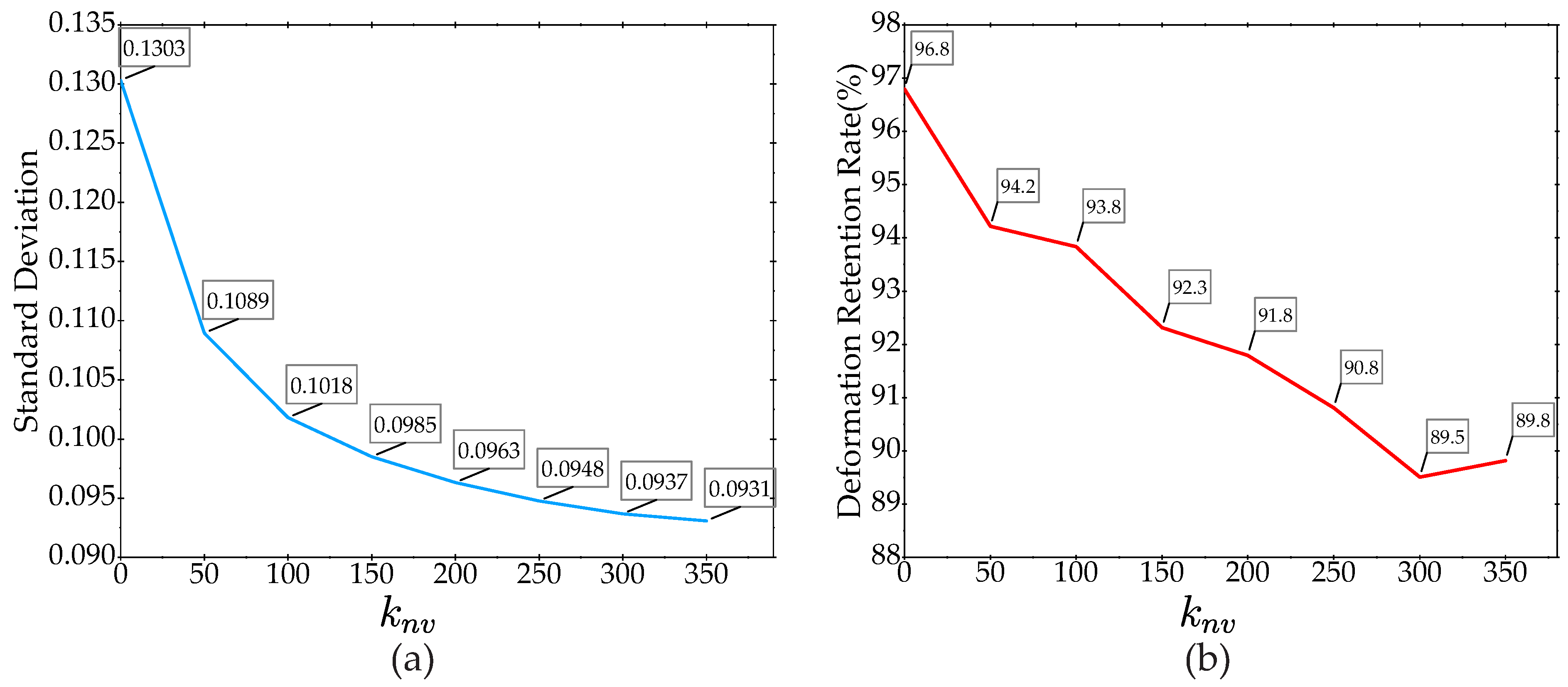
5.3.3. Effect of
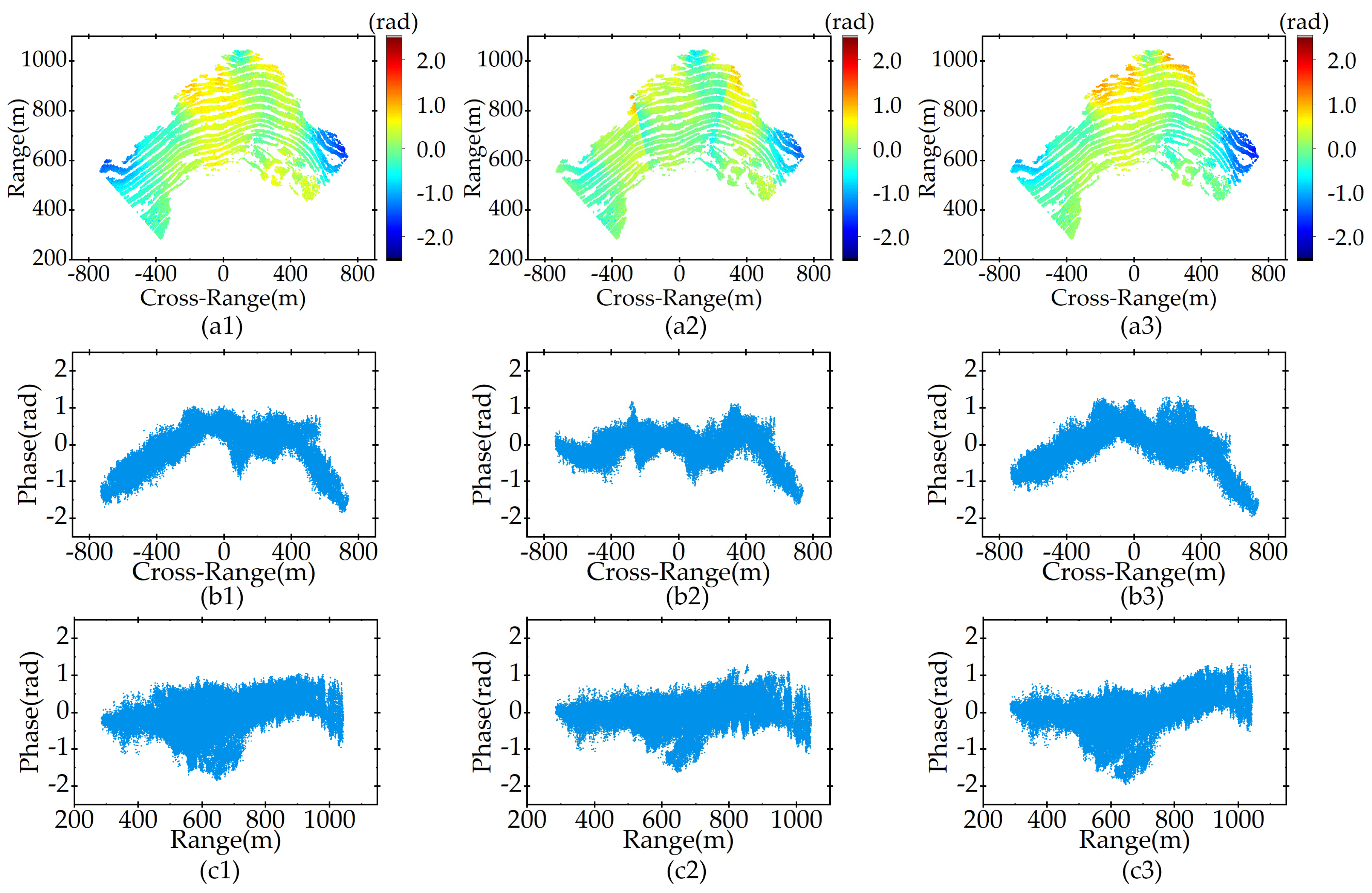
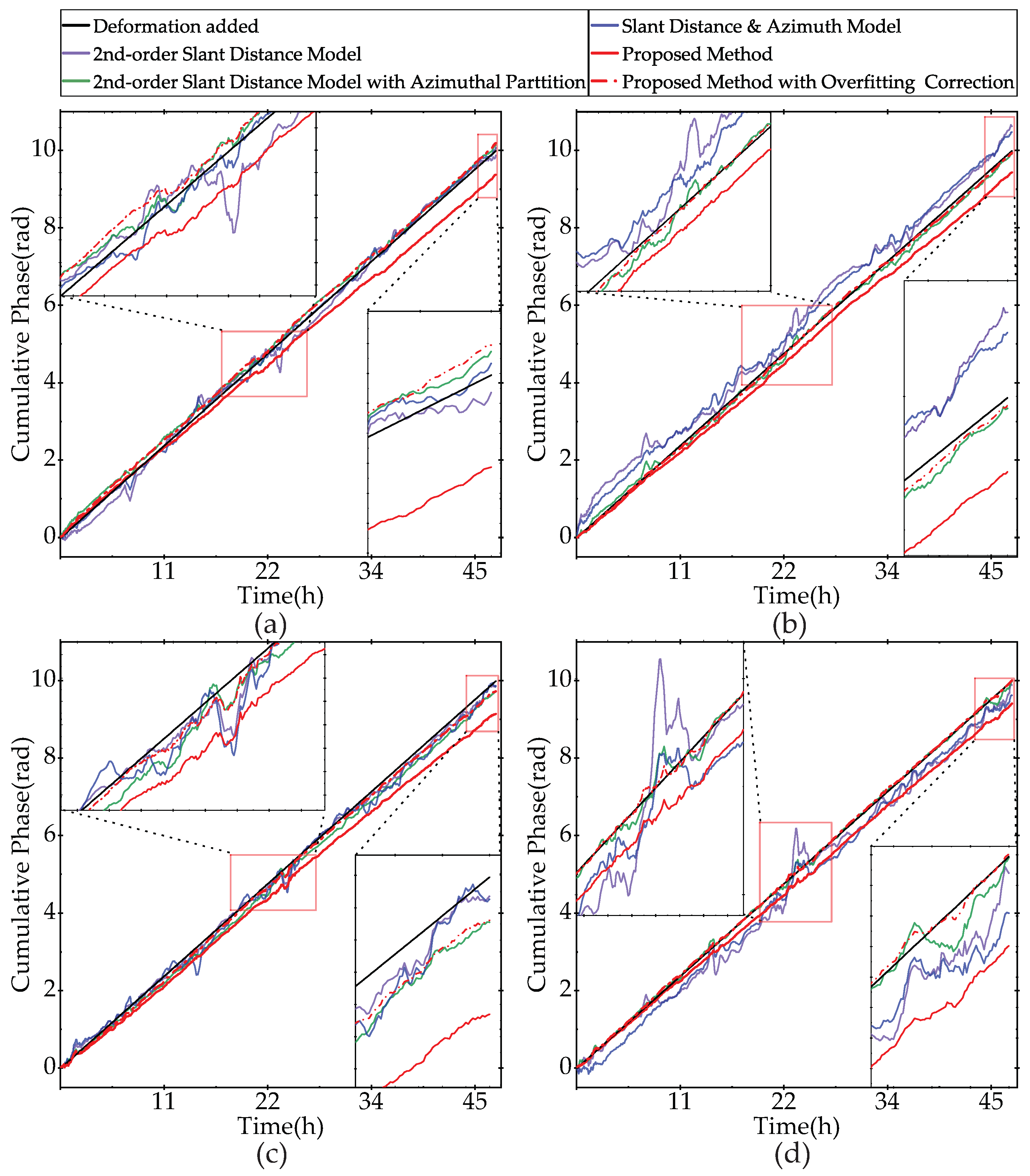
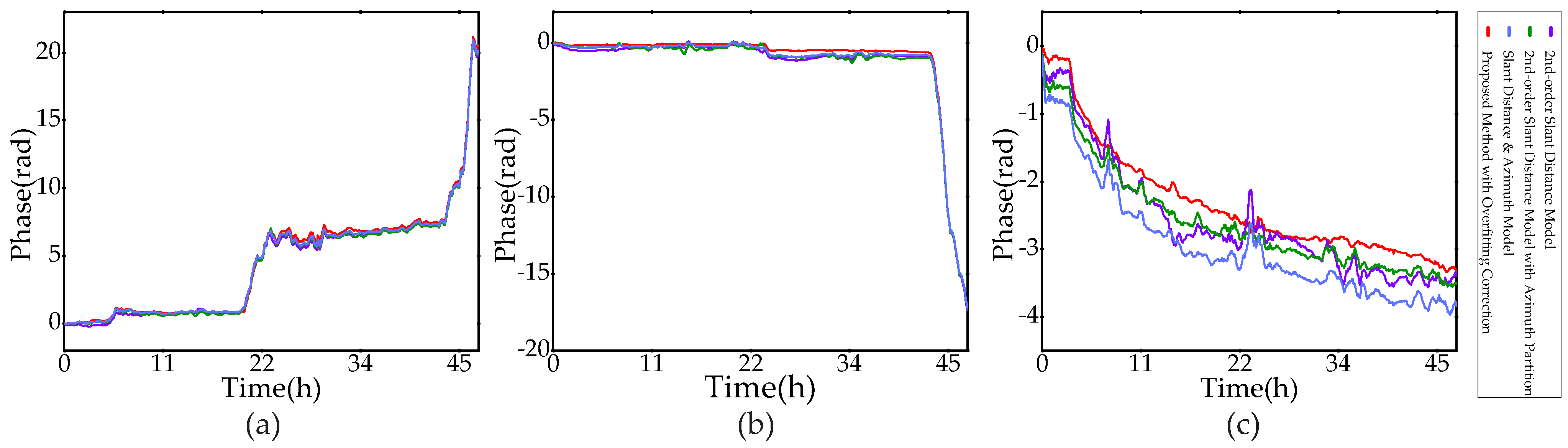
5.4. Time Series Atmospheric Phase Correction
6. Discussions
6.1. Complicated Distribution of Atmospheric Phase
- (1)
- High altitude. The altitude of the Dabao Mountain is between 600 and 800 m. The solar radiation is stronger than that in lower altitude areas, and the air is relatively thin and poorly insulated. This also leads to large changes in atmospheric parameters within a short period of time, and therefore significant diurnal variations. During the daytime, the monitored area is mostly in clear or cloudy weather, and there was no obvious rainfall process during the data acquisition, so the influence of solar irradiation on temperature and humidity is significant. The heat brought by the sun makes the atmospheric parameters change significantly, so the distribution of the AP is more dispersed, and the spatial phase wrapping phenomenon can easily occur. After the rapid loss of heat at night, the change in atmospheric parameters tends to be smooth, and the AP becomes smaller and more stable accordingly.
- (2)
- Steep terrain of the mine. The Dabao Mountain Mine has been mined for many years and the mountain is very steep. The relative elevation from the bottom of the pit to the top of the mine is about 150 m. The difference in elevation makes the spatial distribution of atmospheric parameters non-uniform, resulting in significant changes in the spatial distribution of AP with the change in elevation.
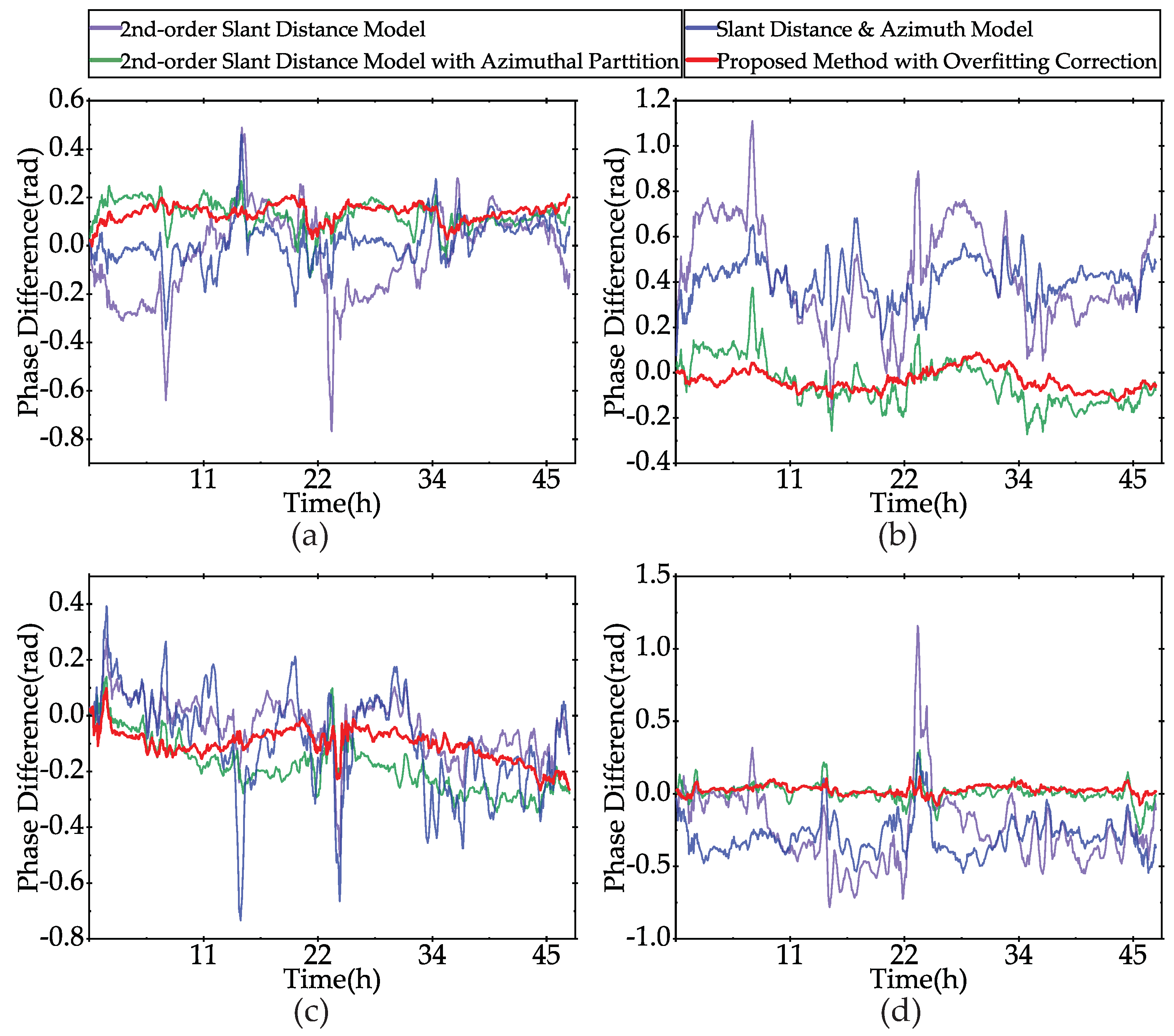
6.2. Comparison of the Conventional Methods and the Proposed Method
6.3. Conflict between Accuracy and Credibility
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pieraccini, M.; Miccinesi, L. Ground-Based Radar Interferometry: A Bibliographic Review. Remote Sens. 2019, 11, 1029. [Google Scholar] [CrossRef]
- Izumi, Y.; Zou, L.; Kikuta, K.; Sato, M. Iterative atmospheric phase screen compensation for near-real-time ground-based InSAR measurements over a mountainous slope. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5955–5968. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, W.; Zhang, Y.; Lin, Y.; Li, Y.; Bai, Z.; Zhang, Q.; Lv, S.; Liu, H.; Song, Y. Ground-Based Differential Interferometry SAR: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 43–70. [Google Scholar] [CrossRef]
- Pipia, L.; Fabregas, X.; Aguasca, A.; Mallorqui, J. A Comparison of Different Techniques for Atmospheric Artefact Compensation in GBSAR Differential Acquisitions. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 3739–3742. [Google Scholar]
- Caduff, R.; Kos, A.; Schlunegger, F.; McArdell, B.W.; Wiesmann, A. Terrestrial Radar Interferometric Measurement of Hillslope Deformation and Atmospheric Disturbances in the Illgraben Debris-Flow Catchment, Switzerland. IEEE Geosci. Remote Sens. Lett. 2014, 11, 434–438. [Google Scholar] [CrossRef]
- Zhao, X. Atmospheric Correction Method for GB-SAR and Its Application to Monitoring Deformation of Landslide. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Tofani, V.; Raspini, F.; Catani, F.; Casagli, N. Persistent Scatterer Interferometry (PSI) Technique for Landslide Characterization and Monitoring. Remote Sens. 2013, 5, 1045–1065. [Google Scholar] [CrossRef]
- Iglesias, R.; Fabregas, X.; Aguasca, A.; Mallorqui, J.J.; Lopez-Martinez, C.; Gili, J.A.; Corominas, J. Atmospheric Phase Screen Compensation in Ground-Based SAR with a Multiple-Regression Model Over Mountainous Regions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2436–2449. [Google Scholar] [CrossRef]
- Karunathilake, A.; Sato, M. Atmospheric Phase Compensation in Extreme Weather Conditions for Ground-Based SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3806–3815. [Google Scholar] [CrossRef]
- Deng, Y.; Hu, C.; Tian, W.; Zhao, Z. A Grid Partition Method for Atmospheric Phase Compensation in GB-SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5206713. [Google Scholar] [CrossRef]
- Hu, C.; Deng, Y.; Tian, W.; Zhao, Z. A Compensation Method for a Time–Space Variant Atmospheric Phase Applied to Time-Series GB-SAR Images. Remote Sens. 2019, 11, 2350. [Google Scholar] [CrossRef]
- Izumi, Y.; Nico, G.; Sato, M. Time-Series Clustering Methodology for Estimating Atmospheric Phase Screen in Ground-Based InSAR Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5206309. [Google Scholar] [CrossRef]
- Noferini, L.; Takayama, T.; Pieraccini, M.; Mecatti, D.; Macaluso, G.; Luzi, G.; Atzeni, C. Analysis of Ground-Based SAR Data with Diverse Temporal Baselines. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1614–1623. [Google Scholar] [CrossRef]
- Iglesias, R.; Aguasca, A.; Fabregas, X.; Mallorqui, J.J.; Monells, D.; López-Martínez, C.; Pipia, L. Ground-Based Polarimetric SAR Interferometry for the Monitoring of Terrain Displacement Phenomena–Part I: Theoretical Description. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 980–993. [Google Scholar] [CrossRef]
- ITU-R. The Radio Refractive Index: Its Formula and Refractivity Data. 2019. Available online: https://www.itu.int/rec/R-REC-P.453-14-201908-I/en (accessed on 22 March 2023).
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Guidi, G.; Moia, F.; Atzeni, C. Ground-based radar interferometry for landslides monitoring: Atmospheric and instrumental decorrelation sources on experimental data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2454–2466. [Google Scholar] [CrossRef]
- Iannini, L.; Guarnieri, A.M. Atmospheric phase screen in ground-based radar: Statistics and compensation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 537–541. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A.; Bruniquel, J.; Vachon, P.W. Coherence estimation for SAR imagery. IEEE Trans. Geosci. Remote Sens. 1999, 37, 135–149. [Google Scholar] [CrossRef]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tamburini, A.; Broccolato, M. Permanent scatterers analysis for atmospheric correction in ground-based SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1471. [Google Scholar] [CrossRef]
- Dematteis, N.; Luzi, G.; Giordan, D.; Zucca, F.; Allasia, P. Monitoring Alpine glacier surface deformations with GB-SAR. Remote Sens. Lett. 2017, 8, 947–956. [Google Scholar] [CrossRef]
- Huang, Z.; Sun, J.; Li, Q.; Tan, W.; Huang, P.; Qi, Y. Time- and Space-Varying Atmospheric Phase Correction in Discontinuous Ground-Based Synthetic Aperture Radar Deformation Monitoring. Sensors 2018, 18, 3883. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Dai, Z.; Zha, X. An Accurate Phase Unwrapping Algorithm Based on Reliability Sorting and Residue Mask. IEEE Geosci. Remote Sens. Lett. 2012, 9, 219–223. [Google Scholar] [CrossRef]
- Huang, Q.; Zhou, H.; Dong, S.; Xu, S. Parallel Branch-Cut Algorithm Based on Simulated Annealing for Large-Scale Phase Unwrapping. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3833–3846. [Google Scholar] [CrossRef]
- Isenburg, M.; Liu, Y.; Shewchuk, J.; Snoeyink, J. Streaming Computation of Delaunay Triangulations. ACM Trans. Graph. 2006, 25, 1049–1056. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Zhang, H.; Ma, G. Multimodal Remote Sensing Image Matching Combining Learning Features and Delaunay Triangulation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Seyed Shirkhorshidi, A.; Ying Wah, T. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning, 1st ed.; Springer: New York, NY, USA, 2006. [Google Scholar]







| Parameters | Value |
|---|---|
| Carrier frequency | 24 GHz |
| Beam coverage | |
| Range resolution | m |
| Angle resolution | 6 mrad |
| Detection range | 4000 m |
| Parameters | Value |
|---|---|
| 50 | |
| 10 | |
| 100 |
| Uncorrected | 2nd-Order Slant Distance Model | 2nd-Order Slant Distance Model with Azimuthal Partition | Slant Distance & Azimuth Model | Proposed Method | |
|---|---|---|---|---|---|
| Mean Value | 0.2310 | 0.2071 | 0.1601 | 0.1897 | 0.1018 |
| Median Value | 0.1766 | 0.1631 | 0.1285 | 0.1523 | 0.0872 |
| 2nd-Order Slant Distance Model | 2nd-Order Slant Distance Model with Azimuthal Partition | Slant Distance & Azimuth Model | Proposed Method with Overfitting Correction | |
|---|---|---|---|---|
| A | 0.1818 | 0.5090 | 0.0910 | 0.0364 |
| B | 0.2170 | 0.1022 | 0.0941 | 0.0469 |
| C | 0.0969 | 0.0786 | 0.1791 | 0.0578 |
| D | 0.2567 | 0.0629 | 0.1278 | 0.0300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, P.; Lai, T.; Huang, S.; Chen, W.; Weng, D. An Atmospheric Phase Correction Method Based on Normal Vector Clustering Partition in Complicated Conditions for GB-SAR. Remote Sens. 2023, 15, 1744. https://doi.org/10.3390/rs15071744
Ou P, Lai T, Huang S, Chen W, Weng D. An Atmospheric Phase Correction Method Based on Normal Vector Clustering Partition in Complicated Conditions for GB-SAR. Remote Sensing. 2023; 15(7):1744. https://doi.org/10.3390/rs15071744
Chicago/Turabian StyleOu, Pengfei, Tao Lai, Shisheng Huang, Wu Chen, and Duojie Weng. 2023. "An Atmospheric Phase Correction Method Based on Normal Vector Clustering Partition in Complicated Conditions for GB-SAR" Remote Sensing 15, no. 7: 1744. https://doi.org/10.3390/rs15071744
APA StyleOu, P., Lai, T., Huang, S., Chen, W., & Weng, D. (2023). An Atmospheric Phase Correction Method Based on Normal Vector Clustering Partition in Complicated Conditions for GB-SAR. Remote Sensing, 15(7), 1744. https://doi.org/10.3390/rs15071744







