Multi-GNSS Combination Multipath Reflectometry Based on IVMD Method for Sea Level Retrieval
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Descriptions
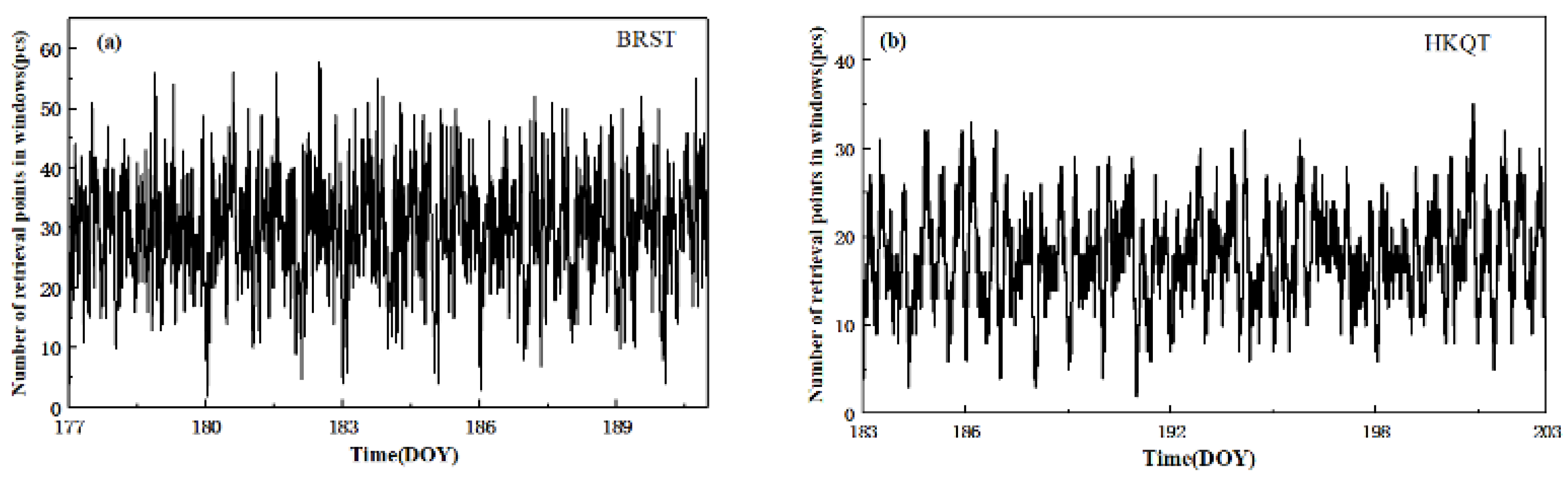
2.2. Data Descriptions
3. Theory and Methods
3.1. Multi-GNSS Combination Algorithm
3.1.1. Classical Sea Level Retrieval Theory
3.1.2. Multi-GNSS Combination Using Robust Regression Solution Strategy
3.2. IVMD Method Based on Multi-GNSS Combination Sea Level Retrieval
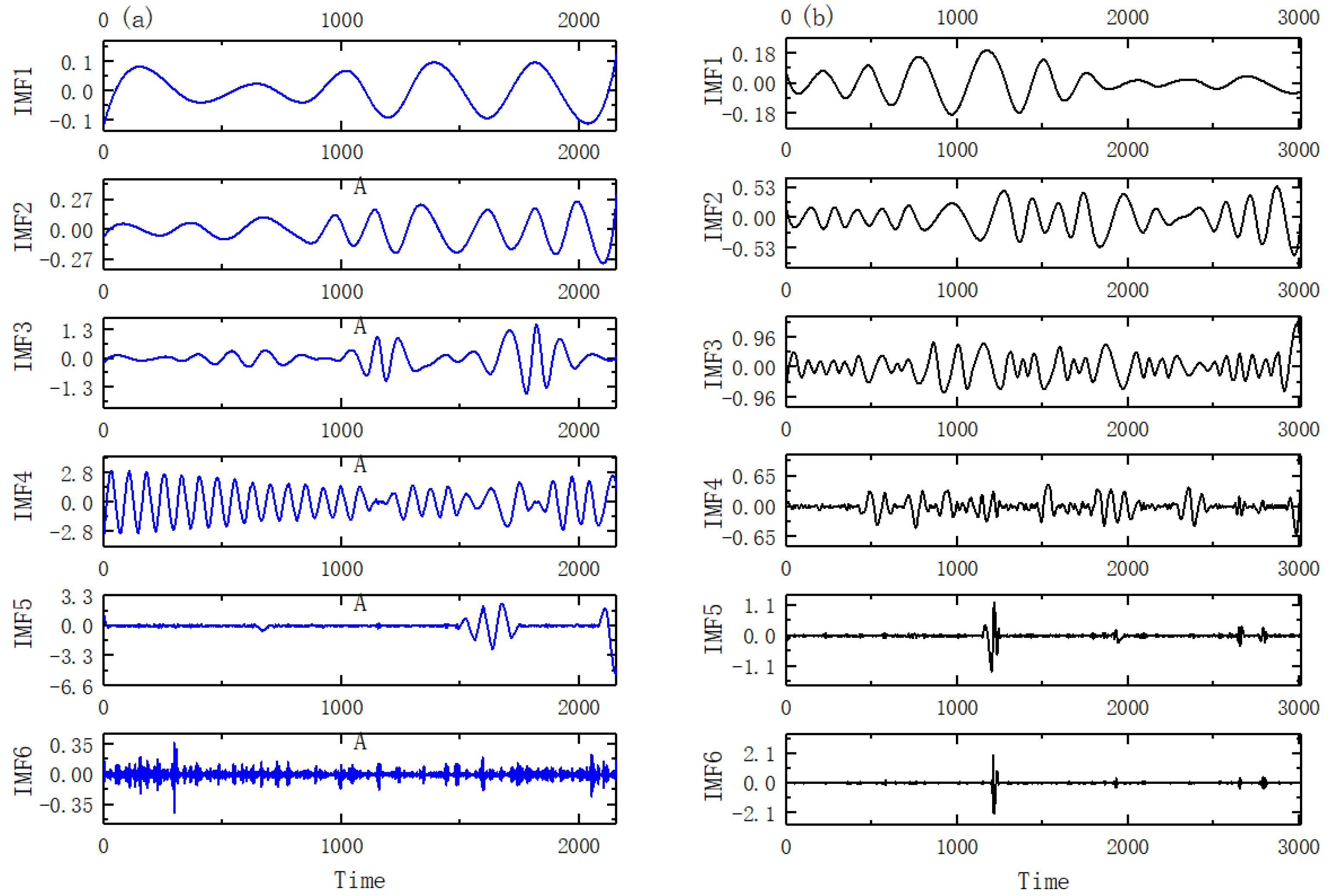
3.2.1. Principles of the VMD Method
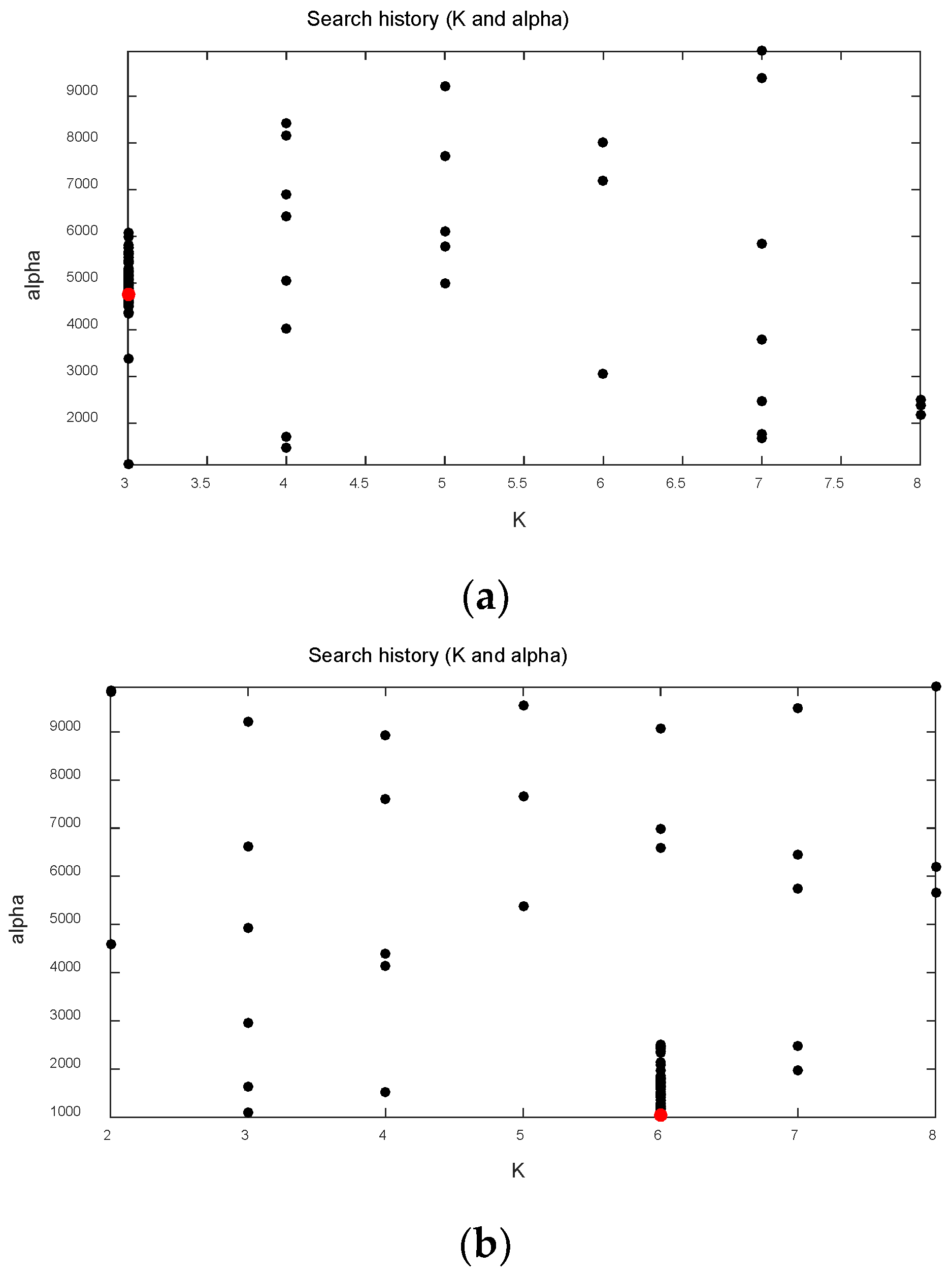
3.2.2. IVMD Algorithm
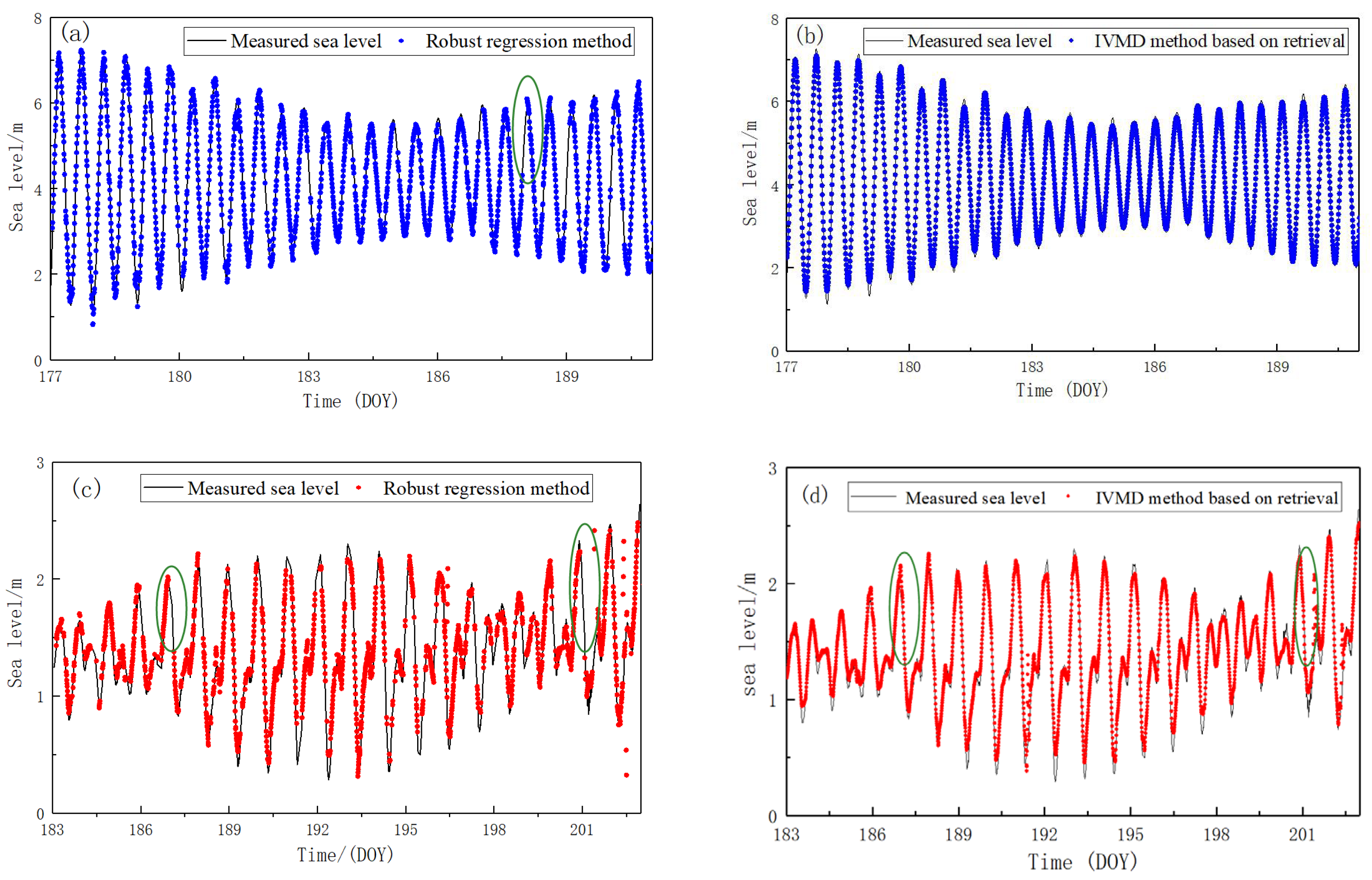
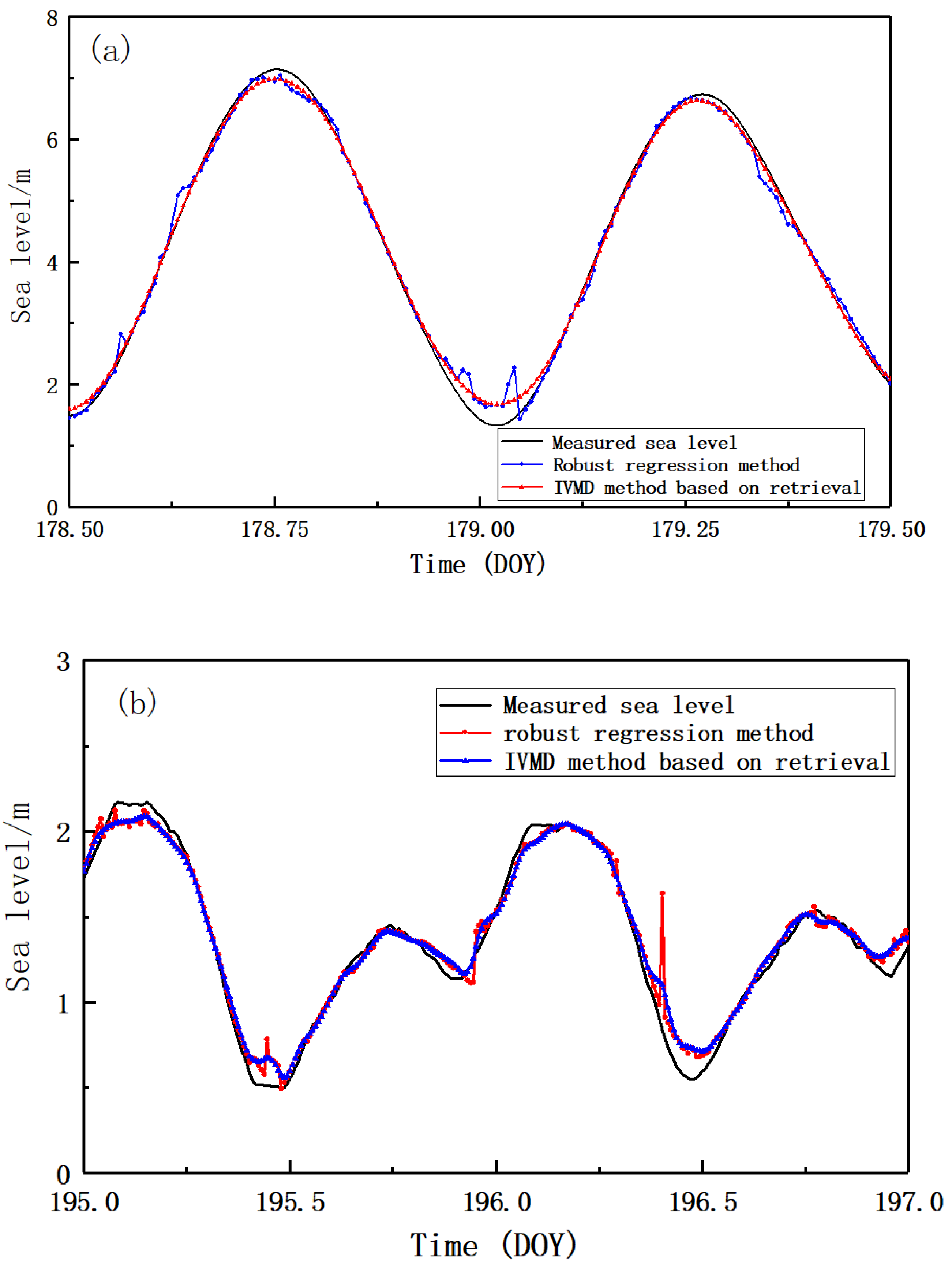
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, G.; Jin, S.; Zhang, T. Coastal sea level changes in Europe from GPS, tide gauge, satellite altimetry and GRACE, 1993–2011. Adv. Space Res. 2013, 51, 1019–1028. [Google Scholar] [CrossRef]
- Coleman, R. Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications. Eos Trans. AGU 2001, 82, 376. [Google Scholar] [CrossRef]
- Larson, K.M.; Löfgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Braun, J.J. Sensing vegetation growth with reflected GPS signals. Geophys. Res. Lett. 2010, 37, L12401. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS multipath to measure soil moisture fluctuations: Initial results. GPS Solut. 2008, 12, 173–177. [Google Scholar] [CrossRef]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, Z.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can we measure snow depth with GPS receivers? Geophys. Res. Lett. 2009, 36, L17502. [Google Scholar] [CrossRef]
- Schöne, T.; Schön, N.; Thaller, D. IGS tide gauge benchmark monitoring pilot project (TIGA): Scientific benefits. J. Geod. 2009, 83, 249–261. [Google Scholar] [CrossRef]
- Hall, C.; Cordey, R. Multistatic scatterometry. In Proceedings of the International Geoscience and Remote Sensing Symposium, ‘Remote Sensing: Moving toward the 21st Century’, Edinburgh, UK, 12–16 September 1988. [Google Scholar] [CrossRef]
- Nakashima, Y.; Heki, K. GPS Tide Gauges Using Multipath Signatures. J. Geod. Soc. Jpn. 2013, 59, 157–162. [Google Scholar]
- Löfgren, J.S.; Haas, R. Sea level measurements using multi-frequency GPS and GLONASS observations. EURASIP J. Adv. Signal Process. 2014, 2014, 50. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, Q.; Qian, X. New Progress and Application Prospects of Global Navigation Satellite System Reflectometry (GNSS + R). Acta Geod. Cartogr. Sin. 2017, 46, 1389–1398. [Google Scholar]
- Ansari, K.; Seok, H.W.; Jamjareegulgarn, P. Quasi zenith satellite system-reflectometry for sea-level measurement and implication of machine learning methodology. Sci. Rep. 2022, 12, 21445. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Haas, R.; Scherneck, H.G. Sea level time series and ocean tide analysis from multipath signals at five GPS sites in different parts of the world. J. Geodyn. 2014, 80, 66–80. [Google Scholar] [CrossRef]
- Tabibi, S.; Geremia-Nievinski, F.; Francis, O.; Dam, T.V. Tidal analysis of gnss reflectometry applied for coastal sea level sensing in antarctica and greenland. Remote Sens. Environ. 2020, 248, 111959. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Nievinski, F.G. Tropospheric delays in ground-based GNSS multipath reflectometry—Experimental evidence from coastal sites. J. Geophys. Res. Solid Earth 2017, 122, 2310–2327. [Google Scholar] [CrossRef]
- Purnell, D.J.; Gomez, N.; Chan, N.H.; Strandberg, J.; Holland, D.M.; Hobiger, T. Quantifying the Uncertainty in Ground-Based GNSS-Reflectometry Sea Level Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4419–4428. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Improving GNSS-R sea level determination through inverse modeling of SNR data. Radio Sci. 2016, 51, 1286–1296. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Watson, C.; Gravelle, M.; King, M.; Wöppelmann, G. Levelling co-located GNSS and tide gauge stations using GNSS reflectometry. J. Geod. 2015, 89, 241–258. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Watson, C. Remote leveling of tide gauges using GNSS reflectometry: Case study at Spring Bay, Australia. GPS Solut. 2016, 21, 451–459. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Zhang, S. Water levels measured with SNR using wavelet decomposition and Lomb–Scargle periodogram. GPS Solut. 2018, 22, 22. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Zhang, Q. Coherent superposition of multi-GNSS wavelet analysis periodogram for sea-level retrieval in GNSS multipath reflectometry. Adv. Space Res. 2019, 65, 1781–1788. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, K.; Liu, Q.; Zhang, C.; Zhang, Q.; Nan, Y. Tide Variation Monitoring Based Improved GNSS-MR by Empirical Mode Decomposition. Adv. Space Res. 2019, 63, 3333–3345. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Real-time sea-level monitoring using Kalman filtering of GNSS-R data. GPS Solut. 2019, 23, 61. [Google Scholar] [CrossRef]
- Roussel, N.; Ramillien, G.; Frappart, F.; Darrozes, J.; Gay, A.; Biancale, R.; Striebig, N.; Hanquiez, V.; Bertin, X.; Allain, D. Sea level monitoring and sea state estimate using a single geodetic receiver. Remote Sens. Environ. 2015, 171, 261–277. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Zhang, Q. Evaluation and combination of quad-constellation multi-GNSS multipath reflectometry applied to sea level retrieval. Remote Sens. Environ. 2019, 231, 111229. [Google Scholar] [CrossRef]
- Tabibi, S.; Geremia-Nievinski, F.; Dam, T.V. Statistical comparison and combination of GPS, GLONASS, and multi-GNSS multipath reflectometry applied to snow depth retrieval. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3773–3785. [Google Scholar] [CrossRef]
- Reinking, J. GNSS-SNR water level estimation using global optimization based on interval analysis. J. Geod. Sci. 2016, 6, 80–92. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Shen, Y.; Zheng, W.; Yin, W.; Xu, A.; Zhu, H. Feature Extraction Algorithm Using a Correlation Coefficient Combined with the VMD and Its Application to the GPS and GRACE. IEEE Access 2021, 9, 17507–17519. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Ahmed, W.A.; Wu, F.; Marlia, D.; Zhao, Y. Mitigation of Ionospheric Scintillation Effects on GNSS Signals with VMD-MFDFA. Remote Sens. 2019, 11, 2867. [Google Scholar] [CrossRef]
- Zhou, C.; Ma, J.; Wu, J.; Yuan, X. An adaptive VMD method based on improved GOA to extract early fault feature of rolling bearings. Int. J. Innov. Comput. Inf. Control. 2019, 15, 1485–1505. [Google Scholar]
- Li, C.; Liu, Y.; Liao, Y. An Improved Parameter-Adaptive Variational Mode Decomposition Method and Its Application in Fault Diagnosis of Rolling Bearings. Shock Vib. 2021, 2021, 2968488. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Dabbakuti, J.R.K.K.; Jacob, A.; Veeravalli, V.R.; Kallakunta, R.K. Implementation of IoT analytics ionospheric forecasting system based on machine learning and ThingSpeak. IET Radar Sonar Navig. 2020, 14, 341–347. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- He, X.; Bos, M.S.; Montillet, J.P.; Fernandes, R.; Melbourne, T.; Jiang, W.; Li, W. Spatial Variations of Stochastic Noise Properties in GPS Time Series. Remote Sens. 2021, 13, 4534. [Google Scholar] [CrossRef]
- Silva, L.K.J.; Ramarakula, M. An efficient interference mitigation approach for NavIC receivers using improved variational mode decomposition and wavelet packet decomposition. Trans. Emerg. Telecommun. Technol. 2021, 32, e4242. [Google Scholar]
- Zhu, J.; Zhang, Z.; Kuang, C. A Reliable Evaluation Indicator of Wavelet Denoising. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 688–694. [Google Scholar]



| Index | Reconstructed Time Series | ||
|---|---|---|---|
| T | 0.6659 | 0.3278 | 0.3341 |
| Index | Reconstructed Time Series | |||||
|---|---|---|---|---|---|---|
| T | 0.6145 | 0.1188 | 0.1159 | 0.1533 | 0.2467 | 0.3855 |
| Station Name | BRST | HKQT | ||
|---|---|---|---|---|
| Method | RMSE of retrieval (cm) | Loss rate of retrieval (%) | RMSE of retrieval (cm) | Loss rate of retrieval (%) |
| Robust regression method | 10.78 | 8.01 | 10.86 | 33.25 |
| IVMD method based on retrieval | 8.78 | 0 | 9.78 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Wen, Y.; Wang, X.; Xu, H. Multi-GNSS Combination Multipath Reflectometry Based on IVMD Method for Sea Level Retrieval. Remote Sens. 2023, 15, 1733. https://doi.org/10.3390/rs15071733
Li R, Wen Y, Wang X, Xu H. Multi-GNSS Combination Multipath Reflectometry Based on IVMD Method for Sea Level Retrieval. Remote Sensing. 2023; 15(7):1733. https://doi.org/10.3390/rs15071733
Chicago/Turabian StyleLi, Runchuan, Yuanlan Wen, Xiaolei Wang, and Huaqing Xu. 2023. "Multi-GNSS Combination Multipath Reflectometry Based on IVMD Method for Sea Level Retrieval" Remote Sensing 15, no. 7: 1733. https://doi.org/10.3390/rs15071733
APA StyleLi, R., Wen, Y., Wang, X., & Xu, H. (2023). Multi-GNSS Combination Multipath Reflectometry Based on IVMD Method for Sea Level Retrieval. Remote Sensing, 15(7), 1733. https://doi.org/10.3390/rs15071733





