Estimation of Anthocyanins in Leaves of Trees with Apple Mosaic Disease Based on Hyperspectral Data
Abstract
1. Introduction
2. Materials and Methods
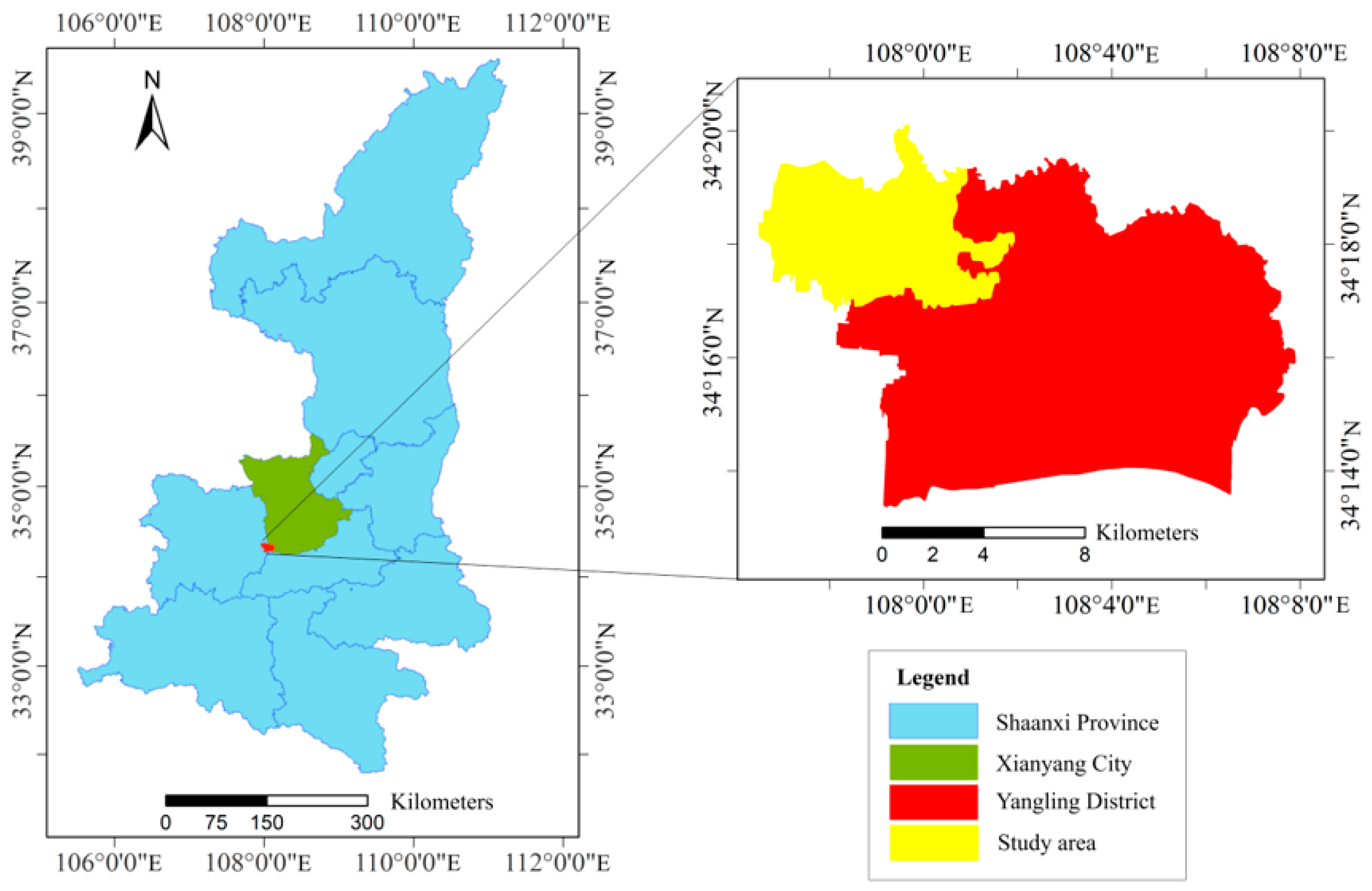
2.1. Study Area Overview and Experimental Design
2.2. Data Acquisition and Preprocessing
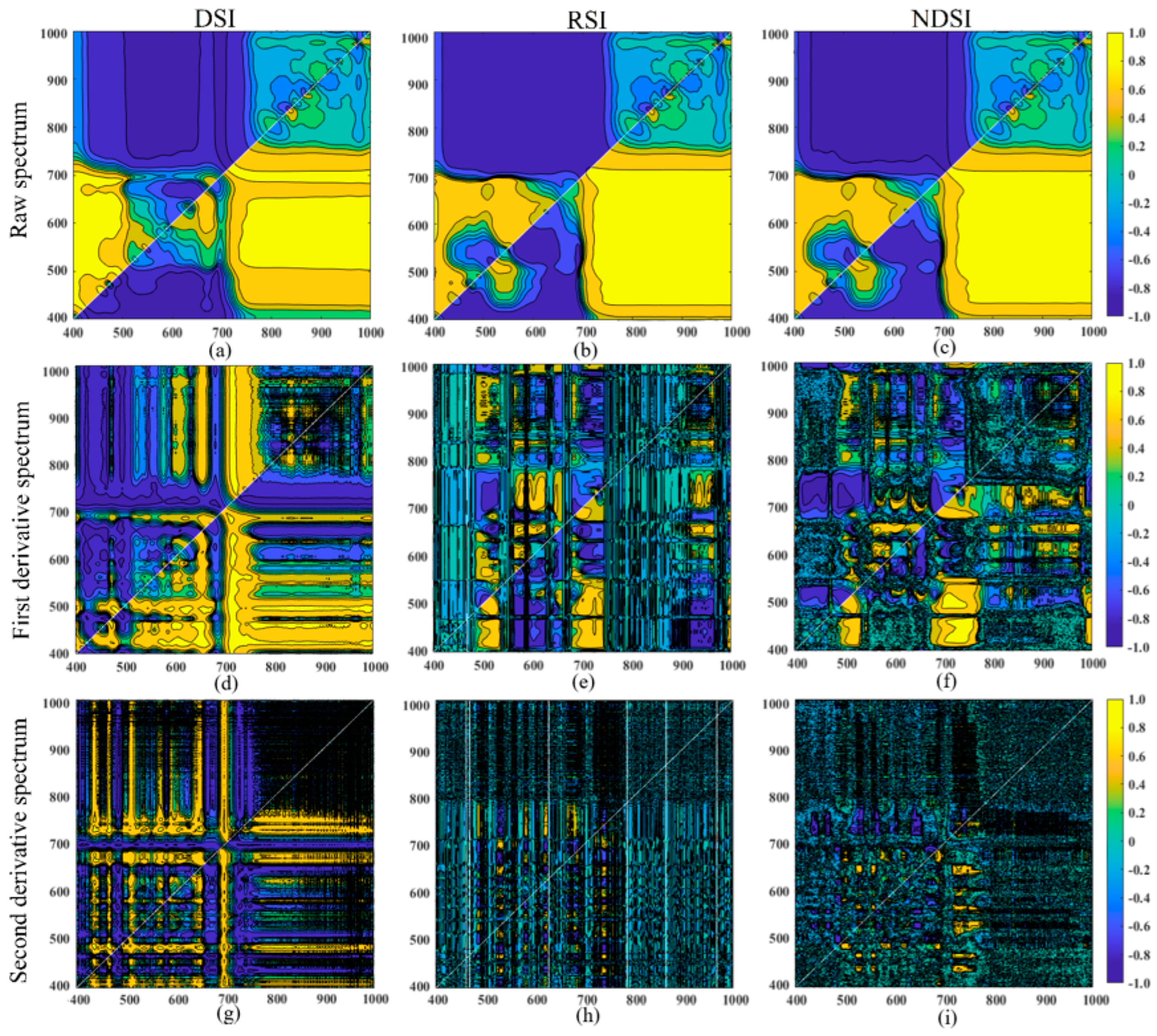
2.3. Construct the Sensitivity Spectral Index of Anthocyanins
2.4. Modeling Method
2.4.1. Variable Importance in Projection (VIP)
2.4.2. Akaike Information Criterion (AIC)
2.4.3. Sparrow Search Algorithm-Random Forest (SSA-RF)
- (1)
- Set initialization population, iteration number, predator ratio, and warning value.
- (2)
- The RF model is established according to the initial population, and the fitness is calculated and ranked.
- (3)
- SSA updates the location of predators, scouts, and entrants.
- (4)
- Feedback the results to the RF model, calculate the fitness, and update the position of the sparrow.
- (5)
- Judge whether the best fitness is obtained. If so, exit SSA and output RF results. Otherwise, repeat steps (2) to (4).
3. Results
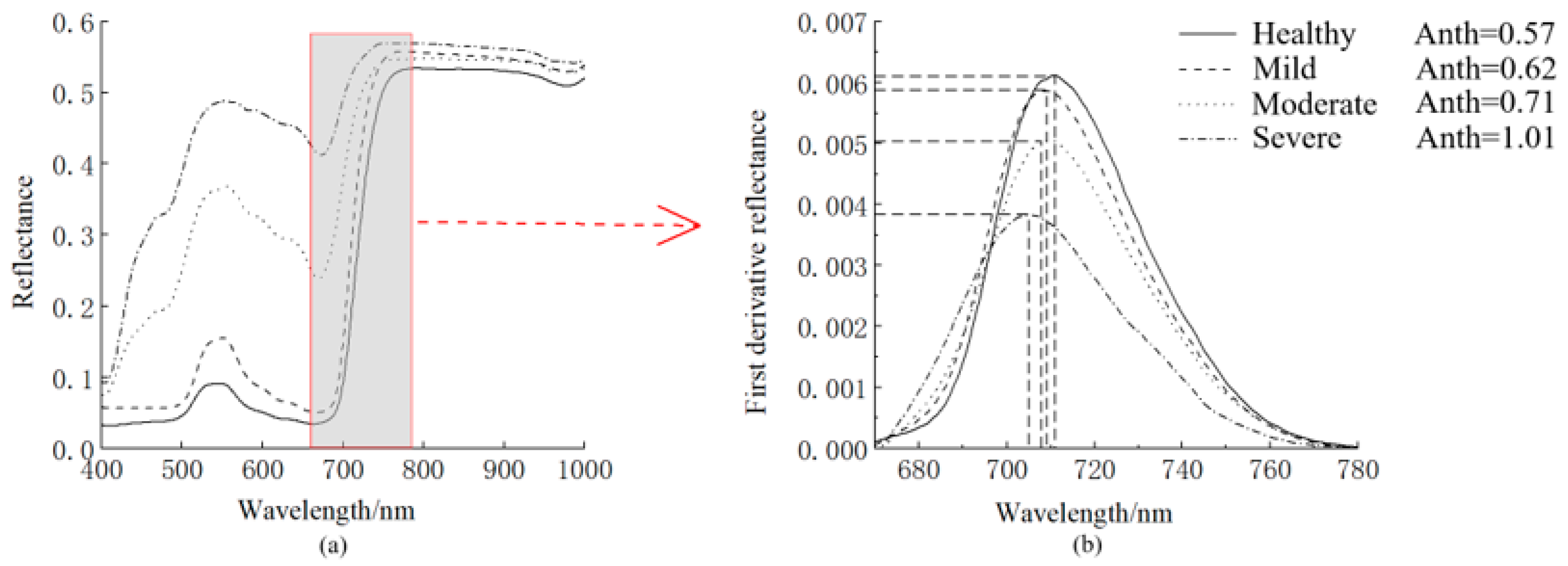
3.1. Spectral Characteristics of Mosaic Leaves
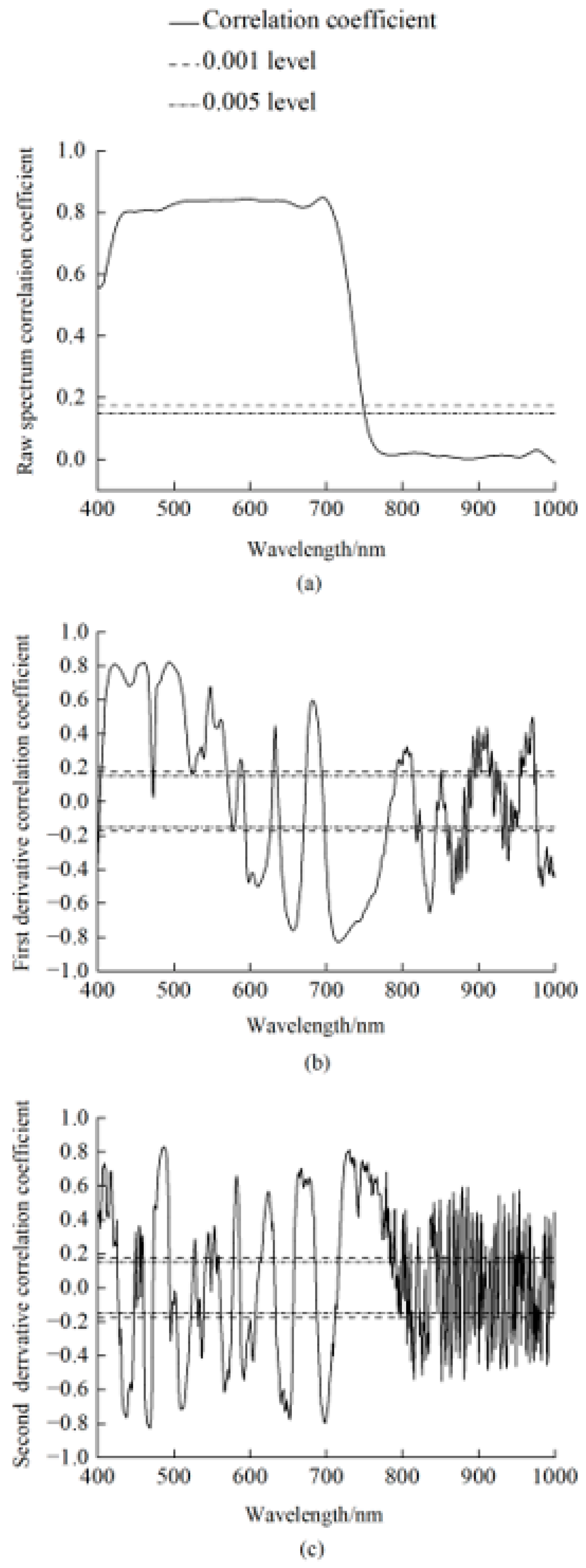
3.2. Correlation Analysis of the Spectral Index and the Anthocyanin Content
3.3. Selection of the Spectral Index Independent Variables Based on the VIP-PLSR-AIC Method
3.3.1. VIP Analysis of Spectral Index and Anthocyanin Content
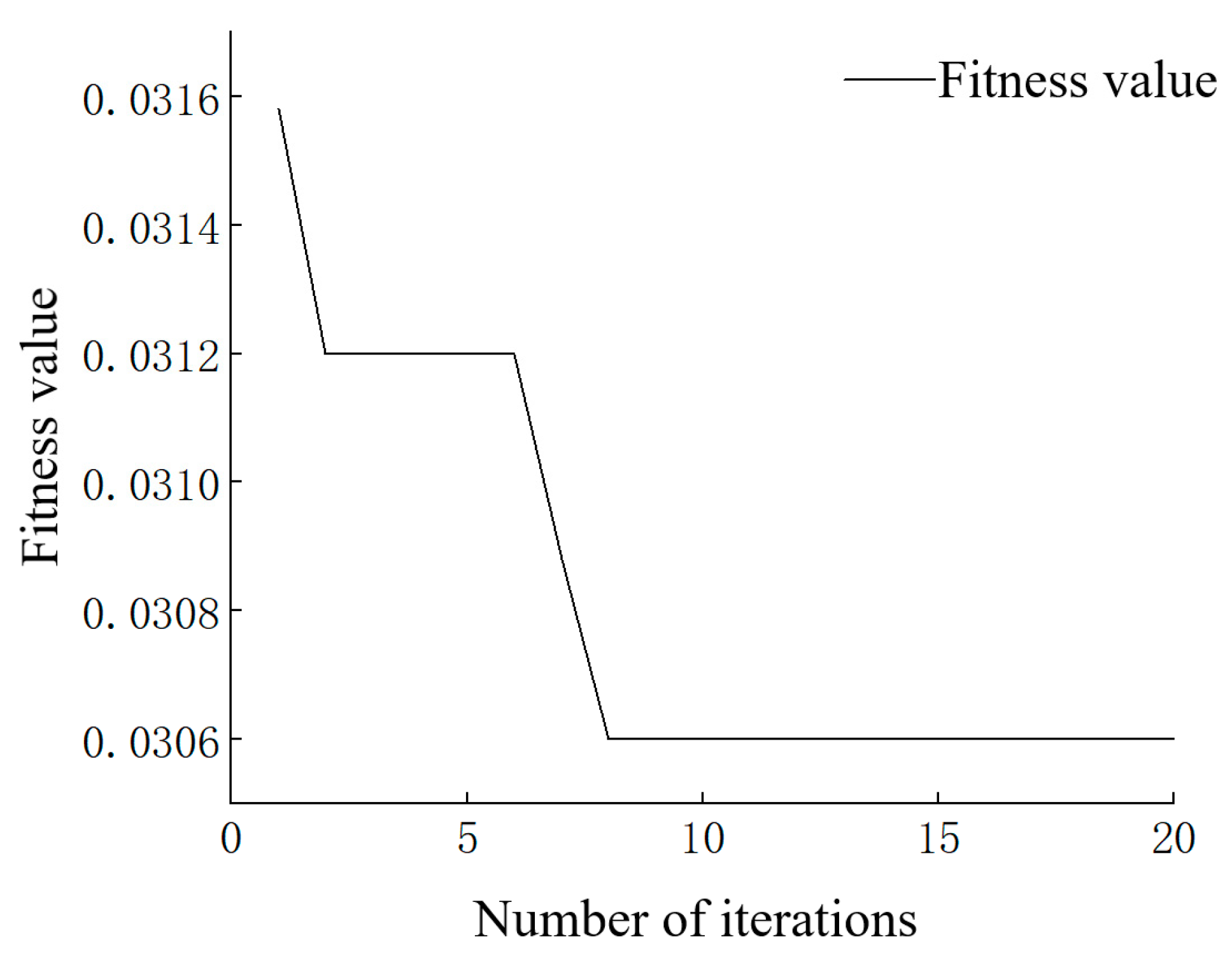
3.3.2. Selection of Optimal Independent Variables
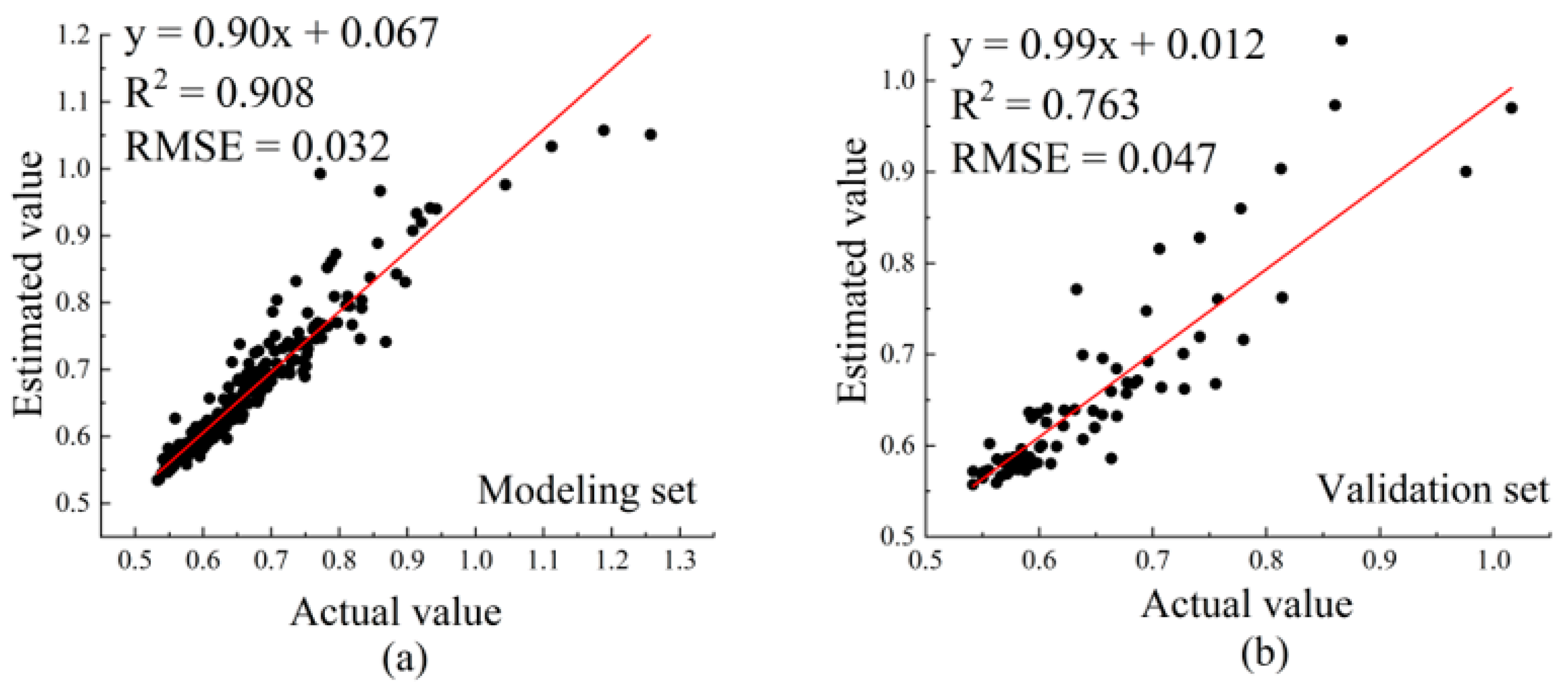
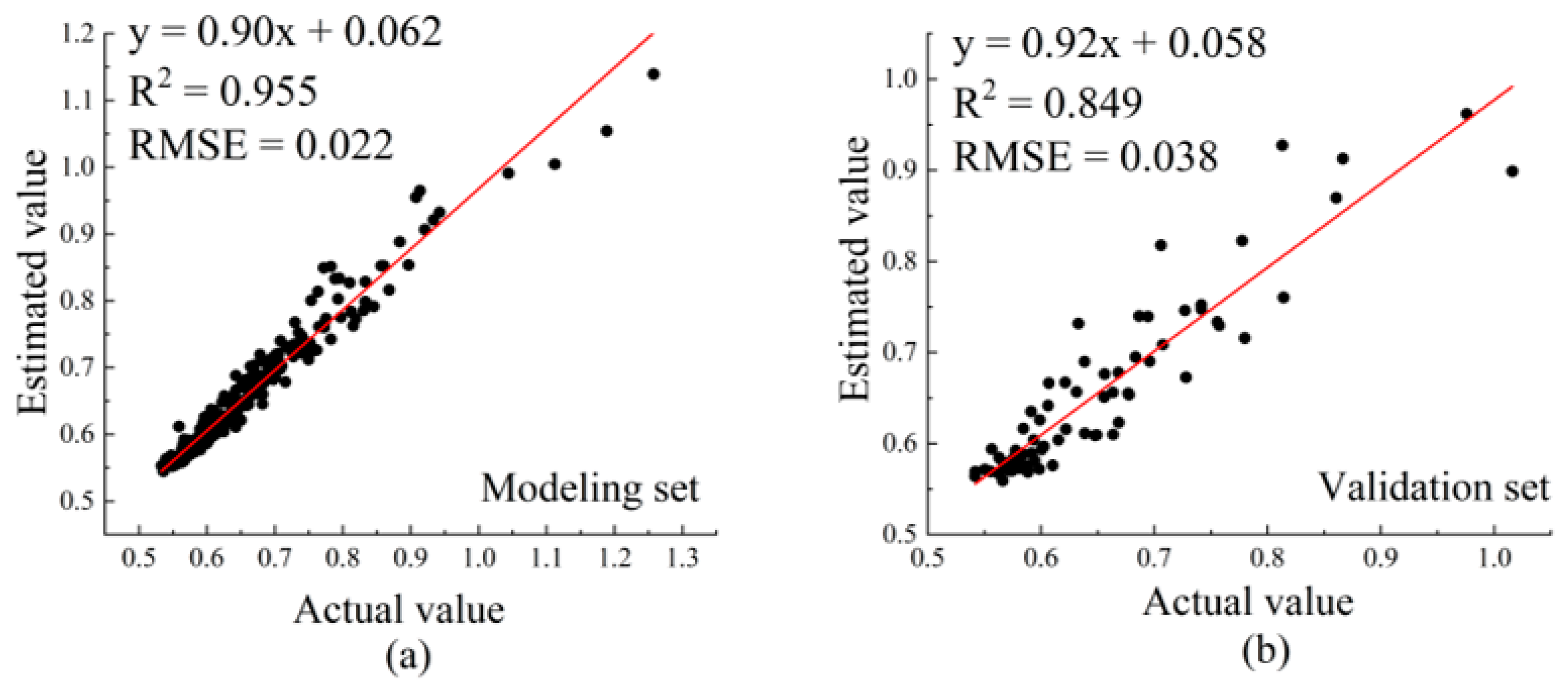
3.3.3. Establishment and Comparison of Hyperspectral Estimation Models for Anthocyanin Content in Apple Leaves
4. Discussion
4.1. Effect of Apple Mosaic Disease on Leaf Spectral Reflectivity and Anthocyanin Content
4.2. VIP-PLSR-AIC Method Selected the Optimal Argument Variables of the Model
4.3. Evaluation of the SSA-RF Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grimova, L.; Winkowska, L.; Konrady, M.; Rysanek, P. Apple mosaic virus. Phytopathol. Mediterr. 2016, 55, 1–19. [Google Scholar] [CrossRef]
- Landi, M.; Tattini, M.; Gould, K.S. Multiple functional roles of anthocyanins in plant-environment interactions. Environ. Exp. Bot. 2015, 119, 4–17. [Google Scholar] [CrossRef]
- Lo Piccolo, E.; Landi, M.; Massai, R.; Remorini, D.; Guidi, L. Girled-induced anthocyanin accumulation in red-leafed Prunus cerasifera: Effect on photosynthesis, photoprotection and sugar metabolism. Plant Sci. 2020, 294, 110456. [Google Scholar] [CrossRef]
- Janeeshma, E.; Rajan, V.K.; Puthur, J.T. Spectral variations associated with anthocyanin accumulation; an apt tool to evaluate zinc stress in Zea mays L. Chem. Ecol. 2021, 37, 32–49. [Google Scholar] [CrossRef]
- Skoneczny, H.; Kubiak, K.; Spiralski, M.; Kotlarz, J. Fire Blight Disease Detection for Apple Trees: Hyperspectral Analysis of Healthy, Infected and Dry Leaves. Remote Sens. 2020, 12, 2101. [Google Scholar] [CrossRef]
- Fernandes, A.M.; Oliveira, P.; Moura, J.P.; Oliveira, A.A.; Falco, V.; Correia, M.J.; Melo-Pinto, P. Determination of anthocyanin concentration in whole grape skins using hyperspectral imaging and adaptive boosting neural networks. J Food Eng. 2011, 105, 216–226. [Google Scholar] [CrossRef]
- Ye, W.X.; Xu, W.; Yan, T.Y.; Yan, J.K.; Gao, P.; Zhang, C. Application of Near-Infrared Spectroscopy and Hyperspectral Imaging Combined with Machine Learning Algorithms for Quality Inspection of Grape: A Review. Foods 2023, 12, 132. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.F.; Zhang, Z.L.; Cai, W.; Yang, N.J.; Zhan, Y. Semi-Supervised Locality Preserving Dense Graph Neural Network With ARMA Filters and Context-Aware Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 12. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Keydan, G.P.; Merzlyak, M.N. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Lett. 2006, 33, 5. [Google Scholar] [CrossRef]
- Huang, J.F.; Wei, C.; Zhang, Y.; Blackburn, G.A.; Wang, X.Z.; Wei, C.W.; Wang, J. Meta-Analysis of the Detection of Plant Pigment Concentrations Using Hyperspectral Remotely Sensed Data. PLoS ONE 2015, 10, e0137029. [Google Scholar] [CrossRef]
- Wang, X.X.; Cai, G.S.; Lu, X.P.; Yang, Z.N.; Zhang, X.J.; Zhang, Q.G. Inversion of Wheat Leaf Area Index by Multivariate Red-Edge Spectral Vegetation Index. Sustainability 2022, 14, 15875. [Google Scholar] [CrossRef]
- Wu, B.; Zheng, H.; Xu, Z.L.; Wu, Z.W.; Zhao, Y.D. Forest Burned Area Detection Using a Novel Spectral Index Based on Multi-Objective Optimization. Forests 2022, 13, 1787. [Google Scholar] [CrossRef]
- Li, D.; Chen, J.M.; Yu, W.G.; Zheng, H.B.; Yao, X.; Cao, W.X.; Wei, D.D.; Xiao, C.C.; Zhu, Y.; Cheng, T. Assessing a soil-removed semi-empirical model for estimating leaf chlorophyll content. Remote Sens. Environ. 2022, 282, 113284. [Google Scholar] [CrossRef]
- Gu, X.H.; Cai, W.Q.; Fan, Y.B.; Ma, Y.; Zhao, X.Y.; Zhang, C. Estimating foliar anthocyanin content of purple corn via hyperspectral model. Food Sci. Nutr. 2018, 6, 572–578. [Google Scholar] [CrossRef]
- Hernandez-Hierro, J.M.; Nogales-Bueno, J.; Rodriguez-Pulido, F.J.; Heredia, F.J. Feasibility Study on the Use of Near-Infrared Hyperspectral Imaging for the Screening of Anthocyanins in Intact Grapes during Ripening. J. Agric. Food Chem. 2013, 61, 9804–9809. [Google Scholar] [CrossRef]
- Yang, Y.C.; Sun, D.W.; Pu, H.B.; Wang, N.N.; Zhu, Z.W. Rapid detection of anthocyanin content in lychee pericarp during storage using hyperspectral imaging coupled with model fusion. Postharvest Biol. Technol. 2015, 103, 55–65. [Google Scholar] [CrossRef]
- Tran, T.V.; Reef, R.; Zhu, X. A Review of Spectral Indices for Mangrove Remote Sensing. Remote Sens. 2022, 14, 4868. [Google Scholar] [CrossRef]
- Anchal, S.; Bahuguna, S.; Priti; Pal, P.K.; Kumar, D.; Murthy, P.V.S.; Kumar, A. Non-destructive method of biomass and nitrogen (N) level estimation in Stevia rebaudiana using various multispectral indices. Geocarto Int. 2022, 37, 6409–6421. [Google Scholar] [CrossRef]
- Mlynarczyk, A.; Konatowska, M.; Krolewicz, S.; Rutkowski, P.; Piekarczyk, J.; Kowalewski, W. Spectral Indices as a Tool to Assess the Moisture Status of Forest Habitats. Remote Sens. 2022, 14, 4267. [Google Scholar] [CrossRef]
- Psiroukis, V.; Darra, N.; Kasimati, A.; Trojacek, P.; Hasanli, G.; Fountas, S. Development of a Multi-Scale Tomato Yield Prediction Model in Azerbaijan Using Spectral Indices from Sentinel-2 Imagery. Remote Sens. 2022, 14, 4202. [Google Scholar] [CrossRef]
- Lopes, D.D.; Moura, L.D.; Neto, A.J.S.; Ferraz, L.D.L.; Carlos, L.D.; Martins, L.M. Spectral Indices for Non-destructive Determination of Lettuce Pigments. Food Anal. Method. 2017, 10, 2807–2814. [Google Scholar] [CrossRef]
- Tian, X.; Wen, B.W.; Qing, B.Z.; Yong, Z. Comparison of hyperspectral remote sensing inversion methods for leaf area index in winter wheat. Trans. Chin. Soc. Agric. Eng. 2013, 29, 139–147. [Google Scholar]
- Xia, J.; Teng, Z.; Qin, Z.; Ju, M.Y.; Ying, Y.D. Construction of remote sensing monitoring model of wheat stripe rust based on fractional differential spectral index. Trans. Chin. Soc. Agric. Eng. 2021, 37, 142–151. [Google Scholar]
- Bhadra, S.; Sagan, V.; Maimaitijiang, M.; Maimaitiyiming, M.; Newcomb, M.; Shakoor, N.; Mockler, T.C. Quantifying Leaf Chlorophyll Concentration of Sorghum from Hyperspectral Data Using Derivative Calculus and Machine Learning. Remote Sens. 2020, 12, 2082. [Google Scholar] [CrossRef]
- Li, C.C.; Wang, Y.L.; Ma, C.Y.; Ding, F.; Li, Y.C.; Chen, W.A.; Li, J.B.; Xiao, Z. Hyperspectral Estimation of Winter Wheat Leaf Area Index Based on Continuous Wavelet Transform and Fractional Order Differentiation. Sensors 2021, 21, 8497. [Google Scholar] [CrossRef] [PubMed]
- Wumuti, A.; Nijiati, K.; Chen, C.; Sawut, M. Estimation of Winter Wheat LAI Based on Multi-dimensional Hyperspectral Vegetation Indices. Trans. Chin. Soc. Agric. Mach. 2022, 53, 181–190. [Google Scholar]
- Ritchie, G.L.; Sullivan, D.G.; Vencill, W.K.; Bednarz, C.W.; Hook, J.E. Sensitivities of Normalized Difference Vegetation Index and a Green/Red Ratio Index to Cotton Ground Cover Fraction. Crop Sci. 2010, 50, 1000–1010. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Chivkunova, O.B.; Merzlyak, M.N. Nondestructive estimation of anthocyanins and chlorophylls in anthocyanic leaves. Am. J. Bot. 2009, 96, 1861–1868. [Google Scholar] [CrossRef]
- Feng, L.; Wu, B.H.; Chen, S.S.; Zhang, C.; He, Y. Application of visible/near-infrared hyperspectral imaging with convolutional neural networks to phenotype aboveground parts to detect cabbage Plasmodiophora brassicae (clubroot). Infrared Phys. Technol. 2022, 121, 14. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Munoz-Mari, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Garcia-Berna, J.A.; Ouhbi, S.; Benmouna, B.; Garcia-Mateos, G.; Fernandez-Aleman, J.L.; Molina-Martinez, J.M. Systematic Mapping Study on Remote Sensing in Agriculture. Appl. Sci. 2020, 10, 3456. [Google Scholar] [CrossRef]
- Le, T.H.; Liu, C.; Yao, B.; Natraj, V.; Yung, Y.L. Application of machine learning to hyperspectral radiative transfer simulations. J. Quant. Spectrosc. Radiat. Transf. 2020, 246, 106928. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.L.; Zhao, X.F.; Hong, D.F.; Li, W.; Cai, W.; Zhan, Y. AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification. Inf. Sci. 2022, 602, 201–219. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.L.; Zhao, X.F.; Cai, W.; Yang, N.J.; Hu, H.J.; Huang, X.X.; Cao, Y.; Cai, W.W. Unsupervised Self-Correlated Learning Smoothy Enhanced Locality Preserving Graph Convolution Embedding Clustering for Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 16. [Google Scholar] [CrossRef]
- Sun, C.J.; Gao, F. Remote Sensing Image Recognition Based on LOG-T-SSA-LSSVM and AE-ELM Network. Comput. Intell. Neurosci. 2022, 2022, 8077563. [Google Scholar] [CrossRef]
- Balaha, H.M.; Hassan, A.E.S. Skin cancer diagnosis based on deep transfer learning and sparrow search algorithm. Neural Comput. Appl. 2023, 35, 815–853. [Google Scholar] [CrossRef]
- Liu, J.; Hu, P.; Xue, H.; Pan, X.; Chen, C. Prediction of milk protein content based on improved sparrow search algorithm and optimized back propagation neural network. Spectrosc. Lett. 2022, 55, 229–239. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Tanaka, Y.; Imachi, Y.; Yamashita, M.; Katsura, K. Feasibility of Combining Deep Learning and RGB Images Obtained by Unmanned Aerial Vehicle for Leaf Area Index Estimation in Rice. Remote Sens. 2021, 13, 84. [Google Scholar] [CrossRef]
- Rong, M.X.; Li, Y.; Guo, X.L.; Zong, T.; Ma, Z.Y.; Li, P.L. An ISSA-RF Algorithm for Prediction Model of Drug Compound Molecules Antagonizing ER? Gene Activity. Oncologie 2022, 24, 309–327. [Google Scholar] [CrossRef]
- Chang, J.Y.; Fu, X.J.; Zhao, C.X.; Lang, P.; Feng, C. Distributed Radar Target Detection Based on RF-SSA in Non-Gaussian Noise. Electronics 2022, 11, 2319. [Google Scholar] [CrossRef]
- Liu, R.; Li, G.L.; Wei, L.S.; Xu, Y.; Gou, X.J.; Luo, S.B.; Yang, X. Spatial prediction of groundwater potentiality using machine learning methods with Grey Wolf and Sparrow Search Algorithms. J. Hydrol. 2022, 610, 127977. [Google Scholar] [CrossRef]
- Cerovic, Z.G.; Masdoumier, G.; Ben Ghozlen, N.; Latouche, G. A new optical leaf-clip meter for simultaneous non-destructive assessment of leaf chlorophyll and epidermal flavonoids. Physiol. Plant. 2012, 146, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Goulas, Y.; Cerovic, Z.G.; Cartelat, A.; Moya, I. Dualex: A new instrument for field measurements of epidermal ultraviolet absorbance by chlorophyll fluorescence. Appl. Optics 2004, 43, 4488–4496. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.Y.; Yu, H.Y.; Liu, X.; Zhang, L.; Sui, Y.Y. Diagnosis of Cucumber Diseases and Insect Pests by Fluorescence Spectroscopy Technology Based on PCA-SVM. Spectrosc. Spectr. Anal. 2010, 30, 3018–3021. [Google Scholar] [CrossRef]
- Choudhury, M.R.; Christopher, J.; Das, S.; Apan, A.; Menzies, N.W.; Chapman, S.; Mellor, V.; Dang, Y.P. Detection of calcium, magnesium, and chlorophyll variations of wheat genotypes on sodic soils using hyperspectral red edge parameters. Environ. Technol. Innov. 2022, 27, 102469. [Google Scholar] [CrossRef]
- Ya, K.Z.; Bin, L.; Da, Y.S.; Peng, S.; Wen, C.L.; Cheng, W.; Chun, J.Z. Estimation of Nitrogen content in soybean canopy based on fractional differential algorithm. Spectrosc. Spectr. Anal. 2018, 38, 3221–3230. [Google Scholar]
- Van den Berg, A.K.; Perkins, T.D. Nondestructive estimation of anthocyanin content in autumn sugar maple leaves. Hortscience 2005, 40, 685–686. [Google Scholar] [CrossRef]
- Steele, M.R.; Gitelson, A.A.; Rundquist, D.C.; Merzlyak, M.N. Nondestructive Estimation of Anthocyanin Content in Grapevine Leaves. Am. J. Enol. Vitic. 2009, 60, 87–92. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.; Liu, Q.H.; Lin, S.R.; Huete, A.; Liu, L.Y.; Croft, H.; Clevers, J.; Zeng, Y.L.; Wang, X.H.; et al. A novel red-edge spectral index for retrieving the leaf chlorophyll content. Methods Ecol. Evol. 2022, 13, 2771–2787. [Google Scholar] [CrossRef]
- Xiao, Y.F.; Zhao, W.J.; Zhou, D.M.; Gong, H.L. Sensitivity Analysis of Vegetation Reflectance to Biochemical and Biophysical Variables at Leaf, Canopy, and Regional Scales. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4014–4024. [Google Scholar] [CrossRef]
- Ta, N.; Chang, Q.R.; Zhang, Y.M. Estimation of Apple Tree Leaf Chlorophyll Content Based on Machine Learning Methods. Remote Sens. 2021, 13, 3902. [Google Scholar] [CrossRef]
- Jia, P.P.; Zhang, J.H.; He, W.; Yuan, D.; Hu, Y.; Zamanian, K.; Jia, K.L.; Zhao, X.N. Inversion of Different Cultivated Soil Types’ Salinity Using Hyperspectral Data and Machine Learning. Remote Sens. 2022, 14, 5639. [Google Scholar] [CrossRef]
- Nie, M.P.; Meng, L.W.; Chen, X.J.; Hu, X.Y.; Li, L.M.; Yuan, L.M.; Shi, W. Tuning parameter identification for variable selection algorithm using the sum of ranking differences algorithm. J. Chemometr. 2019, 33, e3113. [Google Scholar] [CrossRef]
- Farres, M.; Platikanov, S.; Tsakovski, S.; Tauler, R. Comparison of the variable importance in projection (VIP) and of the selectivity ratio (SR) methods for variable selection and interpretation. J. Chemometr. 2015, 29, 528–536. [Google Scholar] [CrossRef]
- Sardar, S.; Shahid, S.S.; Ali, K.T.M. Investigating Wheat Yield and Climate Parameters Regression Model Based on Akaike Information Criteria. Pak. J. Bot. 2021, 53, 1299–1306. [Google Scholar] [CrossRef]
- Fan, X.Y.; He, G.J.; Zhang, W.Y.; Long, T.F.; Zhang, X.M.; Wang, G.Z.; Sun, G.; Zhou, H.K.; Shang, Z.H.; Tian, D.S.; et al. Sentinel-2 Images Based Modeling of Grassland Above-Ground Biomass Using Random Forest Algorithm: A Case Study on the Tibetan Plateau. Remote Sens. 2022, 14, 5321. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.Q.; Fang, M.Y.; Xu, W.Q. Spectral Reflectance Reconstruction Based on BP Neural Network and the Improved Sparrow Search Algorithm. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2022, 105, 1175–1179. [Google Scholar] [CrossRef]
- Hu, Y.T.; Wang, Z.; Li, X.F.; Li, L.; Wang, X.G.; Wei, Y.L. Nondestructive Classification of Maize Moldy Seeds by Hyperspectral Imaging and Optimal Machine Learning Algorithms. Sensors. 2022, 22, 6064. [Google Scholar] [CrossRef]
- Tian, M.L.; Ban, S.T.; Chang, Q.R.; Zhang, Z.R.; Wu, X.M.; Wang, Q. Quantified Estimation of Anthocyanin Content in Mosaic Virus Infected Apple Leaves Based on Hyperspectral Imaging. Spectrosc. Spectr. Anal. 2017, 37, 3187–3192. [Google Scholar]
- Ren, P.; Feng, M.C.; Yang, W.D.; Wang, C.; Liu, T.T.; Wang, H.Q. Response of Winter Wheat (Triticum aestivum L.) Hyperspectral Characteristics to Low Temperature Stress. Spectrosc. Spectr. Anal. 2014, 34, 2490–2494. [Google Scholar]
- Zhang, S.L.; Qin, J.; Tang, X.D.; Wang, Y.J.; Huang, J.L.; Song, Q.L.; Min, J.Y. Spectral Characteristics and Evaluation Model of Pinus Massoniana Suffering from Bursaphelenchus Xylophilus Disease. Spectrosc. Spectr. Anal. 2019, 39, 865–872. [Google Scholar]
- Janik, L.J.; Cozzolino, D.; Dambergs, R.; Cynkar, W.; Gishen, M. The prediction of total anthocyanin concentration in red-grape homogenates using visible-near-infrared spectroscopy and artificial neural networks. Anal. Chim. Acta 2007, 594, 107–118. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.W.; Zou, X.B.; Zhao, J.W.; Shi, J.Y.; Zhang, X.L.; Holmes, M. Measurement of total anthocyanins content in flowering tea using near infrared spectroscopy combined with ant colony optimization models. Food Chem. 2014, 164, 536–543. [Google Scholar] [CrossRef]
- Wold, S.; Sjostrom, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Noda, K.; Miyaoka, E.; Itoh, M. On bias correction of the Akaike information criterion in linear models. Commun. Stat.-Theory Methods 1996, 25, 1845–1857. [Google Scholar] [CrossRef]
- Gao, D.H.; Qiao, L.; An, L.L.; Zhao, R.M.; Sun, H.; Li, M.Z.; Tang, W.J.; Wang, N. Estimation of spectral responses and chlorophyll based on growth stage effects explored by machine learning methods. Crop J. 2022, 10, 1292–1302. [Google Scholar] [CrossRef]
- He, R.Y.; Li, H.; Qiao, X.J.; Jiang, J.B. Using wavelet analysis of hyperspectral remote-sensing data to estimate canopy chlorophyll content of winter wheat under stripe rust stress. Int. J. Remote Sens. 2018, 39, 4059–4076. [Google Scholar] [CrossRef]
- Chi, G.Y.; Huang, B.; Shi, Y.; Chen, X.; Li, Q.; Zhu, J.G. Detecting ozone effects in four wheat cultivars using hyperspectral measurements under fully open-air field conditions. Remote Sens. Env. 2016, 184, 329–336. [Google Scholar] [CrossRef]
- Zhao, S.S.; Blum, J.A.; Ma, F.F.; Wang, Y.Z.; Borejsza-Wysocka, E.; Ma, F.W.; Cheng, L.L.; Li, P.M. Anthocyanin Accumulation Provides Protection against High Light Stress While Reducing Photosynthesis in Apple Leaves. Int. J. Mol. Sci. 2022, 23, 12616. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N.; Chivkunova, O.B. Optical properties and nondestructive estimation of anthocyanin content in plant leaves. Photochem. Photobiol. 2001, 74, 38–45. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Z.Y.; Xu, C.X.; Zhao, X.L.; Pang, L.L.; Li, K.; Shi, Y.X. Heavy metal content prediction based on Random Forest and Sparrow Search Algorithm. J. Chemom. 2022, 36, e3445. [Google Scholar] [CrossRef]
- Verma, B.; Prasad, R.; Srivastava, P.K.; Singh, P.; Badola, A.; Sharma, J. Evaluation of Simulated AVIRIS-NG Imagery Using a Spectral Reconstruction Method for the Retrieval of Leaf Chlorophyll Content. Remote Sens. 2022, 14, 3560. [Google Scholar] [CrossRef]

| Spectral Index | Definition/Formula | Document |
|---|---|---|
| Anthocyanin Content Index (ACI) | R530/R940 | [47] |
| Adjusted anthocyanin Index (MACI) | Raverage(760~800)/Raverage(540~560) | [48] |
| Red-Green Index (RG) | Raverage(660~680)/Raverage(540~560) | [49] |
| Spectral Polygon Vegetation Index (SPVI) | 0.4[3.7(R800 − R670) − 1.2|R530 − R670|] | [50] |
| Composite index 3 (CI3) | [(R800 − R445)/(R800 − R680)]/(R800/R670) | [27] |
| Composite index four (CI4) | [(R550 − R450)/(R550 + R450)]/[(R800 − R670)/(R800 + R670)] | [27] |
| Difference spectral index (DSI0) | Difference between the optimal band combination of the original spectrum | [46] |
| First-order difference value spectral index (DSI1) | Difference between the optimal band combination of the first-order differential spectrum | [46] |
| Second-order difference spectral index (DSI2) | Difference between the optimal band combination of the second-order differential spectrum | [46] |
| Ratio spectral index RSI0 | Ratio of the optimal band combination of the original spectrum | [46] |
| First-order ratio spectral index (RSI1) | Ratio of the optimal band combinations in the first-order differential spectrum | [46] |
| Second-order ratio spectral index (RSI2) | Ratio of the optimal band combinations in the second-order differential spectrum | [46] |
| Normalized difference spectral index (NDSI0) | Difference and ratio of the optimal band combination of the original spectrum | [46] |
| First-order normalized difference spectral index (NDVI1) | Difference and ratio of optimal band combinations in the first-order differential spectrum | [46] |
| Second-order normalized difference spectral index (NDVI2) | Difference and ratio of optimal band combinations in the second-order differential spectrum | [46] |
| Red edge amplitude (Dr) | Maximum of first-order differential spectrum in red band (680~760 nm) | [51] |
| Red edge area (Sr) | Integration of the first-order differential spectrum within the red light band (680~760 nm) | [51] |
| Yellow edge amplitude (Dy) | Maximum of the first-order differential spectrum in the yellow light band (560~640 nm) | [51] |
| Yellow edge area (Sy) | Integration of the first-order differential spectrum within the yellow light band(560~640 nm) | [51] |
| Blue edge amplitude (Db) | Maximum of first-order differential spectrum in blue light band (490~530 nm) | [51] |
| Blue edge area (Sb) | Integration of the first-order differential spectrum within the blue light band (490~530 nm) | [51] |
| Spectral Index | Band 1 | Band 2 | Formula | Correlation Coefficient (r) |
|---|---|---|---|---|
| DSI0 | 477 | 634 | R634 − R477 | 0.854 ** |
| DSI1 | 424 | 656 | R656 − R424 | 0.852 ** |
| DSI2 | 469 | 619 | R619 − R469 | 0.855 ** |
| RSI0 | 696 | 792 | R696/R792 | 0.854 ** |
| RSI1 | 573 | 654 | R654/R573 | 0.829 ** |
| RSI2 | 531 | 652 | R652/R531 | 0.830 ** |
| NDSI0 | 695 | 791 | (R695 − R791)/(R695 + R791) | 0.841 ** |
| NDSI1 | 464 | 750 | (R464 − R750)/(R464 + R750) | 0.854 ** |
| NDSI2 | 469 | 732 | (R469 − R732)/(R469 + R732) | 0.857 ** |
| Spectral Index | VIP Value | Sort |
|---|---|---|
| DSI0 | 1.114 | 5 |
| DSI1 | 1.112 | 6 |
| DSI2 | 1.115 | 2 |
| RSI0 | 1.114 | 4 |
| RSI1 | 1.08 | 10 |
| RSI2 | 1.082 | 9 |
| NDSI0 | 1.097 | 8 |
| NDSI1 | 1.115 | 3 |
| NDSI2 | 1.118 | 1 |
| ACI | 1.106 | 7 |
| MACI | 0.956 | 15 |
| SPVI | 1.044 | 11 |
| RG | 0.850 | 18 |
| CI3 | 1.038 | 12 |
| CI4 | 1.033 | 14 |
| Dr | 0.924 | 16 |
| Sr | 1.037 | 13 |
| Dy | 0.679 | 20 |
| Sy | 0.219 | 21 |
| Db | 0.839 | 19 |
| Sb | 0.872 | 17 |
| Number of Independent Variables | Residual Sum of Squares | AIC |
|---|---|---|
| 5 | 0.823 | −46.009 |
| 6 | 0.823 | −44.015 |
| 7 | 0.822 | −42.326 |
| 8 | 0.812 | −43.803 |
| 9 | 0.800 | −46.101 |
| 10 | 0.797 | −45.459 |
| 11 | 0.796 | −43.755 |
| 12 | 0.788 | −44.629 |
| 13 | 0.775 | −47.290 |
| 14 | 0.775 | −45.303 |
| 15 | 0.769 | −45.462 |
| 16 | 0.764 | −45.689 |
| 17 | 0.722 | −59.632 |
| 18 | 0.721 | −58.201 |
| 19 | 0.711 | −58.205 |
| Data | Methods | RMSE | |
|---|---|---|---|
| Modeling set | PLSR | 0.770 | 0.050 |
| BP | 0.898 | 0.033 | |
| SVM | 0.717 | 0.056 | |
| RF | 0.908 | 0.032 | |
| SSA-RF | 0.955 | 0.022 | |
| Validation set | PLSR | 0.800 | 0.043 |
| BP | 0.734 | 0.049 | |
| SVM | 0.846 | 0.038 | |
| RF | 0.763 | 0.047 | |
| SSA-RF | 0.849 | 0.038 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Jiang, D.; Chang, Q.; Zheng, Z.; Fu, X.; Li, K.; Mo, H. Estimation of Anthocyanins in Leaves of Trees with Apple Mosaic Disease Based on Hyperspectral Data. Remote Sens. 2023, 15, 1732. https://doi.org/10.3390/rs15071732
Zhang Z, Jiang D, Chang Q, Zheng Z, Fu X, Li K, Mo H. Estimation of Anthocyanins in Leaves of Trees with Apple Mosaic Disease Based on Hyperspectral Data. Remote Sensing. 2023; 15(7):1732. https://doi.org/10.3390/rs15071732
Chicago/Turabian StyleZhang, Zijuan, Danyao Jiang, Qingrui Chang, Zhikang Zheng, Xintong Fu, Kai Li, and Haiyang Mo. 2023. "Estimation of Anthocyanins in Leaves of Trees with Apple Mosaic Disease Based on Hyperspectral Data" Remote Sensing 15, no. 7: 1732. https://doi.org/10.3390/rs15071732
APA StyleZhang, Z., Jiang, D., Chang, Q., Zheng, Z., Fu, X., Li, K., & Mo, H. (2023). Estimation of Anthocyanins in Leaves of Trees with Apple Mosaic Disease Based on Hyperspectral Data. Remote Sensing, 15(7), 1732. https://doi.org/10.3390/rs15071732







