AVHRR NDVI Compositing Method Comparison and Generation of Multi-Decadal Time Series—A TIMELINE Thematic Processor
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Sites
2.2. Data
2.2.1. AVHRR
2.2.2. MODIS
2.2.3. NOAA AVHRR CDR
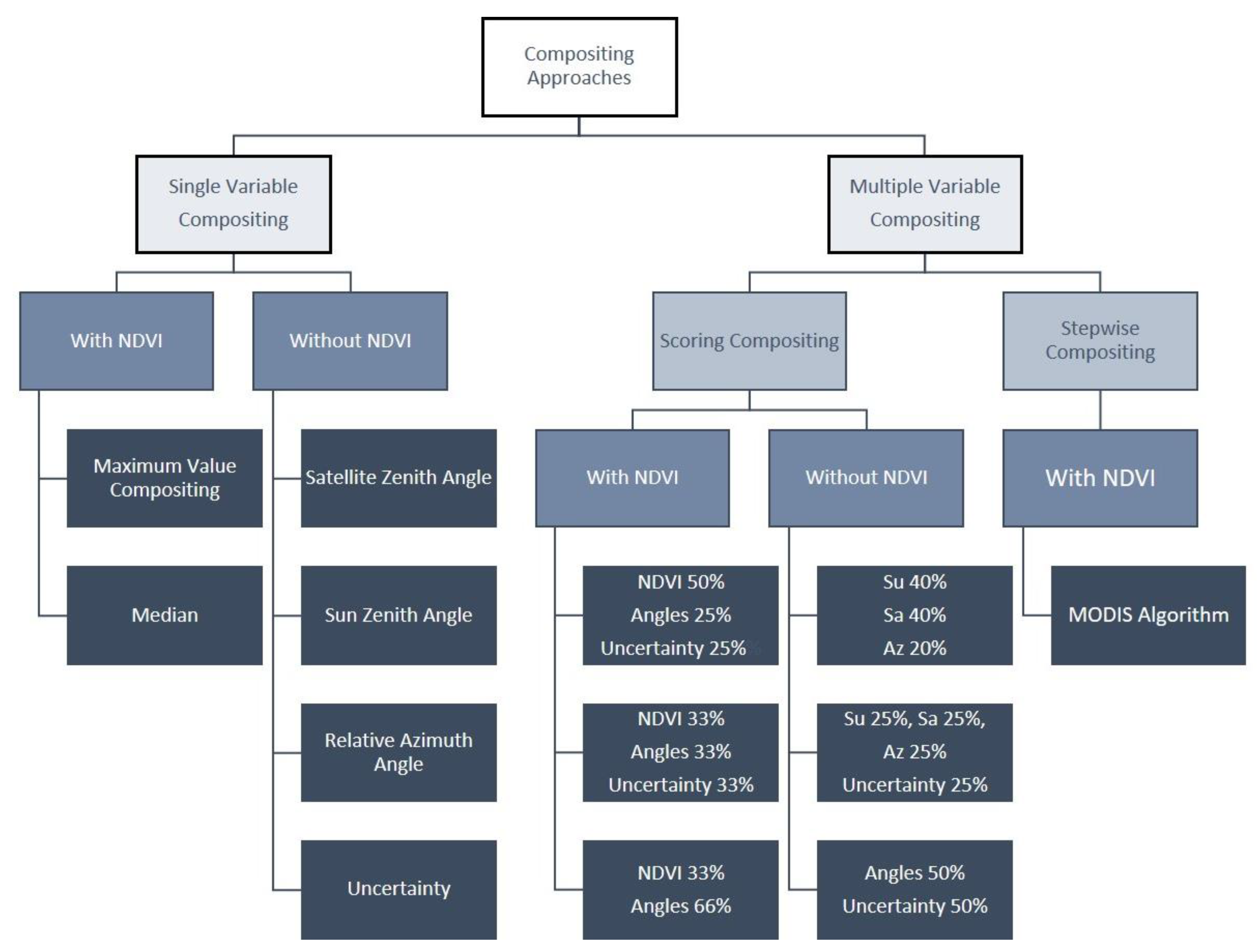
2.3. Compositing Methods
- “MVC”: Maximum Value Compositing. The highest NDVI observation value achieves the highest score, i.e., is selected. This is a standard procedure in image compositing, originally designed for AVHRR compositing (see above). However, studies have shown that MVC selects pixels with large view and solar zenith angles [38,67,110,112]. This is especially true for TOC reflectance [35,113]. The MVC approach thus potentially selects pixels with NDVI greater than the nadir value. Nevertheless, we keep this procedure for comparison reasons.
- “MED”: Median NDVI. The median value of all NDVI observations is selected. This procedure relies on the NDVI values only, and it is thought to reduce signal attenuation effects such as undetected clouds as well saturation or bidirectional reflectance effects, while maintaining an original physical observation.
- “Sa”: Satellite Zenith Angle. The view angle of an observation is used as criterion. As [112] specifies, the directional reflectance factor increases with the off-nadir view angle for any azimuth view direction. Furthermore, the closer an acquisition is to nadir, the lower the effect of atmospheric disturbances is [114]. Hence, previous studies have suggested generating composites approximating images with near-nadir geometry [38,67,110]. Nadir view, i.e., a satellite zenith angle of 0°, is considered best and given highest score while larger angles are given lower scores by ranking the cosine of the satellite zenith angle. Through cosine transformation, an angle of 0° obtains a score of 1, while for example angles of 20°, 40°, or 60°, they obtain scores of 0.93, 0.77, or 0.5, respectively, and a score of 0 is assigned to view angles of 90°.
- “Su”: Sun Zenith Angle. The illumination angle under which an observation is taken is used as selection criterion. An illumination of 45° is considered best (to be in accordance with the TIMELINE BRDF correction, see [12]) and is given the highest score by ranking the cosine of the absolute value of the sun zenith angle minus 45°. The cosine of the absolute, −45°-shifted angle values is in the last step scaled to a range from 0 to 1, resulting in the lowest possible scores of 0 for sun zenith angles of 0° and 90°.
- “Az”: Relative Azimuth Angle. The absolute difference between sun and satellite azimuth angles under which an observation is taken is used as criterion. An equal azimuth angle, i.e., a relative azimuth angle of 0°, is considered best to minimize shadowing effects [112], and is given the highest score by ranking the cosine of the absolute relative azimuth angle, analogous to the scaling of the satellite zenith angle score.
- “Uc”: Uncertainty. The uncertainty value, associated through flags with each pixel in the L2c SDR red and NIR bands and indicating the reflectance uncertainty derived during atmospheric correction, is combined, scaled to 0–1, and used as selection criteria. No uncertainty is considered best and lower uncertainties achieve higher scores through using their reciprocal value.
- “NAUc”: NDVI, Angles, and Uncertainty. For the score calculation, half of the weight is given to the NDVI value, while ¼ of each is given to the average score of the acquisition angles and to the reflectance uncertainty. In this approach, every available criterion is considered for the selection of the best pixel value, but with an emphasis on NDVI.
- “NAUc_33”: NDVI, Angles, and Uncertainty. For the score calculation, equal weight is given to the NDVI value, to the average score of the acquisition angles, and to the reflectance uncertainty. It is hence conceptually similar to the NAUc approach, but with less influence of the NDVI.
- “AN”: Angles and NDVI. For the score calculation, two thirds of the weight is given to the average score of the acquisition angles, while one third is given to the NDVI value. This approach hence gives higher importance to the acquisition geometry than to NDVI, without considering the uncertainty.
- “SuSaAz”: Sun Zenith, Satellite Zenith, and Azimuth. In this approach, only the acquisition geometry, i.e., sun and satellite zenith angles as well as relative azimuth angle, is used for compositing. For the score calculation, 40% of the weight is given to each zenith angle, while the relative azimuth is considered with 20%.
- “SuSaAzUc”: Sun Zenith, Satellite Zenith, Azimuth, and Uncertainty. In this approach, every available criterion but NDVI is considered for selecting the best pixel value. For the score calculation, equal weight is given to each of the four parameters.
- “AUc”: Angles and Uncertainty. In this approach, the uncertainty flag is given a relatively high weight. For the score calculation, half of the weight is given to the uncertainty, and half is given to an average score of the acquisition angles.
- “MOD”: MODIS Algorithm. The algorithm first selects the two highest NDVI values and in a second step selects of those the observation with the smaller satellite zenith angle, called CV-MVC algorithm [47,49,107]. Additionally, other studies found this stepwise procedure to be most effective [38]. This standard MODIS procedure is included for comparison reasons as a benchmark. However, we adapted it using the four highest NDVI values as “preselection” to account for the longer integrating period and higher number of input data compared to MODIS.
2.4. Comparison of Compositing Approaches
2.4.1. Value Distributions
2.4.2. Spatial Consistency
2.4.3. Temporal Consistency
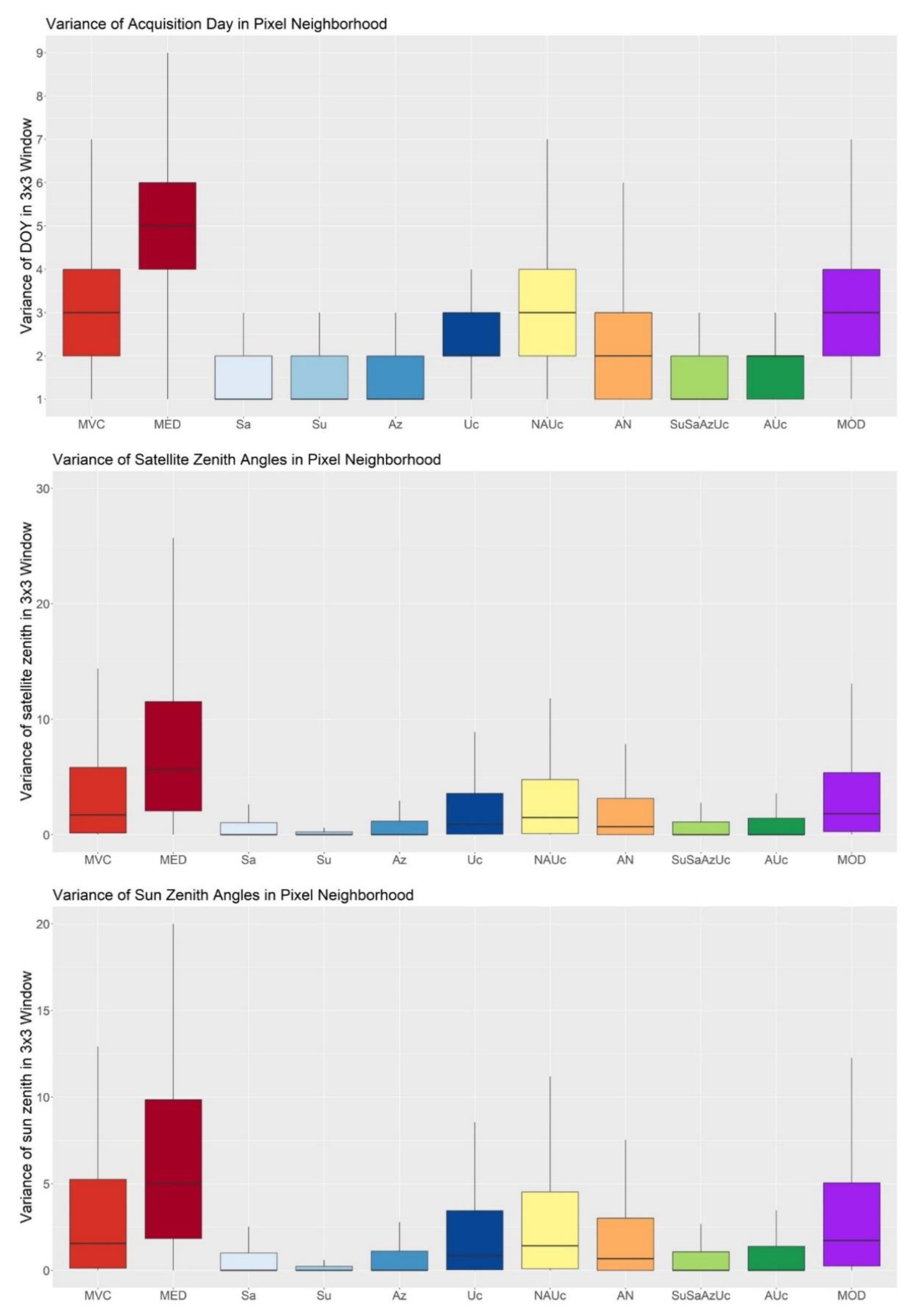
2.4.4. Spatial Consistency of Acquisition Conditions
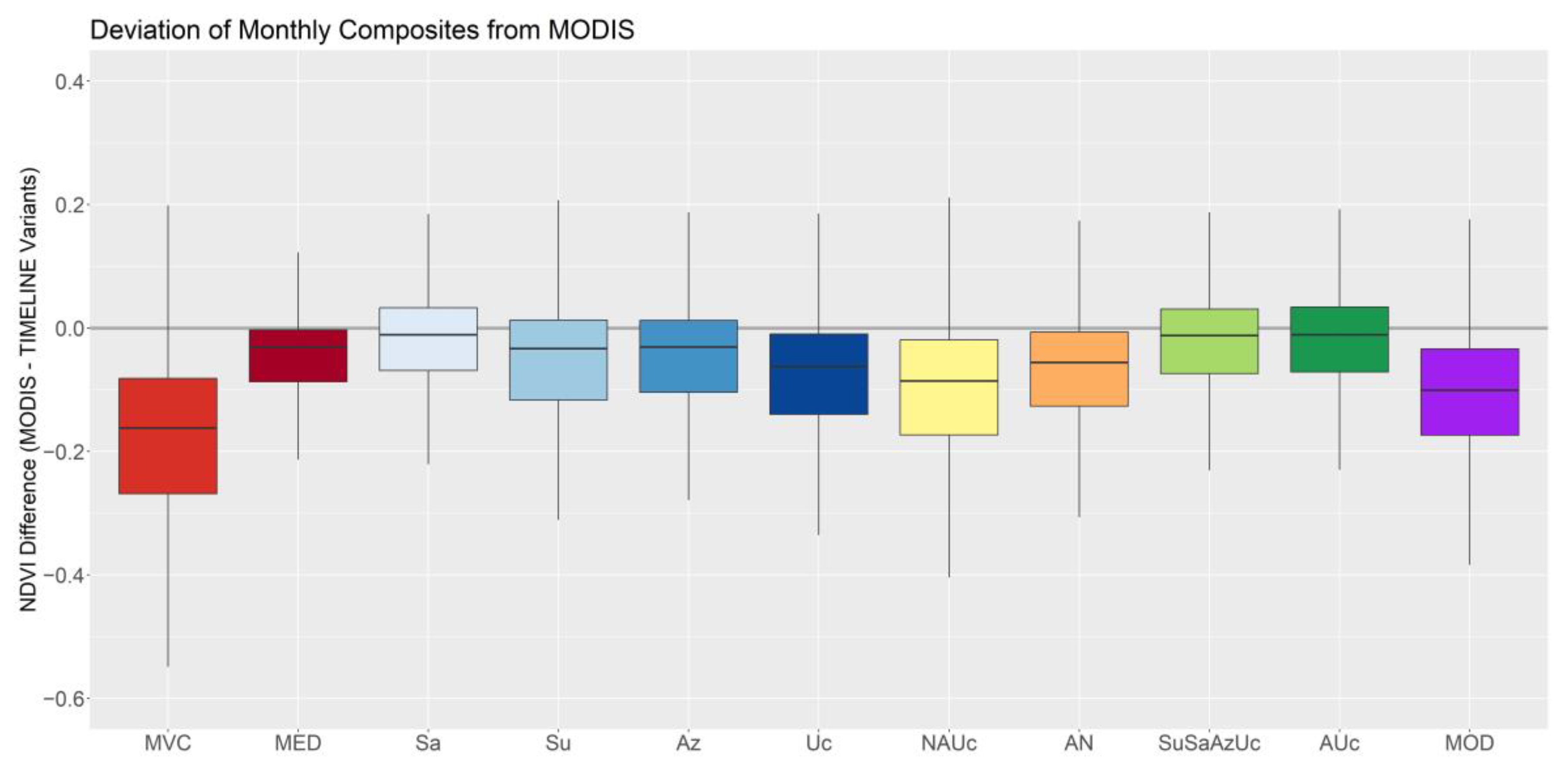
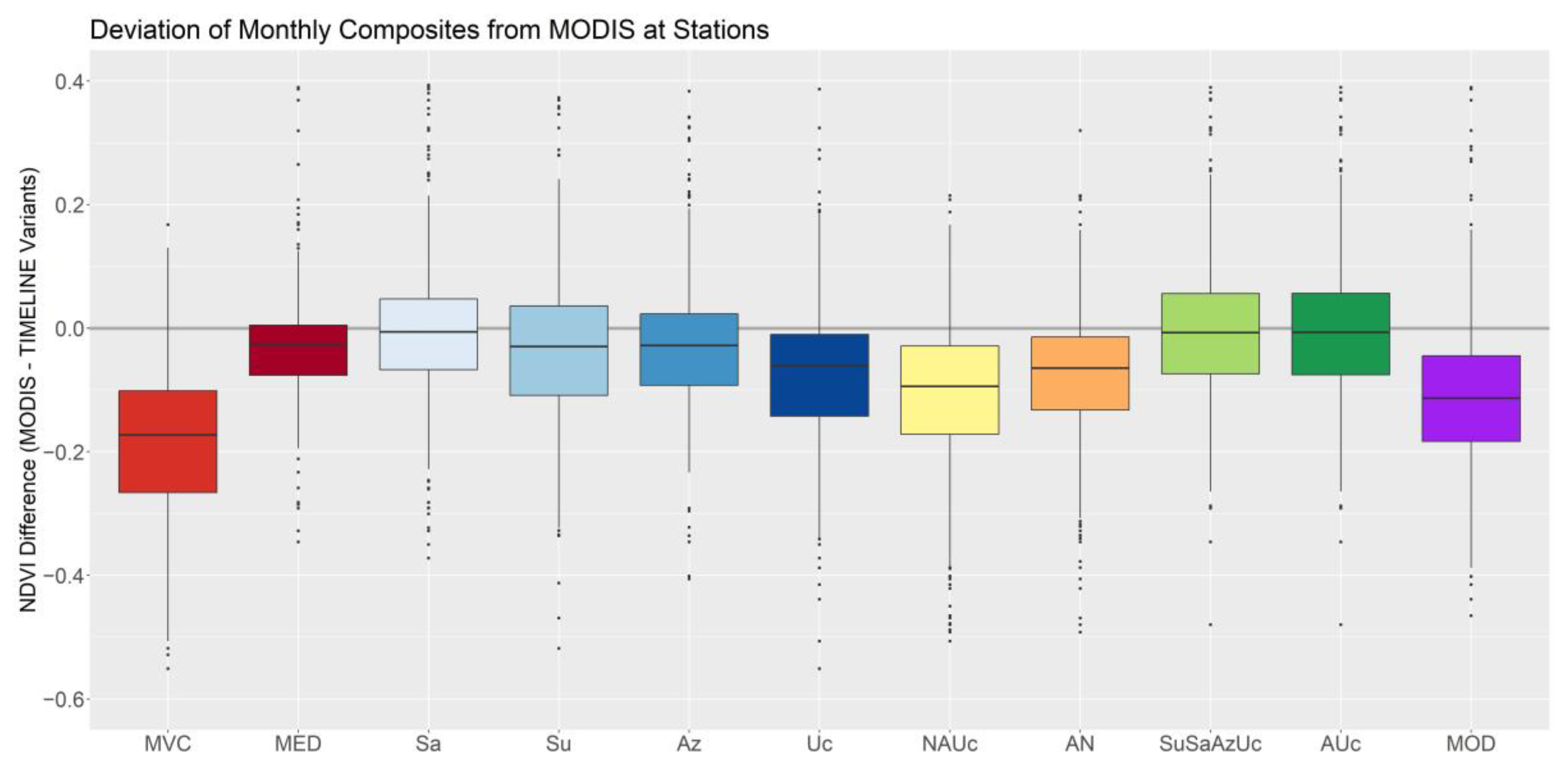
2.4.5. Comparison to MODIS and NOAA CDR NDVI Products
3. Results
3.1. NDVI, Satellite, and Sun Zenith Angle Value Distributions
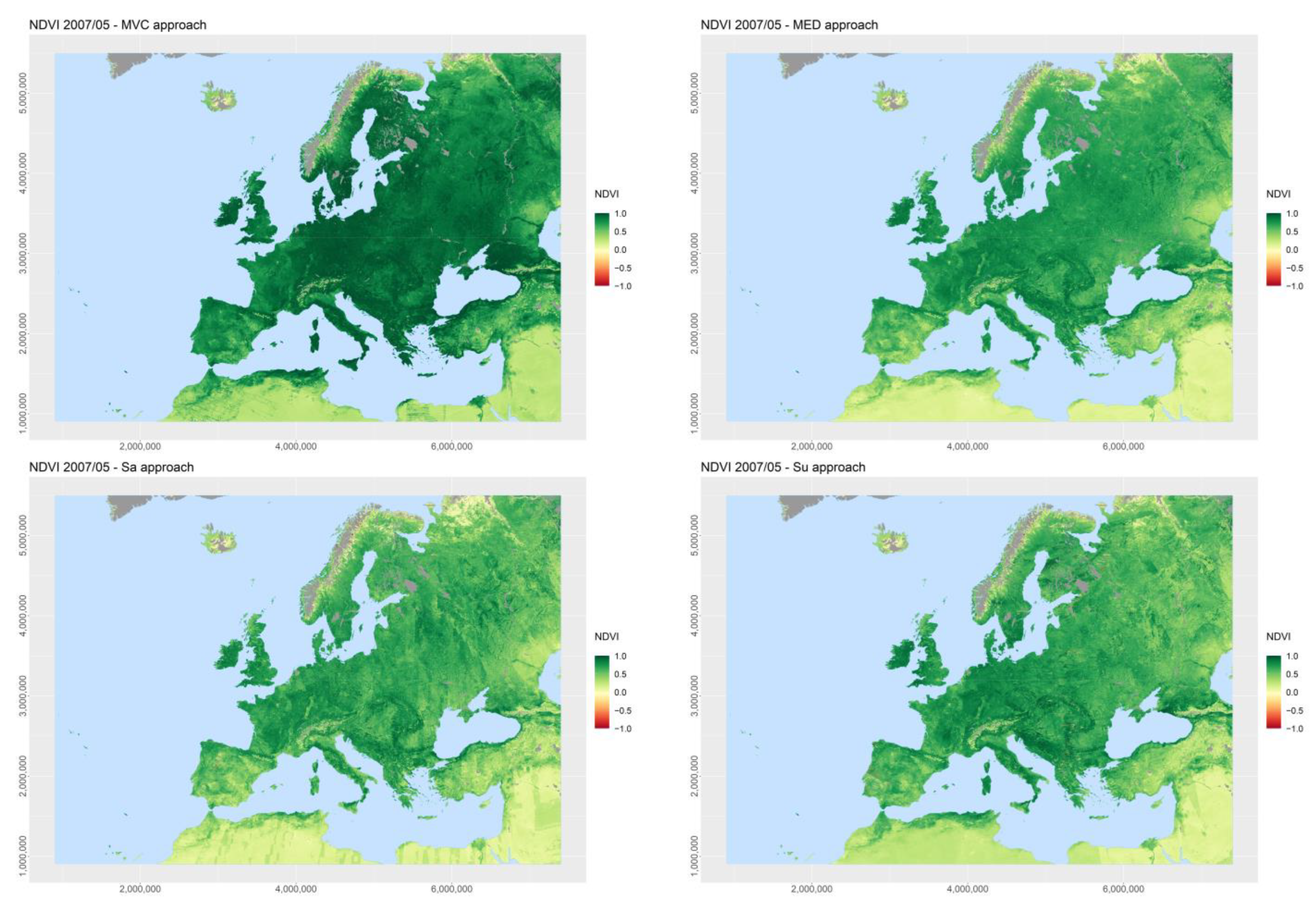
3.2. Spatial Consistency
3.3. Temporal Consistency
3.4. Spatial Consistency of Acquisition Conditions
4. Discussion
4.1. Purely NDVI-Based Approaches: MVC and MED
4.2. Purely Geometry-Based Approaches: Sa, Su, and Az
4.3. Uncertainty Information as Sole Selection Criterion: Uc
4.4. Multiple Variable Compositing Not including NDVI: SuSaAzUc and AUc
4.5. Multiple Variable Compositing including NDVI: NAUc and AN
4.6. Imitating the MODIS Standard Product: MOD
4.7. Algorithm Selection, Limitations, and Further Work
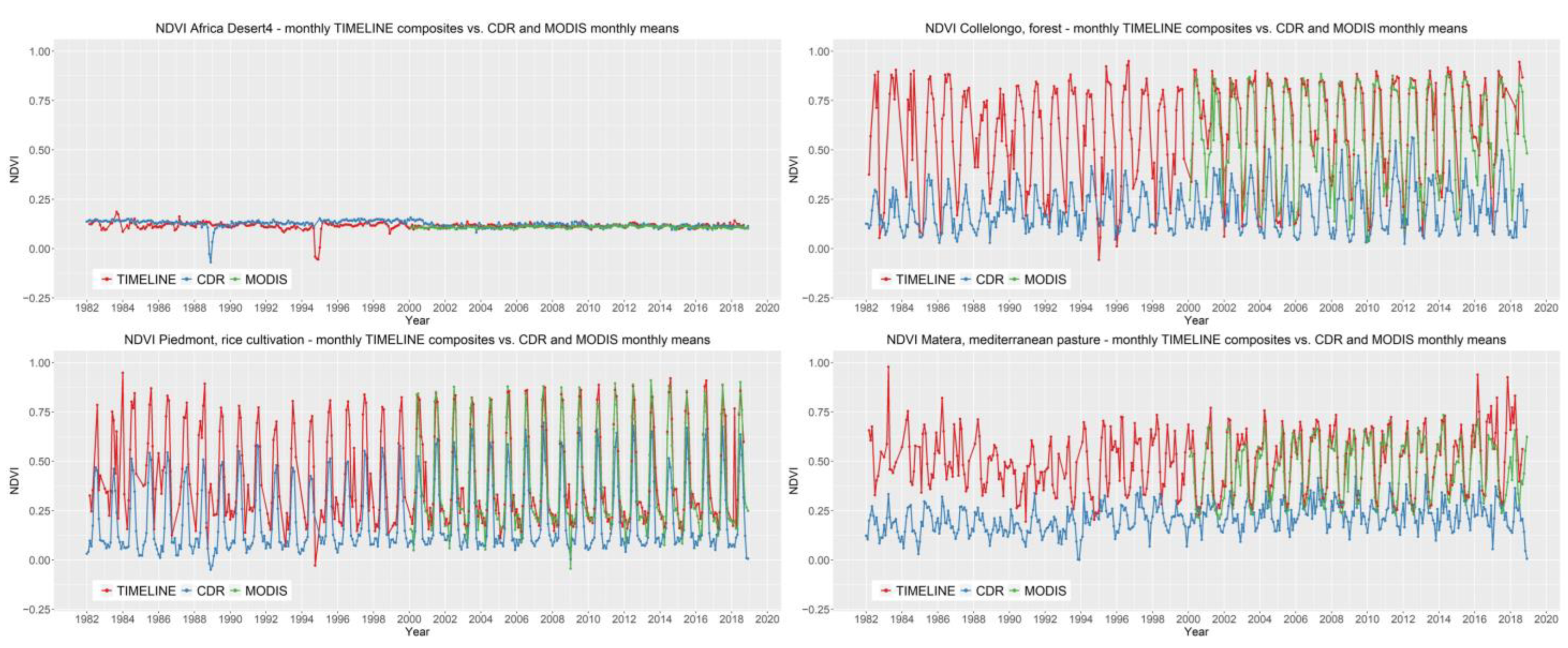
5. Final TIMELINE NDVI Product and Comparison to MODIS and NOAA CDR NDVI
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Piao, S.; Wang, X.; Park, T.; Chen, C.; Lian, X.; He, Y.; Bjerke, J.W.; Chen, A.; Ciais, P.; Tømmervik, H.; et al. Characteristics, drivers and feedbacks of global greening. Nat. Rev. Earth Environ. 2020, 1, 14–27. [Google Scholar] [CrossRef]
- Alkama, R.; Cescatti, A. Biophysical climate impacts of recent changes in global forest cover. Science 2016, 351, 600–604. [Google Scholar] [CrossRef]
- Huang, K.; Xia, J.; Wang, Y.; Ahlström, A.; Chen, J.; Cook, R.B.; Cui, E.; Fang, Y.; Fisher, J.B.; Huntzinger, D.N.; et al. Enhanced peak growth of global vegetation and its key mechanisms. Nat. Ecol. Evol. 2018, 2, 1897–1905. [Google Scholar] [CrossRef]
- Gu, H.; Qiao, Y.; Xi, Z.; Rossi, S.; Smith, N.G.; Liu, J.; Chen, L. Warming-induced increase in carbon uptake is linked to earlier spring phenology in temperate and boreal forests. Nat. Commun. 2022, 13, 3698. [Google Scholar] [CrossRef] [PubMed]
- Peñuelas, J.; Rutishauser, T.; Filella, I. Phenology Feedbacks on Climate Change. Science 2009, 324, 887–888. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Mooney, H.; Larigauderie, A.; Cesario, M.; Elmquist, T.; Hoegh-Guldberg, O.; Lavorel, S.; Mace, G.M.; Palmer, M.; Scholes, R.; Yahara, T. Biodiversity, climate change, and ecosystem services. Curr. Opin. Environ. Sustain. 2009, 1, 46–54. [Google Scholar] [CrossRef]
- Tang, J.; Körner, C.; Muraoka, H.; Piao, S.; Shen, M.; Thackeray, S.J.; Yang, X. Emerging opportunities and challenges in phenology: A review. Ecosphere 2016, 7, e01436. [Google Scholar] [CrossRef]
- Kuenzer, C.; Dech, S.; Wagner, W. Remote Sensing Time Series Revealing Land Surface Dynamics: Status Quo and the Pathway Ahead. In Remote Sensing Time Series: Revealing Land Surface Dynamics; Kuenzer, C., Dech, S., Wagner, W., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–24. [Google Scholar] [CrossRef]
- Yang, J.; Gong, P.; Fu, R.; Zhang, M.; Chen, J.; Liang, S.; Xu, B.; Shi, J.; Dickinson, R. The role of satellite remote sensing in climate change studies. Nat. Clim. Chang. 2013, 3, 875–883. [Google Scholar] [CrossRef]
- Ehrlich, D.; Estes, J.E.; Singh, A. Applications of NOAA-AVHRR 1 km data for environmental monitoring. Int. J. Remote Sens. 1994, 15, 145–161. [Google Scholar] [CrossRef]
- Dech, S.; Holzwarth, S.; Asam, S.; Andresen, T.; Bachmann, M.; Boettcher, M.; Dietz, A.; Eisfelder, C.; Frey, C.; Gesell, G.; et al. Potential and Challenges of Harmonizing 40 Years of AVHRR Data: The TIMELINE Experience. Remote Sens. 2021, 13, 3618. [Google Scholar] [CrossRef]
- Holzwarth, S. TIMELINE DLR Website. Available online: www.timeline.dlr.de (accessed on 2 August 2022).
- Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G. A commentary review on the use of normalized difference vegetation index (NDVI) in the era of popular remote sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Third Symposium on Significant Results Obtained with ERTS-1; NASA SP-351; pp. 309–317. Available online: https://ntrs.nasa.gov/citations/19740022614 (accessed on 12 March 2023).
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Tucker, C.J.; Townshend, J.R.G.; Goff, T.E. African Land-Cover Classification Using Satellite Data. Science 1985, 227, 369–375. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Mueller, T.; Dressler, G.; Tucker, C.J.; Pinzon, J.E.; Leimgruber, P.; Dubayah, R.O.; Hurtt, G.C.; Böhning-Gaese, K.; Fagan, W.F. Human Land-Use Practices Lead to Global Long-Term Increases in Photosynthetic Capacity. Remote Sens. 2014, 6, 5717–5731. [Google Scholar] [CrossRef]
- Fensholt, R.; Rasmussen, K.; Kaspersen, P.; Huber, S.; Horion, S.; Swinnen, E. Assessing Land Degradation/Recovery in the African Sahel from Long-Term Earth Observation Based Primary Productivity and Precipitation Relationships. Remote Sens. 2013, 5, 664–686. [Google Scholar] [CrossRef]
- Atzberger, C.; Klisch, A.; Mattiuzzi, M.; Vuolo, F. Phenological Metrics Derived over the European Continent from NDVI3g Data and MODIS Time Series. Remote Sens. 2014, 6, 257–284. [Google Scholar] [CrossRef]
- Wang, J.; Dong, J.; Liu, J.; Huang, M.; Li, G.; Running, S.W.; Smith, W.K.; Harris, W.; Saigusa, N.; Kondo, H.; et al. Comparison of Gross Primary Productivity Derived from GIMMS NDVI3g, GIMMS, and MODIS in Southeast Asia. Remote Sens. 2014, 6, 2108–2133. [Google Scholar] [CrossRef]
- Dardel, C.; Kergoat, L.; Hiernaux, P.; Grippa, M.; Mougin, E.; Ciais, P.; Nguyen, C.-C. Rain-Use-Efficiency: What it Tells us about the Conflicting Sahel Greening and Sahelian Paradox. Remote Sens. 2014, 6, 3446–3474. [Google Scholar] [CrossRef]
- Stöckli, R.; Vidale, P.L. European plant phenology and climate as seen in a 20-year AVHRR land-surface parameter dataset. Int. J. Remote Sens. 2004, 25, 3303–3330. [Google Scholar] [CrossRef]
- Potter, C.S.; Klooster, S.; Brooks, V. Interannual Variability in Terrestrial Net Primary Production: Exploration of Trends and Controls on Regional to Global Scales. Ecosystems 1999, 2, 36–48. [Google Scholar] [CrossRef]
- Pedelty, J.; Devadiga, S.; Masuoka, E.; Brown, M.; Pinzon, J.; Tucker, C.; Vermote, E.; Prince, S.; Nagol, J.; Justice, C.; et al. Generating a Long-term Land Data Record from the AVHRR and MODIS Instruments. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1021–1025. [Google Scholar]
- Vermote, E.; NOAA CDR Program. NOAA Climate Data Record (CDR) of AVHRR Normalized Difference Vegetation Index (NDVI), Version 5; NOAA National Centers for Environmental Information: Washington, DC, USA, 2019. [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Pinzon, J.E.; Tucker, C.J. A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- LSA SAF. Normalized Difference Vegetation Index CDR Release 2—Metop; EUMETSAT SAF on Land Surface Analysis; 2021; Available online: https://navigator.eumetsat.int/product/EO:EUM:DAT:0385 (accessed on 12 March 2023).
- Trigo, I.F.; DaCamara, C.C.; Viterbo, P.; Roujean, J.-L.; Olesen, F.; Barroso, C.; Camacho-de Coca, F.; Carrer, D.; Freitas, S.C.; Garcí-a-Haro, J.; et al. The Satellite Application Facility on Land Surface Analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- Government of Canada. Corrected representation of the NDVI using historical AVHRR satellite images (1 km resolution) from 1987 to 2021. In Statistics Canada; Government of Canada: Ottawa, ON, Canada, 2021. [Google Scholar]
- Earth Resources Observation and Science (EROS) Center. USGS EROS Archive—AVHRR Normalized Difference Vegetation Index (NDVI) Composites. 2018. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-avhrr-normalized-difference-vegetation-index-ndvi-composites?qt-science_center_objects=0#qt-science_center_objects (accessed on 12 March 2023).
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Griffiths, P.; Nendel, C.; Hostert, P. Intra-annual reflectance composites from Sentinel-2 and Landsat for national-scale crop and land cover mapping. Remote Sens. Environ. 2019, 220, 135–151. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–155. [Google Scholar] [CrossRef]
- Cihlar, J.; Manak, D.; D’ Iorio, M. Evaluation of compositing algorithms for AVHRR data over land. IEEE Trans. Geosci. Remote Sens 1994, 32, 427–437. [Google Scholar] [CrossRef]
- Roy, D.P. Investigation of the maximum Normalized Difference Vegetation Index (NDVI) and the maximum surface temperature (Ts) AVHRR compositing procedures for the extraction of NDVI and Ts over forest. Int. J. Remote Sens. 1997, 18, 2383–2401. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Digirolamo, N.E.; Dorman, T.J. A comparison of reflectances and vegetation indices from three methods of compositing the AVHRR-GAC data over Northern Africa. Remote Sens. Rev. 1994, 10, 245–263. [Google Scholar] [CrossRef]
- Qiu, S.; Zhu, Z.; Olofsson, P.; Woodcock, C.E.; Jin, S. Evaluation of Landsat image compositing algorithms. Remote Sens. Environ. 2023, 285, 113375. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, P.; Feng, X.; Li, H.; Zhang, W.; Lin, J. Effective Compositing Method to Produce Cloud-Free AVHRR Image. IEEE GRSL 2014, 11, 328–332. [Google Scholar] [CrossRef]
- Chuvieco, E.; Ventura, G.; Martín, M.P. AVHRR multitemporal compositing techniques for burned land mapping. Int. J. Remote Sens. 2005, 26, 1013–1018. [Google Scholar] [CrossRef]
- Potapov, P.V.; Turubanova, S.A.; Hansen, M.C.; Adusei, B.; Broich, M.; Altstatt, A.; Mane, L.; Justice, C.O. Quantifying forest cover loss in Democratic Republic of the Congo, 2000–2010, with Landsat ETM+ data. Remote Sens. Environ. 2012, 122, 106–116. [Google Scholar] [CrossRef]
- Roberts, D.; Mueller, N.; Mcintyre, A. High-Dimensional Pixel Composites From Earth Observation Time Series. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6254–6264. [Google Scholar] [CrossRef]
- Flood, N. Seasonal Composite Landsat TM/ETM+ Images Using the Medoid (a Multi-Dimensional Median). Remote Sens. 2013, 5, 6481–6500. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Wolfe, R.E.; Roy, D.P.; Vermote, E. MODIS land data storage, gridding, and compositing methodology: Level 2 grid. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1324–1338. [Google Scholar] [CrossRef]
- Didan, K.; Munoz, A.B.; Solano, R.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series), Version 3.00, June 2015 (Collection 6); Vegetation Index and Phenology Lab, The University of Arizona: Tucson, AZ, USA, 2015. [Google Scholar]
- Pinzon, J.E.; Brown, M.E.; Tucker, C.J. EMD Correction of orbital drift artifacts in satellite data stream. In Hilbert-Huang Transform and Its Applications; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2005; pp. 167–186. [Google Scholar] [CrossRef]
- Swinnen, E.; Veroustraete, F. Extending the SPOT-VEGETATION NDVI Time Series (1998–2006) Back in Time With NOAA-AVHRR Data (1985–1998) for Southern Africa. IEEE Trans. Geosci. Remote Sens. 2008, 46, 558–572. [Google Scholar] [CrossRef]
- Matsuoka, M.; Kajiwara, K.; Hashimoto, T.; Honda, Y. Composite Method over Land for NOAA/AVHRR GAC Global Data Set. J. Jpn. Soc. Photogramm. Remote Sens. 2001, 40, 6–14. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Kline, K.; Scaramuzza, P.L.; Kovalskyy, V.; Hansen, M.; Loveland, T.R.; Vermote, E.; Zhang, C. Web-enabled Landsat Data (WELD): Landsat ETM+ composited mosaics of the conterminous United States. Remote Sens. Environ. 2010, 114, 35–49. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Hobart, G.W.; Luther, J.E.; Hermosilla, T.; Griffiths, P.; Coops, N.C.; Hall, R.J.; Hostert, P.; Dyk, A.; et al. Pixel-Based Image Compositing for Large-Area Dense Time Series Applications and Science. Can. J. Remote Sens. 2014, 40, 192–212. [Google Scholar] [CrossRef]
- Griffiths, P.; van der Linden, S.; Kuemmerle, T.; Hostert, P. A Pixel-Based Landsat Compositing Algorithm for Large Area Land Cover Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2088–2101. [Google Scholar] [CrossRef]
- Frantz, D.; Röder, A.; Stellmes, M.; Hill, J. Phenology-adaptive pixel-based compositing using optical earth observation imagery. Remote Sens. Environ. 2017, 190, 331–347. [Google Scholar] [CrossRef]
- Latifovic, R.; Trishchenko, A.P.; Chen, J.; Park, W.B.; Khlopenkov, K.V.; Fernandes, R.; Pouliot, D.; Ungureanu, C.; Luo, Y.; Wang, S.; et al. Generating historical AVHRR 1 km baseline satellite data records over Canada suitable for climate change studies. Can. J. Remote Sens. 2005, 31, 324–346. [Google Scholar] [CrossRef]
- Vancutsem, C.; Pekel, J.F.; Bogaert, P.; Defourny, P. Mean Compositing, an alternative strategy for producing temporal syntheses. Concepts and performance assessment for SPOT VEGETATION time series. Int. J. Remote Sens. 2007, 28, 5123–5141. [Google Scholar] [CrossRef]
- Rogge, D.; Bauer, A.; Zeidler, J.; Mueller, A.; Esch, T.; Heiden, U. Building an exposed soil composite processor (SCMaP) for mapping spatial and temporal characteristics of soils with Landsat imagery (1984–2014). Remote Sens. Environ. 2018, 205, 1–17. [Google Scholar] [CrossRef]
- Hagolle, O.; Morin, D.; Kadiri, M. Detailed Processing Model for the Weighted Average Synthesis Processor (WASP) for Sentinel-2 (1.4). 2018. Available online: https://zenodo.org/record/1401360 (accessed on 12 March 2023).
- Zhu, Z.; Woodcock, C.E.; Holden, C.; Yang, Z. Generating synthetic Landsat images based on all available Landsat data: Predicting Landsat surface reflectance at any given time. Remote Sens. Environ. 2015, 162, 67–83. [Google Scholar] [CrossRef]
- Vuolo, F.; Ng, W.-T.; Atzberger, C. Smoothing and gap-filling of high resolution multi-spectral time series: Example of Landsat data. Int. J. Appl. Earth. Obs. Geoinf. 2017, 57, 202–213. [Google Scholar] [CrossRef]
- Chen, P.Y.; Srinivasan, R.; Fedosejevs, G.; Kiniry, J.R. Evaluating different NDVI composite techniques using NOAA-14 AVHRR data. Int. J. Remote Sens. 2003, 24, 3403–3412. [Google Scholar] [CrossRef]
- Bicheron, P.; Leroy, M. Bidirectional reflectance distribution function signatures of major biomes observed from space. J. Geophys. Res. 2000, 105, 26669–26681. [Google Scholar] [CrossRef]
- Roy, D.P.; Lewis, P.; Schaaf, C.; Devadiga, S.; Boschetti, L. The Global Impact of Clouds on the Production of MODIS Bidirectional Reflectance Model-Based Composites for Terrestrial Monitoring. IEEE GRSL 2006, 3, 452–456. [Google Scholar] [CrossRef]
- Gao, F.; Jin, Y.; Schaaf, C.B.; Strahler, A.H. Bidirectional NDVI and atmospherically resistant BRDF inversion for vegetation canopy. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1269–1278. [Google Scholar] [CrossRef]
- Goward, S.N.; Markham, B.; Dye, D.G.; Dulaney, W.; Yang, J. Normalized difference vegetation index measurements from the advanced very high resolution radiometer. Remote Sens. Environ. 1991, 35, 257–277. [Google Scholar] [CrossRef]
- Steven, M.D.; Malthus, T.J.; Baret, F.; Xu, H.; Chopping, M.J. Intercalibration of vegetation indices from different sensor systems. Remote Sens. Environ. 2003, 88, 412–422. [Google Scholar] [CrossRef]
- Bachmann, M.; Tungalagsaikhan, P.; Ruppert, T.; Dech, S. Calibration and Pre-processing of a Multi-decadal AVHRR Time Series. In Remote Sensing Time Series: Revealing Land Surface Dynamics; Kuenzer, C., Dech, S., Wagner, W., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 43–74. [Google Scholar] [CrossRef]
- Ji, L.; Brown, J.F. Effect of NOAA satellite orbital drift on AVHRR-derived phenological metrics. Int. J. Appl. Earth. Obs. Geoinf. 2017, 62, 215–223. [Google Scholar] [CrossRef]
- McGregor, J.; Gorman, A.J. Some considerations for using AVHRR data in climatological studies: I. Orbital characteristics of NOAA satellites. Int. J. Remote Sens. 1994, 15, 537–548. [Google Scholar] [CrossRef]
- Gutman, G.; Masek, J.G. Long-term time series of the Earth’s land-surface observations from space. Int. J. Remote Sens. 2012, 33, 4700–4719. [Google Scholar] [CrossRef]
- Kern, A.; Marjanović, H.; Barcza, Z. Evaluation of the Quality of NDVI3g Dataset against Collection 6 MODIS NDVI in Central Europe between 2000 and 2013. Remote Sens. 2016, 8, 955. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Bohn, U.; Zazanashvili, N.; Nakhutsrishvili, G.; Ketskhoveli, N. The Map of the Natural Vegetation of Europe and its application in the Caucasus Ecoregion. Bull. Georgian Natl. Acad. Sci. 2007, 175, 112–121. [Google Scholar]
- ICOS. Standardised Greenhouse Gas Measurements throughout Europe. Available online: https://www.icos-cp.eu/ (accessed on 20 January 2023).
- Pisek, J.; Erb, A.; Korhonen, L.; Biermann, T.; Carrara, A.; Cremonese, E.; Cuntz, M.; Fares, S.; Gerosa, G.; Grünwald, T.; et al. Retrieval and validation of forest background reflectivity from daily Moderate Resolution Imaging Spectroradiometer (MODIS) bidirectional reflectance distribution function (BRDF) data across European forests. Biogeosciences 2021, 18, 621–635. [Google Scholar] [CrossRef]
- CEOS Cal/Val Portal. PICS: Pseudo-Invariant Calibration Sites. Available online: https://calvalportal.ceos.org/pics_sites (accessed on 20 January 2023).
- CEOS Cal/Val Portal. LANDNET SITES (CEOS Reference Sites). Available online: https://calvalportal.ceos.org/ceos-landnet-sites (accessed on 20 January 2023).
- GHG Europe Database. GHG Europe Database. Available online: http://gaia.agraria.unitus.it/ghg-europe (accessed on 20 January 2023).
- National Physical Laboratory, U.o.S.; EOLab. Fiducial Reference Measurements for Vegetation. Available online: https://frm4veg.org/ (accessed on 20 January 2023).
- Forschungszentrum Jülich. TERENO Northeastern Lowland Observatory Test Sites. Available online: https://www.tereno.net/joomla/index.php/observatories/northeast-german-lowland-observatory/test-sites (accessed on 20 January 2023).
- Davidson, A. Joint Experiment for Crop Assessment and Monitoring (JECAM), Germany-DEMMIN. Available online: http://jecam.org/studysite/germany-demmin/ (accessed on 20 January 2023).
- Koslowsky, D. Mehrjährige Validierte und Homogenisierte Reihen des Reflexionsgrades und des Vegetationsindexes von Landoberflächen aus Täglichen AVHRR-Daten Hoher Auflösung. Ph.D. Thesis, Freie Universität Berlin, Berlin, Germany, 1996. [Google Scholar]
- Defourny, P.; Kirches, G.; Militzer, J.; Boettcher, M.; Brockmann, C.; Bontemps, S. Land Cover CCI Product ValidationAnd Intercomparison Report v2; UCL-Geomatics: Louvain-la-Neuve, Belgium, 2017; p. 374. [Google Scholar]
- Cuntz, M.; Aiguier, T.; Courtois, P.; Joetzjer, E.; Lily, J. Hesse ICOS Station. Available online: https://meta.icos-cp.eu/resources/stations/ES_FR-Hes (accessed on 20 January 2023).
- Kidwell, K.B. NOAA Polar Orbiter Data Users Guide: (TIROS-N, NOAA-6, NOAA-7, NOAA-8, NOAA-9, NOAA-10, NOAA-11, NOAA-12, NOAA-13, and NOAA-14); National Oceanic and Atmospheric Administration, and National Climatic Data Center (U.S.), Satellite Data Services Division: Washington, DC, USA, 1995.
- Robel, J.; Graumann, A. NOAA KLM User’s Guide with NOAA-N, N Prime, and MetOp Supplements; National Oceanic and Atmospheric Administration, National Environmental Satellite, Data, and Information Service National Climatic Data Center, Remote Sensing and Applications Division: Washington, DC, USA, 2014.
- Molch, K.; Leone, R.; Frey, C.; Wolfmüller, M.; Tungalagsaikhan, P. NOAA AVHRR Data Curation and Reprocessing—TIMELINE. In Proceedings of the Big Data from Space (BiDS’ 2013), Frascati, Italy, 5–7 June 2013. [Google Scholar]
- Trishchenko, A.P. Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors: Extension to AVHRR NOAA-17, 18 and METOP-A. Remote Sens. Environ. 2009, 113, 335–341. [Google Scholar] [CrossRef]
- Molling, C.C.; Heidinger, A.K.; Straka, W.C.; Wu, X. Calibrations for AVHRR channels 1 and 2: Review and path towards consensus. Int. J. Remote Sens. 2010, 31, 6519–6540. [Google Scholar] [CrossRef]
- Santamaria-Artigas, A.; Vermote, E.F.; Franch, B.; Roger, J.-C.; Skakun, S. Evaluation of the AVHRR surface reflectance long term data record between 1984 and 2011. Int. J. Appl. Earth. Obs. Geoinf. 2021, 98, 102317. [Google Scholar] [CrossRef]
- Dietz, A.J.; Frey, C.M.; Ruppert, T.; Bachmann, M.; Kuenzer, C.; Dech, S. Automated Improvement of Geolocation Accuracy in AVHRR Data Using a Two-Step Chip Matching Approach—A Part of the TIMELINE Preprocessor. Remote Sens. 2017, 9, 303. [Google Scholar] [CrossRef]
- Bachmann, M.; Müller, T. Using spaceborne hyperspectral data for spectral cross-calibration of multispectral sensors. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2813–2815. [Google Scholar]
- Dietz, A.J.; Klein, I.; Gessner, U.; Frey, C.M.; Kuenzer, C.; Dech, S. Detection of Water Bodies from AVHRR Data—A TIMELINE Thematic Processor. Remote Sens. 2017, 9, 57. [Google Scholar] [CrossRef]
- Kriebel, K.T.; Gesell, G.; Kastner, M.; Mannstein, H. The cloud analysis tool APOLLO: Improvements and validations. Int. J. Remote Sens. 2003, 24, 2389–2408. [Google Scholar] [CrossRef]
- Kriebel, K.T.; Saunders, R.W.; Gesell, G. Optical Properties of Clouds Derived from Fully Cloudy AVHRR Pixels. Beiträge zur Physik der Atmosphäre 1989, 62, 165–171. [Google Scholar]
- Saunders, R.W.; Kriebel, K.T. An improved method for detecting clear sky and cloudy radiances from AVHRR data. Int. J. Remote Sens. 1988, 9, 123–150. [Google Scholar] [CrossRef]
- Klüser, L.; Killius, N.; Gesell, G. APOLLO_NG—A probabilistic interpretation of the APOLLO legacy for AVHRR heritage channels. Atmos. Meas. Tech. 2015, 8, 4155–4170. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Shettle, E.P. Modtran® 5.2.0.0 User’s Manual; Air Force Research Laboratory, Space Vehicles Directorate, Air Force Materiel Command Hanscom AFB: Burlington, MA, USA, 2008. [Google Scholar]
- NASA. About MODIS. Available online: https://modis.gsfc.nasa.gov/about/ (accessed on 15 November 2022).
- NASA. MODIS Specifications. Available online: https://modis.gsfc.nasa.gov/about/specifications.php (accessed on 15 November 2022).
- Didan, K. MODIS/Terra Vegetation Indices 16-Day L3 Global 1 km SIN Grid V061 [Data Set]. NASA EOSDIS Land Processes DAAC. Available online: https://lpdaac.usgs.gov/products/mod13a2v061/ (accessed on 15 November 2022).
- Didan, K. MODIS/Terra Vegetation Indices Monthly L3 Global 1 km SIN Grid V061 [Data Set]. NASA EOSDIS Land Processes DAAC. Available online: https://lpdaac.usgs.gov/products/mod13a3v061/ (accessed on 15 November 2022).
- Didan, K. Status for: Vegetation Indices (MOD13). Available online: https://modis-land.gsfc.nasa.gov/ValStatus.php?ProductID=MOD13 (accessed on 3 March 2023).
- Huete, A.; Justice, C.; van Leeuwen, W.J.D.; Jacobson, A.; Solanos, R.; Laing, T.D. MODIS VEGETATION INDEX (MOD 13) Algorithm Theoretucal Basis Document, Version 3; Vegetation Index and Phenology Lab.: Tucson, AZ, USA, 1999. [Google Scholar]
- NASA; EOSDIS; LAADS; DAAC. Long-Term Data Record. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/applications/ltdr/#project-documentation (accessed on 6 March 2023).
- Vermote, E. AVHRR Surface Reflectance and Normalized Difference Vegetation Index—Climate Algorithm Theoretical Basis Document, NOAA Climate Data Record Program CDRP-ATBD-0459 Revsion 2; NOAA Central Library: Washington, DC, USA, 2018. Available online: https://www.ncei.noaa.gov/pub/data/sds/cdr/CDRs/Normalized_Difference_Vegetation_Index/AVHRR/AlgorithmDescriptionAVHRR_01B-20b.pdf (accessed on 12 March 2023).
- Cihlar, J.; Ly, H.; Li, Z.; Chen, J.; Pokrant, H.; Huang, F. Multitemporal, multichannel AVHRR data sets for land biosphere studies—Artifacts and corrections. Remote Sens. Environ. 1997, 60, 35–57. [Google Scholar] [CrossRef]
- Gutman, G.G. Vegetation indices from AVHRR: An update and future prospects. Remote Sens. Environ. 1991, 35, 121–136. [Google Scholar] [CrossRef]
- Kimes, D.S. Dynamics of directional reflectance factor distributions for vegetation canopies. Appl. Opt. 1983, 22, 1364–1372. [Google Scholar] [CrossRef]
- Cihlar, J.; Huang, F. Effect of atmospheric correction and viewing angle restriction on AVHRR data composites. Can. J. Remote Sens. 1994, 20, 132–137. [Google Scholar]
- van Leeuwen, W.J.D.; Huete, A.R.; Laing, T.W. MODIS Vegetation Index Compositing Approach: A Prototype with AVHRR Data. Remote Sens. Environ. 1999, 69, 264–280. [Google Scholar] [CrossRef]
- Meyer, D.; Verstraete, M.; Pinty, B. The effect of surface anisotropy and viewing geometry on the estimation of NDVI from AVHRR. Remote Sens. Rev. 1995, 12, 3–27. [Google Scholar] [CrossRef]
- Vermote, E.F.; Saleous, N.Z. Calibration of NOAA16 AVHRR over a desert site using MODIS data. Remote Sens. Environ. 2006, 105, 214–220. [Google Scholar] [CrossRef]



| Approach | Abbreviation | Score Formula | Logic |
|---|---|---|---|
| Single Variable Compositing | |||
| With NDVI | |||
| Maximum Value Compositing | MVC | Established approach: reduces disturbing influences as clouds, snow, and aerosols typically reduce NDVI. | |
| Median | MED | Reduces signal attenuating and saturation effects alike. | |
| Without NDVI | |||
| Satellite Zenith Angle | Sa | Satellite zenith of 0° (nadir view) is considered best. | |
| Sun Zenith Angle | Su | Illumination of 45° is considered best. | |
| Relative Azimuth Angle | Az | Relative azimuth angle of 0° is considered best. | |
| Uncertainty | Uc | A low uncertainty associated with band 1 + 2 reflectance is considered best. | |
| Multiple Variables Compositing | |||
| Scoring Compositing | |||
| With NDVI | |||
| NDVI 50% Angles 25% Uncertainty 25% | NAUc | Half of the weight for score calculation given to NDVI, and ¼ of weight to acquisition angles and uncertainty each. | |
| NDVI 33% Angles 33% Uncertainty 33% | NAUc_33 | One third of the weight given to angles, uncertainty, and NDVI. | |
| Angles 66% NDVI 33% | AN | Without uncertainty, 2/3 of weight given to angles, and 1/3 of weight to NDVI. | |
| Without NDVI | |||
| Su 40% and Sa 40% Az 20% | SuSaAz | Without uncertainty, 1/5 of weight given to relative azimuth, and 2/5 to each zenith angle. | |
| Su 25%, Sa 25%, and Az 25% Uncertainty 25% | SuSaAzUc | Give equal weight to each angle and to uncertainty. | |
| Angles 50% Uncertainty 50% | AUc | Give half of the weight to angles and to uncertainty each. | |
| Stepwise Compositing | |||
| MODIS Algorithm | MOD | Established approach used in the standard MODIS product: used for comparison as a benchmark. | |
| Criteria | Value Distribution | Spatial Consistency | Spatial Match to MODIS | Time Series Consistency | Time Series Match to MODIS | Neighborhood | |
|---|---|---|---|---|---|---|---|
| Approach | |||||||
| MVC | -- | - | -- | - | -- | - | |
| MED | + | ++ | + | + | + | - | |
| Sa | ++ | -- | ++ | - | ++ | ++ | |
| Su | + | - | + | -- | - | ++ | |
| Az | + | -- | + | - | + | ++ | |
| Uc | ++ | - | - | + | - | + | |
| NAUc | - | + | -- | -- | -- | - | |
| AN | + | + | - | + | - | + | |
| SuSaAzUc | ++ | -- | ++ | - | ++ | ++ | |
| AUc | ++ | -- | ++ | - | ++ | ++ | |
| MOD | - | - | -- | -- | -- | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asam, S.; Eisfelder, C.; Hirner, A.; Reiners, P.; Holzwarth, S.; Bachmann, M. AVHRR NDVI Compositing Method Comparison and Generation of Multi-Decadal Time Series—A TIMELINE Thematic Processor. Remote Sens. 2023, 15, 1631. https://doi.org/10.3390/rs15061631
Asam S, Eisfelder C, Hirner A, Reiners P, Holzwarth S, Bachmann M. AVHRR NDVI Compositing Method Comparison and Generation of Multi-Decadal Time Series—A TIMELINE Thematic Processor. Remote Sensing. 2023; 15(6):1631. https://doi.org/10.3390/rs15061631
Chicago/Turabian StyleAsam, Sarah, Christina Eisfelder, Andreas Hirner, Philipp Reiners, Stefanie Holzwarth, and Martin Bachmann. 2023. "AVHRR NDVI Compositing Method Comparison and Generation of Multi-Decadal Time Series—A TIMELINE Thematic Processor" Remote Sensing 15, no. 6: 1631. https://doi.org/10.3390/rs15061631
APA StyleAsam, S., Eisfelder, C., Hirner, A., Reiners, P., Holzwarth, S., & Bachmann, M. (2023). AVHRR NDVI Compositing Method Comparison and Generation of Multi-Decadal Time Series—A TIMELINE Thematic Processor. Remote Sensing, 15(6), 1631. https://doi.org/10.3390/rs15061631





