Optimization of Multi-Mission CubeSat Constellations with a Multi-Objective Genetic Algorithm
Abstract
1. Introduction
2. Mission Design
2.1. CubeSat Design
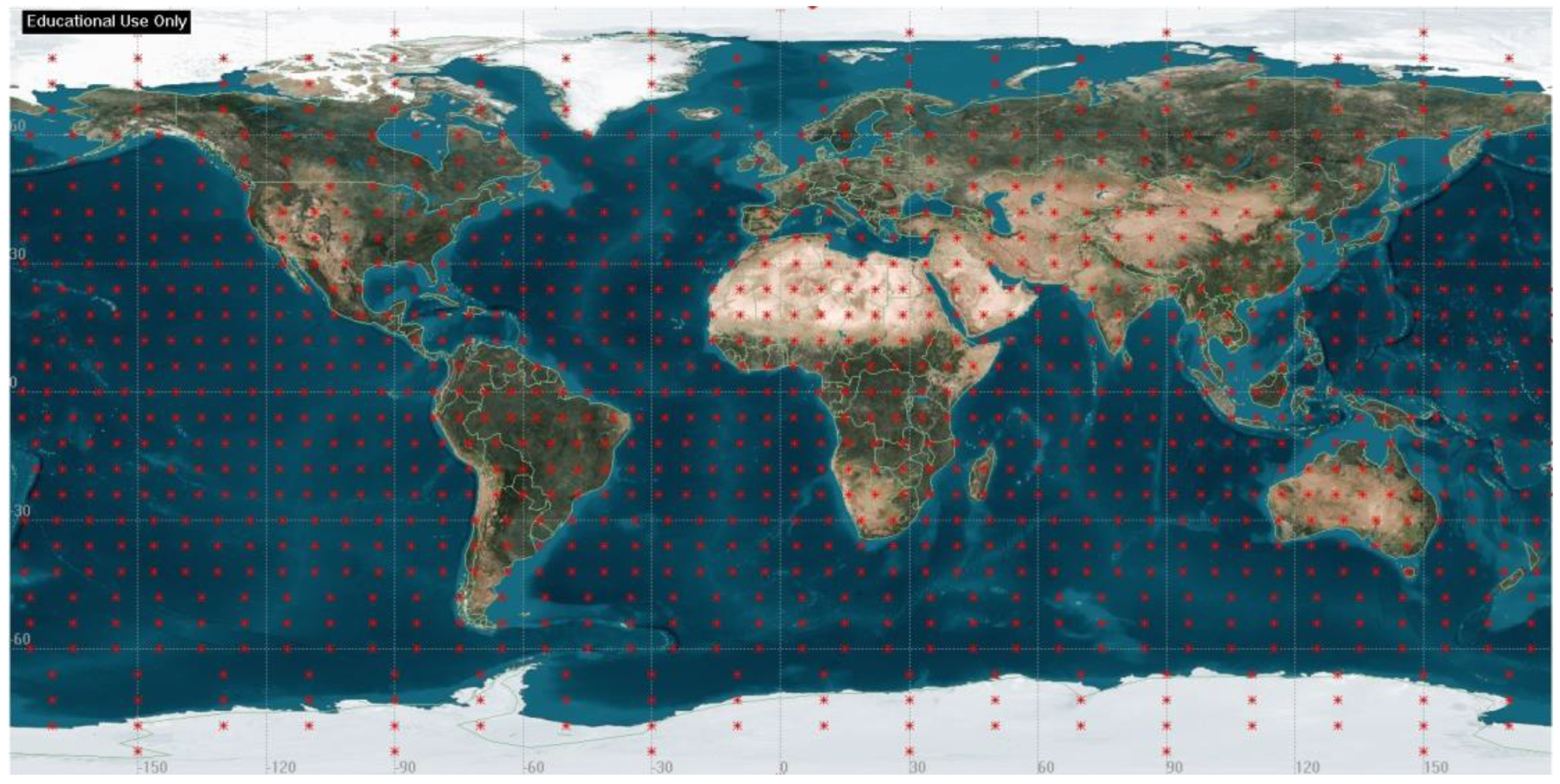
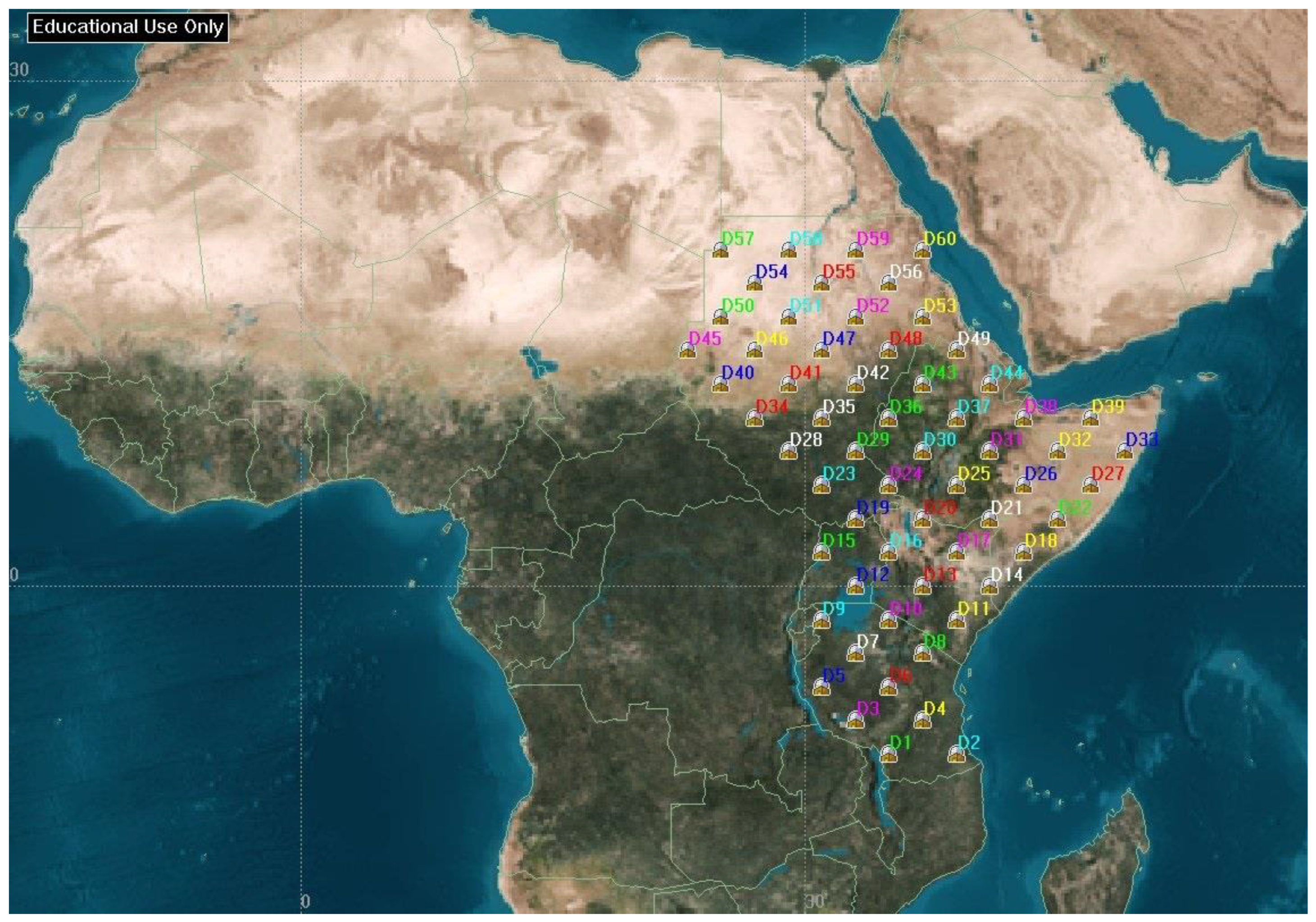
2.2. Target Areas
2.3. Constellation Design
3. Problem and Optimization Formulation
3.1. Problem Statement
3.2. Objective Functions Formulation
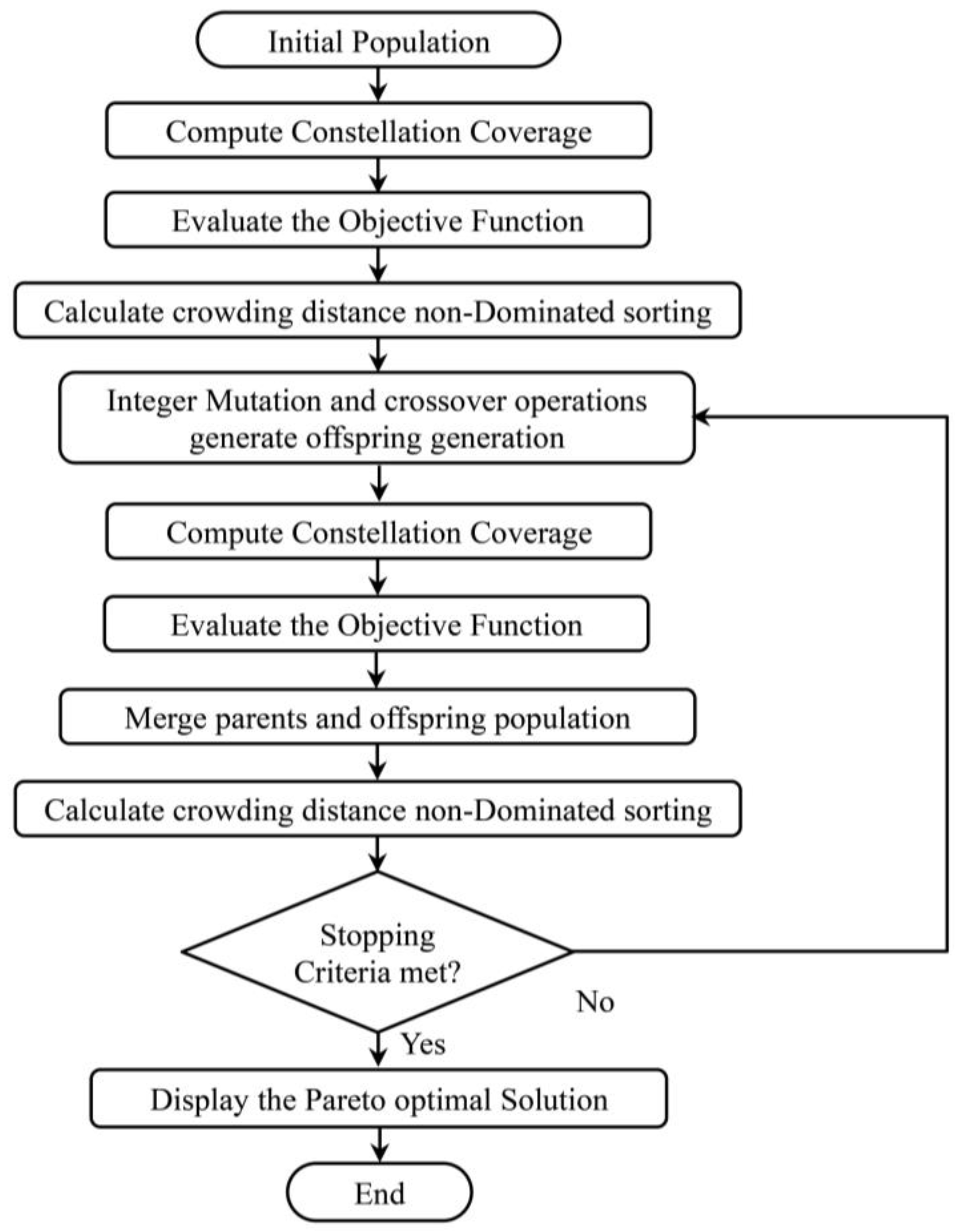
3.3. Multi-Objective Genetic Algorithm
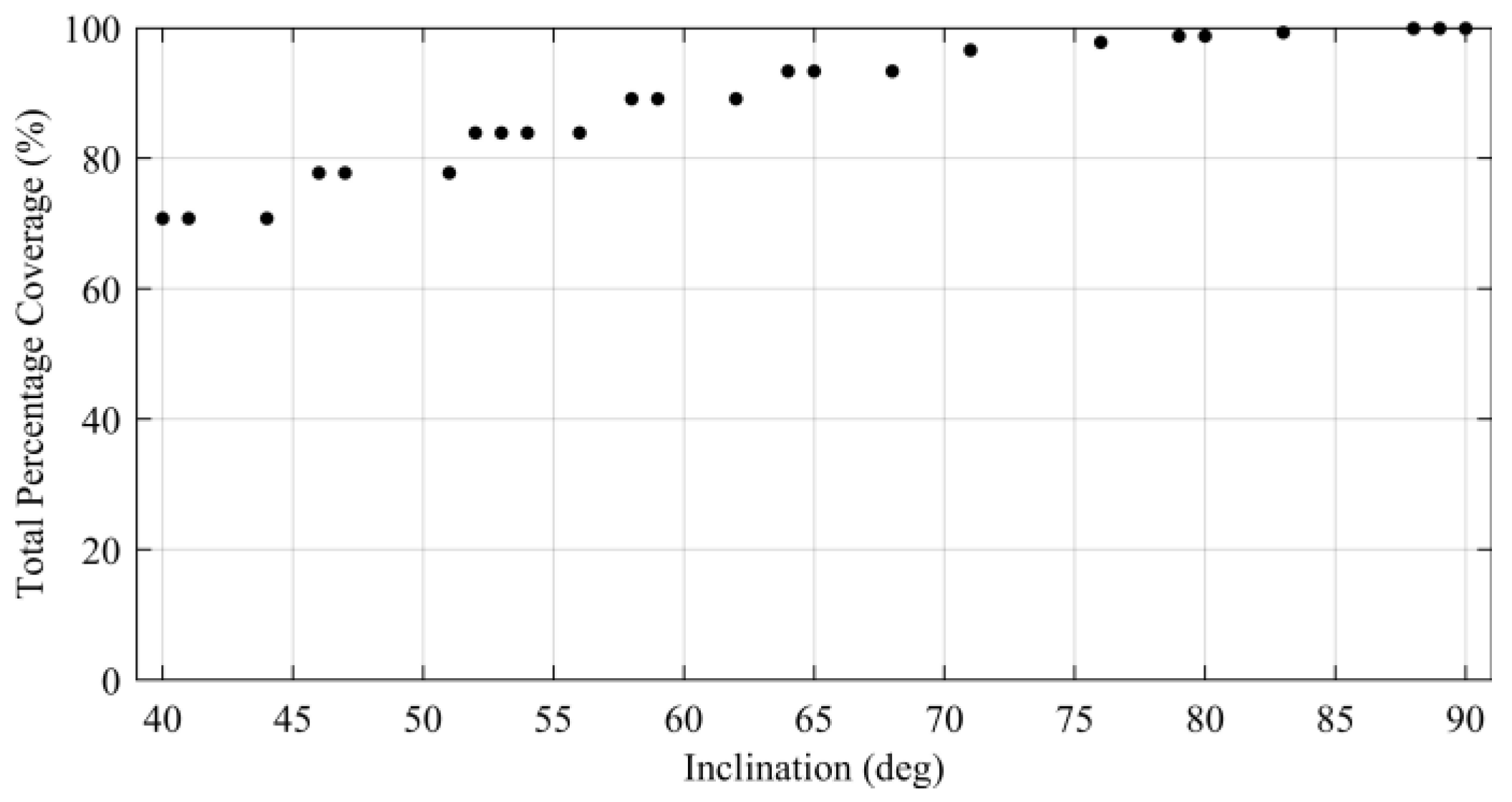
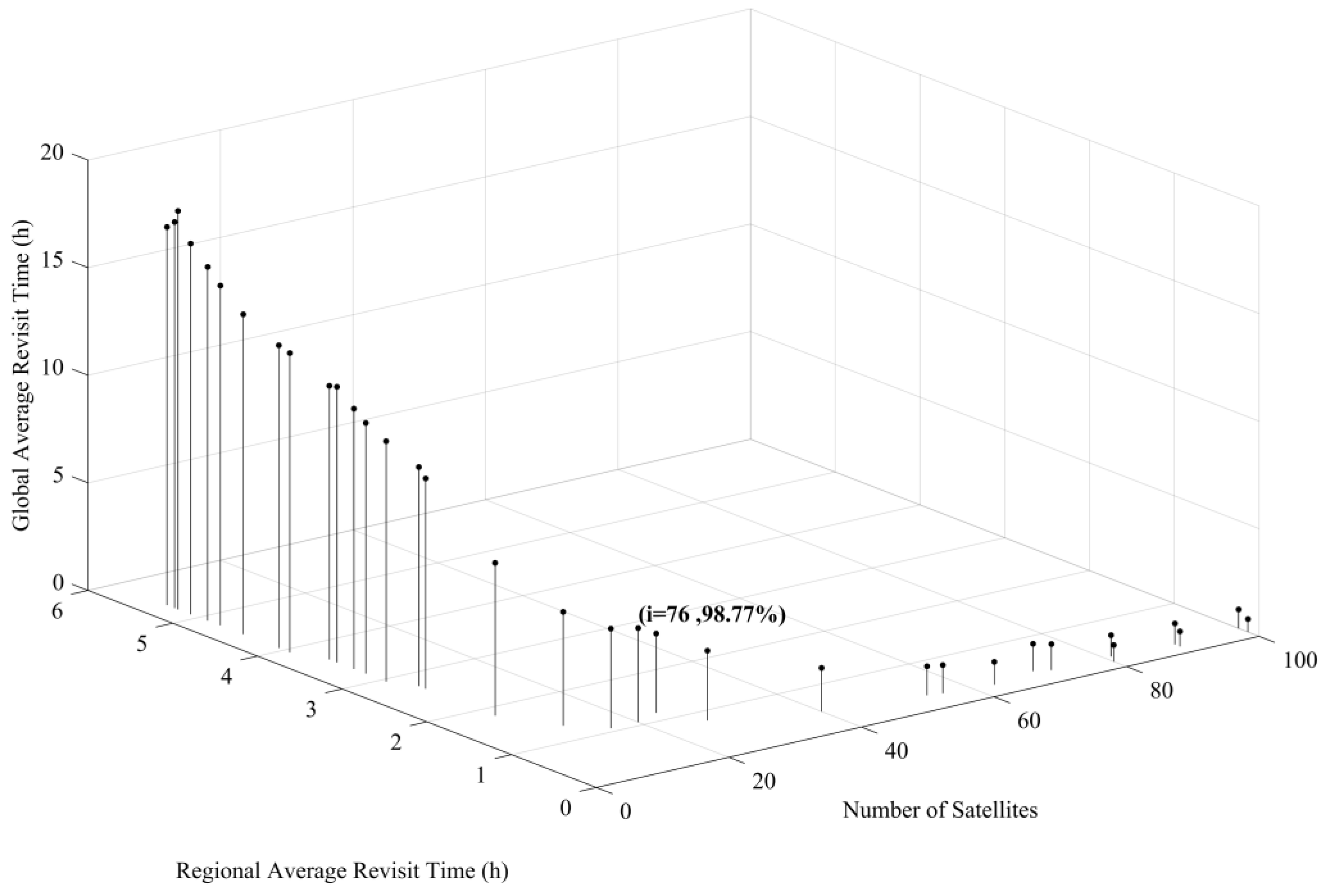
4. Simulation Results and Discussion
4.1. Simulation Setup
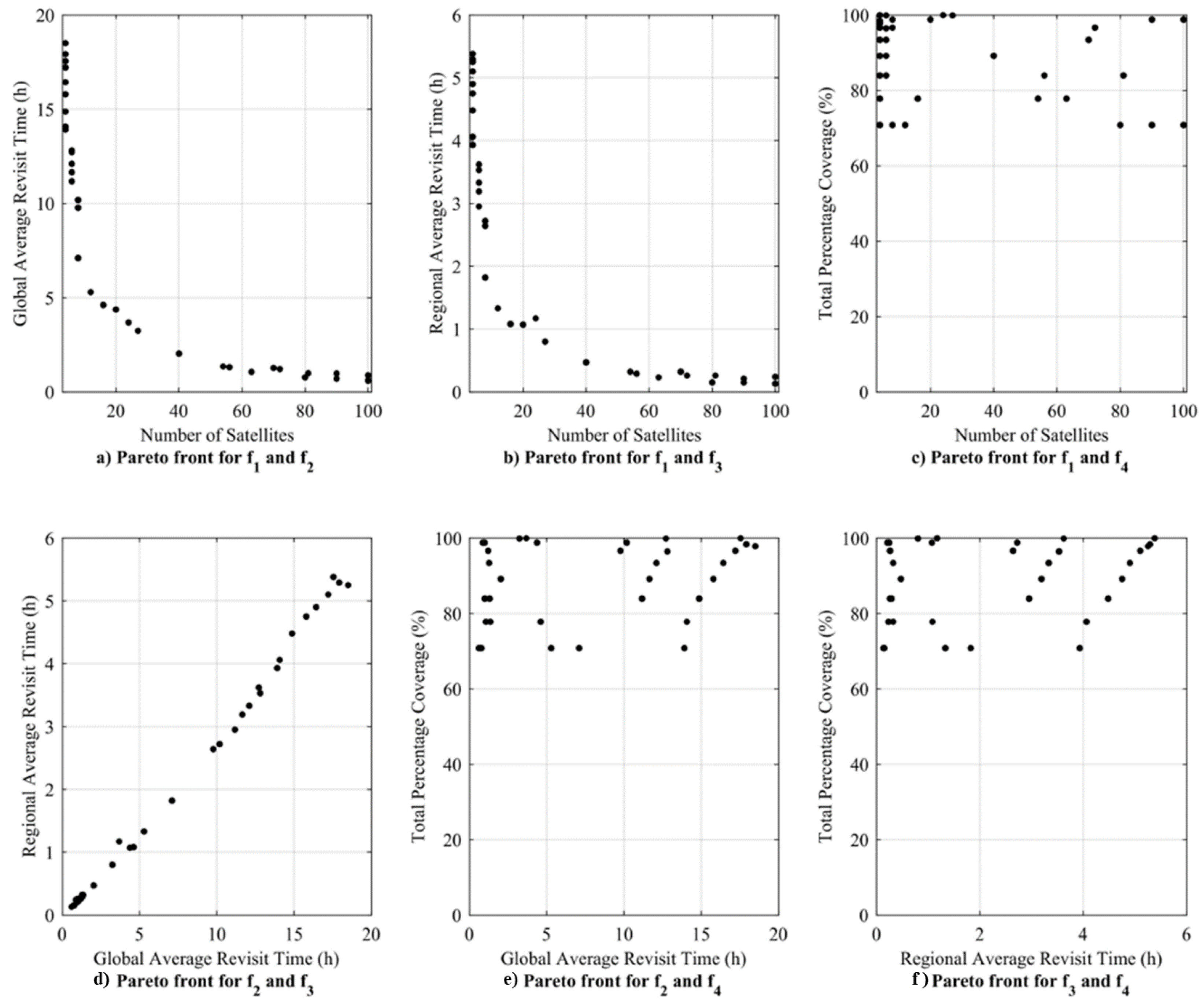
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lazreg, N.; Ben Bahri, O.; Besbes, K. Analysis and design of Cubesat constellation for the Mediterranean south costal monitoring against illegal immigration. Adv. Sp. Res. 2018, 61, 1017–1024. [Google Scholar] [CrossRef]
- Cappelletti, C.; Robson, D. 2—CubeSat Missions and Applications. In Cubesat Handbook; Cappelletti, C., Battistini, S., Malphrus, B.K., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 53–65. [Google Scholar] [CrossRef]
- Villela, T.; Costa, C.A.; Brandão, A.M.; Bueno, F.T.; Leonardi, R. Towards the Thousandth CubeSat: A Statistical Overview. Int. J. Aerosp. Eng. 2019, 2019, 5063145. [Google Scholar] [CrossRef]
- Buzzi, P.G.; Selva, D.; Hitomi, N.; Blackwell, W.J. Assessment of Constellation Designs for Earth Observation: Application to the TROPICS Mission. Acta Astronaut. 2019, 161, 166–182. [Google Scholar] [CrossRef]
- Wu, S.; Chen, W.; Cao, C.; Zhang, C.; Mu, Z. A Multiple-CubeSat Constellation for Integrated Earth Observation and Marine/Air Traffic Monitoring. Adv. Sp. Res. 2021, 67, 3712–3724. [Google Scholar] [CrossRef]
- Saeed, N.; Elzanaty, A.; Almorad, H.; Dahrouj, H.; Al-Naffouri, T.Y.; Alouini, M.-S. CubeSat Communications: Recent Advances and Future Challenges. IEEE Commun. Surv. Tut. 2020, 22, 1839–1862. [Google Scholar] [CrossRef]
- Santilli, G.; Vendittozzi, C.; Cappelletti, C.; Battistini, S.; Gessini, P. CubeSat constellations for disaster management in remote areas. Acta Astronaut. 2018, 145, 11–17. [Google Scholar] [CrossRef]
- Chadalavada, P.; Dutta, A. Regional CubeSat Constellation Design to Monitor Hurricanes. IEEE Trans. Geosci. Remote 2022, 60, 1–8. [Google Scholar] [CrossRef]
- Goncharenko, Y.v.; Berg, W.; Reising, S.C.; Iturbide-Sanchez, F.; Chandrasekar, V. Design and Analysis of CubeSat Microwave Radiometer Constellations to Observe Temporal Variability of the Atmosphere. IEEE J. Sel. Top. Appl. Earth. Obs. Remote Sens. 2021, 14, 11728–11736. [Google Scholar] [CrossRef]
- Meziane-Tani, I.; Métris, G.; Lion, G.; Deschamps, A.; Bendimerad, F.T.; Bekhti, M. Optimization of small satellite constellation design for continuous mutual regional coverage with multi-objective genetic algorithm. Int. J. Comput. Intell. Syst. 2016, 9, 627–637. [Google Scholar] [CrossRef]
- Han, Y.; Wang, L.; Fu, W.; Zhou, H.; Li, T.; Xu, B.; Chen, R. LEO Navigation Augmentation Constellation Design with the Multi-Objective Optimization Approaches. Chinese J. Aeronaut. 2021, 34, 265–278. [Google Scholar] [CrossRef]
- Yan, D.; Liu, C.; You, P.; Shaowei, Y. Multi-objective optimization design of extended Walker constellation for global coverage services. In Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14–17 October 2016; pp. 1309–1313. [Google Scholar] [CrossRef]
- Poghosyan, A.; Golkar, A. CubeSat evolution: Analyzing CubeSat capabilities for conducting science missions. Prog. Aerosp. Sci. 2017, 88, 59–83. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Zhu, P.; Guo, J. Star of AOXiang: An innovative 12U CubeSat to demonstrate polarized light navigation and microgravity measurement. Acta Astronaut. 2018, 147, 97–106. [Google Scholar] [CrossRef]
- Guzmán, R.; López, R.; Ocerin Martínez, E.; Davis, S.; Hernani, J.T.; Brennan-Craddock, R.; Kellerman, N.; Pastena, M.; Melega, N.; Mariani, F. A compact multispectral imager for the MANTIS mission 12U CubeSat. In Proceedings of the CubeSats and SmallSats for Remote Sensing IV; Norton, C.D., Pagano, T.S., Babu, S.R., Eds.; SPIE: Bellingham, DC, USA, 2020; p. 5. [Google Scholar]
- IFRC World Disasters Report—Leaving No One Behind; International Federation of Red Cross and Red Crescent Societies: Geneva, Switzerland, 2018; ISBN 9782970128908.
- Cornara, S.; Beech, T.W.; Belló-Mora, M.; Janin, G. Satellite constellation mission analysis and design. Acta Astronaut. 2001, 48, 681–691. [Google Scholar] [CrossRef]
- Ma, D.M.; Hong, Z.C.; Lee, T.H.; Chang, B.J. Design of a micro-satellite constellation for communication. Acta Astronaut. 2013, 82, 54–59. [Google Scholar] [CrossRef]
- Whittecar, W.R.; Ferringer, M.P. Global coverage constellation design exploration using evolutionary algorithms. AIAA/AAS Astrodyn. Spec. Conf. 2014, 2014, 1–20. [Google Scholar] [CrossRef]
- Kak, A.; Akyildiz, I.F. Designing Large-Scale Constellations for the Internet of Space Things With CubeSats. IEEE Internet Things J. 2021, 8, 1749–1768. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ferringer, M.P.; Spencer, D.B. Satellite constellation design tradeoffs using multiple-objective evolutionary computation. J. Spacecr. Rockets 2006, 43, 1404–1411. [Google Scholar] [CrossRef]
- Savitri, T.; Kim, Y.; Jo, S.; Bang, H. Satellite Constellation Orbit Design Optimization with Combined Genetic Algorithm and Semianalytical Approach. Int. J. Aerosp. Eng. 2017, 2017, 1235692. [Google Scholar] [CrossRef]
- Pu, M.; Wang, J.; Zhang, D.; Jia, Q.; Shao, X. Optimal small satellite orbit design based on robust multi-objective optimization method. Aerosp. Sci. Technol. 2017, 70, 339–350. [Google Scholar] [CrossRef]
- Vallado, D.A.; MacClain, W.D. Fundamentals of Astrodynamics and Applications; Kluwer Academic Publishers: New York, NY, USA, 2001. [Google Scholar]
- Bate, R.R.; Mueller, D.D.; White, J.E. Fundamentals of Astrodynamics; Dover Publications: Mineola, NY, USA, 1971. [Google Scholar]
- Wekerle, T.; Pessoa Filho, J.B.; da Costa, L.E.V.L.; Trabasso, L.G. Status and Trends of Smallsats and Their Launch Vehicles—An Up-to-Date Review. J. Aerosp. Technol. Manag. 2017, 9, 269–286. [Google Scholar] [CrossRef]



| Subsystem | Description |
|---|---|
| Structure | Mass: 24 kg |
| Size: 226mm × 226mm × 340mm | |
| ADCS | High performance up to 0.01° pointing accuracy |
| Power | 90 Wh |
| Communication | S-Band: 1 Mbps |
| X-Band: 150 Mbps | |
| Payload | EOC: Conic sensor FOV angle of 30° |
| UHF receiver: COTS dipole antenna at 436 MHz |
| Optimization Parameter | Range | Unit | |
|---|---|---|---|
| Regional | Multi-Mission | ||
| Altitude | 400, 450, 500 | 450 | km |
| Inclination | 40 | 40–90 | deg. |
| Number of orbital planes | 2–10 | 2–10 | – |
| Number of sat per plane | 2–10 | 2–10 | – |
| No. | N (P,S) | inclination (deg) | Regional ART (h) | Global ART (h) | Coverage (%) |
|---|---|---|---|---|---|
| 1 | 4 (2,2) | 45 | 3.93 | 13.91 | 70.79 |
| 2 | 4 (2,2) | 47 | 4.06 | 14.07 | 77.78 |
| 3 | 4 (2,2) | 53 | 4.48 | 14.87 | 83.92 |
| 4 | 4 (2,2) | 58 | 4.75 | 15.79 | 89.14 |
| 5 | 4 (2,2) | 64 | 4.9 | 16.43 | 93.38 |
| 6 | 4 (2,2) | 70 | 5.1 | 17.21 | 96.61 |
| 7 | 4 (2,2) | 76 | 5.25 | 18.5 | 97.81 |
| 8 | 4 (2,2) | 79 | 5.29 | 17.92 | 98.34 |
| 9 | 4 (2,2) | 89 | 5.38 | 17.55 | 99.93 |
| 10 | 6 (3,2) | 53 | 2.95 | 11.17 | 83.92 |
| 11 | 6 (3,2) | 59 | 3.19 | 11.65 | 89.14 |
| 12 | 6 (3,2) | 64 | 3.33 | 12.1 | 93.38 |
| 13 | 6 (3,2) | 72 | 3.53 | 12.81 | 96.43 |
| 14 | 6 (3,2) | 84 | 3.62 | 12.72 | 99.86 |
| 15 | 8 (2,4) | 40 | 1.82 | 7.1 | 70.79 |
| 16 | 8 (4,2) | 71 | 2.64 | 9.77 | 96.61 |
| 17 | 8 (4,2) | 80 | 2.72 | 10.18 | 98.77 |
| 18 | 12 (2,6) | 45 | 1.33 | 5.29 | 70.79 |
| 19 | 16 (8,2) | 49 | 1.08 | 4.61 | 77.78 |
| 20 | 20 (5,4) | 76 | 1.07 | 4.37 | 98.77 |
| 21 | 24 (4,6) | 88 | 1.17 | 3.68 | 99.93 |
| 22 | 27 (3,9) | 87 | 0.8 | 3.24 | 99.86 |
| 23 | 40 (5,8) | 61 | 0.47 | 2.03 | 89.14 |
| 24 | 54 (6,9) | 47 | 0.32 | 1.35 | 77.78 |
| 25 | 56 (7,8) | 53 | 0.29 | 1.31 | 83.92 |
| 26 | 63 (9,7) | 46 | 0.23 | 1.06 | 77.78 |
| 27 | 70 (10,7) | 66 | 0.32 | 1.27 | 93.38 |
| 28 | 72 (9,8) | 70 | 0.26 | 1.21 | 96.61 |
| 29 | 80 (10,8) | 42 | 0.15 | 0.77 | 70.79 |
| 30 | 81 (9,9) | 57 | 0.26 | 0.99 | 83.92 |
| 31 | 90 (9,10) | 42 | 0.15 | 0.7 | 70.79 |
| 32 | 90 (9,10) | 76 | 0.21 | 0.98 | 98.77 |
| 33 | 100 (10,10) | 41 | 0.13 | 0.6 | 70.79 |
| 34 | 100 (10,10) | 76 | 0.24 | 0.88 | 98.77 |
| 35 | 100 (10,10) | 77 | 0.24 | 0.88 | 98.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melaku, S.D.; Kim, H.-D. Optimization of Multi-Mission CubeSat Constellations with a Multi-Objective Genetic Algorithm. Remote Sens. 2023, 15, 1572. https://doi.org/10.3390/rs15061572
Melaku SD, Kim H-D. Optimization of Multi-Mission CubeSat Constellations with a Multi-Objective Genetic Algorithm. Remote Sensing. 2023; 15(6):1572. https://doi.org/10.3390/rs15061572
Chicago/Turabian StyleMelaku, Shimeles Demissie, and Hae-Dong Kim. 2023. "Optimization of Multi-Mission CubeSat Constellations with a Multi-Objective Genetic Algorithm" Remote Sensing 15, no. 6: 1572. https://doi.org/10.3390/rs15061572
APA StyleMelaku, S. D., & Kim, H.-D. (2023). Optimization of Multi-Mission CubeSat Constellations with a Multi-Objective Genetic Algorithm. Remote Sensing, 15(6), 1572. https://doi.org/10.3390/rs15061572






