A High-Resolution Global Moho Model from Combining Gravimetric and Seismic Data by Using Spectral Combination Methods
Abstract
1. Introduction
2. Materials
2.1. Seismic Models
2.2. XGM2019 Combined Global Gravity Field Model
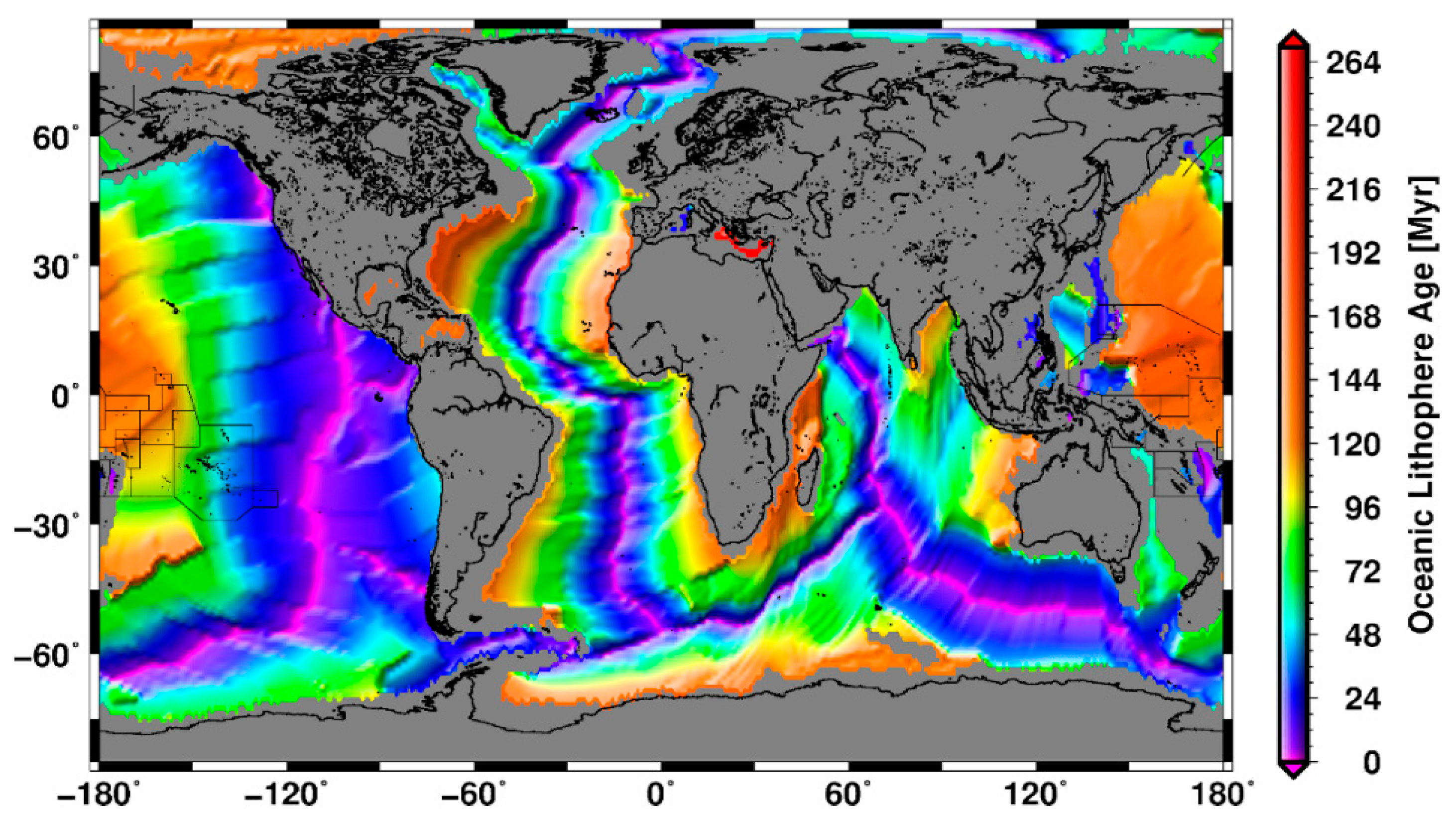
2.3. Earth2014
3. Methods
3.1. VMM Method
3.2. Butterworth Filter
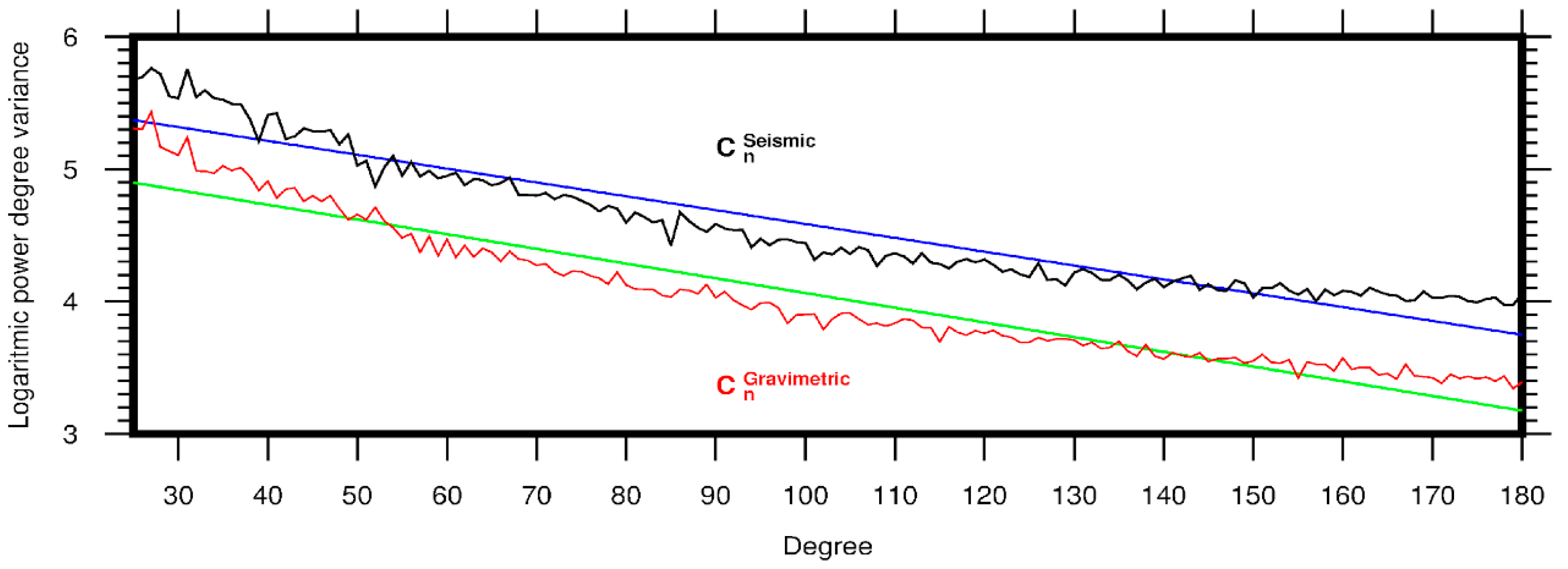
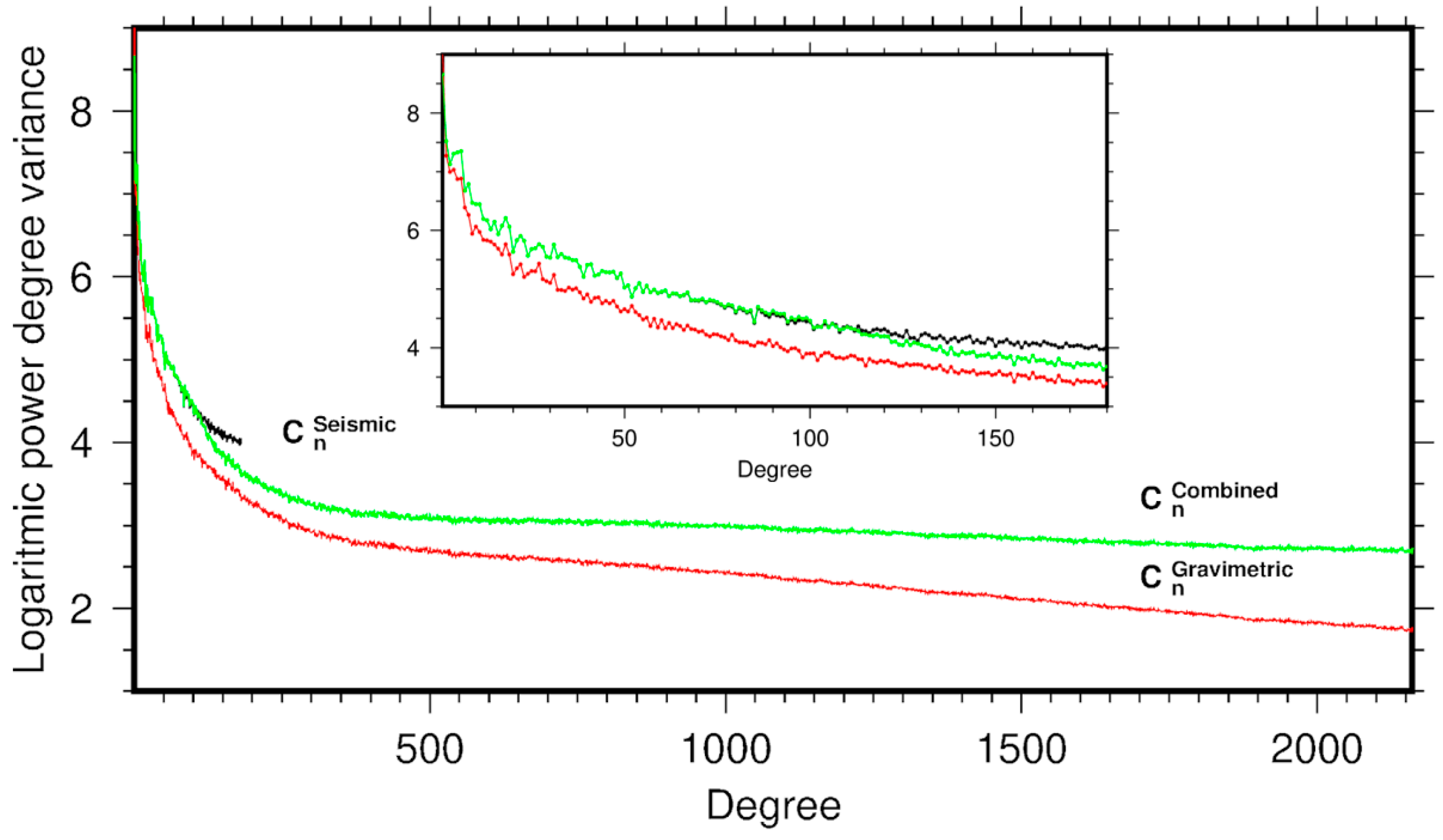
3.3. Spectral Combination
4. Results
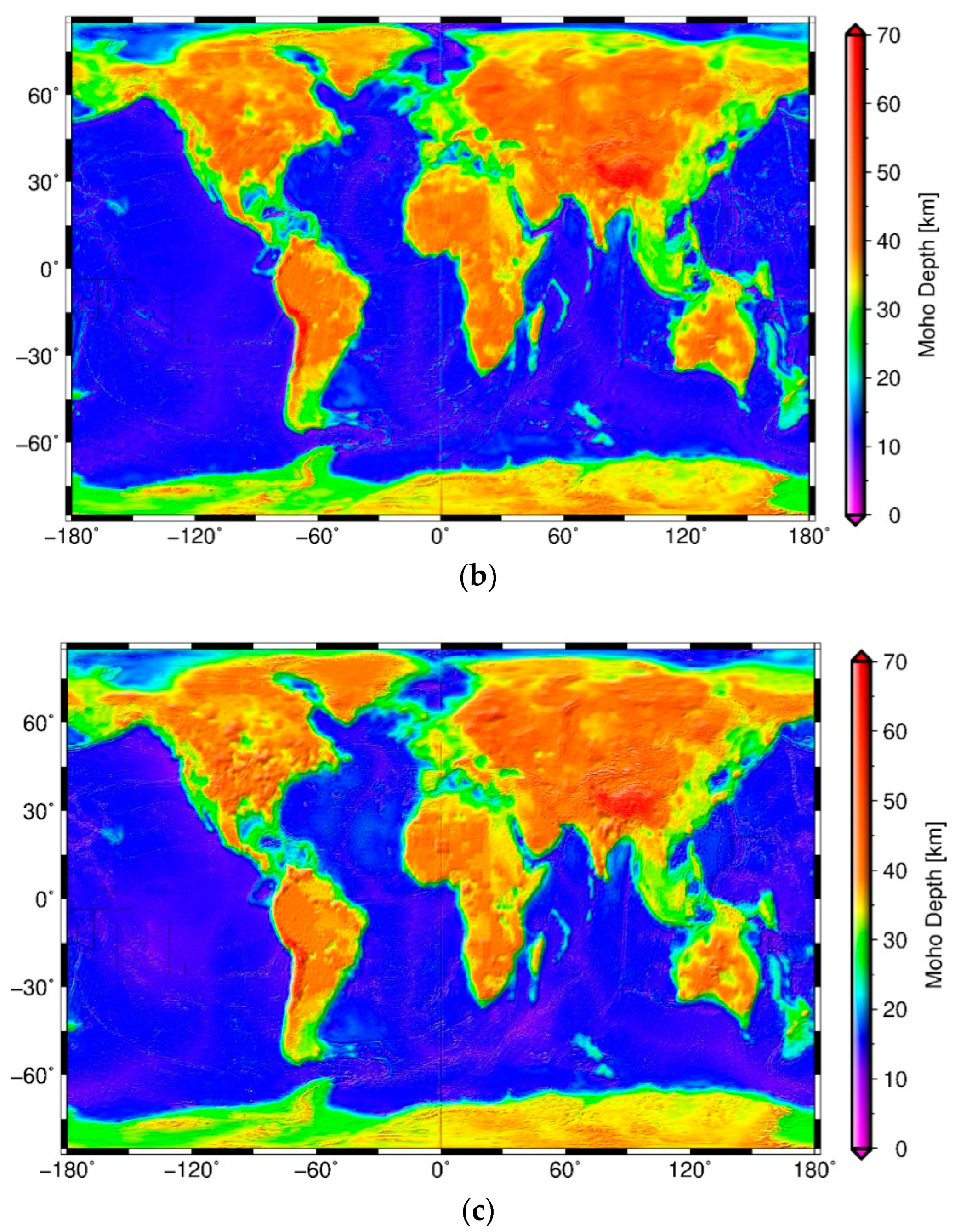
4.1. Global Combined High-Resolution Moho Depth Model
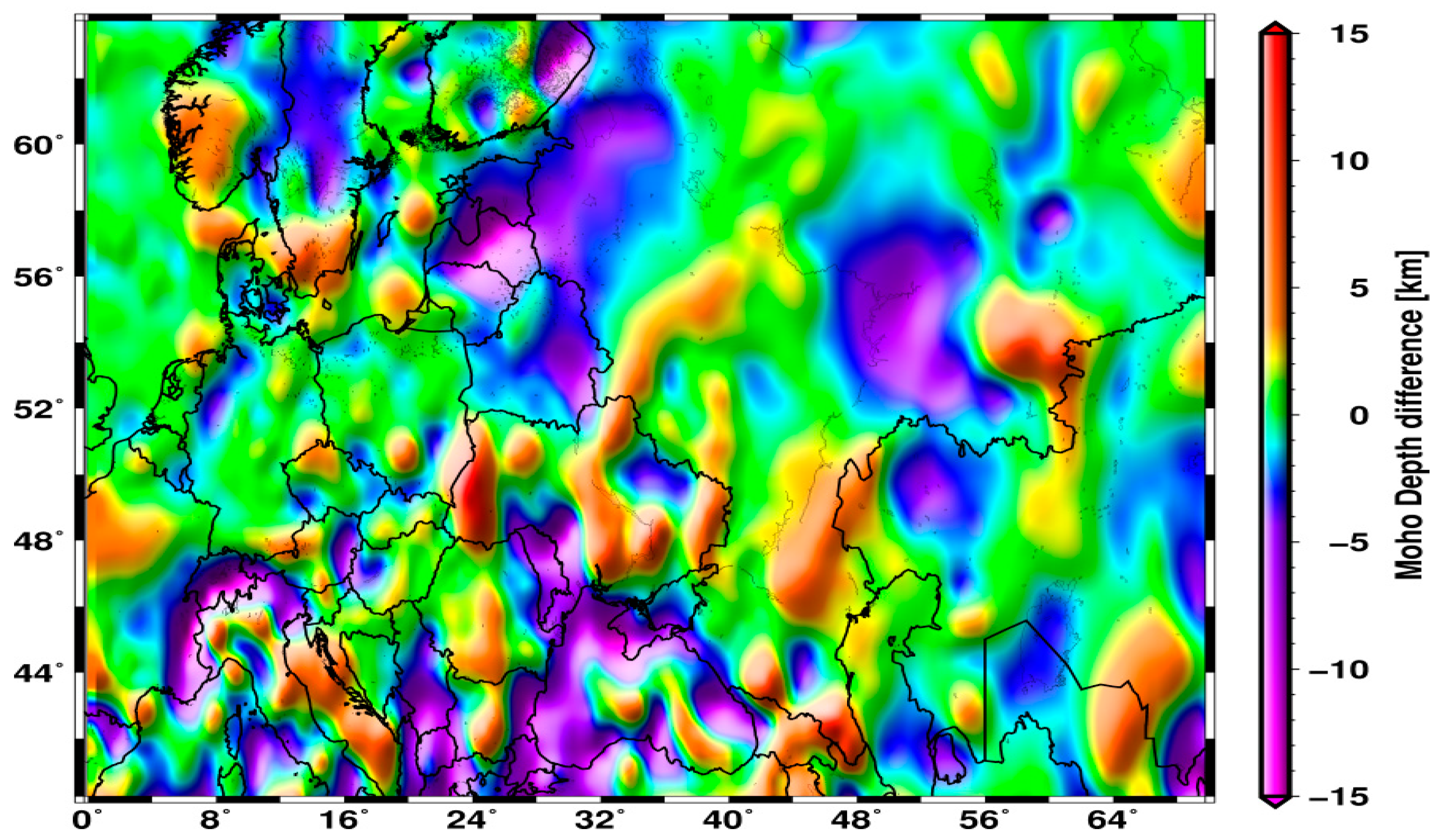
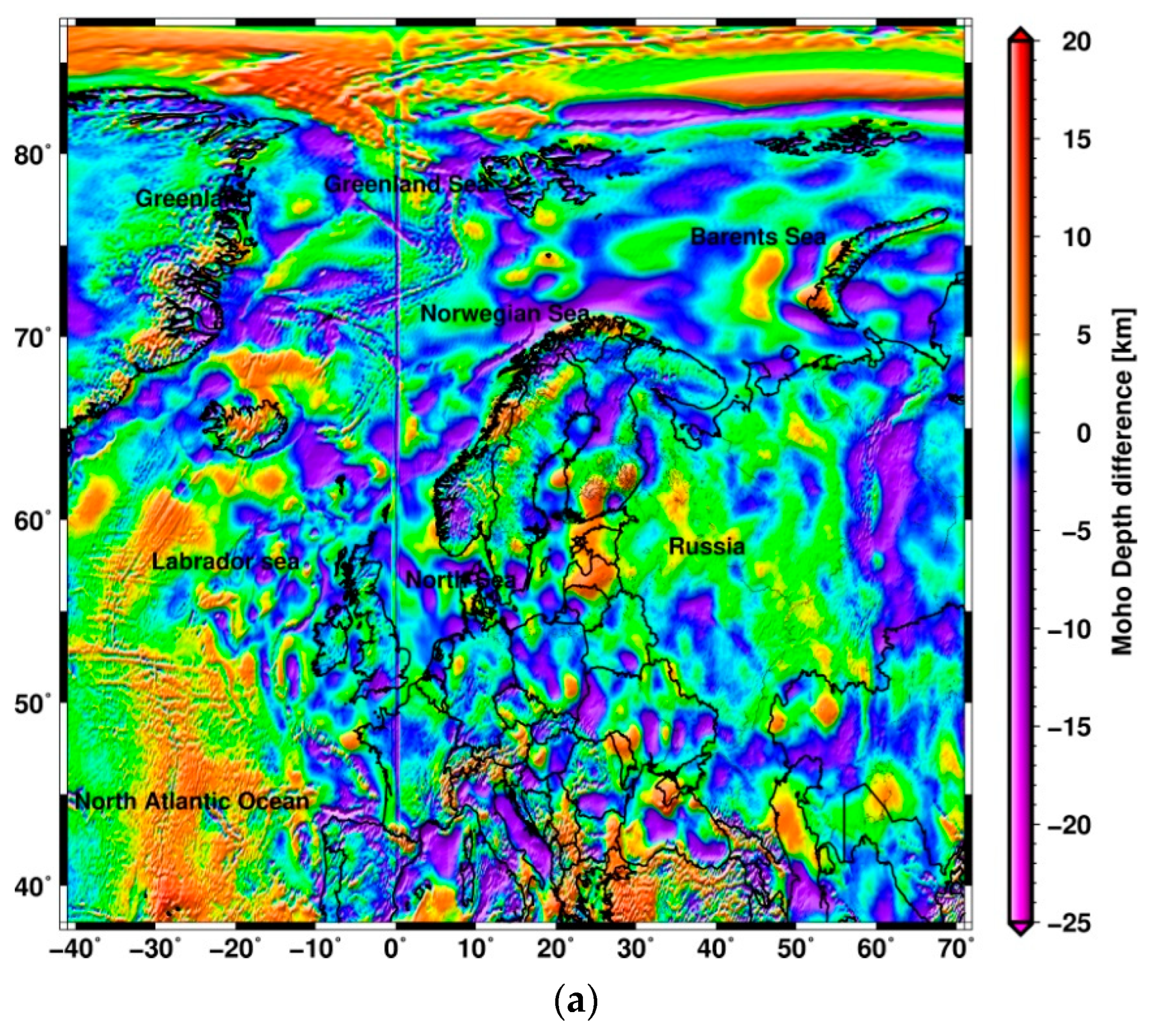
4.2. Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Differences | Percentage (%) |
|---|---|
| Less than |±1| km | 100 |
| Less than |±0.5| km | 99 |
| Less than |±0.2| km | 92 |
| Statistical Parameters | Value |
|---|---|
| Max | −4.0 |
| Mean | −0.0 |
| Min | −3.5 |
| STD | 0.1 |
References
- Martinec, Z. The minimum depth of compensation of topographic masses. Geophys. J. Int. 1994, 117, 545–554. [Google Scholar] [CrossRef]
- Mooney, W.D.; Laske, G.; Masters, T.G. CRUST 5.1: A global crustal model at 5 × 5. J. Geophys. Res. Solid Earth 1998, 103, 727–747. [Google Scholar] [CrossRef]
- Akinrinade, O.J.; Li, C.-F.; Afelumo, A.J. Geodynamic processes inferred from Moho and Curie depths in Central and Southern African Archean Cratons. Tectonophysics 2021, 815, 228993. [Google Scholar] [CrossRef]
- Yuan, X.; Sobolev, S.V.; Kind, R. Moho topography in the central Andes and its geodynamic implications. Earth Planet. Sci. Lett. 2002, 199, 389–402. [Google Scholar] [CrossRef]
- Stolk, W.; Kaban, M.; Beekman, F.; Tesauro, M.; Mooney, W.D.; Cloetingh, S. High resolution regional crustal models from irregularly distributed data: Application to Asia and adjacent areas. Tectonophysics 2013, 602, 55–68. [Google Scholar] [CrossRef]
- Becker, T.W.; Faccenna, C. Mantle conveyor beneath the Tethyan collisional belt. Earth Planet. Sci. Lett. 2011, 310, 453–461. [Google Scholar] [CrossRef]
- Richards, M.A.; Hager, B.H. Geoid anomalies in a dynamic Earth. J. Geophys. Res. Solid Earth 1984, 89, 5987–6002. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Bagherbandi, M. Gravity Inversion and Integration; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ghomsi, F.E.K.; Tenzer, R.; Njinju, E.; Steffen, R. The crustal configuration of the West and Central African Rift System from gravity and seismic data analysis. Geophys. J. Int. 2022, 230, 995–1012. [Google Scholar] [CrossRef]
- Shin, Y.H.; Shum, C.; Braitenberg, C.; Lee, S.M.; Na, S.-H.; Choi, K.S.; Hsu, H.; Park, Y.-S.; Lim, M. Moho topography, ranges and folds of Tibet by analysis of global gravity models and GOCE data. Sci. Rep. 2015, 5, 11681. [Google Scholar] [CrossRef] [PubMed]
- Pratt, J.H.I. On the attraction of the Himalaya Mountains, and of the elevated regions beyond them, upon the plumb-line in India. Philos. Trans. R. Soc. Lond. 1855, 145, 53–100. [Google Scholar]
- Airy, G.B., III. On the computation of the effect of the attraction of mountain-masses, as disturbing the apparent astronomical latitude of stations in geodetic surveys. Philos. Trans. R. Soc. Lond. 1855, 145, 101–104. [Google Scholar] [CrossRef]
- Meinesz, F. Une nouvelle methode pour la reduction isostatique regionale de l’intensite de la pesanteur. Bull. Geod. 1931, 29, 33–51. [Google Scholar] [CrossRef]
- Moritz, H. The Figure of the Earth: Theoretical Geodesy and the Earth’s Interior; Wichmann: Karlsruhe, Germany, 1990. [Google Scholar]
- Sjöberg, L.E. Solving Vening Meinesz-Moritz inverse problem in isostasy. Geophys. J. Int. 2009, 179, 1527–1536. [Google Scholar] [CrossRef]
- Bagherbandi, M.; Eshagh, M. Combined Moho Estimators. Geodyn. Res. Int. Bull. 2014, 1, 1–11. [Google Scholar]
- Tenzer, R.; Chen, W. Expressions for the global gravimetric Moho modeling in spectral domain. Pure Appl. Geophys. 2014, 171, 1877–1896. [Google Scholar] [CrossRef]
- Wan, J.; Xu, C.; Luo, Z.; Wu, Y.; Zhou, B.; Yan, J. An Approach to Moho Topography Recovery Using the On-Orbit GOCE Gravity Gradients and Its Applications in Tibet. Remote Sens. 2019, 11, 1567. [Google Scholar] [CrossRef]
- Ye, Z.; Tenzer, R.; Sneeuw, N.; Liu, L.; Wild-Pfeiffer, F. Generalized model for a Moho inversion from gravity and vertical gravity-gradient data. Geophys. J. Int. 2016, 207, 111–128. [Google Scholar] [CrossRef]
- Bagherbandi, M.; Sjöberg, L.E. A synthetic Earth gravity model based on a topographic-isostatic model. Stud. Geophys. Geod. 2012, 56, 935–955. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Bagherbandi, M. A method of estimating the Moho density contrast with a tentative application of EGM08 and CRUST2.0. Acta Geophys. 2011, 59, 502–525. [Google Scholar] [CrossRef]
- Eshagh, M.; Bagherbandi, M.; Sjöberg, L. A combined global Moho model based on seismic and gravimetric data. Acta Geod. Geophys. Hung. 2011, 46, 25–38. [Google Scholar] [CrossRef]
- Reguzzoni, M.; Sampietro, D.; Sansò, F. Global Moho from the combination of the CRUST2.0 model and GOCE data. Geophys. J. Int. 2013, 195, 222–237. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Willsky, A.; Young, I. Signals and Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 2000. [Google Scholar]
- Sjöberg, L.E. Geoid determination by spectral combination of an Earth gravitational model with airborne and terrestrial gravimetry—A theoretical study. Stud. Geophys. Geod. 2011, 55, 579–588. [Google Scholar] [CrossRef]
- Bagherbandi, M. Combination of seismic and an isostatic crustal thickness models using Butterworth filter in a spectral approach. J. Asian Earth Sci. 2012, 59, 240–248. [Google Scholar] [CrossRef]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1. 0—A 1-degree global model of Earth’s crust. In Proceedings of the Geophysical Research Abstracts, EGU General Assembly, Vienna, Austria, 7–12 April 2013. [Google Scholar]
- Bassin, C. The current limits of resolution for surface wave tomography in North America. Eos Trans. AGU 2000, 81, F897. [Google Scholar]
- Grad, M.; Tiira, T.; Group, E.W. The Moho depth map of the European Plate. Geophys. J. Int. 2009, 176, 279–292. [Google Scholar] [CrossRef]
- Luosto, U. Structure of the Earth’s crust in Fennoscandia as revealed from refraction and wide-angle reflection studies. Geophysica 1997, 33, 3–16. [Google Scholar]
- Abdollahi, S.; Ardestani, V.E.; Zeyen, H.; Shomali, Z.H. Crustal and upper mantle structures of Makran subduction zone, SE Iran by combined surface wave velocity analysis and gravity modeling. Tectonophysics 2018, 747, 191–210. [Google Scholar] [CrossRef]
- Zhang, H.; Ravat, D.; Lowry, A.R. Crustal composition and Moho variations of the central and eastern United States: Improving resolution and geologic interpretation of EarthScope USArray seismic images using gravity. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018537. [Google Scholar] [CrossRef]
- Silvennoinen, H.; Kozlovskaya, E.; Kissling, E.; Kosarev, G.; W.L.P Group. A new Moho boundary map for the northern Fennoscandian Shield based on combined controlled-source seismic and receiver function data. GeoResJ 2014, 1, 19–32. [Google Scholar] [CrossRef]
- Lowry, A.R.; Pérez-Gussinyé, M. The role of crustal quartz in controlling Cordilleran deformation. Nature 2011, 471, 353–357. [Google Scholar] [CrossRef]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The combined global gravity field model XGM2019e. J. Geod. 2020, 94, 66. [Google Scholar] [CrossRef]
- Shako, R.; Förste, C.; Abrikosov, O.; Bruinsma, S.; Marty, J.-C.; Lemoine, J.-M.; Flechtner, F.; Neumayer, H.; Dahle, C. EIGEN-6C: A high-resolution global gravity combination model including GOCE data. In Observation of the System Earth from Space-CHAMP, GRACE, GOCE and Future Missions; Springer: Berlin/Heidelberg, Germany, 2014; pp. 155–161. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B4. [Google Scholar] [CrossRef]
- Hirt, C.; Rexer, M. Earth2014: 1 arc-min shape, topography, bedrock and ice-sheet models–Available as gridded data and degree-10,800 spherical harmonics. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 103–112. [Google Scholar] [CrossRef]
- Haagmans, R. A synthetic Earth for use in geodesy. J. Geod. 2000, 74, 503–511. [Google Scholar] [CrossRef]
- Bagherbandi, M.; Sjöberg, L.E. Non-isostatic effects on crustal thickness: A study using CRUST2.0 in Fennoscandia. Phys. Earth Planet. Inter. 2012, 200, 37–44. [Google Scholar] [CrossRef]
- Claessens, S. A Synthetic Earth Model Analysis, Implementation, Validation and Application. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Kuhn, M.; Featherstone, W. On the construction of a synthetic Earth gravity model. In Proceedings of the Proceed 3rd Meeting of the International Gravity and Geoid Commission, Hrsg. I. Tziavos, Thessaloniki, Greece, 26–30 August 2002; pp. 189–194. [Google Scholar]
- Heiskanen, W.A. Physical geodesy. Determ. Geoid Ground Anom. 1967, 8, 325–330. [Google Scholar] [CrossRef]
- Čadek, O.; Martinec, Z. Spherical harmonic expansion of the Earth’s crustal thickness up to degree and order 30. Stud. Geophys. Geod. 1991, 35, 151–165. [Google Scholar] [CrossRef]
- Müller, R.D.; Sdrolias, M.; Gaina, C.; Roest, W.R. Age, spreading rates, and spreading asymmetry of the world’s ocean crust. Geochem. Geophys. Geosystems 2008, 9. [Google Scholar] [CrossRef]
- Laske, G. Crustal Model at 2 × 2 arc-degrees. 2002. Available online: http://igppweb.ucsd.edu/~gabi/rem.html (accessed on 27 November 2022).
- Pasyanos, M.E.; Walter, W.R.; Flanagan, M.P.; Goldstein, P.; Bhattacharyya, J. Building and testing an a priori geophysical model for western Eurasia and North Africa. Pure Appl. Geophys. 2004, 161, 235–281. [Google Scholar] [CrossRef]
- Braitenberg, C.; Wienecke, S.; Wang, Y. Basement structures from satellite-derived gravity field: South China Sea ridge. J. Geophys. Res. Solid Earth 2006, 111, B5. [Google Scholar] [CrossRef]
- Evenick, J.C. Glimpses into Earth’s history using a revised global sedimentary basin map. Earth-Sci. Rev. 2021, 215, 103564. [Google Scholar] [CrossRef]



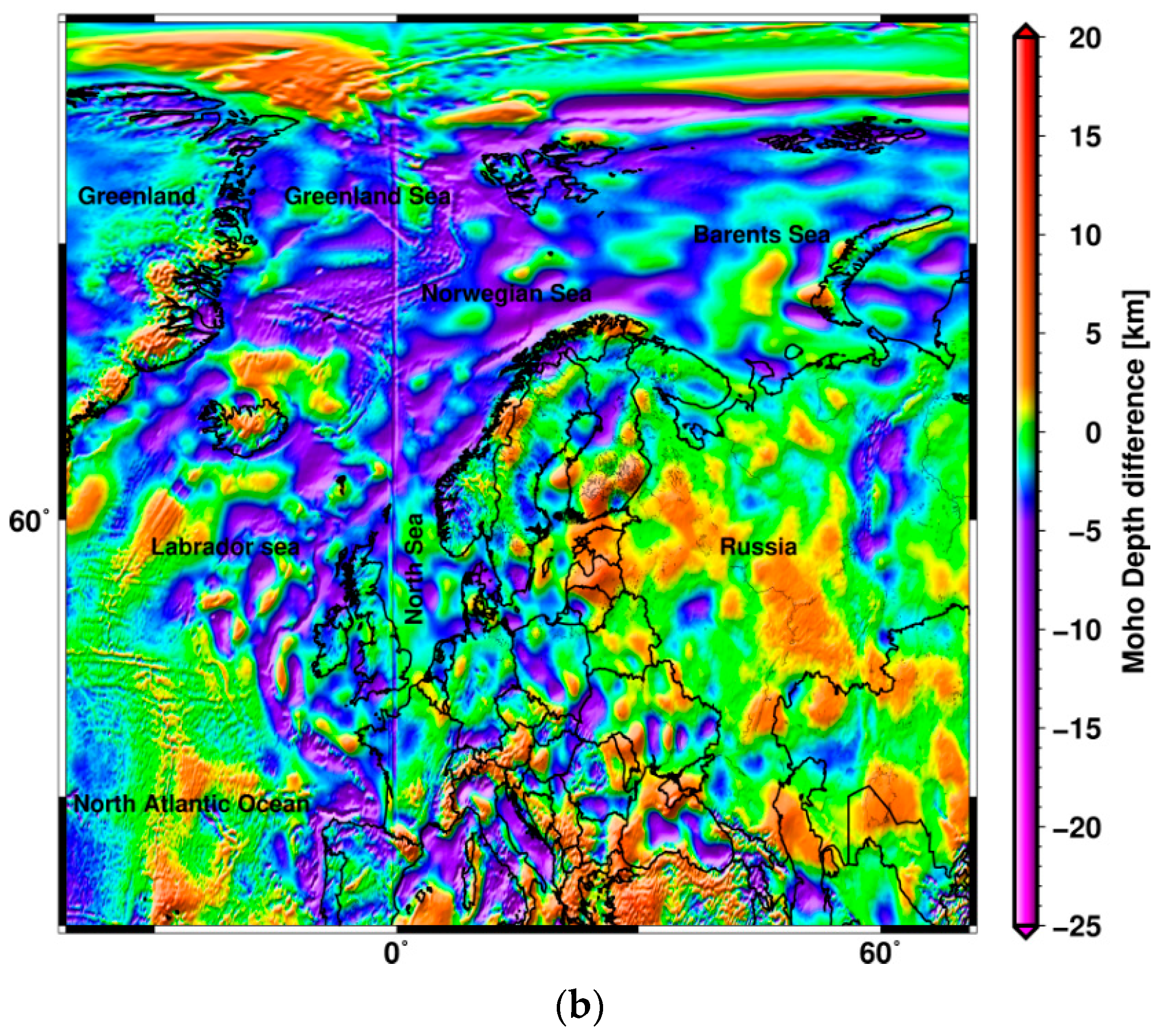
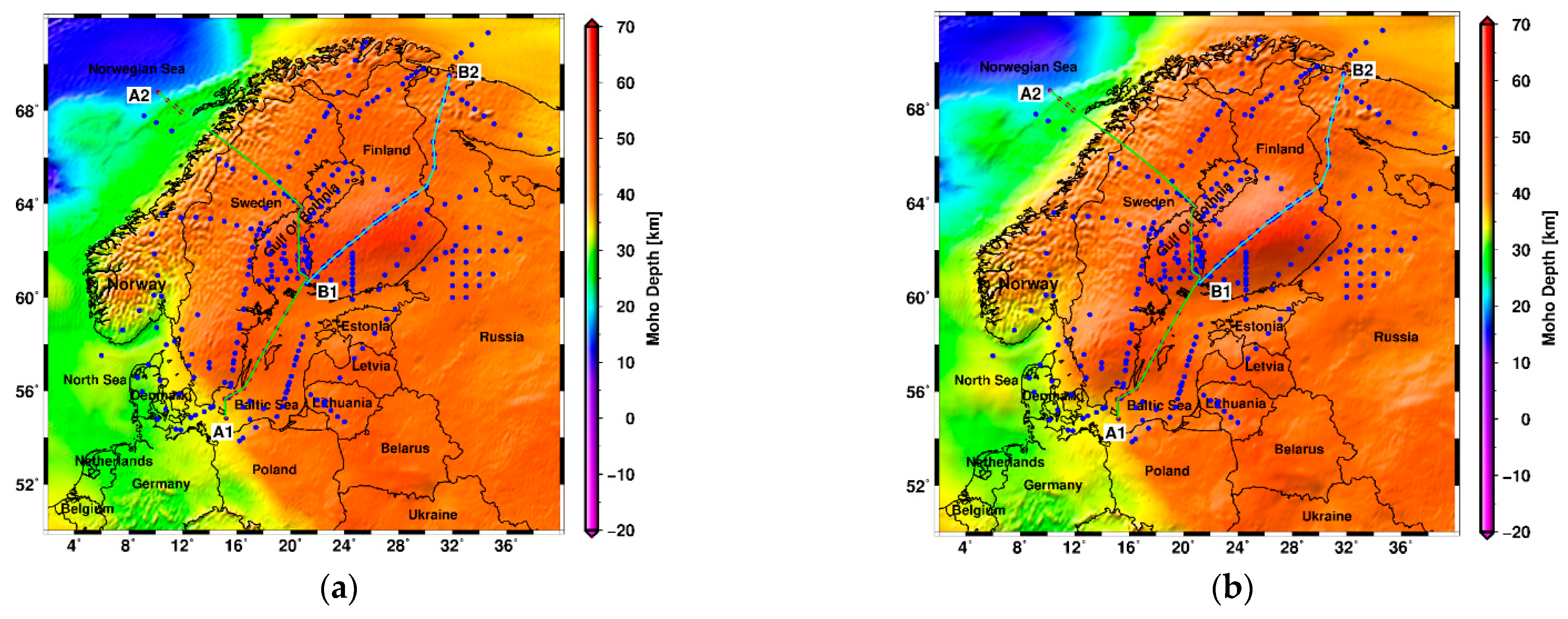
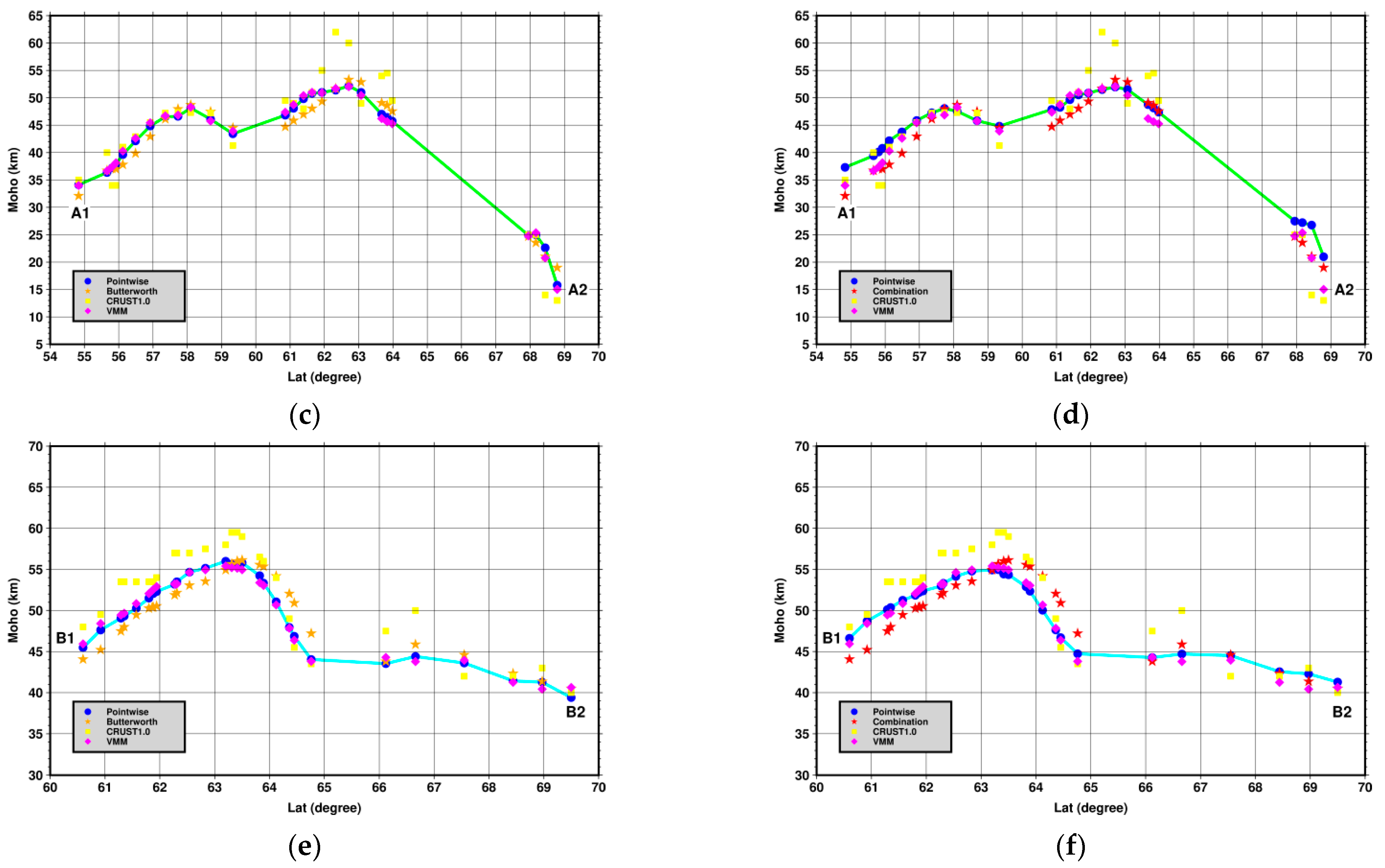
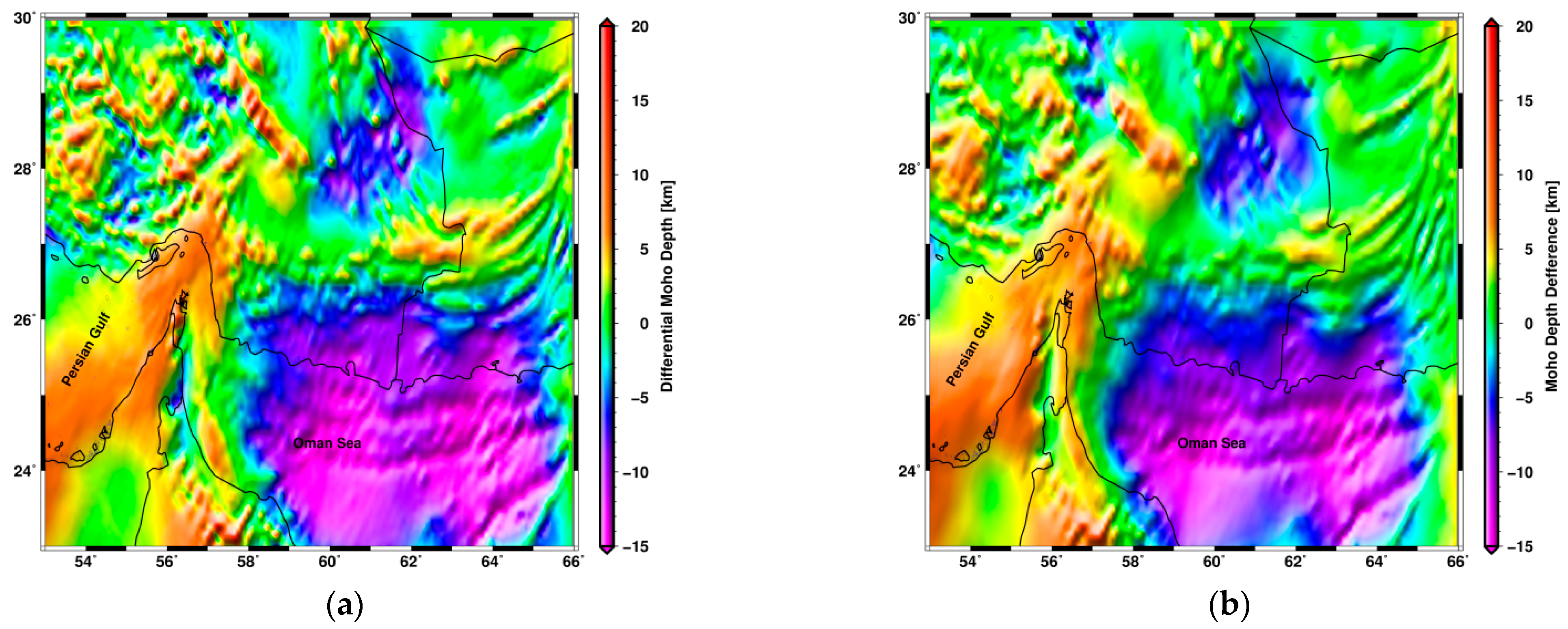

| Method | k | Eurasia | Europe | Fennoscandia | Makran | U.S. | |
|---|---|---|---|---|---|---|---|
| Butterworth | 78 | 1 | 2.9 | 1.7 | 3.9 | 4.8 | 1.9 |
| 2 | 2.9 | 1.7 | 4.1 | 4.8 | 1.9 | ||
| 8 | 2.9 | 1.7 | 4.3 | 4.8 | 1.9 | ||
| 25 | 2.9 | 1.7 | 4.5 | 4.7 | 2.0 | ||
| Spectral combination | 1 | 2.4 | 0.4 | 4.0 | 4.5 | 2.1 |
| Method | Statistics | Eurasia | Europe | Fennoscandia | Makran | U.S. |
|---|---|---|---|---|---|---|
| Butterworth | Max | 37.8 | 20.7 | 8.6 | 19.5 | 39.8 |
| Mean | 0.8 | 1.1 | −1.2 | −2.4 | −1.1 | |
| Min | −23.1 | −27.6 | −15.6 | −46.6 | −13.4 | |
| RMS | 2.9 | 1.7 | 2.8 | 4.7 | 1.9 | |
| Spectral Combination | Max | 38.1 | 15.6 | 12.8 | 14.2 | 39.5 |
| Mean | −0.7 | −1.1 | −0.1 | −1.01 | −2.0 | |
| Min | −20.8 | −19.1 | −14.1 | −46.6 | −13.0 | |
| RMS | 2.4 | 0.4 | 2.9 | 4.1 | 2.1 |
| Method | Differences | Eurasia (%) | Europe (%) | Fennoscandia (%) | Makran (%) | U.S. (%) |
|---|---|---|---|---|---|---|
| Butterworth | Less than ±5 km | 86 | 90 | 100 | 61 | 98 |
| Less than ±10 km | 97 | 99 | 100 | 85 | 100 | |
| Spectral Combination | Less than ±5 km | 86 | 92 | 95 | 62 | 86 |
| Less than ±10 km | 98 | 100 | 100 | 91 | 99 |
| Profiles | |||
|---|---|---|---|
| HRCM Models | A1–A2 | B1–B2 | |
| Butterworth | Max | 8.6 | 1.6 |
| Mean | −1.1 | −2.3 | |
| Min | −10.6 | −5.6 | |
| RMS | 2.9 | 2.0 | |
| Spectral Combination | Max | 12.8 | 2.6 |
| Mean | 0.4 | −2.2 | |
| Min | −10.5 | −5.3 | |
| RMS | 3.4 | 2.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dashtbazi, A.; Voosoghi, B.; Bagherbandi, M.; Tenzer, R. A High-Resolution Global Moho Model from Combining Gravimetric and Seismic Data by Using Spectral Combination Methods. Remote Sens. 2023, 15, 1562. https://doi.org/10.3390/rs15061562
Dashtbazi A, Voosoghi B, Bagherbandi M, Tenzer R. A High-Resolution Global Moho Model from Combining Gravimetric and Seismic Data by Using Spectral Combination Methods. Remote Sensing. 2023; 15(6):1562. https://doi.org/10.3390/rs15061562
Chicago/Turabian StyleDashtbazi, Arash, Behzad Voosoghi, Mohammad Bagherbandi, and Robert Tenzer. 2023. "A High-Resolution Global Moho Model from Combining Gravimetric and Seismic Data by Using Spectral Combination Methods" Remote Sensing 15, no. 6: 1562. https://doi.org/10.3390/rs15061562
APA StyleDashtbazi, A., Voosoghi, B., Bagherbandi, M., & Tenzer, R. (2023). A High-Resolution Global Moho Model from Combining Gravimetric and Seismic Data by Using Spectral Combination Methods. Remote Sensing, 15(6), 1562. https://doi.org/10.3390/rs15061562






