Coherent-on-Receive Synthesis Using Dominant Scatterer in Millimeter-Wave Distributed Coherent Aperture Radar
Abstract
1. Introduction
- We first introduce the coherent-on-receive synthesis into the millimeter-wave distributed coherent aperture radar. This method can be widely used in millimeter-wave radar applications, such as autonomous driving and precision guidance;
- An adaptive compensation approach is proposed to correct the estimated CPs of the dominant scatterer. On the one hand, prior information about the dominant scatterer is not required, and we can choose an unknown target with strong scattering points to estimate the CPs in radar detection scenarios. On the other hand, there is also no need for the spatial position of other targets as prior information;
- The proposed MMW DCAR can be adaptively cohered based on observed target echoes, thus reducing the hardware demands for high-accuracy synchronization.
2. Background
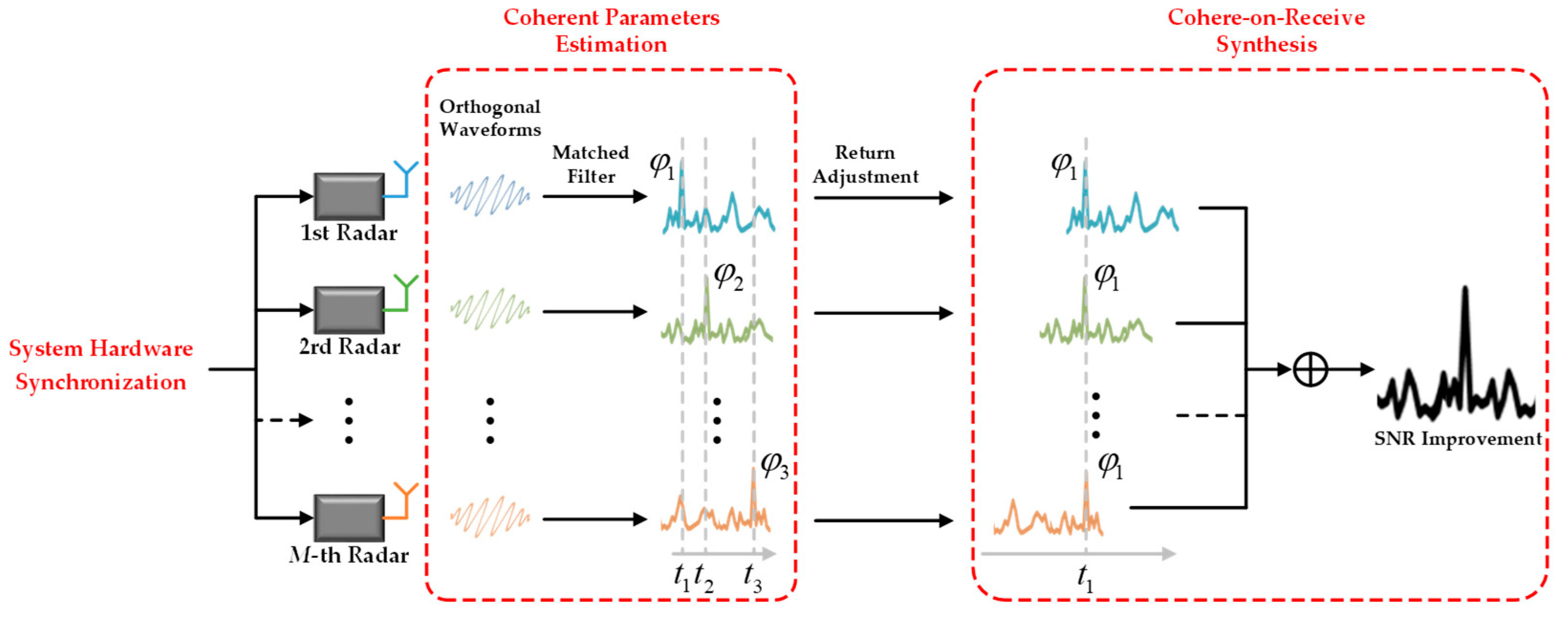
2.1. Workflow of CoRS in DCAR
- The multiple-unit radars within DCAR rely on wired or wireless connections to ensure that they can operate at the same time.
- Due to the imperfect synchronization and the unequal range between different unit radars and targets, there are multidimensional differences between any two radars, called coherent parameters (CPs). To solve this problem, the multiple unit radars transmit the orthogonal waveforms with the same time base, which allows the target echoes to be separated at each receiver’s matched filter output. By detecting the target peaks in different echoes, the CPs can be estimated.
- The estimated CPs are used to adjust the echoes of multiple unit radars, and then the adjusted echoes are added together with the same time and phase to obtain the SNR gain.
2.2. Signal Model
3. Proposed Method
3.1. CP Estimation Using Dominant Scatterer
3.2. Echoes Compensation and Analysis
3.3. Adaptive Compensation for Phases
3.3.1. Compensation for Coupling Term
3.3.2. Compensation for Spatial Phase
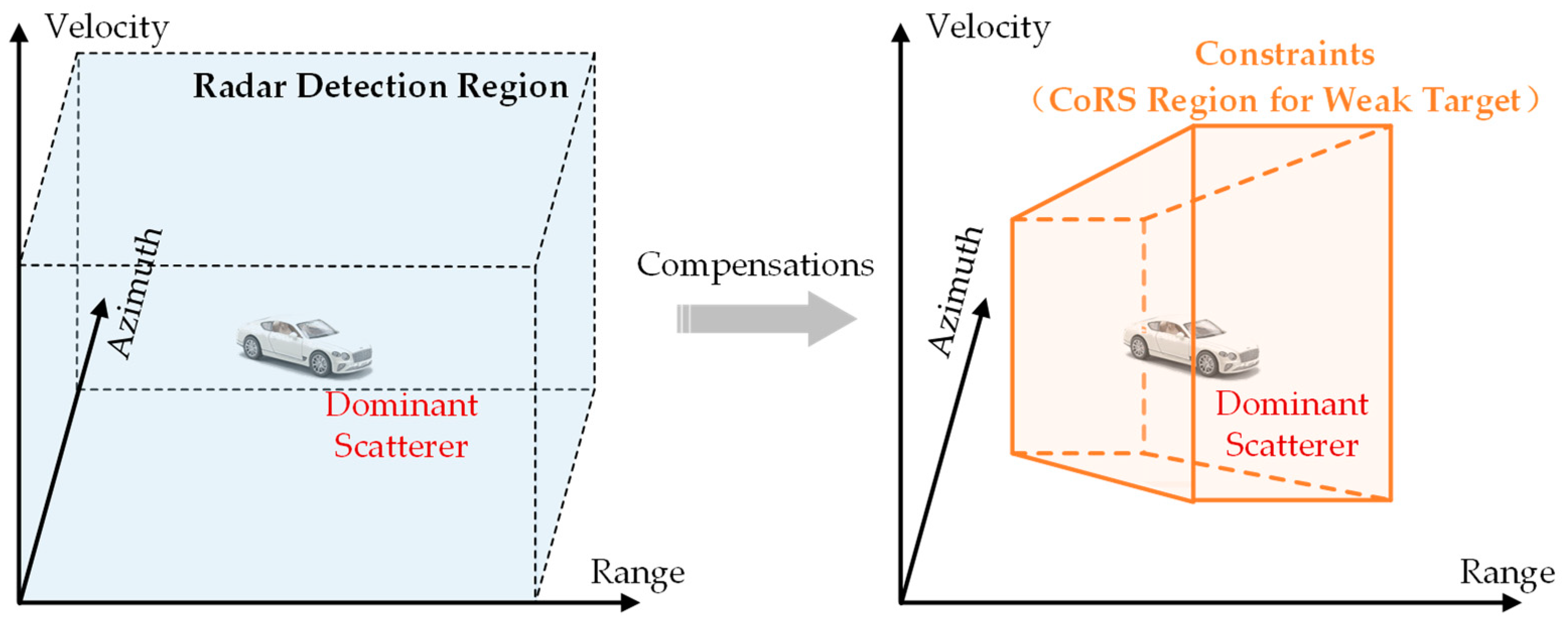
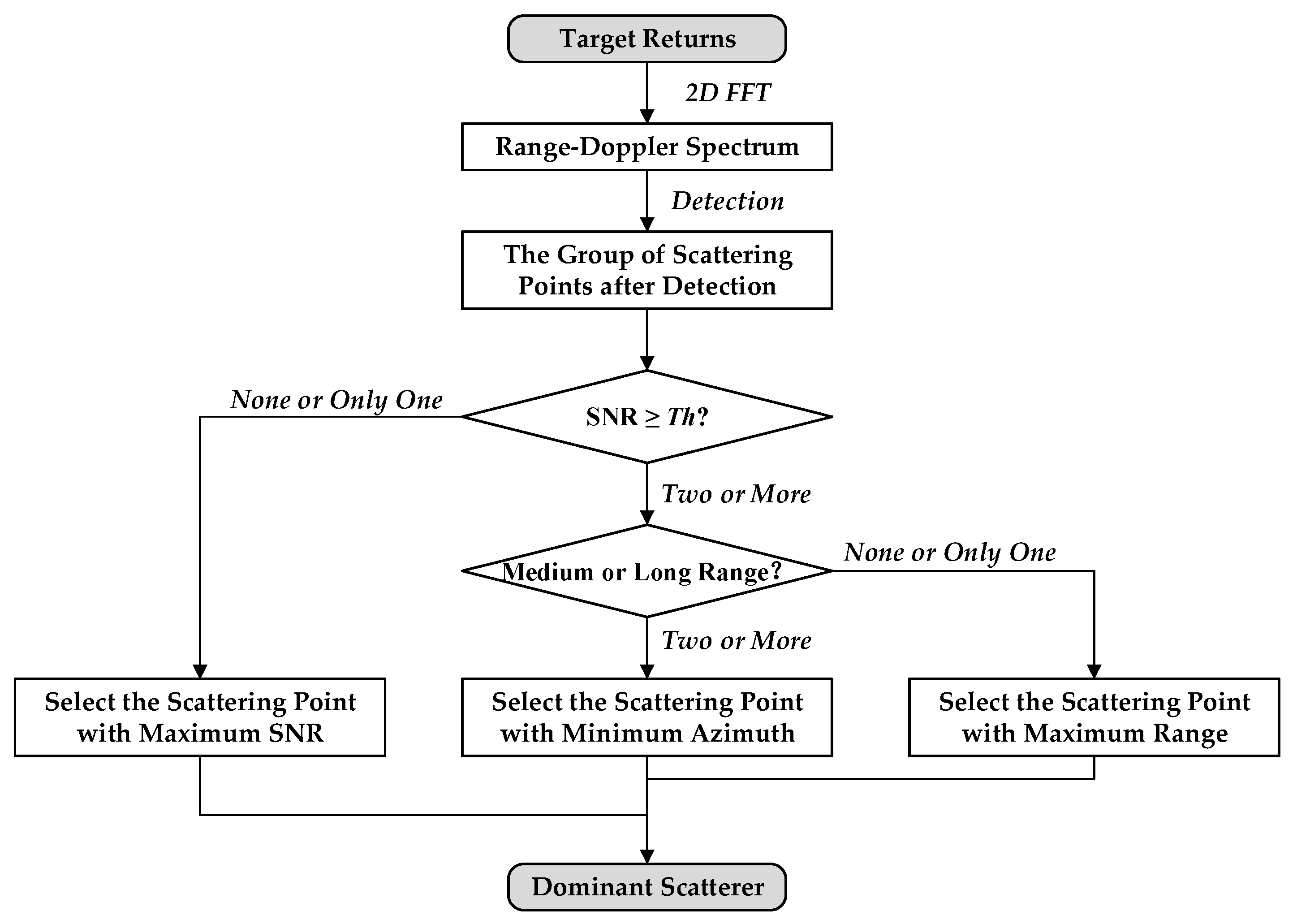
3.4. Selection of Dominant Scatterer
3.4.1. Analysis of Constraints
3.4.2. Selection Criteria
3.5. Derivation of Theoretical Synthetic SNR
4. Simulations
4.1. CoRS for Multiple Targets
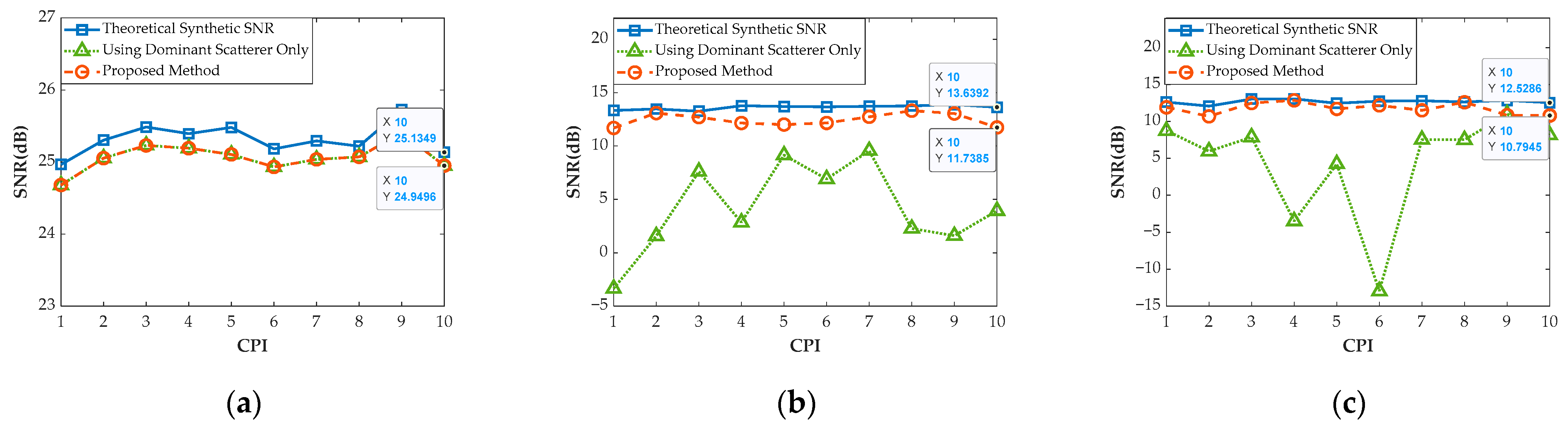
4.1.1. Synthetic Results in Continuous CPIs
4.1.2. Synthetic Results within a Single CPI
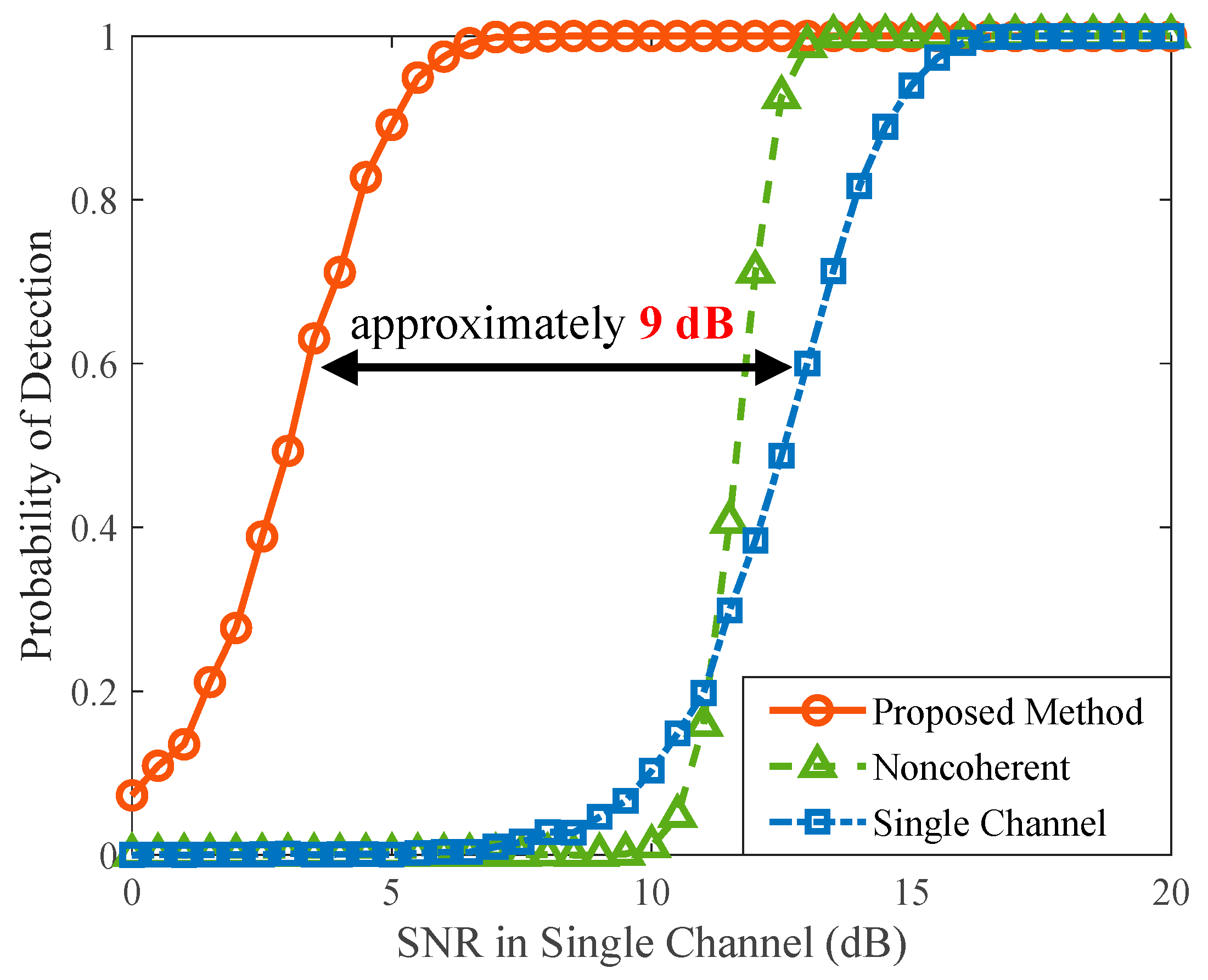
4.2. Detection Performance Comparison
5. Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Coutts, S.; Cuomo, K.; McHarg, J.; Robey, F.; Weikle, D. Distributed Coherent Aperture Measurements for Next Generation BMD Radar. In Proceedings of the IEEE Workshop on Sensor Array and Multichannel Processing, Waltham, MA, USA, 12–14 July 2006. [Google Scholar]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target Localization Accuracy Gain in MIMO Radar-Based Systems. IEEE Trans. Inf. Theory 2010, 56, 2783–2802. [Google Scholar] [CrossRef]
- Dai, F.; Li, Y.; Wang, Y.; Chen, H. Efficient Implementation for SBL-Based Coherent Distributed mmWave Radar Imaging. Remote Sens. 2023, 15, 1054. [Google Scholar] [CrossRef]
- Cuomo, K.M.; Coutts, S.D.; McHarg, J.C.; Pulsone, N.B.; Robey, F.C. Wideband Aperture Coherence Processing for Next Generation Radar (NexGen); MIT Lincoln Laboratory: Lexington, MA, USA, 2004. [Google Scholar]
- Long, T.; Zhang, H.; Zeng, T.; Liu, Q.; Chen, X.; Zheng, L. High Accuracy Unambiguous Angle Estimation Using Multi-Scale Combination in Distributed Coherent Aperture Radar. IET Radar Sonar Nav. 2017, 11, 1090–1098. [Google Scholar] [CrossRef]
- Liang, C.; Wang, Y.; Yang, Z.; Hu, X.; Pei, Q.; Gu, W.; Zhang, L. Cooperative Automotive Radars with Multi-Aperture Multiplexing MIMO Sparse Array Design. Electronics 2022, 11, 1198. [Google Scholar] [CrossRef]
- Fletcher, A.S.; Robey, F.C. Performance Bounds for Adaptive Coherence of Sparse Array Radar. In Proceedings of the 11th Conference Adaptive Sensors Array Processing, Lexington, MA, USA, 11–13 March 2003. [Google Scholar]
- Li, J.; Stoica, P. MIMO Radar with Colocated Antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Gottinger, M.; Hoffmann, M.; Christmann, M.; Schütz, M.; Kirsch, F.; Gulden, P.; Vossiek, M. Coherent Automotive Radar Networks: The Next Generation of Radar-Based Imaging and Mapping. IEEE J. Microw. 2021, 1, 149–163. [Google Scholar] [CrossRef]
- Sun, P.; Tang, J.; He, Q.; Tang, B.; Tang, X. Cramer-Rao bound of parameters estimation and coherence performance for next generation radar. IET Radar Sonar Nav. 2013, 7, 553–567. [Google Scholar] [CrossRef]
- Tang, X.; Tang, J.; He, Q.; Wan, S.; Tang, B.; Sun, P.; Zhang, N. Cramer-Rao Bounds and Coherence Performance Analysis for Next Generation Radar with Pulse Trains. Sensors 2013, 13, 5347–5367. [Google Scholar] [CrossRef]
- Brookner, E. Phased-Array and Radar Breakthroughs. In Proceedings of the IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007. [Google Scholar]
- Kuschel, H.; O’Hagan, D. Passive Radar from History to Future. In Proceedings of the 11-th International Radar Symposium, Vilnius, Lithuania, 16–18 June 2010. [Google Scholar]
- Kuschel, H. Approaching 80 Years of Passive Radar. In Proceedings of the 2013 International Conference on Radar, Adelaide, SA, Australia, 9–12 September 2013. [Google Scholar]
- Stelzer, A.; Jahn, M.; Scheiblhofer, S. Precise Distance Measurement with Cooperative FMCW Radar Units. In Proceedings of the 2008 IEEE Radio and Wireless Symposium, Orlando, FL, USA, 22–24 January 2008. [Google Scholar]
- Feger, R.; Pfeffer, C.; Schmid, C.M.; Lang, M.J.; Tong, Z.; Stelzer, A. A 77-GHz FMCW MIMO Radar Based on Loosely Coupled Stations. In Proceedings of the 7th German Microwave Conference, Ilmenau, Germany, 12–14 March 2012. [Google Scholar]
- Butt, F.A.; Aslam, M.A.; Zafar, M.T.; Naqvi, I.H.; Riaz, U. Synchronization of Long-Range, Widely-Separated MIMO Radar Network using GSM Protocol. In Proceedings of the 19th International Radar Symposium, Bonn, Germany, 20–22 June 2018. [Google Scholar]
- Steiner, M.; Keller, M.; Geiß, J.; Vossiek, M.; Waldschmidt, C. Synchronization of Radar Sensors in a Network Based on Inter-Sensor Interference. In Proceedings of the 2019 16th European Radar Conference (EuRAD), Paris, France, 2–4 October 2019. [Google Scholar]
- Zhang, H.; Lei, Z.; Song, Y. Coherent Parameters Estimation Method Based on MUSIC and KF in Wideband DCAR. In Proceedings of the IET International Radar Conference, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Zeng, T.; Yin, P.; Liu, Q. Wideband Distributed Coherent Aperture Radar Based on Stepped Frequency Signal: Theory and Experimental Results. IET Radar Sonar Nav. 2016, 10, 672–688. [Google Scholar] [CrossRef]
- Edstaller, S.; Mueller, D. Vector Velocity and Position Measurement Using a 77-GHz Cooperative Radar System. In Proceedings of the 2019 IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2019. [Google Scholar]
- Edstaller, S.; Mueller, D. A Cooperative Radar System with Active Reference Target Synchronization for Kinematic Target Analysis. IEEE Trans. Microw. Theory Techn. 2021, 69, 4118–4131. [Google Scholar] [CrossRef]
- Rabideau, D.J. MIMO Radar Waveforms and Cancellation Ratio. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1167–1178. [Google Scholar] [CrossRef]
- Kronauge, M.; Rohling, H. New Chirp Sequence Radar Waveform. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2870–2877. [Google Scholar] [CrossRef]
- Hu, X.; Lu, M.; Li, Y.; Wang, Y. Motion Compensation for TDM MIMO Radar by Sparse Reconstruction. Electron. Lett. 2017, 53, 1604–1606. [Google Scholar] [CrossRef]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive Radars: A Review of Signal Processing Techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Hu, X.; Li, Y.; Lu, M.; Wang, Y.; Yang, X. A Multi-Carrier-Frequency Random-Transmission Chirp Sequence for TDM MIMO Automotive Radar. IEEE Trans. Veh. Technol. 2019, 68, 3672–3685. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving: Advantages and Challenges. IEEE Signal Process. Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Feger, R.; Pfeffer, C.; Stelzer, A. A Frequency-Division MIMO FMCW Radar System Based on Delta–Sigma Modulated Transmitters. IEEE Trans. Microw. Theory Techn. 2014, 62, 3572–3581. [Google Scholar] [CrossRef]
- Kim, E.H.; Kim, K.H. Random Phase Code for Automotive MIMO Radars Using Combined Frequency Shift Keying-Linear FMCW Waveform. IET Radar Sonar Nav. 2018, 12, 1090–1095. [Google Scholar] [CrossRef]
- Benedetto, J.J.; Konstantinidis, I.; Rangaswamy, M. Phase-Coded Waveforms and Their Design. IEEE Signal Process. Mag. 2009, 26, 22–31. [Google Scholar] [CrossRef]
- Uysal, F. Phase-Coded FMCW Automotive Radar: System Design and Interference Mitigation. IEEE Trans. Veh. Technol. 2020, 69, 270–281. [Google Scholar] [CrossRef]
- Overdevest, J.; Jansen, F.; Uysal, F.; Yarovoy, A. Doppler Influence on Waveform Orthogonality in 79 GHz MIMO Phase-Coded Automotive Radar. IEEE Trans. Veh. Technol. 2020, 69, 16–25. [Google Scholar] [CrossRef]
- Ferrari, A.; Berenguer, C.; Alengrin, G. Doppler Ambiguity Resolution Using Multiple PRF. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 738–751. [Google Scholar] [CrossRef]
- Rossum, W.; van Anitori, L. Simultaneous Resolution of Range-Doppler Ambiguities using Agile Pulse Intervals with Sparse Signal Processing. In Proceedings of the 2020 IEEE Radar Conference, Florence, Italy, 21–25 September 2020. [Google Scholar]
- Wang, J. CFAR-Based Interference Mitigation for FMCW Automotive Radar Systems. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12229–12238. [Google Scholar] [CrossRef]
- Xu, Z.; Yuan, M. An Interference Mitigation Technique for Automotive Millimeter Wave Radars in the Tunable Q-Factor Wavelet Transform Domain. IEEE Trans. Microw. Theory Techn. 2021, 69, 5270–5283. [Google Scholar] [CrossRef]
- Xu, Z.; Xue, S.; Wang, Y. Incoherent Interference Detection and Mitigation for Millimeter-Wave FMCW Radars. Remote Sens. 2022, 14, 4817. [Google Scholar] [CrossRef]
- Xu, Z. Bi-Level l1 Optimization-Based Interference Reduction for Millimeter Wave Radars. IEEE Trans. Intell. Transp. Syst. 2023, 24, 728–738. [Google Scholar] [CrossRef]
- Sun, L.; Yu, H.; Lan, J.; Fu, Z.; He, Z.; Pu, J. Tracking of Multiple Maneuvering Random Hypersurface Extended Objects Using High Resolution Sensors. Remote Sens. 2021, 13, 2963. [Google Scholar] [CrossRef]
- Smith, M.E.; Varshney, P.K. Intelligent CFAR Processor Based on Data Variability. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 837–847. [Google Scholar] [CrossRef]
- Tao, D.; Anfinsen, S.N.; Brekke, C. Robust CFAR Detector Based on Truncated Statistics in Multiple-Target Situations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 117–134. [Google Scholar] [CrossRef]
- Cao, Z.; Li, J.; Song, C.; Xu, Z.; Wang, X. Compressed Sensing-Based Multitarget CFAR Detection Algorithm for FMCW Radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9160–9172. [Google Scholar] [CrossRef]
- Bird, J.S. Calculating the Performance of Linear and Square-Law Detectors. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 39–51. [Google Scholar] [CrossRef]
- Morgan, D.R.; Madsen, C.K. Wide-Band System Identification Using Multiple Tones with Allpass Filters and Square-Law Detectors. IEEE Trans. Circuits–I 2006, 53, 1151–1165. [Google Scholar] [CrossRef]



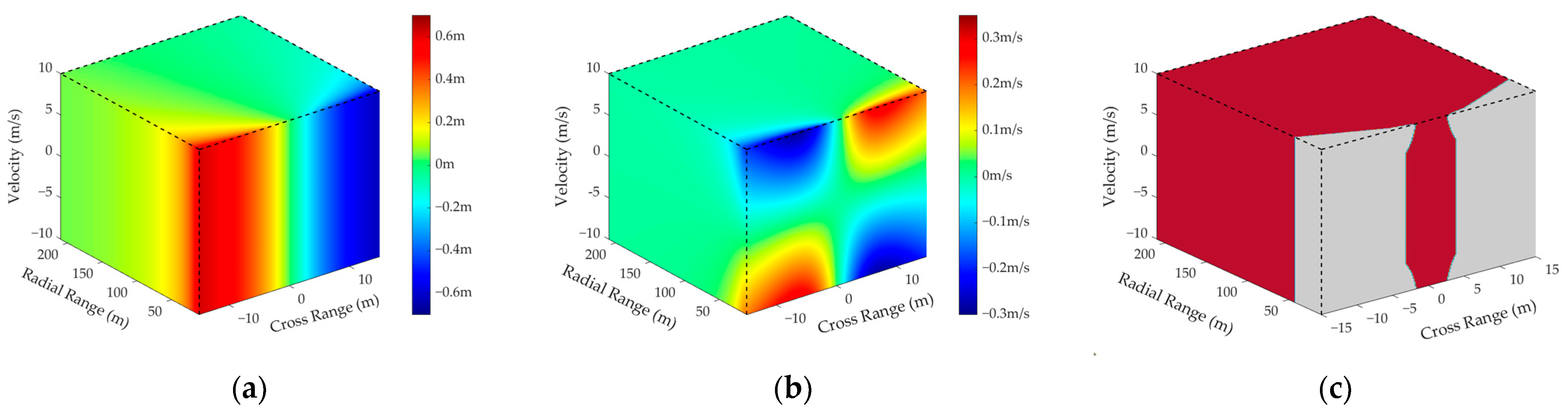
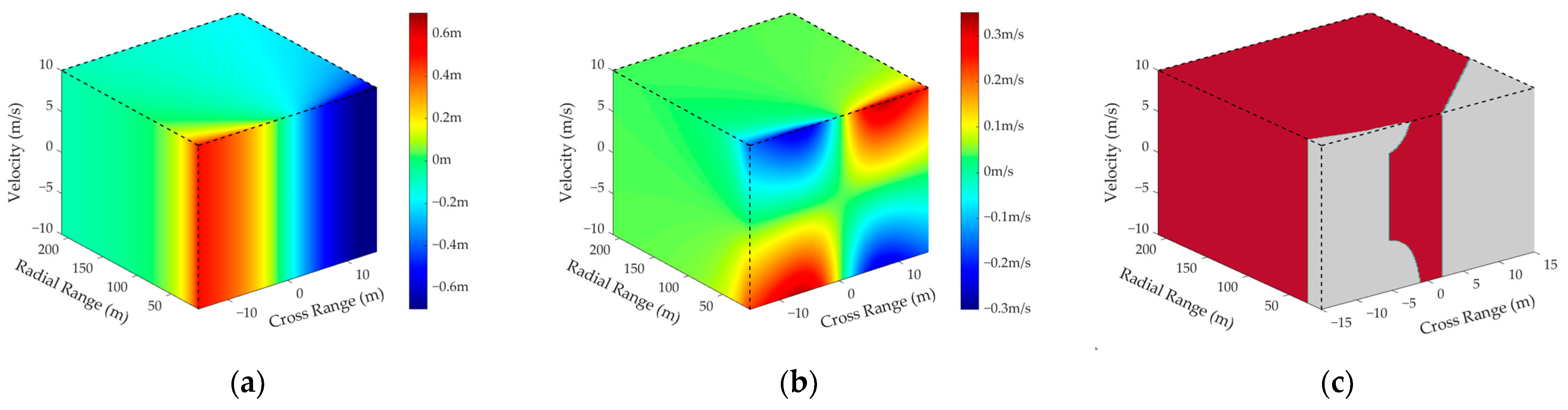
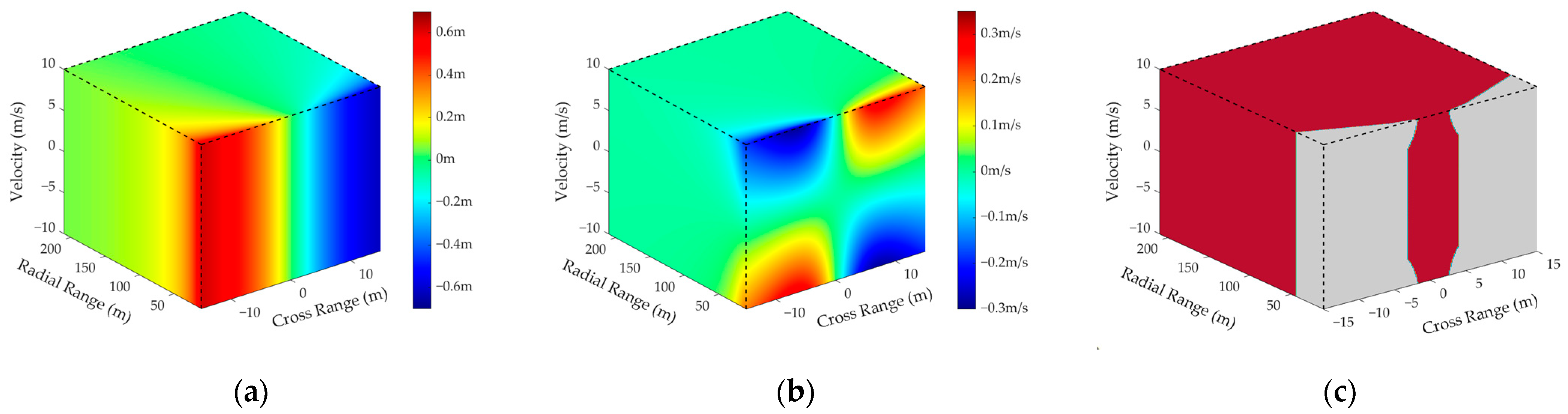

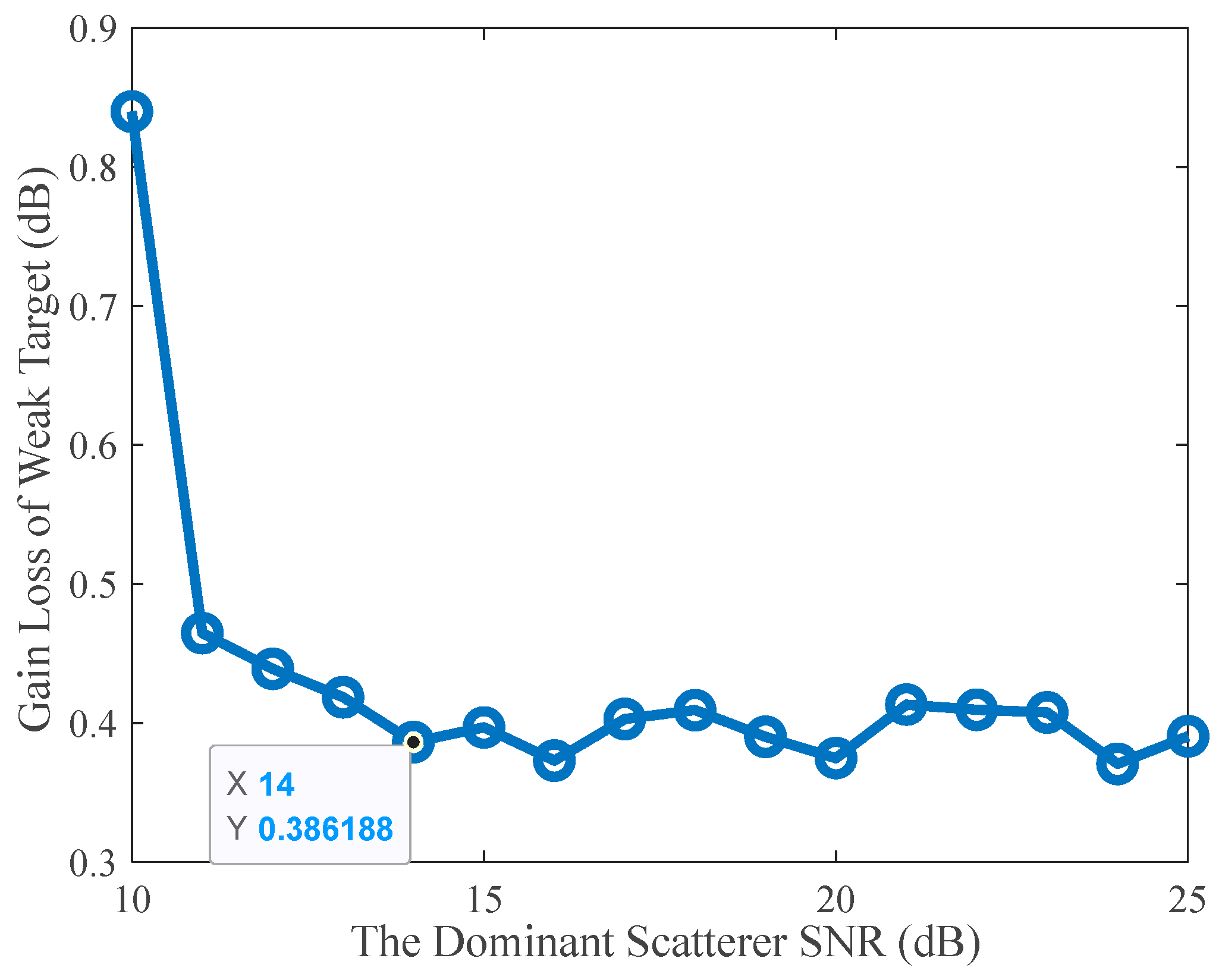
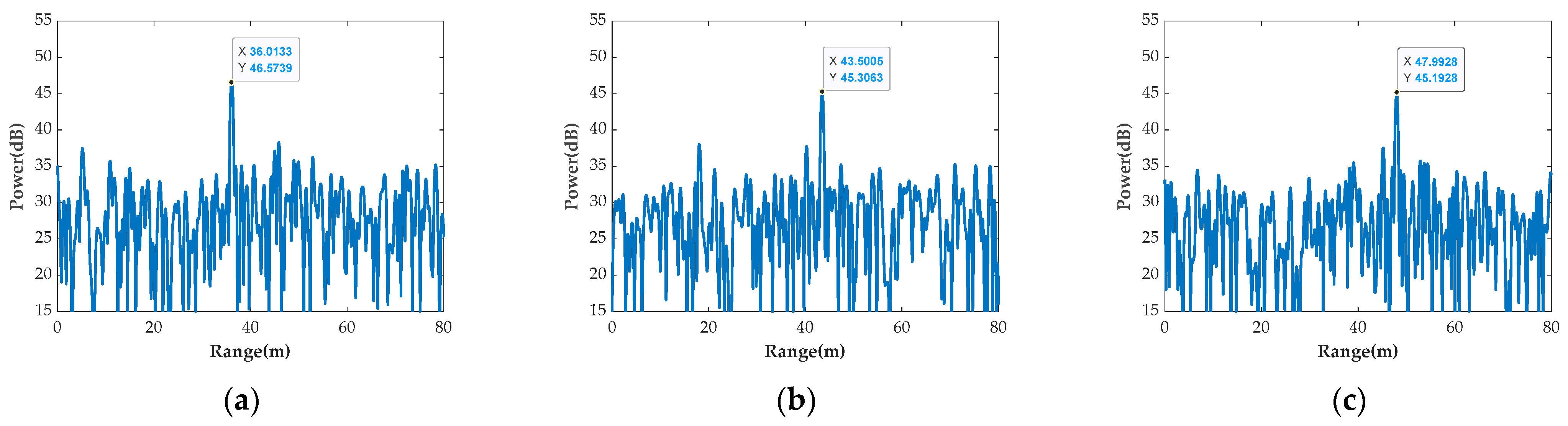

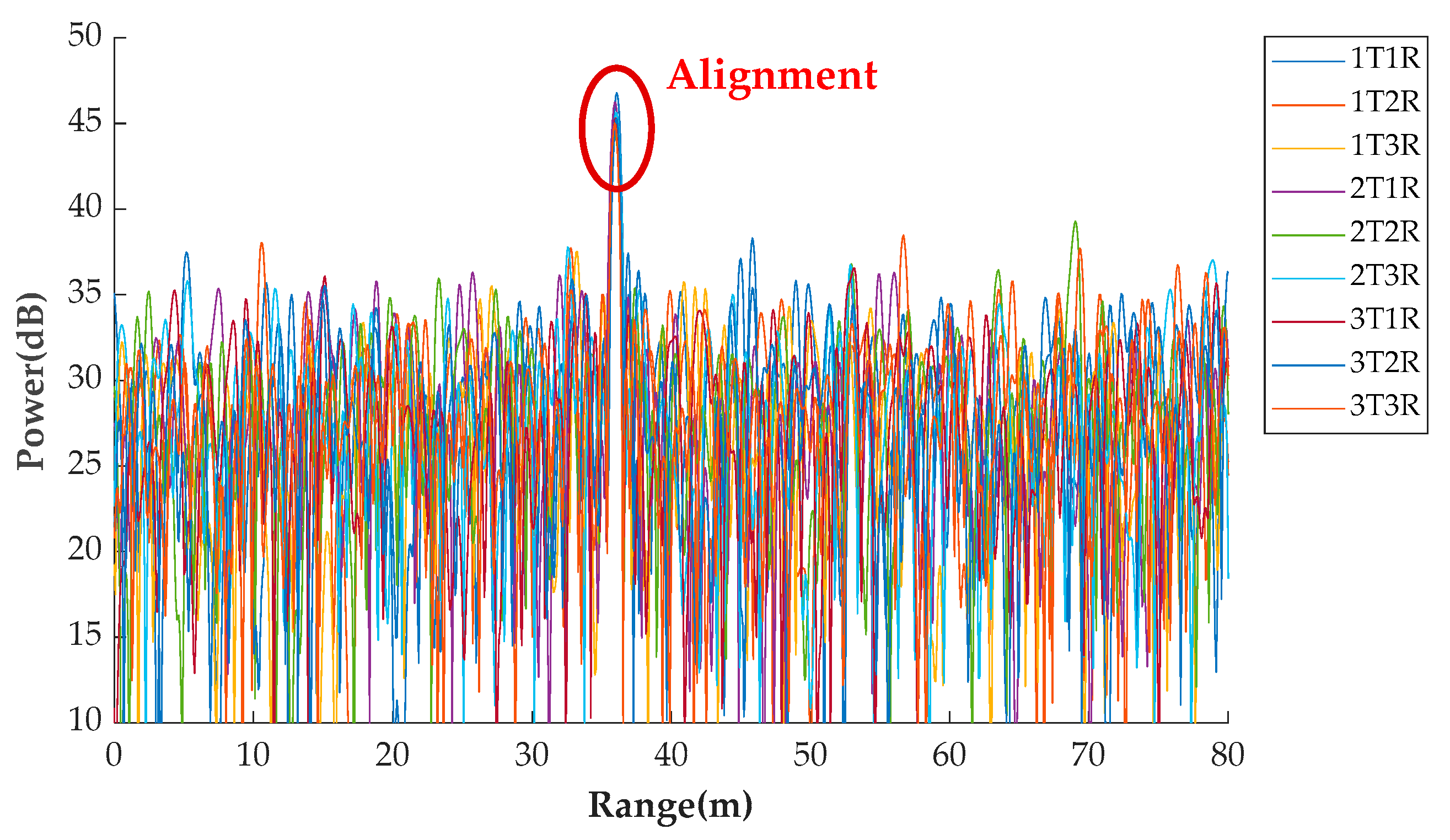
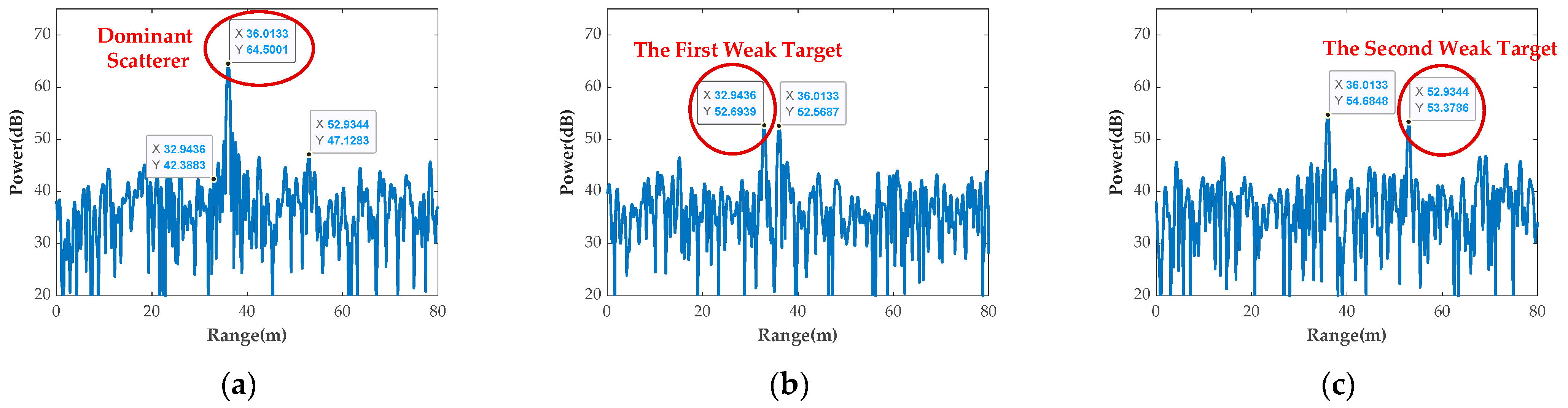
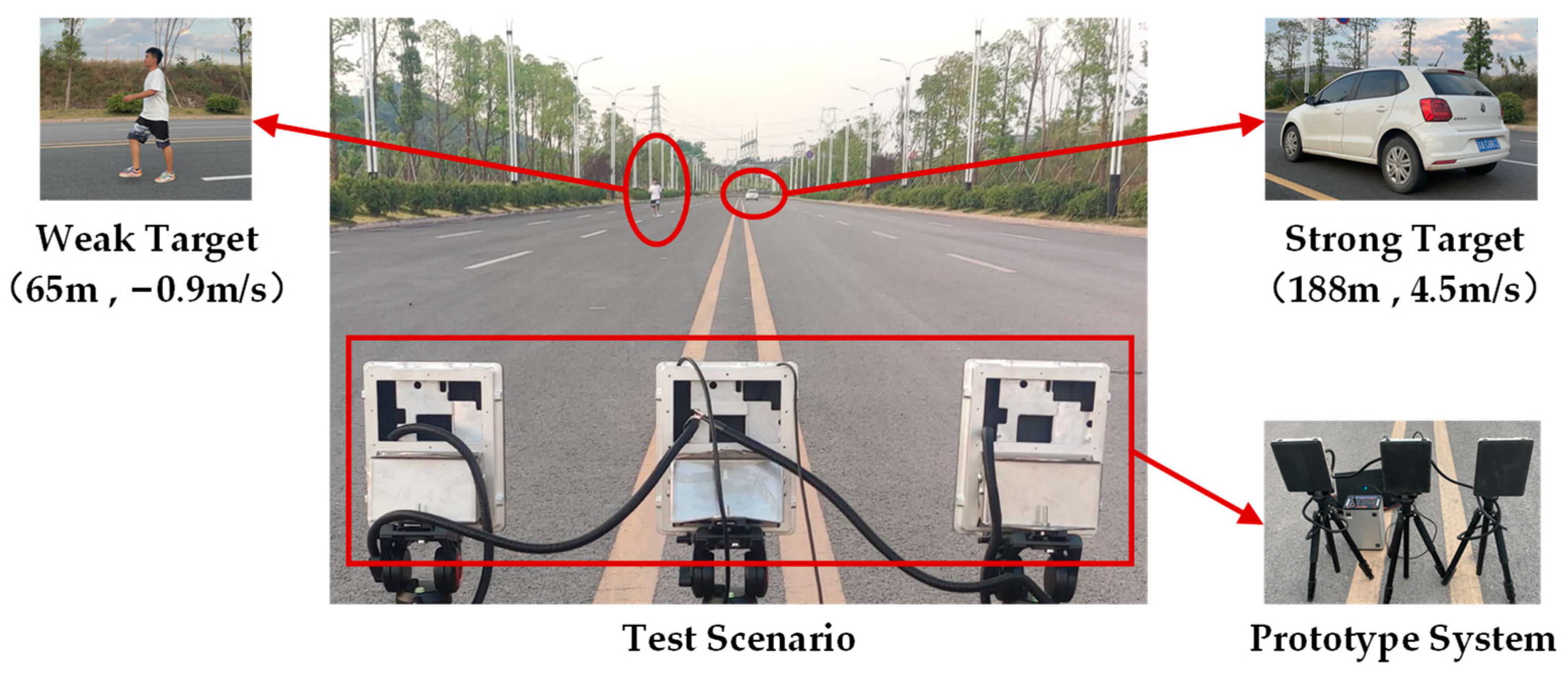

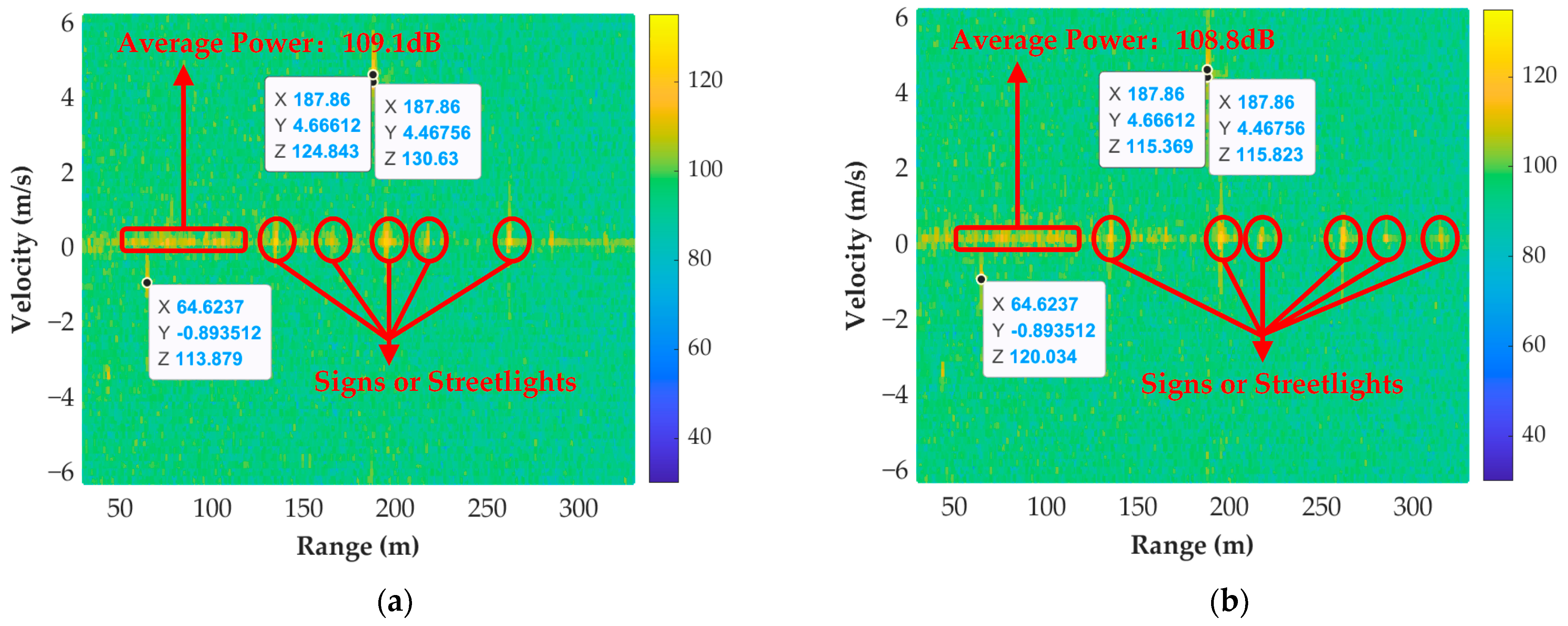
| Parameters | Test 1 | Test 2 | Test 3 | Test 4 |
|---|---|---|---|---|
| Cross range | 0 m | −10 m | 0 m | 0 m |
| Radial range | 60 m | 60 m | 150 m | 60 m |
| Velocity | 20 m/s | 20 m/s | 20 m/s | −5 m/s |
| Parameter | Value | |
|---|---|---|
| MMW DCAR | Carrier frequency | 77 GHz |
| Range resolution | 0.5 m | |
| Velocity resolution | 0.3 m/s | |
| Number of radars | 3 | |
| Radar spacing | 0.3 m/0.2 m | |
| Weak Target | Traversal region in cross range | [−15 m 15 m] |
| Traversal region in radial range | [10 m 210 m] | |
| Traversal region in velocity | [−10 m/s 10 m/s] | |
| Traversal interval in cross range | 0.15 m | |
| Traversal interval in radial range | 1 m | |
| Traversal interval in velocity | 0.2 m/s |
| Test 1 | Test 2 | Test 3 | Test 4 | |
|---|---|---|---|---|
| Proportion | 93.58% | 89.84% | 93.57% | 93.58% |
| Target Classification | Parameters | Value |
|---|---|---|
| Dominant Scatterer | Cross range | −3 m |
| Radial range | 45 m | |
| Radial velocity | −9 m/s | |
| SNR | 15 dB | |
| First Weak Target | Cross range | 0 m |
| Radial range | 30 m | |
| Radial velocity | 3 m/s | |
| SNR | 4 dB | |
| Second Weak Target | Cross range | 3 m |
| Radial range | 55 m | |
| Radial velocity | −2 m/s | |
| SNR | 3 dB |
| Parameters | Channels | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1T1R | 1T2R | 1T3R | 2T1R | 2T2R | 2T3R | 3T1R | 3T2R | 3T3R | ||
| Original signal | Noise power | 30.2 | 29.1 | 30.0 | 29.9 | 30.0 | 30.0 | 30.1 | 29.1 | 29.9 |
| Dominant scatterer SNR | 16.4 | 16.2 | 15.1 | 16.3 | 14.3 | 15.7 | 15.2 | 16.1 | 14.9 | |
| First weak target SNR | 2.9 | 5.3 | 4.1 | 4.0 | 3.7 | 3.8 | 3.2 | 5.7 | 4.2 | |
| Second weak target SNR | 2.4 | 3.0 | 1.8 | 4.3 | 3.5 | 2.7 | 2.2 | 4.8 | 2.0 | |
| Compensated signal | Noise power | 30.2 | 29.4 | 30.0 | 29.5 | 30.0 | 29.6 | 29.8 | 29.1 | 29.9 |
| Dominant scatterer SNR | 16.4 | 15.9 | 15.1 | 16.7 | 14.3 | 16.1 | 15.5 | 16.1 | 14.9 | |
| First weak target SNR | 2.9 | 5.0 | 4.1 | 4.4 | 3.7 | 4.2 | 3.5 | 5.7 | 4.2 | |
| Second weak target SNR | 2.4 | 2.7 | 1.8 | 4.7 | 3.5 | 3.1 | 2.5 | 4.8 | 2.0 | |
| Theoretical SNR | Dominant scatterer | 25.1 | ||||||||
| First weak target | 13.6 | |||||||||
| Second weak target | 12.5 | |||||||||
| Proposed method | Dominant scatterer | 24.9 (Gain loss: 0.2 dB) | ||||||||
| First weak target | 11.7 (Gain loss: 1.9 dB) | |||||||||
| Second weak target | 10.8 (Gain loss: 1.7 dB) | |||||||||
| Parameter | Value |
|---|---|
| Center frequency | 77.0 GHz |
| Bandwidth | 200 MHz |
| Chirp duration | 40 μs |
| Pulse repetition time | 48 μs |
| IF bandwidth | 12.5 MHz |
| Clock frequency | 80 MHz |
| Parameters | Channels | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1T1R | 1T2R | 1T3R | 2T1R | 2T2R | 2T3R | 3T1R | 3T2R | 3T3R | ||
| Original signal | Noise power | 89.2 | 88.6 | 87.8 | 89.8 | 89.4 | 88.5 | 88.8 | 89.0 | 87.9 |
| Vehicle Point 1 SNR | 21.3 | 22.3 | 23.9 | 23.8 | 24.3 | 23.5 | 24.4 | 23.5 | 25.4 | |
| Vehicle Point 2 SNR | 16.1 | 13.3 | 15.6 | 19.8 | 19.3 | 16.5 | 12.8 | 20.4 | 20.8 | |
| Pedestrian SNR | 14.4 | 12.6 | 12.5 | 16.5 | 16.6 | 14.1 | 11.6 | 13.8 | 14.8 | |
| Theoretical SNR | Vehicle Point 1 | 33.2 | ||||||||
| Vehicle Point 2 | 27.2 | |||||||||
| Pedestrian | 23.8 | |||||||||
| Proposed method | Vehicle Point 1 | 32.0 (Gain loss: 1.2 dB) | ||||||||
| Vehicle Point 2 | 26.2 (Gain loss: 1.0 dB) | |||||||||
| Pedestrian | 21.6 (Gain loss: 2.2 dB) | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, C.; Li, Y.; Hu, X.; Wang, Y.; Zhang, L.; Wang, M.; Guo, J. Coherent-on-Receive Synthesis Using Dominant Scatterer in Millimeter-Wave Distributed Coherent Aperture Radar. Remote Sens. 2023, 15, 1505. https://doi.org/10.3390/rs15061505
Liang C, Li Y, Hu X, Wang Y, Zhang L, Wang M, Guo J. Coherent-on-Receive Synthesis Using Dominant Scatterer in Millimeter-Wave Distributed Coherent Aperture Radar. Remote Sensing. 2023; 15(6):1505. https://doi.org/10.3390/rs15061505
Chicago/Turabian StyleLiang, Can, Yang Li, Xueyao Hu, Yanhua Wang, Liang Zhang, Min Wang, and Junliang Guo. 2023. "Coherent-on-Receive Synthesis Using Dominant Scatterer in Millimeter-Wave Distributed Coherent Aperture Radar" Remote Sensing 15, no. 6: 1505. https://doi.org/10.3390/rs15061505
APA StyleLiang, C., Li, Y., Hu, X., Wang, Y., Zhang, L., Wang, M., & Guo, J. (2023). Coherent-on-Receive Synthesis Using Dominant Scatterer in Millimeter-Wave Distributed Coherent Aperture Radar. Remote Sensing, 15(6), 1505. https://doi.org/10.3390/rs15061505








