Abstract
The target signal-to-noise ratio (SNR) can be notably improved by coherent-on-receive synthesis (CoRS) in distributed coherent aperture radar (DCAR). A core challenge of CoRS is to estimate the coherent parameters (CPs), including time, frequency, and phase, in order to cohere the multi-radar within DCAR. Conventional methods usually rely on the target’s own information to estimate the CPs, which is not available in highly dynamic environments. Additionally, the CPs of different targets, especially the phase, are unequal in high-frequency systems. This means that we cannot directly use the CPs of one target to compensate for others. To address these issues, an adaptive CoRS method using the dominant scatterer is proposed for millimeter-wave (MMW) DCAR in this paper. The basic idea is to correct the CPs of the dominant scatterer to compensate for other targets. The novelty lies in the adaptive phase compensation based on the estimated CPs. This phase compensation depends on a series of discrete phase values, which are derived from the limit of synthesis loss within a given configuration. Hence, this method avoids the requirement of prior information or massive searches for the possible locations of other targets. Moreover, the dominant scatterer in this work is an unknown target with strong scattering points in radar detection scenarios, and we focus on analyzing its selection criteria. To validate the proposed method, a prototype system has been fabricated and evaluated through experiments. It is demonstrated that the multi-target can realize CoRS effectively, thus enhancing the target SNR.
1. Introduction
Distributed coherent aperture radar (DCAR), which is composed of several independent unit radars, has potential for radar detection, tracking, and recognition [,,]. These unit radars can be placed in different positions and used together in a coherent and cooperative way to enhance the target energy significantly.
A typical mode of DCAR is coherent-on-receive synthesis (CoRS) [,,]. With this mode, DCAR could promote the target signal-to-noise ratio (SNR) by M2 times, where M is the number of unit radars. In CoRS, the multiple-unit radars rely on hardware for synchronization and transmit orthogonal signals [,,]. This hardware allows the target echoes to be separated at each receiver. By analyzing these echoes, we can estimate the coherent parameters (CPs) between different unit radars, including transmission time, frequency, and phase [,]. The estimated CPs can then be used to carefully adjust the echoes so that the echoes can be added together at the same time and phase. The synthesis performance of DCAR depends on high-accuracy CP estimations. Moreover, the demands for estimation accuracy also increase with the radar carrier frequency and bandwidth. Therefore, the majority of the research on CoRS is focused on the low-frequency system [,,].
To align the time and phase between unit radars, hardware-based methods have been investigated in the literature [,,,]. They utilize wired or wireless connections to obtain high-precision synchronization. However, these methods commonly require highly complex hardware. Additionally, even with almost ideal synchronization, real-time monitoring and calibration are still required in practical applications because of hardware instability.
Estimating the CPs based on observed target echoes is an effective way to solve the above problems. Existing estimation methods can be roughly divided into two categories. One is detecting the target’s own peak in returns for estimations [,], and the other is utilizing a cooperative target with prior information, called the dominant scatterer [,]. However, these methods are quite limited in highly dynamic scenarios. The former will fail when all scattering points of the target are undetectable, and the premise of the latter, requiring prior information, is hardly valid in many applications. Furthermore, using the estimated CPs of one target, the phases of other targets may still not be aligned in multiple-unit radars. This is caused by the spatial phase between different targets, which can be neglected in previous low-frequency systems. In high-frequency systems, such as millimeter-wave (MMW), the spatial phase may vary significantly, so we cannot directly use the estimated CPs of one target to compensate for the others.
In this paper, a novel CoRS method is proposed to solve the above issues for MMW DCAR. The basic idea is to correct the CPs of the dominant scatterer to compensate for other targets. Unlike the previous works that use a pre-positioned corner reflector or active backscatter transponder as the dominant scatterer, the proposed method employs an unknown target with strong scattering points to estimate the CPs in radar detection scenarios. For the dominant scatterer, we focused on analyzing its selection criteria and procedure. Furthermore, an adaptive phase compensation approach was explored to correct the estimated CPs of the dominant scatterer. This approach can compensate for the phases of different targets using a series of discrete phase values. Different from the general approaches that compensate the phases by searching for the possible positions of other targets point-by-point, the determination of discrete phase values in this approach is derived by the limit of synthesis loss within a given MMW DCAR configuration. This approach can simultaneously align the phase of targets located in a certain region based on the phase relationship between multiple unit radars. Hence, it can significantly reduce the number of phase compensations searches and remove the need for the spatial position of other targets. Finally, a prototype system composed of three MMW radars with a common trigger was fabricated, and the proposed concepts were confirmed via measurements with this prototype system. The main contributions in this work can be summarized as follows:
- We first introduce the coherent-on-receive synthesis into the millimeter-wave distributed coherent aperture radar. This method can be widely used in millimeter-wave radar applications, such as autonomous driving and precision guidance;
- An adaptive compensation approach is proposed to correct the estimated CPs of the dominant scatterer. On the one hand, prior information about the dominant scatterer is not required, and we can choose an unknown target with strong scattering points to estimate the CPs in radar detection scenarios. On the other hand, there is also no need for the spatial position of other targets as prior information;
- The proposed MMW DCAR can be adaptively cohered based on observed target echoes, thus reducing the hardware demands for high-accuracy synchronization.
The remainder of this paper is organized as follows. In Section 2, we introduce the workflow and signal model of CoRS in DCAR. In Section 3, the proposed method is described and derived in detail. Moreover, its constraints are also analyzed to present the selection criteria of the dominant scatterer. In Section 4, the proposed method’s evaluation via simulations is reported. Section 5 illustrates the real-data results with a prototype system to verify the feasibility of the proposed method. Finally, we conclude this paper with a summary of the main outcomes in Section 6.
2. Background
2.1. Workflow of CoRS in DCAR
The distributed coherent aperture radar (DCAR) is composed of M unit radars. An M2 SNR gain could be obtained over a unit radar when coherence-on-receive synthesis (CoRS) is realized, which makes it capable of attaining the equivalent performance compared with a large aperture radar.
There are three steps, including system hardware synchronization, coherent parameters estimation, and cohere-on-receive synthesis, in the operation procedure of CoRS, as displayed in Figure 1. The workflow can be illustrated as follows:
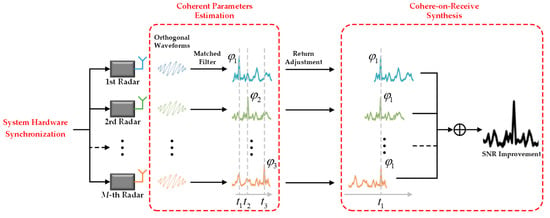
Figure 1.
The workflow diagram of CoRS in DCAR.
- The multiple-unit radars within DCAR rely on wired or wireless connections to ensure that they can operate at the same time.
- Due to the imperfect synchronization and the unequal range between different unit radars and targets, there are multidimensional differences between any two radars, called coherent parameters (CPs). To solve this problem, the multiple unit radars transmit the orthogonal waveforms with the same time base, which allows the target echoes to be separated at each receiver’s matched filter output. By detecting the target peaks in different echoes, the CPs can be estimated.
- The estimated CPs are used to adjust the echoes of multiple unit radars, and then the adjusted echoes are added together with the same time and phase to obtain the SNR gain.
2.2. Signal Model
Multiple-unit radars transmit the orthogonal waveforms to guarantee that mixed echoes can be separated at the receivers. The basis waveform in this work is the fast chirp sequence [,,,,], where a series of chirp signals is successively transmitted in one coherent processing interval (CPI). With the basis waveform, various orthogonal techniques have been reviewed in [], such as time division, frequency division, and code division.
The frequency-division method limits the available bandwidth for each transmitter as well as the range resolution [,]. Moreover, its intermediate frequency (IF) should have a large bandwidth to hold the mixer output, resulting in high hardware costs. The code-division method modulates different phase sequences on the transmission pulses [,,]. Due to its imperfect orthogonality, this waveform will have relatively high sidelobes in the spectrum. The high sidelobes may reduce the estimation accuracy of coherent parameters, resulting in an overall loss of synthesis.
Considering the above issues, we recommend using the time-division method. This method is simple, but the unambiguous Doppler range will be reduced. To solve this problem, staggered PRT or multiple PRT approaches can be used to estimate the ambiguity number [,]. These approaches have a good performance in resolving velocity ambiguity, yet have a relatively low data rate. Additionally, the time-division method will also receive interference signals from other radars in many applications, such as traffic scenarios. Although the parameters of the signals may be different, they may produce non-phase-referenced interference, which will limit the performance of CoRS. In this regard, interference mitigation approaches [,,,] can be employed to solve this issue. Based on these approaches, we can first estimate the interfering signal. Then, after removing the estimated interference, the radar echoes can be restored with sparsity-based techniques.
Utilizing the time-division method, as shown in Figure 2, in a single chirp duration, only one unit radar transmits a linear chirp of the form:
with carrier frequency , frequency slope , where B is the sweep bandwidth and T represents pulse repetition time (PRT).
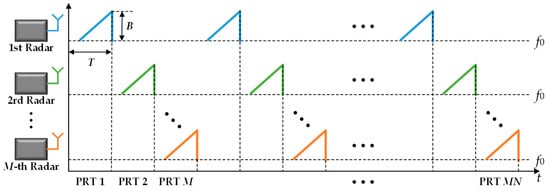
Figure 2.
The fast chirp sequence waveform used in the MMW DCAR with time-division method.
Since the proposed MMW DCAR only relies on a common trigger for synchronization, it leads to multidimensional synchronization errors between any two unit radars. Assuming that the synchronization errors of the m-th radar, compared with the reference radar (the first radar), include time synchronization error , frequency synchronization error , and phase synchronization error , the echo of the m-th transmitting radar and the n-th receiving radar can be expressed as
with
where and represent the sum of the propagation distance and radial velocity of the target, and c is the speed of light.
Further, the beat signal can be obtained with de-chirp processing as
Supposing , where is the sampling time in PRT and denotes the velocity dimension sampling time, the beat signal can be modified as
Note that the quadratic phase terms within the beat signal have been neglected because their contribution to the phase change is small, referring to []. Further, the beat signal can be simplified as
where
The classical signal model with the time-division method was derived. Usually, the sampled data are stacked together in a cube according to the fast time and slow time. Hence, the range and velocity of the targets are separately extracted with a two-dimensional fast Fourier transform (2D-FFT) from this data cube, which can be expressed as
where represents the 2D-FFT processing.
Clearly, the target can be focused on the range–Doppler spectrum; however, there is an uncertain deviation caused by the synchronization errors. To estimate the deviations in range or the Doppler spectrum, we can detect the target peak in different echoes. However, the phase deviation, as in Equation (12), which is proportional to the radar carrier frequency, is related to the target’s spatial position and the synchronization errors. Therefore, it may vary significantly for different targets in high-frequency systems. This means that the available region for estimating CPs of phases is quite limited. When we compensate the phases using the CPs of one target, the phases of other targets cannot be aligned, leading to a great CoRS loss.
3. Proposed Method
To solve the above problem, a novel coherent-on-receive synthesis method using the dominant scatterer is proposed, and its processing flow is presented in Figure 3.
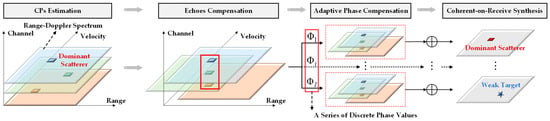
Figure 3.
The processing flow of the proposed method using the dominant scatterer.
First, the proposed method uses the dominant scatterer to estimate CPs, in which the dominant scatterer is realized as an unknown strong target in radar detection scenarios.
Second, the echoes of multiple unit radars can be compensated with the estimated CPs of the dominant scatterer. In this way, the range and velocity of different targets in multiple unit radars can be aligned, but the phase requires further adjustment.
Third, an adaptive compensation approach was explored to align the phases of various targets in multiple unit radars. The phases of different targets are compensated with discrete phase values. Unlike the general approaches that compensate the phases by searching for the possible positions of other targets point-by-point, the determination of discrete phase values in this work is derived by the limit of synthesis loss within a given MMW DCAR configuration. This approach can simultaneously align the phase of targets located in a certain region based on the phase relationship between multiple unit radars. Hence, it can significantly reduce the number of phase compensation searches, and there is no need for the spatial position of other targets.
Furthermore, we derived the constraints of the proposed method and focused on analyzing the selection criteria and procedure of the dominant scatterer. The theoretical CoRS gain is also deduced to evaluate the performance of the proposed method in practice.
3.1. CP Estimation Using Dominant Scatterer
According to the focusing positions, we can estimate the CPs using the dominant scatterer. In previous works, the dominant scatterer was realized as a pre-positioned corner reflector or active backscatter transponder, which is hardly valid in high-dynamic scenarios. Instead, the dominant scatterer in this work is defined as an unknown target with strong scattering points in radar detection scenarios, such as vehicles, signs, etc.
The specific estimation method is similar to conventional methods. Assuming that channel 1T1R is the reference channel, which consists of the first transmitting and receiving radar, according to Equation (9), the beat signal in channel 1T1R without synchronization errors can be derived and simplified as
Correspondingly, the estimated CPs for time can be obtained as
Similarly, the estimated CPs for velocity can be calculated as
Moreover, the CPs for phase can also be estimated as
3.2. Echoes Compensation and Analysis
Using the estimated CPs, as in Equations (15) to (17), the beat signal can be compensated as
After compensation, the multidimensional parameters can be aligned with the reference channel. This means that the echoes can be added together to enhance the SNR of the dominant scatterer. However, due to the spatial difference, the compensated signal of other weak targets may have deviations. These deviations may lead to a great synthesis loss of weak targets. Therefore, we carefully derive the deviations and present an analysis thereof in the following.
Assuming that the CPs of a weak target can be estimated, the ideal compensated signal can be aligned to the reference channel and is expressed as
where and denote the range and velocity of the weak target in reference channel.
Due to the lack of the estimated CPs of the weak target, we can only utilize the CPs of the dominant scatterer to compensate for the beat signal. In this way, the compensated signal can be derived as
Comparing Equations (19) and (20), it is apparent that the results including range, velocity, and phase are shifted. Specifically, the deviations can be calculated as
Herein, the range and velocity deviations are simplified because the neglected terms are much smaller than the reserved ones, which can be expressed as follows.
Obviously, the deviations in range and velocity are caused by the geometry of the target relative to multiple unit radars. It is difficult to further compensate them due to the lack of a weak target position. In this regard, we define the constraints for dominant scatterer compensation so that these two deviations cannot exceed half a resolution cell after compensation. The specific derivation and analysis are presented in Section 3.4.
The phase deviation, as in Equation (23), is composed of two terms. The former is only determined by multi-target spatial positions, and the latter is a coupling term with the spatial positions and the synchronization errors. Similarly, it is difficult to accurately compensate for the phases due to the lack of weak target information. Moreover, the phase deviation is proportional to the radar carrier frequency. It will vary significantly for different targets in the MMW system, and hence is required to be adjusted for effective CoRS.
3.3. Adaptive Compensation for Phases
To align the phases of different targets in multi-channels, an adaptive compensation method is proposed. Considering that the phase deviation is composed of two terms, we performed two-step compensations to align the phases in multi-channels.
First, we utilized the information and CPs of the dominant scatterer to compensate for the coupling term, which is composed of the spatial positions and the synchronization errors. Thereafter, due to the lack of weak target information, we propose to compensate the phase adaptively with discrete phase values. The determination of discrete phase values is derived from the limit of synthesis loss within a given MMW DCAR configuration. Hence, this approach can simultaneously align the phase of targets located in a certain region based on the phase relationship between multiple unit radars. It can significantly reduce the compensation number and remove the need of the spatial position of weak targets.
3.3.1. Compensation for Coupling Term
To eliminate the coupling term of phase deviation, the signal of each channel can be compensated with the CPs of the dominant scatterer and can be expressed as
where represents the cells in range spectrum.
After compensating for the coupling term, the phase deviation of the weak target can be derived as
Herein, it is apparent that the compensated phase deviation only relies on the multi-target spatial positions.
3.3.2. Compensation for Spatial Phase
Although the compensated phase deviation is only related to the multi-target positions, aligning the phases of weak targets is a challenging task. On the one hand, we cannot obtain prior information on weak targets to compensate the phase directly. On the other hand, compensating via searching for the possible positions of the weak targets leads to a large number of compensations. To this end, we propose to compensate the phase adaptively with discrete phase values, which are derived by the limit of synthesis loss within a given MMW DCAR configuration.
First, in a given configuration, the relative relationships of the compensated phase deviations of the weak targets within multi-channel are derived. Second, we define the acceptable synthetic gain loss and construct an inequality equation from this loss. Finally, the phase tolerance is deduced by solving the inequality equation. The phase tolerance is a discrete phase value, which can be defined as the maximum acceptable phase difference between any two channels. According to this tolerance, we can adjust the phases of multi-channel adaptively with the relative relationship. The specific derivation of this approach is described as follows.
The compensated phase deviation in channel mTnR in Equation (27) can be rewritten as
where and represent the one-way propagation range from dominant scatterer and weak target to i-th radar.
In a given MMW DCAR configuration, the relative relationship of the compensated phase deviations can be derived as
Thereafter, we analyzed and derived the signal power after CoRS. Herein, it is assumed that multi-channel signals after compensation have the same amplitude and only the phase deviations. For the MMW DCAR composed of N unit radars, the signal power of channels after CoRS can be expressed as
Correspondingly, the theoretical signal power after synthesis, in which each channel is aligned to the reference channel, can be denoted as
Due to the phase deviations, there is a certain gain loss. We define the acceptable synthetic gain loss as PGL, which can be expressed as
According to the Euler formula, it can be rewritten as
By solving the inequality equation, Equation (33), we can obtain a certain phase tolerance. This tolerance is defined as the maximum acceptable phase difference between any two channels and can be derived as
This phase tolerance is a discrete phase value, that is used to guide the compensation of each channel. For an arbitrary channel, we can cyclically compensate a phase value to satisfy the derived tolerance. Within the phase region , the number of compensations can be denoted as
and the value for each compensation can be expressed as
It should be noted that only the channels from 1T2R to 1TNR are required to be compensated. Owing to the relationship, as in Equation (29), the remaining channels can be compensated adaptively. Therefore, the total number of compensations for N unit radars can be deduced as
Utilizing the proposed method, the phases of the weak target can be aligned in one of the sets of compensations. This method can simultaneously align the phase of targets located in a certain region based on the phase relationship between multiple unit radars. Hence, it can significantly reduce the number of compensations, and there is no need for the spatial position of other targets.
3.4. Selection of Dominant Scatterer
The dominant scatterer in this work is defined as an unknown target with strong scattering points in radar detection scenarios, such as vehicles, signs, etc. Its selection may directly affect the synthetic performance of other targets. Therefore, we focused on analyzing the selection criteria and procedure of the dominant scatterer.
The constraints of the proposed method will vary with the positions of the dominant scatterer, and the synthetic gain of weak targets also relies on the dominant scatterer’s SNR. In this regard, we defined the constraints using the dominant scatterer and performed the simulations on the influence of the dominant scatterer position and SNR. The selection criteria and procedure can be obtained from the results.
3.4.1. Analysis of Constraints
In Section 3.2, we derived and analyzed the deviations in range and velocity after compensation using the dominant scatterer. These two deviations may lead to the failure of the proposed method. This means that the compensations using the dominant scatterer are valid for a certain region, as depicted in Figure 4. Specifically, we defined the constraint that the deviations could not exceed half of a resolution cell after compensation.

Figure 4.
Conceptual diagram of constraints for the compensation using the dominant scatterer.
For the purpose of simplification, the MMW DCAR used in this work was considered a rigid system. Namely, the relative motion states of multi-unit radars can be considered constant. On this basis, a typical scenario composed of the MMW DCAR and two targets is displayed in Figure 5. The specific constraints in this scenario are derived as follows.
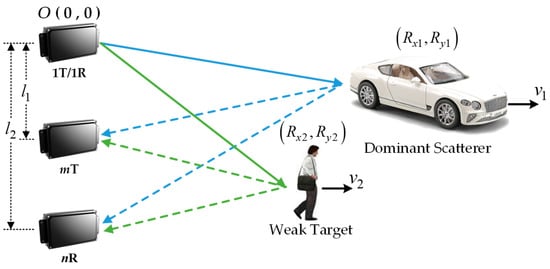
Figure 5.
Geometric diagram of the DCAR and multi-target.
The compensated signals of the weak target should be focused on the same range cell in each channel, which can be expressed as
where represents the range resolution. As shown in Figure 5, the coordinates of the weak target are required to meet the first constraint, which can be further deduced as
Similarly, the compensated signal must be focused on the same velocity cell, which can be denoted as
where represents the velocity resolution. Then, we can derive the second constraint for the weak target as
Furthermore, due to the shift of the range spectrum caused by the synchronization errors, the proposed method requires that the multi-target in all channels must be within the observation region after translation, which can be denoted as
where Rmax is the maximum observation in the range spectrum. Hence, the third constraint can be derived as
In summary, the compensations for weak targets are valid for a certain region that relies on the position and velocity of the dominant scatterer. We performed the simulations on this in the next subsection to analyze the selection criteria for the dominant scatterer.
3.4.2. Selection Criteria
We performed the simulations to determine the influence of the dominant scatterer position and SNR. The selection criteria and procedure can be obtained from the results.
The comparison tests are composed of four scenarios in which the dominant scatterer is located in different positions, as given in Table 1. Moreover, the parameters of the MMW DCAR configuration and the weak target traversal region are presented in Table 2.

Table 1.
Parameters of the dominant scatterer position.

Table 2.
Parameters of the MMW DCAR configuration and weak target.
According to Equations (21) and (22), the deviations in range and velocity are calculated and depicted in Figure 6, Figure 7, Figure 8 and Figure 9. The effective regions, satisfying the constraint that the deviations cannot exceed half of a resolution cell after compensation, are also presented. The part marked in red corresponds to the effective region, which covers the majority of radar detection scenarios. This means that the proposed method can be effectively adapted to many applications.
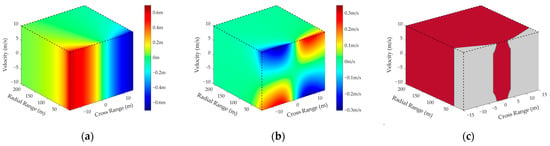
Figure 6.
The simulation results of Test 1. (a,b) display the range and velocity deviations. (c) represents radar detection scenario, including effective region (red) and ineffective region (gray).
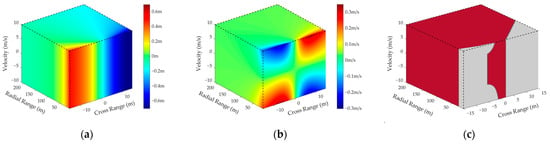
Figure 7.
The simulation results of Test 2. (a,b) display the range and velocity deviations. (c) represents radar detection scenario, including effective region (red) and ineffective region (gray).
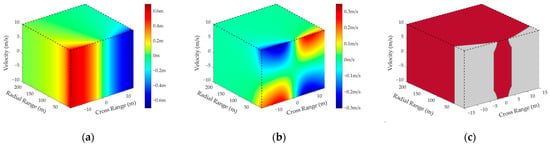
Figure 8.
The simulation results of Test 3. (a,b) display the range and velocity deviations. (c) represents radar detection scenario, including effective region (red) and ineffective region (gray).
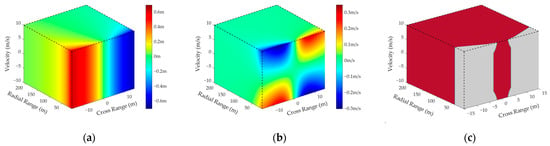
Figure 9.
The simulation results of Test 4. (a,b) display the range and velocity deviations. (c) represents radar detection scenario, including effective region (red) and ineffective region (gray).
As shown in Figure 6, Figure 7, Figure 8 and Figure 9, it is apparent that the radial range and velocity of the dominant scatterer have a negligible impact on the effective region. On the contrary, the deviations will increase with the cross range, and the corresponding effective region will reduce significantly, as shown in Table 3. Therefore, the first criterion is that the dominant scatterer should be close to the normal direction of MMW DCAR, i.e., its azimuth should be relatively small.

Table 3.
The proportion satisfying the constraints.
The dominant scatterer in this work is a non-cooperative target, which may have multiple scattering points at a short range []. The CP estimations require scattering point matching; the multiple scattering points can lead to mismatching and a negative estimation. Thus, we recommend choosing a target with a medium- or long-range as the dominant scatterer, which is the second selection criterion.
Furthermore, the dominant scatterer’s SNR determines the accuracy of the CP estimations, which potentially has an essential impact on the synthetic performance of weak targets. In this regard, we performed the simulations on the synthetic gain loss of the weak target with respect to the dominant scatterer’s SNR. The dominant scatterer SNR was set from 10 dB to 25 dB with a 1 dB interval, and 1000 Monte Carlo simulations were performed for each SNR.
The simulation results are displayed in Figure 10. As the dominant scatterer’s SNR increases, the synthetic performance of the weak target is enhanced. In particular, the synthetic performance tends to be stable with an SNR higher than 13 dB. Hence, the third criterion is to choose one of the targets with a higher SNR as the dominant scatterer. For a scenario containing multiple high SNR targets, these targets can all be used as the dominant scatterer, and can then be further refined using the above two criteria.
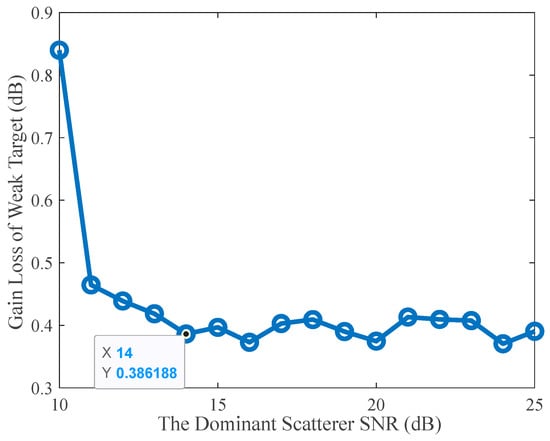
Figure 10.
The synthetic SNR gain loss of the weak target versus the dominant scatterer’s SNR.
In summary, the dominant scatterer in the paper can be defined as a medium- or long-range target that is close to the radar’s normal direction. Moreover, its SNR should be as higher than 13 dB as possible. According to these selection criteria, the selection procedure of the dominant scatterer in practice is illustrated in Figure 11.
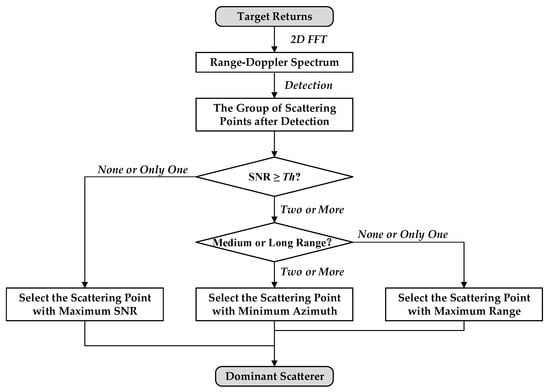
Figure 11.
The selection procedure of the dominant scatterer, where Th is set to 13 dB in this paper.
3.5. Derivation of Theoretical Synthetic SNR
SNRs in multiple unit radars may be different due to the influence of noise. Hence, to evaluate the proposed method, the theoretical synthetic SNR is required to be derived as follows.
Assuming that the signal amplitude and noise power in channel mTnR are Kmn and Pmn, the target SNR can be expressed as
Thereafter, the theoretical signal amplitude after CoRS is the sum of the signal amplitude in each channel, which is expressed as
Similarly, the accumulated noise power after CoRS can be denoted as
Therefore, the theoretical SNR can be obtained as
Let , which indicates the noise power ratio of the channel mTnR to the reference channel. Thereby, we can rewrite Equation (47) as
4. Simulations
We assessed the proposed method via simulations and present an analysis thereof. A typical scenario composed of one dominant scatterer and two weak targets was set up. The synthetic performance of all targets in continuous CPIs is presented, and the specific results are discussed within a single CPI. Moreover, the proposed method is also compared with the noncoherent integration method in terms of detection improvement.
4.1. CoRS for Multiple Targets
The simulation scenario is composed of three targets, the parameters of which are given in Table 4. The used MMW DCAR consists of three unit radars. It is important to note that the acceptable synthetic gain loss is defined as 3 dB in simulation. Therefore, the phase tolerance can be calculated as 27.9° according to Equation (34). Additionally, the compensation number for each channel and the MMW DCAR can be deduced as 7 times and 49 times, respectively.

Table 4.
Parameters of multiple targets.
4.1.1. Synthetic Results in Continuous CPIs
Utilizing the proposed method, the synthetic results of different targets in continuous CPIs are illustrated in Figure 12. Herein, the theoretical SNR, as in Equation (48), was used as a guideline for evaluation.
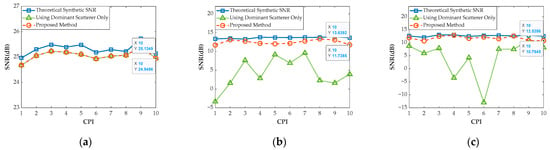
Figure 12.
Multi-target coherent-on-receive synthesis results in consecutive CPIs. (a) Results of the dominant scatterer. (b) Results of the first weak target. (c) Results of the second weak target.
Since the multidimensional parameters of the dominant scatterer can be aligned with its own estimated CPs, the synthetic results in Figure 12a are consistent whether adaptive phase compensation is employed or not. However, due to the phase deviation, the synthetic performance of weak targets will decline significantly when using the dominant scatterer compensation only, as illustrated in Figure 12b,c. Instead, the synthetic results of weak targets can be effectively improved with the proposed method. Particularly, the maximum gain loss of these targets is 1.9 dB, which satisfies the definition.
4.1.2. Synthetic Results within a Single CPI
To demonstrate the synthetic performance, the simulation results of the 10th CPI are presented in Figure 13, Figure 14 and Figure 15. Due to the synchronization errors, these targets focused on different range cells in multi-channel, as illustrated in Figure 13. The echoes can be calibrated with the estimated CPs of the dominant scatterer. Figure 14 shows that the deviations caused by the synchronization errors were eliminated, and thereby the multi-target was aligned in the range spectrum. From Figure 15a, the dominant scatterer can be synthesized effectively, while the weak targets suffer a great loss due to the phase deviation. Utilizing the proposed method, the weak targets can achieve CoRS with adaptive phase compensation, as shown in Figure 15b,c.
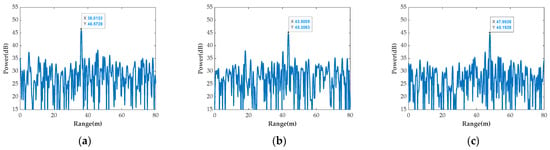
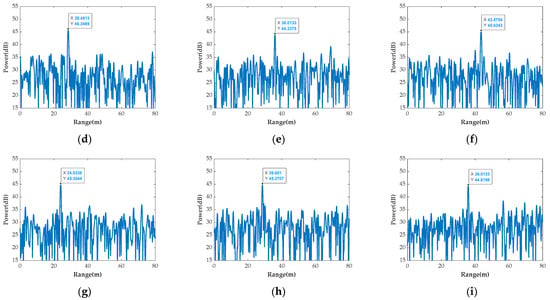
Figure 13.
The range spectra of the original beat signal in multi-channel. (a–i) are the channels 1T1R to 3T3R, respectively.
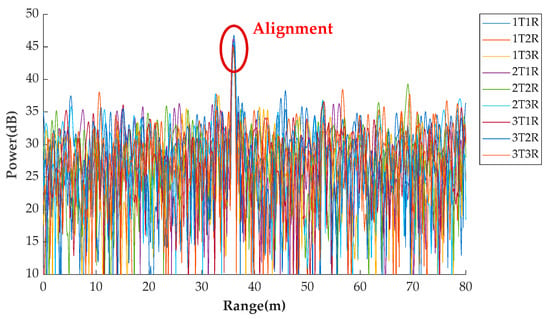
Figure 14.
The range spectra after dominant scatterer compensation.
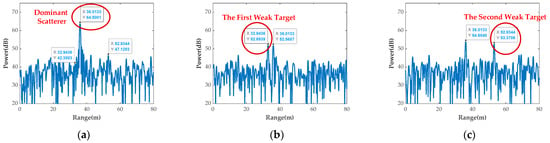
Figure 15.
Multi-target CoRS results via the proposed method. (a) Results of the dominant scatterer. (b) Results of the first weak target. (c) Results of the second weak target.
To specifically verify the effectiveness of the proposed method, Table 5 gives the numerical comparison results. Since the signal discreteness in FFT processing causes a fence effect, the targets’ SNRs have a slight variation after compensation using estimated CPs. It is verified that the targets’ SNRs in multi-channels do not change significantly, and thus their impact can be neglected in the actual processing.

Table 5.
The numerical comparison results (dB) of simulations.
For the dominant scatterer, its synthetic SNR is 24.9 dB, with a gain loss of 0.2 dB compared to the theoretical result. Additionally, with the proposed method, the SNR gain losses of two weak targets are 1.9 dB and 1.7 dB, respectively. In summary, it is demonstrated that these targets can match the defined acceptable synthetic gain loss well. Namely, multi-target can be effectively synthesized, thus improving the target SNR and enhancing the radar detection performance significantly.
4.2. Detection Performance Comparison
The feasibility of the proposed method was further evaluated with the constant false alarm detection (CFAR) algorithm [,,]. We compared it with the noncoherent integration method based on the square law detector [,]. Herein, the dominant scatterer with SNR = 20 dB was fixed, and a weak target was randomly generated in the radar detection region that satisfies the constraints, with the weak target’s SNR in a single channel set from 0 dB to 20 dB. We performed the Monte Carlo simulations 1000 times via different methods, which are demonstrated in Figure 16.
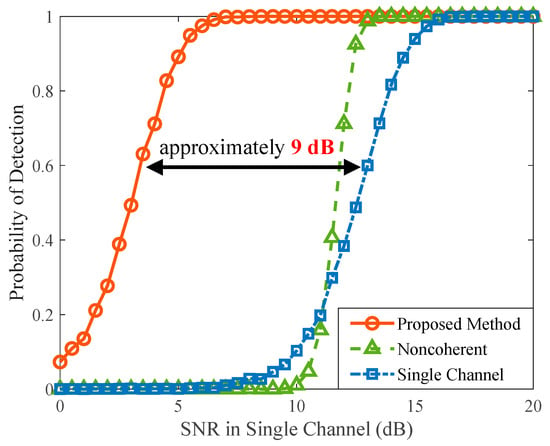
Figure 16.
Detection performance utilizing CFAR algorithm with 1000 Monte Carlo simulations.
Compared with using a single channel, using two types of synthesis methods can improve the detection performance. However, the noncoherent integration method suffers a great loss in the case of a low SNR. As the SNR increases, this method can enhance target detection, with a maximum gain of approximately 3.5 dB. On the contrary, the proposed method is stable at both high and low SNR conditions. With an equivalent detection probability, the proposed method improves by approximately 9 dB.
5. Experiments
The proposed CoRS method using the dominant scatterer was verified by measurements in a typical urban environment. The prototype system was fabricated, and the hardware components of the MMW DCAR are presented.
The prototype system in this work is composed of three radars with an operating frequency range of 76.0 GHz to 81.0 GHz. It employs a wired trigger, which is generated by a separate signal source and provides a trigger pulse to the radars with cables of equal length. An overview of the basic parameters of these radars is given in Table 6.

Table 6.
Parameters of the test radars.
In the prototype system, a certain timing difference between the high levels of the trigger pulse at the radars is unavoidable because of the imperfect electrical length of the lines. Since each radar is independent, there may be an uncertain timing difference when their internal clocks detect the trigger pulse. The combined timing difference is the main factor that contributes to the arbitrary initial time delay. Furthermore, these independent unit radars are also subject to random deviations in carrier frequency and phase.
The prototype system, which contains three MMW radars and a wired trigger, is displayed in Figure 17. The test scenario consisted of a vehicle as the dominant scatterer and a pedestrian as the weak target.

Figure 17.
The prototype system and the test scenario consisting of a vehicle and a pedestrian.
With the time-division method, the multi-channel signals can be separated at each receiver. The range–Doppler spectra are presented in Figure 18. Clearly, due to the system synchronization errors, the focus positions are offset, which can be calibrated with the dominant scatterer.
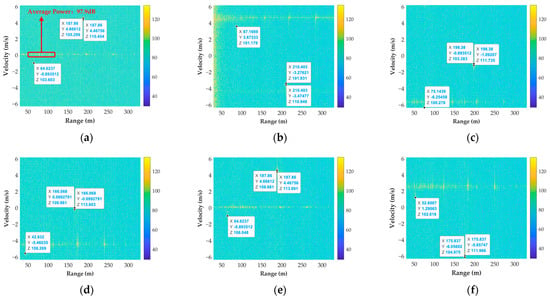
Figure 18.
The range–Doppler spectra of multi-channel with real data. (a–i) are the channels 1T1R to 3T3R, respectively.
In the real-data experiment, the vehicle had two strong scattering points. We chose the stronger scattering point as the dominant scatterer of the proposed method. The optimal synthetic results for the vehicle and the pedestrian are demonstrated in Figure 19a,b, respectively.
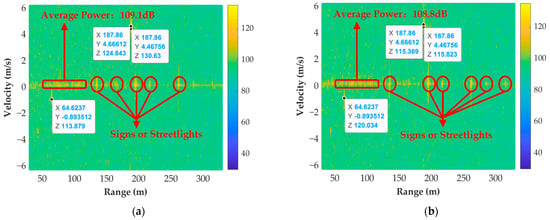
Figure 19.
The optimal CoRS results in multiple-phase compensation groups. (a) Results of the vehicle. (b) Results of the pedestrian.
The numerical comparison results from the real-data experiment are given in Table 7. The theoretical SNR of the stronger scattering point after synthesis is calculated at 33.2 dB, while the actual SNR can be improved to 32.0 dB. For weak scattering points, the CoRS can be realized by using the estimated CPs only. Its theoretical and actual SNR after synthesis are 27.2 dB and 26.2 dB, respectively. The pedestrian is also synthesized with the proposed method, and its theoretical and actual SNR after synthesis can be calculated as 23.8 dB and 21.6 dB. Additionally, it should be noted that several stationary targets including signs and streetlights can also be effectively synthesized, as shown in Figure 19. To sum up, the proposed method satisfies the defined acceptable synthetic gain loss (3 dB) for each target, which can enhance the target SNR effectively.

Table 7.
The numerical comparison results (dB) with real data.
Furthermore, the power near the zero frequency in the Doppler spectrum is higher than that at other frequencies. This is caused by the ground clutter and some stationary targets (e.g., trees, curbs, etc.) in the urban environment. As illustrated in Figure 18a and Figure 19a, the signal power in this part is 97.9 dB and 109.1 dB, with 11.2 dB of gain. It is well known that the ideal synthetic gain for targets is approximately 19.0 dB, while the gain for noise is 9.5 dB. Consequently, the gain of clutter is intermediate between the noise and the target, which may have a negative impact on the improvement of the proposed method for stationary targets.
6. Conclusions
This paper describes a millimeter-wave distributed coherent aperture radar that can be used to improve the target SNR by coherent-on-receive synthesis. The synchronization errors are calibrated with the estimated coherent parameters of the dominant scatterer, which can be defined as an unknown strong target in radar detection scenarios. We focused on the selection criteria of the dominant scatterer by analyzing the constraints of the proposed method. Furthermore, an adaptive compensation approach was further explored to expand the available region for the estimated CPs of the dominant scatterer. This approach can compensate for the phases of different targets within multiple-unit radars using discrete phase values. The determination of discrete phase values is derived from the limit of synthesis loss within a given MMW DCAR configuration. Hence, this approach avoids massive searches for possible locations of other targets and the requirement of prior information.
The presented theory and the corresponding method were evaluated via extensive simulations and experiments. The constraints and limitations of the system were verified to meet the application requirements. Utilizing the proposed method, multi-target can achieve the desired synthetic results in sequential CPIs. Compared with the noncoherent integration method, the proposed method is stable at both high and low SNR conditions, yet with a higher SNR gain. Furthermore, a prototype system was fabricated and used to verify the proposed method. The experiment results match well with the simulations, showing the efficacy of the proposed method.
Author Contributions
Conceptualization, C.L. and Y.L.; methodology, C.L. and Y.W.; validation, C.L., M.W. and J.G.; formal analysis, X.H. and L.Z.; writing—original draft preparation, C.L. and Y.W.; writing—review and editing, Y.W., X.H. and L.Z.; supervision, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (Grant No. 2018YFE0202101, 2018YFE0202103), Natural Science Foundation of Chongqing, China (Grant No. cstc2020jcyj-msxmX0812) and project ZR2021MF134 supported by Shandong Provincial Natural Science Foundation.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Coutts, S.; Cuomo, K.; McHarg, J.; Robey, F.; Weikle, D. Distributed Coherent Aperture Measurements for Next Generation BMD Radar. In Proceedings of the IEEE Workshop on Sensor Array and Multichannel Processing, Waltham, MA, USA, 12–14 July 2006. [Google Scholar]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target Localization Accuracy Gain in MIMO Radar-Based Systems. IEEE Trans. Inf. Theory 2010, 56, 2783–2802. [Google Scholar] [CrossRef]
- Dai, F.; Li, Y.; Wang, Y.; Chen, H. Efficient Implementation for SBL-Based Coherent Distributed mmWave Radar Imaging. Remote Sens. 2023, 15, 1054. [Google Scholar] [CrossRef]
- Cuomo, K.M.; Coutts, S.D.; McHarg, J.C.; Pulsone, N.B.; Robey, F.C. Wideband Aperture Coherence Processing for Next Generation Radar (NexGen); MIT Lincoln Laboratory: Lexington, MA, USA, 2004. [Google Scholar]
- Long, T.; Zhang, H.; Zeng, T.; Liu, Q.; Chen, X.; Zheng, L. High Accuracy Unambiguous Angle Estimation Using Multi-Scale Combination in Distributed Coherent Aperture Radar. IET Radar Sonar Nav. 2017, 11, 1090–1098. [Google Scholar] [CrossRef]
- Liang, C.; Wang, Y.; Yang, Z.; Hu, X.; Pei, Q.; Gu, W.; Zhang, L. Cooperative Automotive Radars with Multi-Aperture Multiplexing MIMO Sparse Array Design. Electronics 2022, 11, 1198. [Google Scholar] [CrossRef]
- Fletcher, A.S.; Robey, F.C. Performance Bounds for Adaptive Coherence of Sparse Array Radar. In Proceedings of the 11th Conference Adaptive Sensors Array Processing, Lexington, MA, USA, 11–13 March 2003. [Google Scholar]
- Li, J.; Stoica, P. MIMO Radar with Colocated Antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Gottinger, M.; Hoffmann, M.; Christmann, M.; Schütz, M.; Kirsch, F.; Gulden, P.; Vossiek, M. Coherent Automotive Radar Networks: The Next Generation of Radar-Based Imaging and Mapping. IEEE J. Microw. 2021, 1, 149–163. [Google Scholar] [CrossRef]
- Sun, P.; Tang, J.; He, Q.; Tang, B.; Tang, X. Cramer-Rao bound of parameters estimation and coherence performance for next generation radar. IET Radar Sonar Nav. 2013, 7, 553–567. [Google Scholar] [CrossRef]
- Tang, X.; Tang, J.; He, Q.; Wan, S.; Tang, B.; Sun, P.; Zhang, N. Cramer-Rao Bounds and Coherence Performance Analysis for Next Generation Radar with Pulse Trains. Sensors 2013, 13, 5347–5367. [Google Scholar] [CrossRef]
- Brookner, E. Phased-Array and Radar Breakthroughs. In Proceedings of the IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007. [Google Scholar]
- Kuschel, H.; O’Hagan, D. Passive Radar from History to Future. In Proceedings of the 11-th International Radar Symposium, Vilnius, Lithuania, 16–18 June 2010. [Google Scholar]
- Kuschel, H. Approaching 80 Years of Passive Radar. In Proceedings of the 2013 International Conference on Radar, Adelaide, SA, Australia, 9–12 September 2013. [Google Scholar]
- Stelzer, A.; Jahn, M.; Scheiblhofer, S. Precise Distance Measurement with Cooperative FMCW Radar Units. In Proceedings of the 2008 IEEE Radio and Wireless Symposium, Orlando, FL, USA, 22–24 January 2008. [Google Scholar]
- Feger, R.; Pfeffer, C.; Schmid, C.M.; Lang, M.J.; Tong, Z.; Stelzer, A. A 77-GHz FMCW MIMO Radar Based on Loosely Coupled Stations. In Proceedings of the 7th German Microwave Conference, Ilmenau, Germany, 12–14 March 2012. [Google Scholar]
- Butt, F.A.; Aslam, M.A.; Zafar, M.T.; Naqvi, I.H.; Riaz, U. Synchronization of Long-Range, Widely-Separated MIMO Radar Network using GSM Protocol. In Proceedings of the 19th International Radar Symposium, Bonn, Germany, 20–22 June 2018. [Google Scholar]
- Steiner, M.; Keller, M.; Geiß, J.; Vossiek, M.; Waldschmidt, C. Synchronization of Radar Sensors in a Network Based on Inter-Sensor Interference. In Proceedings of the 2019 16th European Radar Conference (EuRAD), Paris, France, 2–4 October 2019. [Google Scholar]
- Zhang, H.; Lei, Z.; Song, Y. Coherent Parameters Estimation Method Based on MUSIC and KF in Wideband DCAR. In Proceedings of the IET International Radar Conference, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Zeng, T.; Yin, P.; Liu, Q. Wideband Distributed Coherent Aperture Radar Based on Stepped Frequency Signal: Theory and Experimental Results. IET Radar Sonar Nav. 2016, 10, 672–688. [Google Scholar] [CrossRef]
- Edstaller, S.; Mueller, D. Vector Velocity and Position Measurement Using a 77-GHz Cooperative Radar System. In Proceedings of the 2019 IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2019. [Google Scholar]
- Edstaller, S.; Mueller, D. A Cooperative Radar System with Active Reference Target Synchronization for Kinematic Target Analysis. IEEE Trans. Microw. Theory Techn. 2021, 69, 4118–4131. [Google Scholar] [CrossRef]
- Rabideau, D.J. MIMO Radar Waveforms and Cancellation Ratio. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1167–1178. [Google Scholar] [CrossRef]
- Kronauge, M.; Rohling, H. New Chirp Sequence Radar Waveform. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2870–2877. [Google Scholar] [CrossRef]
- Hu, X.; Lu, M.; Li, Y.; Wang, Y. Motion Compensation for TDM MIMO Radar by Sparse Reconstruction. Electron. Lett. 2017, 53, 1604–1606. [Google Scholar] [CrossRef]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive Radars: A Review of Signal Processing Techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Hu, X.; Li, Y.; Lu, M.; Wang, Y.; Yang, X. A Multi-Carrier-Frequency Random-Transmission Chirp Sequence for TDM MIMO Automotive Radar. IEEE Trans. Veh. Technol. 2019, 68, 3672–3685. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving: Advantages and Challenges. IEEE Signal Process. Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Feger, R.; Pfeffer, C.; Stelzer, A. A Frequency-Division MIMO FMCW Radar System Based on Delta–Sigma Modulated Transmitters. IEEE Trans. Microw. Theory Techn. 2014, 62, 3572–3581. [Google Scholar] [CrossRef]
- Kim, E.H.; Kim, K.H. Random Phase Code for Automotive MIMO Radars Using Combined Frequency Shift Keying-Linear FMCW Waveform. IET Radar Sonar Nav. 2018, 12, 1090–1095. [Google Scholar] [CrossRef]
- Benedetto, J.J.; Konstantinidis, I.; Rangaswamy, M. Phase-Coded Waveforms and Their Design. IEEE Signal Process. Mag. 2009, 26, 22–31. [Google Scholar] [CrossRef]
- Uysal, F. Phase-Coded FMCW Automotive Radar: System Design and Interference Mitigation. IEEE Trans. Veh. Technol. 2020, 69, 270–281. [Google Scholar] [CrossRef]
- Overdevest, J.; Jansen, F.; Uysal, F.; Yarovoy, A. Doppler Influence on Waveform Orthogonality in 79 GHz MIMO Phase-Coded Automotive Radar. IEEE Trans. Veh. Technol. 2020, 69, 16–25. [Google Scholar] [CrossRef]
- Ferrari, A.; Berenguer, C.; Alengrin, G. Doppler Ambiguity Resolution Using Multiple PRF. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 738–751. [Google Scholar] [CrossRef]
- Rossum, W.; van Anitori, L. Simultaneous Resolution of Range-Doppler Ambiguities using Agile Pulse Intervals with Sparse Signal Processing. In Proceedings of the 2020 IEEE Radar Conference, Florence, Italy, 21–25 September 2020. [Google Scholar]
- Wang, J. CFAR-Based Interference Mitigation for FMCW Automotive Radar Systems. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12229–12238. [Google Scholar] [CrossRef]
- Xu, Z.; Yuan, M. An Interference Mitigation Technique for Automotive Millimeter Wave Radars in the Tunable Q-Factor Wavelet Transform Domain. IEEE Trans. Microw. Theory Techn. 2021, 69, 5270–5283. [Google Scholar] [CrossRef]
- Xu, Z.; Xue, S.; Wang, Y. Incoherent Interference Detection and Mitigation for Millimeter-Wave FMCW Radars. Remote Sens. 2022, 14, 4817. [Google Scholar] [CrossRef]
- Xu, Z. Bi-Level l1 Optimization-Based Interference Reduction for Millimeter Wave Radars. IEEE Trans. Intell. Transp. Syst. 2023, 24, 728–738. [Google Scholar] [CrossRef]
- Sun, L.; Yu, H.; Lan, J.; Fu, Z.; He, Z.; Pu, J. Tracking of Multiple Maneuvering Random Hypersurface Extended Objects Using High Resolution Sensors. Remote Sens. 2021, 13, 2963. [Google Scholar] [CrossRef]
- Smith, M.E.; Varshney, P.K. Intelligent CFAR Processor Based on Data Variability. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 837–847. [Google Scholar] [CrossRef]
- Tao, D.; Anfinsen, S.N.; Brekke, C. Robust CFAR Detector Based on Truncated Statistics in Multiple-Target Situations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 117–134. [Google Scholar] [CrossRef]
- Cao, Z.; Li, J.; Song, C.; Xu, Z.; Wang, X. Compressed Sensing-Based Multitarget CFAR Detection Algorithm for FMCW Radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9160–9172. [Google Scholar] [CrossRef]
- Bird, J.S. Calculating the Performance of Linear and Square-Law Detectors. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 39–51. [Google Scholar] [CrossRef]
- Morgan, D.R.; Madsen, C.K. Wide-Band System Identification Using Multiple Tones with Allpass Filters and Square-Law Detectors. IEEE Trans. Circuits–I 2006, 53, 1151–1165. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).