Rotation Invariant Graph Neural Network for 3D Point Clouds
Abstract
1. Introduction
2. Related Work
2.1. Graph Neural Network for 3D Data
2.2. Rotation Invariant Classification and Part Segmentation Networks
3. Theoretical Background
3.1. Background for Graph Neural Networks
3.2. Spectral Graph Convolution Neural Network
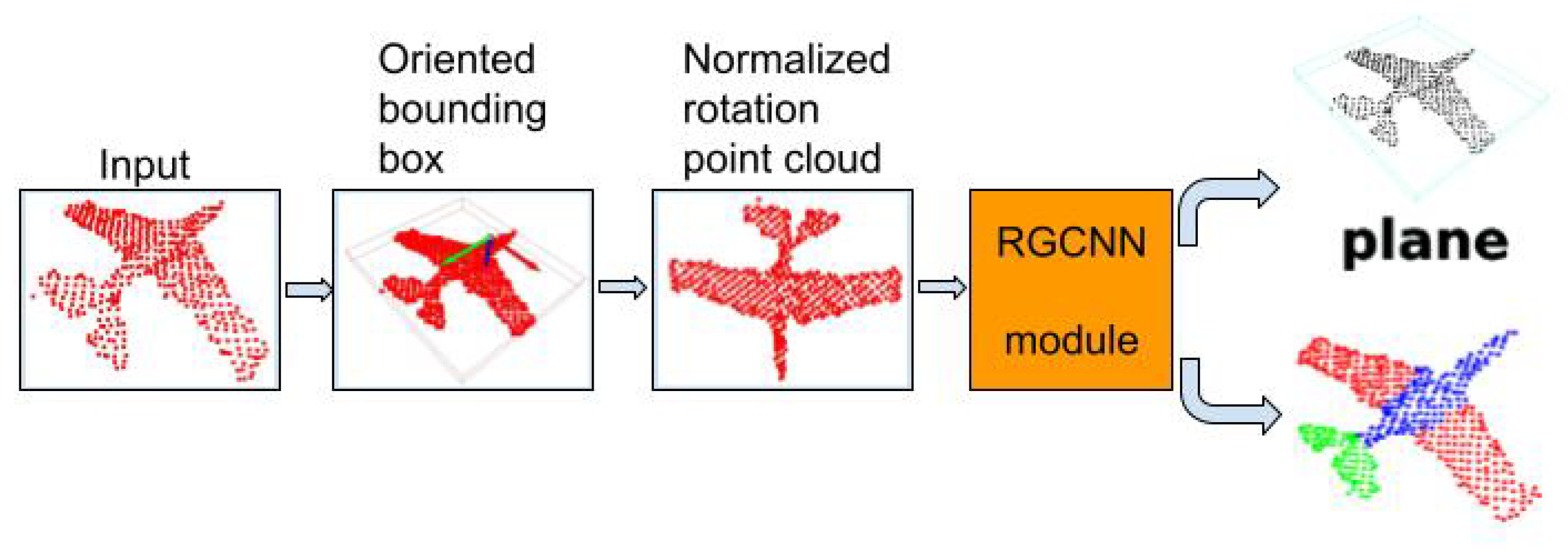
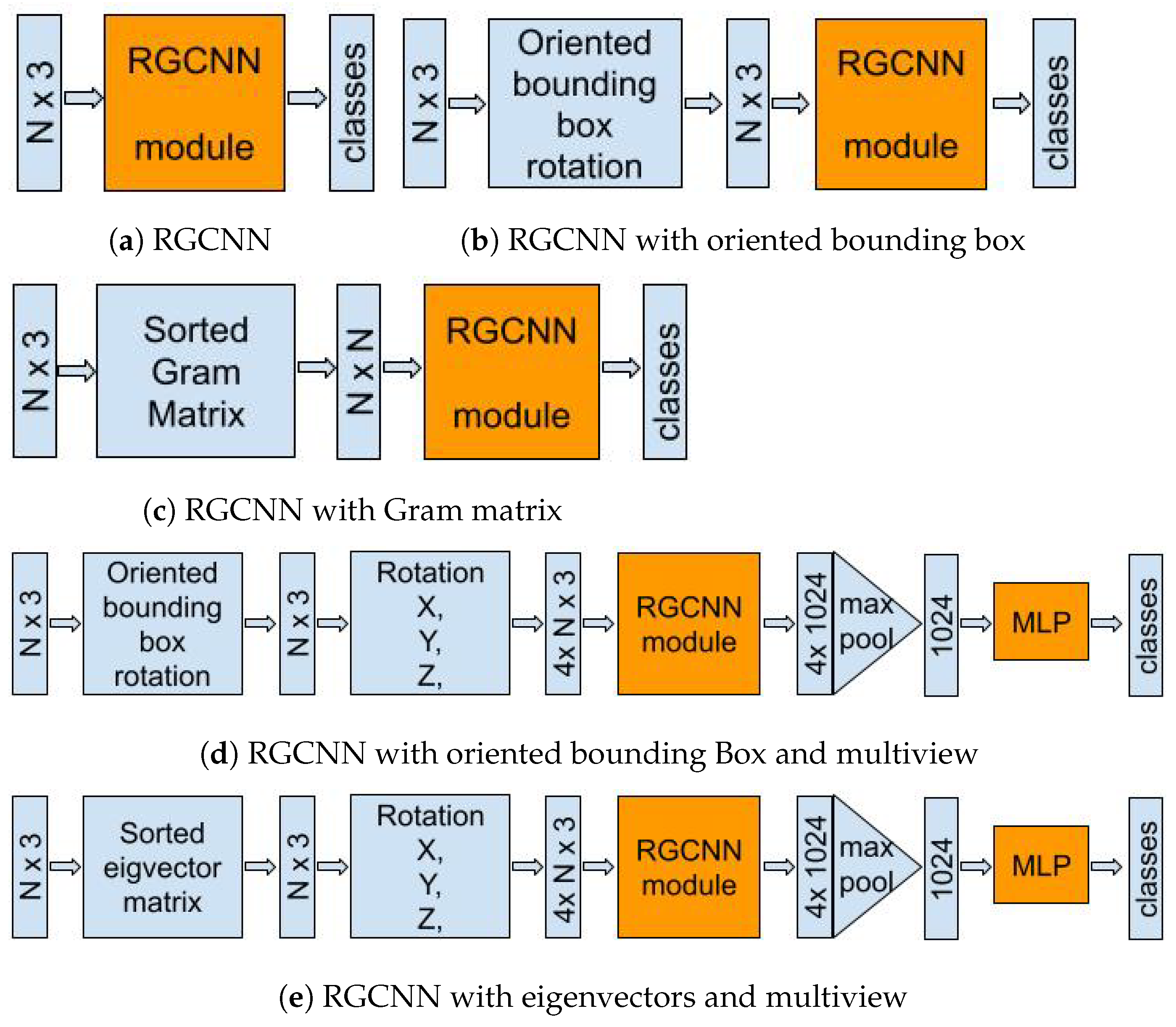
4. Methodology
Proposed Method
5. Datasets
5.1. Synthetic Datasets
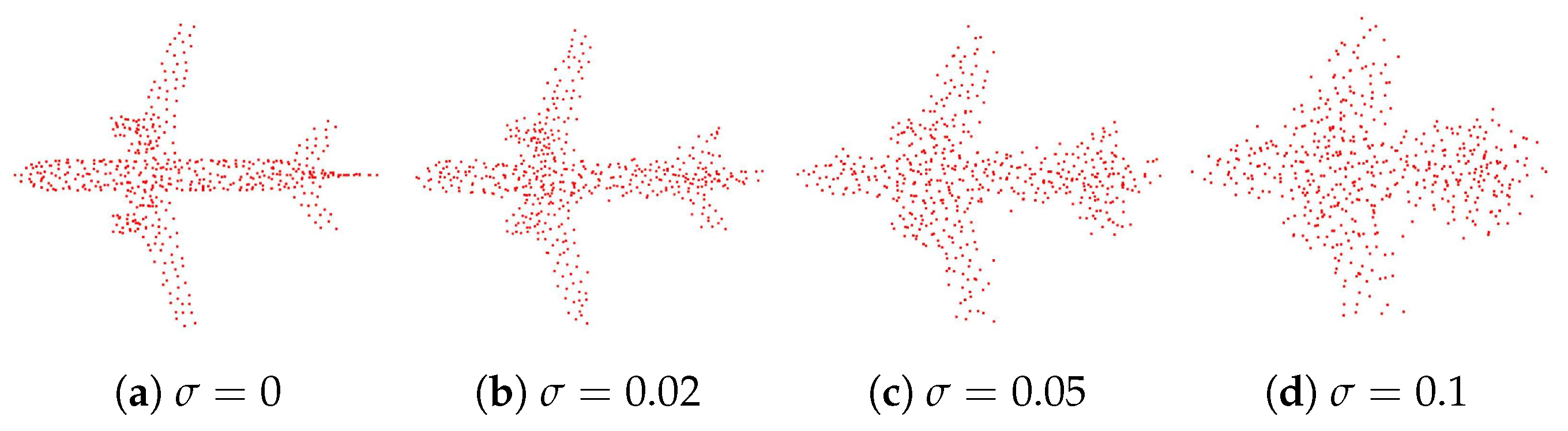
5.1.1. Gaussian Noise
5.1.2. Orientation Noise
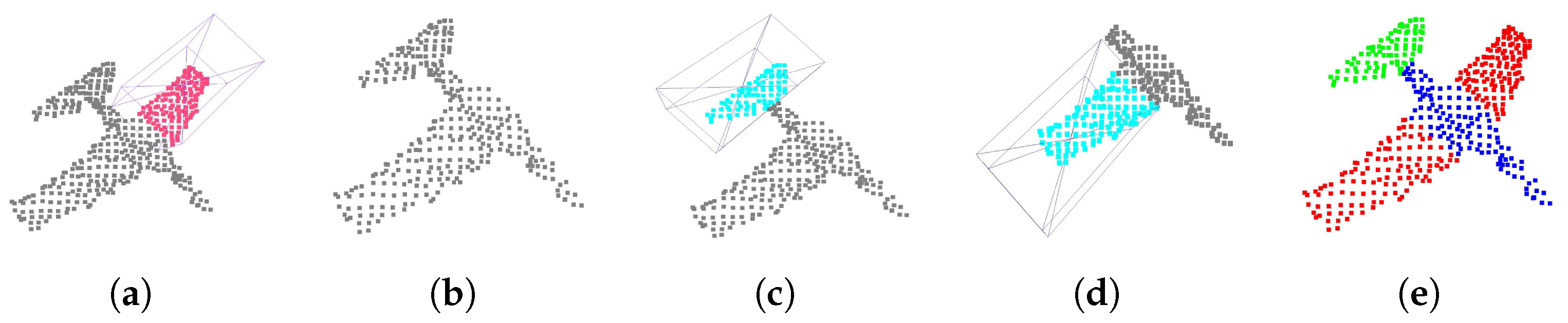
5.1.3. Occlusion Noise
5.2. Custom Camera Datasets
5.2.1. Classification Custom Dataset
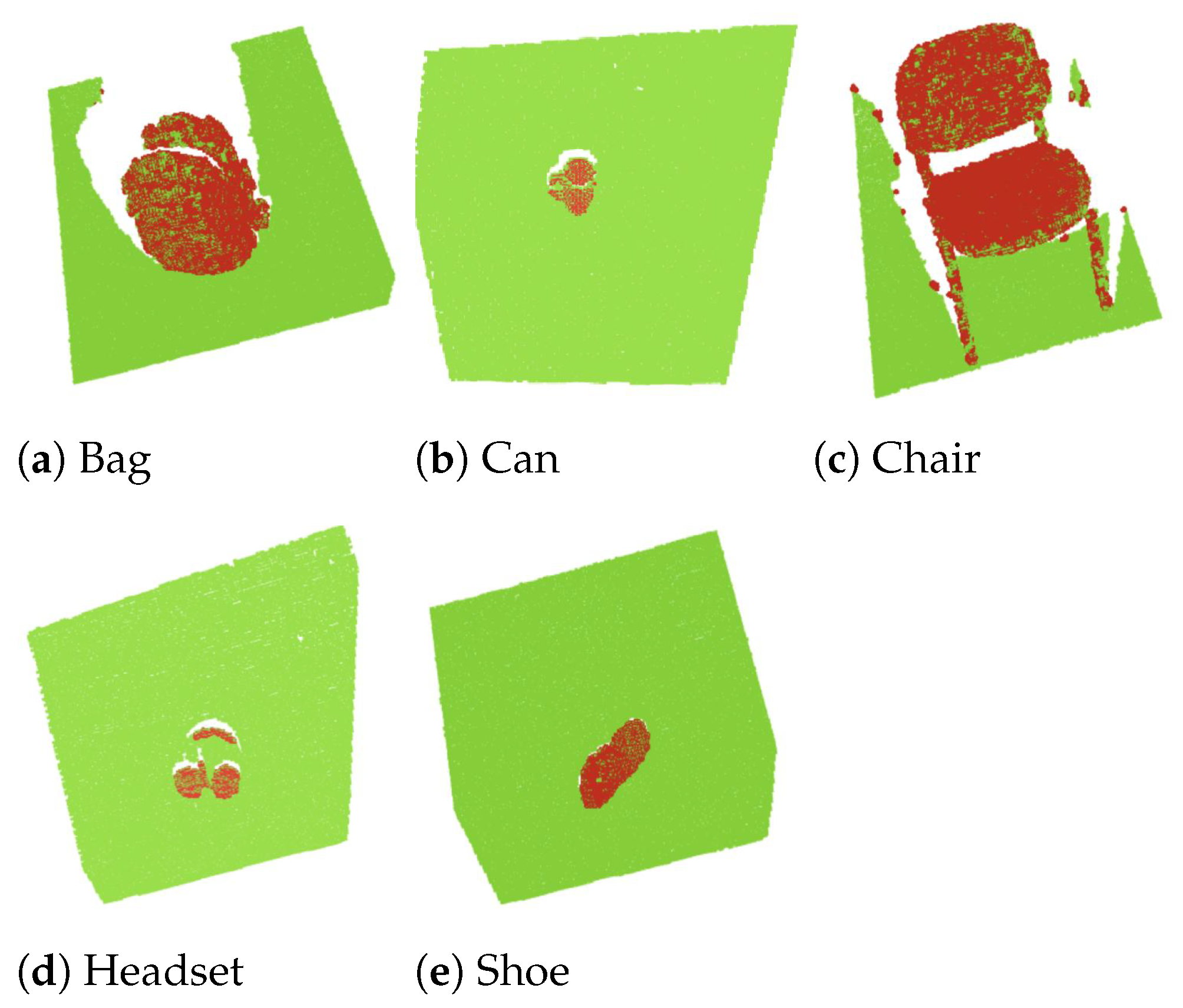
5.2.2. Part Segmentation Custom Dataset
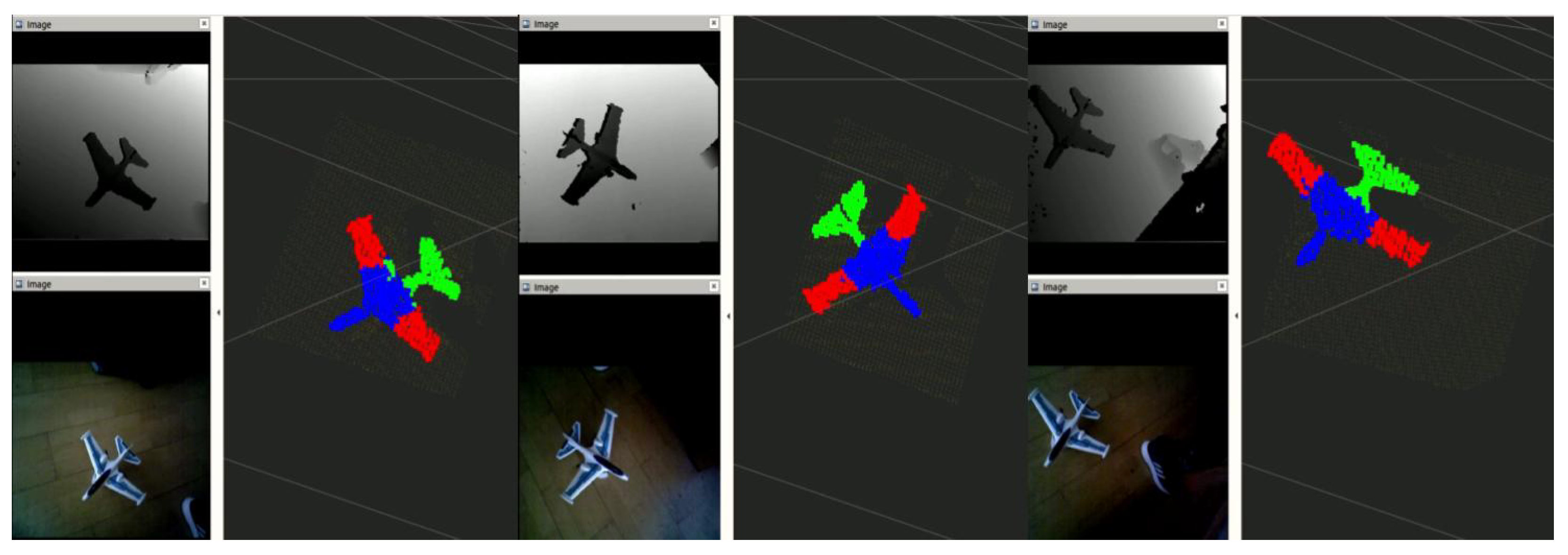
5.3. Implementation on Embedded Device Using Real Data
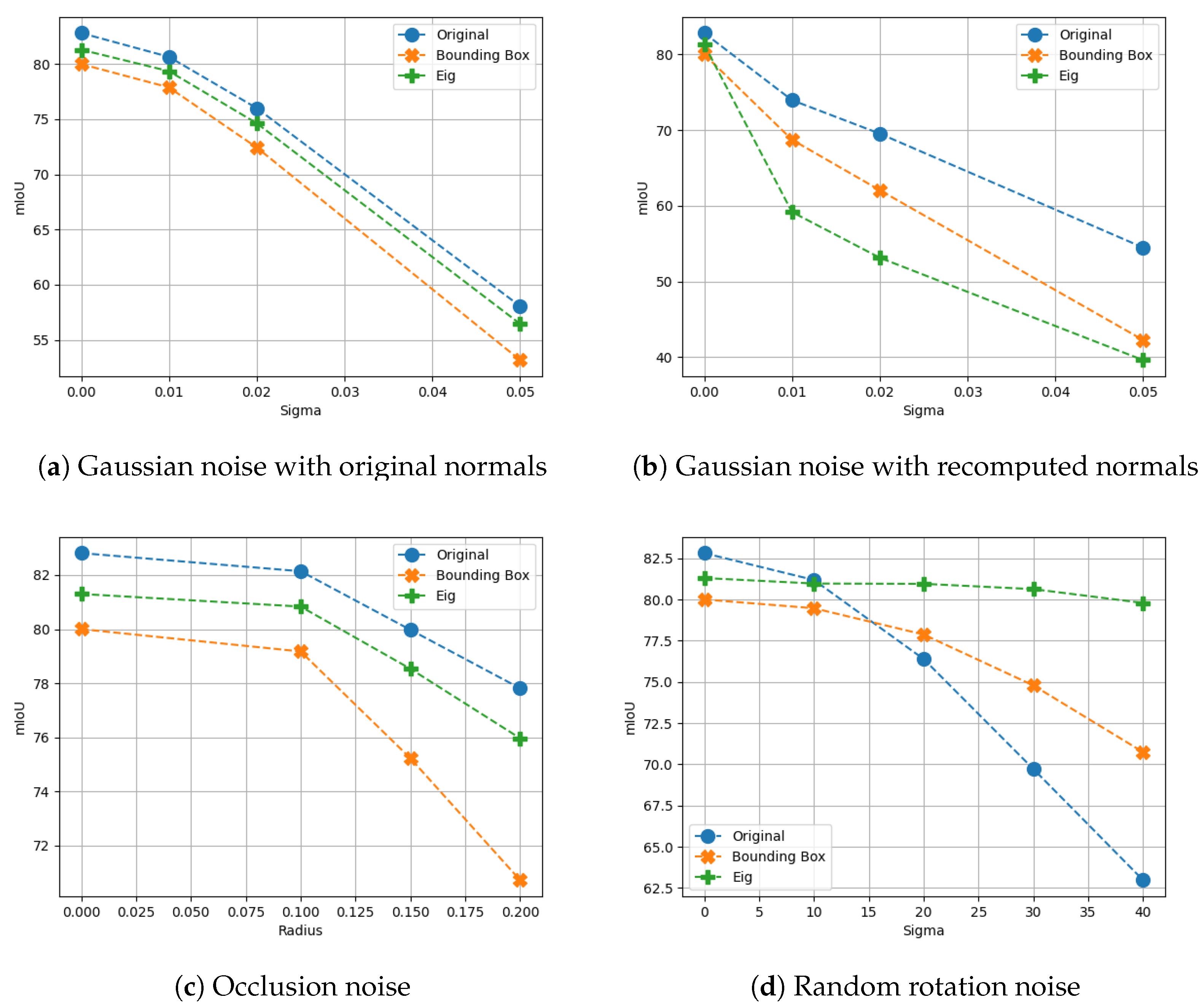
6. Results
6.1. Classification
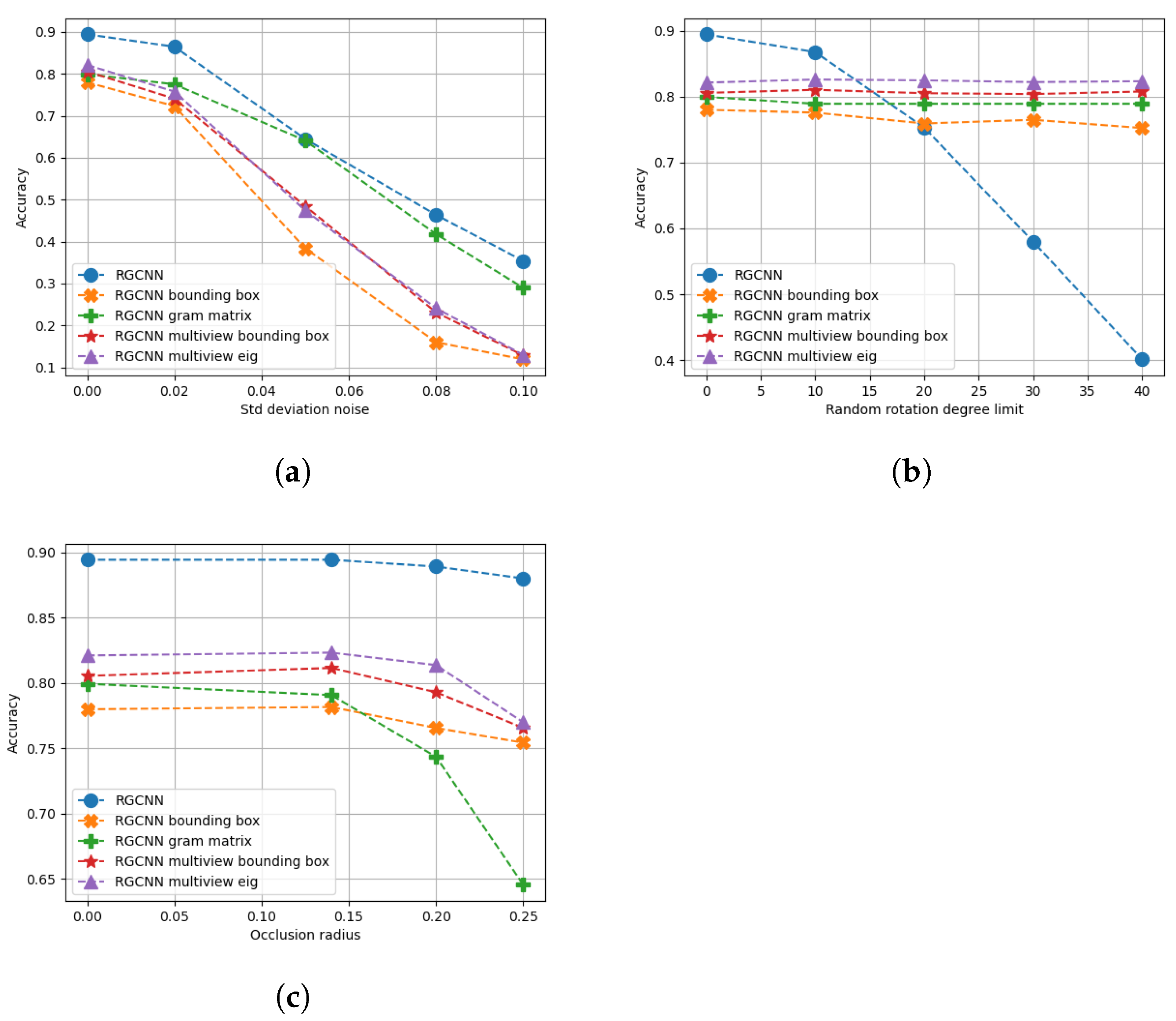
6.1.1. Synthetic Dataset without Noise
6.1.2. Synthetic Dataset Trained with Noise
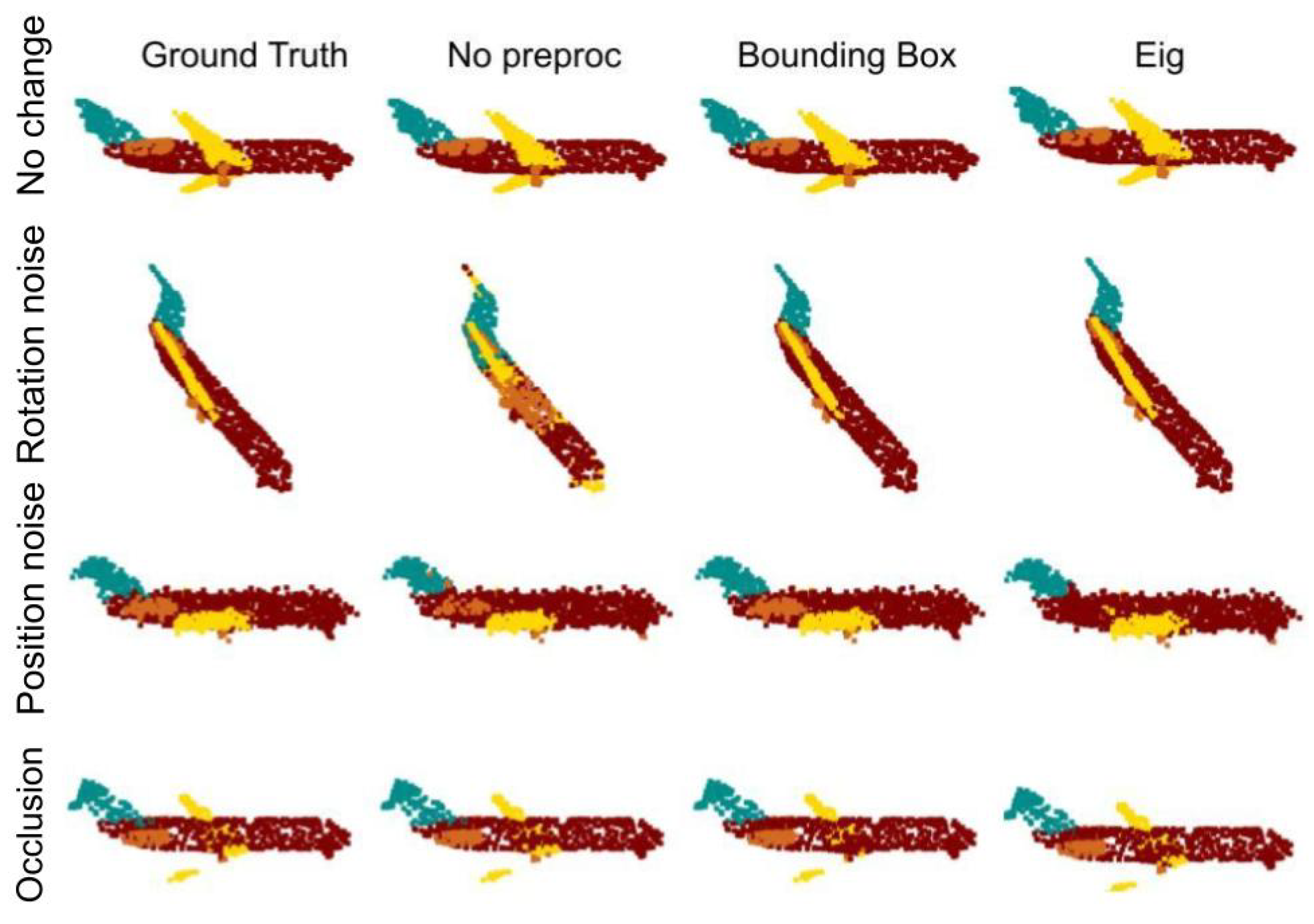
6.2. Part Segmentation
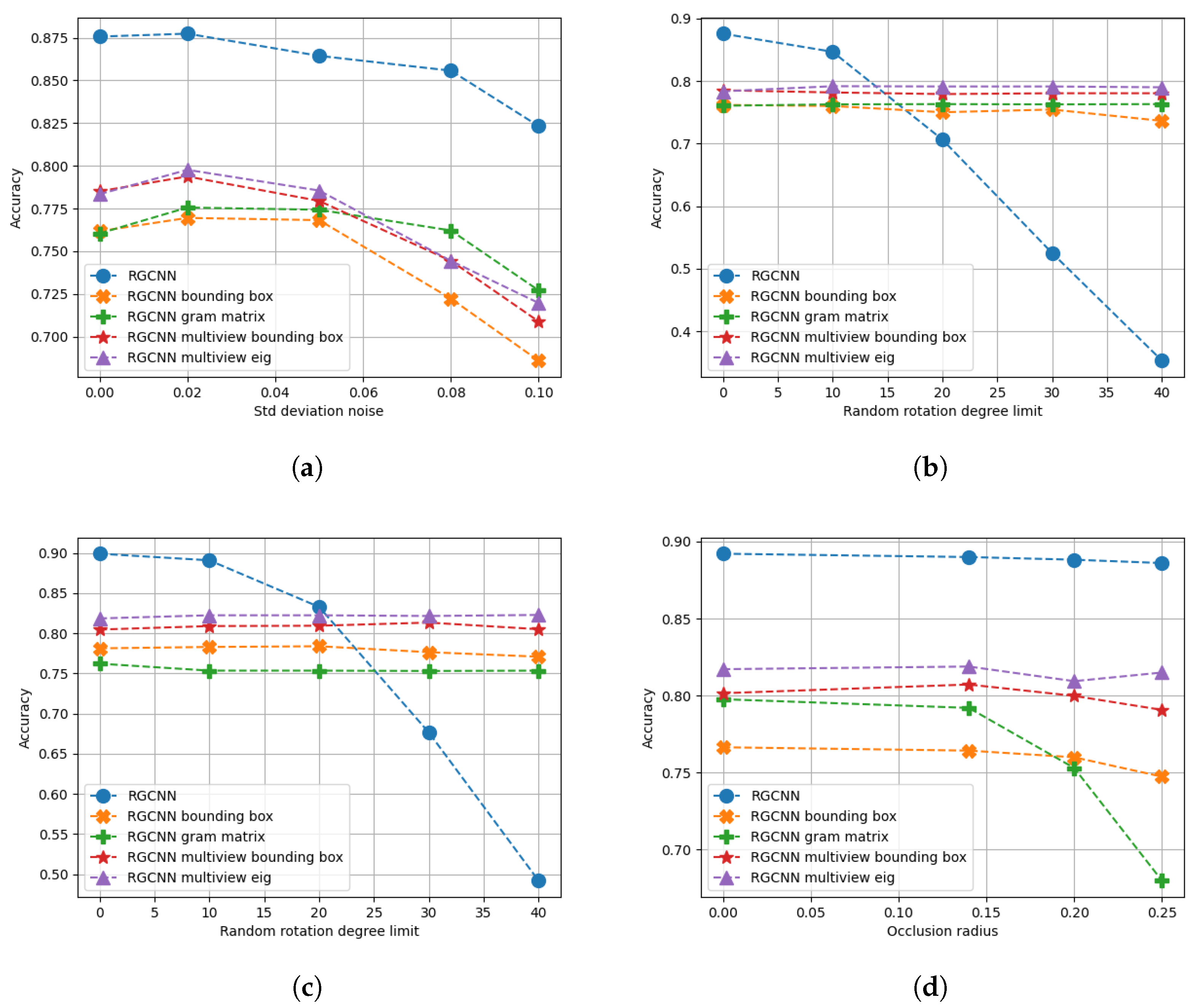
6.2.1. Synthetic Dataset without Noise
6.2.2. Synthetic Dataset Trained with Noise
7. Discussion
7.1. Classification
7.1.1. Synthetic Dataset without Noise
7.1.2. Synthetic Dataset with Noise
7.2. Part segmentation
7.2.1. Synthetic Dataset without Noise
7.2.2. Synthetic Dataset with Noise
7.3. Model Profiling
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| RGCNN | Regularized Graph Convolutional Neural Network |
| DGCNN | Dynamic Graph Convolutional Neural Network |
| RGB-D | Red–Green–Blue-Depth |
| mIoU | Mean Intersection Over Union |
| kNN | K-Nearest Neighbor |
References
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3D model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Tamas, L.; Jensen, B. Robustness analysis of 3D feature descriptors for object recognition using a time-of-flight camera. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1020–1025. [Google Scholar]
- Li, F.; Fujiwara, K.; Okura, F.; Matsushita, Y. A closer look at rotation-invariant deep point cloud analysis. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16218–16227. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. (TOG) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Te, G.; Hu, W.; Zheng, A.; Guo, Z. Rgcnn: Regularized graph cnn for point cloud segmentation. In Proceedings of the 26th ACM International Conference on Multimedia, Seoul, Republic of Korea, 22–26 October 2018; pp. 746–754. [Google Scholar]
- Khan, S.A.; Shi, Y.; Shahzad, M.; Zhu, X.X. Fgcn: Deep feature-based graph convolutional network for semantic segmentation of urban 3D point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 198–199. [Google Scholar]
- Wang, W.; You, Y.; Liu, W.; Lu, C. Point cloud classification with deep normalized Reeb graph convolution. Image Vis. Comput. 2021, 106, 104092. [Google Scholar] [CrossRef]
- Xiao, Z.; Lin, H.; Li, R.; Geng, L.; Chao, H.; Ding, S. Endowing deep 3D models with rotation invariance based on principal component analysis. In Proceedings of the 2020 IEEE International Conference on Multimedia and Expo (ICME), London, UK, 6–10 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Frohlich, R.; Tamas, L.; Kato, Z. Absolute pose estimation of central cameras using planar regions. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 377–391. [Google Scholar] [CrossRef]
- Pan, G.; Wang, J.; Ying, R.; Liu, P. 3DTI-Net: Learn inner transform invariant 3D geometry features using dynamic GCN. arXiv 2018, arXiv:1812.06254. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Dhaka, Bangladesh, 13–14 February 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Shang, C.; Liu, Q.; Tong, Q.; Sun, J.; Song, M.; Bi, J. Multi-view spectral graph convolution with consistent edge attention for molecular modeling. Neurocomputing 2021, 445, 12–25. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Ren, L.; Wang, F. 3D Point Cloud of Single Tree Branches and Leaves Semantic Segmentation Based on Modified PointNet Network. J. Physics Conf. Ser. 2021, 2074, 012026. [Google Scholar] [CrossRef]
- Chen, L.; Xu, G.; Fu, N.; Hu, Z.; Zheng, S.; Li, X. Study on the 3D point cloud semantic segmentation method of fusion semantic edge detection. J. Physics Conf. Ser. 2022, 2216, 012098. [Google Scholar] [CrossRef]
- Li, G.; Muller, M.; Thabet, A.; Ghanem, B. Deepgcns: Can gcns go as deep as cnns? In Proceedings of the the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 9267–9276. [Google Scholar]
- Kim, S.; Park, J.; Han, B. Rotation-invariant local-to-global representation learning for 3D point cloud. Adv. Neural Inf. Process. Syst. 2020, 33, 8174–8185. [Google Scholar]
- Levie, R.; Monti, F.; Bresson, X.; Bronstein, M.M. Cayleynets: Graph convolutional neural networks with complex rational spectral filters. IEEE Trans. Signal Process. 2018, 67, 97–109. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. PPFNET: Global context aware local features for robust 3D point matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 195–205. [Google Scholar]
- Zhang, Z.; Hua, B.S.; Rosen, D.W.; Yeung, S.K. Rotation invariant convolutions for 3D point clouds deep learning. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 204–213. [Google Scholar]
- Xiao, C.; Wachs, J. Triangle-net: Towards robustness in point cloud learning. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 826–835. [Google Scholar]
- Li, X.; Li, R.; Chen, G.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. A rotation-invariant framework for deep point cloud analysis. IEEE Trans. Vis. Comput. Graph. 2021, 28, 4503–4514. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Lian, Z.; Xiao, J. Srinet: Learning strictly rotation-invariant representations for point cloud classification and segmentation. In Proceedings of the the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 980–988. [Google Scholar]
- Poulenard, A.; Rakotosaona, M.J.; Ponty, Y.; Ovsjanikov, M. Effective rotation-invariant point cnn with spherical harmonics kernels. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 47–56. [Google Scholar]
- Chen, R.; Cong, Y. The Devil is in the Pose: Ambiguity-free 3D Rotation-invariant Learning via Pose-aware Convolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 7472–7481. [Google Scholar]
- Xu, J.; Tang, X.; Zhu, Y.; Sun, J.; Pu, S. SGMNet: Learning rotation-invariant point cloud representations via sorted Gram matrix. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10468–10477. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Zhao, C.; Yang, J.; Xiong, X.; Zhu, A.; Cao, Z.; Li, X. Rotation invariant point cloud analysis: Where local geometry meets global topology. Pattern Recognit. 2022, 127, 108626. [Google Scholar] [CrossRef]
- Yu, R.; Wei, X.; Tombari, F.; Sun, J. Deep positional and relational feature learning for rotation-invariant point cloud analysis. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 217–233. [Google Scholar]
- Yang, Z.; Ye, Q.; Stoter, J.; Nan, L. Enriching Point Clouds with Implicit Representations for 3D Classification and Segmentation. Remote Sens. 2023, 15, 61. [Google Scholar] [CrossRef]
- Chen, C.; Li, G.; Xu, R.; Chen, T.; Wang, M.; Lin, L. Clusternet: Deep hierarchical cluster network with rigorously rotation-invariant representation for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019; pp. 4994–5002. [Google Scholar]
- Zhang, Y.; Rabbat, M. A graph-cnn for 3D point cloud classification. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 6279–6283. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and deep locally connected networks on graphs. In Proceedings of the 2nd International Conference on Learning Representations (ICLR 2014), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]







| Network | Fw. (ms) 512 Points | Fw. (ms) 1024 Points | Fw. (ms) 2048 Points |
|---|---|---|---|
| DGCNN Cls | 15.82 | 23.28 | 52.71 |
| DGCNN Part Seg | 13.64 | 17.17 | 38.89 |
| RGCNN Cls | 4.91 | 12.09 | 57.39 |
| RGCNN Part Seg | 7.27 | 15.94 | 61.78 |
| Method | Nr. Points | Preproc (ms) | Inference (ms) | Total (ms) |
|---|---|---|---|---|
| 512 | - | 6.28 | 6.28 | |
| 1024 | - | 6.88 | 6.88 | |
| Pointnet | 2048 | - | 8.46 | 8.46 |
| 512 | - | 4.91 | 4.91 | |
| 1024 | - | 12.09 | 12.09 | |
| RGCNN | 2048 | - | 57.39 | 57.39 |
| 512 | 0.3 | 4.91 | 5.21 | |
| 1024 | 0.5 | 12.09 | 12.59 | |
| RGCNN BB | 2048 | 0.76 | 57.39 | 58.15 |
| 512 | 0.41 | 4.91 | 5.32 | |
| 1024 | 0.4 | 12.09 | 12.49 | |
| RGCNN PCA | 2048 | 0.47 | 57.39 | 57.86 |
| 512 | 0.85 | 6.07 | 6.92 | |
| 1024 | 2.16 | 23.75 | 25.91 | |
| RGCNN Gram (GPU) | 2048 | 10.71 | 143.22 | 153.93 |
| 512 | 0.3 | 12.45 | 12.75 | |
| 1024 | 0.5 | 30.8 | 31.3 | |
| BB multi view | 2048 | 0.76 | 103.49 | 104.25 |
| 512 | 0.41 | 12.45 | 12.86 | |
| 1024 | 0.4 | 30.8 | 31.2 | |
| PCA multi view | 2048 | 0.47 | 103.49 | 103.96 |
| Network | Model Size (MB) | Number of Parameters |
|---|---|---|
| Pointnet | 14 | 3.478.796 |
| DGCNN | 7 | 1.809.576 |
| RGCNN | 16 | 4148680 |
| RGCNN Gram | 18 | 4539592 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pop, A.; Domșa, V.; Tamas, L. Rotation Invariant Graph Neural Network for 3D Point Clouds. Remote Sens. 2023, 15, 1437. https://doi.org/10.3390/rs15051437
Pop A, Domșa V, Tamas L. Rotation Invariant Graph Neural Network for 3D Point Clouds. Remote Sensing. 2023; 15(5):1437. https://doi.org/10.3390/rs15051437
Chicago/Turabian StylePop, Alexandru, Victor Domșa, and Levente Tamas. 2023. "Rotation Invariant Graph Neural Network for 3D Point Clouds" Remote Sensing 15, no. 5: 1437. https://doi.org/10.3390/rs15051437
APA StylePop, A., Domșa, V., & Tamas, L. (2023). Rotation Invariant Graph Neural Network for 3D Point Clouds. Remote Sensing, 15(5), 1437. https://doi.org/10.3390/rs15051437






