Spatiotemporal Prediction of Radar Echoes Based on ConvLSTM and Multisource Data
Abstract
1. Introduction
2. Materials and Methods
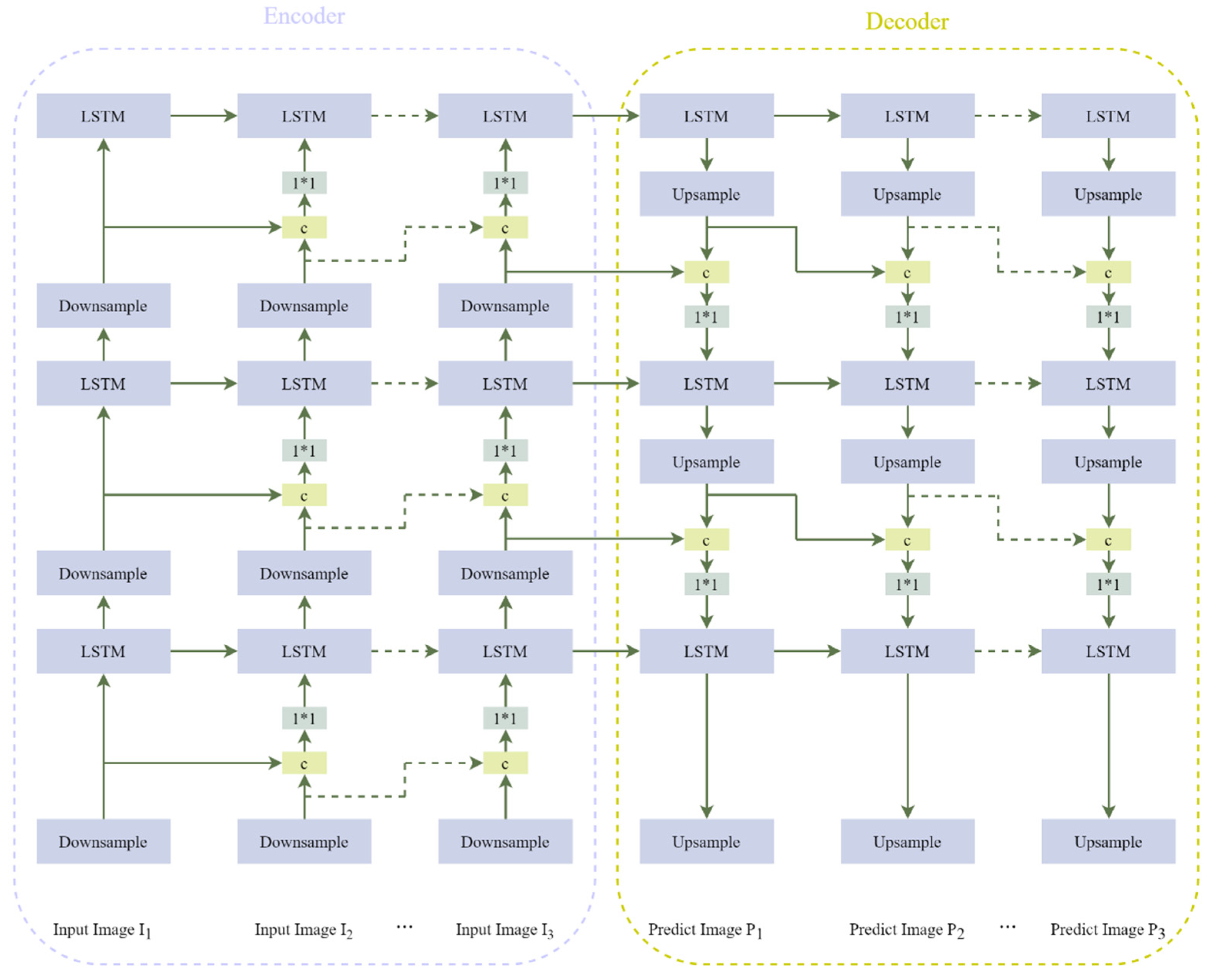
2.1. ConvLSTM Structure
2.2. MS-ConvLSTM
2.2.1. Three-Dimensional Convolutional Operation
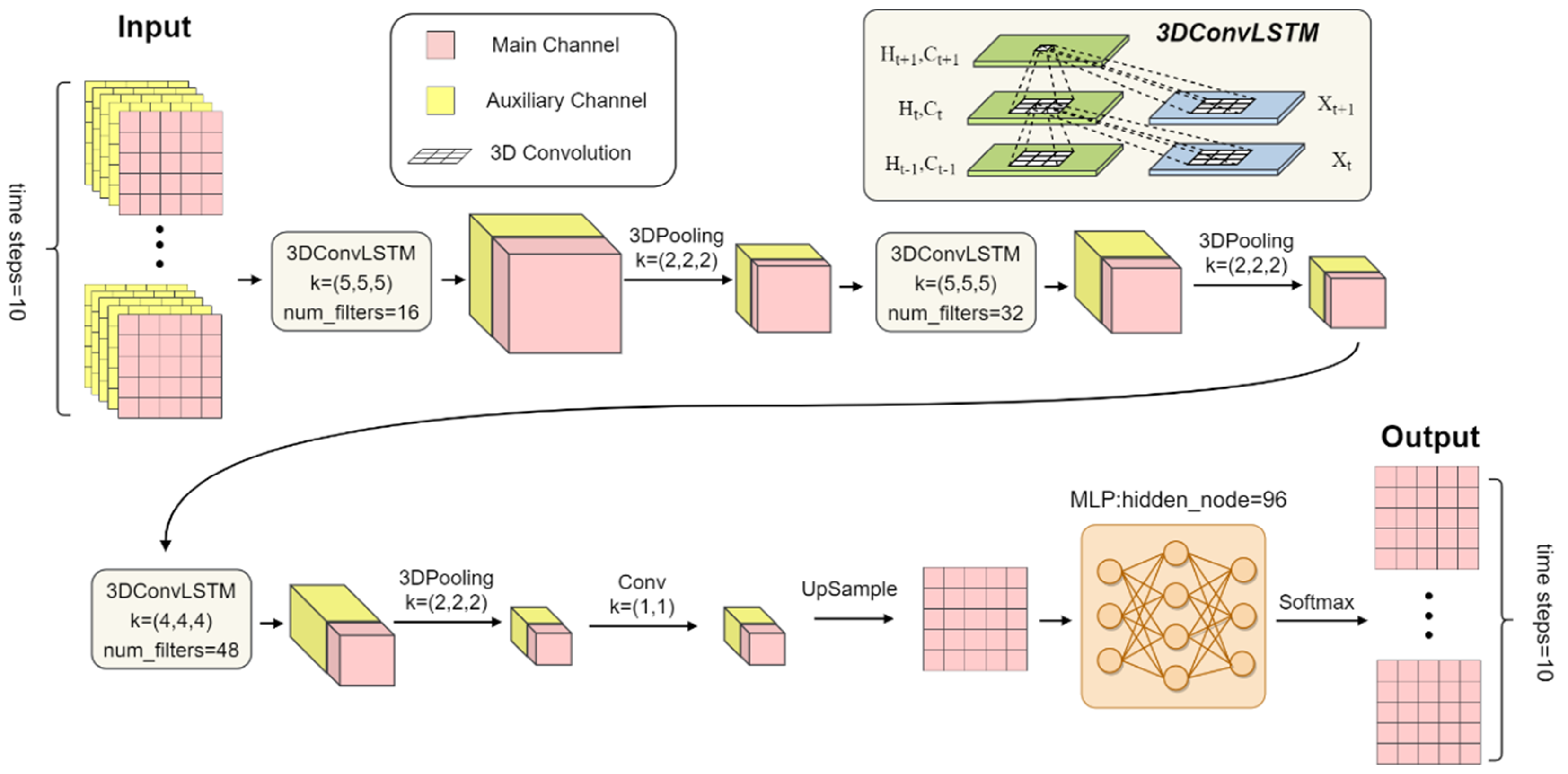
2.2.2. MS-ConvLSTM Architecture
- Input: The model receives two inputs: a main channel and an auxiliary channel. The main channel consists of a sequence of 10 consecutive frames of radar images, with each frame having a spatial size of 459 × 459. The auxiliary channel consists of an auxiliary data sequence corresponding to the main channel information, with the same spatial size of 459 × 459.
- ConvLSTM1 with 3D Convolution: To extract features, a spatiotemporal convolution is conducted, which involves using 16 different 3D convolution kernels, each with a size of 5 × 5 × 5. The size of 5 × 5 in the spatial dimensions represents the size of the convolution kernel in the x and y dimensions of the image. The length of 5 in the temporal dimension represents the number of time steps that the convolution kernel considers when performing the convolution. The convolution operation is performed on the input data, which consists of a sequence of 10 images with a spatial size of 459 × 459. The 3D convolution kernels are applied to the data, sliding across the spatial and temporal dimensions and performing a dot product between the kernel values and the input data at each position. This results in a feature map with eight times the number of channels as the input data.
- Pooling: After the convolution operation, the model performs a pooling operation. Pooling is often used in CNNs to reduce the size of feature maps, which can reduce the computational complexity of the model and improve its ability to generalize to new data. Pooling can also help the model to be invariant to small translations in the input, as the pooling operation aggregates values within a certain region and is not sensitive to the exact positions of the values within that region. The pooling operation involves downsampling the feature maps by taking the average or maximum value within a certain region. In this case, the model performs a downsampling operation with a unit of 2 × 2 in the spatial domain and a downsampling with a unit of 2 in the time domain. This reduces the spatial and temporal resolutions of the feature maps, resulting in the third layer of the model. The specific parameters and configurations used for these operations, such as the size of the convolution kernels and the size of the downsampling operation, can affect the performance of the model and have been determined based on experiments.
- ConvLSTM2 with 3D Convolution: To further extract features, 3D convolution is conducted, which involves using 32 different 3D convolution kernels, each with a size of 5 × 5 × 5. This results in double the number of feature maps in the third layer.
- Pooling: A 2 × 2 downsampling operation is applied to the spatial domain of each feature map in the fifth layer, and a subsampling operation with a sampling unit of 2 is applied to the time domain.
- ConvLSTM3 with 3D Convolution: A 3D convolution operation is applied using 48 different convolution kernels with a size of 4 × 4 × 4, resulting in a feature map that is 1.5 times the size of the fifth layer. This is followed by a downsampling operation with a size of 2 × 2 × 2 to obtain the seventh layer of the model.
- Pooling: This is followed by a downsampling operation with a size of 2 × 2 × 2 to obtain the eighth layer of the model.
- Fully connected classification: After three data feature processing steps using ConvLSTM, the model uses a traditional three-layer fully connected classifier using a softmax activation function for the final radar echo extrapolation. The ninth layer of the model consists of the feature map of a 1 × 1 convolution kernel, which is fully connected to all the feature maps in the eighth layer. This is defined as the input layer of the softmax classifier, and the number of nodes in the middle hidden layer is 96.
- Prediction: The model takes a series of radar echo images and processes them using ConvLSTM1, ConvLSTM2, and ConvLSTM3, and finally makes a prediction about the next 10 consecutive frames. The prediction of the model is then established based on this processing.
2.2.3. Evaluation Metrics
2.2.4. Model Parameter and Experiment Design
2.3. Study Area and Materials
2.3.1. Study Area
2.3.2. Data Description
2.3.3. Training Data Preparation
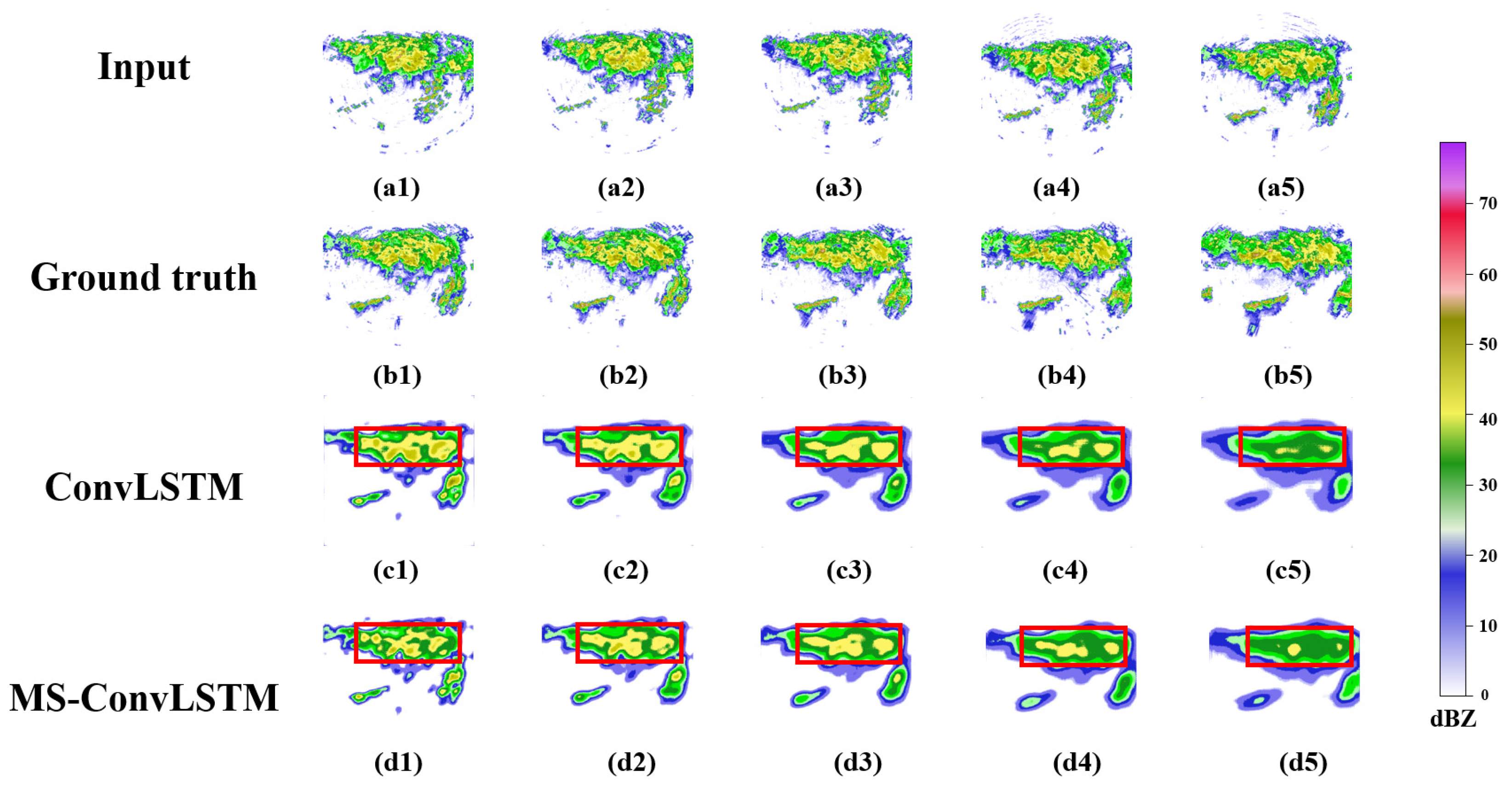
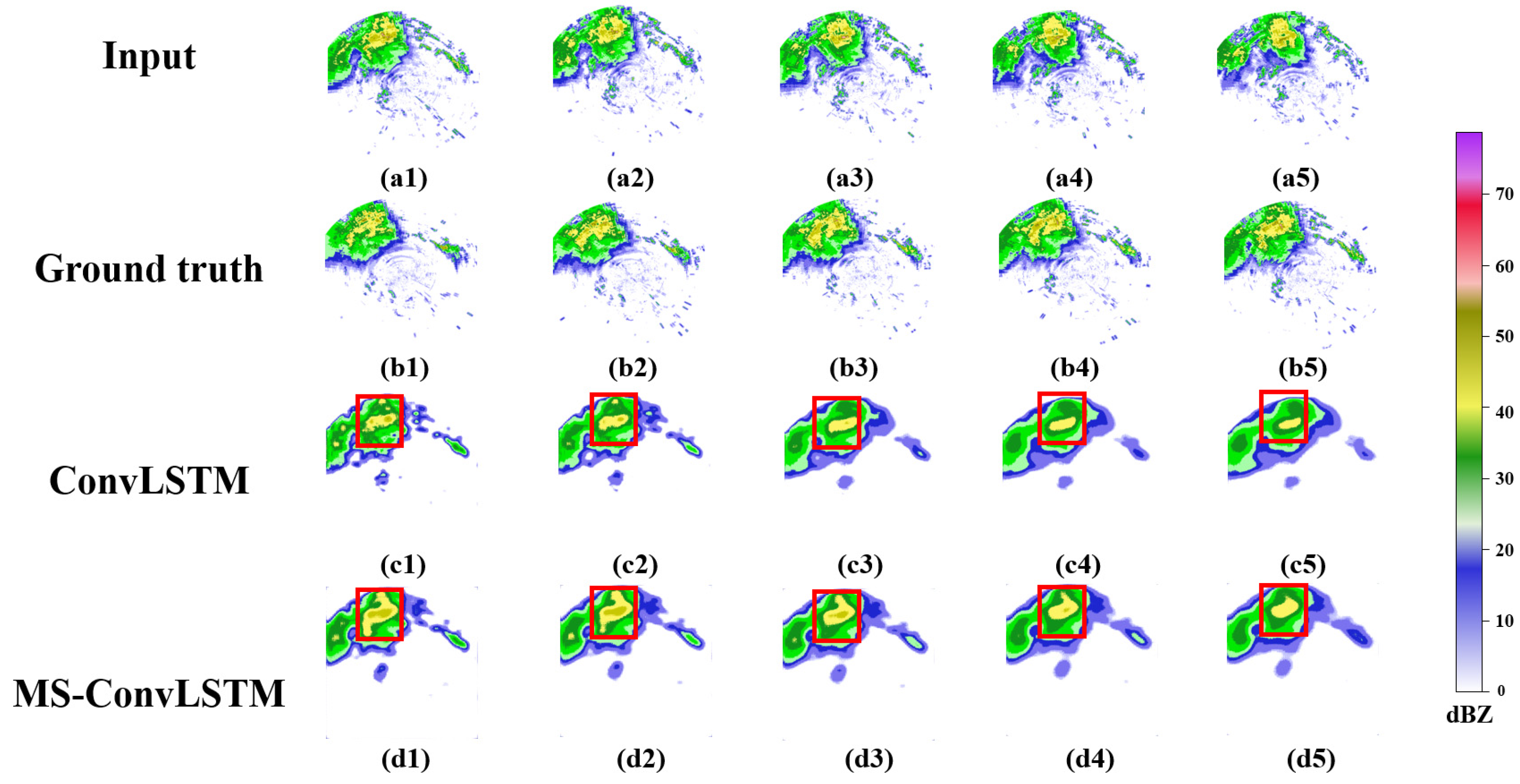
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zaytar, M.A.; El Amrani, C. Sequence to sequence weather forecasting with long short-term memory recurrent neural networks. Int. J. Comput. Appl. 2016, 143, 7–11. [Google Scholar]
- Morris, L.W.; Christopher, D.; Wei, W.; Kevin, W.M.; Joseph, B.K. Experiences with 0–36-hexplicit convective forecasts with the WRF-ARW model. Weather Forecast. 2008, 23, 407–437. [Google Scholar]
- Cong, W.; Ping, W.; Di, W.; Jinyi, H.; Bing, X. Nowcasting multicell short-term intense precipitation using graph models and random forests. Mon. Weather Rev. 2020, 148, 4453–4466. [Google Scholar]
- Houze, R.A., Jr.; Rutledge, S.A.; Biggerstaff, M.I.; Smull, B.F. Interpretation of Doppler weather radar displays of midlatitude mesoscale convective systems. Bull. Am. Meteorol. Soc. 1989, 70, 608–619. [Google Scholar] [CrossRef]
- Jing, J.; Li, Q.; Ma, L.; Chen, L.; Ding, L. REMNet: Recurrent Evolution Memory-Aware Network for Accurate Long-Term Weather Radar Echo Extrapolation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4109313. [Google Scholar] [CrossRef]
- Nitish, S.; Elman, M.; Ruslan, S. Unsupervised learning of video representations using LSTMs. PLMR 2015, 37, 843–852. [Google Scholar]
- Xingjian, S.; Hao, W.; Dit-Yan, Y.; Zhourong, C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Lin, T.; Xutao, L.; Yunming, Y.; Pengfei, X.; Yan, L. A generative adversarial gated recurrent unit model for precipitation nowcasting. IEEE Geosci. Remote Sens. Lett. 2019, 17, 601–605. [Google Scholar]
- Sato, R.; Kashima, H.; Yamamoto, T. Short-term precipitation prediction with skip-connected prednet. In Proceedings of the International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Springer: Cham, Switzerland, 2018; pp. 373–382. [Google Scholar]
- Rane, R.P.; Szügyi, E.; Saxena, V.; Ofner, A.; Stober, S. Prednet and predictive coding: A critical review. In Proceedings of the 2020 International Conference on Multimedia Retrieval, Dublin, Ireland, 8–11 June 2020; pp. 233–241. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Deep learning for precipitation nowcasting: A benchmark and a new model. arXiv 2017, arXiv:1706.03458. [Google Scholar]
- Pulkkinen, S.; Nerini, D.; Pérez Hortal, A.A.; Velasco-Forero, C.; Seed, A.; Germann, U.; Foresti, L. Pysteps: An open-source Python library for probabilistic precipitation nowcasting (v1. 0). Geosci. Model Dev. 2019, 12, 4185–4219. [Google Scholar] [CrossRef]
- Kedong, Z.; Yaping, L.; Wenbo, M.; Feng, L. LSTM enhanced by dual-attention-based encoder-decoder for daily peak load forecasting. Electr. Power Syst. Res. 2022, 208, 107860. [Google Scholar] [CrossRef]
- Feltus, C. Learning Algorithm Recommendation Framework for IS and CPS Security: Analysis of the RNN, LSTM, and GRU Contributions. Int. J. Syst. Softw. Secur. Prot. 2022, 13, 36. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Lin, C.; Vasić, S.; Kilambi, A.; Turner, B.; Zawadzki, I. Precipitation forecast skill of numerical weather prediction models and radar nowcasts. Geophys. Res. Lett. 2005, 32, L14801. [Google Scholar] [CrossRef]
- Datta, L. A survey on activation functions and their relation with xavier and he normal initialization. arXiv 2020, arXiv:2004.06632. [Google Scholar]
- Binetti, M.S.; Campanale, C.; Massarelli, C.; Uricchio, V.F. The Use of Weather Radar Data: Possibilities, Challenges and Advanced Applications. Earth 2022, 3, 157–171. [Google Scholar] [CrossRef]
- Smith, T.M.; Elmore, K.L.; Dulin, S.A. A damaging downburst prediction and detection algorithm for the WSR-88D. Weather Forecast. 2004, 19, 240–250. [Google Scholar] [CrossRef]
- Usharani, B. ILF-LSTM: Enhanced loss function in LSTM to predict the sea surface temperature. Soft Comput. 2022. [Google Scholar] [CrossRef]
- Sun, F.; Li, B.; Min, M.; Qin, D. Deep Learning-Based Radar Composite Reflectivity Factor Estimations from Fengyun-4A Geostationary Satellite Observations. Remote Sens. 2021, 13, 2229. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Hondl, K.; Potvin, C.K.; Preignitz, D. An Improved Method for Estimating Radar Echo-Top Height. Weather Forecast. 2013, 28, 481–488. [Google Scholar] [CrossRef]
- Boudevillain, B.; Andrieu, H. Assessment of vertically integrated liquid (VIL) water content radar measurement. J. Atmos. Ocean. Technol. 2003, 20, 807–819. [Google Scholar] [CrossRef]
- Altube, P.; Bech, J.; Argemí, O.; Rigo, T.; Pineda, N.; Collis, S.; Helmus, J. Correction of Dual-PRF Doppler Velocity Outliers in the Presence of Aliasing. J. Atmos. Ocean. Technol. 2017, 34, 1529–1543. [Google Scholar] [CrossRef]
- Miller, M.L.; Lakshmanan, V.; Smith, T.M. An automated method for depicting mesocyclone paths and intensities. Weather Forecast. 2013, 28, 570–585. [Google Scholar] [CrossRef]

| Model | MAE | MSE | B-MAE | B-MSE |
|---|---|---|---|---|
| ConvLSTM | 7511 | 2973 | 14,647 | 5729 |
| MS-ConvLSTM | 7038 | 2667 | 14,501 | 5613 |
| Model | Time (min) | POD | FAR | CSI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dBZ Threshold | dBZ Threshold | dBZ Threshold | |||||||||||
| 10 | 20 | 30 | avg | 10 | 20 | 30 | avg | 10 | 20 | 30 | avg | ||
| ConvLSTM | 6 | 0.8915 | 0.8581 | 0.5806 | 0.7767 | 0.0953 | 0.0994 | 0.2125 | 0.1357 | 0.8222 | 0.8004 | 0.6048 | 0.7425 |
| 30 | 0.8302 | 0.7372 | 0.4409 | 0.6694 | 0.1682 | 0.1718 | 0.2397 | 0.1932 | 0.7105 | 0.6804 | 0.3870 | 0.5926 | |
| 60 | 0.7540 | 0.5659 | 0.1280 | 0.4826 | 0.1886 | 0.1963 | 0.3628 | 0.2492 | 0.6415 | 0.5337 | 0.1104 | 0.4286 | |
| MS-ConvLSTM | 6 | 0.9002 | 0.8778 | 0.7228 | 0.8336 | 0.0655 | 0.0735 | 0.1403 | 0.0931 | 0.8391 | 0.8031 | 0.5303 | 0.7242 |
| 30 | 0.8411 | 0.7720 | 0.4620 | 0.6917 | 0.1279 | 0.1510 | 0.2367 | 0.1719 | 0.7487 | 0.7165 | 0.4041 | 0.6231 | |
| 60 | 0.7978 | 0.6357 | 0.1646 | 0.5327 | 0.1531 | 0.1842 | 0.4284 | 0.2552 | 0.6972 | 0.5918 | 0.1568 | 0.4818 | |
| Model | Time (min) | POD | FAR | CSI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dBZ Threshold | dBZ Threshold | dBZ Threshold | |||||||||||
| 10 | 20 | 30 | avg | 10 | 20 | 30 | avg | 10 | 20 | 30 | avg | ||
| ConvLSTM | 6 | 0.8616 | 0.8213 | 0.5604 | 0.7477 | 0.1161 | 0.2123 | 0.3772 | 0.2352 | 0.7361 | 0.7182 | 0.5386 | 0.6637 |
| 30 | 0.8020 | 0.7121 | 0.4251 | 0.6464 | 0.1865 | 0.3720 | 0.6384 | 0.3989 | 0.6205 | 0.5732 | 0.3203 | 0.5046 | |
| 60 | 0.7825 | 0.5480 | 0.1346 | 0.4883 | 0.2115 | 0.4975 | 0.7628 | 0.4906 | 0.6115 | 0.5223 | 0.1087 | 0.4141 | |
| MS-ConvLSTM | 6 | 0.8802 | 0.8636 | 0.6282 | 0.7906 | 0.0928 | 0.1807 | 0.3437 | 0.2057 | 0.7491 | 0.7143 | 0.4674 | 0.6402 |
| 30 | 0.8331 | 0.7402 | 0.4517 | 0.6750 | 0.1680 | 0.3531 | 0.6367 | 0.3859 | 0.6487 | 0.6878 | 0.3914 | 0.5759 | |
| 60 | 0.7946 | 0.6194 | 0.1427 | 0.5189 | 0.1931 | 0.3741 | 0.7075 | 0.4249 | 0.6172 | 0.5973 | 0.1582 | 0.4575 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, M.; Li, Y.; Yu, M.; Zhang, Q.; Zhang, Y.; Liu, B.; Wang, M. Spatiotemporal Prediction of Radar Echoes Based on ConvLSTM and Multisource Data. Remote Sens. 2023, 15, 1279. https://doi.org/10.3390/rs15051279
Lu M, Li Y, Yu M, Zhang Q, Zhang Y, Liu B, Wang M. Spatiotemporal Prediction of Radar Echoes Based on ConvLSTM and Multisource Data. Remote Sensing. 2023; 15(5):1279. https://doi.org/10.3390/rs15051279
Chicago/Turabian StyleLu, Mingyue, Yuchen Li, Manzhu Yu, Qian Zhang, Yadong Zhang, Bin Liu, and Menglong Wang. 2023. "Spatiotemporal Prediction of Radar Echoes Based on ConvLSTM and Multisource Data" Remote Sensing 15, no. 5: 1279. https://doi.org/10.3390/rs15051279
APA StyleLu, M., Li, Y., Yu, M., Zhang, Q., Zhang, Y., Liu, B., & Wang, M. (2023). Spatiotemporal Prediction of Radar Echoes Based on ConvLSTM and Multisource Data. Remote Sensing, 15(5), 1279. https://doi.org/10.3390/rs15051279









