Radiative Effects and Costing Assessment of Arctic Sea Ice Albedo Changes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Estimating SIRF Using the Radiative Kernel Method
| Variables | Datasets | Horizontal Resolution | Temporal | Period | Reference |
|---|---|---|---|---|---|
| Surface Albedo | APP-x | 25 km × 25 km | Daily | 1982–2020 | [49] |
| MERRA-2 | 0.5° × 0.625° | Monthly | 1982–2020 | [54] | |
| ERA 5 | 1° × 1° | Monthly | 1982–2020 | [55] | |
| Sea Ice Concentration | SSMR, SSM/I, SSMIS | 25 km × 25 km | Daily | 1982–2020 | [52] |
| Base Period | |||||
| Radiative Kernels | CAM5 | 0.94° × 1.25° | Monthly | 2006–2007 | [56] |
| HadGem2 | 1.25° × 1.88° | 1860 | [57] | ||
| GFDL | 2° × 2.5° | 1979–1995 | [46] | ||
| CMIP5 | Model | RCPs | |||
| BCC-CSM1 | 0.74° × 1° | Monthly | 2006–2100 | 8.5 | |
| CNRM-CM5 | 0.58° × 1° | 2.6, 4.5, 8.5 | |||
| FGOALS-g2 | 0.86° × 1° | 2.6, 4.5, 8.5 | |||
| IPSL-CAM5a-LR | 1.13° × 1.98° | 2.6, 8.5 | |||
| IPSL-CAM5a-MR | 1.13° × 1.98° | 2.6, 4.5, 8.5 | |||
| IPSL-CAM5b-LR | 1.13° × 1.98° | 2.6, 4.5, 8.5 |
2.2. Conversion of SIRF to CO2 Equivalent
2.3. Estimating Economic Value
3. Results
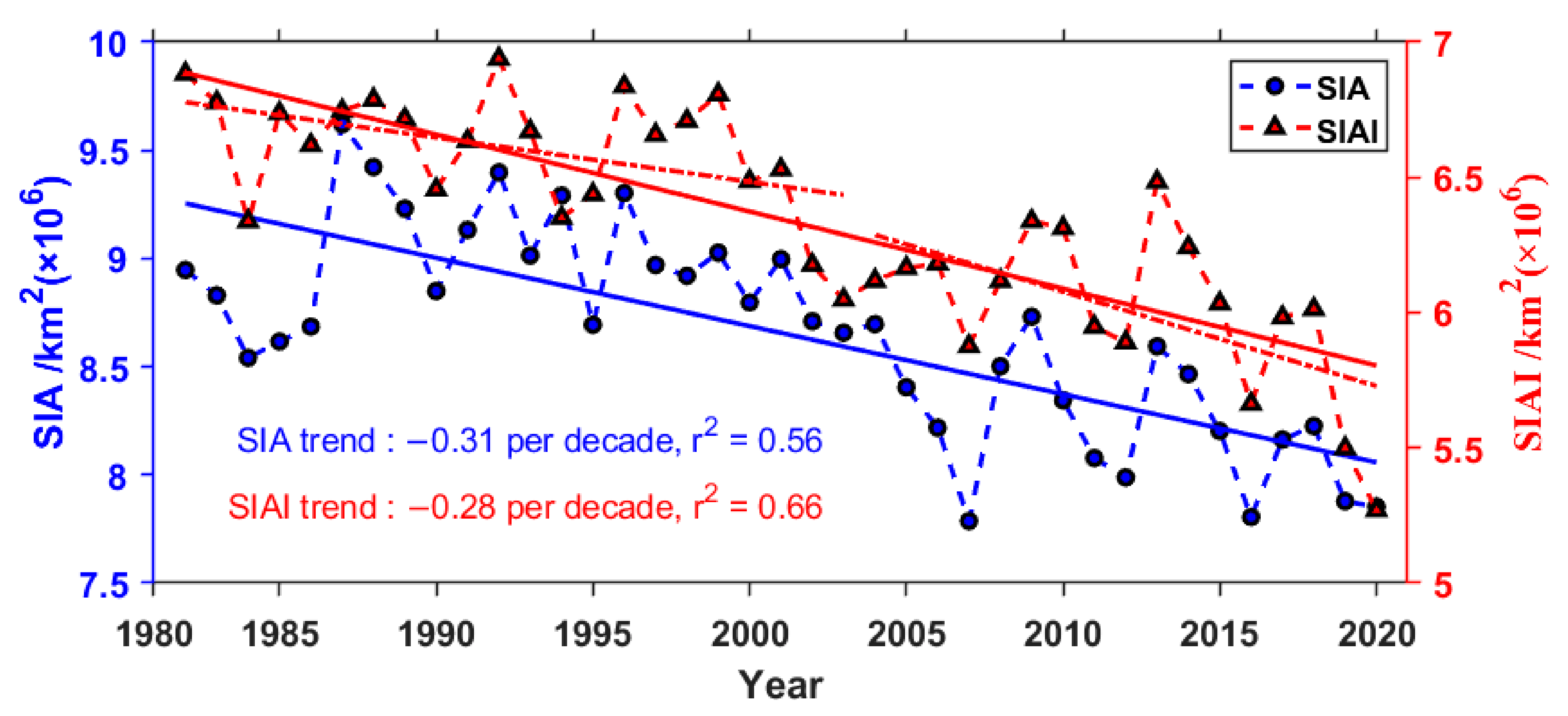
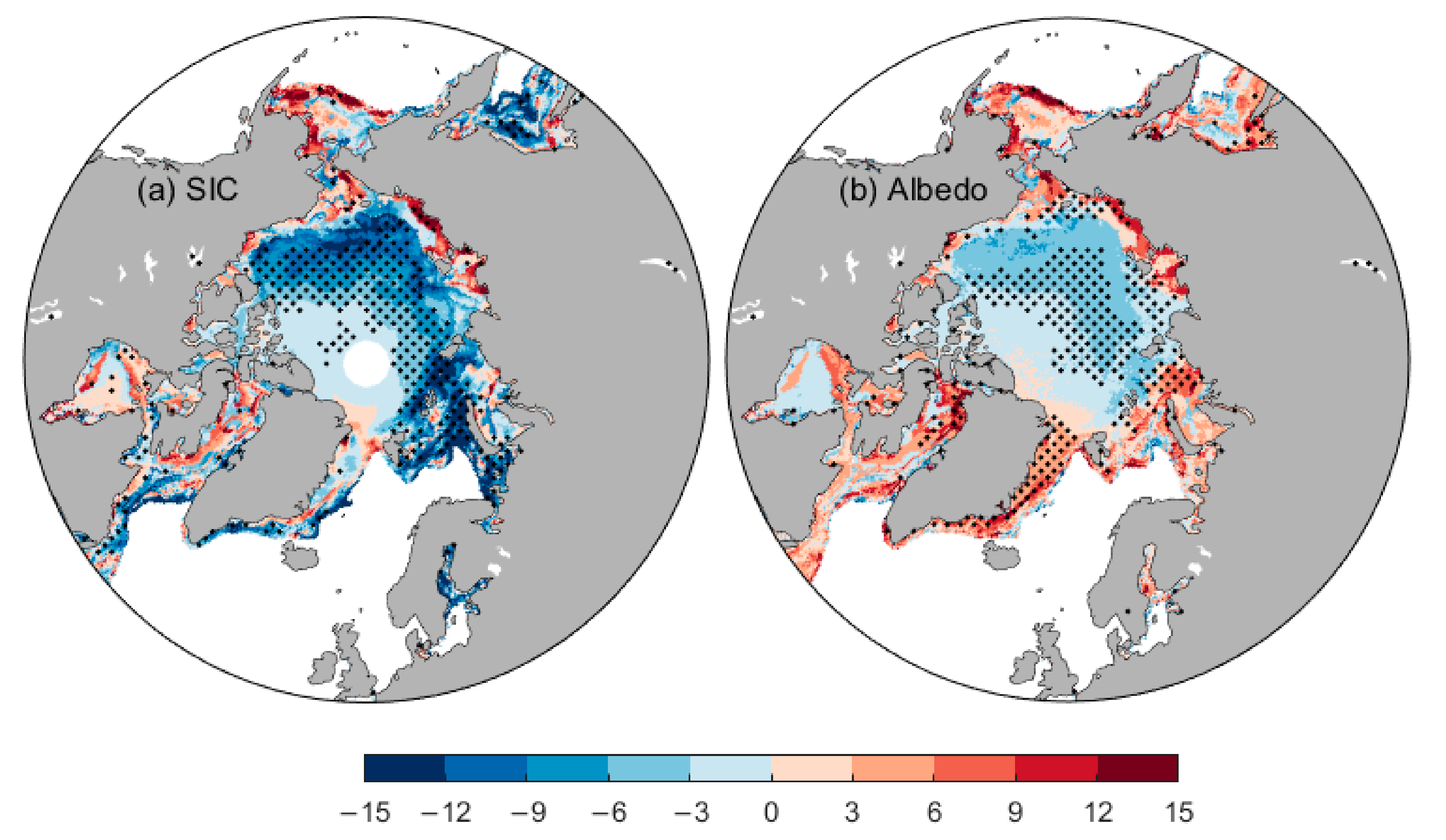
3.1. The Change in Arctic Sea Ice Albedo
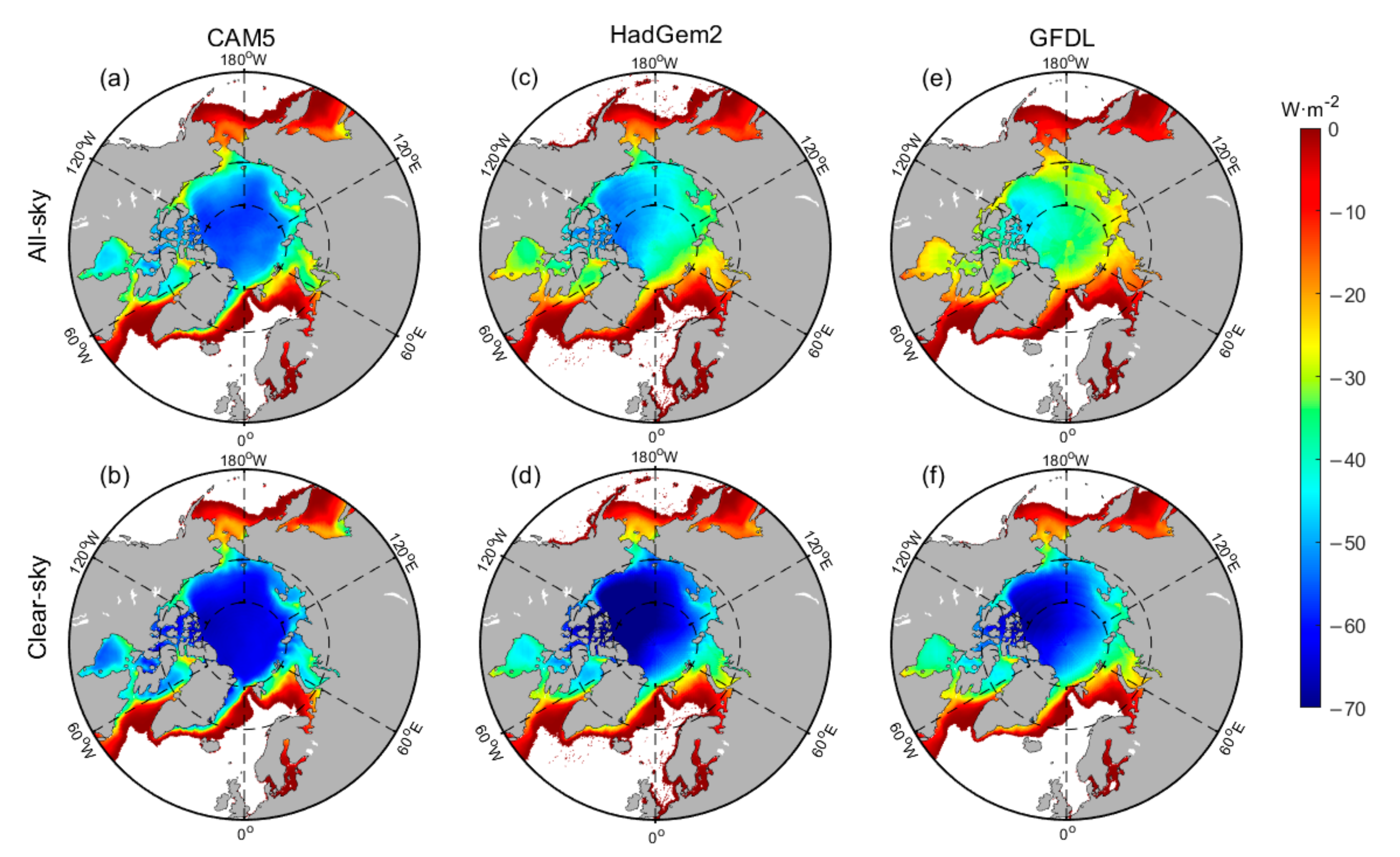
3.2. Arctic SIRF and Seasonal Variation
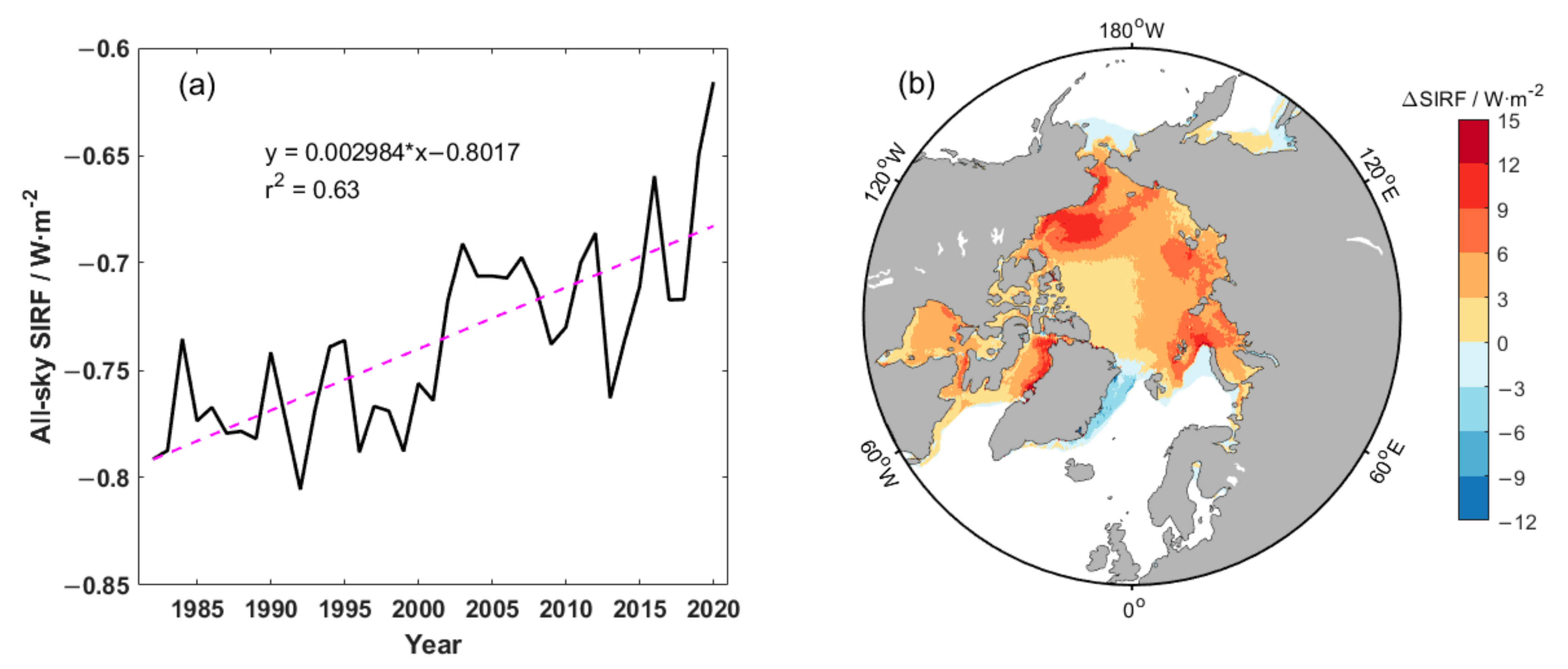
3.3. Past SIRF Changes and Economic Impacts
3.4. Projected Future Arctic SIRF Changes and Economic Impacts
4. Discussion
4.1. Comparison with Previous Studies
4.2. Uncertainties
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Serreze, M.C.; Barry, R.G. Processes and impacts of Arctic amplification: A research synthesis. Glob. Planet. Change 2011, 77, 85–96. [Google Scholar]
- Rantanen, M.; Karpechko, A.Y.; Lipponen, A.; Nordling, K.; Hyvärinen, O.; Ruosteenoja, K.; Vihma, T.; Laaksonen, A. The Arctic has warmed nearly four times faster than the globe since 1979. Commun. Earth Environ. 2022, 3, 168. [Google Scholar] [CrossRef]
- Dai, A.; Luo, D.; Song, M.; Liu, J. Arctic amplification is caused by sea-ice loss under increasing CO2. Nat. Commun. 2019, 10, 121. [Google Scholar] [CrossRef]
- Screen, J.A.; Simmonds, I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 2010, 464, 1334–1337. [Google Scholar] [CrossRef]
- Comiso, J.C. Large decadal decline of the Arctic multiyear ice cover. J. Clim. 2012, 25, 1176–1193. [Google Scholar] [CrossRef]
- Peng, G.; Meier, W.N. Temporal and regional variability of Arctic sea-ice coverage from satellite data. Ann. Glaciol. 2018, 59, 191–200. [Google Scholar] [CrossRef]
- Kwok, R. Arctic sea ice thickness, volume, and multiyear ice coverage: Losses and coupled variability (1958–2018). Environ. Res. Lett. 2018, 13, 105005. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F. Variability of Arctic sea ice thickness and volume from CryoSat-2. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140157. [Google Scholar] [CrossRef]
- Markus, T.; Stroeve, J.C.; Miller, J. Recent changes in Arctic sea ice melt onset, freezeup, and melt season length. J. Geophys. Res. 2009, 114, C12024. [Google Scholar]
- Stroeve, J.C.; Markus, T.; Boisvert, L.N.; Miller, J.A.; Barrett, A.P. Changes in Arctic Melt Season and Implications for Sea Ice Loss. Geophys. Res. Lett. 2014, 41, 1216–1225. [Google Scholar] [CrossRef]
- Smith, A.; Jahn, A.; Burgard, C.; Notz, D. Improving model-satellite comparisons of sea ice melt onset with a satellite simulator. Cryosphere Discuss. 2021, 16, 3235–3248. [Google Scholar] [CrossRef]
- Perovich, D.K.; Polashenski, C. Albedo evolution of seasonal Arctic sea ice. Geophys. Res. Lett. 2012, 39, L08501. [Google Scholar] [CrossRef]
- Riihelä, A.; Manninen, T.; Laine, V. Observed changes in the albedo of the Arctic sea-ice zone for the period 1982–2009. Nat. Clim. Chang. 2013, 3, 895–898. [Google Scholar] [CrossRef]
- Xiao, C.D.; Wang, S.J.; Qin, D.H. A preliminary study of cryosphere service function and value evaluation. Adv. Clim. Chang. Res. 2015, 6, 181–187. [Google Scholar] [CrossRef]
- Su, B.; Xiao, C.; Chen, D.; Qin, D.; Ding, Y. Cryosphere services and human well-being. Sustainability 2019, 11, 4365. [Google Scholar] [CrossRef]
- Xiao, C.; Su, B.; Wang, X.; Qin, D. Cascading risks to the deterioration in cryospheric functions and services. Kexue Tongbao Chin. Sci. Bull. 2019, 64, 1975–1984. [Google Scholar] [CrossRef]
- Gacheno, D.; Amare, G. Review of Impact of Climate Change on Ecosystem Services—A Review. Int. J. Food Sci. Agric. 2021, 5, 363–369. [Google Scholar] [CrossRef]
- Burke, M.; Hsiang, S.M.; Miguel, E. Global non-linear effect of temperature on economic production. Nature 2015, 527, 235–239. [Google Scholar] [CrossRef]
- Whiteman, G.; Hope, C.; Wadhams, P. Vast costs of Arctic change—Methane released by melting permafrost will have global impacts. Nature 2013, 499, 401–403. [Google Scholar] [CrossRef]
- Andry, O.; Bintanja, R.; Hazeleger, W. Time-dependent variations in the Arctic’s surface albedo feedback and the link to seasonality in sea ice. J. Clim. 2017, 30, 393–410. [Google Scholar] [CrossRef]
- Thackeray, C.W.; Hall, A. An emergent constraint on future Arctic sea-ice albedo feedback. Nat. Clim. Chang. 2019, 9, 972–978. [Google Scholar] [CrossRef]
- Petrich, C.; Eicken, H.; Polashenski, C.M.; Sturm, M.; Harbeck, J.P.; Perovich, D.K.; Finnegan, D.C. Snow dunes: A controlling factor of melt pond distribution on Arctic sea ice. J. Geophys. Res. Ocean. 2012, 117, C09029. [Google Scholar] [CrossRef]
- Kashiwase, H.; Ohshima, K.I.; Nihashi, S.; Eicken, H. Evidence for ice-ocean albedo feedback in the Arctic Ocean shifting to a seasonal ice zone. Sci. Rep. 2017, 7, 8170. [Google Scholar] [CrossRef]
- Pinker, R.T.; Niu, X.M.; Ma, Y. Solar heating of the Arctic Ocean in the context of ice-albedo feedback. J. Geophys. Res. Ocean. 2014, 119, 8395–8409. [Google Scholar] [CrossRef]
- Letterly, A.; Key, J.; Liu, Y. Arctic climate: Changes in sea ice extent outweigh changes in snow cover. Cryosphere 2018, 12, 3373–3382. [Google Scholar] [CrossRef]
- Graversen, R.G.; Wang, M. Polar amplification in a coupled climate model with locked albedo. Clim. Dyn. 2009, 33, 629–643. [Google Scholar] [CrossRef]
- Peng, H.T.; Ke, C.Q.; Shen, X.; Li, M.; Shao, Z. De Summer albedo variations in the Arctic Sea ice region from 1982 to 2015. Int. J. Climatol. 2020, 40, 3008–3020. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, H.; Fu, Q.; Rasch, P.J.; Wang, X. Unraveling driving forces explaining significant reduction in satellite-inferred Arctic surface albedo since the 1980s. Proc. Natl. Acad. Sci. USA 2019, 116, 23947–23953. [Google Scholar] [CrossRef]
- Flanner, M.G.; Shell, K.M.; Barlage, M.; Perovich, D.K.; Tschudi, M.A. Radiative forcing and albedo feedback from the Northern Hemisphere cryosphere between 1979 and 2008. Nat. Geosci. 2011, 4, 151–155. [Google Scholar] [CrossRef]
- Pistone, K.; Eisenman, I.; Ramanathan, V. Observational determination of albedo decrease caused by vanishing Arctic sea ice. Proc. Natl. Acad. Sci. USA 2014, 111, 3322–3326. [Google Scholar] [CrossRef]
- Cao, Y.; Liang, S.; Chen, X.; He, T. Assessment of sea ice albedo radiative forcing and feedback over the Northern Hemisphere from 1982 to 2009 using satellite and reanalysis data. J. Clim. 2015, 28, 1248–1259. [Google Scholar] [CrossRef]
- Riihelä, A.; Bright, R.M.; Anttila, K. Recent strengthening of snow and ice albedo feedback driven by Antarctic sea-ice loss. Nat. Geosci. 2021, 14, 832–836. [Google Scholar] [CrossRef]
- Seong, N.-H.; Kim, H.-C.; Choi, S.; Jin, D.; Jung, D.; Sim, S.; Woo, J.; Kim, N.; Seo, M.; Lee, K.-S.; et al. Evaluation of Sea Ice Radiative Forcing according to Surface Albedo and Skin Temperature over the Arctic from 1982–2015. Remote Sens. 2022, 14, 2512. [Google Scholar] [CrossRef]
- Holland, M.M.; Serreze, M.C.; Stroeve, J. The sea ice mass budget of the Arctic and its future change as simulated by coupled climate models. Clim. Dyn. 2010, 34, 185–200. [Google Scholar] [CrossRef]
- Overland, J.E.; Wang, M. When will the summer Arctic be nearly sea ice free? Geophys. Res. Lett. 2020, 40, 2097–2101. [Google Scholar] [CrossRef]
- Niederdrenk, A.L.; Notz, D. Arctic Sea Ice in a 1.5 °C Warmer World. Geophys. Res. Lett. 2018, 45, 1963–1971. [Google Scholar] [CrossRef]
- Pistone, K.; Eisenman, I.; Ramanathan, V. Radiative Heating of an Ice-Free Arctic Ocean. Geophys. Res. Lett. 2019, 46, 7474–7480. [Google Scholar] [CrossRef]
- Hudson, S.R. Estimating the global radiative impact of the sea ice-albedo feedback in the Arctic. J. Geophys. Res. Atmos. 2011, 116, D16102. [Google Scholar] [CrossRef]
- Notz, D.; Stroeve, J. The Trajectory Towards a Seasonally Ice-Free Arctic Ocean. Curr. Clim. Chang. Rep. 2018, 4, 407–416. [Google Scholar] [CrossRef]
- Crawford, A.; Stroeve, J.; Smith, A.; Jahn, A. Arctic open-water periods are projected to lengthen dramatically by 2100. Commun. Earth Environ. 2021, 2, 109. [Google Scholar] [CrossRef]
- Euskirchen, E.S.; Goodstein, E.S.; Huntington, H.P. An estimated cost of lost climate regulation services caused by thawing of the Arctic cryosphere. Ecol. Appl. 2013, 23, 1869–1880. [Google Scholar] [CrossRef]
- Badina, S.; Pankratov, A. Assessment of the Impacts of Climate Change on the Russian Arctic Economy (including the Energy Industry). Energies 2022, 15, 2849. [Google Scholar] [CrossRef]
- Yumashev, D.; Hope, C.; Schaefer, K.; Riemann-Campe, K.; Iglesias-Suarez, F.; Jafarov, E.; Burke, E.J.; Young, P.J.; Elshorbany, Y.; Whiteman, G. Climate policy implications of nonlinear decline of Arctic land permafrost and other cryosphere elements. Nat. Commun. 2019, 10, 1900. [Google Scholar] [CrossRef]
- Nordhaus, W.D.; Boyer, J. Warming the World: Economic Models of Global Warming; The MIT Press: Cambridge, MA, USA, 2000; Volume 7. [Google Scholar]
- Nordhaus, W. Economics of the disintegration of the Greenland ice sheet. Proc. Natl. Acad. Sci. USA 2019, 116, 12261–12269. [Google Scholar] [CrossRef]
- Soden, B.J.; Held, I.M.; Colman, R.C.; Shell, K.M.; Kiehl, J.T.; Shields, C.A. Quantifying climate feedbacks using radiative kernels. J. Clim. 2008, 21, 3504–3520. [Google Scholar] [CrossRef]
- Seitz, R. Bright water: Hydrosols, water conservation and climate change. Clim. Chang. 2010, 105, 365–381. [Google Scholar] [CrossRef]
- Maslanik, J.A.; Key, J.; Fowler, C.W.; Nguyen, T.; Wang, X. Spatial and Temporal Variability of Satellite-derived Cloud and Surface Characteristics During FIRE-ACE. J. Geophys. Res. Atmos. 2001, 106, 233–249. [Google Scholar]
- Key, J.; Wang, X.; Liu, Y.; Dworak, R.; Letterly, A. The AVHRR polar Pathfinder climate data records. Remote Sens. 2016, 8, 167. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; Van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef]
- Cavalieri, D.; Parkinson, C.; Gloersen, P.; Zwally, H. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 1996; p. 29. [Google Scholar] [CrossRef]
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-Grid 2.0: Incremental but significant improvements for earth-gridded data sets. ISPRS Int. J. Geo-Inf. 2012, 1, 32–45. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Conley, A.; Vitt, F.M. Surface and top-of-Atmosphere radiative feedback kernels for cesm-cam5. Earth Syst. Sci. Data 2018, 10, 317–324. [Google Scholar] [CrossRef]
- Smith, C.J.; Kramer, R.J.; Myhre, G.; Forster, P.M.; Soden, B.J.; Andrews, T.; Boucher, O.; Faluvegi, G.; Fläschner, D.; Hodnebrog, M.K.; et al. Understanding Rapid Adjustments to Diverse Forcing Agents. Geophys. Res. Lett. 2018, 45, 12023–12031. [Google Scholar] [CrossRef]
- Nordhaus, W.D. Estimates of the Social Cost of Carbon:Concepts and Results from the DICE-2013R Model and Alternative Approaches. SSRN Electron. J. 2014, 1, 273–312. [Google Scholar] [CrossRef]
- Nordhaus, W.D. Revisiting the social cost of carbon. Proc. Natl. Acad. Sci. USA 2017, 114, 1518–1523. [Google Scholar] [CrossRef]
- World Bank. State and Trends of Carbon Pricing 2021; World Bank: Washington, DC, USA, 2020; ISBN 9781464815867. [Google Scholar]
- Moritz, R.E.; Gawel, A. Increasing Climate Ambition: Analysis of an International Carbon Price Floor; World Economic Forum: Geneva, Switzerland; PwC: Geneva, Switzerland, 2021. [Google Scholar]
- Stiglitz, J.E.; Stern, N.; Duan, M.; Edenhofer, O.; Giraud, G.; Heal, G.M.; la Rovere, E.L.; Morris, A.; Moyer, E.; Pangestu, M.; et al. Report of the High-Level Commission on Carbon Prices; International Bank for Reconstruction and Development: Washington, DC, USA; International Development Association: Washington, DC, USA, 2017. [Google Scholar]
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic sea ice cover. Geophys. Res. Lett. 2008, 35, L01703. [Google Scholar] [CrossRef]
- Hegyi, B.M.; Taylor, P.C. The Unprecedented 2016–2017 Arctic Sea Ice Growth Season: The Crucial Role of Atmospheric Rivers and Longwave Fluxes. Geophys. Res. Lett. 2018, 45, 5204–5212. [Google Scholar] [CrossRef]
- Jeffries, M.O.; Richter-Menge, J.A.; Overland, J.E. Arctic Report Card 2013. Ann. Neurol. 2013, 74, A11–A12. Available online: http://www.arctic.noaa.gov/reportcard (accessed on 14 June 2022).
- Light, B.; Smith, M.M.; Perovich, D.K.; Webster, M.A.; Holland, M.M.; Linhardt, F.; Raphael, I.A.; Clemens-Sewall, D.; Macfarlane, A.R.; Anhaus, P.; et al. Arctic sea ice albedo: Spectral composition, spatial heterogeneity, and temporal evolution observed during the MOSAiC drift. Elementa 2022, 10, 000103. [Google Scholar] [CrossRef]
- Huang, Y.; Chou, G.; Xie, Y.; Soulard, N. Radiative Control of the Interannual Variability of Arctic Sea Ice. Geophys. Res. Lett. 2019, 46, 9899–9908. [Google Scholar] [CrossRef]
- Perovich, D.; Meier, W.; Tschudi, M.; Hendricks, S.; Petty, A.A.; Divine, D.; Farrell, S.; Gerland, S.; Haas, C.; Kaleschke, L.; et al. Arctic Report Card 2020: Sea ice. NOAA Arct. Rep. Card 2020 2021. [Google Scholar] [CrossRef]
- Selyuzhenok, V.; Bashmachnikov, I.; Ricker, R.; Vesman, A.; Bobylev, L. Sea ice volume variability and water temperature in the Greenland Sea. Cryosphere 2020, 14, 477–495. [Google Scholar] [CrossRef]
- Chen, J.L.; Kang, S.C.; Meng, X.H.; You, Q.L. Assessments of the Arctic amplification and the changes in the Arctic sea surface. Adv. Clim. Chang. Res. 2019, 10, 193–202. [Google Scholar] [CrossRef]
- Chernokulsky, A.V.; Esau, I.; Bulygina, O.N.; Davy, R.; Mokhov, I.I.; Outten, S.; Semenov, V.A. Climatology and interannual variability of cloudiness in the Atlantic Arctic from surface observations since the late nineteenth century. J. Clim. 2017, 30, 2103–2120. [Google Scholar] [CrossRef]
- Huang, Y.; Dong, X.; Bailey, D.A.; Holland, M.M.; Xi, B.; DuVivier, A.K.; Kay, J.E.; Landrum, L.L.; Deng, Y. Thicker Clouds and Accelerated Arctic Sea Ice Decline: The Atmosphere-Sea Ice Interactions in Spring. Geophys. Res. Lett. 2019, 46, 6980–6989. [Google Scholar] [CrossRef]
- Matveeva, T.A.; Semenov, V.A. Regional Features of the Arctic Sea Ice Area Changes in 2000–2019 versus 1979–1999 Periods. Atmosphere 2022, 13, 1434. [Google Scholar] [CrossRef]
- Marcianesi, F.; Aulicino, G.; Wadhams, P. Arctic sea ice and snow cover albedo variability and trends during the last three decades. Polar Sci. 2021, 28, 100617. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Y.; Yin, C. Contribution of changes in snow cover extent to shortwave radiation perturbations at the top of the atmosphere over the northern hemisphere during 2000–2019. Remote Sens. 2021, 13, 4938. [Google Scholar] [CrossRef]
- Liu, S.; Qi, J.; Liang, S.; Wang, X.; Wu, X.; Xiao, C. Cascading costs of snow cover reduction trend in northern hemisphere. Sci. Total Environ. 2022, 806, 150970. [Google Scholar] [CrossRef]
- Jarraud, M.; Steiner, A. Summary for Policymakers. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012; Volume 9781107025, pp. 3–22. [Google Scholar] [CrossRef]
- Notz, D.; Community, S. Arctic Sea Ice in CMIP6. Geophys. Res. Lett. 2020, 47, e2019GL086749. [Google Scholar] [CrossRef]
- Kramer, R.J.; Matus, A.V.; Soden, B.J.; L’Ecuyer, T.S. Observation-Based Radiative Kernels From CloudSat/CALIPSO. J. Geophys. Res. Atmos. 2019, 124, 5431–5444. [Google Scholar] [CrossRef]



| All-Sky | Clear-Sky | |||||||
|---|---|---|---|---|---|---|---|---|
| CAM5 | HadGem2 | GFDL | Mean | CAM5 | HadGem2 | GFDL | Mean | |
| APP-x | −1.09 ± 0.16 | −0.95 ± 0.13 | −0.75 ± 0.10 | −0.93 ± 0.13 | −1.29 ± 0.20 | −1.34 ± 0.21 | −1.16 ± 0.19 | −1.26 ± 0.20 |
| MERRA2 | −1.25 ± 0.16 | −1.07 ± 0.10 | −0.81 ± 0.07 | −1.04 ± 0.11 | −1.51 ± 0.16 | −1.56 ± 0.17 | −1.34 ± 0.15 | −1.47 ± 0.16 |
| ERA5 | −1.13 ± 0.12 | −0.97 ± 0.10 | −0.75 ± 0.07 | −0.95 ± 0.10 | −1.36 ± 0.16 | −1.40 ± 0.17 | −1.22 ± 0.15 | −1.33 ± 0.16 |
| Mean | −1.16 ± 0.15 | −1.00 ± 0.11 | −0.77 ± 0.08 | −1.39 ± 0.17 | −1.43 ± 0.18 | −1.24 ± 0.16 | ||
| Model | RCP2.6 | RCP4.5 | RCP8.5 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | MAE | RMSE | Mean | MAE | RMSE | Mean | MAE | RMSE | |
| BCC-CSM1 | nan | nan | nan | nan | nan | nan | −0.05 | 0.15 | 0.17 |
| CNRM-CM5 | 0.15 | 0.15 | 0.20 | −0.05 | 0.15 | 0.17 | 0.16 | 0.17 | 0.21 |
| FGOALS-g2 | 0.13 | 0.15 | 0.22 | 0.16 | 0.16 | 0.21 | 0.12 | 0.15 | 0.21 |
| IPSL-CAM5a-LR | 0.03 | 0.08 | 0.11 | nan | nan | nan | 0.03 | 0.09 | 0.12 |
| IPSL-CAM5a-MR | −0.07 | 0.09 | 0.11 | 0.13 | 0.15 | 0.21 | −0.06 | 0.08 | 0.10 |
| IPSL-CAM5b-LR | nan | nan | nan | −0.05 | 0.07 | 0.09 | 0.13 | 0.15 | 0.22 |
| MMEM | 0.06 | 0.09 | 0.13 | 0.09 | 0.11 | 0.16 | 0.09 | 0.11 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, H.; Su, B.; Liu, S.; Zhuo, W. Radiative Effects and Costing Assessment of Arctic Sea Ice Albedo Changes. Remote Sens. 2023, 15, 970. https://doi.org/10.3390/rs15040970
Hao H, Su B, Liu S, Zhuo W. Radiative Effects and Costing Assessment of Arctic Sea Ice Albedo Changes. Remote Sensing. 2023; 15(4):970. https://doi.org/10.3390/rs15040970
Chicago/Turabian StyleHao, Hairui, Bo Su, Shiwei Liu, and Wenqin Zhuo. 2023. "Radiative Effects and Costing Assessment of Arctic Sea Ice Albedo Changes" Remote Sensing 15, no. 4: 970. https://doi.org/10.3390/rs15040970
APA StyleHao, H., Su, B., Liu, S., & Zhuo, W. (2023). Radiative Effects and Costing Assessment of Arctic Sea Ice Albedo Changes. Remote Sensing, 15(4), 970. https://doi.org/10.3390/rs15040970









