Abstract
This paper investigates possible anomalies on the occasion of the ML = 3.3 earthquake, which occurred on 1st January 2023 close to Guidonia Montecelio (Rome, Italy). This earthquake followed another very close event recorded on 23 December 2022 with a magnitude ML = 3.1 (epicentral distance of less than 1 km). Seismological investigations clearly show an acceleration of seismicity in the preceding six months in a circular area of about a 60 km radius. Two conclusions coming from the time-to-failure power law fitting to the cumulative Benioff strain curve are the most probable: the ML3.3 of 1 January 2023 is the mainshock of the seismic sequence, or an incoming earthquake of a magnitude of about 4.1 provides a slightly better fit (higher determination coefficient) of the seismic data. Further investigations are necessary to assess whether the accumulated stress has been totally released. No atmospheric anomalies related to this seismic activity have been identified, even if some SO2 emissions seem to be induced by the tectonic and volcanic sources in the south Tyrrhenian Sea. Swarm satellite magnetic data show about 20 anomalous tracks six months before the Guidonia earthquake. In particular, on 16 December 2022, anomalous oscillations of the east component of the geomagnetic field are temporally compatible with the seismic acceleration, but other sources are also possible. Other anomalous magnetic signals are more likely to be associated with the ongoing seismic activity offshore of the Marche region in Italy (the strongest event up to now is Mw = 5.5 on 9 November 2022 close to Pesaro Urbino).
1. Introduction
On 1 January 2023 at 13:07:46 Universal Time—UT (14:07 Central European Time—CET)—an earthquake of magnitude ML = 3.3 was localised northeast of the capital of Italy, Rome, by the Italian National Institute of Geophysics and Volcanology (INGV). In particular, the epicenter was 3 km southeast of Guidonia Montecelio town, at the coordinates of 41.982°N and 12.750°E. The earthquake’s depth was shallow, estimated at about 9 km (http://cnt.rm.ingv.it/event/33781261, accessed on 2 January 2023). The event was relatively low in magnitude, but it obtained particular interest because it followed another seismic event with a slightly lower magnitude ML = 3.1 that occurred on 23 December 2022 at 16:35:13 UT (17:35 CET) with almost the same epicentre (41.984°N and 12.756°E, distance from the abovementioned event of about 0.5 km). This event’s hypocentral depth was estimated at 10 km (http://terremoti.ingv.it/event/33714971, accessed on 2 January 2023). Based on the data on the INGV website, at least 681 people (last update 1 January 2023 at 19:31 CET) felt the event on 23 December 2022, filling out the form on https://www.hsit.it/ (accessed on 2 January 2023) and 765 people after the event on 1 January 2023 (last update 2 January 2023 at 3:55 CET). From 1977, around this event, within ~50 km, previous earthquakes were characterised by different focal mechanisms. Some thrust earthquakes have been historically recorded towards the northeast, while strike-slip and normal fault events have been localised on the southeast and west sides. In particular, the Guidonia earthquakes that occurred on 23 December 2022 and 1 January 2023 could have been produced by a strike-slip fault proposed by Faccenna et al. [1] starting on the Cornicolani Mounts and ending at the Colli Albani volcano district, crossing the city of Guidonia city (dashed line in Figure 1 of their paper, depicted here as the green dashed-dot line in Figure 1b). In the box delimited by 41.9°N ≤ latitude ≤ 42.1°N and 12.6°E ≤ longitude ≤ 12.8°E, the highest magnitude event between 1985 and 2023 was Md = 3.3 on 16 February 1999, 2 km north of Tivoli, which seems located on a northeast parallel fault. Other magnitude 2.9 earthquakes were recorded on the same fault close to Tivoli town on 22 September 2005 (doublet) and on 20 August 2013. After 1 January 2023, an event of magnitude Mw = 3.2 was recorded 8 km northwest of Colonna town on 22 January 2023 at 1:46:11 UT (http://cnt.rm.ingv.it/event/33960061, accessed on 29 January 2023). This event was localised on the southern side of the same strike-slip fault (dashed-dot green line in Figure 1b). In conclusion, the ML3.3 Guidonia earthquake of 1 January 2023 is presently the strongest event ever reported with the instrumental catalogue (from 1985) on this fault.
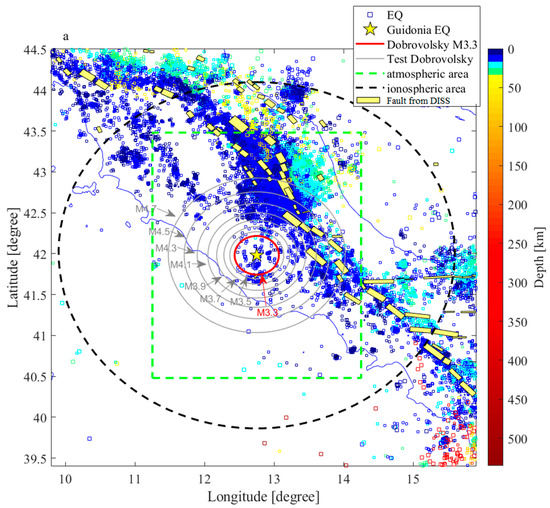
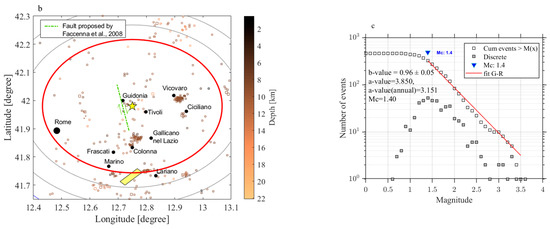
Figure 1.
Earthquakes that occurred in Central Italy from 1st January 2018 until 1st January 2023. (a) Geographical map of the earthquake (EQ) events with active seismic fault from DISS: the yellow star represents the event of Guidonia 1 January 2023, ML = 3.3; the red circle is its Dobrovolsky area; grey circles are the tested Dobrovolsky areas; the green dashed rectangle is the area used to calculate atmospheric time series, and the black dashed circle is the research area for ionospheric investigations. The adapted colour bar scale shows the hypocentral depth. (b) Enlargement of the map around the Guidonia (Rome) earthquake. In addition to previous details, the principal local towns are shown in relation to recorded seismicity. The transcurrent fault proposed by Faccenna [1] is reported with a dashed-dot green line. (c) The Gutenberg–Richter (G–R) distribution of the magnitude of the earthquakes, excluding the seismicity in the northeast corner of the map, i.e., within a radius of 50 km from Guidonia epicentres. The magnitude of completeness and G–R parameters are reported.
One basic question is whether the events are parts of a seismic sequence or a swarm. A seismic sequence is characterised by a higher magnitude event (the mainshock) followed by aftershocks, and could be preceded by foreshocks of lower magnitude. In contrast, a seismic swarm is a chain of comparable and low-magnitude earthquakes without a clear mainshock [2]. If this is a seismic sequence, it is crucial to know if the event of magnitude ML = 3.3 of 1 January 2023 is the mainshock or if a future event of higher magnitude is likely to occur. Furthermore, for seismic sequences, the decay of the aftershocks generally follows the Omori-Utsu law [3]; in contrast, a seismic swarm has an almost constant seismic rate. The peculiarities of the seismic earthquakes of 22 December 2022 and 1 January 2023 localised close to Guidonia (Rome, Italy) motivates a further investigation that we report in this short paper. The research is based on our previous experience in the field of lithosphere, atmosphere, and ionosphere analysis prior to seismic events.
2. Materials and Methods
In this paper, we investigated the earthquake catalogue, the atmospheric data from a climatological archive, and the magnetic field and electron density data from the Swarm satellite constellation.
2.1. Earthquake Catalogue
The earthquake catalogue was acquired from the INGV ISIDE [4] earthquake web portal (http://cnt.rm.ingv.it/, accessed on 2 January 2023) by the selection of the events inside the square box delimited by 34.4°N ≤ latitude ≤ 44.5°N and 9.8°E ≤ longitude ≤ 15.9°E from 1st January 2018 until 1st January 2023. No constraints were selected for magnitude and depth. The geographical positions of all the events are shown in Figure 1a. The seismicity induced by the very long Italian Seismic Sequence of Amatrice-Norcia-Capitigliano (Montereale) 2016–2017 [5] is visible in the diagonal from the northwest to the southeast sides of the map of Figure 1a.
The completeness magnitude “Mc” was analysed by the ZMap software [6], excluding the events associated with the Amatrice-Norcia-Capitigliano Italian Seismic sequence (i.e., the event more than 50 km from the Guidonia 2023 earthquake) to avoid a bias in the analysis. In fact, the Apennines central region of Italy, affected by this sequence, was more thoroughly covered with permanent seismic stations and temporary stations after the start of the same sequence. The completeness magnitude was estimated to be Mc = 1.4, as visible in the graph in Figure 1c. In addition, this graph represents the Gutenberg–Richter law [7] with “a” and “b” values, which represent the amount of recorded seismicity and the ratio between smaller and higher magnitude events in the region, respectively. The “a” value is the decimal logarithm of the amount of M0+ earthquakes in the investigated area in the analysed time, or during one year. The b-value is generally found to be equal to 1 at a global or regional scale. Before large earthquakes, its value can decrease, indicating a lack of larger-magnitude events in the statistic [8,9]. Only earthquakes with magnitude M ≥ Mc will be considered in the following analyses. The cumulative Benioff stress was computed for the events inside the Dobrovolsky radius. Benioff stress is an indication of the stress accumulating on a fault [10]. The Dobrovolsky radius is a distance typically used to estimate the preparation area of an earthquake [11].
In particular, Dobrovolsky’s radius in kilometres is
The Benioff cumulative stress S(t) could be empirically estimated by the following formula:
where “i” is the i-th earthquake with magnitude Mi, and N(t) is the total number of earthquakes that occurred until the time t. According to Mignan et al. [12] and Cianchini et al. [13], the following analytical model, in the form of a time-to-failure power law, has been fitted to the Benioff cumulative stress:
where parameters A and B are proportional to the final and initial accumulated stress, respectively, and m is an exponential factor in the range from 0 to 1, typically equal to 0.3 [13]. We underline that the time-to-failure power law analytical model assumes that the mainshock is incoming at the time tf, and it is not expected to work in the case of the aftershock sequence, a swarm of earthquakes, or a seismic quiescence.
Fitting such a curve is equivalent to resolving the following equation:
In this work, m has been fixed to m = 3 to guarantee the stability of the power law fit. The graphs report “tf”, which is the time to failure, i.e., the likelihood estimation of the mainshock time.
2.2. Atmospheric Data Processing
The data from the climatological archive MERRA-2 by NASA [14] have been investigated to monitor the atmosphere. With the experience of the earthquakes previously studied, the MEANS software was used, with the removal of a linear trend to take into account the possible effect of global warming, as done in De Santis et al. [14] for the Ridgecrest, US, 2019 earthquake analysis. The MEANS algorithm was used for the first time by Piscini et al. [15] to investigate volcano eruptions, and later applied to several other volcano eruptions and earthquakes [14,16,17,18,19,20]. The algorithm essentially estimates the typical value of the atmospheric parameter for the day and region, constructing a historical time series, particularly the mean and standard deviation of the parameter for the area under study. If, in the year with the natural hazard event, the parameter exceeds two standard deviations of the historical time series, it is considered anomalous. This report investigated surface air temperature, aerosol, surface total energy flux, sulphur dioxide, surface specific humidity, and total precipitation.
2.3. Ionospheric Data Processing
The ionosphere is monitored by the European Space Agency (ESA) Swarm constellation. The Swarm mission is composed of three identical satellites in low-Earth quasi-polar orbits, called Alpha, Bravo and Charlie, aiming to measure the geomagnetic field with state-of-the-art precision [21]. The use of Swarm data to study earthquake preparation has been explored by several researchers in the last few years by using a single case study approach [20,22,23,24,25,26,27,28,29,30,31,32,33], or by statistically correlating the magnetic and electron density anomalies of Swarm data with M5.5+ earthquakes that occurred in the first 4.7 years of Swarm mission (De Santis et al. [34]), or the first eight years (Marchetti et al. [35]), or by using machine learning (Xiong et al. [36]).
In this report, we applied the MASS algorithm to Swarm magnetic field data defined with all the details in [29,33,34,35], and the NeLOG algorithm defined with all the details in [29], which was used recently in [37] to study the 2020 Samos (Greece) earthquake. MASS analyses the data track-by-track removing the background, by estimating the derivative and subtracting a cubic spline. Such data processing also intrinsically removes the long-term trend of the geomagnetic field from the residuals. The residuals are monitored within a moving window comparing the root mean square of the window with the root mean square of the entire track along −50°S and +50°N geomagnetic latitude. Higher latitude values are excluded to avoid the influence of polar activity.
NeLOG investigates the electron density latitudinal profiles, removing a polynomial of ten degrees from the investigated track and searching for tracks with at least ten anomalous residual samples. The sample is marked as anomalous if its value exceeds “kt” times the standard deviation of the whole residuals.
3. Results
Here, we discuss the results of the seismological, atmospheric, and ionospheric investigations.
3.1. Seismological Investigation
The cumulative Benioff stress was calculated inside the Dobrovolsky area, testing several mainshocks from magnitude 3.3 to 5.5, as listed in Table 1. The lower limit corresponds to the assumption that the 1 January 2023 event is the mainshock. The higher-magnitude events correspond to the hypothesis that a stronger event is incoming. In addition, Table 1 provides the b-value of the Gutenberg–Richter distribution, calculated in the real or tested Dobrovoslky area by ZMap software [6], using the maximum curvature method for more stable solutions. The detailed graphs are reported in Supplementary Materials Figure S1. As previously mentioned, a low b-value could indicate a lack of higher-magnitude events. This low b-value was found in Dobrovolsky’s area of tested events with a magnitude between 3.7 and 4.1.

Table 1.
List of the real (in bold) and tested earthquake magnitudes with the corresponding Dobrovolsky’s radius. All the events are centred at the epicentre of the ML3.3 Guidonia 1 January 2023 earthquake (41.982°N, 12.750°E). The b-value of the Gutenberg–Richter distribution is computed during the six months before the Guidonia earthquake by the maximum curvature method, and details and graphs are provided in Supplementary Materials Figure S1.
For each fit, the adjusted statistic coefficient of determination “adj-R2” and the estimated time of failure are reported in Figures S2 and S3 (in Supplementary Materials), and in Figure 2 for 5 years, 1 year, and 6 months before the ML = 3.3 Guidonia 1 January 2023 earthquake, respectively.
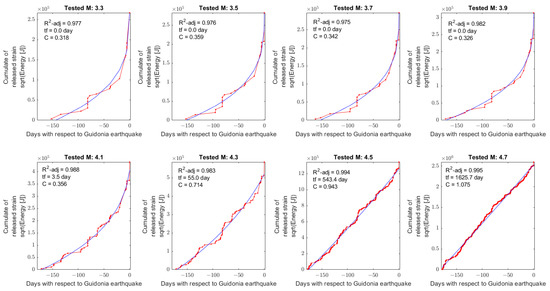
Figure 2.
Benioff cumulative stress curves (in red) calculated within six months of the ML = 3.3 1 January 2023 Guidonia earthquake. Each graph is based on a circular area centred on the 1 January 2023 ML3.3 Guidonia earthquake with a Dobrovolsky’s radius of earthquakes with a magnitude from 3.3 to 4.7. For each plot, the blue curve represents the time-to-failure power law fit, whose adjusted coefficient of determination R2-adj and the time to failure (tf) are reported. The acceleration coefficient C is also reported.
In addition, the acceleration coefficient C defined by Cianchini et al. [13] has been reported in Figures S2 and S3 and Figure 2, and Table 1, calculated as:
where “rmspower law” and “rmslinear fit” are the root mean square errors of samples “Si” (i = 1…N) with respect to their fits “f”; in particular, rms is estimated as:
For lower values of C, the fit represents more acceleration. On the other hand, C = 1 indicates that the trend is linear, and C > 1 indicates that a linear fit is better than the power law. Such a situation could be due to a trend influenced by the aftershocks of another seismic sequence, such as the one of Amatrice-Norcia-Capitigliano (Montereale) Central Italy 2016–2017, in particular for a long trend and a larger radius of analysis.
The investigations for 5 years and 1 year before ML = 3.3 Guidonia 1st January 2023 earthquake do not provide interesting results (Supplementary Materials Figures S2 and S3). In fact, the trends are dominated by another important seismicity which occurred in the area (the Mw = 3.3 11 April 2022, Ciciliano, Rome event, http://cnt.rm.ingv.it/event/30543871, accessed on 2 January 2023). The Apennine residual sequence instead dominates the tests, with a larger magnitude cited above. This is the reason why a magnitudes higher than 4.7 are not reliable to be tested, as the crossing with seismicity from the Central Apennines region becomes predominant.
On the other hand, the investigation in the 6 months before the ML = 3.3 Guidonia 1st January 2023 earthquake, reported in Figure 2, provided interesting results. From magnitude 3.3 to 3.9, the estimated time-to-failure is 0.0 days, and the maximum acceleration reported for M = 3.3 is C = 0.318. Considering that no higher events were recorded in this area on 1 January 2023, among these four analyses, the M = 3.3 test, i.e., the hypothesis that the past earthquake was the mainshock, must be considered the most reliable. Despite this, the analysis for M = 4.1 and M = 4.3 provided good fits, with a time to failure of a few days or weeks (for M4.1, tf = 3.5 days and for M4.3, tf = 55 days). The investigations of M4.5 and M4.7 provided very good fits (R2-adj very close to 1), although they are almost linear (as underlined by their C being close to 1). So, selecting the analysis with the highest adjusted R2 and the most reliable result is the analysis of M4.1 with R2-adj = 0.988 and C = 0.356. Even though this could appear as a prediction, that interpretation is not totally correct. Firstly, it is necessary to estimate the maximum magnitude that the fault could generate. Secondly, it is crucial to determine if these events have totally or partially released the accumulated stress. Furthermore, the time-to-failure power law could not account for several geological and tectonic factors, so it cannot be used alone. Finally, the proper interpretation for the authors is that, in the past six months, in the circular area of a radius of 58 km centred on the Guidonia 1 January 2023 earthquake, a clear seismic acceleration was recorded, but further studies are necessary to propose eventual future scenarios.
3.2. Atmospheric Investigations
In this section, we present the atmospheric investigation six months the ML3.3 Guidonia 1st January 2023 earthquake. The results in terms of time series and maps of surface air temperature, aerosol, surface total energy flux (also known as surface latent heat flux), SO2, surface specific humidity, and total precipitation are provided in Supplementary Materials in Figures S4–S7, Figure 3, Figure 4, Figure 5 and Figure 6. All the time series were calculated in a square box centred on the Guidonia 1st January 2023 earthquake with a 3° side. The surface air temperature time series has some anomalous values. Still, none have multi-day persistence, a criterion found effective for Central Italy by Piscini et al. [38].
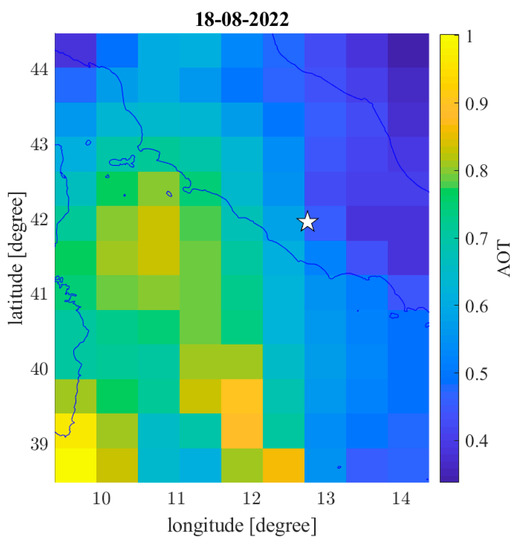
Figure 3.
The aerosol map on 18 August 2022. The epicentre of Guidonia 1 January 2023 earthquake is shown with a white star.
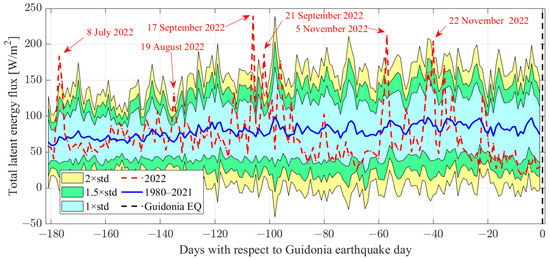
Figure 4.
Total latent energy flux time series from 4 July 2022 to 31 December 2022 (i.e., from six months before until the day before the ML = 3.3 Guidonia 1 January 2023 earthquake, red dashed line). The blue line represents the historical mean calculated from 1980 to 2021 in the same period and region. Cyan, green, and yellow bands represent 1.0, 1.5, and 2.0 standard deviations of the historical values from 1980 to 2021. The horizontal axis represents the day before the Guidonia earthquake for the red dashed line (i.e., the 2022 time series), and the mean and standard deviation of the historical values are computed on the same day of the previous years. The vertical dashed black line represents the Guidonia earthquake (EQ) occurrence time. A red arrow with the specific date is reported for the anomalous days, i.e., the values that exceeded two standard deviations.
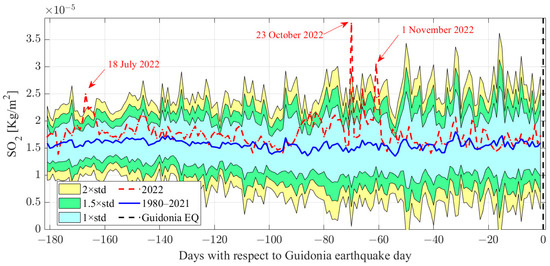
Figure 5.
SO2 time series from 4 July 2022 until 31 December 2022 (i.e., from six months before until the day before the ML = 3.3 1 January 2023 Guidonia earthquake). The years 1985, 1989, and 1993 have been excluded automatically as particularly anomalous. The representation graphic is the same as Figure 4.
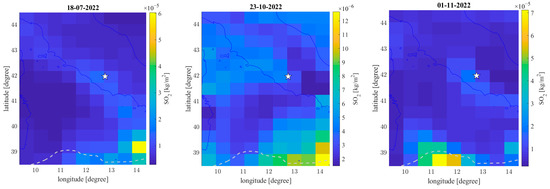
Figure 6.
SO2 maps on 17 July, 23 October and 1 November 2022. The epicentre of Guidonia 1 January 2023 earthquake is shown with a white star.
The aerosol, humidity, total precipitation, and especially SO2 investigations revealed several anomalous days, and we provided some geographical maps to better investigate if the increase in these quantities was local or global. The aerosol on 18 August 2022 was particularly anomalous, and its map is shown in Figure 3. From the aerosol distribution, it seems that all of the Tyrrhenian Sea recorded a high value of aerosol, probably due to particular weather conditions. In any case, it does not seem related to the earthquake.
Figure 4 reports the time series of the surface total energy flux, known as surface latent heat flux (SLHF), in the six months before the ML3.3 Guidonia 1 January 2023 earthquake. Several days exceeded the two-standard-deviation threshold, and they can be considered anomalous. Their occurrence dates (8 July, 19 August, 17 and 21 September, and 5 and 22 November 2022) are reported in red in Figure 4.
Figure 5 shows the time series of sulphur dioxide in the six months before the ML3.3 Guidonia 1 January 2023 earthquake. Figure 6 reports three anomalous days of SO2 in the investigated area, i.e., 18 July, 23 October, and 1 November 2022. The 18 July and 1 November dates show a slightly higher value of SO2 along almost all the coastline, excluding a local phenomenon. Despite this, in all three maps, the highest values are recorded in the sea, corresponding to an important subduction slab of the Tyrrhenian Sea (dashed grey line). The emission of this SO2 could be due to the stress on the subduction slab, and the important volcanic activity of the several volcanos close to this area (the Stromboli in the Aeolian Islands, submersed Marsili, or Etna, in Sicily). These volcanos are well known to emit SO2, and contribute significantly to the global budget of SO2 emissions [39].
A summary of all the identified anomalies in the atmosphere is reported in Table 2. An “X” in the table reports any day for which the surface air temperature, aerosol, SO2, surface total energy latent heat flux, or total precipitation parameter exceeded the positive threshold of 2 standard deviations of the 40-year background (1980–2021). For surface specific humidity, we extracted the anomalous days when the parameter was below the negative threshold of 2 standard deviations. This choice relied on the fact that the lithosphere, atmosphere, and ionosphere coupling mechanism proposed by Pulinets and Ouzonouv [40] predicts an anomalous decrease in humidity due to the chemical bonds of water vapour molecules in the air with the ionised charges produced by the release of radon or the positive holes emitted from the fault according to Freund [41].

Table 2.
List of the atmospheric anomalies identified inside the square area of 3° sides, centred on the ML3.3 Guidonia 1 January 2023 earthquake. The parameter which is anomalous on a specific day is marked with a “X” in the table.
Finally, we compared the volcanic activity in nearby regions in the same period to determine if the atmospheric anomalies could be caused by wind transport of volcanic gases and ash above the research area. Figure 7 compares the SO2 time series we obtained in the research area with the SO2 measured by the Italian National Institute of Geophysics and Volcanology (INGV) for three volcanoes (Etna, Stromboli, and Vulcano) and provided in the official weekly or monthly active volcano reports. Considering that the data from the Etna volcano are already normalised, we decided to normalise the other data also, including our time series. Notably, the SO2 anomalies identified in July 2022 followed some Vulcano degassing. Consequently, they could be due to volcanic activity. On the other hand, the SO2 anomalies of October and November 2022 could be excluded as not being induced by volcanic activity, as some emissions from the calderas of these volcanos did not precede, but followed these anomalies. We propose that the emissions recorded in October and November 2022 could be from a tectonic source in the Tyrrhenian Sea subduction slab.
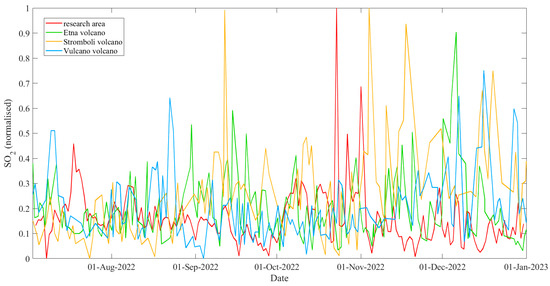
Figure 7.
Comparison of SO2 time series in the research area with SO2 measured in the craters of three active close volcanos: Etna, Stromboli, and Vulcano. All the data were normalised in the range from 0 to 1.
3.3. Ionospheric Investigations
Although the ionosphere is typically investigated inside Dobrovolsky’s area, we take into account that, in this particular case, such an area would be too small (see Figure 1) compared with the altitude of the Swarm satellites (about 470 km above sea level for Alpha and Charlie). So, we decided to consider an area with a diameter equal to the altitude of the two lower-orbit satellites, i.e., a radius equal to 235 km. The MASS algorithm was run for the data from 3 July 2022 to 1 January 2023. In order to avoid external disturbances, only quiet geomagnetic time was considered, using geomagnetic indexes shown in Figure 8. It is possible to note that there are several periods with geomagnetic activity, which is reasonable, as the time under investigation is during the solar activity increase of the 25th solar cycle.
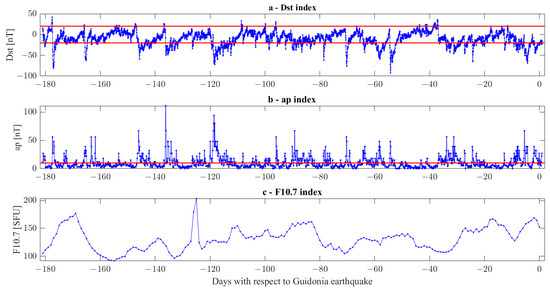
Figure 8.
Geomagnetic indexes Dst (a), ap (b) and solar activity F10.7 index (c) in the six months before the ML = 3.3 Guidonia 1 January 2023 earthquake. Red lines show the thresholds used in the automatic codes to distinguish quiet or disturbed conditions (|Dst| > 20 nT or ap > 10 nT).
After processing all the tracks of Swarm Alpha, Bravo and Charlie, about 20 tracks present some anomalies inside the research area in quiet geomagnetic conditions (|Dst| ≤ 20 nT and ap ≤ 10 nT), using a window of 1° latitude (found optimal in the Central Italy Swarm investigation [42]), and a threshold of rms inside the window of more than 2.5 times the threshold of rms of the whole track. Table 3 reports the list of anomalous tracks, and their cumulate number versus time is shown in Figure S8 in the supplementary materials. No anomalies were identified in the absolute scalar intensity of the geomagnetic field with the selected parameters.

Table 3.
List of the Swarm anomalous tracks in the circular research area of 235 km of radius centred on the ML3.3 Guidonia 1 January 2023 earthquake.
We note that the track of Swarm Bravo on 9 July 2022 followed one day after the surface latent heat flux anomaly reported in Table 2 and Figure 4, suggesting a bottom-up transmission of the anomalous phenomenon.
The three most interesting tracks in the Y-East component of the geomagnetic field are reported in Figure 9, Figure 10 and Figure 11, and the other anomalous tracks are presented in Supplementary Materials from Figure S9 to Figure S22. In particular, Figure 9 shows an anomalous signal of about 3 nT/s peak-peak intensity, but the geomagnetic index Dst is at the upper boundary limit of 20 nT. In fact, looking at the trend of Dst (e.g., on https://wdc.kugi.kyoto-u.ac.jp/dst_realtime/202208/index.html, accessed on 2 January 2023), it continues to increase in the following hours, and reaches −58 nT on 8 August 2022, so this track was acquired at the sudden commencement of a moderate geomagnetic storm. Although the signal was perfectly centred on the incoming earthquake, the external source was the most reliable one to explain this signal.
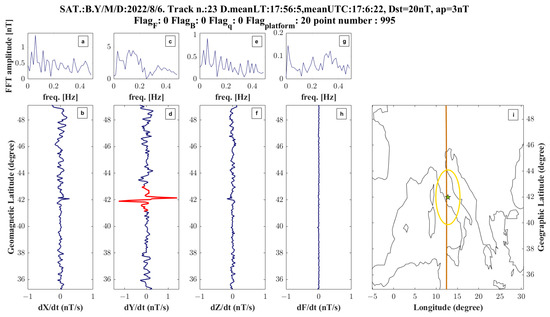
Figure 9.
Swarm Bravo magnetic field analysis on 6 August 2022, track 23. The title reports the first satellite letter, date of acquisition, track number, mean local time and UT time, geomagnetic indexes, and the total number of original samples acquired with anomalous ESA Swarm data quality flags. Map (i) shows the projection of the satellite track in brown, and eventual anomalous flags are marked with red. The green star represents the epicentre of the M3.3 Guidonia 1 January 2023 earthquake, and the yellow circle is the Dobrovolsky of an earthquake of magnitude 4.1. The residuals of geomagnetic signals for X-North (b), Y-East (d), Z-Center (f) and F absolute scalar intensity (h) are represented with blue lines on the left, in correspondence with the map, and eventual anomalies inside the research area are marked with red lines. A spectrum of the signal made by Fast Fourier Transform (FFT) inside the minimum and maximum latitudes of the area is reported in (a), (c), (e) and (g) subfigures for X, Y, Z and F, respectively.
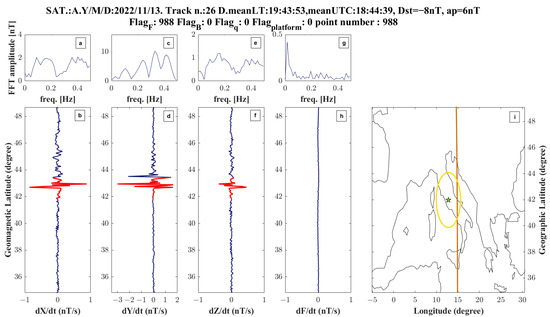
Figure 10.
Swarm Alpha magnetic field analysis on 13 November 2022, track 26. The title reports the first satellite letter, date of acquisition, track number, mean local time and UT time, geomagnetic indexes, and the total number of original samples acquired with anomalous ESA Swarm data quality flags. Map (i) shows the projection of the satellite track in brown, and eventual anomalous flags are marked with red. The green star represents the epicentre of the M3.3 Guidonia 1 January 2023 earthquake, and the yellow circle is the Dobrovolsky of an earthquake of magnitude 4.1. The residuals of geomagnetic signals for X-North (b), Y-East (d), Z-Center (f) and F absolute scalar intensity (h) are represented with blue lines on the left, in correspondence with the map, and eventual anomalies inside the research area are marked with red lines. A spectrum of the signal made by Fast Fourier Transform (FFT) inside the minimum and maximum latitudes of the area is reported in (a), (c), (e) and (g) subfigures for X, Y, Z and F, respectively.
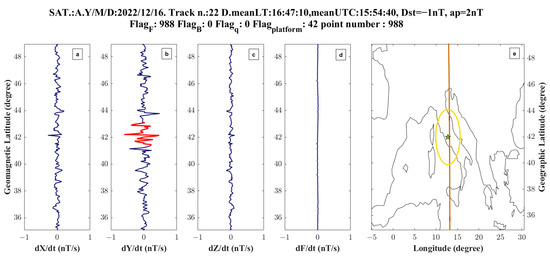
Figure 11.
Swarm Bravo magnetic field analysis on 16 December 2022, track 22. The reported information is the same as in Figure 9, except for the absence of FFT spectra due to some badly flagged samples. The X, Y, and Z components are shown in (a–c), while the absolute scalar intensity is shown in (d) and the map with satellite track projection is shown in (e). The part of the track with bad samples is marked with red colour instead of brown.
Figure 10 reports an interesting track acquired on 13 November 2022 by the Swarm Alpha satellite, with an anomaly superposed on the seismic activity recorded in the North Adriatic Sea close to the Marche Italian region, especially in November 2022 but still ongoing (in January 2023). In particular, on 9 November 2022, offshore Pesaro Urbino town, a shallow (depth estimated equal to 5 km) Mw = 5.5 earthquake was recorded with epicentral coordinates 43.983°N, 13.324°E (http://cnt.rm.ingv.it/event/33301831, accessed on 28 January 2023). The anomaly depicted by Swarm Alpha in the geomagnetic field could have been induced by the aftershock activity recorded at the same coordinates, due to the compression of the two regional tectonic plates. Noticing that anomalous precipitation had been recorded on the same day (see Table 2 and Figure S7 in Supplementary Materials), we checked if there was evidence of lightning activity. We looked at the data from the Lightning Image Sensor (LIS) onboard the International Space Station (ISS) [43], acquired just one hour after the Swarm track above Italy, and presented this in Figure S32 in Supplementary Materials. There is no evidence of lightning activity in Italy, as it was detected only in Brazil and the Papua New Guinea region. We tend to exclude that a thunderstorm could have induced this Swarm anomaly, and that a seismo-induced origin is still plausible.
Figure 11 shows a track of Swarm Bravo acquired during very quiet geomagnetic conditions (Dst = −1 nT, ap = 2 nT), with an anomalous geomagnetic field Y-East component signal recorded above Central Italy. Though the track preceded by about one week the first shock of ML3.1 on 23 December 2022, and was acquired during the seismic acceleration phase, the diffuse nature of the anomaly makes it difficult to confirm that it could be seismo-induced, though that cannot be excluded.
The analysis of electron density measured by Swarm Alpha, Bravo, and Charlie in the six months before the ML3.3 Guidonia 1 January 2023 earthquake is provided in supplementary materials. In particular, Figure S23 shows the cumulate of all the anomalous tracks extracted by applying the NeLOG algorithm with a threshold kt = 2.0. The algorithm selected five anomalous tracks, shown in detail in Figures S24–S28. Among them, the only track which could have an interesting signal is the one acquired by Swarm Bravo on 16 July 2022 (Figure S24), which show oscillations with long period of electron density from a geographical latitude of 42.5°N to 44.5°N. The oscillation is between the Central Apennines and Marche regions. Furthermore, the same track reported anomalies in the geomagnetic field in all three components (Figure S11). Contemporary anomalies in the magnetic field and electron density could be produced by plasma bubbles, which are a possible pre-earthquake phenomenon, as simulated by Kuo et al. [44]. Finally, the anomalous electromagnetic signals recorded by Swarm Bravo on 16 July 2022 could be considered good candidates as pre-seismo-induced phenomena of the seismic activity of November 2022–January 2023 in the Adriatic Sea and Marche region. The other anomalous tracks presented in Figures S25–S28 show an anomalous signal typical of some period in Swarm electron density from the Langmuir probe already found in [29] for the M6.9 Aegean Sea (Greece) 2015 earthquake. Such a signal is surely not due to earthquakes, as it affects all the orbits of the Swarm satellites globally in certain periods. Further specific investigations are necessary to identify its nature, particularly if it is some instrumental noise or ionospheric signal.
4. Discussion and Conclusions
In this paper, we investigated the ML = 3.3 Guidonia (Rome, Italy) earthquake that occurred on 1 January 2023 by the analysis of seismic, atmospheric and ionospheric data. From a preliminary investigation, seismological analysis identified an acceleration of the seismicity around this epicentre, especially in the previous six months. On the other hand, the atmospheric and ionospheric investigations did not provide any results that seemed to be linked to this seismic event, but some anomalies could be seismo-induced by the other seismic activity in the same period in the Adriatic Sea and Marche Italian region. The absence of possible coupling of the lithosphere with the atmosphere and ionosphere is in agreement with the low magnitude of the Guidonia seismic event (ML = 3.3). Such a low magnitude is, in fact, not expected to produce any ionospheric effect, per Marchetti et al. [35], which proposed at least M = 5.5 or even M = 6.0, and per Perevalova [45], which suggested M6.5.
Finally, the seismological investigation not only clearly identified a seismic acceleration, but suggested that these events were likely part of a seismic sequence, and the analyses were compatible with two main hypotheses:
- The ML3.3 of 1 January 2023 is the mainshock of the seismic quiescence (R2-adj = 0.977 and acceleration coefficient C = 0.32);
- The mainshock, of magnitude M4.1 (R2-adj = 0.988 and acceleration coefficient C = 0.36), could be an incoming event in the following weeks/months.
The second hypothesis seems mathematically slightly more probable, but both hypotheses describe well the seismicity recorded in the previous months around Guidonia (Rome, Italy). In any case, the acceleration nature (C << 1) of all the reliable solutions tends to exclude that the events are part of a seismic swarm.
Even though some speculation on the evolution of the seismic activity can be done, it cannot be considered as a prediction because no tests have been ever made, so, without a validation of the method by an independent body (e.g., CSEP, https://cseptesting.org/, accessed on 2 January 2023), the analysis has no predictive value. Furthermore, the correct interpretation of the time-to-failure power law fit is that a seismic acceleration during the last six months, in a 58 km radius circle centred on Guidonia, has been detected. Further investigations are absolutely necessary to propose the future evolution of the seismic sequence. Due to the peculiarity observed in the past months, the installation of geochemical and seismic multiparametric stations could be evaluated to detect eventual gases or fluids released from the ground and improve the completeness magnitude of the area.
Finally, this example shows how these techniques could be applied in real time for monitoring (but not yet prediction) purposes. In particular, Figure 12 shows a conceptual idea of a multiparametric platform to investigate the lithosphere, atmosphere, and ionosphere. This platform could automatically download new data when available; specific algorithms need to explore the particular dataset. Finally, more complex modules would search for possible LAIC, considering the mechanism’s physics (analogous to Wu et al. [46]). An external clock would trigger the several stages of the multiparametric platform. For example, in the first submission of this paper, atmospheric data for December 2022 were unavailable, and we produced the limited time series to 30 November (see Figures S29–S31 and the preprint [47] of the first submission). In the revision stage, the atmospheric data of December 2022 became available, permitting us to provide the full time series. In the future, all of these stages will be automatically executed in order to concentrate on the upper level of the geophysical interpretation and investigation of the results. Beyond this, a real-time geophysical remote sensing multiparametric platform could permit us to provide operative products, not only to better understand and monitor our vulnerable planet, but to mitigate possible negative consequences of natural hazards.
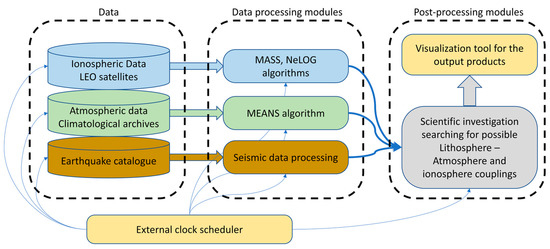
Figure 12.
Concept of a real-time geophysical multiparametric platform to investigate and systematically search for lithosphere, atmosphere, and ionosphere coupling phenomena.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15040942/s1. Figure S1: Gutenberg-Richeter distributions of the earthquake in the areas listed in Table 1; Figures S2 and S3: Benioff cumulative stress curves in the 5 years and 1 year before the ML=3.3 1 January 2023 Guidonia earthquake; Figure S4: Surface air temperature time series; Figure S5: Aerosol time series; Figure S6: Surface specific humidity time series; Figure S7: Total precipitation time series; Figure S8: cumulate number of Swarm Alpha, Bravo and Charlie geomagnetic field anomalies; Figures S9–S22: Swarm anomalous geomagnetic field tracks; Figure S23: cumulate number of Swarm Alpha, Bravo and Charlie electron density (Ne) anomalies; Figures S24–S28: Swarm anomalous Ne tracks; Figures S29–S31: Preliminary atmospheric time series processed immediately after the EQ occurrence (on 2 January 2023); Figure S32: Lightning activity recorded by Lightning Image Sensors (LIS) mounted on International Space Station (ISS) on 13 November 2023 between 19:29:59 UT and 21:02:59 UT. Reference [6] is cited in the supplementary materials.
Author Contributions
Conceptualisation, methodology, software, writing—original draft preparation, formal analysis, investigation, data curation, visualisation, D.M.; supervision, K.Z.; validation, L.M.; resources, project administration, funding acquisition, K.Z. and D.M; writing—review and editing, L.M., D.M., Y.Z., K.Z., W.C., Y.C., M.F., T.W., S.W., J.W., D.Z. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 41974084; the China Postdoctoral Science Foundation, grant number 2021M691190; the International Cooperation Project of the Department of Science and Technology of Jilin Province, grant number 20200801036GH. The APC has been funded by Dedalo Marchetti.
Data Availability Statement
We acknowledge the INGV for the seismic catalogue used in this paper, freely available at http://cnt.rm.ingv.it/, accessed on 3 January 2023. MERRA-2 data can be downloaded from https://disc.gsfc.nasa.gov/datasets?project=MERRA-2 (accessed on 2 January 2023) with Earth Observation NASA free credential. Swarm data are freely available via ftp and http at swarm-diss.eo.esa.int server (accessed on 2 January 2023). We acknowledge INGV for free provision of Database of Individual Seismogenic Sources (DISS) and available at https://diss.ingv.it/ (accessed on 22 January 2023). We acknowledge Lang, Timothy 2022. Non-Quality Controlled Lightning Imaging Sensor (LIS) on International Space Station (ISS) Science Data. Dataset available online from the NASA Global Hydrometeorology Resource Center DAAC, Huntsville, Alabama, U.S.A. doi: http://dx.doi.org/10.5067/LIS/ISSLIS/DATA110.
Acknowledgments
We would acknowledge Alessandro Piscini, Rita Di Giovambattista, Gianfranco Cianchini, Francisco Javier Pavón-Carrasco, Saioa Arquero Campuzano, Dario Sabbagh, Loredana Perrone, Maurizio Soldani, and Angelo De Santis for their contributions in the preparation, writing, and optimisation of some codes re-used in this work, originally developed for some of the cited papers and constructive scientific discussion on previous work whose concepts are here re-applied. We also acknowledge the International Space Science Institute (ISSI at Bern, Switzerland) for supporting International Team 553 led by Essam Ghamry and Zeren Zhima.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Faccenna, C.; Soligo, M.; Billi, A.; De Filippis, L.; Funiciello, R.; Rossetti, C.; Tuccimei, P. Late Pleistocene Depositional Cycles of the Lapis Tiburtinus Travertine (Tivoli, Central Italy): Possible Influence of Climate and Fault Activity. Glob. Planet. Chang. 2008, 63, 299–308. [Google Scholar] [CrossRef]
- Frepoli, A.; Cimini, G.B.; De Gori, P.; De Luca, G.; Marchetti, A.; Monna, S.; Montuori, C.; Pagliuca, N.M. Seismic Sequences and Swarms in the Latium-Abruzzo-Molise Apennines (Central Italy): New Observations and Analysis from a Dense Monitoring of the Recent Activity. Tectonophysics 2017, 712–713, 312–329. [Google Scholar] [CrossRef]
- Utsu, T.; Ogata, Y.; Matsu’ura, S.R. The Centenary of the Omori Formula for a Decay Law of Aftershock Activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
- ISIDe Working Group. Italian Seismological Instrumental and Parametric Database (ISIDe); Istituto Nazionale di Geofisica e Vulcanologia (INGV): Rome, Italy, 2007. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Di Stefano, R.; Tinti, E.; Scognamiglio, L.; Michele, M.; Casarotti, E.; Cattaneo, M.; De Gori, P.; Chiarabba, C.; Monachesi, G.; et al. The 2016 Central Italy Seismic Sequence: A First Look at the Mainshocks, Aftershocks, and Source Models. Seismol. Res. Lett. 2017, 88, 757–771. [Google Scholar] [CrossRef]
- Wiemer, S. A Software Package to Analyse Seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Gutenberg, B. Seismicity of the Earth and Associated Phenomena; Read Books Ltd.: Worcestershire, UK, 2013. [Google Scholar]
- Montuori, C.; Murru, M.; Falcone, G. Spatial Variation of the B-Value Observed for the Periods Preceding and Following the 24 August 2016, Amatrice Earthquake (ML 6.0) (Central Italy). Ann. Geophys. 2016, 59, 12. [Google Scholar] [CrossRef]
- De Santis, A.; Cianchini, G.; Favali, P.; Beranzoli, L.; Boschi, E. The Gutenberg-Richter Law and Entropy of Earthquakes: Two Case Studies in Central Italy. Bull. Seismol. Soc. Am. 2011, 101, 1386–1395. [Google Scholar] [CrossRef]
- Mignan, A. The Stress Accumulation Model: Accelerating Moment Release and Seismic Hazard. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 2008; Volume 49, pp. 67–201. ISBN 978-0-12-374231-5. [Google Scholar]
- Dobrovolsky, I.P.; Zubkov, S.I.; Miachkin, V.I. Estimation of the Size of Earthquake Preparation Zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Mignan, A.; King, G.C.P.; Bowman, D. A Mathematical Formulation of Accelerating Moment Release Based on the Stress Accumulation Model. J. Geophys. Res. Solid Earth 2007, 112, B07308. [Google Scholar] [CrossRef]
- Cianchini, G.; De Santis, A.; Di Giovambattista, R.; Abbattista, C.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; Cesaroni, C.; De Santis, A.; Marchetti, D.; et al. Revised Accelerated Moment Release Under Test: Fourteen Worldwide Real Case Studies in 2014–2018 and Simulations. Pure Appl. Geophys. 2020, 177, 4057–4087. [Google Scholar] [CrossRef]
- De Santis, A.; Cianchini, G.; Marchetti, D.; Piscini, A.; Sabbagh, D.; Perrone, L.; Campuzano, S.A.; Inan, S. A Multiparametric Approach to Study the Preparation Phase of the 2019 M7.1 Ridgecrest (California, United States) Earthquake. Front. Earth Sci. 2020, 8, 540398. [Google Scholar] [CrossRef]
- Piscini, A.; Marchetti, D.; De Santis, A. Multiparametric Climatological Analysis Associated with Global Significant Volcanic Eruptions During 2002–2017. Pure Appl. Geophys. 2019, 176, 3629–3647. [Google Scholar] [CrossRef]
- Marchetti, D.; de Santis, A.; D’Arcangelo, S.; Poggio, F.; Piscini, A.; Campuzano, S.A.; de Carvalho, W.V.J.O. Pre-Earthquake Chain Processes Detected from Ground to Satellite Altitude in Preparation of the 2016–2017 Seismic Sequence in Central Italy. Remote Sens. Environ. 2019, 229, 93–99. [Google Scholar] [CrossRef]
- Marchetti, D.; Zhu, K.; Zhang, H.; Zhima, Z.; Yan, R.; Shen, X.; Chen, W.; Cheng, Y.; He, X.; Wang, T.; et al. Clues of Lithosphere, Atmosphere and Ionosphere Variations Possibly Related to the Preparation of La Palma 19 September 2021 Volcano Eruption. Remote Sens. 2022, 14, 5001. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Wang, T. Developing a Deep Learning-Based Detector of Magnetic, Ne, Te and TEC Anomalies from Swarm Satellites: The Case of Mw 7.1 2021 Japan Earthquake. Remote Sens. 2022, 14, 1582. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; Marchetti, D. Developing a Fuzzy Inference System Based on Multi-Sensor Data to Predict Powerful Earthquake Parameters. Remote Sens. 2022, 14, 3203. [Google Scholar] [CrossRef]
- Marchetti, D.; de Santis, A.; Shen, X.; Campuzano, S.A.; Perrone, L.; Piscini, A.; Di Giovambattista, R.; Jin, S.; Ippolito, A.; Cianchini, G.; et al. Possible Lithosphere-Atmosphere-Ionosphere Coupling Effects Prior to the 2018 Mw = 7.5 Indonesia Earthquake from Seismic, Atmospheric and Ionospheric Data. J. Asian Earth Sci. 2020, 188, 104097. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A Constellation to Study the Earth’s Magnetic Field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Piscini, A.; Cianchini, G. Multi Precursors Analysis Associated with the Powerful Ecuador (MW = 7.8) Earthquake of 16 April 2016 Using Swarm Satellites Data in Conjunction with Other Multi-Platform Satellite and Ground Data. Adv. Space Res. 2018, 61, 248–263. [Google Scholar] [CrossRef]
- Zhu, K.; Li, K.; Fan, M.; Chi, C.; Yu, Z. Precursor Analysis Associated With the Ecuador Earthquake Using Swarm A and C Satellite Magnetic Data Based on PCA. IEEE Access 2019, 7, 93927–93936. [Google Scholar] [CrossRef]
- Zhu, K.; Fan, M.; He, X.; Marchetti, D.; Li, K.; Yu, Z.; Chi, C.; Sun, H.; Cheng, Y. Analysis of Swarm Satellite Magnetic Field Data Before the 2016 Ecuador (Mw = 7.8) Earthquake Based on Non-Negative Matrix Factorization. Front. Earth Sci. 2021, 9, 621976. [Google Scholar] [CrossRef]
- Fan, M.; Zhu, K.; De Santis, A.; Marchetti, D.; Cianchini, G.; Piscini, A.; He, X.; Wen, J.; Wang, T.; Zhang, Y.; et al. Analysis of Swarm Satellite Magnetic Field Data for the 2015 Mw 7.8 Nepal Earthquake Based on Nonnegative Tensor Decomposition. IEEE Trans. Geosci. Remote Sens. 2022, 60, 2006119. [Google Scholar] [CrossRef]
- Ghamry, E.; Mohamed, E.K.; Sekertekin, A.; Fathy, A. Integration of Multiple Earthquakes Precursors before Large Earthquakes: A Case Study of 25 April 2015 in Nepal. J. Atmos. Sol. Terr. Phys. 2023, 242, 105982. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Campuzano, S.A.; Soldani, M.; Piscini, A.; Sabbagh, D.; Cianchini, G.; Perrone, L.; Orlando, M. Swarm Satellite Magnetic Field Data Analysis Prior to 2019 Mw = 7.1 Ridgecrest (California, USA) Earthquake. Geosciences 2020, 10, 502. [Google Scholar] [CrossRef]
- De Santis, A.; Perrone, L.; Calcara, M.; Campuzano, S.A.; Cianchini, G.; D’Arcangelo, S.; Di Mauro, D.; Marchetti, D.; Nardi, A.; Orlando, M.; et al. A Comprehensive Multiparametric and Multilayer Approach to Study the Preparation Phase of Large Earthquakes from Ground to Space: The Case Study of the June 15 2019, M7.2 Kermadec Islands (New Zealand) Earthquake. Remote Sens. Environ. 2022, 283, 113325. [Google Scholar] [CrossRef]
- De Santis, A.; Marchetti, D.; Spogli, L.; Cianchini, G.; Pavón-Carrasco, F.J.; de Franceschi, G.; Di Giovambattista, R.; Perrone, L.; Qamili, E.; Cesaroni, C.; et al. Magnetic Field and Electron Density Data Analysis from Swarm Satellites Searching for Ionospheric Effects by Great Earthquakes: 12 Case Studies from 2014 to 2016. Atmosphere 2019, 10, 371. [Google Scholar] [CrossRef]
- Marchetti, D.; Akhoondzadeh, M. Analysis of Swarm Satellites Data Showing Seismo-Ionospheric Anomalies around the Time of the Strong Mexico (Mw = 8.2) Earthquake of 08 September 2017. Adv. Space Res. 2018, 62, 614–623. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; de Santis, A.; Marchetti, D.; Shen, X. Swarm-TEC Satellite Measurements as a Potential Earthquake Precursor Together With Other Swarm and CSES Data: The Case of Mw7.6 2019 Papua New Guinea Seismic Event. Front. Earth Sci. 2022, 10, 820189. [Google Scholar] [CrossRef]
- Christodoulou, V.; Bi, Y.; Wilkie, G. A Tool for Swarm Satellite Data Analysis and Anomaly Detection. PLoS ONE 2019, 14, e0212098. [Google Scholar] [CrossRef]
- de Santis, A.; Balasis, G.; Pavón-Carrasco, F.J.; Cianchini, G.; Mandea, M. Potential Earthquake Precursory Pattern from Space: The 2015 Nepal Event as Seen by Magnetic Swarm Satellites. Earth Planet. Sci. Lett. 2017, 461, 119–126. [Google Scholar] [CrossRef]
- de Santis, A.; Marchetti, D.; Pavón-Carrasco, F.J.; Cianchini, G.; Perrone, L.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; et al. Precursory Worldwide Signatures of Earthquake Occurrences on Swarm Satellite Data. Sci. Rep. 2019, 9, 20287. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Campuzano, S.A.; Zhu, K.; Soldani, M.; D’Arcangelo, S.; Orlando, M.; Wang, T.; Cianchini, G.; Di Mauro, D.; et al. Worldwide Statistical Correlation of Eight Years of Swarm Satellite Data with M5.5+ Earthquakes: New Hints about the Preseismic Phenomena from Space. Remote Sens. 2022, 14, 2649. [Google Scholar] [CrossRef]
- Xiong, P.; Marchetti, D.; De Santis, A.; Zhang, X.; Shen, X. SafeNet: SwArm for Earthquake Perturbations Identification Using Deep Learning Networks. Remote Sens. 2021, 13, 5033. [Google Scholar] [CrossRef]
- Sasmal, S.; Chowdhury, S.; Kundu, S.; Politis, D.Z.; Potirakis, S.M.; Balasis, G.; Hayakawa, M.; Chakrabarti, S.K. Pre-Seismic Irregularities during the 2020 Samos (Greece) Earthquake (M = 6.9) as Investigated from Multi-Parameter Approach by Ground and Space-Based Techniques. Atmosphere 2021, 12, 1059. [Google Scholar] [CrossRef]
- Piscini, A.; de Santis, A.; Marchetti, D.; Cianchini, G. A Multiparametric Climatological Approach to Study the 2016 Amatrice–Norcia (Central Italy) Earthquake Preparatory Phase. Pure Appl. Geophys. 2017, 174, 3673–3688. [Google Scholar] [CrossRef]
- Allard, P.; Carbonnelle, J.; Métrich, N.; Loyer, H.; Zettwoog, P. Sulphur Output and Magma Degassing Budget of Stromboli Volcano. Nature 1994, 368, 326–330. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) Model—An Unified Concept for Earthquake Precursors Validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Freund, F. Pre-Earthquake Signals: Underlying Physical Processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; D’Arcangelo, S.; Poggio, F.; Jin, S.; Piscini, A.; Campuzano, S.A. Magnetic Field and Electron Density Anomalies from Swarm Satellites Preceding the Major Earthquakes of the 2016–2017 Amatrice-Norcia (Central Italy) Seismic Sequence. Pure Appl. Geophys. 2020, 177, 305–319. [Google Scholar] [CrossRef]
- Lang, T. Non-Quality Controlled Lightning Imaging Sensor (LIS) on International Space Station (ISS) Science Data; NASA Global Hydrology Resource Center DAAC: Huntsville, AL, USA, 2022. [Google Scholar] [CrossRef]
- Kuo, C.L.; Lee, L.C.; Huba, J.D. An Improved Coupling Model for the Lithosphere-Atmosphere-Ionosphere System. J. Geophys. Res. Space Phys. 2014, 119, 3189–3205. [Google Scholar] [CrossRef]
- Perevalova, N.P.; Sankov, V.A.; Astafyeva, E.I.; Zhupityaeva, A.S. Threshold Magnitude for Ionospheric TEC Response to Earthquakes. J. Atmos. Sol. Terr. Phys. 2014, 108, 77–90. [Google Scholar] [CrossRef]
- Wu, L.; Qi, Y.; Mao, W.; Lu, J.; Ding, Y.; Peng, B.; Xie, B. Scrutinizing and Rooting the Multiple Anomalies of Nepal Earthquake Sequence in 2015 with the Deviation–Time–Space Criterion and Homologous Lithosphere–Coversphere–Atmosphere–Ionosphere Coupling Physics. Nat. Hazards Earth Syst. Sci. 2023, 23, 231–249. [Google Scholar] [CrossRef]
- Marchetti, D.; Zhu, K.; Marchetti, L.; Zhang, Y.; Chen, W.; Cheng, Y.; Fan, M.; Wang, S.; Wang, T.; Wen, J.; et al. Quick Report of the ML = 3.3 on 1 January 2023 Guidonia (Rome, Italy) Earthquake: Evidence of a Seismic Acceleration. Preprints 2023, 2023010067. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).