Analysis and Correction of Water Forward-Scattering-Induced Bathymetric Bias for Spaceborne Photon-Counting Lidar
Abstract
1. Introduction
- (1)
- What is the magnitude of the bathymetric bias caused by the water column forward scattering for spaceborne photon-counting lidars and specific to ICESat-2? When and where can it be ignored?
- (2)
- If the bias cannot be ignored, how to effectively correct this bias? What are the specific bathymetric accuracies before and after the water forward-scattering correction?
- (3)
- Is the influence of the FOV of spaceborne lidars similar to that of ALBs? Can a larger FOV of spaceborne lidars increase the received signal level to achieve a better bathymetric capability?
2. Bathymetric Bias Model of Water forward Scattering
2.1. Basic Model of Bathymetric Bias Caused by Water forward Scattering
2.2. Monte Carlo Simulation Process
2.2.1. Parameter Initialization
2.2.2. Photon Packet Penetration in Water Column
2.2.3. Seafloor Reflection
2.2.4. Termination Conditions
2.3. Empirical Formula on Correcting Bias for ICESat-2
3. Experiments and Validations
3.1. Study Area Selection and Data Pre-Processing
3.2. Description of Study Areas and Used Data
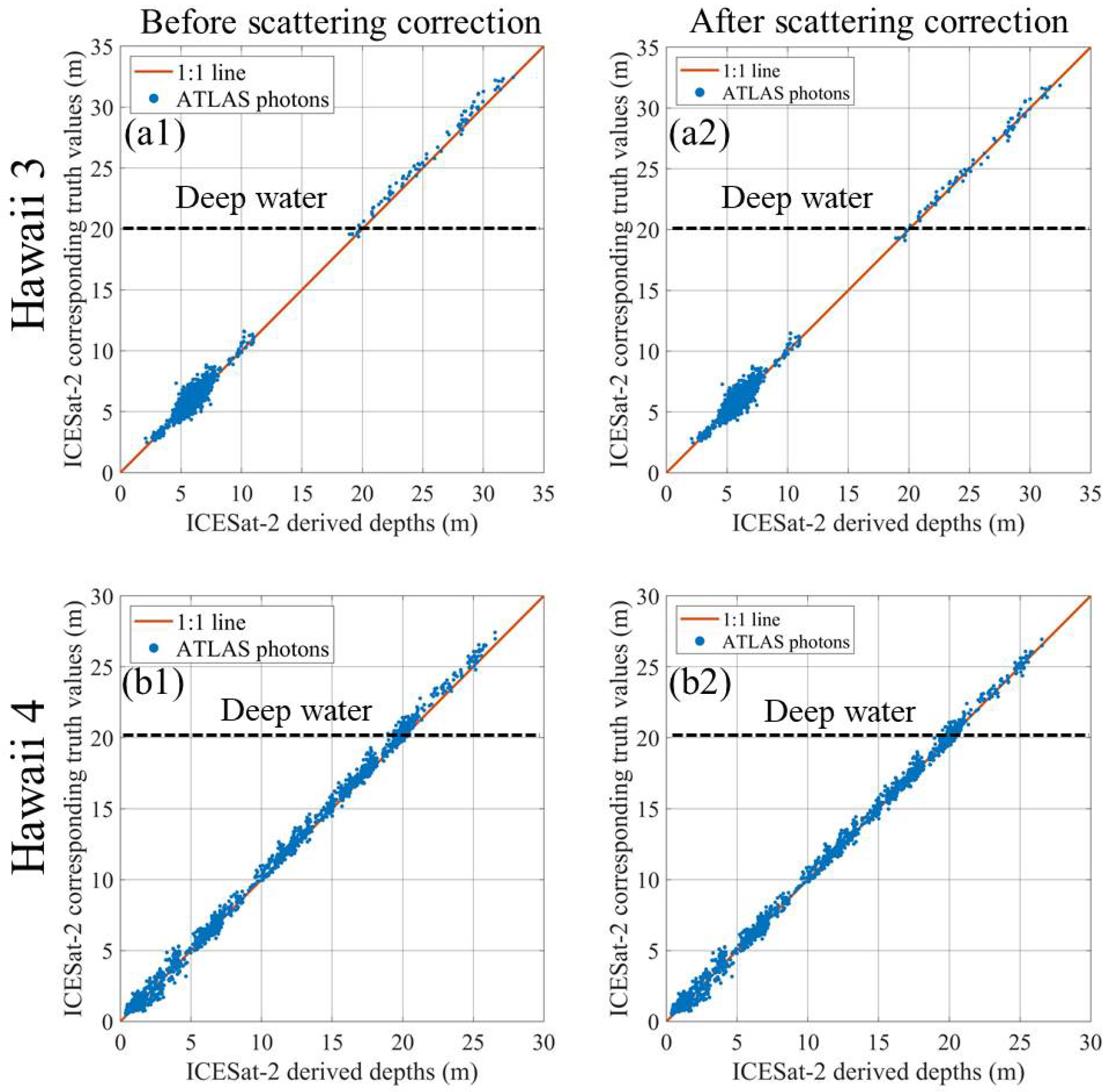
3.3. Experimental Results
3.4. Result Analysis
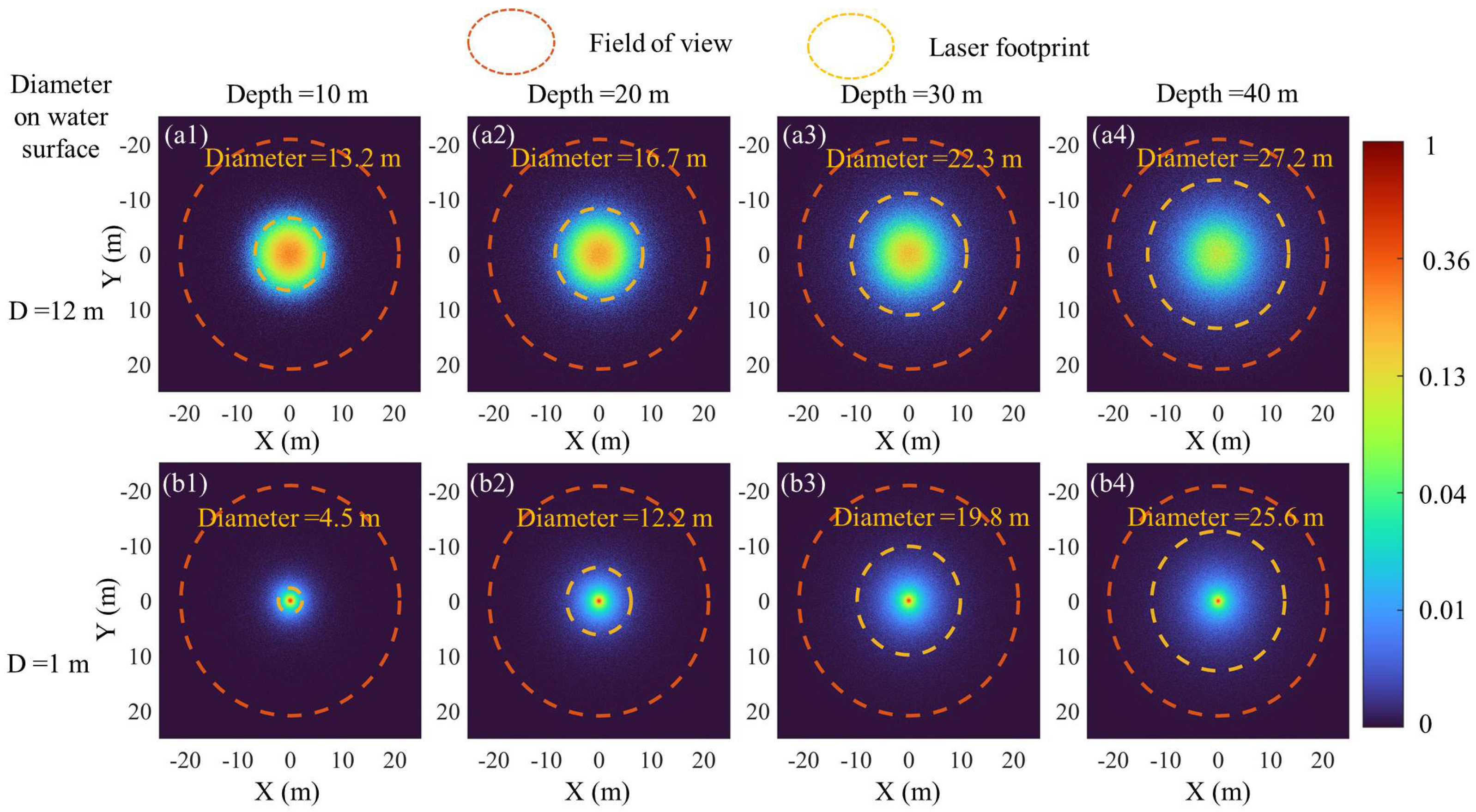
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geog. 2009, 33, 103–116. [Google Scholar]
- Nicholls, R.J.; Cazenave, A. Sea-Level Rise and Its Impact on Coastal Zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Su, D.; Yang, F.; Ma, Y.; Zhang, K.; Huang, J.; Wang, M. Classification of Coral Reefs in the South China Sea by Combining Airborne LiDAR Bathymetry Bottom Waveforms and Bathymetric Features. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 815–828. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, Y.; Hu, C.; Xu, B. Coral reef geomorphology of the Spratly Islands: A simple method based on time-series of Landsat-8 multi-band inundation maps. ISPRS J. Photogramm. Remote. Sens. 2019, 157, 137–154. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Sun, J.; Wang, X.H.; Yang, F.; Li, S. Estimating water levels and volumes of lakes dated back to the 1980s using Landsat imagery and photon-counting lidar datasets. Remote. Sens. Environ. 2019, 232, 111287. [Google Scholar] [CrossRef]
- Babbel, B.J.; Parrish, C.E.; Magruder, L.A. ICESat-2 Elevation Retrievals in Support of Satellite-Derived Bathymetry for Global Science Applications. Geophys Res Lett. 2021, 48, e2020GL090629. [Google Scholar]
- Lee, Z.-P.; Darecki, M.; Carder, K.L.; Davis, C.O.; Stramski, D.; Rhea, W.J. Diffuse attenuation coefficient of downwelling irradiance: An evaluation of remote sensing methods. J. Geophys. Res. Atmos. 2005, 110, C02017. [Google Scholar] [CrossRef]
- Barton, J.S.; Jasinski, M.F. Sensitivity of Depth-Integrated Satellite Lidar to Subaqueous Scattering. Remote. Sens. 2011, 3, 1492–1515. [Google Scholar] [CrossRef]
- Holman, R.; Haller, M.C. Remote Sensing of the Nearshore. Annu. Rev. Mar. Sci. 2013, 5, 95–113. [Google Scholar] [CrossRef]
- Mehdi, G.; Tiit, K.; Abbas, E.S.; Ali, A.; Babak, N. Remotely Sensed Empirical Modeling of Bathymetry in the Southeastern Caspian Sea. Remote Sensing 2013, 5, 2746–2762. [Google Scholar]
- Maas, H.-G. On the Accuracy Potential in Underwater/Multimedia Photogrammetry. Sensors 2015, 15, 18140–18152. [Google Scholar] [CrossRef]
- Forfinski-Sarkozi, N.A.; Parrish, C.E. Analysis of MABEL Bathymetry in Keweenaw Bay and Implications for ICESat-2 ATLAS. Remote. Sens. 2016, 8, 772. [Google Scholar] [CrossRef]
- Yang, F.; Su, D.; Yue, M.; Feng, C.; Yang, A.; Wang, M. Refraction correction of airborne LiDAR bathymetry based on sea surface profile and ray tracing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6141–6149. [Google Scholar] [CrossRef]
- Westfeld, P.; Maas, H.-G.; Richter, K.; Weiß, R. Analysis and correction of ocean wave pattern induced systematic coordinate errors in airborne LiDAR bathymetry. ISPRS J. Photogramm. Remote. Sens. 2017, 128, 314–325. [Google Scholar] [CrossRef]
- Mandlburger, G.; Pfennigbauer, M.; Schwarz, R.; Flöry, S.; Nussbaumer, L. Concept and Performance Evaluation of a Novel UAV-Borne Topo-Bathymetric LiDAR Sensor. Remote Sens. 2020, 12, 986. [Google Scholar] [CrossRef]
- Pereira, P.; Baptista, P.; Cunha, T.; Silva, P.; Romão, S.; Lafon, V. Estimation of the nearshore bathymetry from high temporal resolution Sentinel-1A C-band SAR data A case study. Remote. Sens. Environ. 2019, 223, 166–178. [Google Scholar] [CrossRef]
- Kutser, T.; Hedley, J.; Giardino, C.; Roelfsema, C.; Brando, V.E. Remote sensing of shallow waters A 50 year retrospective and future directions. Remote. Sens. Environ. 2020, 240, 111619. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-derived bathymetry using the ICESat-2 lidar and Sentinel-2 imagery datasets. Remote. Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Chen, B.; Yang, Y.; Xu, D.; Huang, E. A dual band algorithm for shallow water depth retrieval from high spatial resolution imagery with no ground truth. ISPRS J. Photogramm. Remote. Sens. 2019, 151, 1–13. [Google Scholar] [CrossRef]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote. Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-waveform topographic lidar: State-of-the-art. ISPRS J. Photogramm. Remote. Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Liu, Y.; Wu, G.; Liu, P.; Ding, X. A comparison of waveform processing algorithms for single-wavelength LiDAR bathymetry. ISPRS J. Photogramm. Remote. Sens. 2015, 101, 22–35. [Google Scholar] [CrossRef]
- Pan, Z.; Glennie, C.; Hartzell, P.; Fernandez-Diaz, J.C.; Legleiter, C.; Overstreet, B. Performance Assessment of High Res-olution Airborne Full Waveform LiDAR for Shallow River Bathymetry. Remote Sensing 2015, 7, 5133–5159. [Google Scholar]
- Forfinski-Sarkozi, N.A.; Parrish, C.E. Active-Passive Spaceborne Data Fusion for Mapping Nearshore Bathymetry. Photogramm. Eng. Remote. Sens. 2019, 85, 281–295. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Jasinski, M.F.; Zhang, S.; Stoll, J.D. Deriving High-Resolution Reservoir Bathymetry From ICESat-2 Pro-totype Photon-Counting Lidar and Landsat Imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7883–7893. [Google Scholar]
- Armon, M.; Dente, E.; Shmilovitz, Y.; Mushkin, A.; Cohen, T.J.; Morin, E.; Enzel, Y. Determining Bathymetry of Shallow and Ephemeral Desert Lakes Using Satellite Imagery and Altimetry. Geophys. Res. Lett. 2020, 47, e2020GL087367. [Google Scholar] [CrossRef]
- Albright, A.; Glennie, C. Nearshore Bathymetry From Fusion of Sentinel-2 and ICESat-2 Observations. IEEE Geosci. Remote. Sens. Lett. 2021, 18, 900–904. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Zhou, H.; Zhang, W.; Zhang, Z.; Wang, X.H. A Method to Derive Bathymetry for Dynamic Water Bodies Using ICESat-2 and GSWD Data Sets. IEEE Geosci. Remote. Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Thomas, N.; Pertiwi, A.; Traganos, D.; Lagomasino, D.; Poursanidis, D.; Moreno, S.; Fatoyinbo, L. Space-Borne Cloud-Native Satellite-Derived Bathymetry (SDB) Models Using ICESat-2 and Sentinel-2. Geophys. Res. Lett. 2021, 48, e2020GL092170. [Google Scholar] [CrossRef]
- Hsu, H.J.; Huang, C.Y.; Jasinski, M.; Li, Y.; Gao, H.; Yamanokuchi, T.; Wang, C.G.; Chang, T.M.; Ren, H.; Kuo, C.Y. A semi-empirical scheme for bathymetric mapping in shallow water by ICESat-2 and Sentinel-2: A case study in the South China Sea. ISPRS J. Photogramm. Remote Sens. 2021, 178, 1–19. [Google Scholar] [CrossRef]
- Fassoni-Andrade, A.C.; Durand, F.; Moreira, D.; Azevedo, A.; Fassoni-Andrade, A. Comprehensive bathymetry and in-tertidal topography of the Amazon estuary. Earth Syst. Sci. Data 2021, 13, 2275–2291. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Z.; Le, Y.; Qiu, Z.; Chen, G.; Wang, L. Refraction correction and coordinate displacement compensation in nearshore bathymetry using ICESat-2 lidar data and remote-sensing images. Opt. Express 2021, 29, 2411–2430. [Google Scholar] [CrossRef]
- Cossio, T.; Slatton, K.C.; Carter, W.; Shrestha, K.; Harding, D. Predicting Topographic and Bathymetric Measurement Performance for Low-SNR Airborne Lidar. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 2298–2315. [Google Scholar] [CrossRef]
- Eren, F.; Jung, J.; Parrish, C.E.; Sarkozi-Forfinski, N.; Calder, B.R. Total Vertical Uncertainty (TVU) Modeling for Topo-Bathymetric LIDAR Systems. Photogramm. Eng. Remote. Sens. 2019, 85, 585–596. [Google Scholar] [CrossRef]
- Su, D.; Yang, F.; Ma, Y.; Wang, X.H.; Yang, A.; Qi, C. Propagated Uncertainty Models Arising From Device, Environment, and Target for a Small Laser Spot Airborne LiDAR Bathymetry and its Verification in the South China Sea. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 3213–3231. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K.; Boss, E. Phase function effects on oceanic light fields. Appl. Opt. 2002, 41, 1035–1050. [Google Scholar] [CrossRef]
- Guenther, G.C.; Cunningham, A.; LaRocque, P.E.; Reid, D.J. Meeting the accuracy challenge in airborne lidar bathymetry. In Proceedings of the EARSeL-SIG-Workshop LIDAR, Dresden/FRG, EARSeL, Silver Spring, MD, USA, 16–17 June 2000. [Google Scholar]
- Philpot, W.; Wozencraft, J. Airborne Laser Hydrography II. In American Geophysical Union, Ocean Sciences Meeting; AGU: New Orleans, Louisiana, USA, 2016. [Google Scholar]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Martino, A.J.; Neumann, T.A.; Kurtz, N.T.; McLennan, D. ICESat-2 mission overview and early performance. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXIII, Strasbourg, France, 9–12 September 2019; p. 111510C. [Google Scholar]
- Guenther, G.C. Airborne Laser Hydrography System Design and Performance Factors. In NOAA Professional Paper Series; Nat. Ocean Service 1, Nat. Oceanic Atmos. Admin.; U.S. Dept. Commerce: Washington, DC, USA, 1985; pp. 1–385. Available online: https://repository.library.noaa.gov/view/noaa/2811/noaa_2811_DS1.pdf (accessed on 1 December 2021).
- Cox, W.; Muth, J. Simulating channel losses in an underwater optical communication system. J. Opt. Soc. Am. A 2014, 31, 920–934. [Google Scholar] [CrossRef]
- Sahu, S.K.; Shanmugam, P. A theoretical study on the impact of particle scattering on the channel characteristics of un-derwater optical communication system. Opt. Commun. 2018, 408, 3–14. [Google Scholar] [CrossRef]
- Gordon, H.R. Interpretation of airborne oceanic lidar: Effects of multiple scattering. Appl. Opt. 1982, 21, 2996–3001. [Google Scholar] [CrossRef]
- Punjabi, A.; Venable, D.D. Effects of multiple scattering on time- and depth-resolved signals in airborne lidar systems. Int. J. Remote. Sens. 1986, 7, 615–626. [Google Scholar] [CrossRef]
- Duda, D.P.; Spinhirne, J.D.; Eloranta, E.W. Atmospheric multiple scattering effects on GLAS altimetry. I. calculations of single pulse bias. IEEE Trans. Geosci. Remote Sens. 2001, 39, 92–101. [Google Scholar]
- Mahesh, A.; Spinhirne, J.; Duda, D.; Eloranta, E. Atmospheric multiple scattering effects on GLAS altimetry. II. Analysis of expected errors in Antarctic altitude measurements. IEEE Trans. Geosci. Remote. Sens. 2002, 40, 2353–2362. [Google Scholar] [CrossRef]
- Schwarz, R.; Pfeifer, N.; Pfennigbauer, M.; Mandlburger, G. Depth Measurement Bias in Pulsed Airborne Laser Hydrog-raphy Induced by Chromatic Dispersion. IEEE Geosci. Remote Sens Lett. 2021, 18, 1332–1336. [Google Scholar] [CrossRef]
- Abdallah, H.; Baghdadi, N.; Bailly, J.; Pastol, Y.; Fabre, F. Wa-LiD: A new lidar simulator for waters. IEEE Geosci. Remote Sens. Lett. 2012, 9, 744–748. [Google Scholar] [CrossRef]
- Sahu, S.K.; Shanmugam, P. Scattering phase function for particulates-in-water: Modeling and validation. Remote Sens. Model. Atmos. Ocean. Interact. VI 2016, 9882, 98821. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, W.; Cui, X.; Malinka, A.; Liu, Q.; Han, B.; Wang, X.; Zhuo, W.; Che, H.; Song, Q.; et al. Validation of the Analytical Model of Oceanic Lidar Returns: Comparisons with Monte Carlo Simulations and Experimental Results. Remote. Sens. 2019, 11, 1870. [Google Scholar] [CrossRef]
- Liu, Q.; Cui, X.; Jamet, C.; Zhu, X.; Mao, Z.; Chen, P.; Bai, J.; Liu, D. A Semianalytic Monte Carlo Simulator for Spaceborne Oceanic Lidar: Framework and Preliminary Results. Remote. Sens. 2020, 12, 2820. [Google Scholar] [CrossRef]
- Chen, P.; Jamet, C.; Mao, Z.; Pan, D. OLE: A Novel Oceanic Lidar Emulator. IEEE Trans. Geosci. Remote. Sens. 2021, 59, 9730–9744. [Google Scholar] [CrossRef]
- Yin, T.; Lauret, N.; Gastellu-Etchegorry, J.-P. Simulation of satellite, airborne and terrestrial LiDAR with DART (II): ALS and TLS multi-pulse acquisitions, photon counting, and solar noise. Remote. Sens. Environ. 2016, 184, 454–468. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Y.; Yin, T.; Wang, C.; Lauret, N.; Regaieg, O.; Xi, X.; Gastellu-Etchegorry, P. Comprehensive LiDAR simulation with efficient physically-based DART-Lux model (I): Theory, novelty, and consistency validation. Remote Sens. Environ. 2022, 272, 112952. [Google Scholar]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef]
- Eugene, H. Optics, 5th ed.; Pearson: New York, NY, USA, 2016. [Google Scholar]
- Sophocles, J. Orfanidis, Electromagnetic Waves and Antennas. 2016. Available online: http://eceweb1.rutgers.edu/~orfanidi/ewa/ewa-1up.pdf (accessed on 1 December 2021).
- Poole, L.R.; Venable, D.D.; Campbell, J.W. Semianalytic Monte Carlo radiative transfer model for oceanographic lidar systems. Appl. Opt. 1981, 20, 3653–3656. [Google Scholar] [CrossRef]
- Petzold, T.J. Volume Scattering Functions for Selected Ocean Waters. In Proceedings of the Scripps Institution of Oceanography La Jolla Ca Visibility Lab, Naval Air Development Center, Warminster, PA, USA, 1 October 1972. [Google Scholar]
- Yang, J.; Ma, Y.; Li, S.; Liu, X.; Zhang, W.; Zhang, Z. Theoretical model considering optimal ranging performance and energy efficiency for photon-counting lidars with multiple detectors. Appl. Opt. 2021, 60, 8838–8850. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, N.; Ma, Y.; Yang, B.; Zhang, Z.; Wang, X.H.; Li, S. A maximum bathymetric depth model to simulate satellite photon-counting lidar performance. ISPRS J. Photogramm. Remote. Sens. 2021, 174, 182–197. [Google Scholar] [CrossRef]
- Gardner, C.S. Target signatures for laser altimeters: An analysis. Appl. Opt. 1982, 21, 448–453. [Google Scholar] [CrossRef]
- Tsai, B.M.; Gardner, C.S. Remote sensing of sea state using laser altimeters. Appl. Opt. 1982, 21, 3932–3940. [Google Scholar] [CrossRef]
- Fournier, G.R.; Forand, J.L. Analytic phase function for ocean water. In Ocean Optics XII; International Society for Optics and Photonics: Bellingham, WA, USA, 1994; Volume 2258, pp. 194–201. [Google Scholar]
- Fournier, G.R.; Jonasz, M. Computer-based underwater imaging analysis. In Airborne and In-Water Underwater Imaging; SPIE: Bellingham, DC, USA, 1999; pp. 62–71. [Google Scholar]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Mobley, C.; Boss, E.; Roesler, C. Ocean Optics Web book. 2021. Available online: https://oceanopticsbook.info/ (accessed on 1 December 2021).
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Feygels, V.I.; Kopilevich, Y.; Park, J.Y.; Kim, M.; Aitken, J. Particularities of hydro lidar missions in the Asia-Pacific region. In Lidar Remote Sensing for Environmental Monitoring; SPIE: Bellingham, DC, USA, 2014; pp. 62–70. [Google Scholar]
- Wang, J.; Myers, E.; Jeong, I.; White, S. VDatum for the Coastal Waters of Puerto Rico and the U. S. Virgin Islands: Tidal Datums, Marine Grid, and Sea Surface Topography; NOAA Technical Memorandum NOS CS 33: Silver Spring, MD, USA, 2013. [Google Scholar]
- Wright, C.W.; Kranenburg, C.; Battista, T.A.; Parrish, C. Depth Calibration and Validation of the Experimental Advanced Airborne Research Lidar, EAARL-B. J. Coast. Res. 2016, 76, 4–17. [Google Scholar] [CrossRef]
- Feygels, V.I.; Park, J.Y.; Wozencraft, J.; Aitken, J.; Macon, C.; Mathur, A.; Payment, A.; Ramnath, V. CZMIL (coastal zone mapping and imaging lidar): From first flights to first mission through system validation. In Ocean Sensing and Monitoring V; SPIE: Bellingham, DC, USA, 2013; Volume 8724. [Google Scholar] [CrossRef]
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.B.; Rebold, T. AT-LAS/ICESat-2 L2A Global Geolocated Photon Data, Version 4; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021; Available online: https://nsidc.org/sites/default/files/atl03-v004-userguide_1.pdf (accessed on 1 December 2021).
- Neumann, T.; Brenner, A.; Hancock, D.; Luthcke, S.; Lee, J.; Robbins, J.; Harbeck, K.; Bae, S.; Brunt, K.; Gibbons, A.; et al. Ice, Cloud, and Land Elevation Satellite—2 (ICESat-2) Project, Algorithm Theoretical Basis Document (ATBD) for Global Geolocated Photons ATL03; Goddard Space Flight Center: Greenbelt, MD, USA, 2019. [Google Scholar]
- Tian, X.; Shan, J. Comprehensive Evaluation of the ICESat-2 ATL08 Terrain Product. IEEE Trans. Geosci. Remote. Sens. 2021, 59, 8195–8209. [Google Scholar] [CrossRef]
- Feygels, V.I.; Wright, C.W.; Kopilevich, Y.I.; Surkov, A.I. Narrow-field-of-view bathymetrical lidar: Theory and field test. In Ocean Remote Sensing and Imaging II; SPIE: Bellingham, DC, USA, 2003. [Google Scholar]
- Feygels, V.I.; Park, J.Y.; Aitken, J.; Kim, M.; Payment, A.; Ramnath, V. Coastal Zone Mapping and Imaging Lidar (CZMIL): First flights and system validation. In Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions; SPIE: Bellingham, DC, USA, 2012; 85321C–85321C-10. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef]
- Churnside, J.H. Review of profiling oceanographic lidar. Opt. Eng. 2013, 53, 051405. [Google Scholar] [CrossRef]


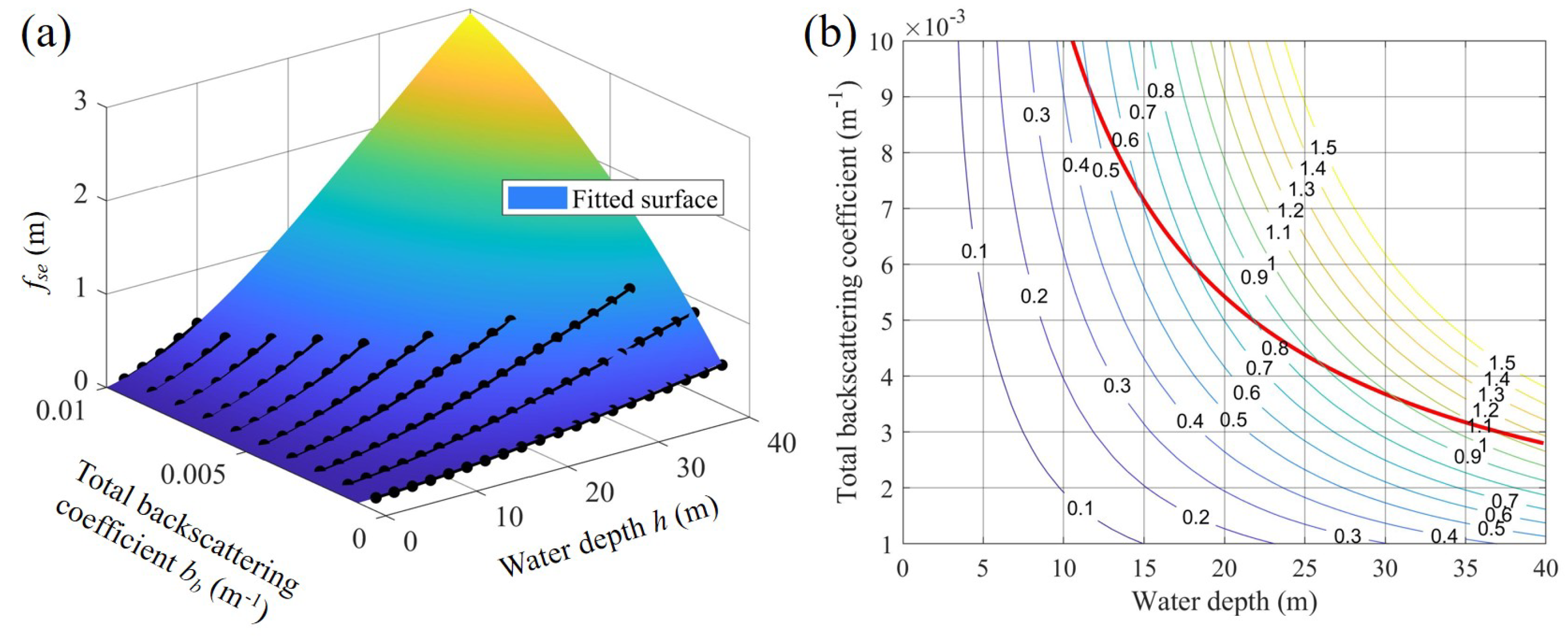

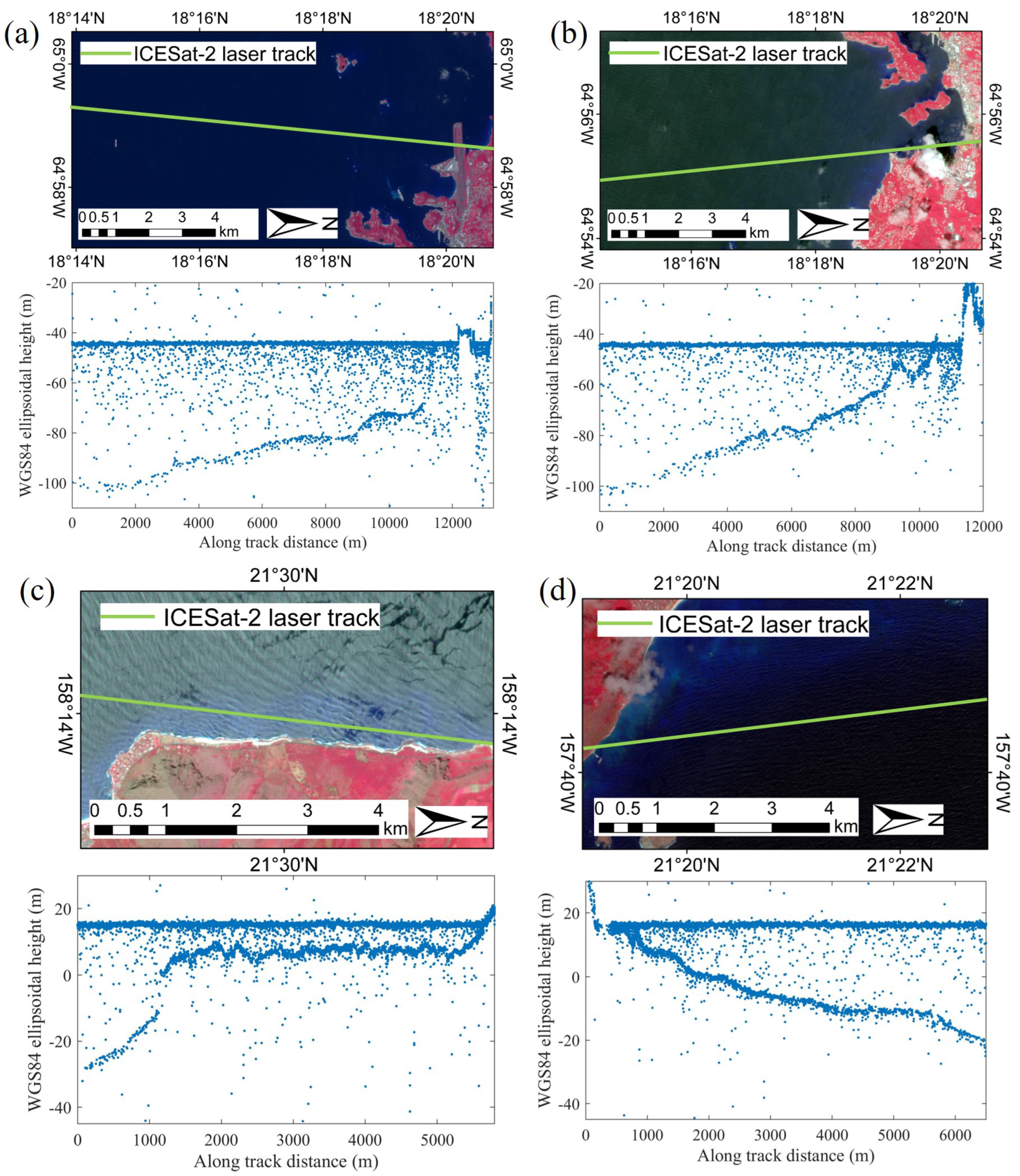

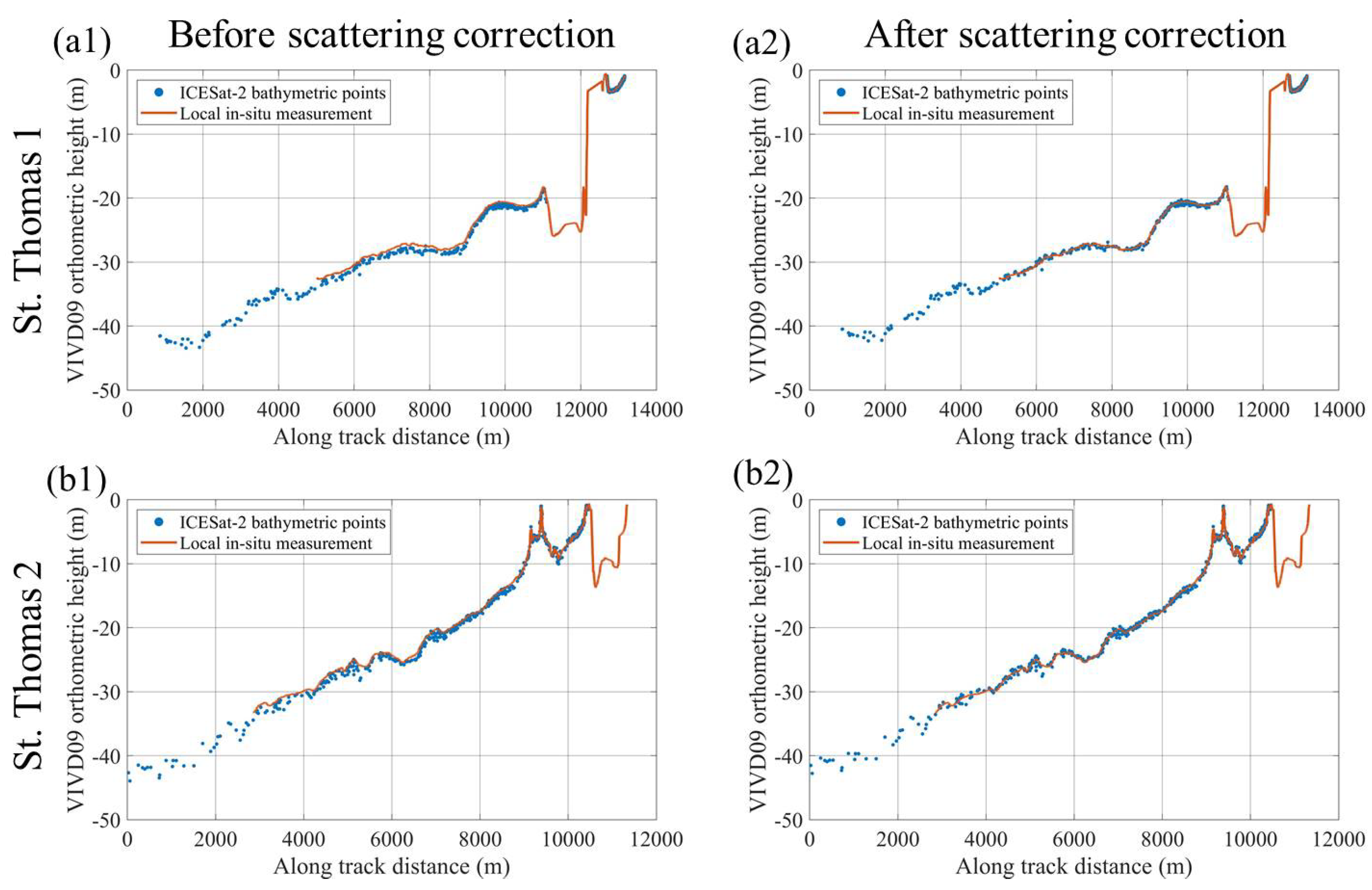

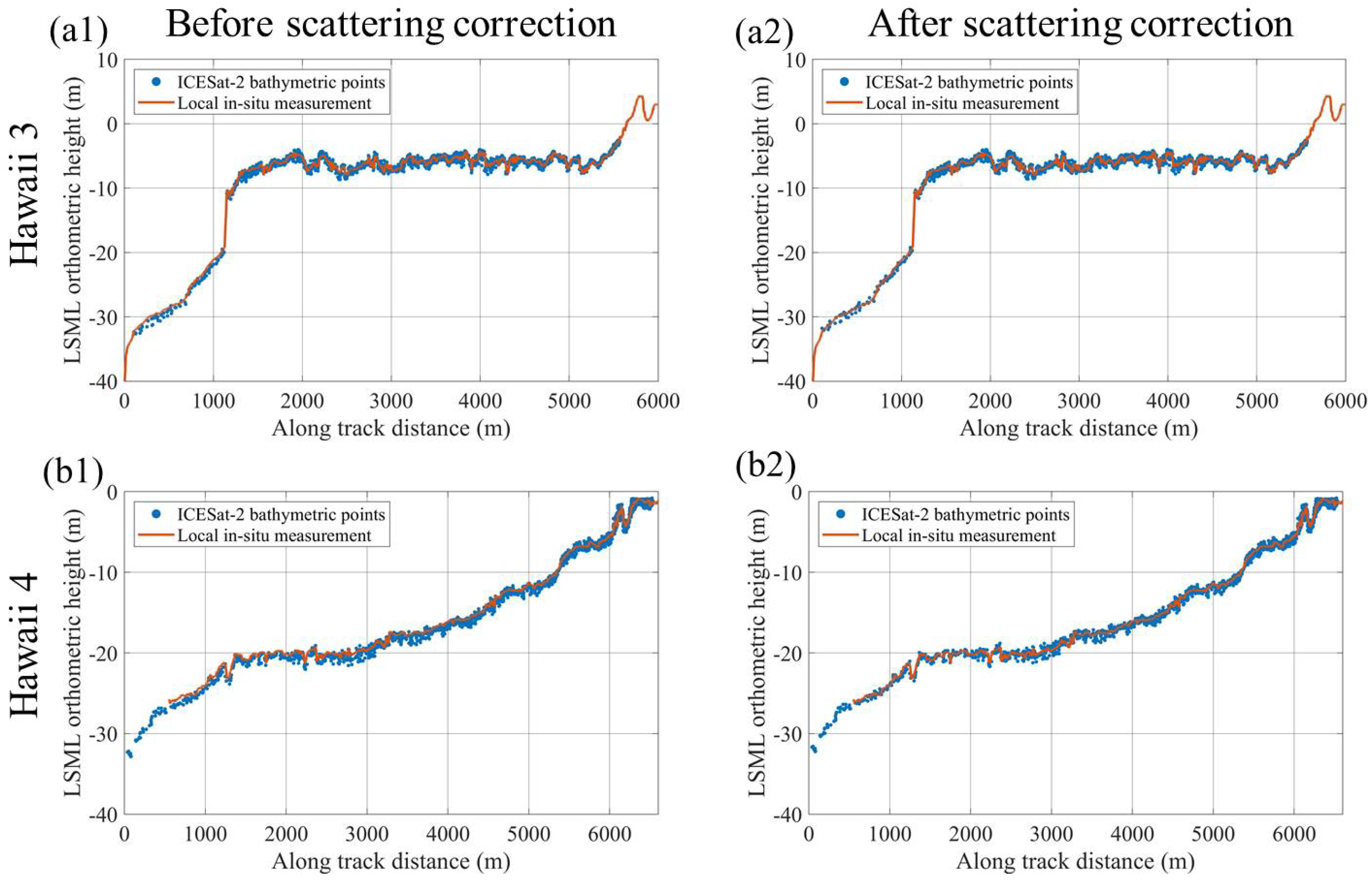

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Field of view 2θr | 83.5 µrad | Laser nadir angle θp | ~0.38° |
| Laser divergence 2θt | 24 µrad | Flight altitude Rh | 500 km |
| Result Figures | Site | Geographical Location | Date | a (m−1) | bb (m−1) |
|---|---|---|---|---|---|
| Figure 5a, Figure 6a, Figure 7a, Figure 8a and Figure 11a | St. Thomas Island 1 | [18.29°N, 64.98°W] | 2018/11/22 | 0.0501 | 0.00244 |
| Figure 5b, Figure 6b, Figure 7b, Figure 8b and Figure 11b | St. Thomas Island 2 | [18.29°N, 64.92°W] | 2019/12/15 | 0.0503 | 0.00255 |
| Figure 5c, Figure 6c, Figure 7c, Figure 8c and Figure 11c | Hawaii Island 3 | [21.50°N, 158.23°W] | 2019/04/16 | 0.0451 | 0.00181 |
| Figure 5d, Figure 6d, Figure 7d, Figure 8d and Figure 11d | Hawaii Island 4 | [21.35°N, 158.67°W] | 2019/06/09 | 0.0447 | 0.00197 |
| Tracks | Parameters | Water Depths (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0~5 | 5~10 | 10~15 | 15~20 | 20~25 | 25~30 | 30~35 | >20 | All | |||
| St. Thomas 1 | Number of ICESat-2 Points | 446 | 0 | 0 | 11 | 131 | 91 | 27 | 249 | 706 | |
| MEs (m) | Uncorrected | −0.02 | NaN | NaN | −0.48 | −0.49 | −0.73 | −0.75 | −0.61 | −0.23 | |
| Corrected | −0.01 | NaN | NaN | −0.13 | −0.07 | −0.10 | 0.00 | −0.07 | −0.03 | ||
| RMSEs (m) | Uncorrected | 0.17 | NaN | NaN | 0.52 | 0.53 | 0.78 | 0.84 | 0.67 | 0.43 | |
| Corrected | 0.17 | NaN | NaN | 0.23 | 0.21 | 0.29 | 0.37 | 0.26 | 0.21 | ||
| St. Thomas 2 | Number of ICESat-2 Points | 41 | 151 | 43 | 73 | 85 | 76 | 31 | 192 | 500 | |
| MEs (m) | Uncorrected | 0.00 | −0.08 | −0.35 | −0.29 | −0.53 | −0.60 | −0.76 | −0.60 | −0.33 | |
| Corrected | 0.03 | −0.01 | −0.14 | 0.04 | −0.06 | 0.01 | 0.01 | −0.02 | −0.01 | ||
| RMSEs (m) | Uncorrected | 0.48 | 0.38 | 0.53 | 0.39 | 0.66 | 0.78 | 0.91 | 0.75 | 0.57 | |
| Corrected | 0.48 | 0.36 | 0.40 | 0.27 | 0.39 | 0.48 | 0.47 | 0.44 | 0.40 | ||
| Tracks | Parameters | Water Depths (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0~5 | 5~10 | 10~15 | 15~20 | 20~25 | 25~30 | 30~35 | >20 | All | |||
| Hawaii 3 | Number of ICESat-2 Points | 343 | 1912 | 16 | 8 | 34 | 39 | 10 | 83 | 2362 | |
| MEs (m) | Uncorrected | −0.06 | −0.06 | −0.30 | −0.28 | −0.58 | −0.52 | −0.60 | −0.56 | −0.08 | |
| Corrected | −0.03 | −0.02 | −0.19 | −0.01 | −0.22 | −0.04 | −0.03 | −0.11 | −0.02 | ||
| RMSEs (m) | Uncorrected | 0.39 | 0.43 | 0.61 | 0.41 | 0.64 | 0.69 | 0.73 | 0.67 | 0.44 | |
| Corrected | 0.39 | 0.42 | 0.57 | 0.29 | 0.35 | 0.43 | 0.42 | 0.40 | 0.42 | ||
| Hawaii 4 | Number of ICESat-2 Points | 204 | 351 | 368 | 449 | 177 | 26 | 0 | 203 | 1575 | |
| MEs (m) | Uncorrected | −0.02 | −0.15 | −0.28 | −0.35 | −0.49 | −0.51 | NaN | −0.49 | −0.26 | |
| Corrected | −0.01 | −0.09 | −0.14 | −0.09 | −0.15 | −0.06 | NaN | −0.13 | −0.09 | ||
| RMSEs (m) | Uncorrected | 0.44 | 0.38 | 0.44 | 0.49 | 0.60 | 0.62 | NaN | 0.61 | 0.49 | |
| Corrected | 0.44 | 0.36 | 0.35 | 0.36 | 0.36 | 0.34 | NaN | 0.36 | 0.38 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Ma, Y.; Zheng, H.; Gu, Y.; Zhou, H.; Li, S. Analysis and Correction of Water Forward-Scattering-Induced Bathymetric Bias for Spaceborne Photon-Counting Lidar. Remote Sens. 2023, 15, 931. https://doi.org/10.3390/rs15040931
Yang J, Ma Y, Zheng H, Gu Y, Zhou H, Li S. Analysis and Correction of Water Forward-Scattering-Induced Bathymetric Bias for Spaceborne Photon-Counting Lidar. Remote Sensing. 2023; 15(4):931. https://doi.org/10.3390/rs15040931
Chicago/Turabian StyleYang, Jian, Yue Ma, Huiying Zheng, Yuanfei Gu, Hui Zhou, and Song Li. 2023. "Analysis and Correction of Water Forward-Scattering-Induced Bathymetric Bias for Spaceborne Photon-Counting Lidar" Remote Sensing 15, no. 4: 931. https://doi.org/10.3390/rs15040931
APA StyleYang, J., Ma, Y., Zheng, H., Gu, Y., Zhou, H., & Li, S. (2023). Analysis and Correction of Water Forward-Scattering-Induced Bathymetric Bias for Spaceborne Photon-Counting Lidar. Remote Sensing, 15(4), 931. https://doi.org/10.3390/rs15040931











