A New Strategy to Fuse Remote Sensing Data and Geochemical Data with Different Machine Learning Methods
Abstract
1. Introduction
2. Material and Methodologies
2.1. Geological Background
2.2. Data Sets
2.2.1. Remote Sensing
2.2.2. Geochemical Data
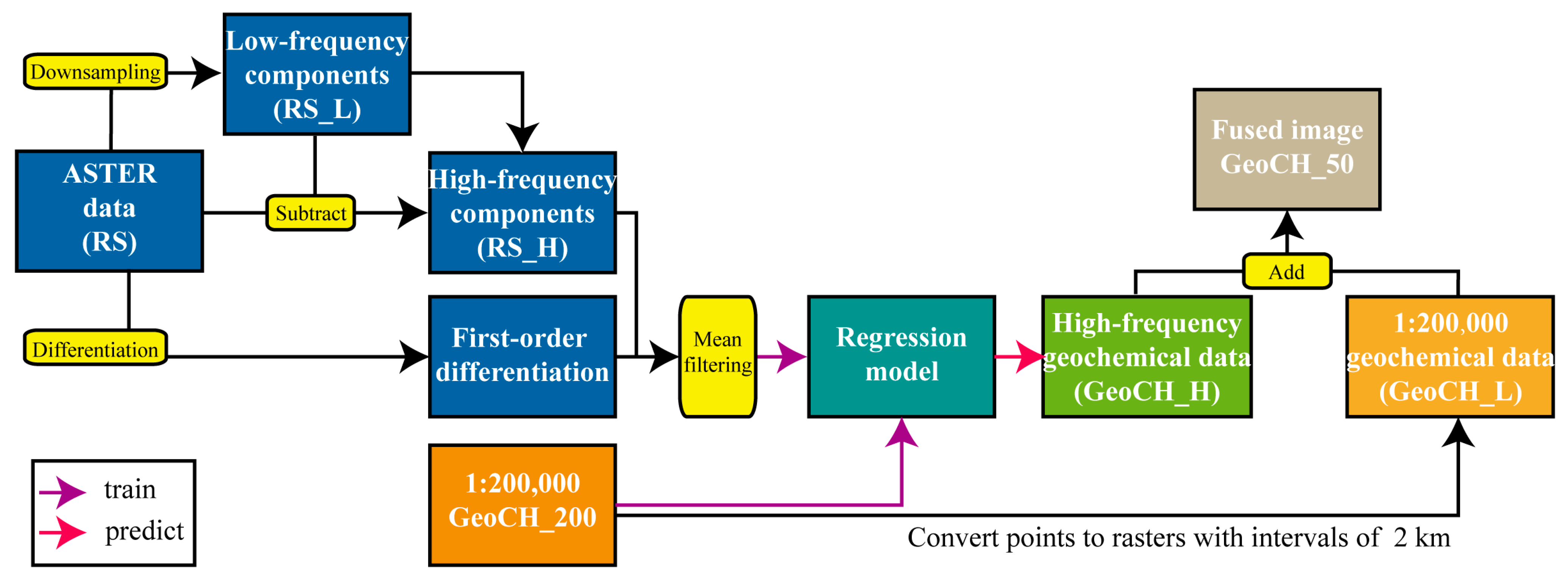
2.3. Data Fusion Strategy
2.4. Regression Models
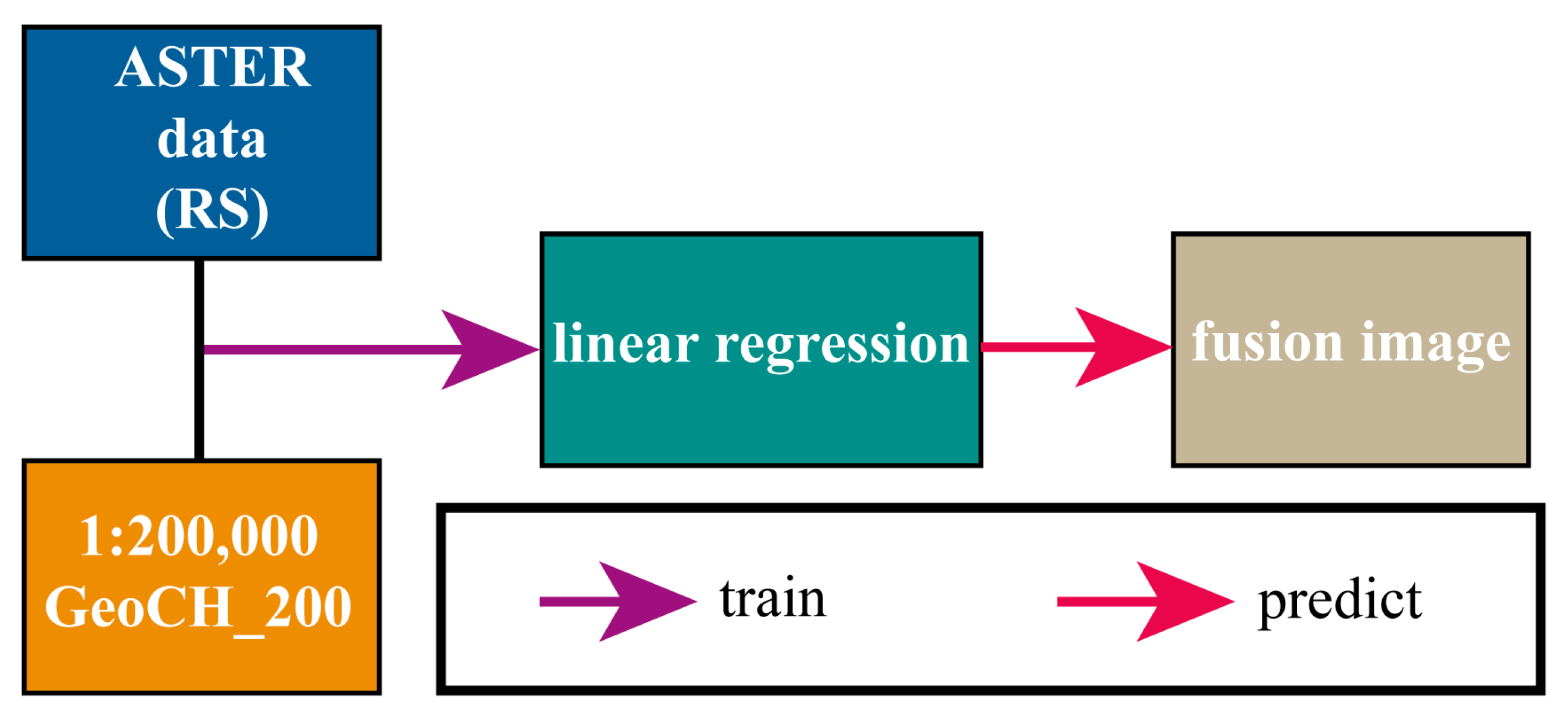
2.4.1. Linear
2.4.2. Random Forest (RF)
2.4.3. Support Vector Regression (SVR)
2.5. Reference of Data Fusion
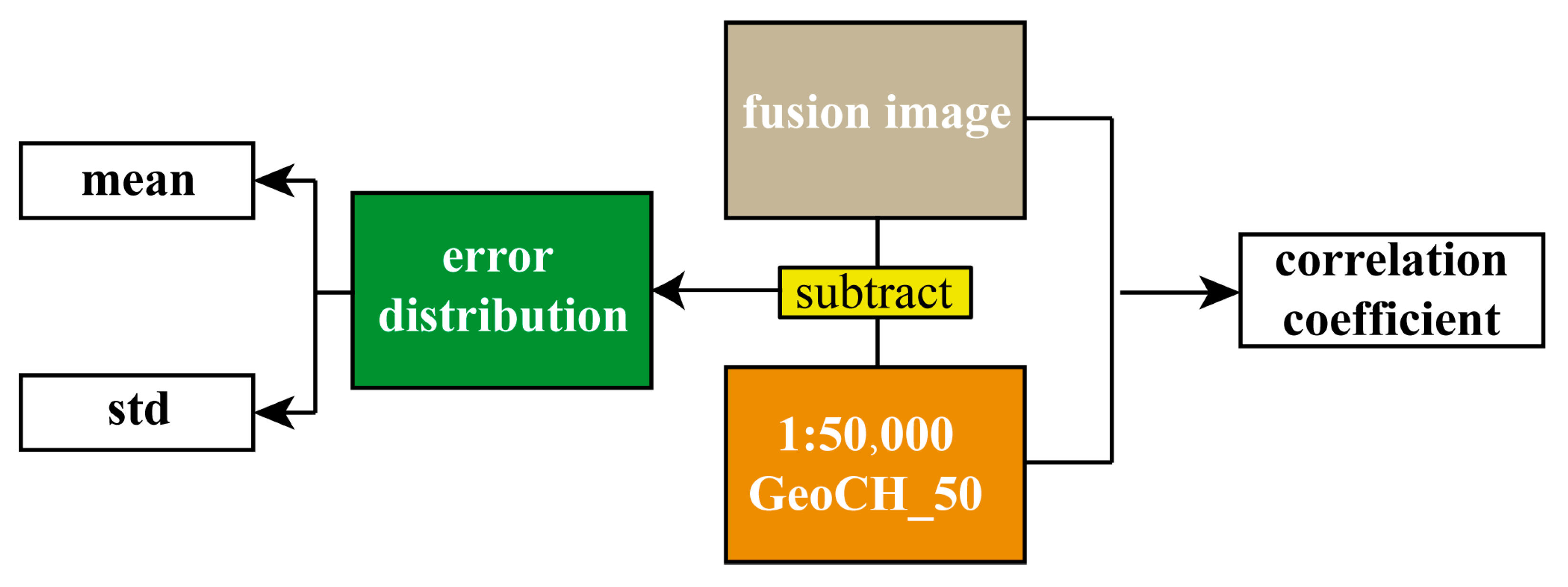
2.6. Evaluation Method
- (1)
- Mean
- (2)
- Standard deviation
- (3)
- Correlation coefficient
3. Results
3.1. Fused Results
3.2. Statistical Evaluation on the Fused Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doran, J.W.; Coleman, D.C.; Bezdicek, D.; Stewart, B. Defining Soil Quality for a Sustainable Environment; Food and Agriculture Organization of the United Nations: Rome, Italy, 1994. [Google Scholar]
- West, T.O.; Post, W.M. Soil organic carbon sequestration rates by tillage and crop rotation: A global data analysis. Soil Sci. Soc. Am. J. 2002, 66, 1930–1946. [Google Scholar] [CrossRef]
- Beus, A.A.; Grigorian, S.V. Geochemical Exploration Methods for Mineral Deposits. 1977. Available online: https://www.osti.gov/biblio/7211784 (accessed on 23 April 2021).
- Krishnakumar, S.; Ramasamy, S.; Chandrasekar, N.; Peter, T.S.; Godson, P.S.; Gopal, V.; Magesh, N. Spatial risk assessment and trace element concentration in reef associated sediments of Van Island, southern part of the Gulf of Mannar, India. Mar. Pollut. Bull. 2017, 115, 444–450. [Google Scholar] [PubMed]
- Krishnakumar, S.; Ramasamy, S.; Peter, T.S.; Godson, P.S.; Chandrasekar, N.; Magesh, N. Geospatial risk assessment and trace element concentration in reef associated sediments, northern part of Gulf of Mannar biosphere reserve, Southeast Coast of India. Mar. Pollut. Bull. 2017, 125, 522–529. [Google Scholar]
- Xie, X.; Cheng, H. Sixty years of exploration geochemistry in China. J. Geochem. Explor. 2014, 139, 4–8. [Google Scholar]
- Wang, Z.; Zuo, R.; Liu, H. Lithological mapping based on fully convolutional network and multi-source geological data. Remote Sens. 2021, 13, 4860. [Google Scholar]
- Yang, N.; Zhang, Z.; Yang, J.; Hong, Z.; Shi, J. A convolutional neural network of GoogLeNet applied in mineral prospectivity prediction based on multi-source geoinformation. Nat. Resour. Res. 2021, 30, 3905–3923. [Google Scholar]
- Campbell, J.B.; Wynne, R.H. Introduction to Remote Sensing; Guilford Press: New York, NY, USA, 2011. [Google Scholar]
- Gupta, R.P. Remote Sensing Geology; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Tappert, M.C.; Rivard, B.; Giles, D.; Tappert, R.; Mauger, A. The mineral chemistry, near-infrared, and mid-infrared reflectance spectroscopy of phengite from the Olympic Dam IOCG deposit, South Australia. Ore Geol. Rev. 2013, 53, 26–38. [Google Scholar]
- Kokaly, R.; Graham, G.E.; Hoefen, T.M.; Kelley, K.D.; Johnson, M.R.; Hubbard, B.E.; Buchhorn, M.; Prakash, A. Multiscale hyperspectral imaging of the Orange Hill Porphyry Copper Deposit, Alaska, USA, with laboratory-, field-, and aircraft-based imaging spectrometers. Proc. Explor. 2017, 17, 923–943. [Google Scholar]
- Meyer, J.M.; Kokaly, R.F.; Holley, E. Hyperspectral remote sensing of white mica: A review of imaging and point-based spectrometer studies for mineral resources, with spectrometer design considerations. Remote Sens. Environ. 2022, 275, 113000. [Google Scholar]
- Swayze, G.A.; Clark, R.N.; Pearson, R.M.; Livo, K.E. Mapping Acid-Generating Minerals at the California Gulch Superfund Site in Leadville, Colorado Using Imaging Spectroscopy; NASA: Washington, DC, USA, 1996. [Google Scholar]
- Kopačková-Strnadová, V.; Rapprich, V.; McLemore, V.; Pour, O.; Magna, T. Quantitative estimation of rare earth element abundances in compositionally distinct carbonatites: Implications for proximal remote-sensing prospection of critical elements. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102423. [Google Scholar] [CrossRef]
- Huadong, G.; Pinliang, D. Integrated MSS-SAR-SPOT-geophysical and geochemical data for exploration geology in Yeder area. Adv. Space Res. 1992, 12, 27–30. [Google Scholar] [CrossRef]
- Fazliani, H.; Kamkar-Rouhani, A.; Arab-Amiri, A. Integration and analysis of geological, geochemical and remote sensing data of south of Neyshabur using principal component analysis. Int. J. Min. Geo-Eng. 2021, 55, 161–170. [Google Scholar]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide susceptibility assessment using SVM machine learning algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar]
- Zuo, R. Machine learning of mineralization-related geochemical anomalies: A review of potential methods. Nat. Resour. Res. 2017, 26, 457–464. [Google Scholar] [CrossRef]
- Lucey, P.G.; Blewett, D.T.; Hawke, B.R. Mapping the FeO and TiO2 content of the lunar surface with multispectral imagery. J. Geophys. Res. Planets 1998, 103, 3679–3699. [Google Scholar] [CrossRef]
- Wang, Z.; Zuo, R.; Jing, L. Fusion of geochemical and remote-sensing data for lithological mapping using random forest metric learning. Math. Geosci. 2021, 53, 1125–1145. [Google Scholar] [CrossRef]
- Moradpour, H.; Rostami Paydar, G.; Feizizadeh, B.; Blaschke, T.; Pour, A.B.; Valizadeh Kamran, K.; Muslim, A.M.; Hossain, M.S. Fusion of ASTER satellite imagery, geochemical and geology data for gold prospecting in the Astaneh granite intrusive, West Central Iran. Int. J. Image Data Fusion 2022, 13, 71–94. [Google Scholar] [CrossRef]
- Contreras, C.; Khodadadzadeh, M.; Tusa, L.; Loidolt, C.; Tolosana-Delgado, R.; Gloaguen, R. Geochemical and Hyperspectral Data Fusion for Drill-Core Mineral Mapping. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019. [Google Scholar]
- Jiang, L.; Xing, L.; Liang, Y.; Pan, J.; Liang, L.-H.; Huang, J.-C. Anomalies information extraction from geochemical data and remote sensing fusion. J. Jilin Univ. (Earth Sci. Ed.) 2011, 41, 932–936. [Google Scholar]
- Li, Z.; Zhang, X.; Zhu, R.; Zhang, Z.; Weng, Z. Integrating data-to-data correlation into inverse distance weighting. Comput. Geosci. 2020, 24, 203–216. [Google Scholar]
- Mao, J.; Pirajno, F.; Zhang, Z.; Chai, F.; Yang, J.; Wu, H.; Chen, S.; Cheng, S.; Zhang, C. Late Variscan post-collisional Cu-Ni sulfide deposits in East Tianshan and Altay in China: Principal characteristics and possible relationship with mantle plume. Acta Geol. Sin. 2006, 80, 925–942. [Google Scholar]
- Windley, B.; Allen, M.; Zhang, C.; Zhao, Z.; Wang, G. Paleozoic accretion and Cenozoic redeformation of the Chinese Tien Shan range, central Asia. Geology 1990, 18, 128–131. [Google Scholar] [CrossRef]
- Şengör, A.; Natal’In, B.; Burtman, V. Evolution of the Altaid tectonic collage and Palaeozoic crustal growth in Eurasia. Nature 1993, 364, 299–307. [Google Scholar] [CrossRef]
- Jahn, B.-m.; Windley, B.; Natal’in, B.; Dobretsov, N. Phanerozoic continental growth in Central Asia. J. Asian Earth Sci. 2004, 5, 599–603. [Google Scholar]
- Xiao, W.-J.; Zhang, L.-C.; Qin, K.-Z.; Sun, S.; Li, J.-L. Paleozoic accretionary and collisional tectonics of the Eastern Tianshan (China): Implications for the continental growth of central Asia. Am. J. Sci. 2004, 304, 370–395. [Google Scholar] [CrossRef]
- Qin, K.; Sun, S.; Li, J.; Fang, T.; Wang, S.; Liu, W. Paleozoic epithermal Au and porphyry Cu deposits in North Xinjiang, China: Epochs, features, tectonic linkage and exploration significance. Resour. Geol. 2002, 52, 291–300. [Google Scholar] [CrossRef]
- Xiao, W.; Han, C.; Yuan, C.; Sun, M.; Lin, S.; Chen, H.; Li, Z.; Li, J.; Sun, S. Middle Cambrian to Permian subduction-related accretionary orogenesis of Northern Xinjiang, NW China: Implications for the tectonic evolution of central Asia. J. Asian Earth Sci. 2008, 32, 102–117. [Google Scholar] [CrossRef]
- Long, L.; Wang, J.; Wang, Y.; Deng, X.; Mao, Q.; Sun, Y.; Sun, Z.; Zhang, Z. Metallogenic regularity and metallogenic model of the paleo arc-basin system in eastern Tianshan. Acta Petrol. Sin. 2019, 35, 3161–3188. [Google Scholar]
- Mao, Q.; Yu, M.; Xiao, W.; Windley, B.F.; Li, Y.; Wei, X.; Zhu, J.; Lü, X. Skarn-mineralized porphyry adakites in the Harlik arc at Kalatage, E. Tianshan (NW China): Slab melting in the Devonian-early Carboniferous in the southern Central Asian Orogenic Belt. J. Asian Earth Sci. 2018, 153, 365–378. [Google Scholar]
- Zhang, Z.; Xiao, W.; Zheng, X.; Yang, G.; Gao, J. Composition, structure and the late Paleozoic evolution of Kanggurtag structural belt in eastern Tianshan. Miner. Explor. 2021, 12, 1530–1538. [Google Scholar]
- Wang, J.; Wang, Y.; He, Z. Ore deposits as a guide to the tectonic evolution in the East Tianshan Mountains, NW China. Geol. China 2006, 33, 461–469. [Google Scholar]
- Xiao, W.; Windley, B.F.; Allen, M.B.; Han, C. Paleozoic multiple accretionary and collisional tectonics of the Chinese Tianshan orogenic collage. Gondwana Res. 2013, 23, 1316–1341. [Google Scholar] [CrossRef]
- Rowan, L.C.; Mars, J.C. Lithologic mapping in the Mountain Pass, California area using advanced spaceborne thermal emission and reflection radiometer (ASTER) data. Remote Sens. Environ. 2003, 84, 350–366. [Google Scholar] [CrossRef]
- Gabr, S.; Ghulam, A.; Kusky, T. Detecting areas of high-potential gold mineralization using ASTER data. Ore Geol. Rev. 2010, 38, 59–69. [Google Scholar]
- Shirazi, A.; Hezarkhani, A.; Beiranvand Pour, A.; Shirazy, A.; Hashim, M. Neuro-Fuzzy-AHP (NFAHP) Technique for Copper Exploration Using Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) and Geological Datasets in the Sahlabad Mining Area, East Iran. Remote Sens. 2022, 14, 5562. [Google Scholar]
- Kurata, K.; Yamaguchi, Y. Integration and visualization of mineralogical and topographical information derived from ASTER and DEM data. Remote Sens. 2019, 11, 162. [Google Scholar] [CrossRef]
- Goshtasby, A. Registration of images with geometric distortions. IEEE Trans. Geosci. Remote Sens. 1988, 26, 60–64. [Google Scholar]
- Chavez, P.S. Image-based atmospheric corrections-revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1035. [Google Scholar]
- Department of Geology and Mineral Resources Survey and Technology Division. Regional Geochemistry Exploration Specifications—Proportional Scale 1:200,000; National Standardization Technical Committee of Geology and Mineral Resources Technical Committee Geophysical and Geochemical: Beijing China, 1996. [Google Scholar]
- Xuejing, X.; Xuzhan, M.; Tianxiang, R. Geochemical mapping in China. J. Geochem. Explor. 1997, 60, 99–113. [Google Scholar] [CrossRef]
- Zhuang, D.; Liu, T.; Hu, J.; Wang, X. The review and prospect of regional geochemical exploration in Xinjiang. Geophys. Geochem. Explor. 2003, 27, 425–427. [Google Scholar]
- Wang, H.; Yuan, Z.; Cheng, Q.; Zhang, S.; Sadeghi, B. Geochemical anomaly definition using stream sediments landscape modeling. Ore Geol. Rev. 2022, 142, 104715. [Google Scholar] [CrossRef]
- Manyika, J.; Durrant-Whyte, H. Data Fusion and Sensor Management: A Decentralized Information-Theoretic Approach; Prentice Hall PTR: Hoboken, NJ, USA, 1995. [Google Scholar]
- Jing, L.; Cheng, Q. A technique based on non-linear transform and multivariate analysis to merge thermal infrared data and higher-resolution multispectral data. Int. J. Remote Sens. 2010, 31, 6459–6471. [Google Scholar] [CrossRef]
- Grunsky, E.; Agterberg, F. Spatial and multivariate analysis of geochemical data from metavolcanic rocks in the Ben Nevis area, Ontario. Math. Geol. 1988, 20, 825–861. [Google Scholar]
- Reimann, C.; Garrett, R.G. Geochemical background—Concept and reality. Sci. Total Environ. 2005, 350, 12–27. [Google Scholar] [CrossRef] [PubMed]
- McLennan, S.M.; Taylor, S.; Kröner, A. Geochemical evolution of Archean shales from South Africa. I. The Swaziland and Pongola Supergroups. Precambrian Res. 1983, 22, 93–124. [Google Scholar] [CrossRef]
- Cheng, Q.; Agterberg, F.; Ballantyne, S. The separation of geochemical anomalies from background by fractal methods. J. Geochem. Explor. 1994, 51, 109–130. [Google Scholar] [CrossRef]
- Povarennykh, A. The use of infrared spectra for the determination of minerals. Am. Mineral. 1978, 63, 956–959. [Google Scholar]
- Wu, M.; Zhou, K.; Wang, Q.; Wang, J. Mapping hydrothermal zoning pattern of porphyry Cu deposit using absorption feature parameters calculated from ASTER data. Remote Sens. 2019, 11, 1729. [Google Scholar] [CrossRef]
- Chattoraj, S.L.; Prasad, G.; Sharma, R.U.; van der Meer, F.D.; Guha, A.; Pour, A.B. Integration of remote sensing, gravity and geochemical data for exploration of Cu-mineralization in Alwar basin, Rajasthan, India. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102162. [Google Scholar] [CrossRef]
- Karimpour, M.H.; Mazhari, N.; Shafaroudi, A.M. Discrimination of different erosion levels of porphyry Cu deposits using ASTER image processing in eastern Iran: A case study in the Maherabad, Shadan, and Chah Shaljami Areas. Acta Geol. Sin.-Engl. Ed. 2014, 88, 1195–1213. [Google Scholar]
- Aiken, L.S.; West, S.G.; Reno, R.R. Multiple Regression: Testing and Interpreting Interactions; Sage: Thousand Oaks, CA, USA, 1991. [Google Scholar]
- Chung, C.-J.F.; Fabbri, A.G.; Westen, C.J.V. Multivariate regression analysis for landslide hazard zonation. In Geographical Information Systems in Assessing Natural Hazards; Springer: Berlin/Heidelberg, Germany, 1995; pp. 107–133. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar]
- Burges, C.J. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Shevade, S.K.; Keerthi, S.S.; Bhattacharyya, C.; Murthy, K.R.K. Improvements to the SMO algorithm for SVM regression. IEEE Trans. Neural Netw. 2000, 11, 1188–1193. [Google Scholar] [CrossRef] [PubMed]
- Soentpiet, R. Advances in Kernel Methods: Support Vector Learning; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Yu, L.; Liu, H. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 856–863. [Google Scholar]






| Data Type | Mean | Std | Min | Max |
|---|---|---|---|---|
| 1:50,000 | 26.23 | 12.90 | 0.00 | 63.00 |
| 1:200,000 | 22.86 | 11.25 | 3.00 | 64.00 |
| Method | Mean | Std | Correlation (Geochemical) | Correlation (RS) |
|---|---|---|---|---|
| Cu | ||||
| Direct linear | 59.07 | 68.91 | 0.33 | 0.13 |
| Linear | 4.29 | 6.70 | 0.70 | 0.39 |
| Random forest | 3.45 | 5.04 | 0.71 | 0.31 |
| SVR | 5.09 | 5.02 | 0.72 | 0.32 |
| 20-5 | 7.22 | 7.00 | 0.67 | 0.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, S.; Zhao, J. A New Strategy to Fuse Remote Sensing Data and Geochemical Data with Different Machine Learning Methods. Remote Sens. 2023, 15, 930. https://doi.org/10.3390/rs15040930
Bai S, Zhao J. A New Strategy to Fuse Remote Sensing Data and Geochemical Data with Different Machine Learning Methods. Remote Sensing. 2023; 15(4):930. https://doi.org/10.3390/rs15040930
Chicago/Turabian StyleBai, Shi, and Jie Zhao. 2023. "A New Strategy to Fuse Remote Sensing Data and Geochemical Data with Different Machine Learning Methods" Remote Sensing 15, no. 4: 930. https://doi.org/10.3390/rs15040930
APA StyleBai, S., & Zhao, J. (2023). A New Strategy to Fuse Remote Sensing Data and Geochemical Data with Different Machine Learning Methods. Remote Sensing, 15(4), 930. https://doi.org/10.3390/rs15040930








