Statistical Characteristics of the Multiscale SST Fractal Structure over the Kuroshio Extension Region Using VIIRS Data
Abstract
1. Introduction
2. Data
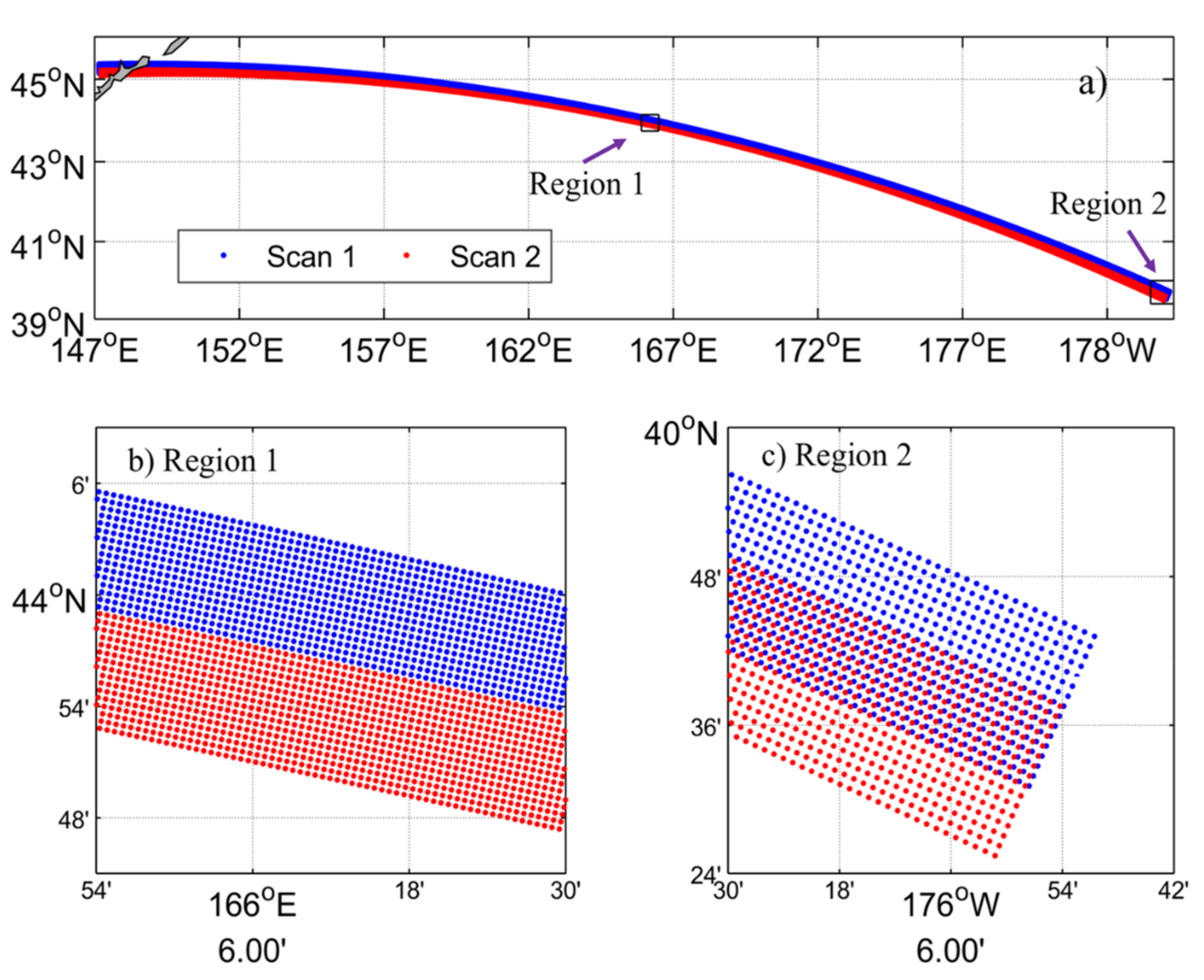
2.1. VIIRS L2P SST
2.2. GHRSST L4 SST
3. Methods
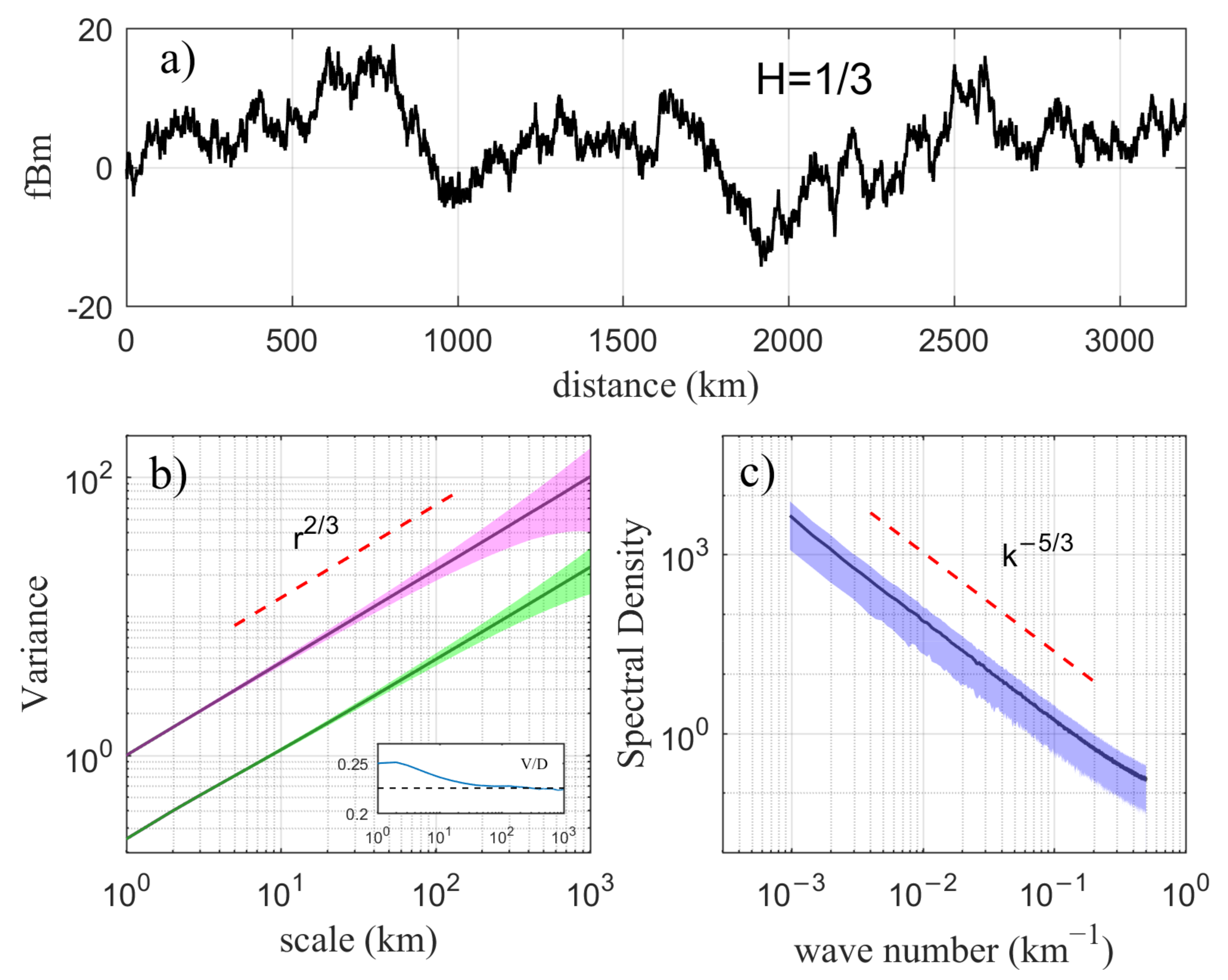
3.1. Spectral Approach and Second-Order Structure Function
3.2. Spatial Variance Method
3.3. Method Framework
3.4. Fractional Brownian Motion Experiments
4. Results
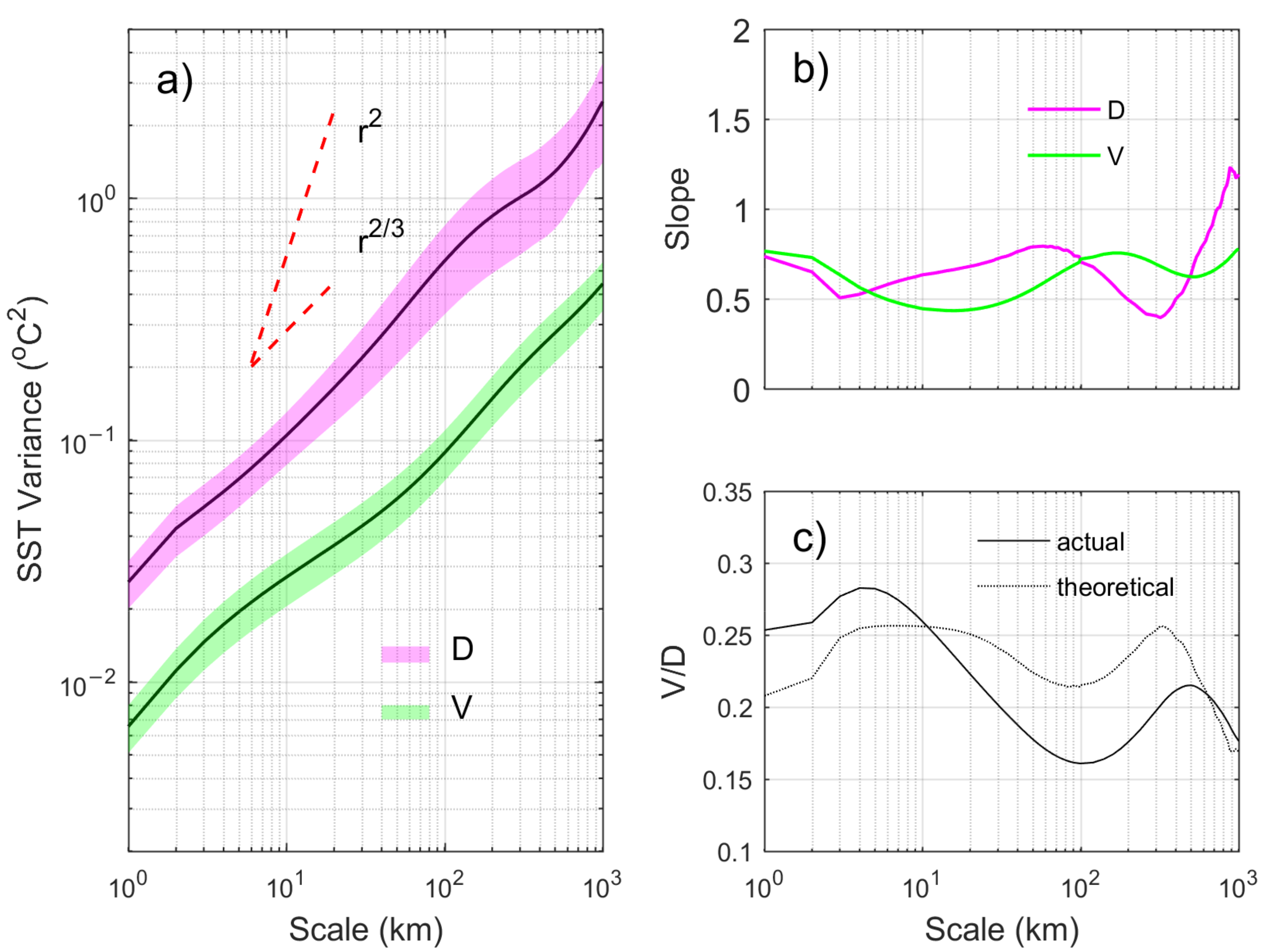
4.1. Power-Law of the Multiscale Fractal Structure
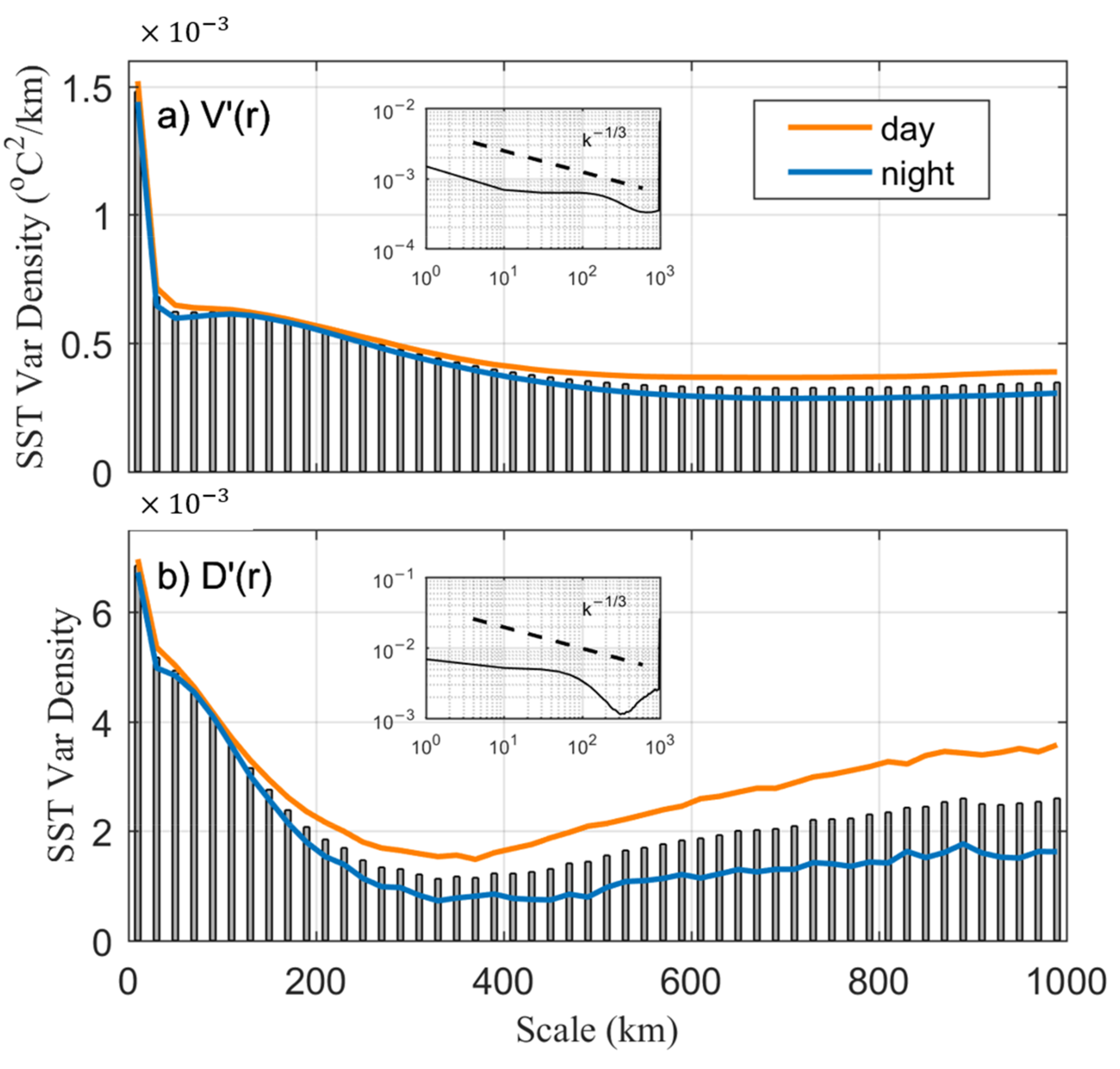
4.2. Spatial Variance Density
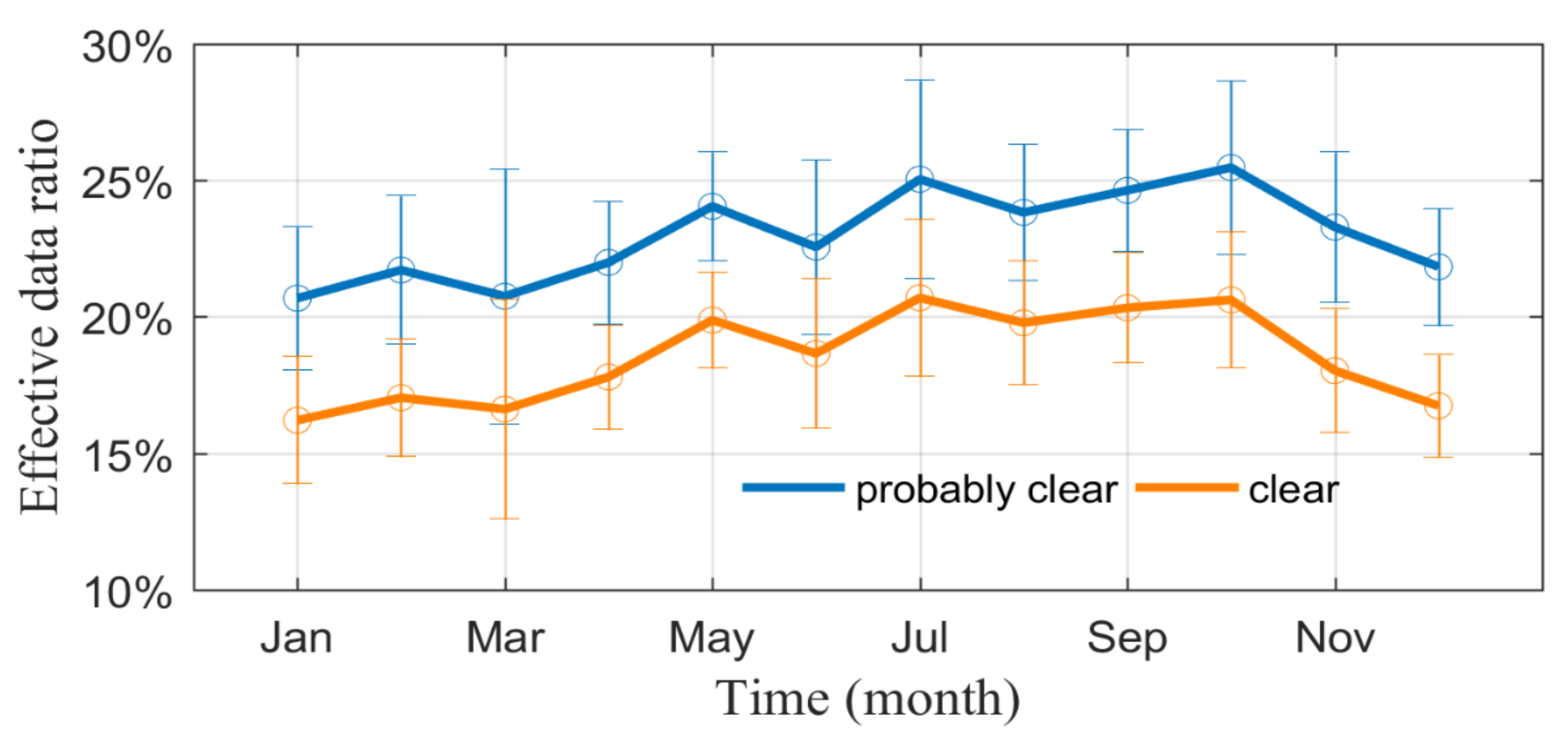
4.2.1. Mean State and Diurnal Variability
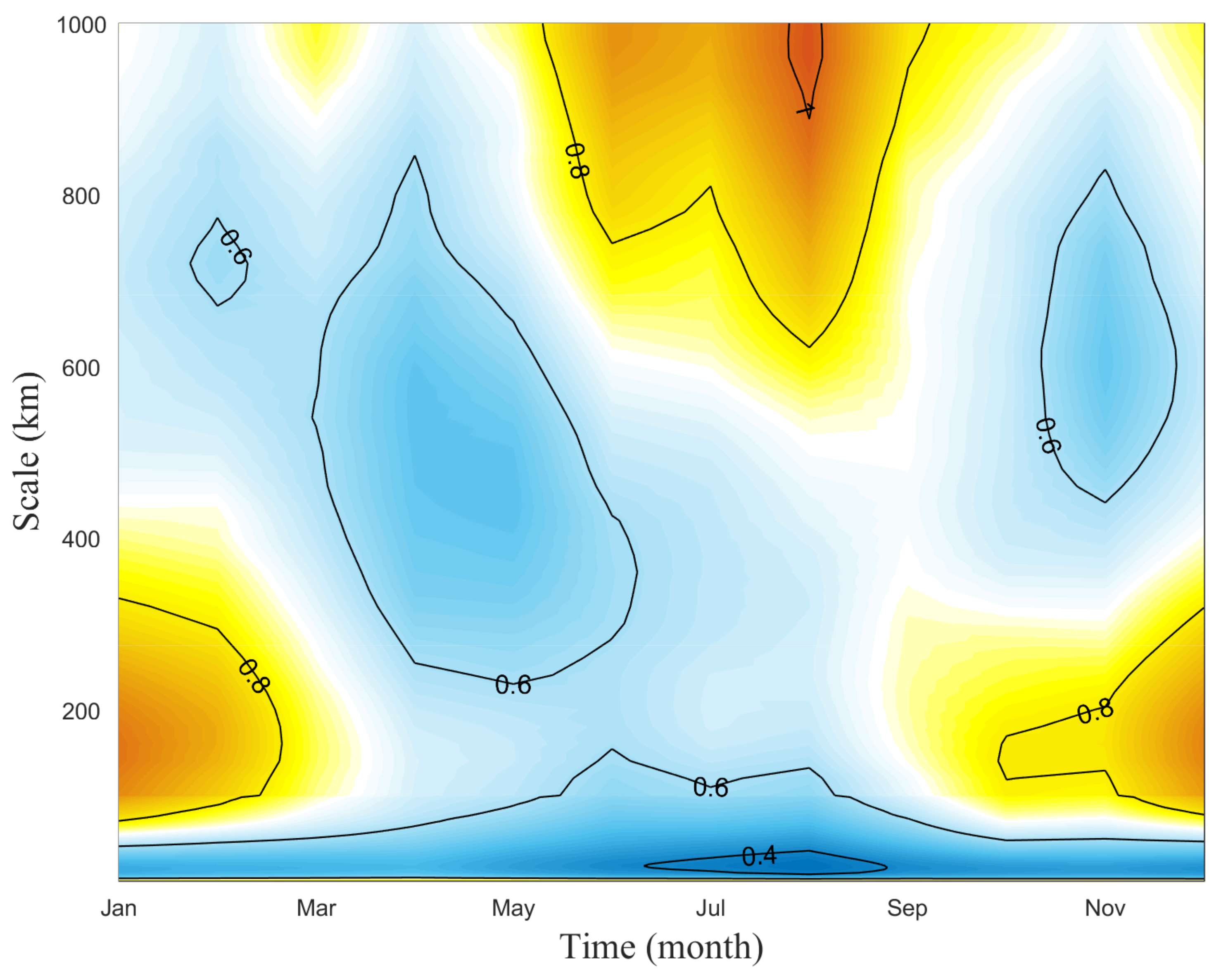
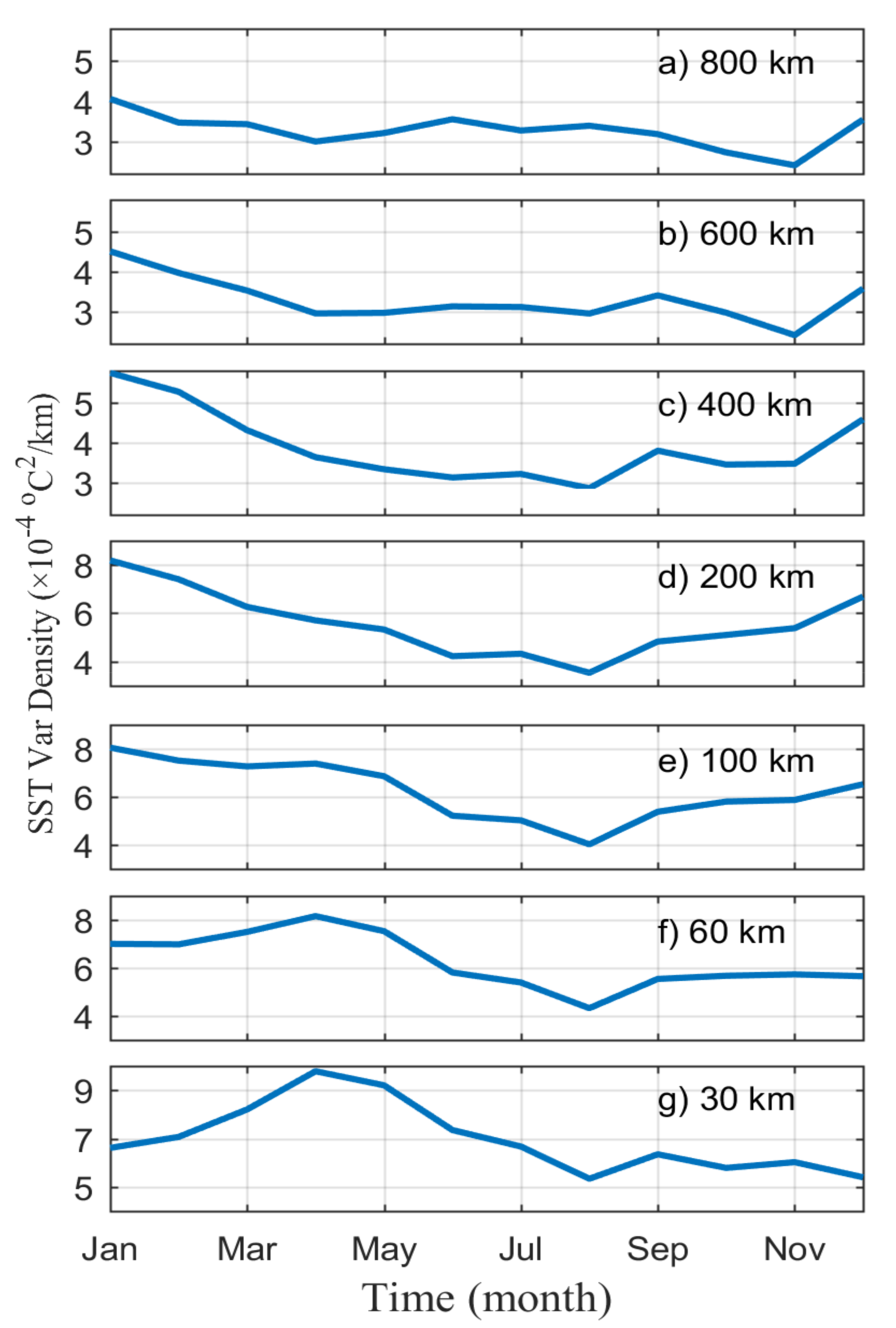
4.2.2. Seasonal Variability
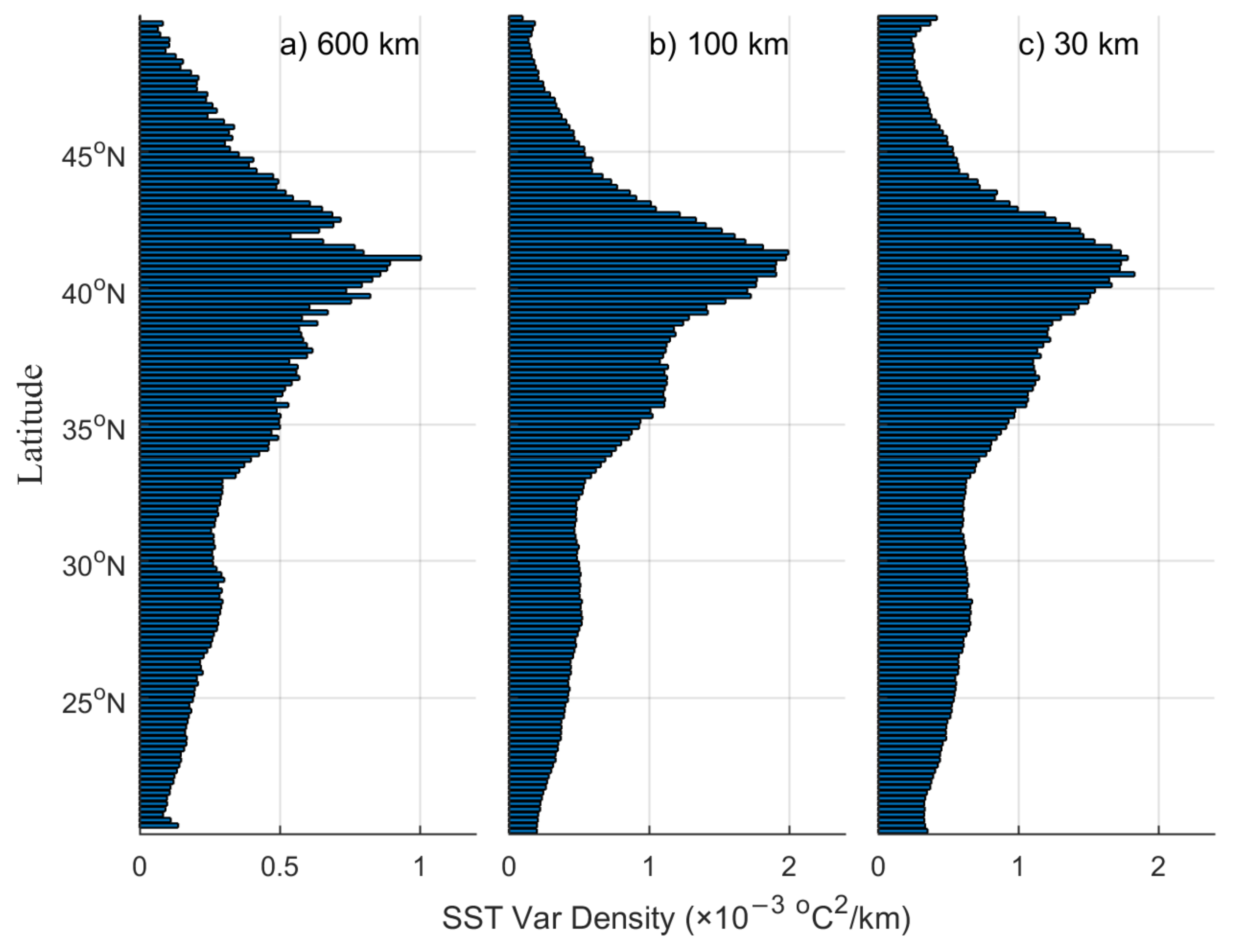
4.2.3. Latitudinal Variability
5. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kolmogrov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR. 1941, 30, 299–303. [Google Scholar]
- Kraichnan, R.H. Inertial ranges in two-dimensional turbulence. Phys. Fluids. 1967, 10, 1417–1423. [Google Scholar] [CrossRef]
- Charney, J.G. Geostrophic turbulence. J. Atmos. Sci. 1971, 28, 1087–1095. [Google Scholar] [CrossRef]
- Blumen, W. Uniform potential vorticity flow. Part I: Theory of wave interactions and two-dimensional turbulence. J. Atmos. Sci. 1978, 35, 774–783. [Google Scholar] [CrossRef]
- Klein, P.; Treguier, A.M.; Hua, B.L. Three-dimensional stirring of thermohaline fronts. J. Mar. Res. 1998, 56, 589–612. [Google Scholar] [CrossRef]
- Gage, K.S. Evidence for a k-5/3 law inertial range in mesoscale two-dimensional turbulence. J. Atmos. Sci. 1979, 36, 1950–1954. [Google Scholar] [CrossRef]
- Nastrom, G.D.; Gage, K.S. A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 1985, 42, 950–960. [Google Scholar] [CrossRef]
- Lindborg, E. Can the atmospheric kinetic energy spectrum be explained by two-dimensional turbulence? J. Fluid Mech. 1999, 388, 259–288. [Google Scholar] [CrossRef]
- Scott, R.B.; Wang, F. Direct evidence of an oceanic inverse kinetic energy cascade from satellite altimetry. J. Phys. Oceanogr. 2005, 35, 1650–1666. [Google Scholar] [CrossRef]
- Callies, J.; Ferrari, R. Interpreting energy and tracer spectra of upper-ocean turbulence in the submesoscale range (1–200 km). J. Phys. Oceanogr. 2013, 43, 2456–2474. [Google Scholar] [CrossRef]
- McCaffrey, K.; Fox-Kemper, B.; Forget, G. Estimates of ocean macroturbulence: Structure function and spectral slope from Argo profiling floats. J. Phys. Oceanogr. 2015, 45, 1773–1793. [Google Scholar] [CrossRef]
- Cao, C.; DeLuccia, F.; Xiong, X.; Wolfe, R.; Weng, F. Early on- orbit performance of the Visible Infrared Imaging Radiometer Suite (VIIRS) onboard the Suomi National Polar-orbiting Partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1142–1156. [Google Scholar] [CrossRef]
- Lee, E.L.; Miller, S.D.; Turk, F.J. The NPOESS VIIRS day/night visible sensor. Bull. Am. Meteorol. Soc. 2010, 87, 191–199. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California Current System. Part III: Energy balance and flux. J. Phys. Oceanogr. 2008, 38, 2256–2269. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, S.P.; Sasaki, H.; Sasai, Y. Seasonal mesoscale and submesoscale eddy variability along the North Pacific Subtropical Countercurrent. J. Phys. Oceanogr. 2014, 44, 3079–3098. [Google Scholar] [CrossRef]
- Callies, J.; Ferrari, R.; Klymak, J.; Gula, J. Seasonality in submesoscale turbulence. Nat. Commun. 2015, 6, 6862. [Google Scholar] [CrossRef]
- Rocha, C.B.; Gille, S.T.; Chereskin, T.K.; Menemenlis, D. Seasonality of submesoscale dynamics in the Kuroshio Extension. Geophys. Res. Lett. 2016, 43, 11304–11311. [Google Scholar] [CrossRef]
- Sasaki, H.; Klein, P.; Sasai, Y.; Qiu, B. Regionality and seasonality of submesoscale and mesoscale turbulence in the North Pacific Ocean. Ocean Dynam. 2017, 67, 1195–1216. [Google Scholar] [CrossRef]
- Zhong, Y.; Bracco, A.; Tian, J.; Dong, J.; Zhao, W.; Zhang, Z. Observed and simulated submesoscale vertical pump of an anticyclonic eddy in the South China Sea. Sci. Rep. 2017, 7, 44011. [Google Scholar] [CrossRef]
- Vogelzang, J.; King, G.P.; Stoffelen, A. Spatial variances of wind fields and their relation to second-order structure functions and spectra. J. Geophys. Res. Oceans 2015, 120, 1048–1064. [Google Scholar] [CrossRef]
- Yu, K.; Dong, C.; King, G.P. Turbulent kinetic energy of the ocean winds over the Kuroshio Extension from QuikSCAT winds (1999–2009). J. Geophys. Res. Oceans 2017, 122, 4482–4499. [Google Scholar] [CrossRef]
- Kelly, K.; Small, R.; Samelson, R.; Qiu, B.; Joyce, T.; Kwon, Y.; Cronin, M. Western boundary currents and frontal air-sea interaction: Gulf stream and Kuroshio extension. J. Clim. 2010, 23, 5644–5667. [Google Scholar] [CrossRef]
- Booth, J.F.; Thompson, L.; Patoux, J.; Kelly, K.A.; Dickinson, S. The signature of the midlatitude tropospheric storm tracks in the surface winds. J. Clim. 2010, 23, 1160–1174. [Google Scholar] [CrossRef]
- Wyrtki, K.; Magaard, L.; Hagar, J. Eddy energy in the oceans. J. Geophys. Res. Oceans 1976, 81, 2641–2646. [Google Scholar] [CrossRef]
- Qiu, B. Variability and energetics of the Kuroshio Extension and its recirculation gyre from the first two-year TOPEX data. J. Phys. Oceanogr. 1995, 25, 1827–1842. [Google Scholar] [CrossRef]
- Dong, J.; Fox-Kemper, B.; Zhang, H.; Dong, C. The seasonality of submesoscale energy production, content, and cascade. Geophys. Res. Lett. 2020, 47, e2020GL087388. [Google Scholar] [CrossRef]
- Webb, E.K. Ratio of spectrum and structure-function constants in the inertial subrange. Quart. J. Roy. Meteor. Soc. 1964, 90, 344–345. [Google Scholar] [CrossRef]
- Boyd, J.P. The energy spectrum of fronts: Time evolution of shocks in Burgers’ equation. J. Atmos. Sci. 1992, 49, 128–139. [Google Scholar] [CrossRef]
- Erickson, Z.K.; Thompson, A.F.; Callies, J.; Yu, X.; Garabato, A.N.; Klein, P. The vertical structure of open-ocean submesoscale variability during a full seasonal cycle. J. Phys. Oceanogr. 2020, 50, 145–160. [Google Scholar] [CrossRef]
- Nonaka, M.; Nakamura, H.; Tanimoto, Y.; Kagimoto, T.; Sasaki, H. Decadal variability in the Kuroshio–Oyashio extension simulated in an eddy-resolving OGCM. J. Clim. 2006, 19, 1970–1989. [Google Scholar] [CrossRef]
- Jing, Z.; Chang, P.; Shan, X.; Wang, S.; Wu, L.; Kurian, J. Mesoscale SST dynamics in the Kuroshio–Oyashio extension region. J. Phys. Oceanogr. 2019, 49, 1339–1352. [Google Scholar] [CrossRef]
- VanZandt, T.E. A universal spectrum of buoyancy waves in the atmosphere. Geophys. Res. Lett. 1982, 9, 575–578. [Google Scholar] [CrossRef]
- Lilly, D.K. Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 1983, 40, 749–761. [Google Scholar] [CrossRef]
- Vallis, G.K.; Shutts, G.J.; Gray, M.E.B. Balanced mesoscale motion and stratified turbulence forced by convection. Q. J. R. Meteorol. Soc. 1997, 123, 1621–1652. [Google Scholar] [CrossRef]
- Cho, J.Y.N.; Lindborg, E. Horizontal velocity structure functions in the upper troposphere and lower stratosphere: 1. Observations. J. Geophys. Res. 2001, 106, 10223–10232. [Google Scholar] [CrossRef]
- Hamilton, K.; Takahashi, Y.O.; Ohfuchi, W. Mesoscale spectrum of atmospheric motions investigated in a very fine resolution global general circulation model. J. Geophys. Res. 2008, 113, D18110. [Google Scholar] [CrossRef]
- Waite, M.L.; Snyder, C. Mesoscale energy spectra of moist baroclinic waves. J. Atmos. Sci. 2013, 70, 1242–1256. [Google Scholar] [CrossRef]
- D’Asaro, E.; Lee, C.; Rainville, L.; Thomas, L. Enhanced turbulence and energy dissipation at ocean fronts. Science 2011, 332, 318–322. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Qiu, B.; Zhao, W.; Chang, P.; Wu, D.; Wan, X. Observed 3D structure, generation, and dissipation of oceanic mesoscale eddies in the South China Sea. Sci. Rep. 2016, 6, 24349. [Google Scholar] [CrossRef]
- Menemenlis, D.; Campin, J.; Heimbach, P.; Hill, C.; Lee, T.; Nguyen, A.; Schodlok, M.; Zhang, H. ECCO2: High resolution global ocean and sea ice data synthesis. Mercator Ocean Quart. Newsl. 2008, 31, 13–21. [Google Scholar]
- Forget, G.; Campin, J.-M.; Heimbach, P.; Hill, C.N.; Ponte, R.M.; Wunsch, C. ECCO version 4: An integrated framework for non-linear inverse modeling and global ocean state estimation. Geosci. Model Dev. 2015, 8, 3653–3743. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Dong, C.; Wang, J.; Cheng, X.; Yu, Y. Statistical Characteristics of the Multiscale SST Fractal Structure over the Kuroshio Extension Region Using VIIRS Data. Remote Sens. 2023, 15, 881. https://doi.org/10.3390/rs15040881
Yu K, Dong C, Wang J, Cheng X, Yu Y. Statistical Characteristics of the Multiscale SST Fractal Structure over the Kuroshio Extension Region Using VIIRS Data. Remote Sensing. 2023; 15(4):881. https://doi.org/10.3390/rs15040881
Chicago/Turabian StyleYu, Kai, Changming Dong, Jin Wang, Xuhua Cheng, and Yi Yu. 2023. "Statistical Characteristics of the Multiscale SST Fractal Structure over the Kuroshio Extension Region Using VIIRS Data" Remote Sensing 15, no. 4: 881. https://doi.org/10.3390/rs15040881
APA StyleYu, K., Dong, C., Wang, J., Cheng, X., & Yu, Y. (2023). Statistical Characteristics of the Multiscale SST Fractal Structure over the Kuroshio Extension Region Using VIIRS Data. Remote Sensing, 15(4), 881. https://doi.org/10.3390/rs15040881






