Examining Thresholding and Factors Impacting Snow Cover Detection Using Nighttime Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study Areas
2.2. Data Collection
2.3. Data Preparation
2.4. Methodology
3. Results
3.1. Overall Thresholding Results
3.2. Land Cover Discrimination
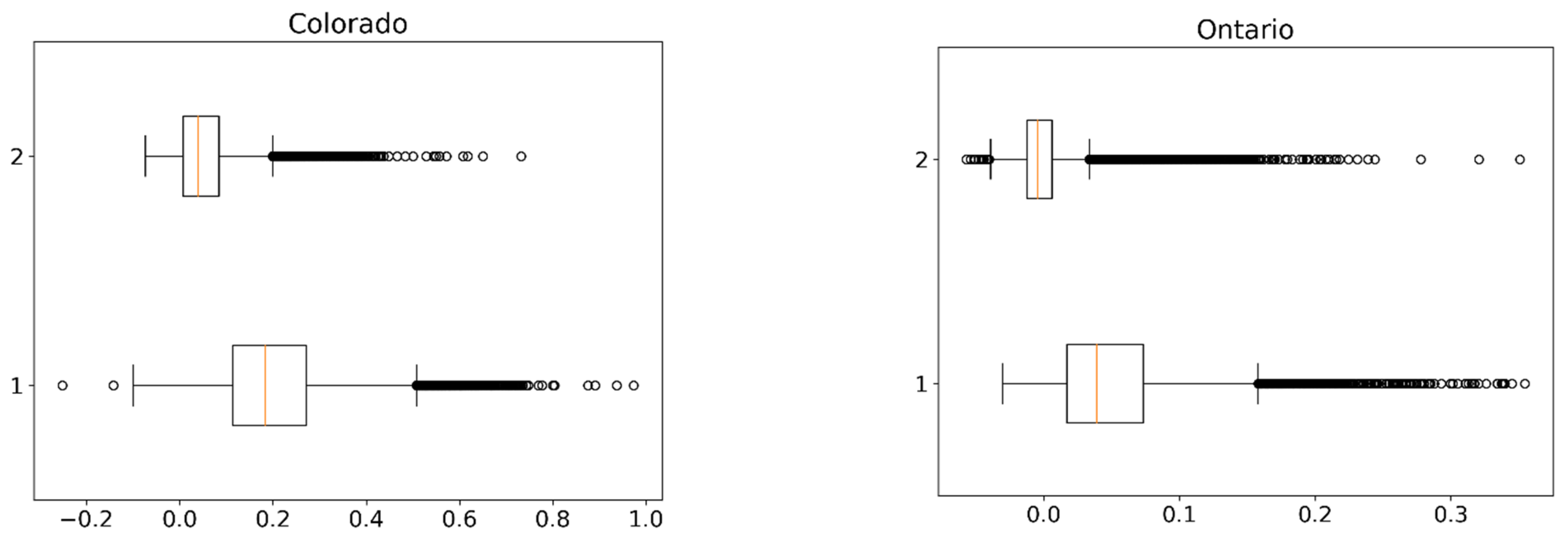
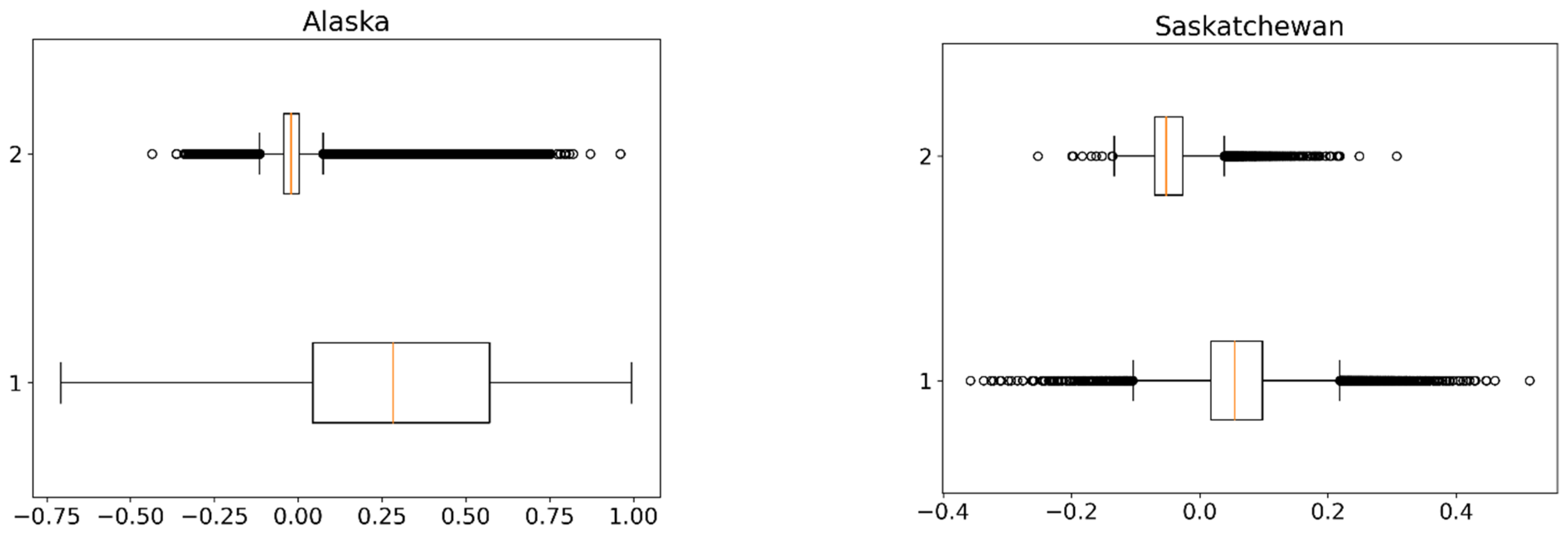
3.3. NDVI Influence
3.4. Additional Factors
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Levis, S.; Bonan, G.B.; Lawrence, P.J. Present-Day Springtime High-Latitude Surface Albedo as a Predictor of Simulated Climate Sensitivity. Geophys. Res. Lett. 2007, 34, 1–4. [Google Scholar] [CrossRef]
- Musselman, K.N.; Clark, M.P.; Liu, C.; Ikeda, K.; Rasmussen, R. Slower Snowmelt in a Warmer World. Nat. Clim. Chang. 2017, 7, 214–219. [Google Scholar] [CrossRef]
- Foster, J.L.; Hall, D.K. Observations of Snow and Ice Features during the Polar Winter Using Moonlight as a Source of Illumination. Remote Sens. Environ. 1991, 37, 77–88. [Google Scholar] [CrossRef]
- Da Ronco, P.; Avanzi, F.; De Michele, C.; Notarnicola, C.; Schaefli, B. Comparing MODIS Snow Products Collection 5 with Collection 6 over Italian Central Apennines. Int. J. Remote Sens. 2020, 41, 4174–4205. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. MODIS/Aqua Snow Cover Daily L3 Global 500 m Grid, Version 61; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA. [CrossRef]
- Miller, S.D.; Straka, W.; Mills, S.P.; Elvidge, C.D.; Lee, T.F.; Solbrig, J.; Walther, A.; Heidinger, A.K.; Weiss, S.C. Illuminating the Capabilities of the Suomi National Polar-Orbiting Partnership (NPP) Visible Infrared Imaging Radiometer Suite (VIIRS) Day/Night Band. Remote Sens. 2013, 5, 6717–6766. [Google Scholar] [CrossRef]
- Huang, Y.; Song, Z.; Yang, H.; Yu, B.; Liu, H.; Che, T.; Chen, J.; Wu, J.; Shu, S.; Peng, X.; et al. Snow Cover Detection in Mid-Latitude Mountainous and Polar Regions Using Nighttime Light Data. Remote Sens. Environ. 2022, 268, 112766. [Google Scholar] [CrossRef]
- Lee, T.E.; Miller, S.D.; Turk, F.J.; Schueler, C.; Julian, R.; Deyo, S.; Dills, P.; Wang, S. The NPOESS VIIRS Day/Night Visible Sensor. Bull. Am. Meteorol. Soc. 2006, 87, 191–200. [Google Scholar] [CrossRef]
- Foster, J.L. Observations of the Earth Using Nighttime Visible Imagery; Aitken, G.W., Ed.; SPIE: Arlington, MA, USA, 1983; pp. 187–193. [Google Scholar]
- Wiesnet, D.R.; Mcginnis, J.; Matson, M.; Pritchard, J.A. Evaluation of Hcmm Satellite Data for Estuarine Tidal Circulation Patterns and Thermal Inertia Soil Moisture Measurements; Interim; Final Report; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1981. [Google Scholar]
- Liu, D.; Zhang, Q.; Wang, J.; Wang, Y.; Shen, Y.; Shuai, Y. The Potential of Moonlight Remote Sensing: A Systematic Assessment with Multi-Source Nightlight Remote Sensing Data. Remote Sens. 2021, 13, 4639. [Google Scholar] [CrossRef]
- Yin, D.; Cao, X.; Chen, X.; Shao, Y.; Chen, J. Comparison of Automatic Thresholding Methods for Snow-Cover Mapping Using Landsat TM Imagery. Int. J. Remote Sens. 2013, 34, 6529–6538. [Google Scholar] [CrossRef]
- Levin, N. The Impact of Seasonal Changes on Observed Nighttime Brightness from 2014 to 2015 Monthly VIIRS DNB Composites. Remote Sens. Environ. 2017, 193, 150–164. [Google Scholar] [CrossRef]
- LAADS DAAC VIIRS/NPP Day/Night Band 6-Min L1 Swath SDR 750m—LAADS DAAC. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/products/NPP_VDNES_L1#overview (accessed on 6 May 2022).
- Buchhorn, M.; Smets, B.; Bertels, L.; Roo, B.D.; Lesiv, M.; Tsendbazar, N.-E.; Herold, M.; Fritz, S. Copernicus Global Land Service: Land Cover 100 m: Collection 3: Epoch 2018: Globe 2020. Available online: https://zenodo.org/record/3518038 (accessed on 7 May 2022).
- Buchhorn, M.; Smets, B.; Bertels, L.; Roo, B.D.; Lesiv, M.; Tsendbazar, N.-E.; Herold, M.; Fritz, S. Copernicus Global Land Service: Land Cover 100m: Collection 3: Epoch 2019: Globe 2020. Available online: https://zenodo.org/record/3939050 (accessed on 7 May 2022).
- Vermote, E.; Wolfe, R. MODIS/Terra Surface Reflectance Daily L2G Global 1 km and 500 m SIN Grid V061 2021. Available online: https://lpdaac.usgs.gov/products/mod09gav061/ (accessed on 7 May 2022).
- Huang, Y.; Liu, H.; Yu, B.; Wu, J.; Kang, E.L.; Xu, M.; Wang, S.; Klein, A.; Chen, Y. Improving MODIS Snow Products with a HMRF-Based Spatio-Temporal Modeling Technique in the Upper Rio Grande Basin. Remote Sens. Environ. 2018, 204, 568–582. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Li, C.H.; Tam, P.K.S. An Iterative Algorithm for Minimum Cross Entropy Thresholding. Pattern Recognit. Lett. 1998, 19, 771–776. [Google Scholar] [CrossRef]
- Yen, J.-C.; Chang, F.-J.; Chang, S. A New Criterion for Automatic Multilevel Thresholding. IEEE Trans. Image Process. 1995, 4, 370–378. [Google Scholar] [CrossRef] [PubMed]
- Zack, G.W.; Rogers, W.E.; Latt, S.A. Automatic Measurement of Sister Chromatid Exchange Frequency. J. Histochem. Cytochem. 1977, 25, 741–753. [Google Scholar] [CrossRef] [PubMed]
- Glasbey, C.A. An Analysis of Histogram-Based Thresholding Algorithms. CVGIP Graph. Models Image Process. 1993, 55, 532–537. [Google Scholar] [CrossRef]
- Ridler, T.W.; Calvard, S. Picture Thresholding Using an Iterative Selection Method. IEEE Trans. Syst. Man Cybern. 1978, 8, 630–632. [Google Scholar] [CrossRef]
- Sekertekin, A. A Survey on Global Thresholding Methods for Mapping Open Water Body Using Sentinel-2 Satellite Imagery and Normalized Difference Water Index. Arch. Comput. Methods Eng. 2021, 28, 1335–1347. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Ménard, C.B.; Luojus, K.; Lemmetyinen, J.; Pulliainen, J. Evaluation of Snow Products over the Tibetan Plateau. Hydrol. Process. 2015, 29, 3247–3260. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. MODIS/Terra Snow Cover 5-Min L2 Swath 500 m, Version 5; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2006. [Google Scholar]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Zhang, G.; Che, T.; Yan, W.; Ye, M.; Ma, N. Ground-Based Evaluation of MODIS Snow Cover Product V6 across China: Implications for the Selection of NDSI Threshold. Sci. Total Environ. 2019, 651, 2712–2726. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote Sensing of Snow—A Review of Available Methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Webster, C.; Jonas, T. Influence of Canopy Shading and Snow Coverage on Effective Albedo in a Snow-Dominated Evergreen Needleleaf Forest. Remote Sens. Environ. 2018, 214, 48–58. [Google Scholar] [CrossRef]
- Buchhorn, M.; Smets, B.; Bertels, L.; Roo, B.D.; Lesiv, M.; Tsendbazar, N.-E.; Li, L.; Tarko, A. Copernicus Global Land Service: Land Cover 100 m: Version 3 Globe 2015–2019: Product User Manual; Zenodo: Geneve, Switzerland, September 2020. [Google Scholar] [CrossRef]
- Tong, K.P.; Kyba, C.C.M.; Heygster, G.; Kuechly, H.U.; Notholt, J.; Kolláth, Z. Angular Distribution of Upwelling Artificial Light in Europe as Observed by Suomi–NPP Satellite. J. Quant. Spectrosc. Radiat. Transf. 2020, 249, 107009. [Google Scholar] [CrossRef]
- Román, M.O.; Wang, Z.; Sun, Q.; Kalb, V.; Miller, S.D.; Molthan, A.; Schultz, L.; Bell, J.; Stokes, E.C.; Pandey, B.; et al. NASA’s Black Marble Nighttime Lights Product Suite. Remote Sens. Environ. 2018, 210, 113–143. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K.; Román, M.O. MODIS Snow Products Collection 6.1 User Guide; National Snow and Ice Data Center: Boulder, CO, USA, 2019; Volume 66. [Google Scholar]
- Levin, N.; Kyba, C.C.M.; Zhang, Q.; Sánchez de Miguel, A.; Román, M.O.; Li, X.; Portnov, B.A.; Molthan, A.L.; Jechow, A.; Miller, S.D.; et al. Remote Sensing of Night Lights: A Review and an Outlook for the Future. Remote Sens. Environ. 2020, 237, 111443. [Google Scholar] [CrossRef]
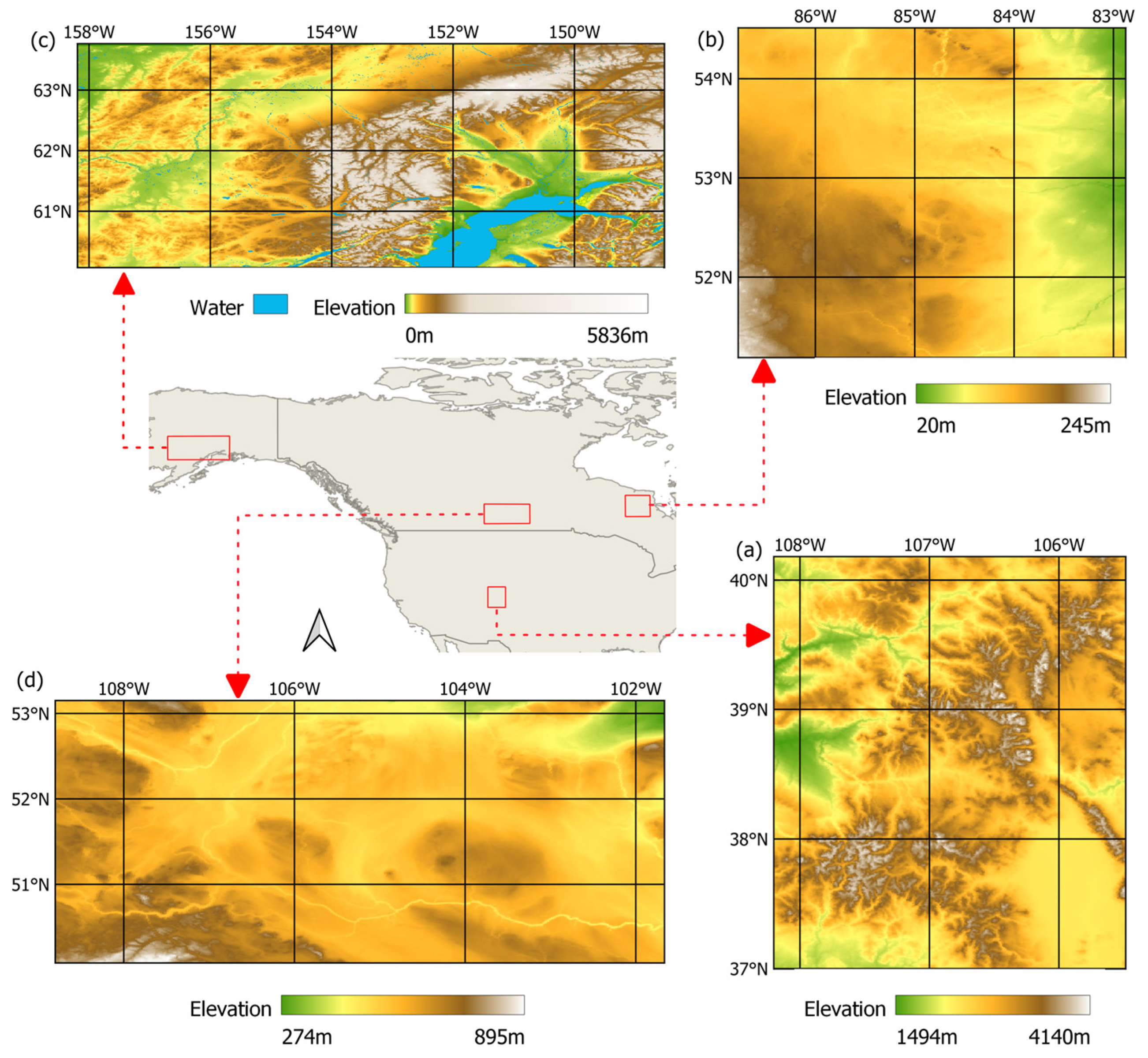
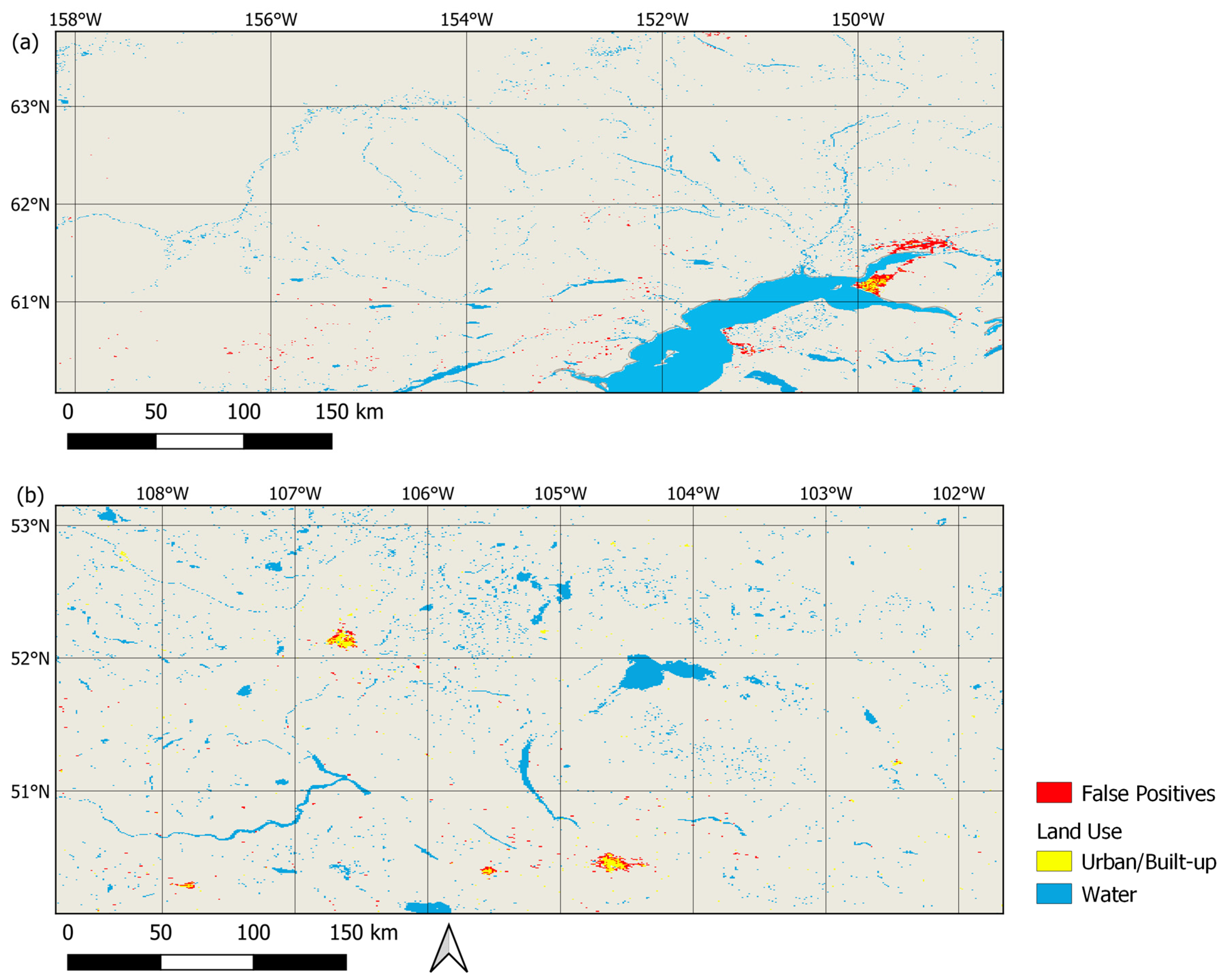
| Case Study | Location | VIIRS/MODIS Collection Date | VIIRS Time (Local) |
|---|---|---|---|
| a | Colorado | 2 March 2018 | 01:30 |
| b | Ontario | 2 March 2018 | 03:24 |
| c | Alaska | 13 October 2019 | 05:06 |
| d | Saskatchewan | 21 March 2019 | 04:06 |
| Dataset | Dates | Resolution |
|---|---|---|
| VIIRS DNB 1 | 2018–2019 | 750 m |
| MODIS Snow Cover 2 | 2018–2019 | 500 m |
| MODIS NDVI 3 | 2018–2019 | 500 m |
| Copernicus Land Use 4 | 2018–2019 | 10 m |
| Case Study | Thresholding Algorithm | TP | TN | FP | FN | Overall Accuracy | Kappa |
|---|---|---|---|---|---|---|---|
| a. Colorado | Otsu | 28.42 | 31.32 | 0.14 | 40.13 | 59.73 | 0.31 |
| Li | 36.86 | 31.19 | 0.26 | 31.68 | 68.05 | 0.42 | |
| Yen | 0.03 | 31.44 | 0.01 | 68.51 | 31.47 | 0.00 | |
| Triangle | 7.98 | 31.42 | 0.04 | 60.57 | 39.40 | 0.08 | |
| Minimum | 0.01 | 31.45 | 0.00 | 68.54 | 31.45 | 0.00 | |
| Mean | 38.36 | 31.15 | 0.30 | 30.19 | 69.51 | 0.44 | |
| Isodata | 29.73 | 31.30 | 0.16 | 38.82 | 61.02 | 0.32 | |
| b. Ontario | Otsu | 62.34 | 0.00 | 0.00 | 37.66 | 62.34 | n/a |
| Li | 69.17 | 0.00 | 0.00 | 30.83 | 69.17 | n/a | |
| Yen | 77.91 | 0.00 | 0.00 | 22.09 | 77.91 | n/a | |
| Triangle | 0.07 | 0.00 | 0.00 | 99.93 | 0.07 | n/a | |
| Minimum | 0.00 | 0.00 | 0.00 | 100.00 | 0.00 | n/a | |
| Mean | 54.75 | 0.00 | 0.00 | 45.25 | 54.75 | n/a | |
| Isodata | 64.97 | 0.00 | 0.00 | 35.03 | 64.94 | n/a | |
| c. Alaska | Otsu | 19.17 | 40.25 | 0.22 | 40.36 | 59.42 | 0.27 |
| Li | 25.72 | 40.16 | 0.31 | 33.81 | 65.88 | 0.37 | |
| Yen | 0.01 | 40.42 | 0.05 | 59.53 | 40.42 | 0.00 | |
| Triangle | 0.20 | 40.39 | 0.08 | 59.33 | 40.59 | 0.00 | |
| Minimum | 0.00 | 40.47 | 0.00 | 59.53 | 40.47 | 0.00 | |
| Mean | 30.50 | 40.03 | 0.44 | 29.03 | 70.53 | 0.45 | |
| Isodata | 23.38 | 40.19 | 0.27 | 36.15 | 63.57 | 0.34 | |
| d. Saskatchewan | Otsu | 55.10 | 22.26 | 0.17 | 22.47 | 77.36 | 0.52 |
| Li | 59.37 | 22.21 | 0.22 | 18.20 | 81.58 | 0.59 | |
| Yen | 0.02 | 22.38 | 0.04 | 77.55 | 22.41 | 0.00 | |
| Triangle | 0.15 | 22.34 | 0.08 | 77.42 | 22.50 | 0.00 | |
| Minimum | 0.00 | 22.42 | 0.00 | 77.57 | 22.42 | 0.00 | |
| Mean | 52.68 | 22.27 | 0.16 | 24.89 | 74.95 | 0.48 | |
| Isodata | 55.10 | 22.26 | 0.17 | 22.47 | 77.36 | 0.52 |
| Case Study | Thresholding Algorithm | TP | TN | FP | FN | Overall Accuracy | Kappa |
|---|---|---|---|---|---|---|---|
| a. Colorado | Shrubs | 25.45 | 58.43 | 0.73 | 15.39 | 83.88 | 0.65 |
| Herbaceous vegetation | 46.45 | 41.22 | 0.46 | 11.88 | 87.67 | 0.76 | |
| Cultivated and managed vegetation/agriculture | 7.72 | 86.68 | 0.64 | 4.95 | 94.40 | 0.70 | |
| Bare/sparse vegetation | 73.37 | 24.09 | 0.13 | 2.37 | 97.50 | 0.93 | |
| Closed forest, evergreen needle leaf | 22.81 | 15.33 | 0.08 | 61.77 | 38.15 | 0.10 | |
| Closed forest, deciduous broad leaf | 70.13 | 0.11 | 0.03 | 29.74 | 70.24 | 0.00 | |
| Closed forest, unknown | 43.42 | 20.74 | 0.14 | 35.69 | 64.16 | 0.33 | |
| Open forest, evergreen needle leaf | 34.72 | 21.94 | 0.18 | 43.15 | 56.66 | 0.26 | |
| Open forest, deciduous broad leaf | 72.95 | 0.07 | 0.00 | 26.99 | 73.01 | 0.00 | |
| Open forest, unknown | 43.14 | 29.40 | 0.24 | 27.22 | 75.86 | 0.54 | |
| b. Ontario | Shrubs | 85.81 | 0.00 | 0.00 | 14.19 | 85.81 | n/a |
| Herbaceous vegetation | 94.17 | 0.00 | 0.00 | 5.83 | 94.17 | n/a | |
| Herbaceous wetland | 97.09 | 0.00 | 0.00 | 2.91 | 97.09 | n/a | |
| Closed forest, evergreen needle leaf | 36.94 | 0.00 | 0.00 | 63.06 | 36.94 | n/a | |
| Open forest, evergreen needle leaf | 63.92 | 0.00 | 0.00 | 36.08 | 63.92 | n/a | |
| Open forest, unknown | 74.73 | 0.00 | 0.00 | 25.27 | 74.73 | n/a | |
| c. Alaska | Shrubs | 20.65 | 56.49 | 0.25 | 22.61 | 77.14 | 0.50 |
| Herbaceous vegetation | 48.50 | 33.71 | 0.31 | 17.48 | 82.21 | 0.65 | |
| Bare/sparse vegetation | 84.51 | 1.14 | 0.28 | 14.06 | 85.66 | 0.12 | |
| Snow and Ice | 78.48 | 0.18 | 0.03 | 21.30 | 78.67 | 0.01 | |
| Herbaceous wetland | 3.37 | 82.83 | 2.28 | 11.52 | 86.20 | 0.27 | |
| Closed forest, evergreen needle leaf | 6.13 | 38.31 | 0.35 | 55.22 | 44.44 | 0.07 | |
| Closed forest, mixed | 0.95 | 69.95 | 2.47 | 26.63 | 70.90 | 0.00 | |
| Closed forest, unknown | 6.66 | 56.01 | 0.74 | 36.59 | 62.67 | 0.16 | |
| Open forest, evergreen needle leaf | 11.60 | 31.55 | 0.91 | 55.93 | 43.16 | 0.10 | |
| Open forest, unknown | 12.24 | 58.13 | 0.45 | 29.18 | 70.37 | 0.32 | |
| d. Saskatchewan | Herbaceous vegetation | 48.16 | 37.93 | 0.59 | 13.33 | 86.08 | 0.72 |
| Cultivated and managed vegetation/agriculture | 67.79 | 20.76 | 0.13 | 11.31 | 88.55 | 0.71 | |
| Herbaceous wetland | 62.41 | 20.66 | 0.18 | 16.75 | 83.07 | 0.60 | |
| Closed forest, evergreen needle leaf | 6.43 | 0.08 | 0.00 | 93.50 | 6.50 | 0.00 | |
| Closed forest, deciduous broad leaf | 29.14 | 0.22 | 0.00 | 70.63 | 29.37 | 0.00 | |
| Closed forest, mixed | 3.46 | 0.07 | 0.00 | 96.48 | 3.52 | 0.00 | |
| Closed forest, unknown | 35.92 | 5.77 | 0.00 | 58.31 | 41.69 | 0.07 | |
| Open forest, evergreen needle leaf | 57.12 | 0.92 | 0.00 | 41.96 | 58.04 | 0.02 | |
| Open forest, deciduous broad leaf | 58.94 | 0.26 | 0.00 | 40.80 | 59.20 | 0.01 | |
| Open forest, unknown | 60.25 | 7.63 | 0.08 | 32.03 | 67.88 | 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stopic, R.; Dias, E. Examining Thresholding and Factors Impacting Snow Cover Detection Using Nighttime Images. Remote Sens. 2023, 15, 868. https://doi.org/10.3390/rs15040868
Stopic R, Dias E. Examining Thresholding and Factors Impacting Snow Cover Detection Using Nighttime Images. Remote Sensing. 2023; 15(4):868. https://doi.org/10.3390/rs15040868
Chicago/Turabian StyleStopic, Renato, and Eduardo Dias. 2023. "Examining Thresholding and Factors Impacting Snow Cover Detection Using Nighttime Images" Remote Sensing 15, no. 4: 868. https://doi.org/10.3390/rs15040868
APA StyleStopic, R., & Dias, E. (2023). Examining Thresholding and Factors Impacting Snow Cover Detection Using Nighttime Images. Remote Sensing, 15(4), 868. https://doi.org/10.3390/rs15040868








