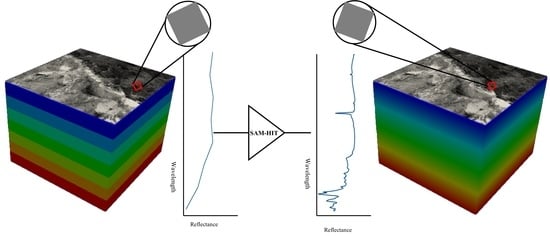
SAM-HIT: A Simulated Annealing Multispectral to Hyperspectral Imagery Data Transformation
Abstract
1. Introduction
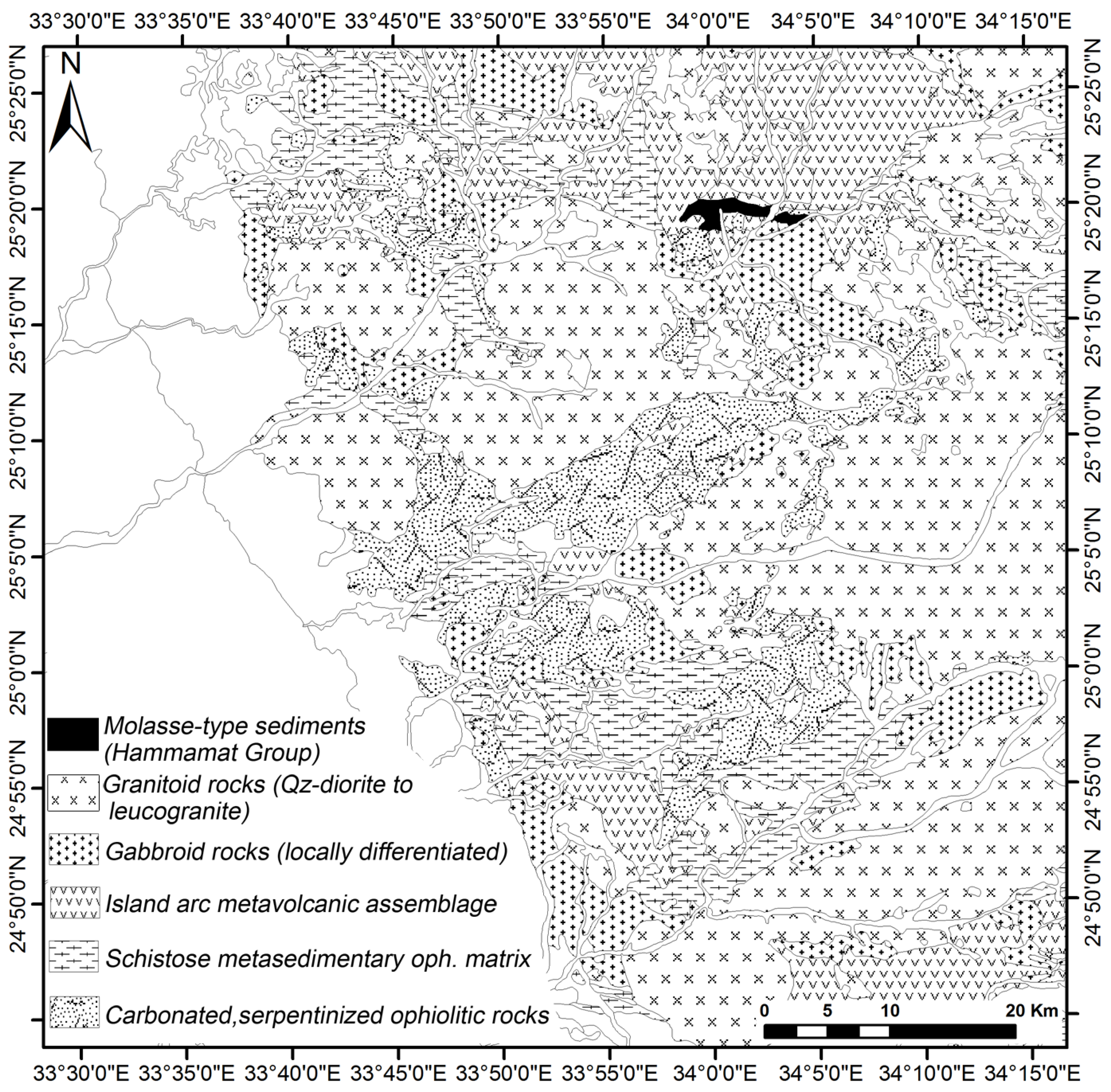
2. Materials and Methods
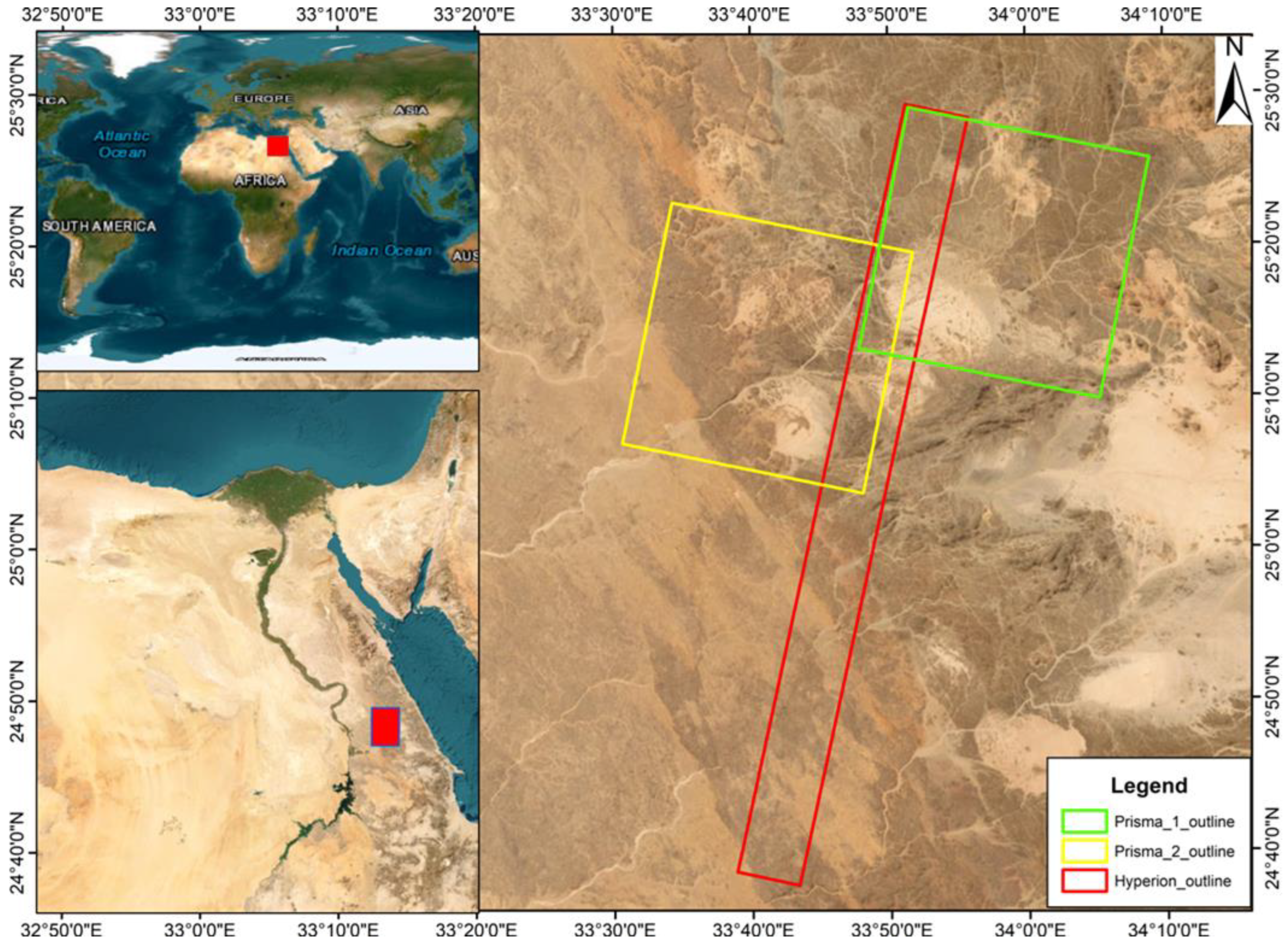
2.1. Data and Method
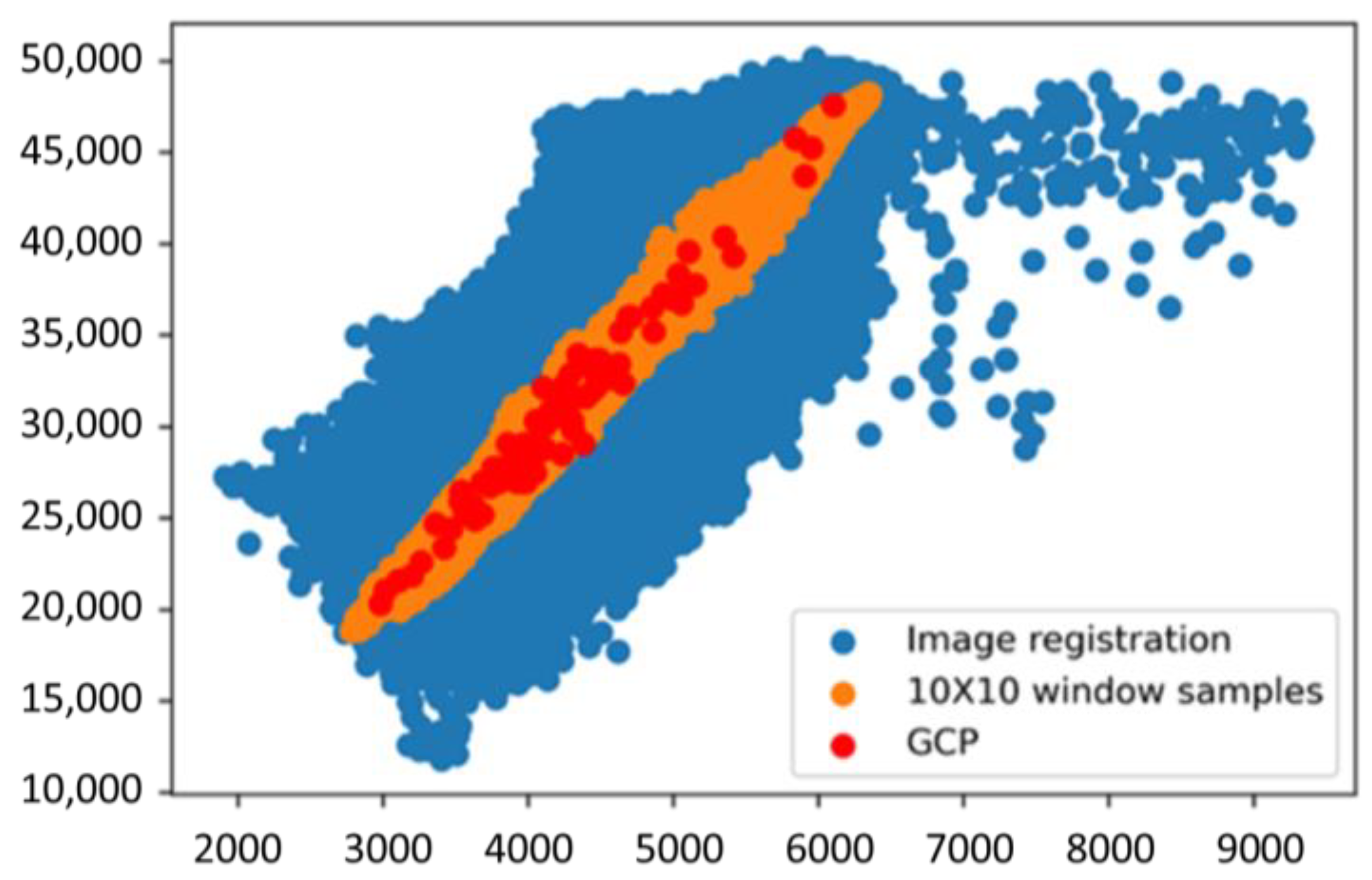
2.2. Pre-Processing of Hyperion and L8 Images
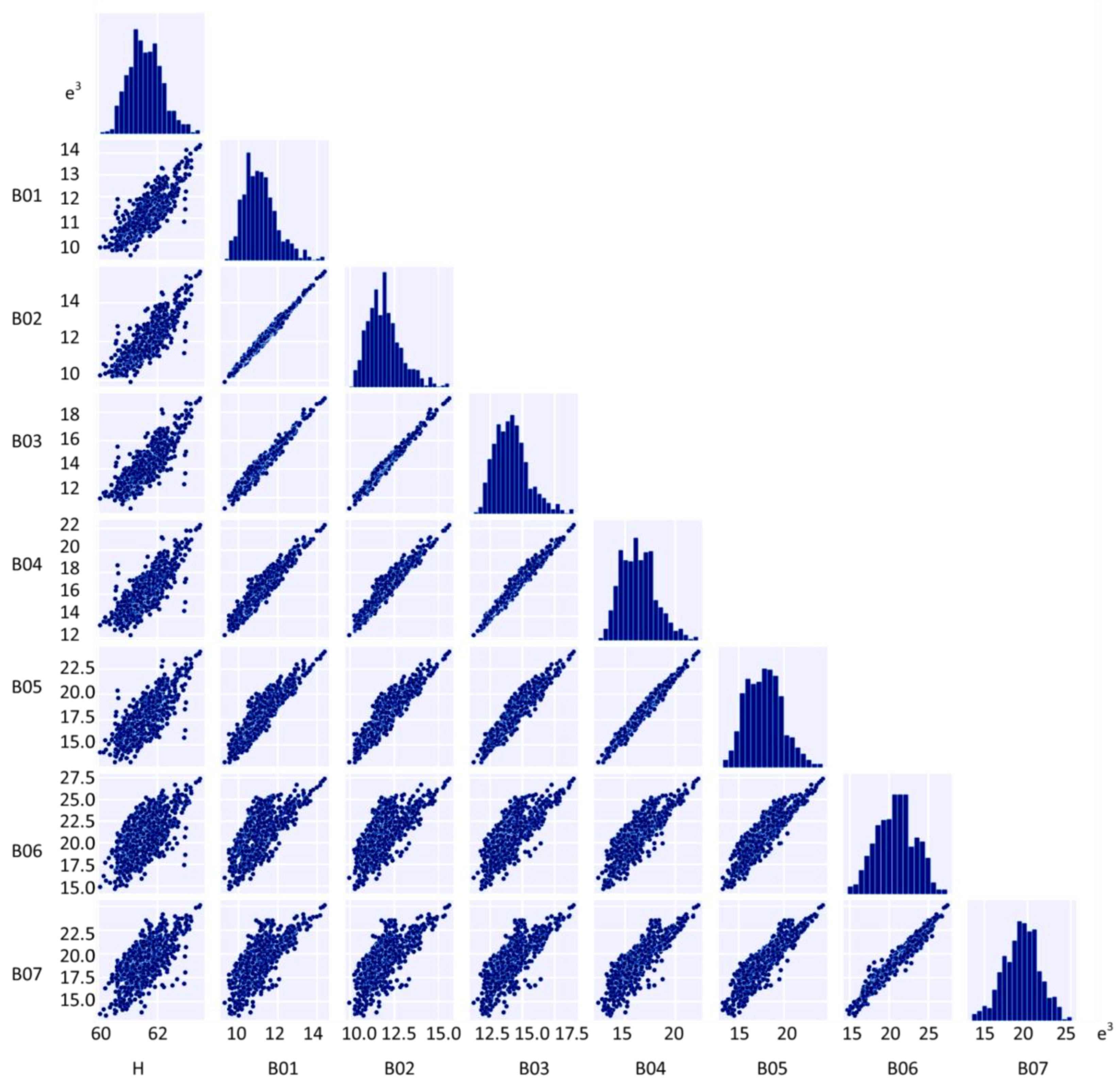
2.3. SAM-HIT Implementation
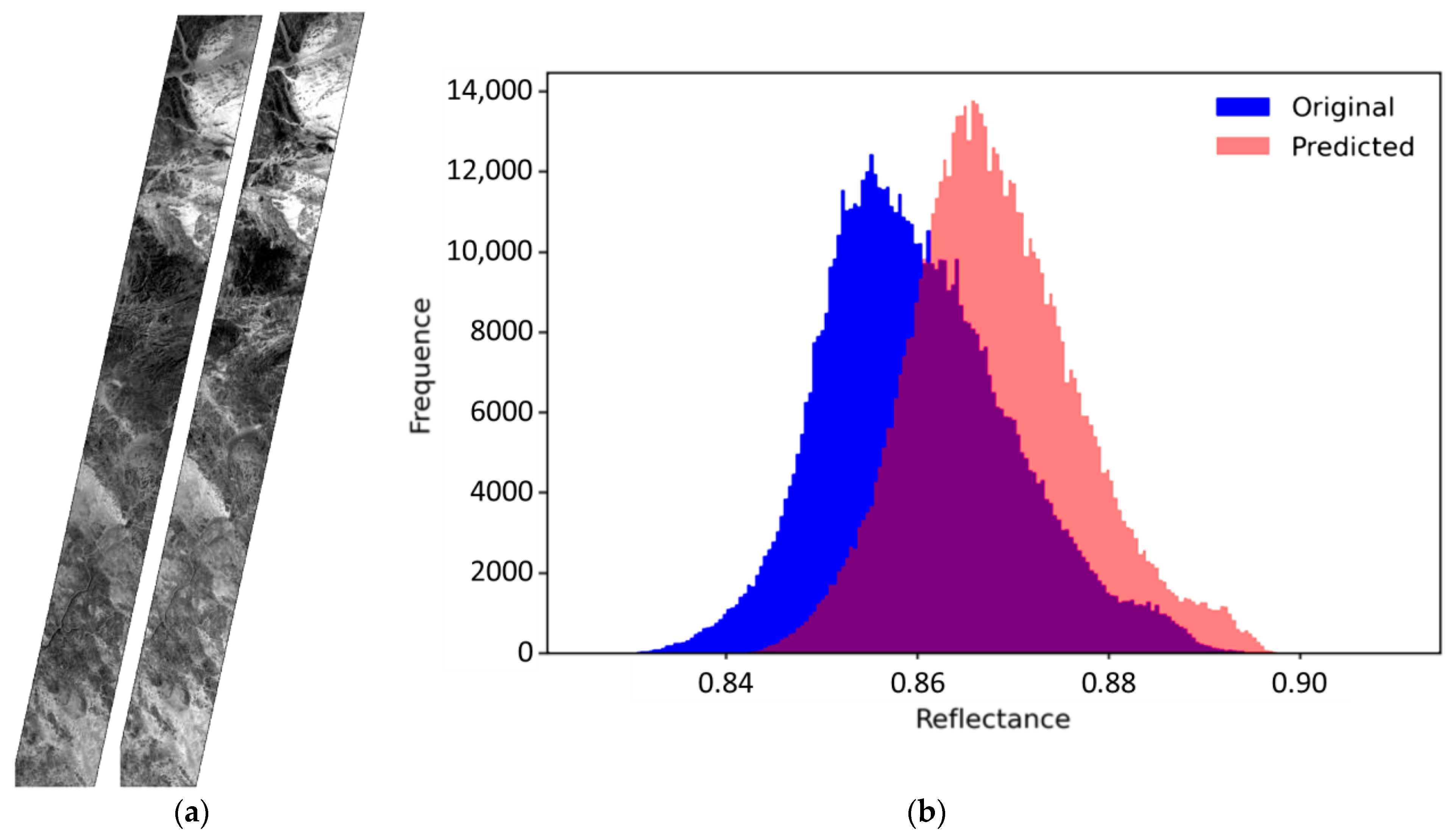
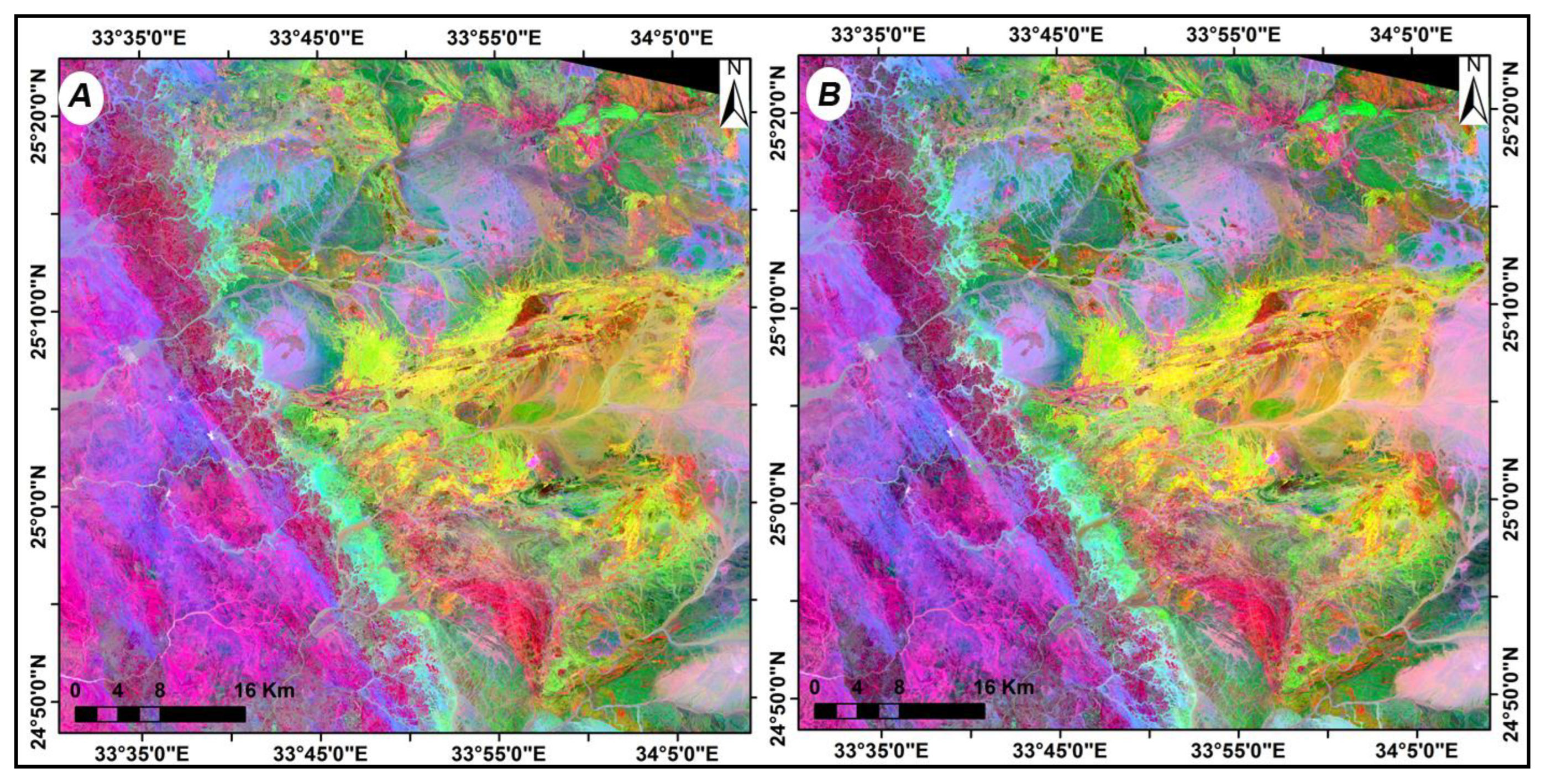
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, F.; Niu, Z.; Sun, G.; Wang, C.; Teng, J. Using Low-spectral-resolution Images to Acquire Simulated Hyperspectral Images. Int. J. Remote Sens. 2008, 29, 2963–2980. [Google Scholar] [CrossRef]
- Berezowski, T.; Chormanski, J.; Chan, J.C. Preliminary Validation of a Method for Simulating Hyperspectral Bands from Multispectral Images. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4283–4286. [Google Scholar]
- Liu, B.; Zhang, L.; Zhang, X.; Zhang, B.; Tong, Q. Simulation of EO-1 Hyperion Data from ALI Multispectral Data Based on the Spectral Reconstruction Approach. Sensors 2009, 9, 3090–3108. [Google Scholar] [CrossRef]
- Hoang, N.T.; Koike, K. Transformation of Landsat Imagery into Pseudo-Hyperspectral Imagery by a Multiple Regression-Based Model with Application to Metal Deposit-Related Minerals Mapping. ISPRS J. Photogramm. Remote Sens. 2017, 133, 157–173. [Google Scholar] [CrossRef]
- Winter, M.E.; Winter, E.M.; Beaven, S.G.; Ratkowski, A.J. Hyperspectral Image Sharpening Using Multispectral Data. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–9. [Google Scholar]
- Cudahy, T.J.; Hewson, R.; Huntington, J.F.; Quigley, M.A.; Barry, P.S. The Performance of the Satellite-Borne Hyperion Hyperspectral VNIR-SWIR Imaging System for Mineral Mapping at Mount Fitton, South Australia. In Proceedings of the IGARSS 2001. Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, Australia, 9–13 July 2001; Volume 1, pp. 314–316. [Google Scholar]
- Jupp, D.; Datt, B.; Lovell, J.; Campbell, S.; King, E. Discussions Around Hyperion Data: Background Notes for the Hyperion Data; CSIRO Earth Observation Centre: Perth, Australia, 2002. [Google Scholar]
- Guarini, R.; Loizzo, R.; Facchinetti, C.; Longo, F.; Ponticelli, B.; Faraci, M.; Dami, M.; Cosi, M.; Amoruso, L.; De Pasquale, V.; et al. Prisma Hyperspectral Mission Products. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 179–182. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Ingber, L. Very Fast Simulated Re-Annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
- Zoheir, B.; Lehmann, B. Listvenite–Lode Association at the Barramiya Gold Mine, Eastern Desert, Egypt. Ore Geol. Rev. 2011, 39, 101–115. [Google Scholar] [CrossRef]
- San, R.T. Hyperspectral Image Processing of eo-1 Hyperion Data for Lithological and Mineralogical Mapping. Middle East Technical University. 2008. Available online: https://etd.lib.metu.edu.tr/upload/3/12610057/index.pdf (accessed on 24 January 2023).
- ITT Visual Information Solutions ENVI User’s Guide; 2009; p. 1272. Available online: https://www.tetracam.com/PDFs/Rec_Cite9.pdf (accessed on 24 January 2023).
- Farifteh, J.; Nieuwenhuis, W.; García-Meléndez, E. Mapping Spatial Variations of Iron Oxide By-Product Minerals from EO-1 Hyperion. Int. J. Remote Sens. 2013, 34, 682–699. [Google Scholar] [CrossRef]
- Kumar, V.; Yarrakula, K. Comparison of Efficient Techniques of Hyper-Spectral Image Preprocessing for Mineralogy and Vegetation Studies. Indian J. Geo-Mar. Sci. 2017, 46, 1008–1021. [Google Scholar]
- Abrams, M.J.; Brown, D.; Lepley, L.; Sadowski, R. Remote Sensing for Porphyry Copper Deposits in Southern Arizona. Econ. Geol. 1983, 78, 591–604. [Google Scholar] [CrossRef]
- Clark, R.N.; King, T.V.V.; Klejwa, M.; Swayze, G.A.; Vergo, N. High Spectral Resolution Reflectance Spectroscopy of Minerals. J. Geophys. Res. Solid Earth 1990, 95, 12653–12680. [Google Scholar] [CrossRef]
- CLOUTIS, E.A. Review Article Hyperspectral Geological Remote Sensing: Evaluation of Analytical Techniques. Int. J. Remote Sens. 1996, 17, 2215–2242. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Drury, S.A. 1993. Image Interpretation in Geology, 2nd Ed. Xi + 283 Pp. London, Glasgow, New York, Tokyo, Melbourne, Madras: Chapman ’ Hall. Price £24.95 (Paperback). ISBN 0 412 48880 9. Geol. Mag. 1994, 131, 704–706. [Google Scholar] [CrossRef]
- Hunt, G.R.; Salisbury, J.W. Visible and near Infrared Spectra of Minerals and Rocks. II. Carbonates. Mod. Geol. 1971, 2, 23–30. [Google Scholar]
- Hunt, G.R. Electromagnetic Radiation: The Communication Link in Remote Sensing. Remote Sens. Geol. 1980, 5, 4–45. [Google Scholar]
- EGSMA. Geological Maps of Marsa Alam 1:100,000 Scale; The Egyptian Geologic Survay and Mining Authority, Cairo (EGSMA): Abbasiya, Egypt, 1992. [Google Scholar]










| Hyperion Band | C1 | C2 | C3 | C4 | C5 | C6 | C7 | Intercept |
|---|---|---|---|---|---|---|---|---|
| B018 | 0.743531 | 1.949537 | −0.00211 | 0.796674 | 0.129633 | 0.245029 | 0.264724 | 2924.863 |
| PCs | Eigenvalue | Weight | Cumulative Weight |
|---|---|---|---|
| PC 1 | 77,483,511.41 | 0.821410385 | 0.821410385 |
| PC 2 | 11,958,992.1 | 0.126778461 | 0.948188845 |
| PC 3 | 4,186,135.111 | 0.044377633 | 0.992566478 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| Sum | 94,329,841.53 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, A.; Emam, A.; Zoheir, B. SAM-HIT: A Simulated Annealing Multispectral to Hyperspectral Imagery Data Transformation. Remote Sens. 2023, 15, 1154. https://doi.org/10.3390/rs15041154
Mohamed A, Emam A, Zoheir B. SAM-HIT: A Simulated Annealing Multispectral to Hyperspectral Imagery Data Transformation. Remote Sensing. 2023; 15(4):1154. https://doi.org/10.3390/rs15041154
Chicago/Turabian StyleMohamed, Ali, Ashraf Emam, and Basem Zoheir. 2023. "SAM-HIT: A Simulated Annealing Multispectral to Hyperspectral Imagery Data Transformation" Remote Sensing 15, no. 4: 1154. https://doi.org/10.3390/rs15041154
APA StyleMohamed, A., Emam, A., & Zoheir, B. (2023). SAM-HIT: A Simulated Annealing Multispectral to Hyperspectral Imagery Data Transformation. Remote Sensing, 15(4), 1154. https://doi.org/10.3390/rs15041154