Coupled Thorens and Soil Conservation Service Models for Soil Erosion Assessment in a Loess Plateau Watershed, China
Abstract
1. Introduction
2. Materials and Methods
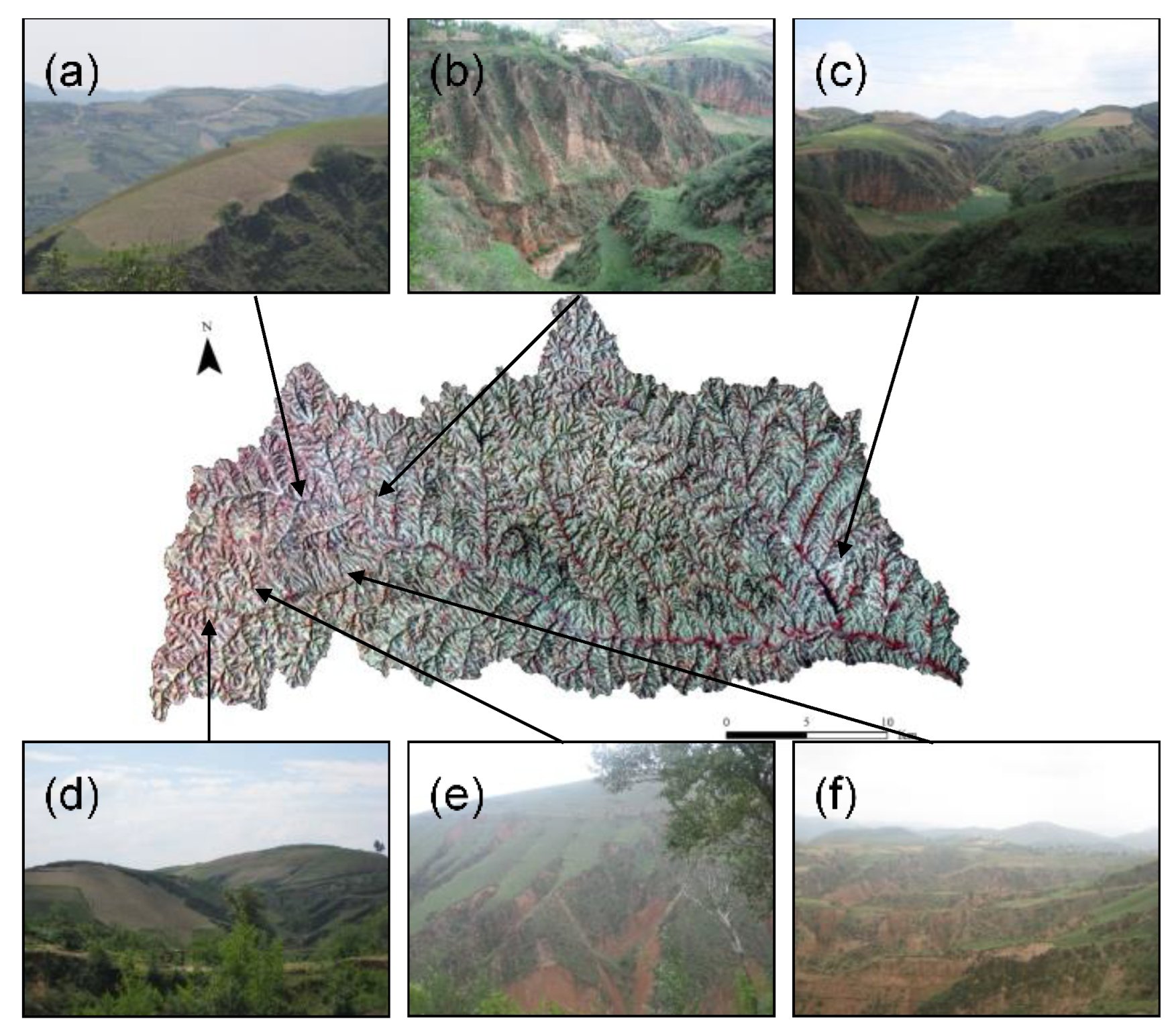
2.1. Study Area
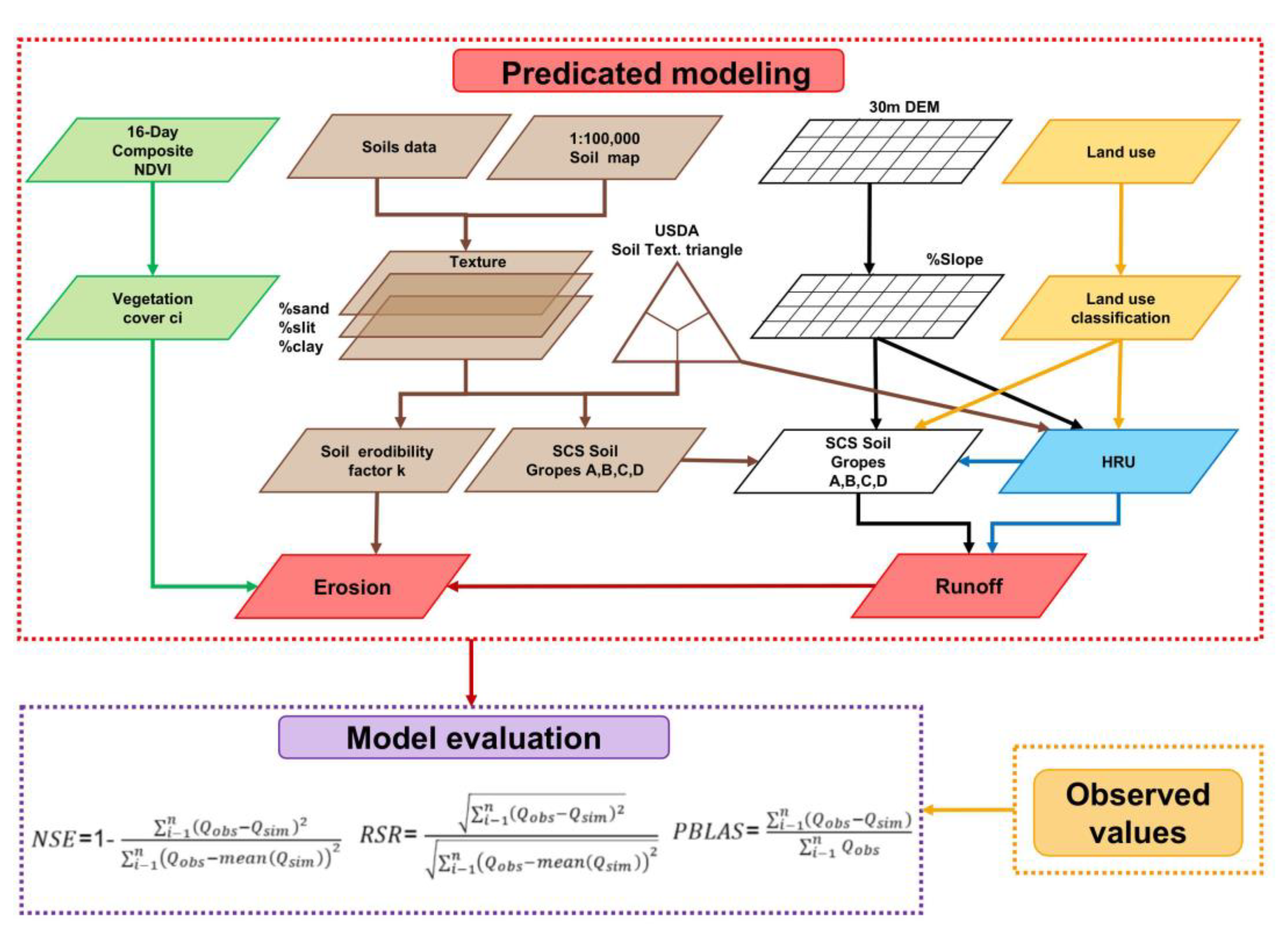
2.2. Model Descriptions
2.3. Data Collection and Model Input
2.3.1. Hydrology
2.3.2. Topography
2.3.3. Soil Properties
2.3.4. Land Use
2.3.5. Vegetation Cover
3. Results
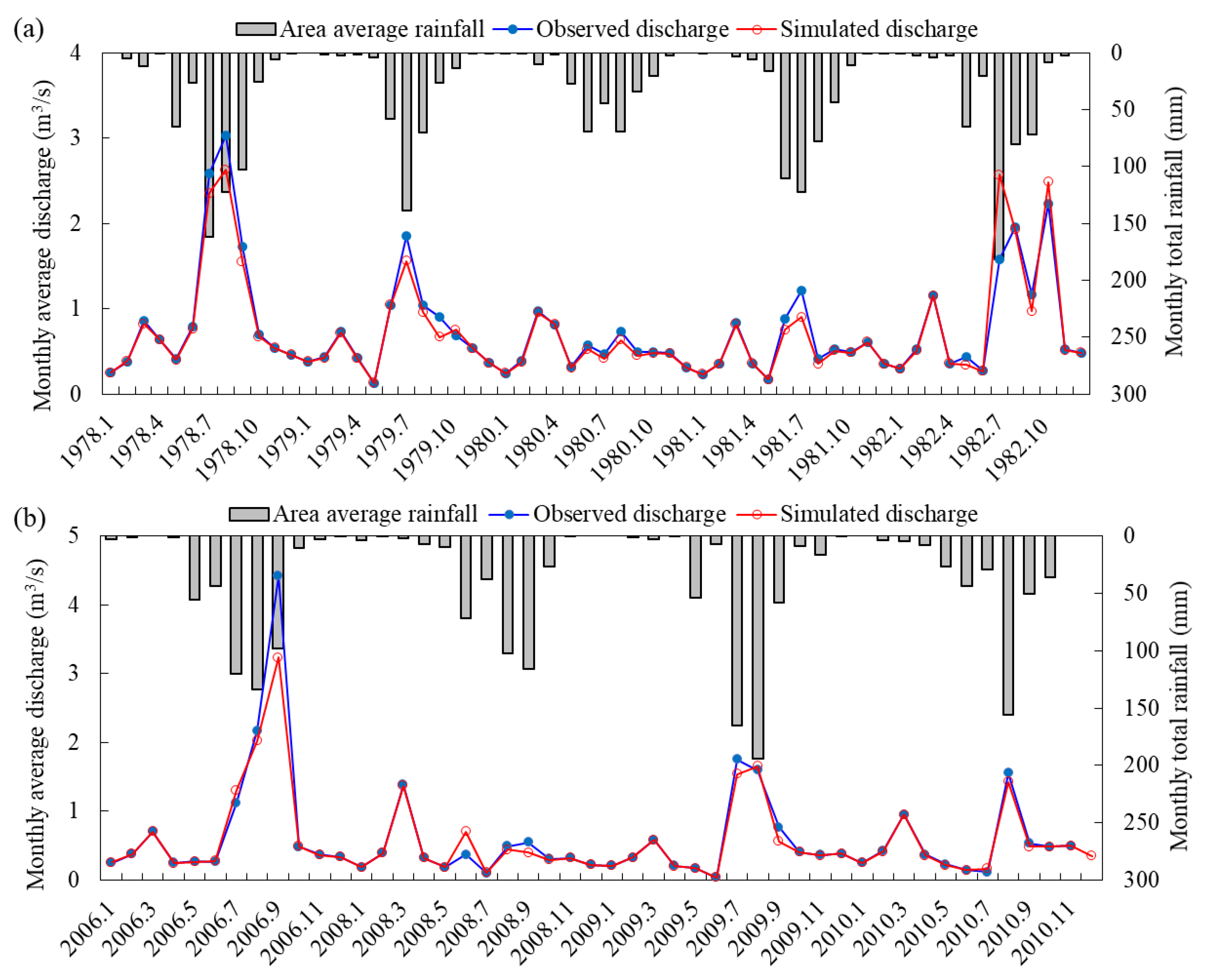
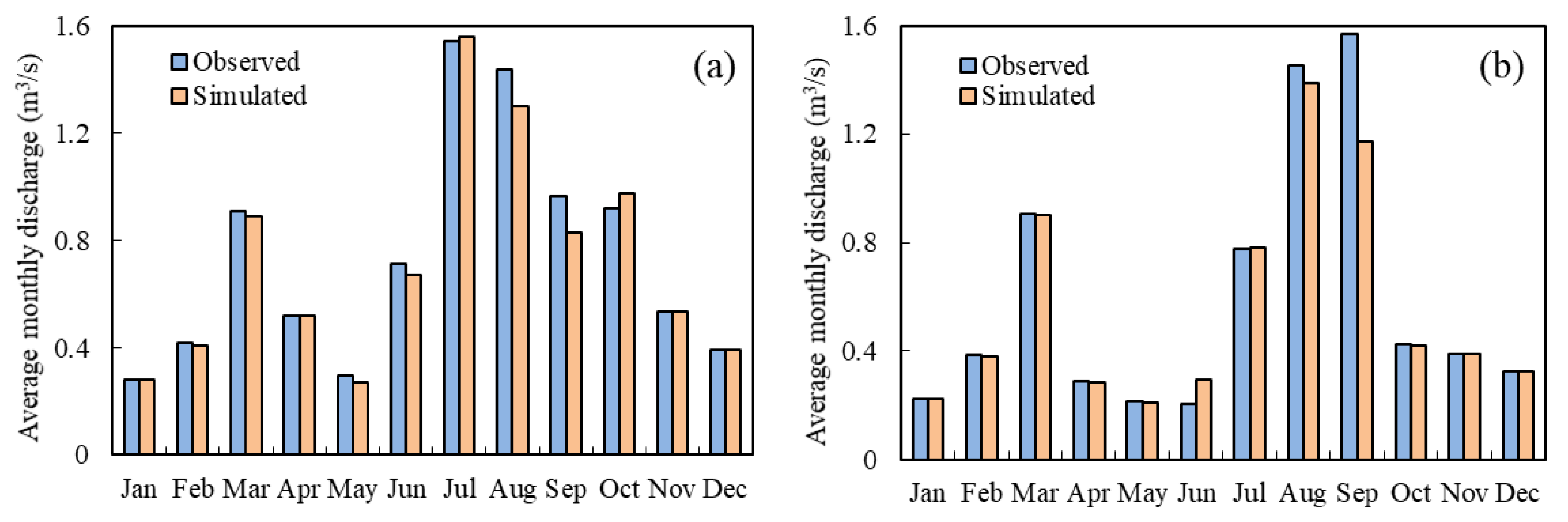
3.1. Modelling Monthly Runoff
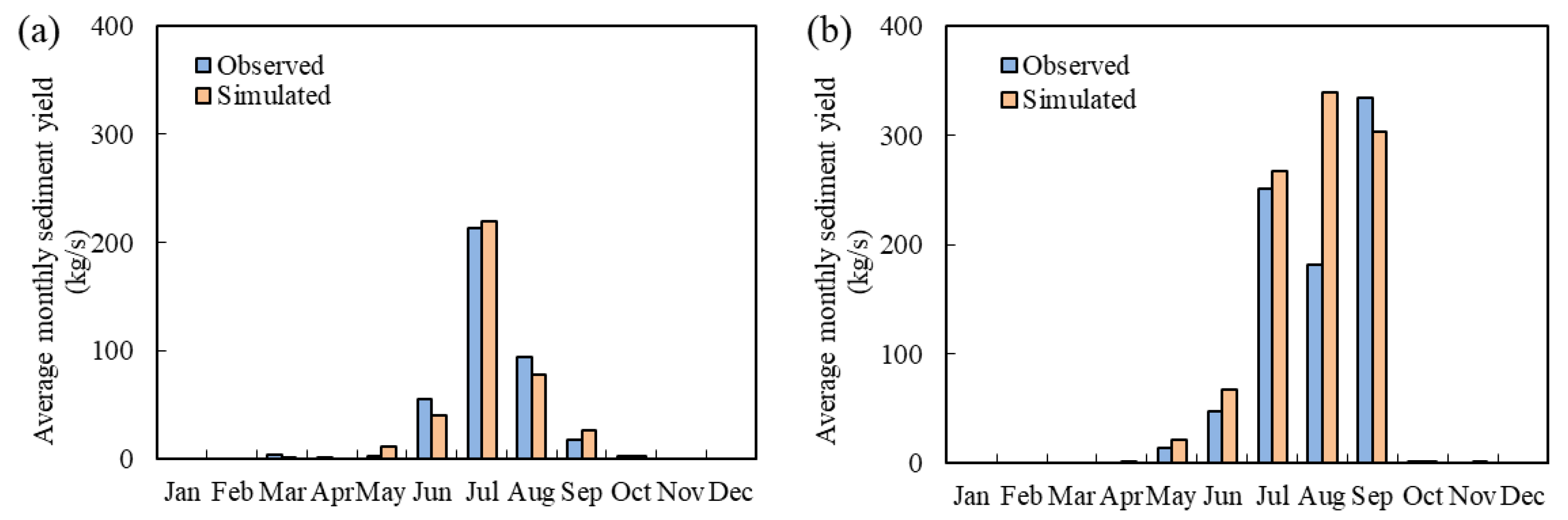
3.2. Modelling Monthly Sediment
3.3. Effects of Land Use Change on Runoff and Sediment
3.4. The Combined Effects of Rainfall and Land Use Change on the Temporal and Spatial Patterns of Erosion Rates
4. Discussion
4.1. Application of the Proposed Modelling Framework
4.2. Advantages and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Fu, B.; Wang, S.; Stringer, L.C.; Wang, Y.; Li, Z.; Liu, Y.; Zhou, W. Drivers and impacts of changes in China’s drylands. Nat. Rev. Earth Environ. 2021, 2, 858–873. [Google Scholar] [CrossRef]
- Li, C.; Holden, J.; Grayson, R.; Li, P. Erosion in peatlands: Recent research progress and future directions. Earth-Sci. Rev. 2018, 185, 870–886. [Google Scholar] [CrossRef]
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef] [PubMed]
- Borrelli, P.; Robinson, D.A.; Panagos, P.; Lugato, E.; Yang, J.E.; Alewell, C.; Wuepper, D.; Montanarella, L.; Ballabio, C. Land use and climate change impacts on global soil erosion by water (2015–2070). Proc. Natl. Acad. Sci. USA 2020, 117, 21994–22001. [Google Scholar] [CrossRef]
- Miao, C.; Ni, J.; Borthwick, A.G. Recent changes of water discharge and sediment load in the Yellow River basin, China. Prog. Phys. Geogr. 2010, 34, 541–561. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Liang, W. Developing policy for the Yellow River sediment sustainable control. Natl. Sci. Rev. 2016, 3, 162–164. [Google Scholar] [CrossRef]
- Zuo, D.; Xu, Z.; Yao, W.; Jin, S.; Xiao, P.; Ran, D. Assessing the effects of changes in land use and climate on runoff and sediment yields from a watershed in the Loess Plateau of China. Sci. Total Environ. 2016, 544, 238–250. [Google Scholar] [CrossRef]
- Zhao, G.; Mu, X.; Wen, Z.; Wang, F.; Gao, P. Soil erosion, conservation, and eco-environment changes in the Loess Plateau of China. Land Degrad. Dev. 2013, 24, 499–510. [Google Scholar] [CrossRef]
- Gao, P.; Mu, X.-M.; Wang, F.; Li, R. Changes in streamflow and sediment discharge and the response to human activities in the middle reaches of the Yellow River. Hydrol. Earth Syst. Sci. 2011, 15, 1–10. [Google Scholar] [CrossRef]
- Shi, H.; Shao, M. Soil and water loss from the Loess Plateau in China. J. Arid Environ. 2000, 45, 9–20. [Google Scholar] [CrossRef]
- Chen, L.; Wei, W.; Fu, B.; Lü, Y. Soil and water conservation on the Loess Plateau in China: Review and perspective. Prog. Phys. Geogr. 2007, 31, 389–403. [Google Scholar] [CrossRef]
- Fu, B.; Wang, S.; Liu, Y.; Liu, J.; Liang, W.; Miao, C. Hydrogeomorphic ecosystem responses to natural and anthropogenic changes in the Loess Plateau of China. Annu. Rev. Earth Planet. Sci. 2017, 45, 223–243. [Google Scholar] [CrossRef]
- Wu, X.; Wei, Y.; Fu, B.; Wang, S.; Zhao, Y.; Moran, E.F. Evolution and effects of the social-ecological system over a millennium in China’s Loess Plateau. Sci. Adv. 2020, 6, eabc0276. [Google Scholar] [CrossRef] [PubMed]
- Hessel, R. Consequences of hyperconcentrated flow for process-based soil erosion modelling on the Chinese Loess Plateau. Earth Surf. Process. Landf. 2006, 31, 1100–1114. [Google Scholar] [CrossRef]
- Sun, W.; Shao, Q.; Liu, J.; Zhai, J. Assessing the effects of land use and topography on soil erosion on the Loess Plateau in China. Catena 2014, 121, 151–163. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Piao, S.; Lü, Y.; Ciais, P.; Feng, X.; Wang, Y. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Ali, K.F.; de Boer, D.H. Spatially distributed erosion and sediment yield modeling in the upper Indus River basin. Water Resour. Res. 2010, 46, W08504. [Google Scholar] [CrossRef]
- Li, P.; Mu, X.; Holden, J.; Wu, Y.; Irvine, B.; Wang, F.; Gao, P.; Zhao, G.; Sun, W. Comparison of soil erosion models used to study the Chinese Loess Plateau. Earth-Sci. Rev. 2017, 170, 17–30. [Google Scholar] [CrossRef]
- Wen, X.; Deng, X. Current soil erosion assessment in the Loess Plateau of China: A mini-review. J. Clean. Prod. 2020, 276, 123091. [Google Scholar] [CrossRef]
- Wu, B.; Wang, Z.; Zhang, Q.; Shen, N.; Liu, J. Modelling sheet erosion on steep slopes in the loess region of China. J. Hydrol. 2017, 553, 549–558. [Google Scholar] [CrossRef]
- Borrelli, P.; Alewell, C.; Alvarez, P.; Anache, J.A.A.; Baartman, J.; Ballabio, C.; Bezak, N.; Biddoccu, M.; Cerdà, A.; Chalise, D. Soil erosion modelling: A global review and statistical analysis. Sci. Total Environ. 2021, 780, 146494. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.; Zhao, W.; Chen, L.; Zhang, Q.; Lü, Y.; Gulinck, H.; Poesen, J. Assessment of soil erosion at large watershed scale using RUSLE and GIS: A case study in the Loess Plateau of China. Land Degrad. Dev. 2005, 16, 73–85. [Google Scholar] [CrossRef]
- Jin, F.; Yang, W.; Fu, J.; Li, Z. Effects of vegetation and climate on the changes of soil erosion in the Loess Plateau of China. Sci. Total Environ. 2021, 773, 145514. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.; Liu, Y.; Lü, Y.; He, C.; Zeng, Y.; Wu, B. Assessing the soil erosion control service of ecosystems change in the Loess Plateau of China. Ecol. Complex. 2011, 8, 284–293. [Google Scholar] [CrossRef]
- Li, P.; Chen, J.; Zhao, G.; Holden, J.; Liu, B.; Chan, F.K.S.; Hu, J.; Wu, P.; Mu, X. Determining the drivers and rates of soil erosion on the Loess Plateau since 1901. Sci. Total Environ. 2022, 823, 153674. [Google Scholar] [CrossRef]
- Hessel, R.; van Asch, T. Modelling gully erosion for a small catchment on the Chinese Loess Plateau. Catena 2003, 54, 131–146. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.-Z.; Zhang, X.-C.; Zheng, F.-L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Feng, X.; Wang, Y.; Chen, L.; Fu, B.; Bai, G. Modeling soil erosion and its response to land-use change in hilly catchments of the Chinese Loess Plateau. Geomorphology 2010, 118, 239–248. [Google Scholar] [CrossRef]
- Jetten, V.; Govers, G.; Hessel, R. Erosion models: Quality of spatial predictions. Hydrol. Process. 2003, 17, 887–900. [Google Scholar] [CrossRef]
- Nearing, M.; Romkens, M.; Norton, L.; Stott, D.; Rhoton, F.; Laflen, J.; Flanagan, D.; Alonso, C.; Binger, R.; Dabney, S. Measurements and models of soil loss rates. Science 2000, 290, 1300–1301. [Google Scholar] [CrossRef]
- Thornes, J. The ecology of erosion. Geography 1985, 70, 222–235. [Google Scholar]
- Thornes, J. The interaction of erosional and vegetational dynamics in land degradation: Spatial outcomes. In Vegetation and Erosion: Processes and Environments; Thornes, J.B., Ed.; CABI: Chichester, UK, 1990; pp. 41–53. [Google Scholar]
- Zhang, X.; Drake, N.; Wainwright, J. Scaling land surface parameters for global-scale soil erosion estimation. Water Resour. Res. 2002, 38, 1180. [Google Scholar] [CrossRef]
- Saavedra, C. Estimating Spatial Patterns of Soil Erosion and Deposition of the Andean Region Using Geo-Information Techniques: A Case study in Cochabamba, Bolivia. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2005. [Google Scholar]
- Saavedra, C.; Mannaerts, C. Erosion estimation in an Andean catchment combining coarse and fine resolution satellite imagery. In Proceedings of the 31st International Symposium on Remote Sensing of Environment: Global Monitoring for Sustainability and Security, Saint Petersburg, Russia, 20–24 June 2005. [Google Scholar]
- Symeonakis, E.; Calvo-Cases, A.; Arnau-Rosalen, E. Land use change and land degradation in southeastern Mediterranean Spain. Environ. Manag. 2007, 40, 80–94. [Google Scholar] [CrossRef]
- Symeonakis, E.; Robinson, T.; Drake, N. GIS and multiple-criteria evaluation for the optimisation of tsetse fly eradication programmes. Environ. Monit. Assess. 2007, 124, 89–103. [Google Scholar] [CrossRef]
- Feng, X.; Fu, B.; Piao, S.; Wang, S.; Ciais, P.; Zeng, Z.; Lü, Y.; Zeng, Y.; Li, Y.; Jiang, X. Revegetation in China’s Loess Plateau is approaching sustainable water resource limits. Nat. Clim. Change 2016, 6, 1019–1022. [Google Scholar] [CrossRef]
- Hessel, R.; Messing, I.; Liding, C.; Ritsema, C.; Stolte, J. Soil erosion simulations of land use scenarios for a small Loess Plateau catchment. Catena 2003, 54, 289–302. [Google Scholar] [CrossRef]
- Zheng, M.; Qin, F.; Sun, L.; Qi, D.; Cai, Q. Spatial scale effects on sediment concentration in runoff during flood events for hilly areas of the Loess Plateau, China. Earth Surf. Process. Landf. 2011, 36, 1499–1509. [Google Scholar] [CrossRef]
- He, L.; Wang, G.; Fu, X. Disaggregation model of daily rainfall and its application in the Xiaolihe Watershed, Yellow River. J. Environ. Inform. 2015, 16, 11–18. [Google Scholar] [CrossRef]
- Jiongxin, X. Erosion caused by hyperconcentrated flow on the Loess Plateau of China. Catena 1999, 36, 1–19. [Google Scholar] [CrossRef]
- Walling, D.E. The sediment delivery problem. J. Hydrol. 1983, 65, 209–237. [Google Scholar] [CrossRef]
- Huang, M.; Gallichand, J.; Dong, C.; Wang, Z.; Shao, M. Use of soil moisture data and curve number method for estimating runoff in the Loess Plateau of China. Hydrol. Process. 2007, 21, 1471–1481. [Google Scholar] [CrossRef]
- Huang, M.; Gallichand, J.; Wang, Z.; Goulet, M. A modification to the Soil Conservation Service curve number method for steep slopes in the Loess Plateau of China. Hydrol. Process. 2006, 20, 579–589. [Google Scholar] [CrossRef]
- Boughton, W. A review of the USDA SCS curve number method. Soil Res. 1989, 27, 511–523. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, S.; Yang, Y.; Zhao, R.; Shi, Z.; Rossel, R.A.V. National digital soil map of organic matter in topsoil and its associated uncertainty in 1980’s China. Geoderma 2019, 335, 47–56. [Google Scholar] [CrossRef]
- Hessel, R.; Jetten, V. Suitability of transport equations in modelling soil erosion for a small Loess Plateau catchment. Eng. Geol. 2007, 91, 56–71. [Google Scholar] [CrossRef]
- Stone, R.; Hilborn, D. Universal Soil Loss Equation (USLE); Ontario Ministry of Agriculture, Food and Rural Affairs: Guelph, ON, Canada, 2000; Volume 9. [Google Scholar]
- Luo, Y.; Yang, S.; Liu, X.; Liu, C.; Zhang, Y.; Zhou, Q.; Zhou, X.; Dong, G. Suitability of revision to MUSLE for estimating sediment yield in the Loess Plateau of China. Stoch. Environ. Res. Risk Assess. 2016, 30, 379–394. [Google Scholar] [CrossRef]
- Drake, N.A.; Zhang, X.; Berkhout, E.; Bonifacio, R.; Grimes, D.; Wainwright, J.; Mulligan, M. Modelling soil erosion at global and regional scales using remote sensing and GIS techniques. Adv. Remote Sens. GIS Anal. 1999, 241–262. [Google Scholar]
- Flügel, W.A. Delineating hydrological response units by geographical information system analyses for regional hydrological modelling using PRMS/MMS in the drainage basin of the River Bröl, Germany. Hydrol. Process. 1995, 9, 423–436. [Google Scholar] [CrossRef]
- Shi, W.; Huang, M. Predictions of soil and nutrient losses using a modified SWAT model in a large hilly-gully watershed of the Chinese Loess Plateau. Int. Soil Water Conserv. Res. 2021, 9, 291–304. [Google Scholar] [CrossRef]
- Wall, G.; Coote, D.; Pringle, E.; Shelton, I. RUSLEFAC—Revised Universal Soil Loss Equation for Application in Canada: A Handbook for Estimating Soil Loss from Water Erosion in Canada; Research Branch, Agriculture and Agri-Food Canada: Ottawa, ON, Canada, 2002; Volume 117. [Google Scholar]
- Li, C.; Pan, C. The relative importance of different grass components in controlling runoff and erosion on a hillslope under simulated rainfall. J. Hydrol. 2018, 558, 90–103. [Google Scholar] [CrossRef]
- Li, C.; Pan, C. Overland runoff erosion dynamics on steep slopes with forages under field simulated rainfall and inflow. Hydrol. Process. 2020, 34, 1794–1809. [Google Scholar] [CrossRef]
- Nie, W.; Yuan, Y.; Kepner, W.; Nash, M.S.; Jackson, M.; Erickson, C. Assessing impacts of Landuse and Landcover changes on hydrology for the upper San Pedro watershed. J. Hydrol. 2011, 407, 105–114. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, G.; Wang, N.; Luo, L. Initial abstraction ratio in the SCS-CN method in the Loess Plateau of China. Trans. ASABE 2011, 54, 163–169. [Google Scholar] [CrossRef]
- King, K.W.; Arnold, J.; Bingner, R. Comparison of Green-Ampt and curve number methods on Goodwin Creek watershed using SWAT. Trans. ASAE 1999, 42, 919. [Google Scholar] [CrossRef]
- Shi, W.; Huang, M.; Barbour, S.L. Storm-based CSLE that incorporates the estimated runoff for soil loss prediction on the Chinese Loess Plateau. Soil Tillage Res. 2018, 180, 137–147. [Google Scholar] [CrossRef]
- Shi, W.; Huang, M.; Gongadze, K.; Wu, L. A modified SCS-CN method incorporating storm duration and antecedent soil moisture estimation for runoff prediction. Water Resour. Manag. 2017, 31, 1713–1727. [Google Scholar] [CrossRef]
- Hessel, R.; Jetten, V.; Liu, B.; Zhang, Y.; Stolte, J. Calibration of the LISEM model for a small Loess Plateau catchment. Catena 2003, 54, 235–254. [Google Scholar] [CrossRef]


| Land Use Type | 1980s | 2010s | Changes | ||
|---|---|---|---|---|---|
| Area (km2) | Percentage (%) | Area (km2) | Percentage (%) | Area (km2) | |
| Farmland total | 465.41 | 57.24 | 431.57 | 53.07 | −33.84 |
| Plain cropland | 449.87 | 55.33 | 422.55 | 51.97 | −27.32 |
| Montanic cropland | 15.53 | 1.91 | 9.02 | 1.11 | −6.51 |
| Forest total | 22.24 | 2.74 | 45.43 | 5.59 | +23.19 |
| Forest land | 0.10 | 0.01 | 4.18 | 0.51 | +4.08 |
| Shrubland | 6.11 | 0.75 | 12.89 | 1.59 | +6.78 |
| Open forest land | 11.75 | 1.45 | 22.37 | 2.75 | +10.61 |
| Other forest land | 4.28 | 0.53 | 5.99 | 0.74 | +1.71 |
| Grassland total | 323.47 | 39.78 | 334.11 | 41.09 | +10.64 |
| High-coverage grassland | 0.11 | 0.01 | 0.11 | 0.01 | — |
| Moderate-coverage grassland | 65.71 | 8.08 | 330.88 | 40.69 | +265.17 |
| Low-coverage grassland | 257.65 | 31.69 | 3.13 | 0.38 | −254.53 |
| Water area | 1.15 | 0.14 | 1.15 | 0.14 | — |
| Construction land | 0.84 | 0.10 | 0.84 | 0.10 | — |
| Land Use Type | Antecedent Moisture Conditions | ||
|---|---|---|---|
| AMC I | AMC II | AMC III | |
| Urban area | 85 | 93 | 97 |
| Forest | 26 | 45 | 65 |
| Grassland | 15 | 30 | 50 |
| Farmland | 43 | 64 | 80 |
| Water body | 100 | 100 | 100 |
| Land Use Change Types | Changed Area, km2 | Percent Change in Converted Land Use, % |
|---|---|---|
| Plain cropland to forest land | 3.43 | 0.76 |
| Plain cropland to shrubland | 6.78 | 1.51 |
| Plain cropland to open forest land | 9.98 | 2.22 |
| Plain cropland to moderate-coverage grassland | 7.13 | 1.58 |
| Montanic cropland to open forest land | 0.64 | 4.12 |
| Montanic cropland to moderate-coverage grassland | 5.88 | 37.86 |
| Moderate-coverage grassland to other forest land | 1.71 | 2.60 |
| Low-coverage grassland to moderate-coverage grassland | 254.53 | 98.78 |
| Scenarios | Rainfall Occurrence /% | Year | Precipitation (mm) | Observed Values | Simulated Values | ||
|---|---|---|---|---|---|---|---|
| Runoff (m3/s) | Sediment Yield (kg/s) | Runoff (m3/s) | Sediment Yield (kg/s) | ||||
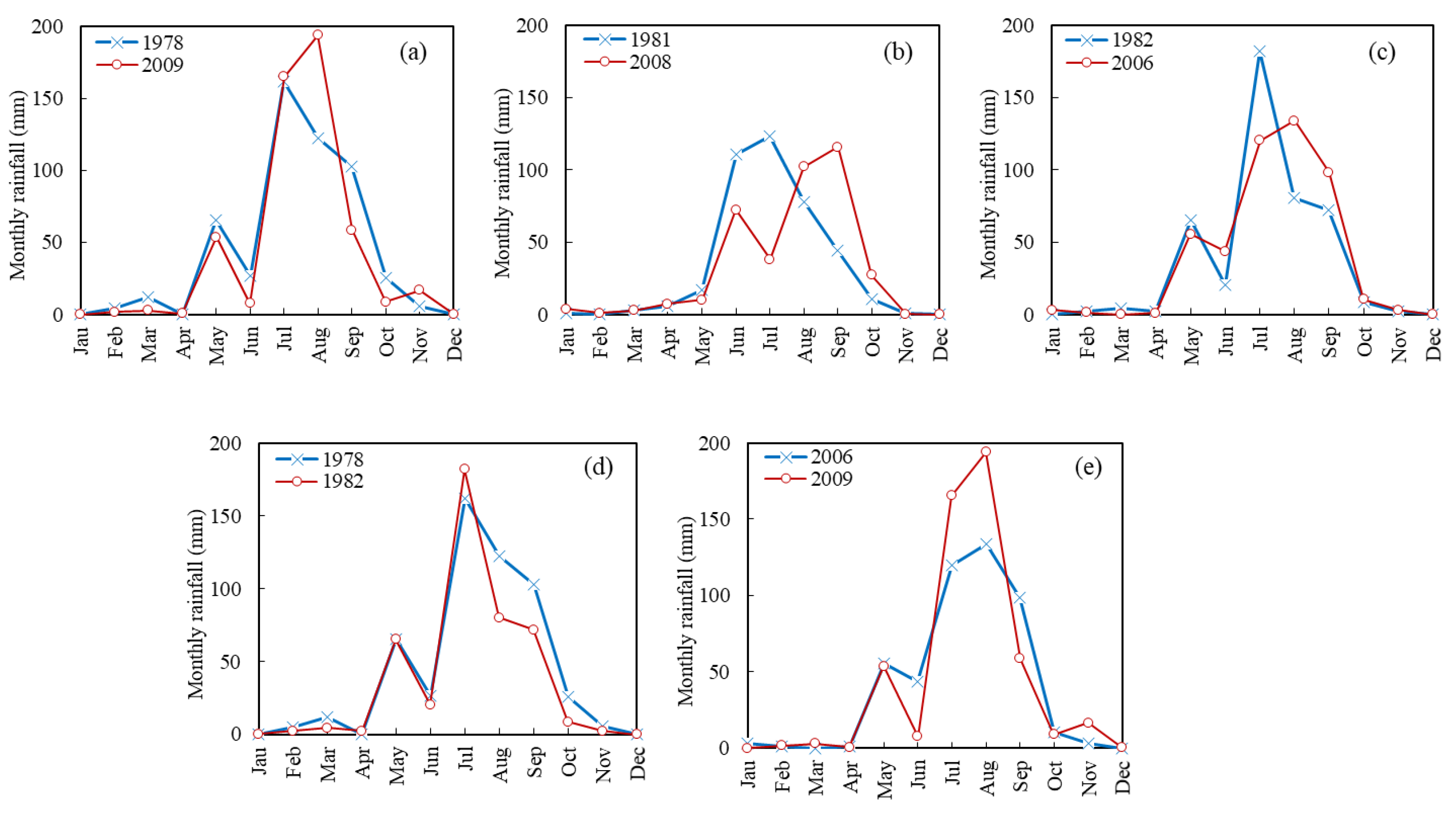
| 1 | 25 | 1978 | 528 a | 1.03 a | 56.96 a | 0.96 a | 49.83 a |
| 2009 | 510 a | 0.57 b | 77.84 a | 0.54 b | 76.45 a | ||
| 1978–2009 | −18 | −0.46 (−45%) | 20.88 (+37%) | −0.42 (−44%) | 26.61 (+53%) | ||
| 2 | 50 | 1981 | 394 a | 0.54 a | 12.03 a | 0.49 a | 10.23 a |
| 2008 | 380 a | 0.40 a | 14.86 a | 0.41 a | 24.50 a | ||
| 1981–2008 | −14 | −0.13 (−25%) | 2.83 (+24%) | −0.08 (−16%) | 14.26 (+139%) | ||
| 3 | 50 | 1982 | 439 a | 0.92 a | 54.47 a | 0.99 a | 67.17 a |
| 2006 | 471 a | 0.92 a | 180.23 a | 0.82 a | 222.35 a | ||
| 1982–2006 | 32 | 0.00 (+0.47%) | 125.76 (+231%) | −0.16 (−17%) | 155.18 (+231%) | ||
| Erosion Rate (mm/year) | Group 1 | Group 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| 1978 | 2009 | 1981 | 2008 | |||||
| Area | Percentage | Area | Percentage | Area | Percentage | Area | Percentage | |
| (km2) | (%) | (km2) | (%) | (km2) | (%) | (km2) | (%) | |
| 0–0.2 | 399 | 49.13 | 426 | 52.45 | 743 | 91.61 | 429 | 52.92 |
| 0.2–1.0 | 334 | 41.10 | 266 | 32.72 | 1 | 0.16 | 266 | 32.76 |
| 1.0–5.0 | 12 | 1.54 | 4 | 0.50 | 11 | 1.32 | 24 | 2.99 |
| 5.0–10.0 | 0 | 0.00 | 0 | 0.00 | 25 | 3.14 | 14 | 1.74 |
| >10.0 | 67 | 8.23 | 116 | 14.33 | 31 | 3.77 | 78 | 9.59 |
| Erosion Rate (mm/year) | Group 3 | Group 4 | ||||||
| 1982 | 2006 | 1978 | 1982 | |||||
| Area | Percentage | Area | Percentage | Area | Percentage | Area | Percentage | |
| (km2) | (%) | (km2) | (%) | (km2) | (%) | (km2) | (%) | |
| 0–0.2 | 399 | 49.13 | 426 | 52.45 | 399 | 49.13 | 399 | 49.13 |
| 0.2–1.0 | 318 | 39.18 | 0 | 0.00 | 334 | 41.10 | 318 | 39.18 |
| 1.0–5.0 | 28 | 3.46 | 10 | 1.27 | 12 | 1.54 | 28 | 3.46 |
| 5.0–10.0 | 0 | 0.00 | 244 | 30.06 | 0 | 0.00 | 0 | 0.00 |
| >10.0 | 67 | 8.23 | 132 | 16.22 | 67 | 8.23 | 67 | 8.23 |
| Erosion Rate (mm/year) | Group 5 | |||||||
| 2006 | 2009 | |||||||
| Area | Percentage | Area | Percentage | |||||
| (km2) | (%) | (km2) | (%) | |||||
| 0–0.2 | 426 | 52.45 | 426 | 52.45 | ||||
| 0.2–1.0 | 0 | 0.00 | 266 | 32.72 | ||||
| 1.0–5.0 | 10 | 1.27 | 4 | 0.50 | ||||
| 5.0–10.0 | 244 | 30.06 | 0 | 0.00 | ||||
| >10.0 | 132 | 16.22 | 116 | 14.33 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Lu, T.; Wang, S.; Xu, J. Coupled Thorens and Soil Conservation Service Models for Soil Erosion Assessment in a Loess Plateau Watershed, China. Remote Sens. 2023, 15, 803. https://doi.org/10.3390/rs15030803
Li C, Lu T, Wang S, Xu J. Coupled Thorens and Soil Conservation Service Models for Soil Erosion Assessment in a Loess Plateau Watershed, China. Remote Sensing. 2023; 15(3):803. https://doi.org/10.3390/rs15030803
Chicago/Turabian StyleLi, Changjia, Tong Lu, Shuai Wang, and Jiren Xu. 2023. "Coupled Thorens and Soil Conservation Service Models for Soil Erosion Assessment in a Loess Plateau Watershed, China" Remote Sensing 15, no. 3: 803. https://doi.org/10.3390/rs15030803
APA StyleLi, C., Lu, T., Wang, S., & Xu, J. (2023). Coupled Thorens and Soil Conservation Service Models for Soil Erosion Assessment in a Loess Plateau Watershed, China. Remote Sensing, 15(3), 803. https://doi.org/10.3390/rs15030803









