An Innovative Signal Processing Scheme for Spaceborne Integrated GNSS Remote Sensors

Abstract

The vigorous development of the global navigation satellite system (GNSS) has led to a boom in GNSS radio occultation (GNSS RO) and GNSS reflectometry (GNSS-R) techniques. Consequently, we have proposed an innovative signal processing scheme for spaceborne integrated GNSS remote sensors (SIGRS), combining a GNSS RO and a GNSS-R module. In the SIGRS, the GNSS-R module shares one precise orbit determination (POD) module with the GNSS RO module, and the GNSS-R module first achieves compatibility with GPS, BDS, and Galileo. Moreover, the programmable non-uniform delay resolution was introduced and first used by the SIGRS to generate the output DDM, which achieves a high delay resolution in the DDM central region around the specular point to improve the accuracy of basic observables but requires fewer delay bins than the conventional DDM with uniform delay resolution. The SIGRS has been successfully used to design the GNOS II onboard the Chinese FY-3E satellite, and the results of in-orbit operation validate the performance of the SIGRS, which means the SIGRS is an economically and technically efficient design and has become the first successful signal processing scheme for spaceborne integrated GNSS remote sensors around the world.

1. Introduction

The vigorous development of the global navigation satellite system (GNSS) in the last few decades has led to a boom in GNSS-based remote sensing techniques. Among all these techniques, GNSS radio occultation (GNSS RO) and GNSS reflectometry (GNSS-R) are the most successful applications. There are many successful missions of GNSS RO, such as the GPS meteorology (GPS/MET) [1], the CHAllenging minisatellite payload (CHAMP) [2,3], the meteorology, ionosphere, and climate (COSMIC) [4], the gravity recovery and, additionally, climate experiment (GRACE) [5], the meteorological operational (Metop) satellite [6] and the GNSS occultation sounder (GNOS) [7] and of GNSS-R such as the UK disaster monitoring constellation (UK-DMC) [8], the UK TechDemoSat-1 (TDS-1) [9], the NASA cyclone global navigation satellite system (CYGNSS) [10], the Chinese BuFeng-1 A/B twin satellite [11], and the ESA FSSCat mission [12].

To the authors’ knowledge, the spaceborne integrated GNSS remote sensor combining a GNSS RO and a GNSS-R module is capable of processing both GNSS occultation signals and reflected GNSS signals simultaneously so as to obtain information about the ionosphere, neutral atmosphere, ocean, ice, and land at the same time, which is of great significance for observations of the Earth. However, none of the above missions combined GNSS RO and GNSS-R techniques together.

Additionally, it is well known that GNSS-R observation benefits from receiving as many reflected GNSS signals of opportunity as possible. However, GNSS-R missions, such as UK-DMC, TDS-1, and CYGNSS, are merely based on GPS, BuFeng-1 is based on both GPS and BeiDou navigation satellite system (BDS), and FSSCat is based on both GPS and the European GNSS (Galileo). So far, there is no one that has achieved compatibility with GPS, BDS, and Galileo.

The GNOS receiver is designed and produced by the National Space Science Center (NSSC), Chinese Academy of Sciences (CAS), under a contract with the China Meteorological Administration (CMA). This receiver has been successfully providing GNSS RO data on-board FY-3C (launched in 2013) and FY-3D (launched in 2017) satellites, which are sun-synchronous polar-orbiting meteorological satellites from China. Up to now, the data provided by GNOS has supported much research [7,13,14,15,16], and the products of GNOS have made contributions to several forecast models.

After foregoing successful GNSS RO missions and taking the above-mentioned motivations into account, NSSC turned its focus to the spaceborne integrated GNSS remote sensor [17]. As a result, the authors proposed an innovative signal processing scheme for spaceborne integrated GNSS remote sensors (SIGRS). In comparison to the signal processing scheme for the GNOS, the SIGRS not only improves designs in GNSS RO and POD modules but also adds a brand-new GNSS-R module. In the SIGRS, the GNSS-R module shares the POD module with the GNSS RO module, and it is capable of processing reflected signals from three GNSS systems, including GPS, BDS, and Galileo, which makes the GNSS-R module obtain more opportunity signals than existing instruments.

The fundamental measurement of the GNSS-R module in the SIGRS is the delay-doppler map (DDM) in raw counts. In order to improve the accuracy of basic observables, the programmable non-uniform delay resolution has been proposed to generate the output DDM of the GNSS-R module. Moreover, the GNSS-R module in the SIGRS also contains one raw intermediate frequency (IF) data collection module to collect sampling data of the reflected signals, which contributes to ground-based post-processing, analysis, and other remote sensing experiments.

The SIGRS has been successfully used to design the spaceborne integrated GNSS remote sensing payload, GNOS II onboard the Chinese FY-3E satellite, and the GNOS II is the first spaceborne integrated GNSS remote sensor around the world. The FY-3E satellite, launched on 5 July 2021, is in a sun-synchronous polar-orbiting orbit at an altitude of 836 km and an inclination of 98.5º. As a consequence, the FY-3E satellite reaches nearly global coverage for Earth observation, and its global data latency is less than 3 h [18]. Certainly, the SIGRS will be improved and used for future GNSS remote sensing missions such as FY-3F and FY-3G.

Since the GNSS RO module has been sufficiently discussed in previous papers [19,20], this paper only gives a brief overview of the GNSS RO module. The main focus of this paper is the GNSS-R module in the SIGRS. Section 2 introduces the structure of the SIGRS. The signal processing of the GNSS RO module in the SIGRS is briefly introduced in Section 3. Section 4 describes the signal processing of the GNSS-R module in the SIGRS in detail. Some results of in-orbit operation validating the performance of the SIGRS are introduced in Section 5. Finally, some discussions and conclusions are made in Section 6 and Section 7, respectively.

2. Structure of the SIGRS

Before introducing the structure of the SIGRS, it is necessary to briefly illuminate the spaceborne integrated GNSS remote sensor because the SIGRS is specially designed for spaceborne integrated GNSS remote sensor missions.

2.1. Spaceborne Integrated GNSS Remote Sensor

When combining a GNSS RO and a GNSS-R module together, the spaceborne integrated GNSS remote sensor is capable of processing both GNSS occultation signals and reflected GNSS signals simultaneously so as to obtain information about the ionosphere, neutral atmosphere, ocean, ice, and land at the same time, which is of great significance for Earth observations.

What is more, the GNSS RO and GNSS-R modules in the spaceborne integrated GNSS remote sensor share many other modules such as the POD module, state-monitoring module, communication module, and power-supply module. Thus, the spaceborne integrated GNSS remote sensor has a lower cost than the two separated designs, as Figure 1 and

Table 1. Comparison of number of different modules between two separated designs, and the spaceborne integrated GNSS remote sensor.

	Module	POD	GNSS RO	GNSS-R	State-Monitoring	Communication	Power-Supply
Sensor
Spaceborne GNSS RO sensor		1	1	0	1	1	1
Spaceborne GNSS-R sensor		1	0	1	1	1	1
Two separated designs		2	1	1	2	2	2
Spaceborne integrated GNSS remote sensor		1	1	1	1	1	1

show.

2.2. SIGRS Overview

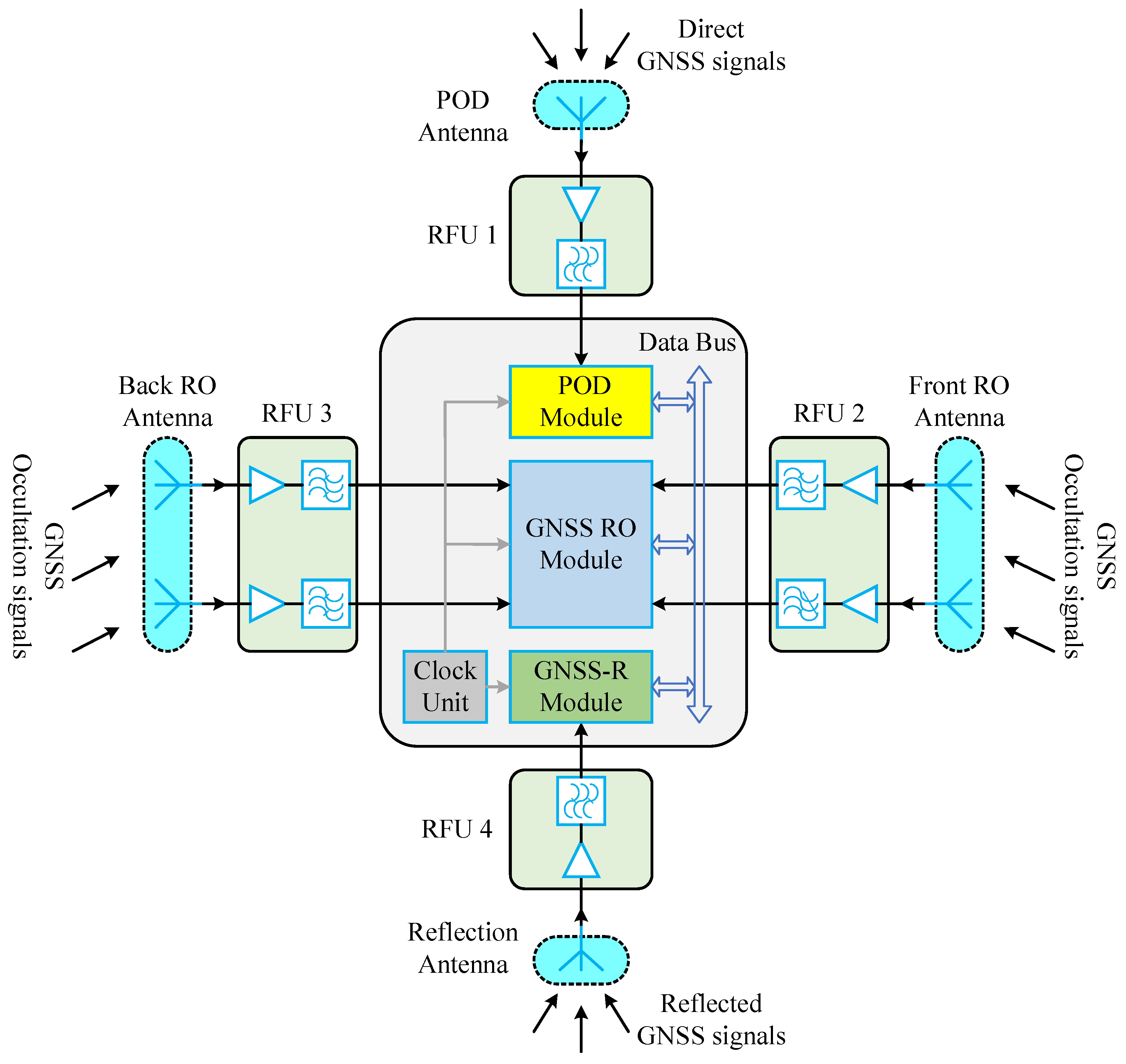
The scientific goal of the SIGRS is to provide precise position and timing information for high-demand space missions and monitor the ionosphere, neutral atmosphere, ocean, ice, and land. To achieve this goal, the SIGRS is composed of three main functional modules: POD, GNSS RO, and GNSS-R. The structure of the SIGRS is shown in Figure 2.

Figure 2 shows that the POD, GNSS RO, and GNSS-R modules process direct GNSS signals, GNSS occultation signals, and reflected GNSS signals, respectively. Since these three types of GNSS signals come from completely different directions with respect to the spaceborne integrated GNSS remote sensor, the POD, GNSS RO, and GNSS-R modules correspond to independent and insulated antennas and radio frequency units (RFUs), respectively. As a consequence, there is no inter-interference among the POD, GNSS RO, and GNSS-R modules.

The clock unit is based on one ultra-stable oven-controlled crystal oscillator (OCXO) with 1-sec stability (Allan deviation) at the level of ${10}^{-12}$ to generate synchronous ultra-stable clock signals for POD, GNSS RO, and GNSS-R modules, which not only guarantees that no clock bias exists among these three modules but also ensures that these three modules are able to generate accurate local replicas and obtain precise measurements.

In addition, the POD module acquires direct GNSS signals by an acquisition engine and then tracks the GNSS signals through closed-loop tracking channels. Finally, the POD module calculates the receiver position, velocity, and time (PVT) and obtains GNSS satellite ephemerides and almanacs before sending the PVT data of the receiver and GNSS satellites to the GNSS RO and GNSS-R modules and also to the satellite platform by a data bus.

Based on the receiver and GNSS satellite PVT information received from the POD module, the GNSS RO module first conducts the occultation event prediction according to the geometry of GNSS RO observation. Subsequently, regarding the predicted upcoming occultation events, the GNSS RO module acquires GNSS occultation signals as soon as possible by a specific acquisition engine and then tracks GNSS occultation signals by open-loop or closed-loop tracking channels to obtain carrier phase observables.

Meanwhile, the GNSS-R module, also based on the receiver and GNSS satellite PVT information received from the POD module, under the geometry of GNSS-R observation, first calculates the specular point position by means of a specular point prediction algorithm. Afterward, the whole reflection path delay and Doppler shift are estimated based on the calculated specular point position, which further assists DDM generation channels of the GNSS-R module to generate DDMs in raw counts.

It is worth noting that the specular point prediction algorithm applied in TDS-1 and CYGNSS is called the quasi-spherical Earth (QSE) approach [21], and it brings about a three-kilometer-level position error [22], which may cause trouble in DDM data processing and blur the boundary of the land-sea interface. Another conventional specular point prediction method named the minimum path length (MPL) [23,24], however, has a huge computation burden, and its accuracy varies with latitude.

In order to improve specular point prediction precision and reduce the calculation time, an improved algorithm named the self-adaptive learning rate gradient descent (SALRGD) [25] has been especially proposed for the GNSS-R module in the SIGRS. On the one hand, the SALRGD calculates the specular point on the ellipsoidal surface, which makes SALRGD fit the ellipsoid better than the QSE. On the other hand, the SALRGD calculates the longitude and latitude of the specular point by applying a self-adaptive learning rate algorithm to find a solution that minimizes the reflection path and makes the time consumption of the SALRGD competitive with the QSE.

3. Signal Processing of the GNSS RO Module

The signal processing of the GNSS RO module in the SIGRS mainly includes GNSS occultation signal acquisition, open-loop tracking, and closed-loop tracking. The open-loop tracking is based on predicted code delays and Doppler frequencies of GNSS occultation signals, and the closed-loop tracking is based on the phase lock loop (PLL). One GNSS occultation tracking channel consists of one open-loop tracking channel as well as one closed-loop tracking channel.

As Figure 3 shows, the GNSS RO acquisition engine works for GNSS occultation signal acquisition. Based on the predicted upcoming occultation events, the GNSS RO acquisition engine acquires GNSS occultation signals as soon as possible because the duration of a GNSS occultation event is only about one minute. After acquiring a GNSS occultation signal successfully, the GNSS acquisition engine sends the acquisition results to a vacant open-loop tracking channel or to a vacant closed-loop tracking channel, which assists in GNSS occultation signal tracking.

Since the lower atmosphere usually has a strong atmospheric modulation, GNSS occultation signals traveling through the lower atmosphere generally have high dynamic stress, which easily causes the conventional closed-loop tracking channel to lose lock. As a result, the GNSS RO open-loop tracking channels are used to track GNSS occultation signals traveling through the lower atmosphere, which is based on the CIRA86+Q atmospheric model to calculate code delays and Doppler frequencies of GNSS occultation signals [19]. On the contrary, the GNSS RO closed-loop tracking channels are used to track GNSS occultation signals which travel through the high atmosphere and therefore have low dynamic stress.

Finally, the GNSS occultation open-loop and closed-loop tracking channels output their carrier phases and amplitudes of GNSS occultation signals, from which accurate and precise vertical bending angle profiles are obtained. Based on the bending angles, profiles of atmospheric/ionospheric refractivity are calculated.

4. Signal Processing of the GNSS-R Module

The signal processing of the GNSS-R module in the SIGRS mainly involves DDM generation, raw IF data collection, generating programmable non-uniform delay resolution, and compatibility with GPS, BDS, and Galileo.

4.1. DDM Generation

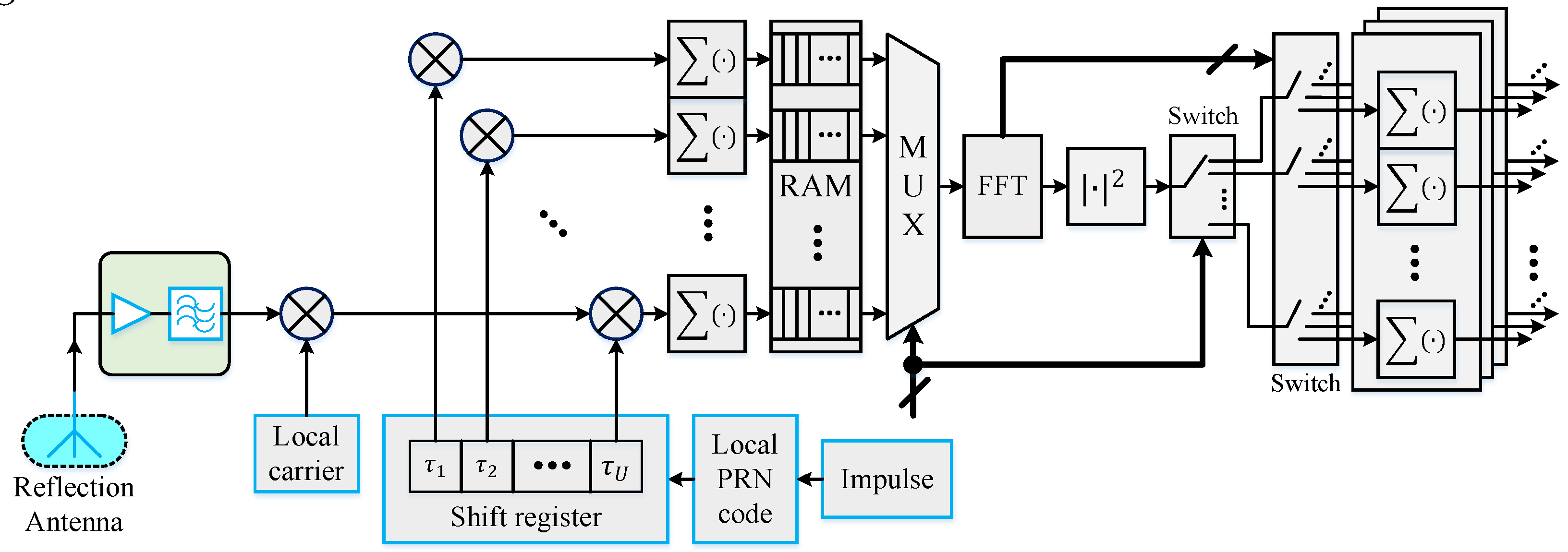
The fundamental measurement of the GNSS-R module in the SIGRS is the DDM in raw counts, and the DDM is a two-dimensional map formed by cross-correlating received reflected GNSS signals with a local replica, which is a function of code delay and Doppler frequency. In addition, the GNSS signals reflected off the rough sea surface have a wide range of code delays and Doppler shifts. In order to collect as many signals as possible, multiple measurements are required. The signal processing structure of a DDM generation sub-channel of the GNSS-R module in the SIGRS is shown in Figure 4, and a DDM generation channel consists of two sub-channels.

As Figure 4 shows, after the processing of the RFU, the received reflected signal is first sampled and quantified and then correlates with a locally generated carrier to demodulate its carrier, which can be written as:

$$s\left(n\right)=r\left(n\right)\left[cos\left(2\pi f_{l}n\Delta T\right)+j·sin\left(2\pi f_{l}n\Delta T\right)\right]$$

(1)

where $n$ is the sample index with a sampling interval of $\Delta T$, $f_l$ is the locally estimated carrier frequency, $r\left(n\right)$ is the digitally received reflected signal, and $s\left(n\right)$ is a complex digital signal.

Then, the signal $s\left(n\right)$ correlates with $U$ ($U\in N^{+}$) local pseudo-random noise (PRN) code sequences with different delays, which can be written as:

$$S_u\left(n\right)=s\left(n\right)c\left(n\Delta T+u\Delta \tau \right)$$

(2)

where $c$ is the local PRN code, $u$ denotes the $u$th local PRN code sequence corresponding to the $u$th correlator, and $u\in \left[1,U\right]$.

The $\Delta \tau$ in chips denotes the delay resolution, and it is given by:

$$\Delta \tau =\frac{R_{PRN}}{f_{Impulse}}$$

(3)

where $R_{PRN}$ in chips per second is the PRN code rate and $f_{Impulse}$ in hertz is the impulse frequency of the impulse module shown in Figure 4. The impulse frequency $f_{Impulse}$ is programmable.

After that, segment coherent accumulation is conducted to down sample the signal $S_u\left(n\right)$ to a sampling frequency of $M$ Hz, which can be written as:

$$I_u\left(m\right)={\displaystyle \sum }_{n=mN}^{\left(m+1\right)N-1}{S}_u\left(n\right)$$

(4)

where $m$ is the sample index under the sampling frequency of $M$ Hz and $N$ is the number of accumulated samples of the signal $S_u\left(n\right)$ plus padding zeros (if necessary).

The short-time coherent integration result $I_u\left(m\right)$ is firstly buffered into the random access memory (RAM) with a depth twice the size of $2LU$ short-time coherent integration results, and then the FFT operation is performed on $L$ consecutive short-time coherent integration results with padding $L$ zeros, which polls all correlators by means of time division multiple access (TDMA). As a result, all correlators share one FFT and one square module, which reduces both system’s complexity and hardware resource consumption.

The FFT operation can be expressed as:

$$F\left(g,k,u\right)={\displaystyle \sum }_{m=0}^{L-1}{I}_u\left(m+gL\right)exp\left(-j\frac{2\pi mk}{2L}\right)$$

(5)

where the length of the FFT is $2L$, $g$ ($g\in N$) denotes the $g$th FFT operation, and $k$ ($k\in \left[0,2L-1\right]$) denotes the $k$th Doppler frequency bin with a resolution of $M/2L$ Hz. Based on the FFT results, a squaring operation is subsequently conducted, which can be written as:

$$P\left(g,k,u\right)={\left|F\left(g,k,u\right)\right|}^2=F\left(g,k,u\right)F{\left(g,k,u\right)}^{*}$$

(6)

where the superscript $*$ means conjugate operation.

After the calculation has been operated on all code delays, the DDM sample with a sampling rate of $M/L$ Hz can be derived, and then non-coherent integration is performed on the consecutive DDM samples to obtain the final DDM data with an output rate of $Q$ Hz, which can be written as:

$$DDM\left(q,k,u\right)={\displaystyle \sum }_{g=qG}^{\left(q+1\right)G-1}P\left(g,k,u\right)$$

(7)

where $q\in N$ and denotes the $q$th DDM data and $G=QM/L$.

Based on Equations (1), (4), and (5), the coherent integration time $T_{coh}$ is given by:

$$T_{coh}=L·N·\Delta T$$

(8)

where the coherent integration time $T_{coh}$ usually has a value of $1 \mathrm{ms}$ in practice. According to paper [26], the $1 \mathrm{ms}$ coherent integration is appropriate to ensure that signals correlate due to random phase changes. In addition, the $1 \mathrm{ms}$ coherent integration is convenient for avoiding the bit transition. Certainly, the coherent integration time is adjustable, which is based on the geometry and sensitivity of missions. Fox example, the $4 \mathrm{ms}$ coherent integration is employed by the FSSCat mission to process reflected Galileo E1 signals [27]. In general, the longer the coherent integration time, the higher the system complexity.

As far as the number of non-coherent integration times is concerned, it is mainly determined by the desired sensitivity and spatial resolution of the GNSS-R receiver. In order to improve the sensitivity, increasing the number of non-coherent integration times is useful. On the contrary, decreasing the number of non-coherent integration times is necessary to improve spatial resolution. It is obvious that there is a trade-off in determining the number of non-coherent integration times. In general, the number of non-coherent integration times is $1000$, namely $G=1000$.

4.2. Raw IF Data Collection

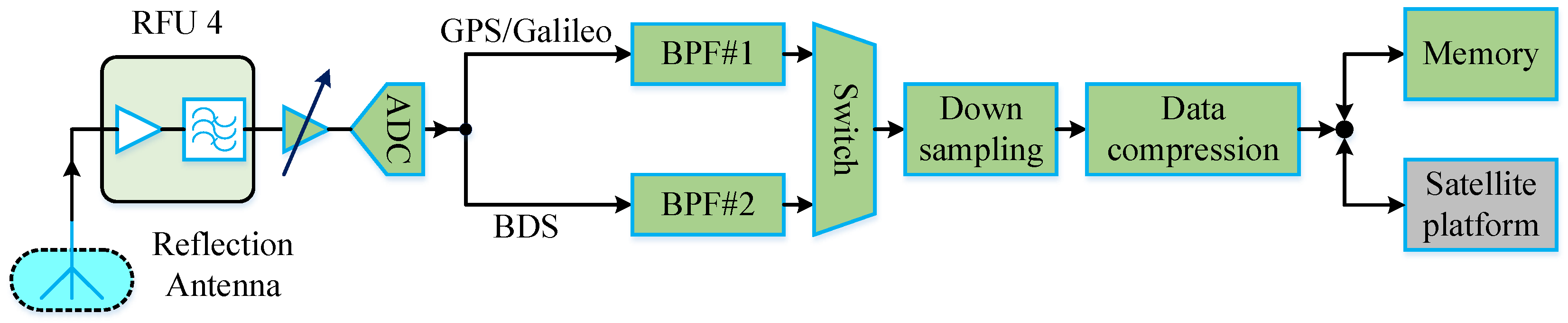
Apart from generating DDMs, the GNSS-R module in the SIGRS is capable of collecting raw IF data of reflected GNSS signals, which, despite the huge data rate, is valuable to ground-based post-processing and analysis because of the abundant information it contains. For example, the ground-based GNSS-R software-defined receiver (SDR) processes the raw IF data to generate DDMs, which can be used to compare with satellite downlink DDMs and to validate the performance and monitor the status of the GNSS-R module on-board the satellite. Moreover, some remote sensing experiments can be conducted based on the raw IF data.

Figure 5 shows that there are two channels that correspond to reflected GPS/Galileo (1575.42 MHz) signals and reflected BDS (1561.098 MHz) signals, respectively. Based on bandpass sampling technology, these two channels share the same analog-to-digital converter (ADC). The first band pass filter (BPF#1) is designed to filter GPS/Galileo signals, and the second BPF (BPF#2) is designed to filter BDS signals. After BPFs, each signal sample is truncated to 4 bits. Then, the switch is controlled by the software to select either GPS/Galileo signals or BDS signals. To decrease the data rate, down-sampling and data compression are consecutively performed before storing the raw IF data in memory. It should be noted that the down-sampling is achieved by decimation.

It should be pointed out that BPF#1 and BPF#2 are all finite impulse response (FIR) filters, and their length and quantized bits are related to the desired magnitude frequency response, filtering gain, and system complexity. Moreover, these two filters produce a length-related delay in collected signals. The delay can be described through the following equation:

$$\Delta d=\mathrm{ceil}\left(\frac{L_{BPF}}{2}\right)$$

(9)

where $L_{BPF}$ is the length of the BPF, $\Delta d$ is the delay in sample numbers, and $\mathrm{ceil}(\bullet )$ is the round-up function. Then, multiplying $\Delta d$ by sampling the interval is the delay in seconds. If the raw IF data are used for delay-sensitive experiments such as GNSS-R altimetry, the filter-induced delay must be considered.

4.3. Programmable Non-Uniform Delay Resolution

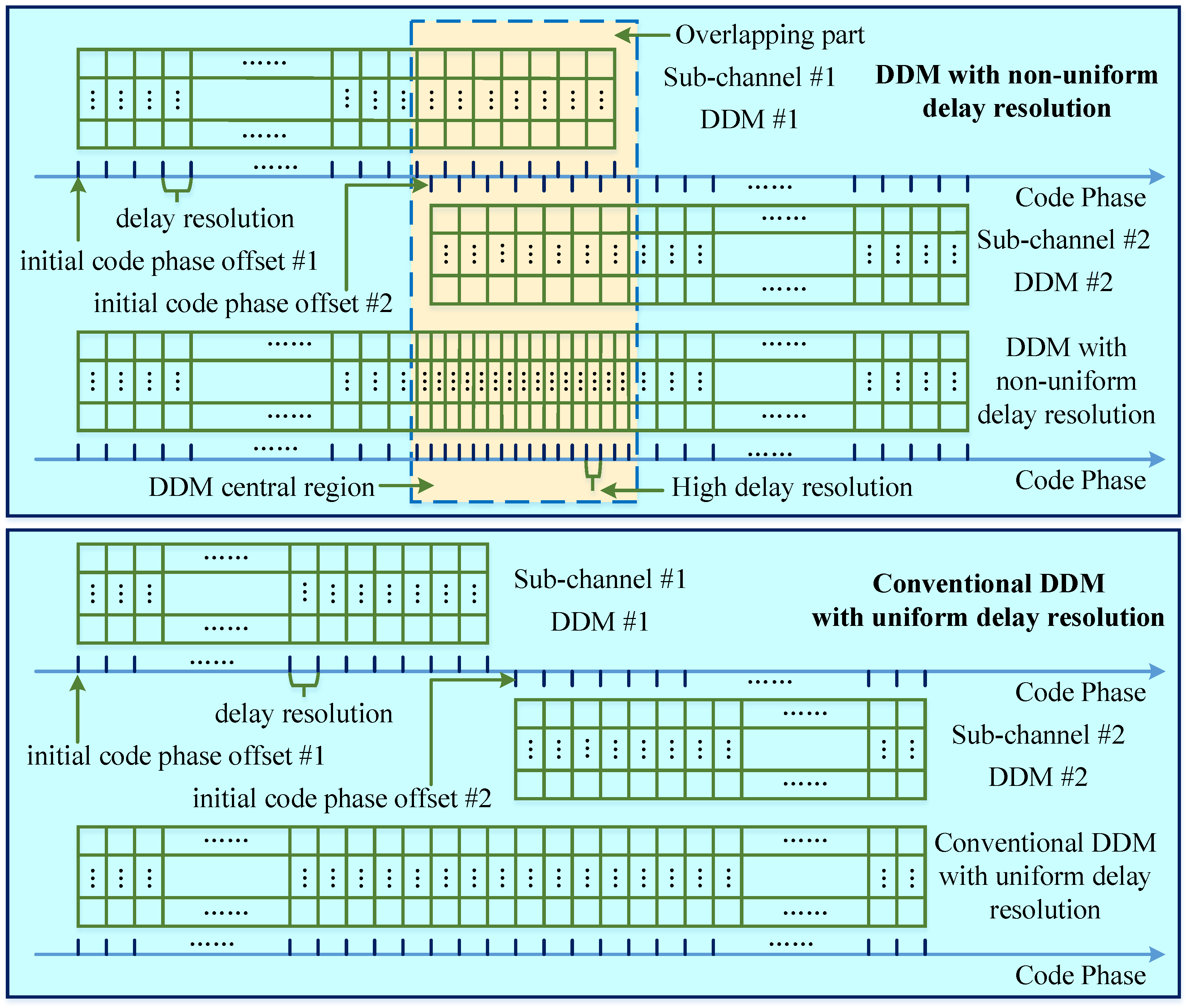
In terms of existing instruments, the delay resolution of the DDM is fixed and uniform, while in SIGRS, the delay resolution of the DDM is programmable and non-uniform. The final output DDM of the GNSS-R module in the SIGRS contains $2U$ code bins and $V$ ($V\le 2L$) frequency bins because it is obtained by either partially overlapping or cascading two DDMs that are generated by two independent DDM generation sub-channels, as these two independent DDM generation sub-channels handle the same reflected GNSS signal. In addition, these two independent DDM generation sub-channels have the same delay resolution $\Delta \tau$ but different initial code phase offsets, which are configured by the software.

Figure 6 shows how the GNSS-R module generates the DDM with a non-uniform delay resolution when the difference between the two different initial code phase offsets is not equal to the integer multiple of the configured delay resolution, and there is an overlapping part between two independent DDMs. It is obvious that the overlapping part has a high delay resolution. This high delay resolution is usually set to $\Delta \tau /2$, which not only ensures that the overlapping part has a uniform delay resolution but also simplifies the calculation regarding the difference between two different initial code phase offsets. On the contrary, the GNSS-R module generates the conventional DDM with uniform delay resolution when the difference between two different initial code phase offsets is equal to the integer multiple of the configured delay resolution, and there is no overlapping part between two independent DDMs.

Since the DDM central region around the specular point plays a key role in obtaining basic observables, such as the leading edge slope (LES) and normalized bistatic radar cross section (NBRCS), the programmable non-uniform delay resolution achieves a high delay resolution only in the DDM central region around the specular point and not only improves the accuracy of basic observables but also requires fewer delay bins than the conventional DDM with a uniform delay resolution when covering the same delay scope and achieving same delay resolution in the central region around the specular point, as

Table 2. Based on a typical DDM delay scope of −12.25–12.125 chips, the comparison of number of delay bins between DDM with non-uniform delay resolution and conventional DDM with uniform delay resolution is shown.

DDM	Central Regional Delay			Elsewhere Delay			Total Delay Bins (Counts)
	Resolution (Chips)	Scope (Chips)	Bins (Counts)	Resolution (Chips)	Scope (Chips)	Bins (Counts)
Programmable non-uniform delay resolution	0.125	−2.875 to 2.875	47	0.25	−12.25 to −3 and 3.125 to 12.125	75	122
Conventional uniform delay resolution				0.125		149	196

shows. It should be pointed out that the programmable non-uniform delay resolution is heavily dependent on precise specular point position estimates calculated by the algorithm of SALRGD because the precise specular point position estimate ensures that the specular point is located in the central region of the DDM data.

4.4. Compatibility with GPS, BDS, and Galileo

The reflected GNSS signal that satisfies the strict geometric relationship can be received only by the GNSS-R instruments, which means that the available observations are sparse for a single GNSS constellation. Therefore, it is of great importance for a GNSS-R instrument to be compatible with multiple GNSS constellations to increase observations.

Since the GPS L1 C/A signal and the BDS-2/3 B1I signal all adopt the modulation mode of the binary phase shift key (BPSK), these signals can be processed directly by the DDM generation sub-channel shown in Figure 4 without any extra word. However, the Galileo E1 signal is different from the GPS L1 C/A signal and the BDS-2/3 B1I signal with respect to the signal modulation mode because it employs a combined binary offset carrier (CBOC) [28] modulation mode. Thus, how the GNSS-R module in the SIGRS processes Galileo E1 signals is the focus of this paper.

The Galileo E1 signal consists of a data component, E1B, and a pilot component, E1C. Since both data and pilot components are modulated onto the same carrier component, with a power-sharing of 50 percent, only the data component E1B is processed by the GNSS-R module in the SIGRS. The carrier frequency of the Galileo E1B signal is the same as the GPS L1 C/A signal. As a result, the RFU used for processing the GPS L1 C/A signal is also capable of processing the Galileo E1B signal.

In addition, the CBOC modulation mode employed by the Galileo E1B signal comprises two components, BOC(1,1) and BOC(6,1), respectively, and the power of the BOC(1,1) component accounts for 10/11 of the total power of the Galileo E1B signal. As a consequence, only the BOC(1,1) component is processed by the GNSS-R module in the SIGRS, which is a useful simplification for the system design. For the convenience of description, this paper takes the Galileo E1B signal as a BOC(1,1) signal hereinafter when there are no special instructions.

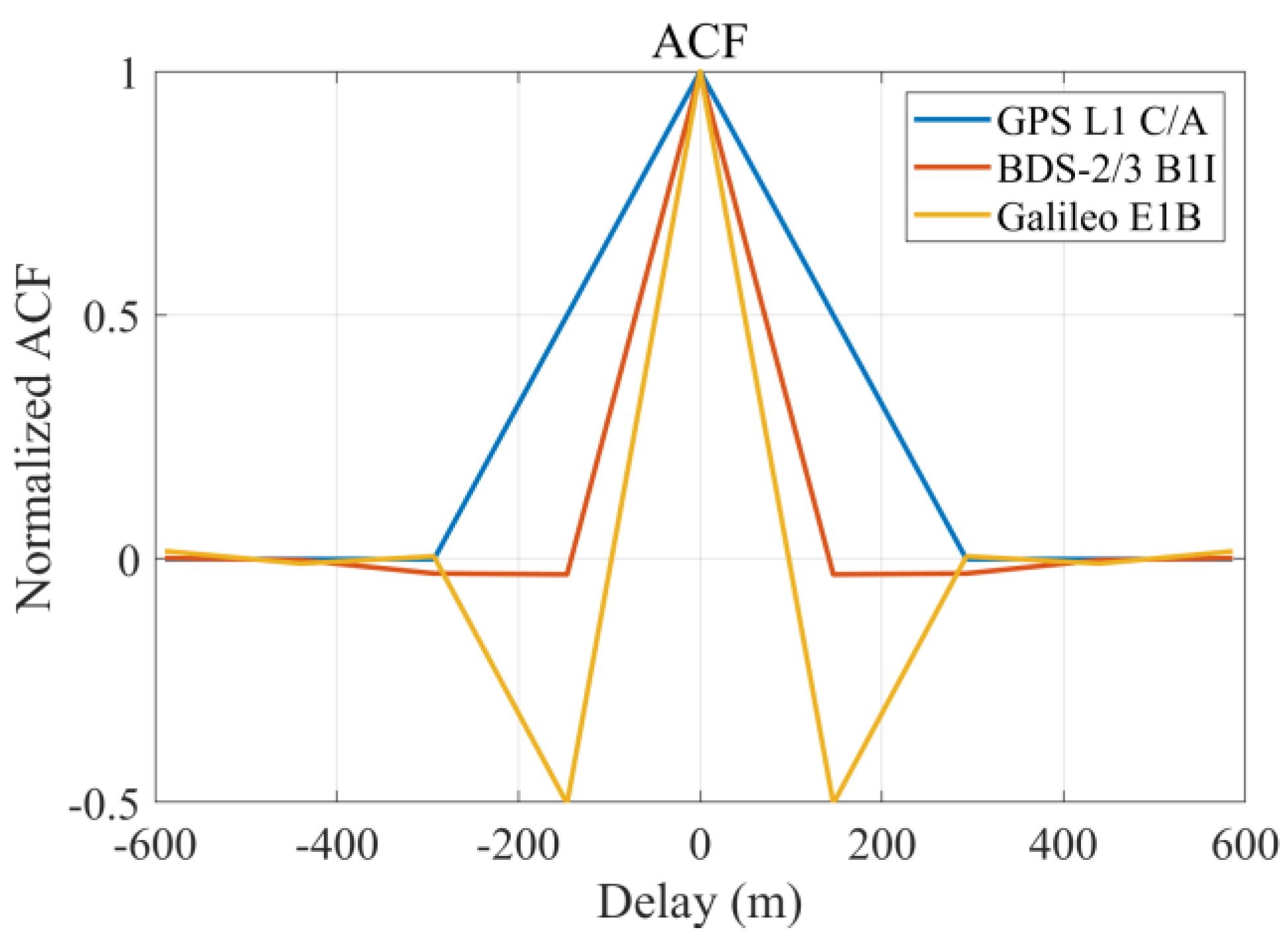
As Figure 7 shows, the auto-correlation function (ACF) of the Galileo E1B signal has two side peaks and one sharpest main peak. In order to reserve as much information about the scattering surface as possible, the GNSS-R module in the SIGRS processes the reflected Galileo E1B signal without side peak removal, and therefore the locally generated PRN code is a composite code that is the product of the primary code and the sub-carrier and has an equivalent chip rate of 2.046 Mega chip per second (Mcps). Moreover, the coherent integration time is also 1 ms for the Galileo E1B signal, although its PRN code period is 4 ms, which merely leads to a slight degradation in its ACF gain and no obvious influence on its DDM data. It is of significant convenience for the low-complexity compatible design of the GNSS-R module that the above-mentioned three-aspect strategies are employed [29].

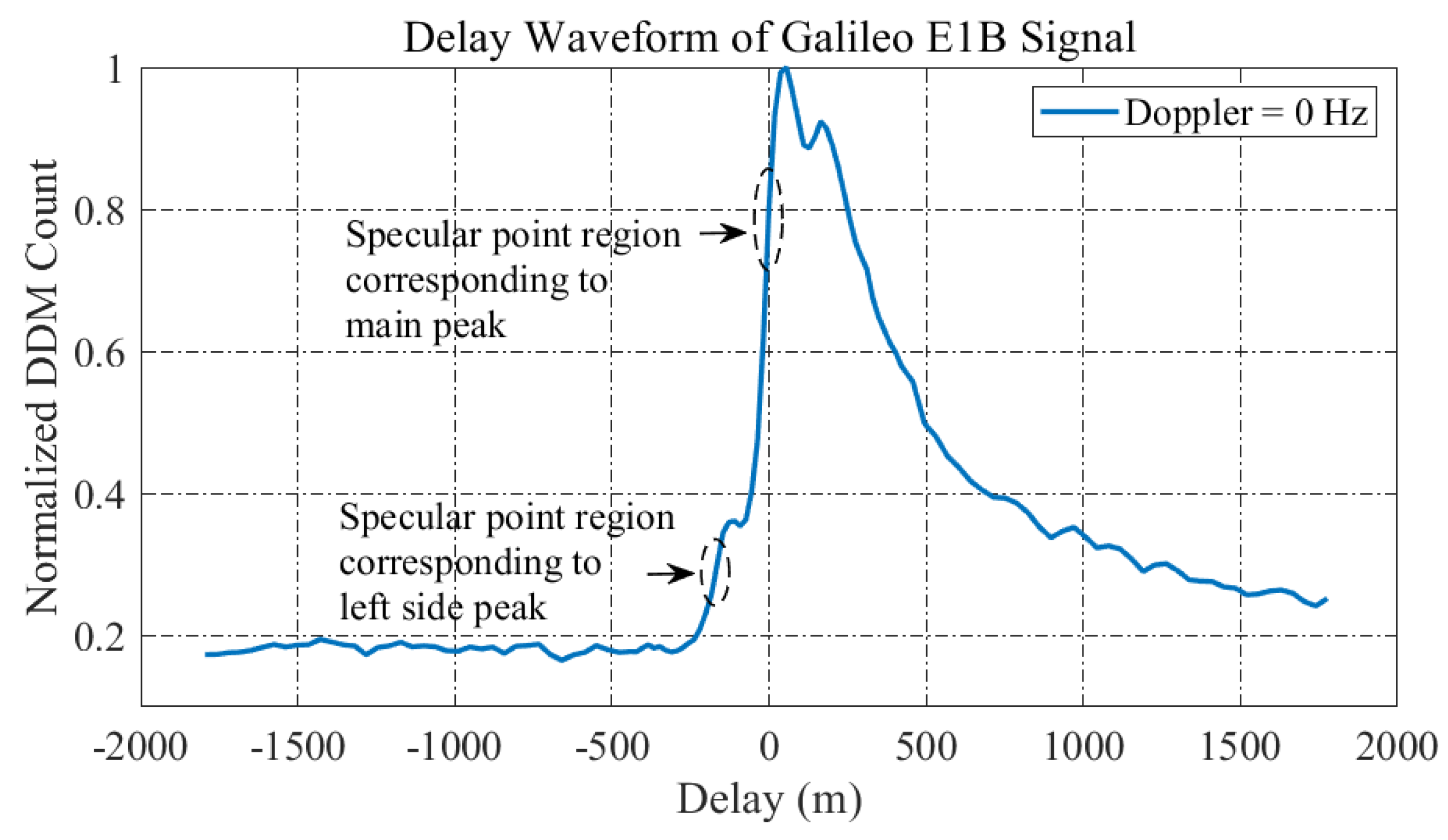
Since the ACF of the Galileo E1B signal has two side peaks and these two side peaks are not only a half primary chip away from the main peak but also have values reaching half of the ACF value of the main peak, two side peaks have a special effect on the delayed waveforms in the DDM. As Figure 8 shows, the left side peak can be ‘geolocated’ in the delay waveform, which means that the left side peak has the potential in obtaining basic observables so as to either perform or facilitate the retrieval of geophysical parameters.

5. In-Orbit Validation

Based on the SIGRS, the GNSS remote sensing payload, GNOS-II onboard the FY-3E satellite was designed. After the successful in-orbit operation, the GNOS-II became the world’s first integrated GNSS remote sensor to combine GNSS RO and GNSS R modules.

Table 3. Parameters of the GNSS-R module of the GNOS-II onboard the FY-3E satellite.

Parameters	Values
Signal	GPS L1 C/A + BDS-2/3 B1I + Galileo E1B
DDM channels	8 (4 of GPS, 3 of BDS-2/3, 1 of Galileo)
Code bin interval	Programmable. The default value is 0.125 chips for the central region and 0.25 chips elsewhere
Code bin number	122
Frequency bin interval	500 Hz
Frequency bin number	20 (−5000 Hz~4500 Hz)
Coherent integration	1 ms
Non-coherent integration	1000
DDM output rate	1 Hz

shows the parameters of the GNSS-R module of the GNOS-II.

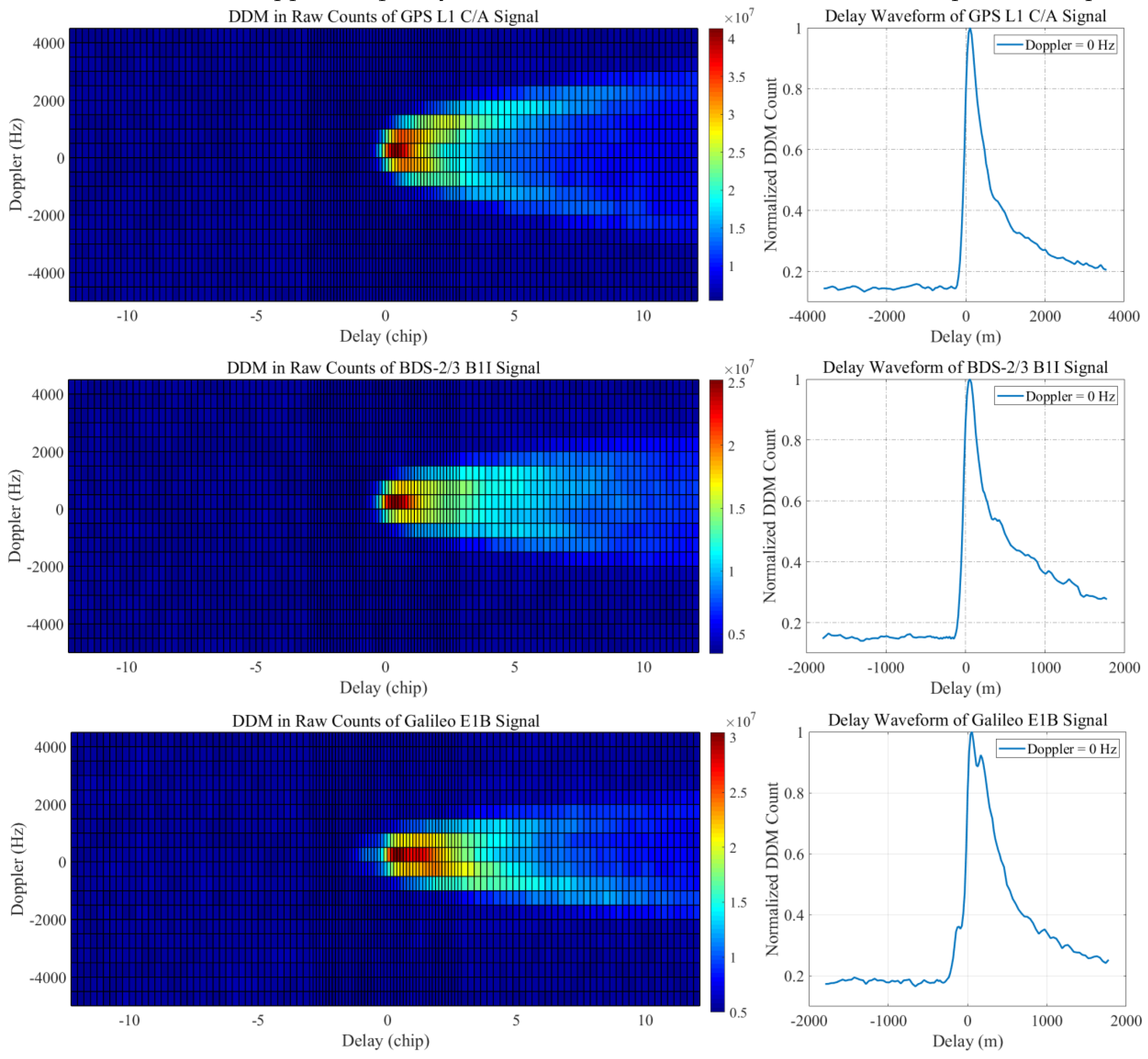
In practice, the GNSS-R module of the GNOS-II generates the DDM with a non-uniform delay resolution, and the delay resolution is programmed as 0.25 chips. Thus, the overlapping part has a high delay resolution of 0.125 chips. Figure 9 shows that the resolution of delay is 0.125 chips from −2.875 to 2.875 chips with respect to the specular point and 0.25 chips elsewhere in the range from −12.25 to 12.125 chips, and the resolution of Doppler frequency is 500 Hz from −5000 Hz to 4500 Hz with respect to the specular point.

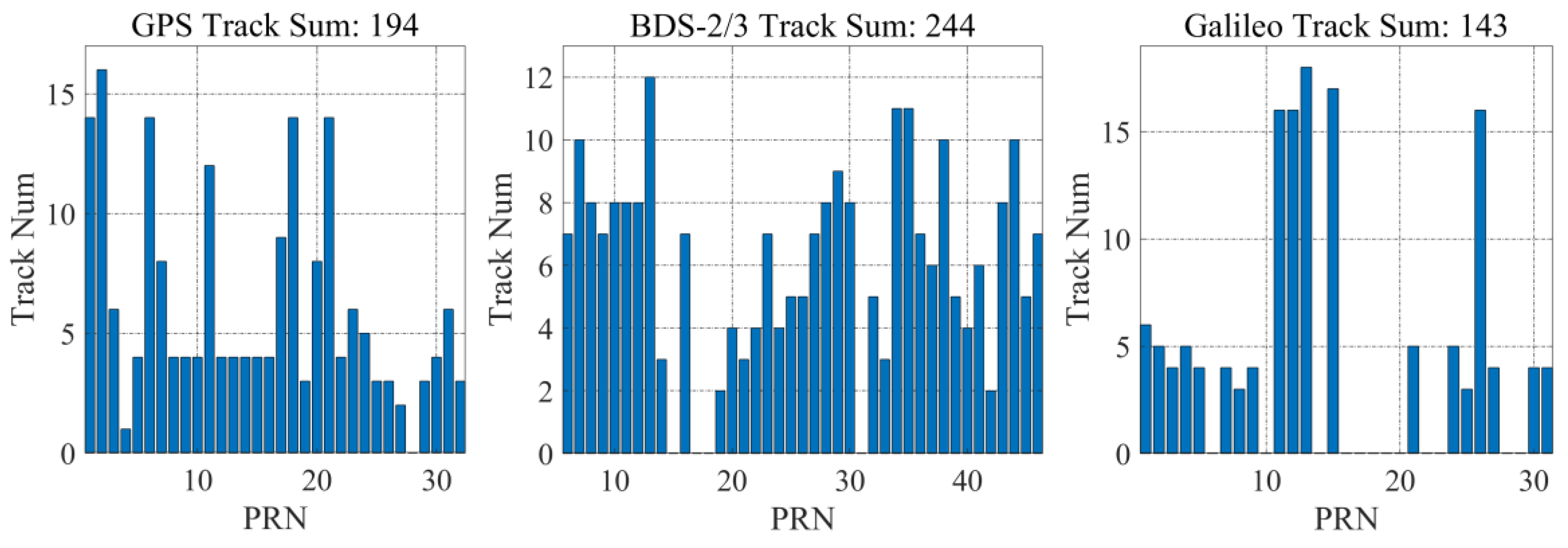
The GNSS-R module of the GNOS-II can collect about 158,180 DDMs over the ocean, about 90,550 DDMs over the land, and about 41,623 DDMs over the ice, on average, each day during August 2022, with a 1 Hz DDM output rate. Figure 10 shows the number of tracks for each GNSS satellite from GPS, BDS-2/3, and Galileo in one day (17 July 2022), where a track is defined as a series of consecutive specular points corresponding to the same GNSS satellite. Based on the data on 17 July 2022, in terms of GPS, one track contained 579 DDMs on average and 1017 DDMs at most, and as far as BDS-2/3, one track contained 534 DDMs on average and 1000 DDMs at most. Regarding Galileo, one track contained 411 DDMs on average and 920 DDMs at most. Figure 11 shows the global distribution of the specular point tracks of the FY-3E satellite in one day (17 July 2022).

The global sea surface wind speed (SWS) is the primary product of the GNOS-II on board the FY-3E satellite, and the Chinese National Satellite Meteorological Center (NSMC) has been releasing the SWS product since 1 June 2022 for global users. The SWS product provides the wind speed at a 10-meter height over the sea surface corresponding to the specular point and covers the Earth between the latitude $\pm 85°$ with a spatial resolution of 25 Km ✕ 25 Km. As a result, the SWS product is used for numerical weather prediction (NWP). However, the SWS product of Galileo was not released until 15 December 2022.

In order to validate the SWS product, the SWS product in 7 days (1–7 September 2022) containing 215,797 SWS observations for GPS and 190,245 SWS observations for BDS-2/3 is used for validation in this paper. Each SWS observation is collocated with the wind speed from the ECMWF ERA5 reanalysis. In terms of the comparison between the SWS and ECMWF wind speeds, Figure 12 shows the root mean square error (RMSE) values for GPS and BDS-2/3 are 1.59 m/s and 1.49 m/s, respectively, and the correlation coefficients for GPS and BDS-2/3 are 0.90 and 0.91, respectively.

As far as the GNSS RO module of the GNOS-II is concerned, it is able to detect about 1200 atmospheric GNSS occultation events on average each day, of which there are about 600 atmospheric GPS occultation events and about 600 atmospheric BDS occultation events. Since the GNSS RO module of the GNOS-II is designed to merely use one GNSS occultation tracking channel to track Galileo occultation signals, the number of detected atmospheric Galileo occultation events is much less than the number of atmospheric GPS and BDS occultation events.

As a consequence, the atmospheric Galileo occultation products have not been assessed and released up to now. Based on the atmospheric GPS and BDS occultation measurements, accurate and precise vertical bending angle profiles are obtained, and then profiles of atmospheric refractivity are calculated. Against the National Centers for Environmental Prediction (NCEP) and FNL (final) operational global analysis data, the inferred refractivity bias and standard deviation of GPS and BDS are shown in Figure 13.

6. Discussions

The results of the in-orbit operation prove that the GNSS-R module of the GNOS-II onboard the FY-3E satellite is able to conduct global observation and output sufficient corresponding DDMs. Based on these DDMs, SWS products are obtained and then released for global users by NSMC, and many other forms of research involving the ice extent, snow depth, soil moisture, and so on, which are being carried out now. In addition, other products of the GNOS-II, such as the atmospheric temperature profile (ATP), electron density profile (EDP), and wet atmosphere profile (WAP), have also been released for global users by NSMC. All of this means that the performance of the GNOS-II meets the expected requirements of CMA. What is more, the success of the GNOS-II indicates that the spaceborne integrated GNSS remote sensor has a broad prospect in Earth observations and will play a key role in future GNSS remote sensing missions.

7. Conclusions

Since the SIGRS has been successfully used to design the GNOS-II onboard the FY-3E satellite, it has become the world’s first successful signal processing scheme for spaceborne integrated GNSS remote sensors to combine a GNSS RO and a GNSS-R module. In addition, the SIGRS is capable of processing GNSS occultation signals and reflected GNSS signals simultaneously to provide information about the ionosphere, neutral atmosphere, ocean, ice, and land, which is of great significance for Earth observation. Moreover, there is no inter-interference among GNSS RO, GNSS-R, and POD modules of the SIGRS, and GNSS RO and GNSS-R modules that share the same POD module, which means that the SIGRS has a lower cost than two separated signal processing designs.

The SIGRS is the first to achieve compatibility with GPS, BDS, and Galileo around the world. In order to reduce the system complexity of the GNSS-R module and reserve as much information about the reflective surface as possible, a series of simplification strategies are used to process reflected Galileo E1B signals, including (1) processing the BOC(1,1) component only, (2) cross-correlating signals without side peak removal using a composite code, and (3) performing 1 ms coherent integration under a PRN code period of 4 ms. Furthermore, it has been pointed out that the left side peak of the ACF of Galileo E1B signals has the potential to obtain basic observables, and the compatibility with Galileo E1B signals sets up a template for future compatibility with other BOC-modulation GNSS signals such as GPS L1C signals, and BDS-3 B1C signals.

Finally, the generation of the programmable non-uniform delay resolution is introduced, and the SIGRS is the first one that is able to generate the DDM with a non-uniform delay resolution. The programmable non-uniform delay resolution achieves a high delay resolution in key central regions around the specular point and then improves the accuracy of basic observables. In comparison to the conventional DDM with uniform delay resolution, the DDM with non-uniform delay resolution requires fewer delay bins when covering the same delay scope and achieving the same high delay resolution in key central regions around the specular point, which leads to an obvious reduction in DDM size.

All in all, the SIGRS represents an economically and technically efficient design with low cost and high effectiveness.