Estimation of Handheld Ground-Penetrating Radar Antenna Position with Pendulum-Model-Based Extended Kalman Filter
Abstract
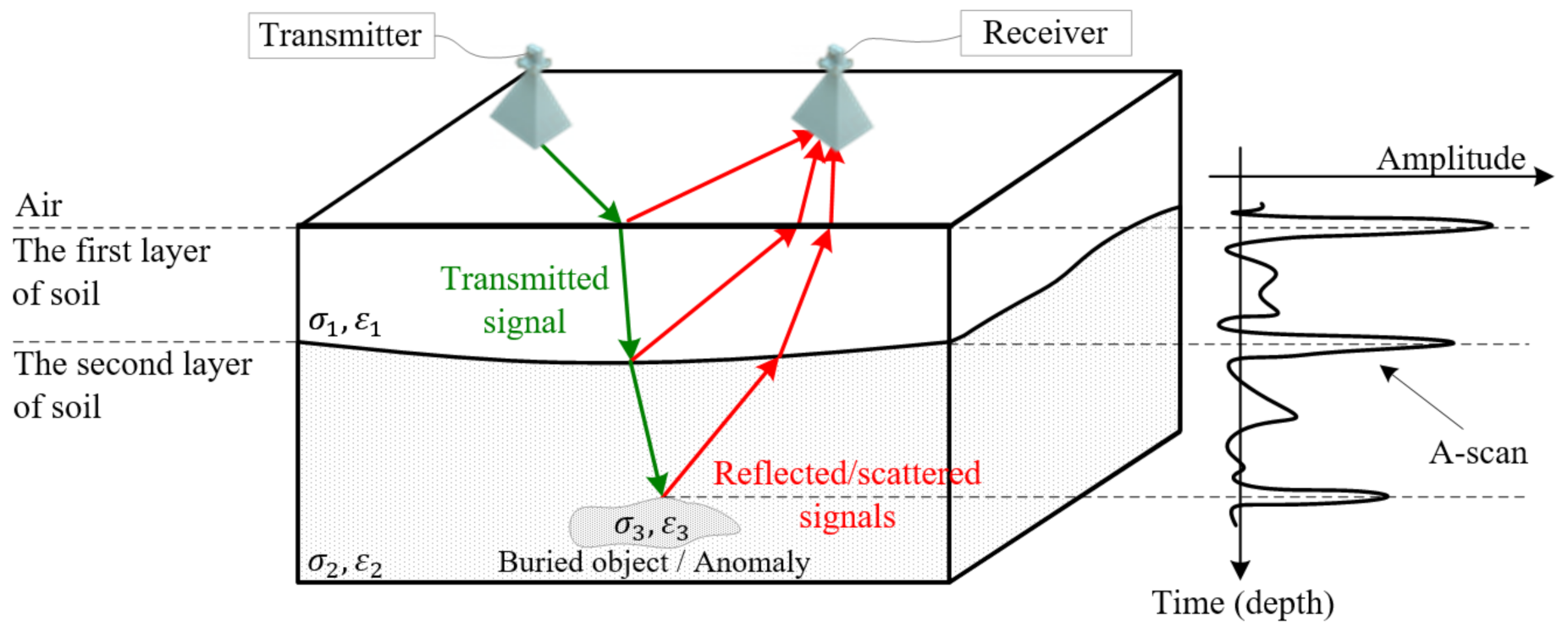
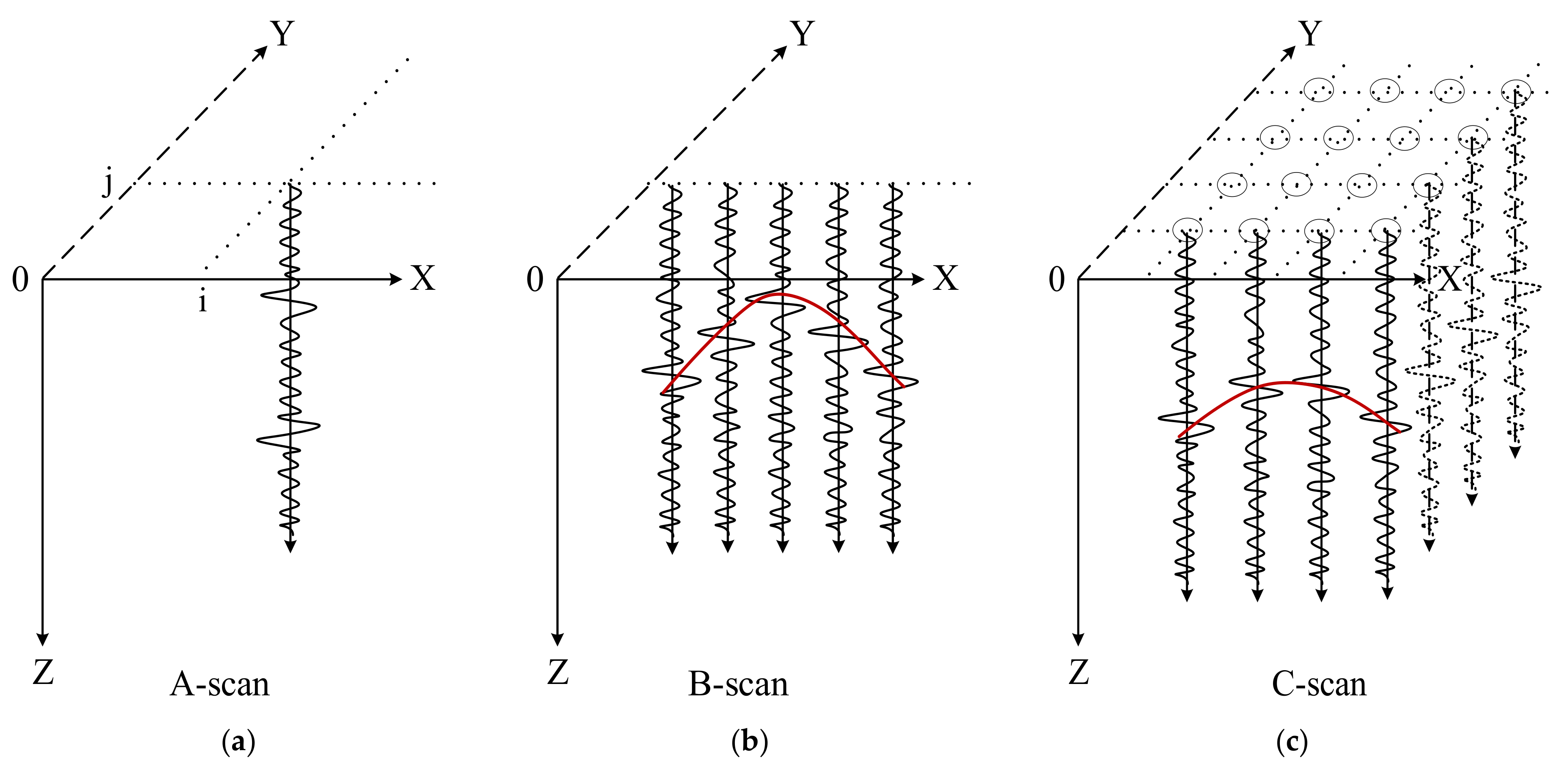
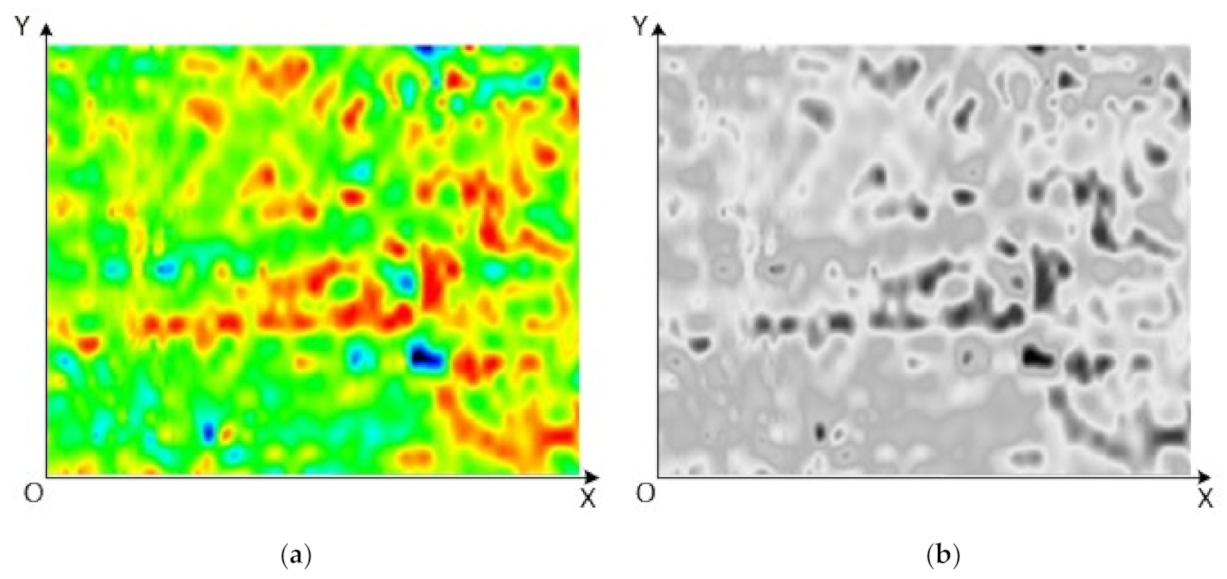
1. Introduction
- Elaboration and detailed presentation of an advanced and practically applicable dynamics and observation model of the UWB-based GPR antenna positioning system, with relinquished simplifying assumptions of the model presented in [41];
- Elaboration and detailed presentation of the estimation algorithm used in the proposed GPR antenna positioning system;
- Presentation of new and detailed results of simulative tests of the positioning system for various realistic system configurations.
2. Materials and Methods
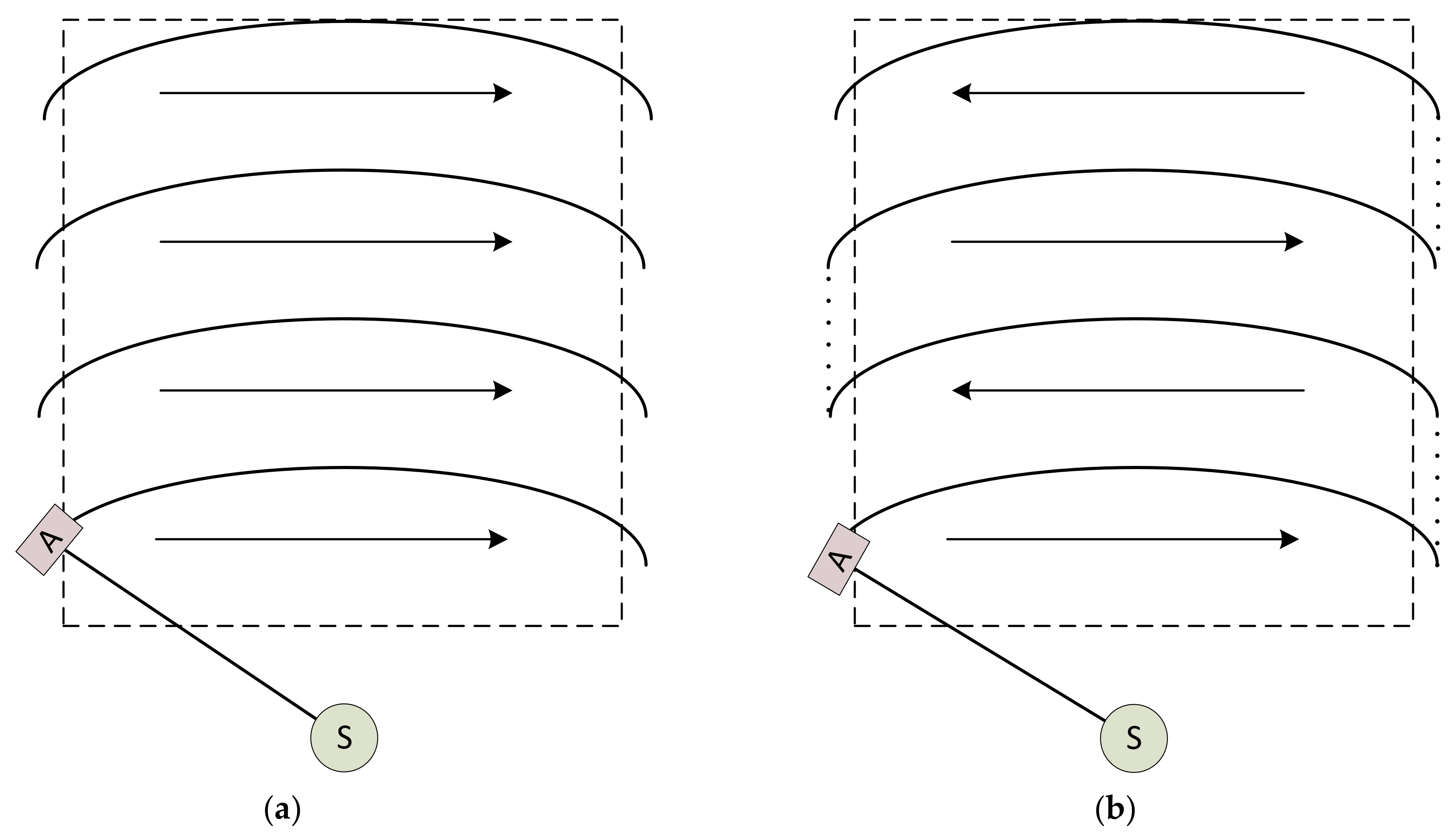
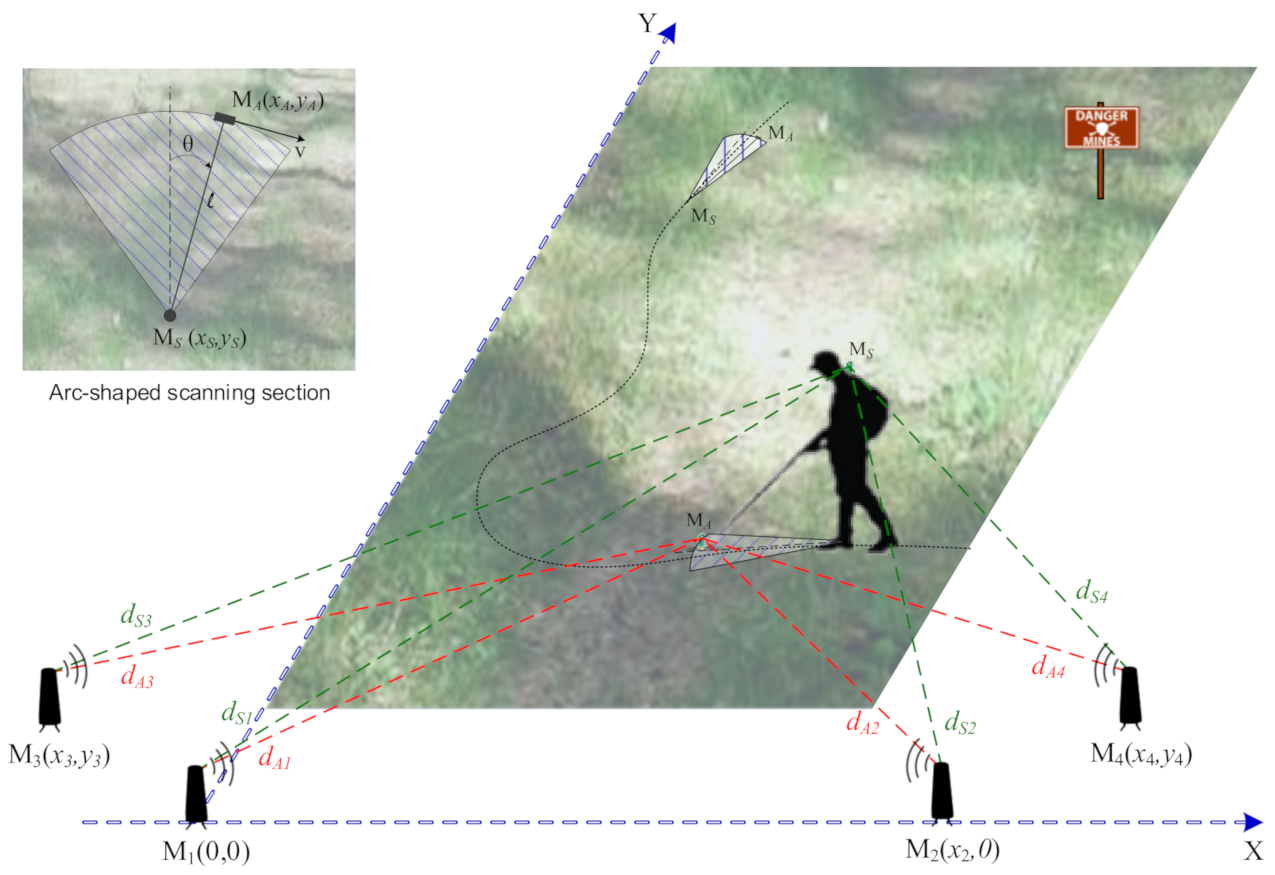
2.1. Scanning Profiles
2.2. UWB Positioning System
- —distance between a j-th beacon and the antenna module ,
- —distance between a j-th beacon and the sapper module ,
- —coordinates of a j-th beacon position,
- —coordinates of the module position,
- —coordinates of the module position,
- —length of the HH-GPR handle (horizontal distance between and ),
- —angle between the horizontal projection of the GPR antenna handle and the central axis of the scanning section.
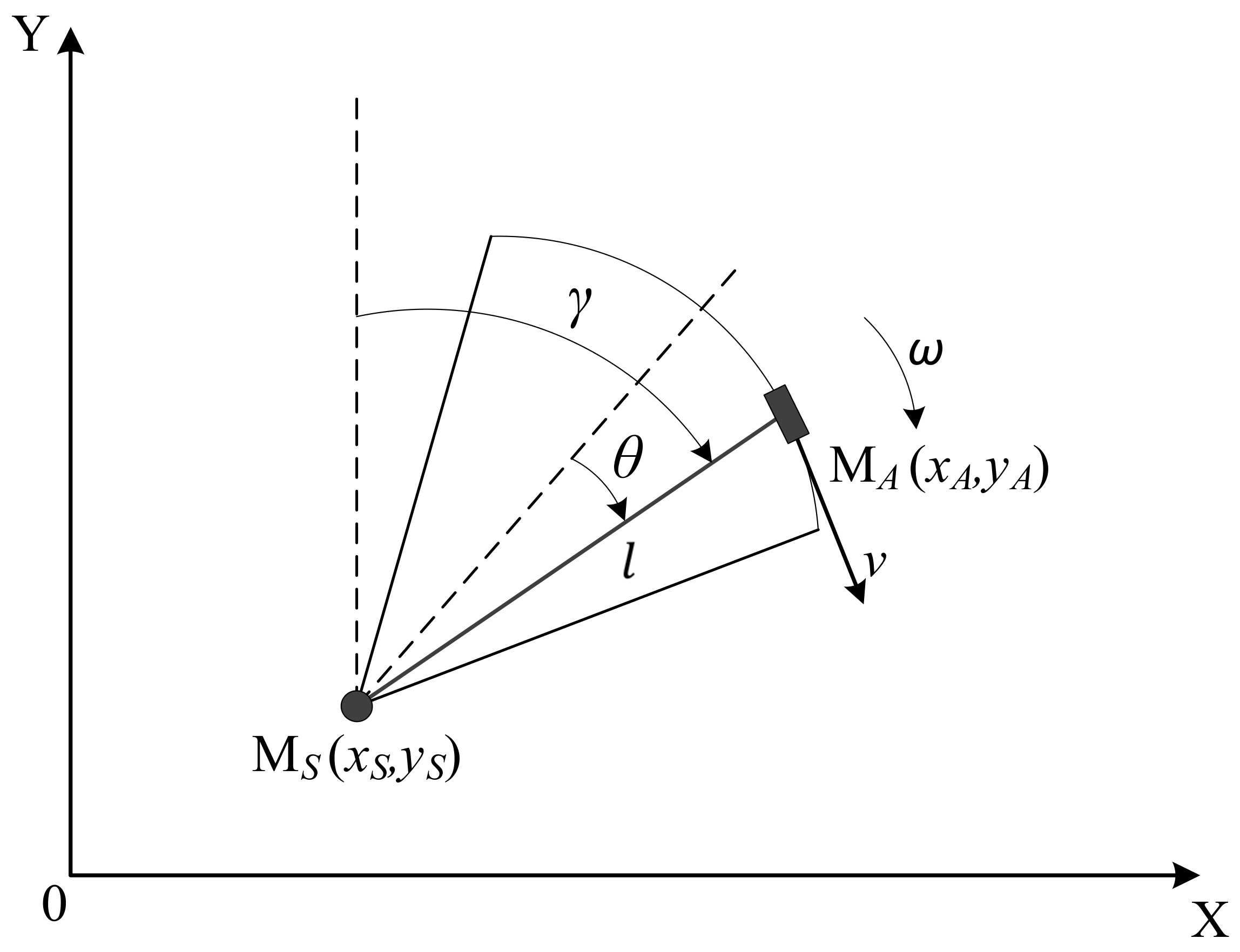
2.3. Mathematical Model
- —coordinates of the HH-GPR antenna ( module) position,
- —coordinates of the sapper’s arm ( module) position,
- —Gaussian white noises representing random components of the sapper’s arm ( module) motion,
- —length of the HH-GPR handle (horizontal distance between and ),
- —angle between the horizontal projection of the GPR antenna handle and the central axis of the scanning section,
- —angle between the horizontal projection of the GPR antenna handle and the axis of the frame of reference,
- —angular velocity of the HH-GPR antenna ( module) motion,
- —acceleration forcing the HH-GPR antenna ( module) motion,
- —Gaussian white noise representing random changes of .
- —distance between a j-th beacon and the antenna module ,
- —distance between a j-th beacon and the sapper module ,
- —coordinates of a j-th beacon position,
- —coordinates of the module position,
- —coordinates of the module position,
- —sapper’s arm height,
- —distance measuring errors for and modules.
2.4. Estimation Algorithm
2.5. Alternative Positioning Algorithms
- —coordinates of antenna position,
- —components of antenna velocity,
- —components of antenna acceleration,
- —Gaussian white noises representing random disturbances of CV motion,
- —Gaussian white noises representing random disturbances of CA motion.
3. Results
3.1. Influence of UWB Beacons’ Locations on System’s Accuracy
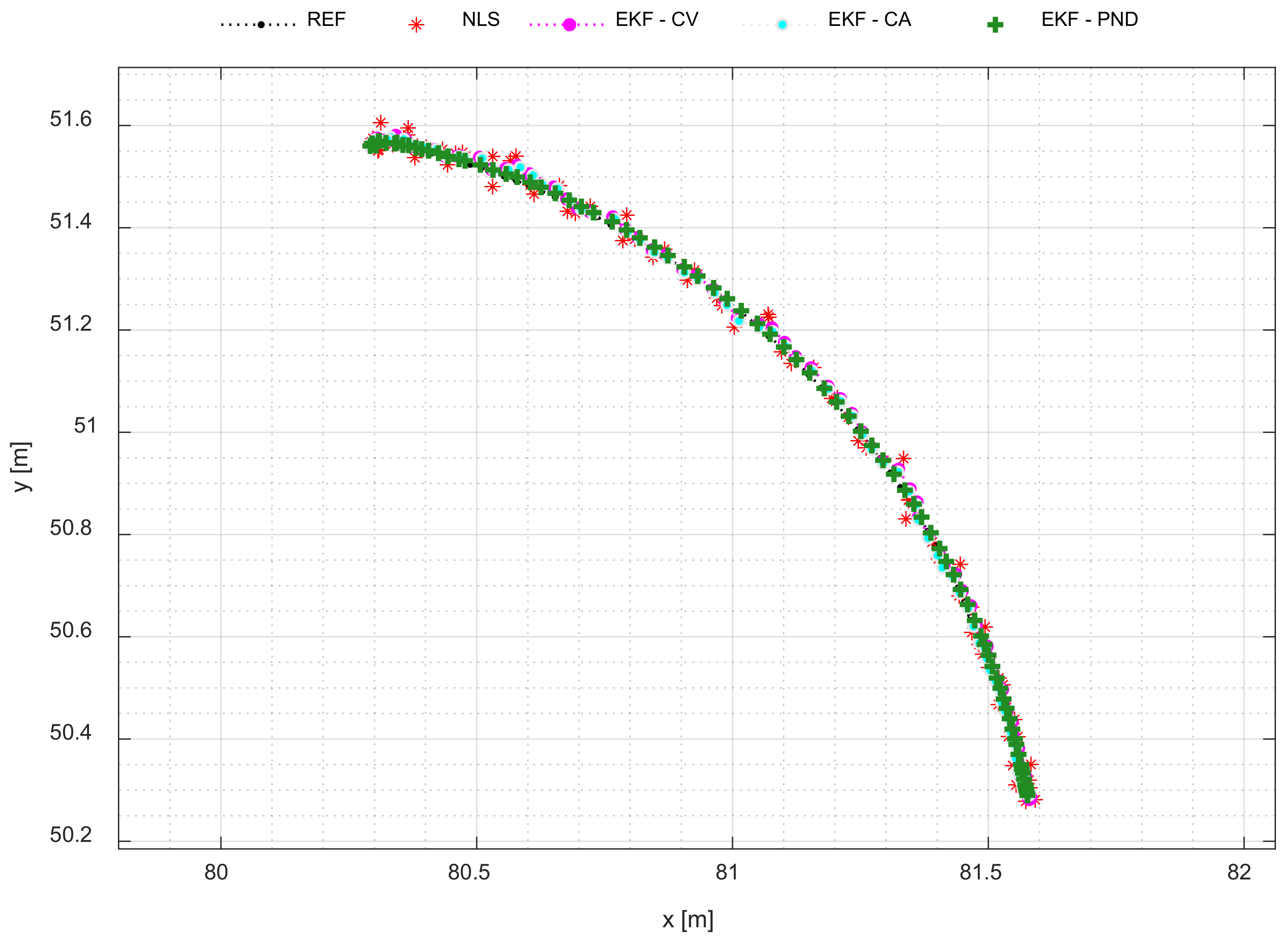
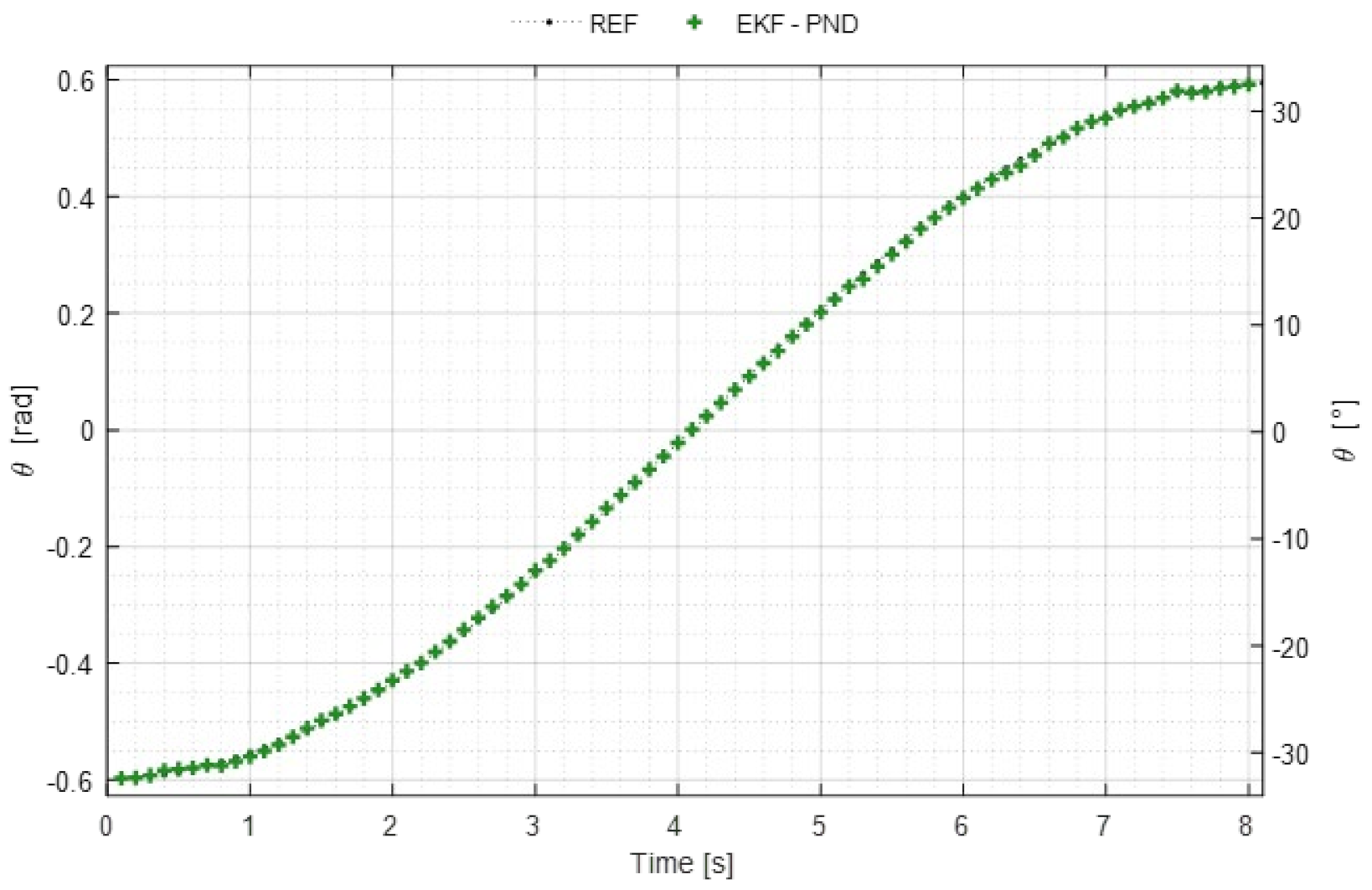
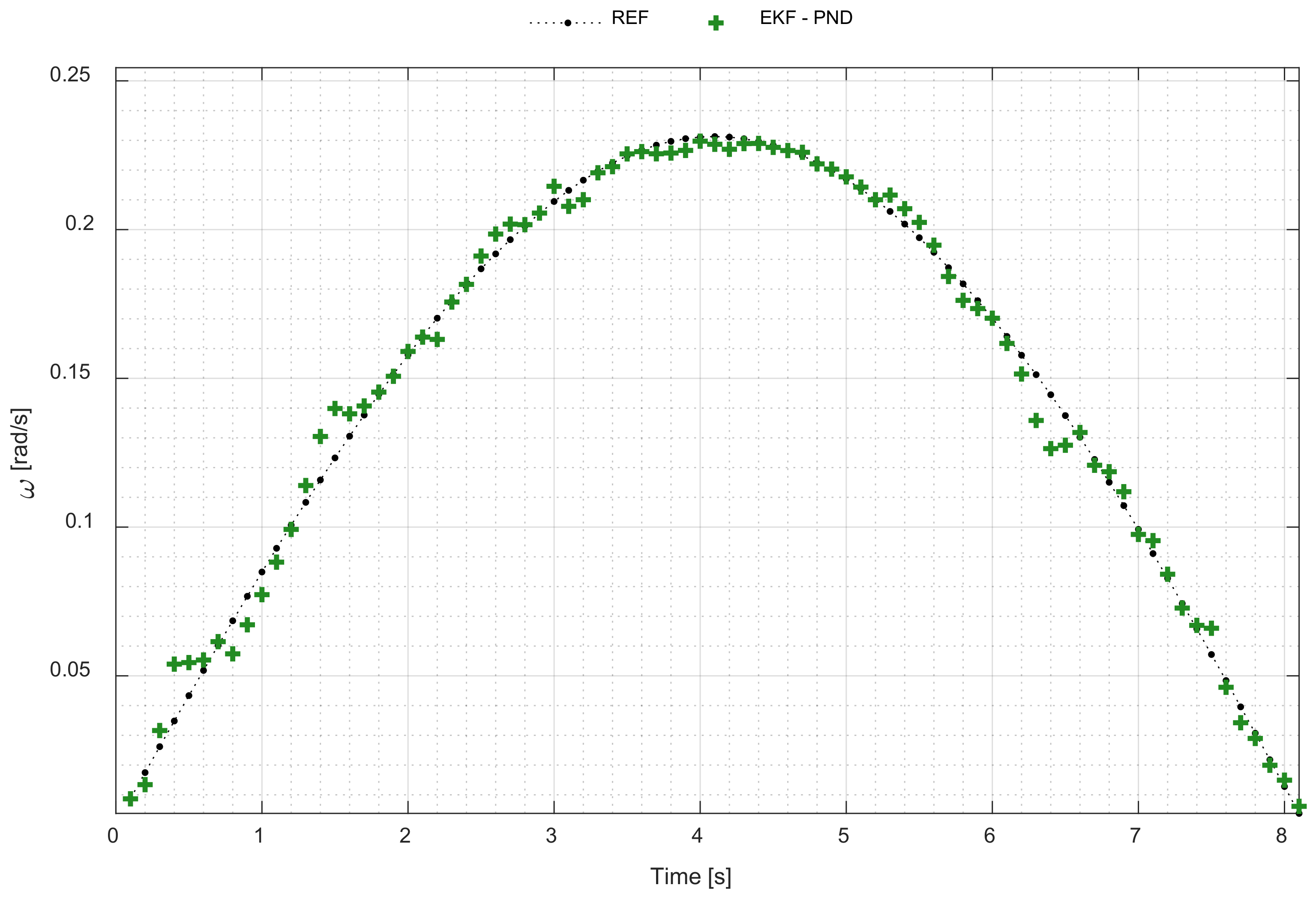
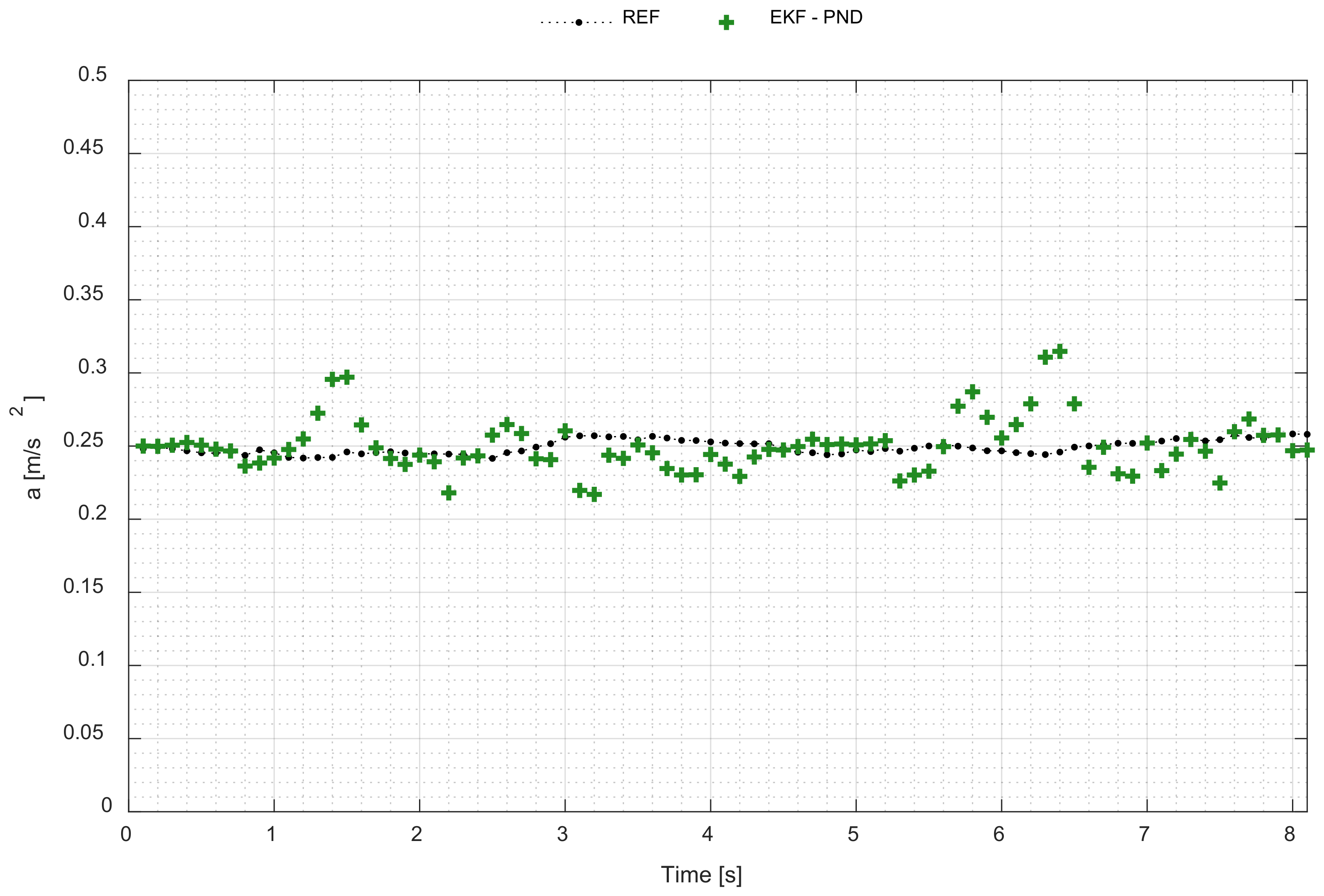
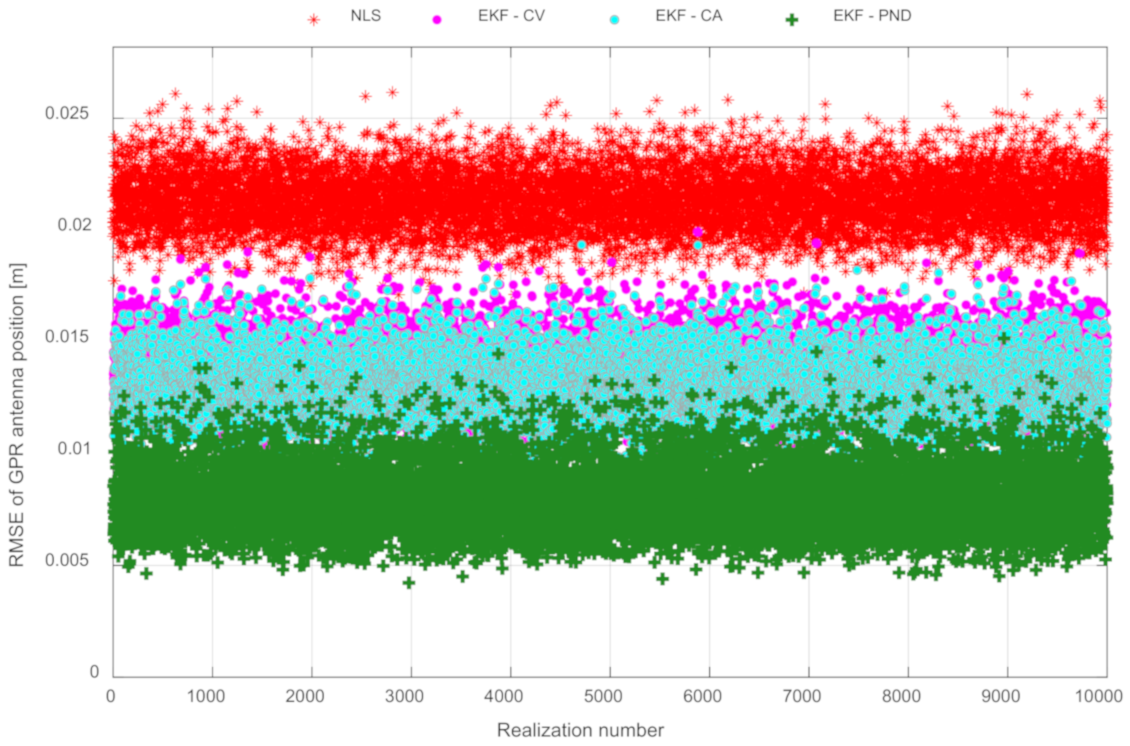
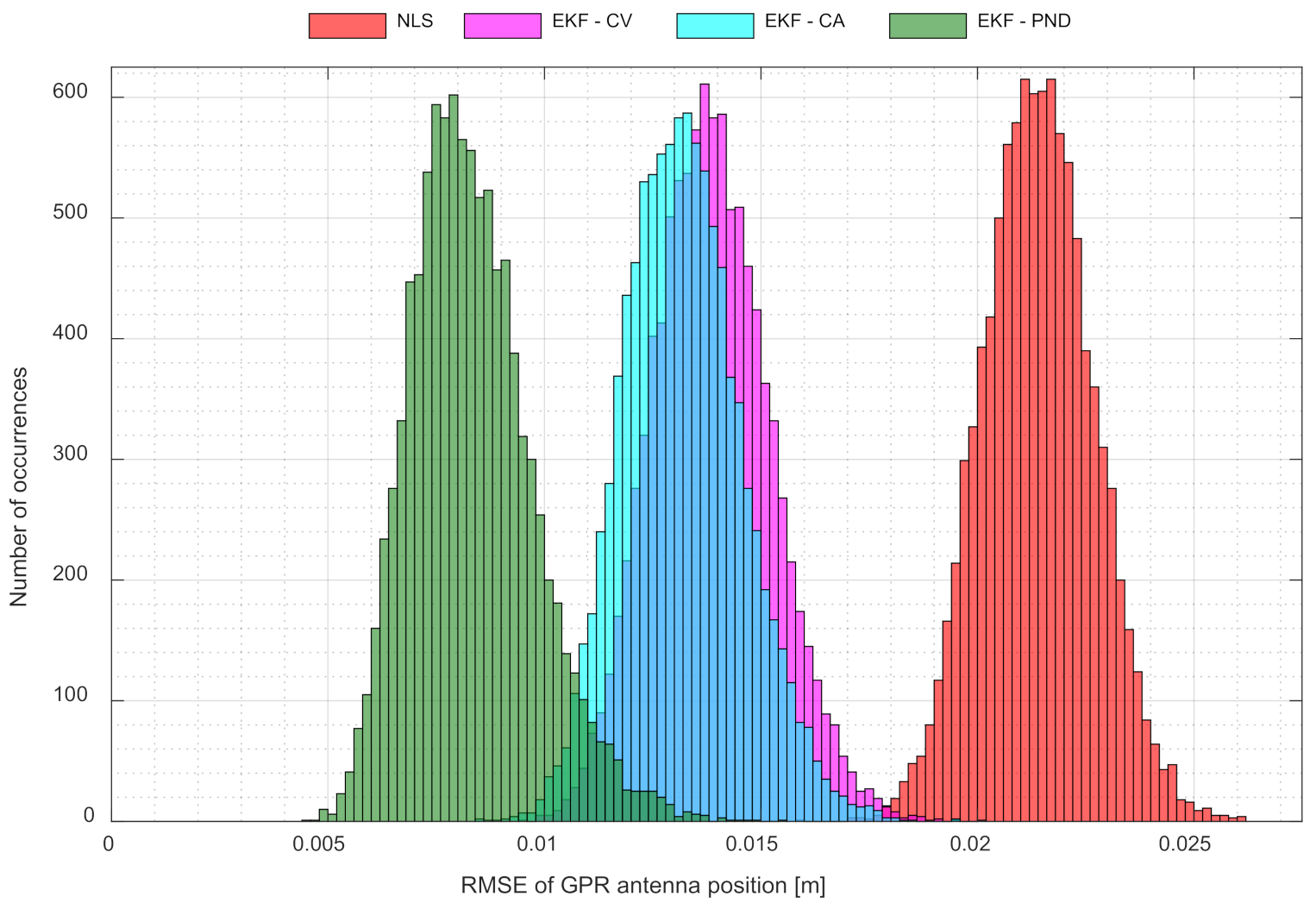
3.2. Positioning Accuracy
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Landmine Monitor 2017. International Campaign to Ban Landmines; Cluster Munition Coalition (ICBL-CMC): Geneva, Switzerland, 2017. [Google Scholar]
- Landmine Monitor 2021. 23rd Annual ed., International Campaign to Ban Landmines; Cluster Munition Coalition (ICBL-CMC): Geneva, Switzerland, 2021. [Google Scholar]
- Daniels, D.J. Ground Penetrating Radar, 2nd ed.; IEE Radar, Sonar and Navigation Series 15; The Institution of Electrical Engineers: London, UK, 2004. [Google Scholar] [CrossRef]
- Kruger, H.; Ewald, H. Handheld metal detector with online visualisation and classification for the humanitarian mine clearance. In Proceedings of the 2008 IEEE SENSORS, Lecce, Italy, 26–29 October 2008. [Google Scholar] [CrossRef]
- Bryakin, I.V.; Bochkarev, I.V.; Khramshin, V.R.; Khramshina, E.A. Developing a Combined Method for Detection of Buried Metal Objects. Machines 2021, 9, 92. [Google Scholar] [CrossRef]
- Guelle, D.; Smith, A.; Lewis, A.; Bloodworth, T. Metal Detector Handbook for Humanitarian Demining; Office for Official Publications of the European Communities: Luxembourg, 2003.
- Furuta, K.; Ishikawa, J. Anti-Personnel Landmine Detection for Humanitarian Demining: The Current Situation and Future Direction for Japanese Research and Development; Springer-Verlag London Limited: London, UK, 2009. [Google Scholar] [CrossRef]
- Barrowes, B.; Prishvin, M.; Jutras, G.; Shubitidze, F. High-Frequency Electromagnetic Induction (HFEMI) Sensor Results from IED Constituent Parts. Remote Sens. 2019, 11, 2355. [Google Scholar] [CrossRef]
- Bruschini, C.; Gros, B.; Guerne, F.; Piece, P.-Y.; Carmona, O. Ground penetrating radar and induction coil sensor imaging for antipersonnel mines detection. In Proceedings of the 6th International Conference on Ground Penetrating Radar (GPR’96), Sendai, Japan, 30 September–3 October 1996. [Google Scholar]
- Szynkarczyk, P.; Wrona, J.; Pasternak, M.; Rubiec, A.; Serafin, P. Unmanned Ground Vehicle Equipped with Ground Penetrating Radar for Improvised Explosives Detection. J. Autom. Mob. Robot. Intell. Syst. 2022, 15, 20–31. [Google Scholar] [CrossRef]
- Daniels, D. Unexploded Ordnance Detection and Mitigation; NATO Science for Peace and Security Series B: Physics and Biophysics; Byrnes, J., Ed.; Springer Science & Business Media: Dordrecht, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Siegel, R. Land mine detection. IEEE Instrum. Meas. Mag. 2002, 5, 22–28. [Google Scholar] [CrossRef]
- Bechtel, T.; Truskavetsky, S.; Capineri, L.; Pochanin, G.; Simic, N.; Viatkin, K.; Sherstyuk, A.; Byndych, T.; Falorni, P.; Bulletti, A.; et al. A survey of electromagnetic characteristics of soils in the Donbass region (Ukraine) for evaluation of the applicability of GPR and MD for landmine detection. In Proceedings of the 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016. [Google Scholar] [CrossRef]
- Ebrahim, S.M.; Medhat, N.I.; Mansour, K.K.; Gaber, A. Examination of soil effect upon GPR detectability of landmine with different orientations. NRIAG J. Astron. Geophys. 2018, 7, 90–98. [Google Scholar] [CrossRef]
- Jol, H.M. Ground Penetrating Radar. Theory and Applications, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Pasternak, M. Radarowa Penetracja Gruntu; Wydawnictwa Komunikacji i Łączności WKŁ: Sulejówek, Poland, 2015. [Google Scholar]
- Li, W.; Cui, X.; Guo, L.; Chen, J.; Chen, X.; Cao, X. Tree Root Automatic Recognition in Ground Penetrating Radar Profiles Based on Randomized Hough Transform. Remote Sens. 2016, 8, 430. [Google Scholar] [CrossRef]
- Karsznia, K.R.; Onyszko, K.; Borkowska, S. Accuracy Tests and Precision Assessment of Localizing Underground Utilities Using GPR Detection. Sensors 2021, 21, 6765. [Google Scholar] [CrossRef]
- Sun, H.; Pashoutani, S.; Zhu, J. Nondestructive Evaluation of Concrete Bridge Decks with Automated Acoustic Scanning System and Ground Penetrating Radar. Sensors 2018, 18, 1955. [Google Scholar] [CrossRef]
- Dong, Z.; Ye, S.; Gao, Y.; Fang, G.; Zhang, X.; Xue, Z.; Zhang, T. Rapid Detection Methods for Asphalt Pavement Thicknesses and Defects by a Vehicle-Mounted Ground Penetrating Radar (GPR) System. Sensors 2016, 16, 2067. [Google Scholar] [CrossRef]
- Kelly, T.B.; Angel, M.N.; O’Connor, D.E.; Huff, C.C.; Morris, L.E.; Wach, G.D. A novel approach to 3D modelling ground-penetrating radar (GPR) data—A case study of a cemetery and applications for criminal investigation. Forensic Sci. Int. 2021, 325, 110882. [Google Scholar] [CrossRef]
- Harari, Z. Ground-penetrating radar (GPR) for imaging stratigraphic features and groundwater in sand dunes. J. Appl. Geophys. 1996, 36, 43–52. [Google Scholar] [CrossRef]
- Zan, Y.; Li, Z.; Su, G.; Zhang, X. An innovative vehicle-mounted GPR technique for fast and efficient monitoring of tunnel lining structural conditions. Case Stud. Nondestruct. Test. Eval. 2016, 6, 63–69. [Google Scholar] [CrossRef]
- Ahmed, S.A.; El Qassas, R.A.Y.; El Salam, H.F.A. Mapping the possible buried archaeological targets using magnetic and ground penetrating radar data, Fayoum, Egypt. Egypt. J. Remote Sens. Space Sci. 2020, 23, 321–332. [Google Scholar] [CrossRef]
- Marsh, L.A.; van Verre, W.; Davidson, J.L.; Gao, X.; Podd, F.J.W.; Daniels, D.J.; Peyton, A.J. Combining Electromagnetic Spectroscopy and Ground-Penetrating Radar for the Detection of Anti-Personnel Landmines. Sensors 2019, 19, 3390. [Google Scholar] [CrossRef]
- Ivashov, S.I.; Makarenkov, V.; Masterkov, A.V.; Razevig, V.V.; Sablin, V.N.; Sheyko, A.P.; Vasilyev, I.A. Remote control mine-detection system with GPR and metal detector. In Proceedings of the SPIE 4084, 8th International Conference on Ground Penetrating Radar, Gold Coast, Australia, 23–26 May 2000. [Google Scholar] [CrossRef]
- Sato, M.; Yokota, Y.; Takahashi, K. ALIS: GPR System for Humanitarian Demining and Its Deployment in Cambodia. J. Korean Inst. Electromagn. Eng. Sci. 2012, 12, 55–62. [Google Scholar] [CrossRef]
- Daniels, D.J.; Curtis, P.; Lockwood, O. Classification of landmines using GPR. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar] [CrossRef]
- De Benedetto, D.; Montemurro, F.; Diacono, M. Mapping an Agricultural Field Experiment by Electromagnetic Induction and Ground Penetrating Radar to Improve Soil Water Content Estimation. Agronomy 2019, 9, 638. [Google Scholar] [CrossRef]
- Frigui, H.; Zhang, L.; Gader, P.D. Context-Dependent Multisensor Fusion and Its Application to Land Mine Detection. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2528–2543. [Google Scholar] [CrossRef]
- AMULET Vehicle-Mounted EODS. Available online: https://www.chelton.com/land/explosive-ordnance-detection-systems/amulet-vehicle-mounted-eods/ (accessed on 29 August 2022).
- Super Buffalo. Available online: https://www.defensemedianetwork.com/stories/general-dynamics-develops-super-buffalo-to-enhance-counter-ied-operations-part-i-multi-functionality/ (accessed on 29 August 2022).
- Ground Penetrating Radar System. Available online: https://www.exponent.com/experience/ground-penetrating-radar-system, (accessed on 29 August 2022).
- Husky Mounted Detection System (HMDS). Available online: https://www.militaryaerospace.com/sensors/article/14175811/groundpenetrating-radar-ied-detection (accessed on 29 August 2022).
- Chemring Sensors & Electronic System. Available online: https://www.chemring.com/what-we-do/sensors-and-information/ied-detection, (accessed on 4 September 2022).
- Arvaniti, A.; Orzeł-Tatarczuk, E.; Popkowski, J.; Kaczmarek, P.; Kawalec, A.M.; Pasternak, M.L. Mobilna platforma z ultraszerokopasmowym radarem do wykrywania ukrytych w ziemi niebezpiecznych obiektów. In Urządzenia i systemy radioelektroniczne. Wybrane problemy 2; Wojskowa Akademia Techniczna: Warszawa, Poland, 2012. [Google Scholar]
- The GPR for UGV project. Available online: https://www.australiandefence.com.au/land/sme-proves-radar-equipped-ugv-concept-for-mine-and-ied-detection (accessed on 29 August 2022).
- Defence Research & Development Organisation. Available online: https://www.drdo.gov.in/muntra-m (accessed on 29 August 2022).
- Knox, M.; Torrione, P.; Collins, L.; Morton, K., Jr. Buried threat detection using a handheld ground penetrating radar system. In Proceedings of the SPIE 9454, Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XX, 94540F, Baltimore, MD, USA, 20–23 April 2015. [Google Scholar] [CrossRef]
- Ho, K.C.; Collins, L.M.; Huettel, L.G.; Gader, P.D. Discrimination mode processing for EMI and GPR sensors for hand-held land mine detection. IEEE Trans. Geosci. Remote Sens. 2004, 42, 249–263. [Google Scholar] [CrossRef]
- Kaniewski, P.; Kraszewski, T. Novel Algorithm for Position Estimation of Handheld Ground-Penetrating Radar Antenna. In Proceedings of the 21st International Radar Symposium (IRS), Warsaw, Poland, 5–8 October 2020. [Google Scholar] [CrossRef]
- Pasternak, M.; Miluski, W.; Czarnecki, W.; Pietrasiński, J. An optoelectronic-inertial system for handheld GPR positioning. In Proceedings of the 15th International Radar Symposium (IRS), Gdansk, Poland, 16–18 June 2014. [Google Scholar] [CrossRef]
- Zoubir, A.M.; Chant, I.J.; Brown, C.L.; Barkat, B.; Abeynayake, C. Signal processing techniques for landmine detection using impulse ground penetrating radar. IEEE Sens. J. 2002, 2, 41–51. [Google Scholar] [CrossRef]
- Lee, J.S.; Nguyen, C.; Scullion, T. A novel, compact, low-cost, impulse ground-penetrating radar for nondestructive evaluation of pavements. IEEE Trans. Instrum. Meas. 2004, 53, 1502–1509. [Google Scholar] [CrossRef]
- Suksmono, A.B.; Bharata, E.; Lestari, A.A.; Yarovoy, A.G.; Ligthart, L.P. Compressive Stepped-Frequency Continuous-Wave Ground-Penetrating Radar. IEEE Geosci. Remote Sens. Lett. 2010, 7, 665–669. [Google Scholar] [CrossRef]
- Iftimie, N.; Savin, A.; Steigmann, R.; Dobrescu, G.S. Underground Pipeline Identification into a Non-Destructive Case Study Based on Ground-Penetrating Radar Imaging. Remote Sens. 2021, 13, 3494. [Google Scholar] [CrossRef]
- Bigman, D.P.; Day, D.J. Ground penetrating radar inspection of a large concrete spillway: A case-study using SFCW GPR at a hydroelectric dam. Case Stud. Constr. Mater. 2022, 16, e00975. [Google Scholar] [CrossRef]
- Jing, H.; Vladimirova, T. Novel algorithm for landmine detection using C-scan ground penetrating radar signals. In Proceedings of the Seventh International Conference on Emerging Security Technologies (EST), Canterbury, UK, 6–8 September 2017; pp. 68–73. [Google Scholar] [CrossRef]
- Grasmueck, M.; Viggiano, D.A. Integration of Ground-Penetrating Radar and Laser Position Sensors for Real-Time 3-D Data Fusion. IEEE Trans. Geosci. Remote Sens. 2007, 45, 130–137. [Google Scholar] [CrossRef]
- Doerksen, K.; McNaughton, A. Positioning system for ground penetrating radar instruments. U.S. Patent US 2003/0112170 A1, 19 June 2003. [Google Scholar]
- Pasternak, M.; Kaczmarek, P. Continuous wave ground penetrating radars: State of the art. In Proceedings of the SPIE, Event: XII Conference on Reconnaissance and Electronic Warfare Systems, Oltarzew, Poland, 19–21 November 2018; SPIE: Bellingham, WA, USA, 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Ferrara, V.; Pietrelli, A.; Chicarella, S.; Pajewski, L. GPR/GPS/IMU system as buried objects locator. Measurement 2018, 114, 534–541. [Google Scholar] [CrossRef]
- Barzaghi, R.; Cazzaniga, N.E.; Pagliari, D.; Pinto, L. Vision-Based Georeferencing of GPR in Urban Areas. Sensors 2016, 16, 132. [Google Scholar] [CrossRef]
- Kaniewski, P.; Kraszewski, T.; Pasek, P. UWB-Based Positioning System for Supporting Lightweight Handheld Ground-Penetrating Radar. In Proceedings of the IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel Aviv, Israel, 4–6 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- TDSR. Data Sheet/User Guide P440 UWB Module; TDSR: Petersburg, TN, USA, 2020.
- Awrejcewicz, J. Mathematical and Physical Pendulum. In Classical Mechanics. Advances in Mechanics and Mathematics, 2012th Edition; Springer: New York, NY, USA, 2012; Volume 29. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory, Algorithms and Software; Wiley-Interscience; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Balakrishnan, A.V. Introduction to Random Processes in Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Szabados, T. An elementary introduction to the Wiener process and stochastic integrals. In Studia Scientiarum Mathematicarum Hungarica; Akadémiai Kiadó: Budapest, Hungary, 2010. [Google Scholar]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering with Matlab Exercises, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kaniewski, P.T. Struktury, Modele i Algorytmy w Zintegrowanych Systemach Pozycjonujących i Nawigacyjnych; Wojskowa Akademia Techniczna: Warszawa, Poland, 2010. [Google Scholar]
- Zarchan, P.; Musoff, H. Fundamentals of Kalman Filtering: A Practical Approach, 3rd ed.; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2009. [Google Scholar]
- Setoodeh, P.; Habibi, S.; Haykin, S. Nonlinear Filters: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Frogerais, P.; Bellanger, J.-J.; Senhadji, L. Various Ways to Compute the Continuous-Discrete Extended Kalman Filter. IEEE Trans. Autom. Control. 2012, 57, 1000–1004. [Google Scholar] [CrossRef]
- Takeno, M.; Katayama, T. A numerical method for continuous-discrete unscented Kalman filter. Int. J. Innov. Comput. Inf. Control. 2012, 8, 2261–2274. [Google Scholar]
- Chapra, S.V.R. Numerical Methods for Engineers; McGraw Hill: New York, NY, USA, 2010. [Google Scholar]
- Hellevik, L.F. Numerical Methods for Engineers; Department of Structural Engineering, Norwegian University of Science and Technology: Trondheim, Norway, 2020. [Google Scholar]
- Pańczyk, B.; Łukasik, E.; Sikora, J.; Guziak, T. Metody Numeryczne w Przykładach; Politechnika Lubelska: Lublin, Poland, 2012. [Google Scholar]
- Cheung, K.W.; So, H.C.; Ma, W.-K.; Chan, Y.T. Least squares algorithms for time-of-arrival-based mobile location. IEEE Trans. Signal Process. 2004, 52, 1121–1130. [Google Scholar] [CrossRef]
- Wu, X.; Tan, S. Error Estimation of Iterative Localization Based on Non-linear Least Square Residuals. In Proceedings of the International Conference on Computer Science and Service System, Nanjing, China, 11–13 August 2012; pp. 1579–1582. [Google Scholar] [CrossRef]
- Rong, X.L.; Jilkov, V.P. Survey of maneuvering target tracking. Part I. Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar] [CrossRef]
- Kolat, M.; Törő, O.; Bécsi, T. Performance Evaluation of a Maneuver Classification Algorithm Using Different Motion Models in a Multi-Model Framework. Sensors 2022, 22, 347. [Google Scholar] [CrossRef]
- Pant, B.; Alkin, O. Correlated movement mobility model and constant acceleration model for EKF-based tracking applications. In Proceedings of the IEEE 8th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Barcelona, Spain, 8–10 October 2012; pp. 869–874. [Google Scholar] [CrossRef]
- Blackman, S.; Popoli, R. Design and Analysis of Modern Tracking Systems. Artech House Inc.: Norwood, MA, USA, 1999. [Google Scholar]
- Stawowy, M.; Duer, S.; Paś, J.; Wawrzyński, W. Determining Information Quality in ICT Systems. Energies 2021, 14, 5549. [Google Scholar] [CrossRef]
- Candy, J.V. Bayesian Signal Processing: Classical, Modern, and Particle Filtering Methods, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]


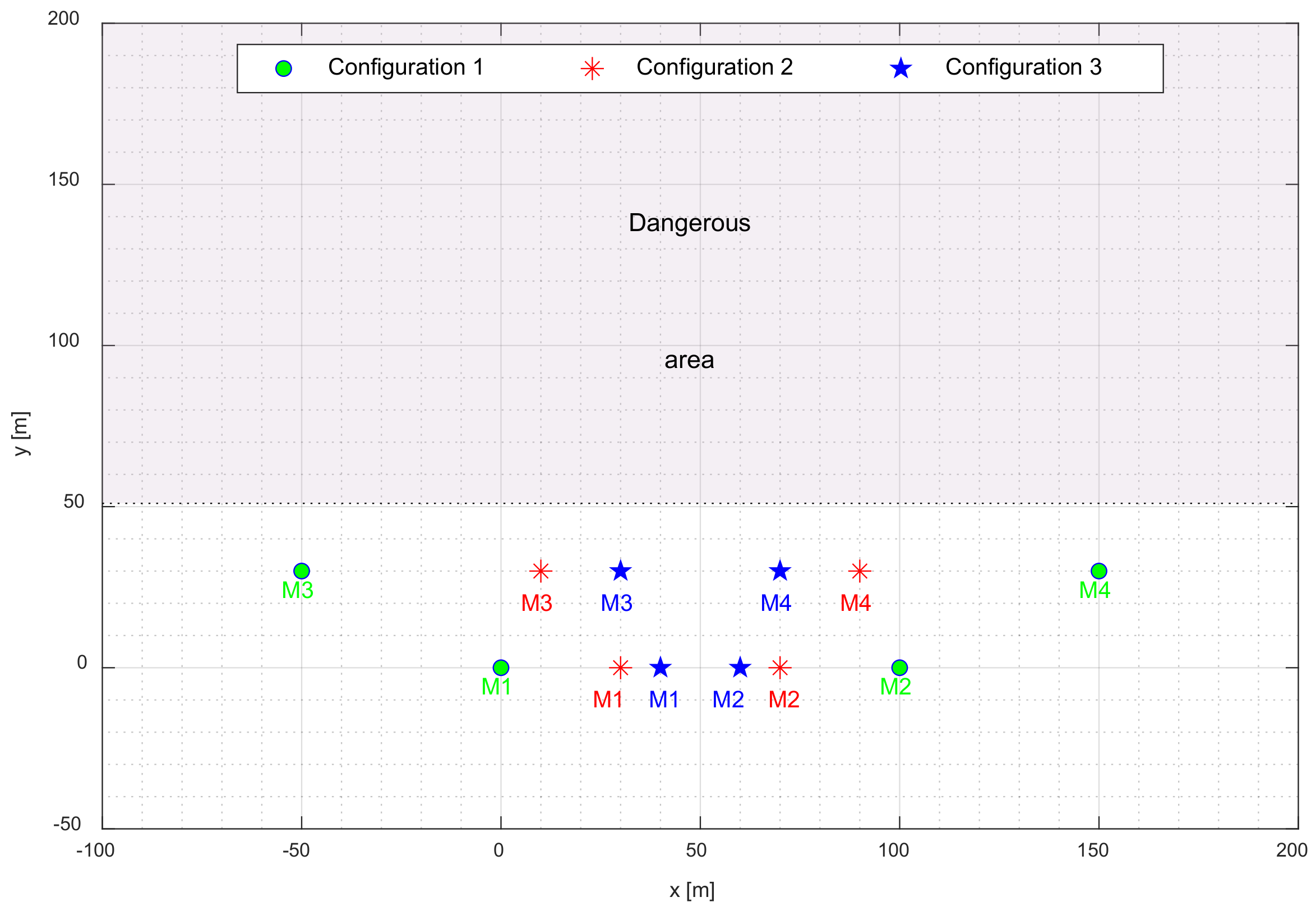
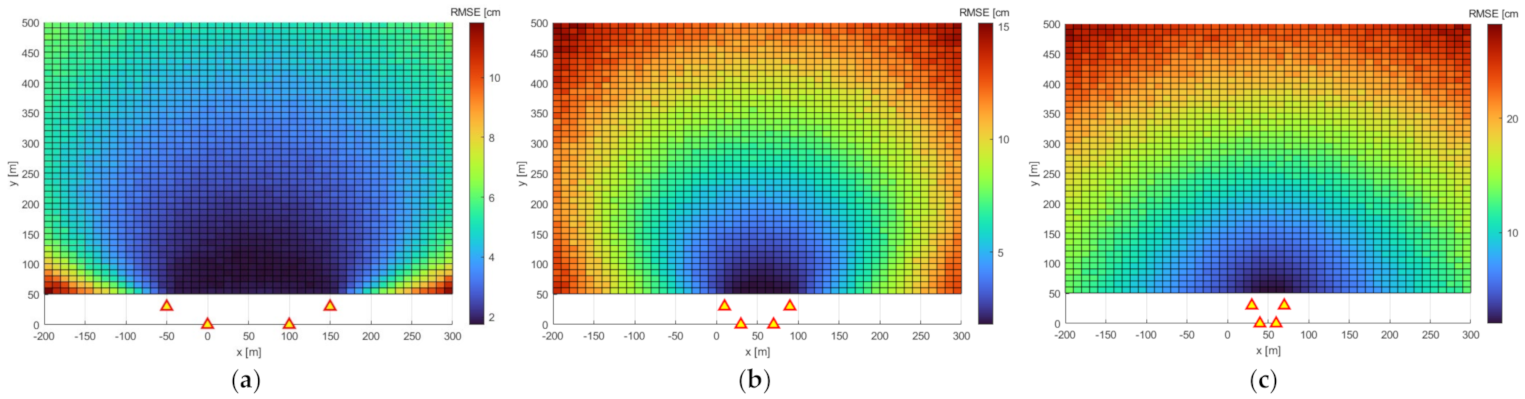

| Configuration Number | Coordinates of the UWB Modules | |||
|---|---|---|---|---|
| M1 | M2 | M3 | M4 | |
| C1 | [0,0] | [100,0] | [−50,30] | [150,30] |
| C2 | [30,0] | [70,0] | [10,30] | [90,30] |
| C3 | [40,0] | [60,0] | [30,30] | [70,30] |
| Configuration Number | The Area of Interest | |||||
|---|---|---|---|---|---|---|
| RMSE Values [cm] | ||||||
| Mean | Max | Mean | Max | Mean | Max | |
| C1 | 4.0786 | 11.8357 | 2.0348 | 2.4603 | 1.9048 | 2.1324 |
| C2 | 8.9495 | 15.1545 | 3.6597 | 4.9420 | 3.1985 | 4.0216 |
| C3 | 15.5555 | 28.2914 | 6.6283 | 9.1209 | 5.6234 | 6.9220 |
| Parameter Name | Symbol | Value | Unit |
|---|---|---|---|
| Length of the HH-GPR handle | l | ||
| Starting angle of the scanning section | |||
| Nominal acceleration | |||
| Standard deviations of all the distance measuring errors | |||
| -coordinate of the initial sapper position | |||
| -coordinate of the initial sapper position | |||
| Sapper’s arm height | |||
| Period between two successive time steps | 0.1 | s | |
| Power spectral density of disturbances | |||
| Power spectral density of disturbances | |||
| Power spectral density of disturbances |
| NLS | EKF-CV | EKF-CA | EKF-PND | |
|---|---|---|---|---|
| Mean RMSE [cm] | 2.14 | 1.39 | 1.32 | 0.83 |
| Improvement vs. NLS [%] | --- | 35.2 | 38.3 | 61.1 |
| Improvement vs. CV [%] | --- | --- | --- | 40.0 |
| Improvement vs. CA [%] | --- | --- | --- | 36.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaniewski, P.; Kraszewski, T. Estimation of Handheld Ground-Penetrating Radar Antenna Position with Pendulum-Model-Based Extended Kalman Filter. Remote Sens. 2023, 15, 741. https://doi.org/10.3390/rs15030741
Kaniewski P, Kraszewski T. Estimation of Handheld Ground-Penetrating Radar Antenna Position with Pendulum-Model-Based Extended Kalman Filter. Remote Sensing. 2023; 15(3):741. https://doi.org/10.3390/rs15030741
Chicago/Turabian StyleKaniewski, Piotr, and Tomasz Kraszewski. 2023. "Estimation of Handheld Ground-Penetrating Radar Antenna Position with Pendulum-Model-Based Extended Kalman Filter" Remote Sensing 15, no. 3: 741. https://doi.org/10.3390/rs15030741
APA StyleKaniewski, P., & Kraszewski, T. (2023). Estimation of Handheld Ground-Penetrating Radar Antenna Position with Pendulum-Model-Based Extended Kalman Filter. Remote Sensing, 15(3), 741. https://doi.org/10.3390/rs15030741







