Fast Wideband Beamforming Using Convolutional Neural Network
Abstract
1. Introduction
2. Wideband Signal Model
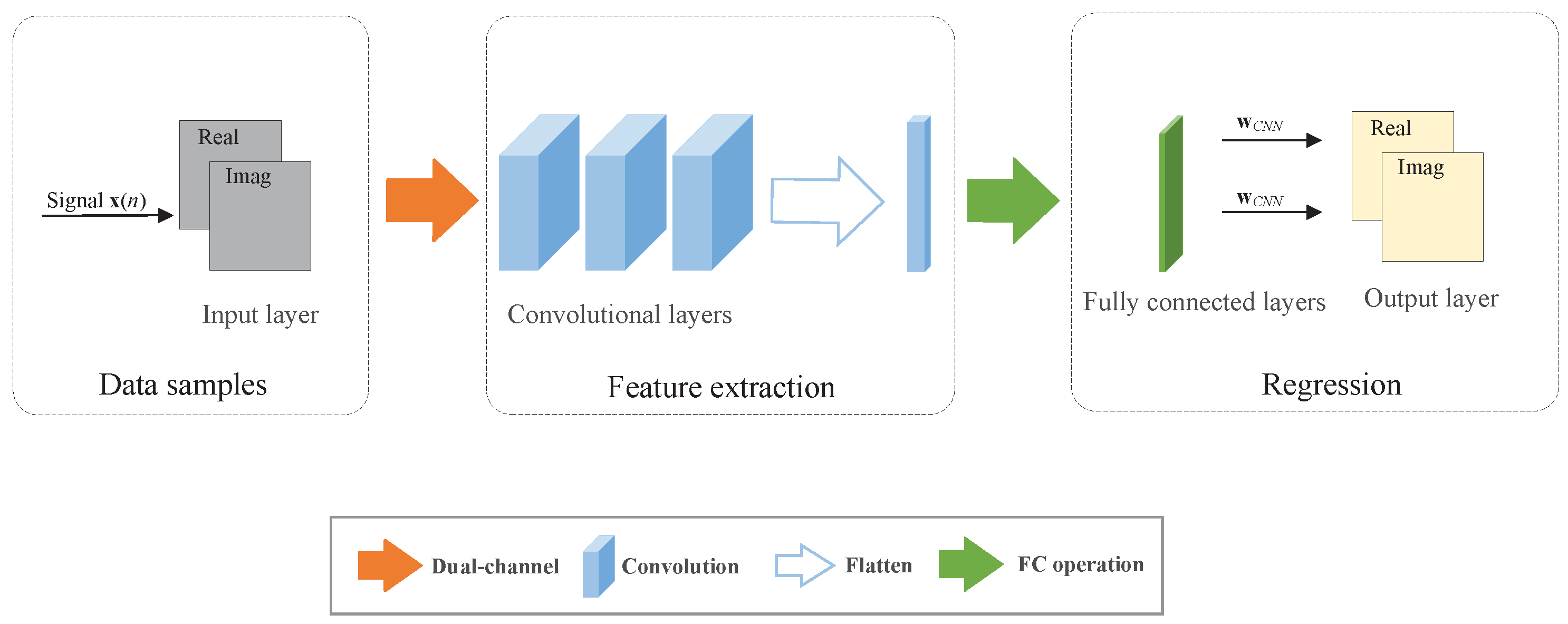
3. Wideband Beamforming Prediction Network
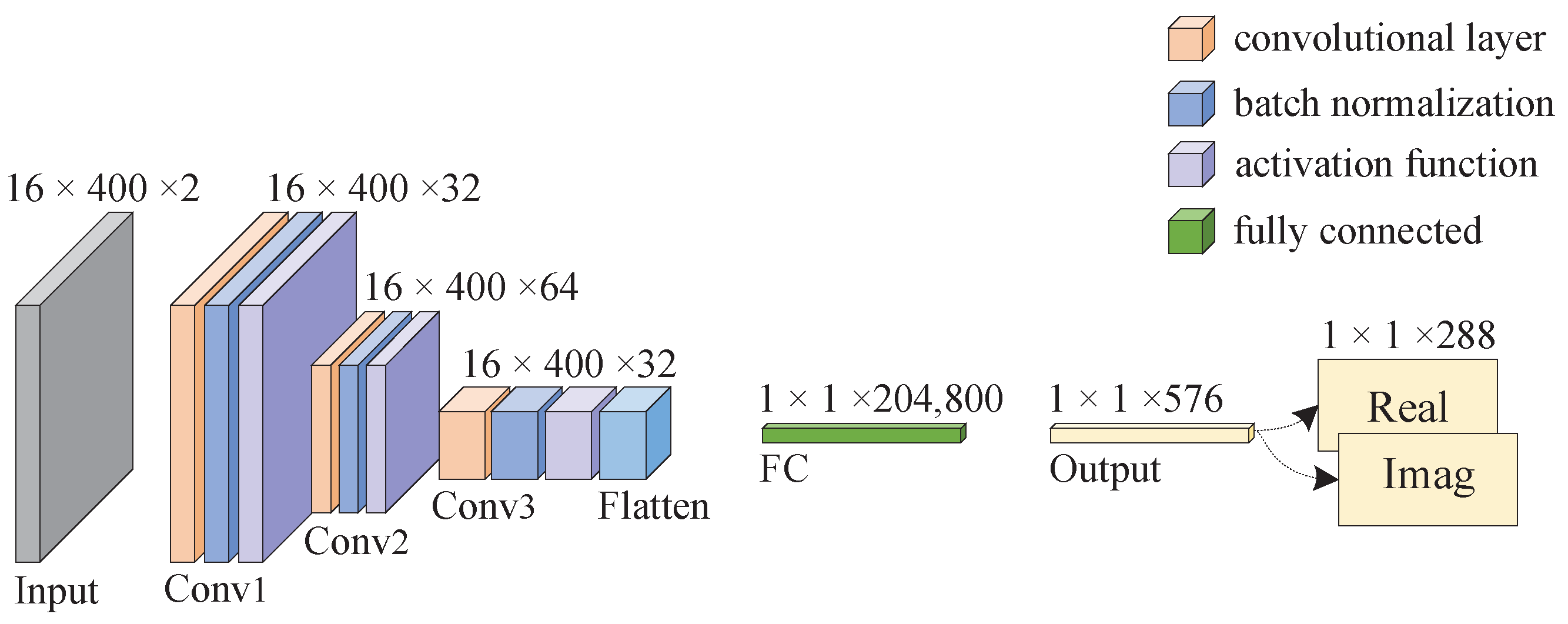
3.1. WBPNet Model
3.2. Training the WBPNet
| Algorithm 1: WBPNet Training. |
| 1: Input: , , , and the number of epoch E |
| 2: Initialization: , using the Kaiming criteria; |
| 3: for : E, do |
| 4: if () do else ifend |
| 5: CONV1: |
| 6: CONV2: |
| 7: CONV3: |
| 8: FC: |
| 9: , where l is the residual error, L is the loss function and we use MSE criterion. |
| 10: if () do |
| , , |
| ifend |
| 11: back-propagation: |
| 12: , |
| 13: forend |
| 14: output:, |
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bollian, T.; Osmanoglu, B.; Rincon, R.; Lee, S.K.; Fatoyinbo, T. Adaptive antenna pattern notching of interference in synthetic aperture radar data using digital beamforming. Remote Sens. 2019, 11, 1346. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Wang, R.; Qiu, J.; Wang, W.; Zhao, Q.; Liu, D. An Advanced Echo Separation Scheme for Space-Time Waveform-Encoding SAR Based on Digital Beamforming and Blind Source Separation. Remote Sens. 2022, 14, 3585. [Google Scholar] [CrossRef]
- Younis, M.; Fischer, C.; Wiesbeck, W. Digital beamforming in SAR systems. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 1735–1739. [Google Scholar] [CrossRef]
- Wiesbeck, W. SDRS: Software-defined radar sensors. In Proceedings of the IGARSS 2001. Scanning the Present and Resolving the Future, IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No. 01CH37217), Sydney, Australia, 9–13 July 2001; Volume 7, pp. 3259–3261. [Google Scholar]
- Wen, W.; Ning, L.; Jun, T.; Yingning, P. Broadband digital beamforming based on fractional delay in SAR systems. In Proceedings of the 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, China, 26–30 October 2009; pp. 575–578. [Google Scholar]
- Zhang, B.; Xu, G.; Zhou, R.; Zhang, H.; Hong, W. Multi-Channel Back-Projection Algorithm for MMWave Automotive MIMO SAR Imaging with Doppler-Division Multiplexing. IEEE J. Sel. Top. Signal Process. 2022. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Chen, J.; Wu, F.; Sheng, J.; Hong, W. Sparse Inverse Synthetic Aperture Radar Imaging Using Structured Low-Rank Method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Nordholm, S.E.; Dam, H.H.; Lai, C.C.; Lehmann, E.A. Broadband beamforming and optimization. In Academic Press Library in Signal Processing; Elsevier: Amsterdam, The Netherlands, 2014; Volume 3, pp. 553–598. [Google Scholar]
- Frost, O.L. An algorithm for linearly constrained adaptive array processing. Proc. IEEE 1972, 60, 926–935. [Google Scholar] [CrossRef]
- Zhang, S.; Gu, Q.; Wu, X.; Luo, J.; Sheng, W. Non-Uniform Decomposition Method Used for Obtaining the Frequency-Constrained Matrix of Broadband Laguerre Beamforming. IEEE Wirel. Commun. Lett. 2022, 11, 1359–1363. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Seydnejad, S.R. Elimination of pre-steering delays in space-time broadband beamforming using frequency domain constraints. IEEE Commun. Lett. 2013, 17, 769–772. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Chen, J.; Hong, W. Structured Low-rank and Sparse Method for ISAR Imaging with 2D Compressive Sampling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Baskin, C.; Zheltonozhkii, E.; Rozen, T.; Liss, N.; Chai, Y.; Schwartz, E.; Giryes, R.; Bronstein, A.M.; Mendelson, A. Nice: Noise injection and clamping estimation for neural network quantization. Mathematics 2021, 9, 2144. [Google Scholar] [CrossRef]
- Oveis, A.H.; Giusti, E.; Ghio, S.; Martorella, M. A Survey on the Applications of Convolutional Neural Networks for Synthetic Aperture Radar: Recent Advances. IEEE Aerosp. Electron. Syst. Mag. 2021, 37, 18–42. [Google Scholar] [CrossRef]
- Kuno, Y.M.; Masiero, B.; Madhu, N. A neural network approach to broadband beamforming. In Proceedings of the 23rd International Congress on Acoustics (ICA 2019), Aachen, Germany, 9–13 September 2019; pp. 6961–6968. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A convolutional neural network for modelling sentences. arXiv 2014, arXiv:1404.2188. [Google Scholar]
- Jeon, M.; Jeong, Y.S. Compact and accurate scene text detector. Appl. Sci. 2020, 10, 2096. [Google Scholar] [CrossRef]
- Vu, T.; Van Nguyen, C.; Pham, T.X.; Luu, T.M.; Yoo, C.D. Fast and efficient image quality enhancement via desubpixel convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Gu, Y.; Wu, J.; Fang, Y.; Zhang, L.; Zhang, Q. End-to-End Moving Target Indication for Airborne Radar Using Deep Learning. Remote Sens. 2022, 14, 5354. [Google Scholar] [CrossRef]
- Sallam, T.; Attiya, A.M. Convolutional neural network for 2D adaptive beamforming of phased array antennas with robustness to array imperfections. Int. J. Microw. Wirel. Technol. 2021, 13, 1096–1102. [Google Scholar] [CrossRef]
- Ramezanpour, P.; Mosavi, M.R. Two-stage beamforming for rejecting interferences using deep neural networks. IEEE Syst. J. 2020, 15, 4439–4447. [Google Scholar] [CrossRef]
- Ramezanpour, P.; Rezaei, M.J.; Mosavi, M.R. Deep-learning-based beamforming for rejecting interferences. IET Signal Process. 2020, 14, 467–473. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Liu, F. Fast and robust adaptive beamforming method based on complex-valued RBF neural network. J. Eng. 2019, 2019, 5917–5921. [Google Scholar] [CrossRef]
- Lin, T.; Zhu, Y. Beamforming design for large-scale antenna arrays using deep learning. IEEE Wirel. Commun. Lett. 2019, 9, 103–107. [Google Scholar] [CrossRef]
- Lovato, R.; Gong, X. Phased antenna array beamforming using convolutional neural networks. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, Georgia, 7–12 July 2019; pp. 1247–1248. [Google Scholar]
- Mizumachi, M. Neural Network-Based Broadband Beamformer with Less Distortion. In Proceedings of the 23rd International Congress on Acoustics (ICA 2019), Aachen, Germany, 9–13 September 2019; pp. 2760–2874. [Google Scholar]
- Fernandes, J.d.C.V.; de Moura Junior, N.N.; de Seixas, J.M. Deep learning models for passive sonar signal classification of military data. Remote Sens. 2022, 14, 2648. [Google Scholar] [CrossRef]
- Brown, A.D. Electronically Scanned Arrays MATLAB® Modeling and Simulation; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ali, R.; Chuah, J.H.; Talip, M.S.A.; Mokhtar, N.; Shoaib, M.A. Structural crack detection using deep convolutional neural networks. Autom. Constr. 2022, 133, 103989. [Google Scholar] [CrossRef]
- Huang, H.; Peng, Y.; Yang, J.; Xia, W.; Gui, G. Fast beamforming design via deep learning. IEEE Trans. Veh. Technol. 2019, 69, 1065–1069. [Google Scholar] [CrossRef]
- Duan, B.; Yang, Y.; Dai, X. Feature Activation through First Power Linear Unit with Sign. Electronics 2022, 11, 1980. [Google Scholar] [CrossRef]
- Xia, W.; Zheng, G.; Wong, K.K.; Zhu, H. Model-driven beamforming neural networks. IEEE Wirel. Commun. 2020, 27, 68–75. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, C.; Wang, J.; Yue, X.G.; Lim, S.J.; Al-Makhadmeh, Z.; Tolba, A. Training convolutional neural networks with multi-size images and triplet loss for remote sensing scene classification. Sensors 2020, 20, 1188. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Qi, F.; Feng, Y. Deep-learning-based multiple beamforming for 5g uav iot networks. IEEE Netw. 2020, 34, 32–38. [Google Scholar] [CrossRef]
- Smith, L.N. A disciplined approach to neural network hyper-parameters: Part 1–learning rate, batch size, momentum, and weight decay. arXiv 2018, arXiv:1803.09820. [Google Scholar]
- Zhang, H.; Yang, N.; Huangfu, W.; Long, K.; Leung, V.C. Power control based on deep reinforcement learning for spectrum sharing. IEEE Trans. Wirel. Commun. 2020, 19, 4209–4219. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; Chen, V.C. Hand Gesture Recognition Using Radial and Transversal Dual Micro-Motion Features. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5963–5973. [Google Scholar] [CrossRef]
- Liu, S.; Huang, Y.; Wu, H.; Tan, C.; Jia, J. Efficient multitask structure-aware sparse Bayesian learning for frequency-difference electrical impedance tomography. IEEE Trans. Ind. Inform. 2020, 17, 463–472. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1026–1034. [Google Scholar]
- Martin-Donas, J.M.; Gomez, A.M.; Gonzalez, J.A.; Peinado, A.M. A deep learning loss function based on the perceptual evaluation of the speech quality. IEEE Signal Process. Lett. 2018, 25, 1680–1684. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, W.; Greco, M.; Gini, F. Cognitive Sparse Beamformer Design in Dynamic Environment via Regularized Switching Network. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltmore, MD, USA, 2013. [Google Scholar]
- Sallam, T.; Abdel-Rahman, A.B.; Alghoniemy, M.; Kawasaki, Z.; Ushio, T. A neural-network-based beamformer for phased array weather radar. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 5095–5104. [Google Scholar] [CrossRef]
- Rong, J.; Liu, F.; Miao, Y. High-Efficiency Optimization Algorithm of PMEPR for OFDM Integrated Radar and Communication Waveform Based on Conjugate Gradient. Remote Sens. 2022, 14, 1715. [Google Scholar] [CrossRef]
- Miao, P.; Yin, W.; Peng, H.; Yao, Y. Study of the performance of deep learning-based channel equalization for indoor visible light communication systems. Photonics 2021, 8, 453. [Google Scholar] [CrossRef]
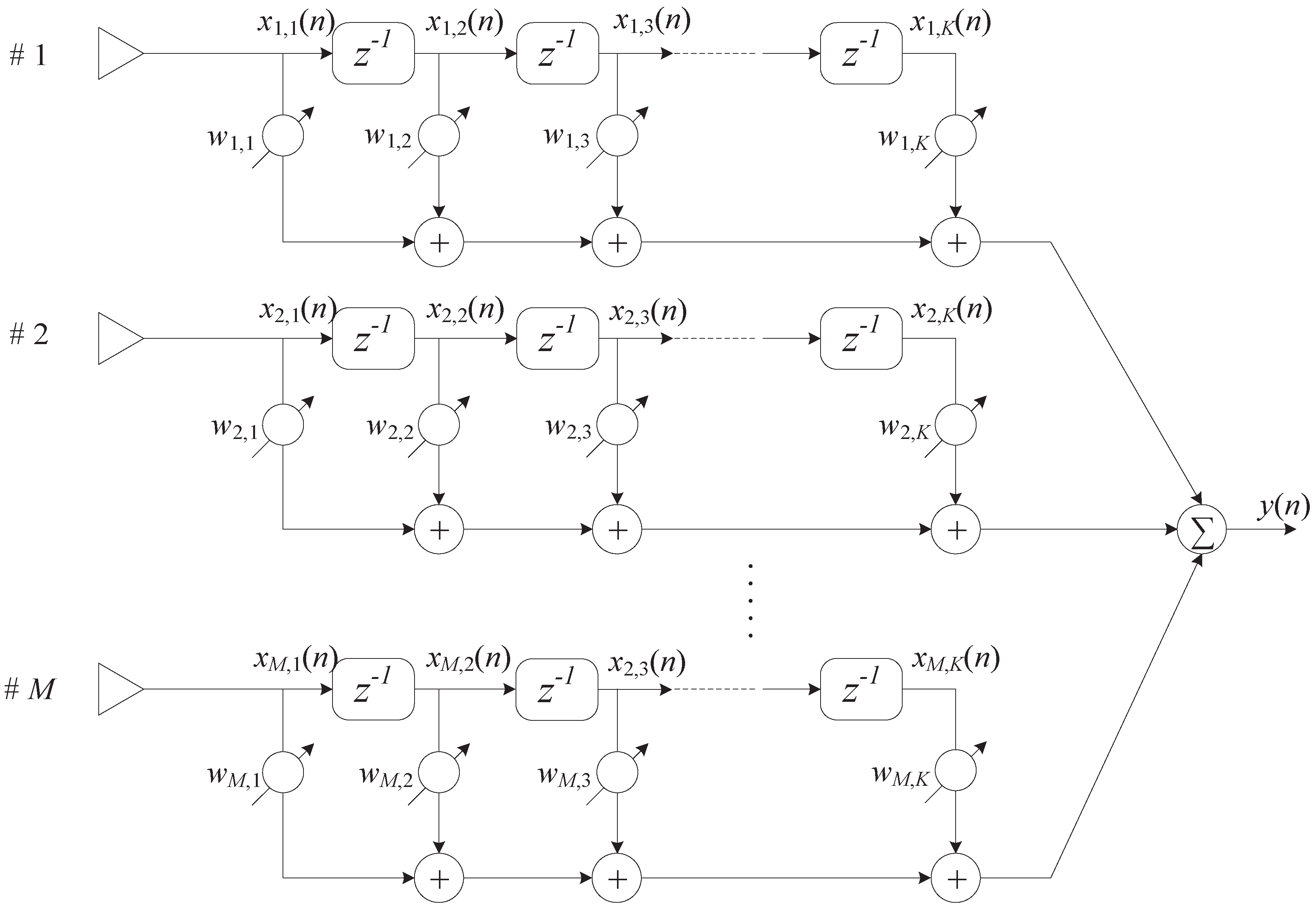
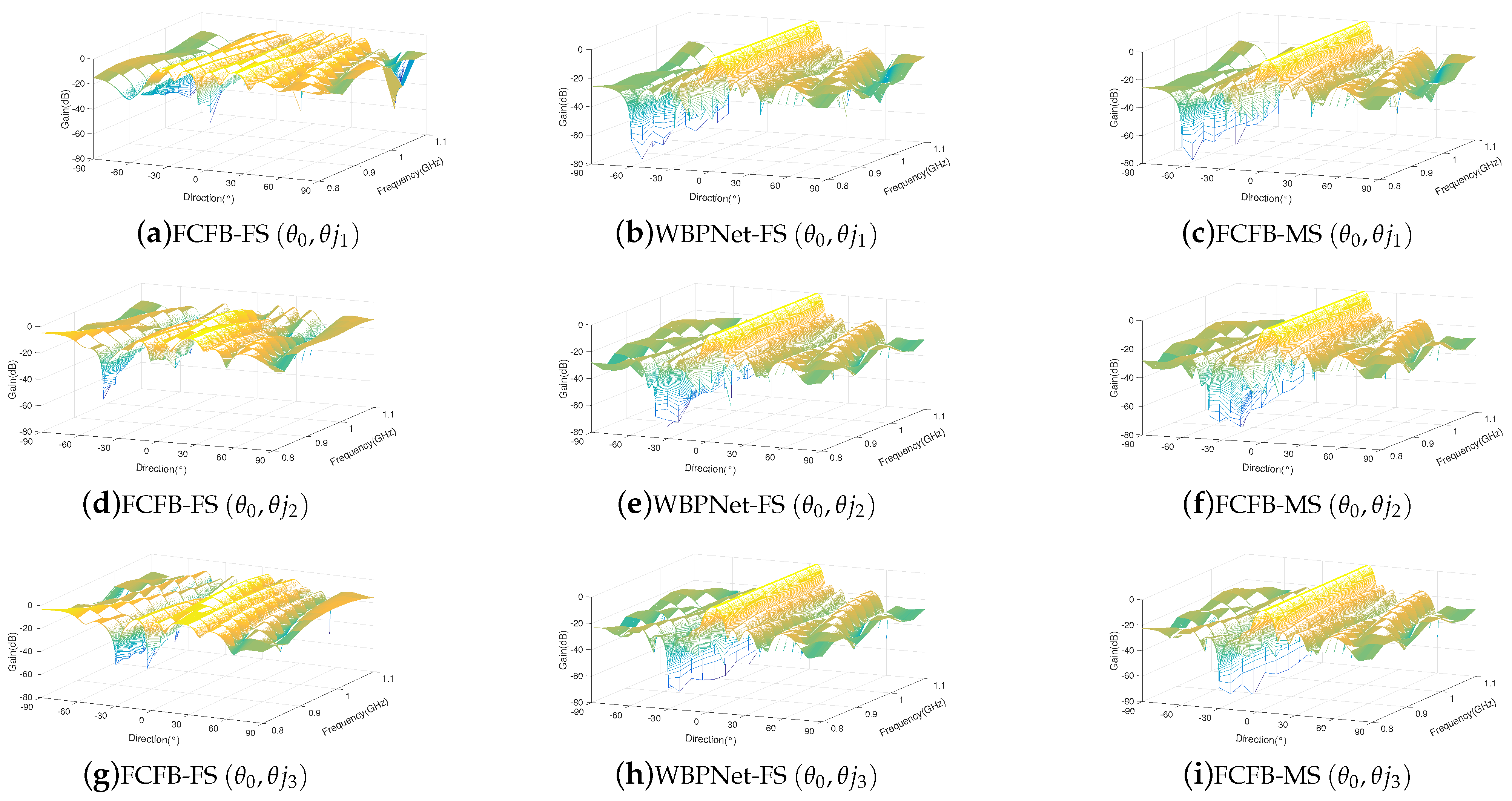
| FCFB-FS | FCFB-MS | WBPNet-FS (Proposed) | |
|---|---|---|---|
| () | () | () | |
| Undistorted response to the SOI | x | √ | √ |
| Deep nulls to anti-jamming | x | √ | √ |
| Direction | FCFB-FS | FCFB-MS | WBPNet-FS (Proposed) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| () | () | ||||||||||
| 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | ||||
| FCFB-FS/FCFB-MS | WBPNet (Proposed) | ||
|---|---|---|---|
| Estimate the covariance matrix | Conv1 | ||
| The inversion of covariance matrix | Conv2 | ||
| Obtain the optimal weight vector | Conv3 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Luo, J.; Li, G.; Zhang, S.; Sheng, W. Fast Wideband Beamforming Using Convolutional Neural Network. Remote Sens. 2023, 15, 712. https://doi.org/10.3390/rs15030712
Wu X, Luo J, Li G, Zhang S, Sheng W. Fast Wideband Beamforming Using Convolutional Neural Network. Remote Sensing. 2023; 15(3):712. https://doi.org/10.3390/rs15030712
Chicago/Turabian StyleWu, Xun, Jie Luo, Guowei Li, Shurui Zhang, and Weixing Sheng. 2023. "Fast Wideband Beamforming Using Convolutional Neural Network" Remote Sensing 15, no. 3: 712. https://doi.org/10.3390/rs15030712
APA StyleWu, X., Luo, J., Li, G., Zhang, S., & Sheng, W. (2023). Fast Wideband Beamforming Using Convolutional Neural Network. Remote Sensing, 15(3), 712. https://doi.org/10.3390/rs15030712






