Assessing the Vertical Structure of Forests Using Airborne and Spaceborne LiDAR Data in the Austrian Alps
Abstract
1. Introduction
- How well are LiDAR data in general suitable for explaining vertical forest structure and the number of layers (NoL) in a near-natural mountainous forest?
- How well are GEDI data specifically suited for this purpose?
- What waveform-based indicators are best suited for explaining vertical forest structure?
2. Materials and Methods
2.1. Materials
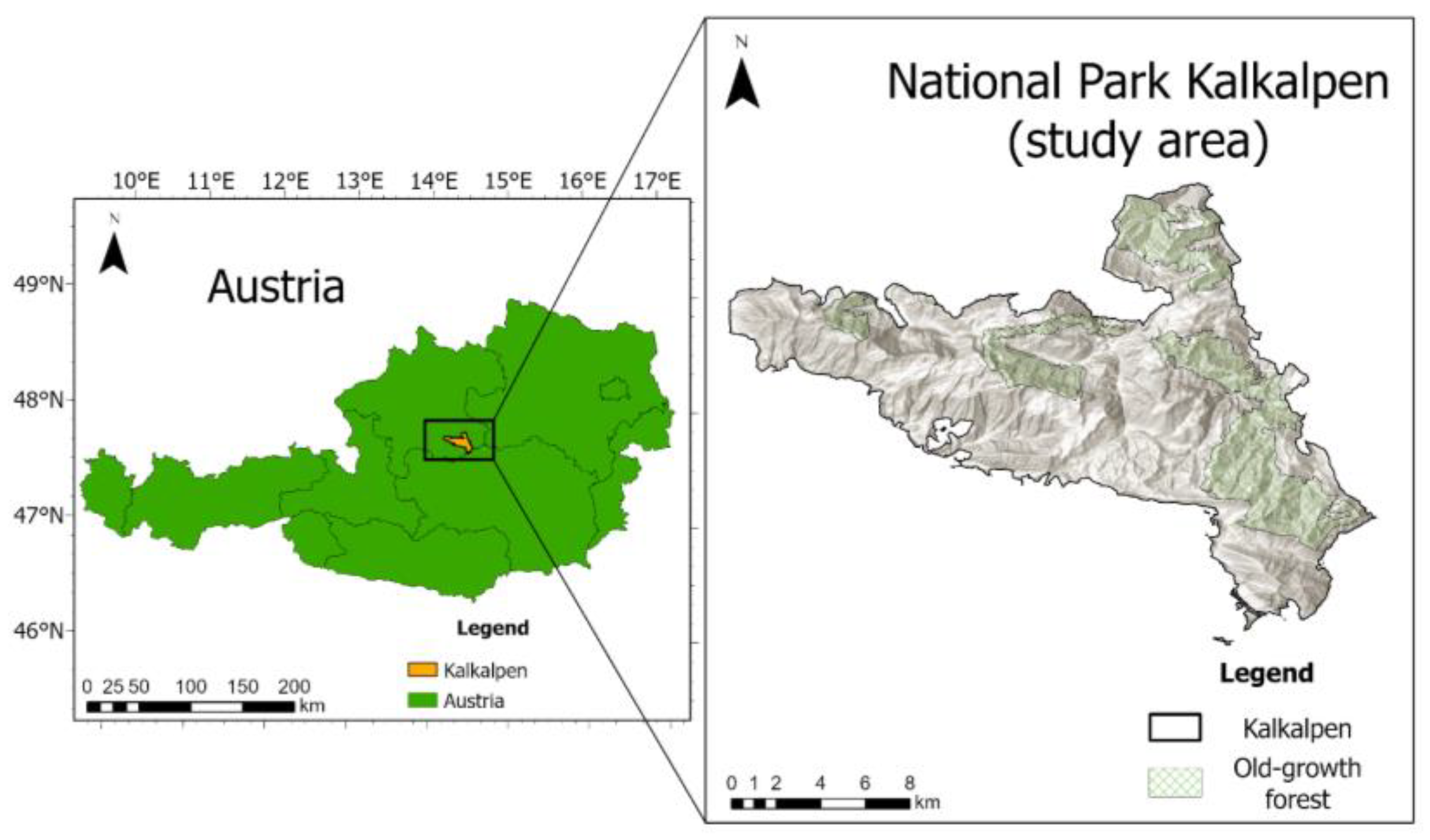
2.1.1. Study Area
2.1.2. GEDI Data
2.1.3. ALS
2.2. Methods
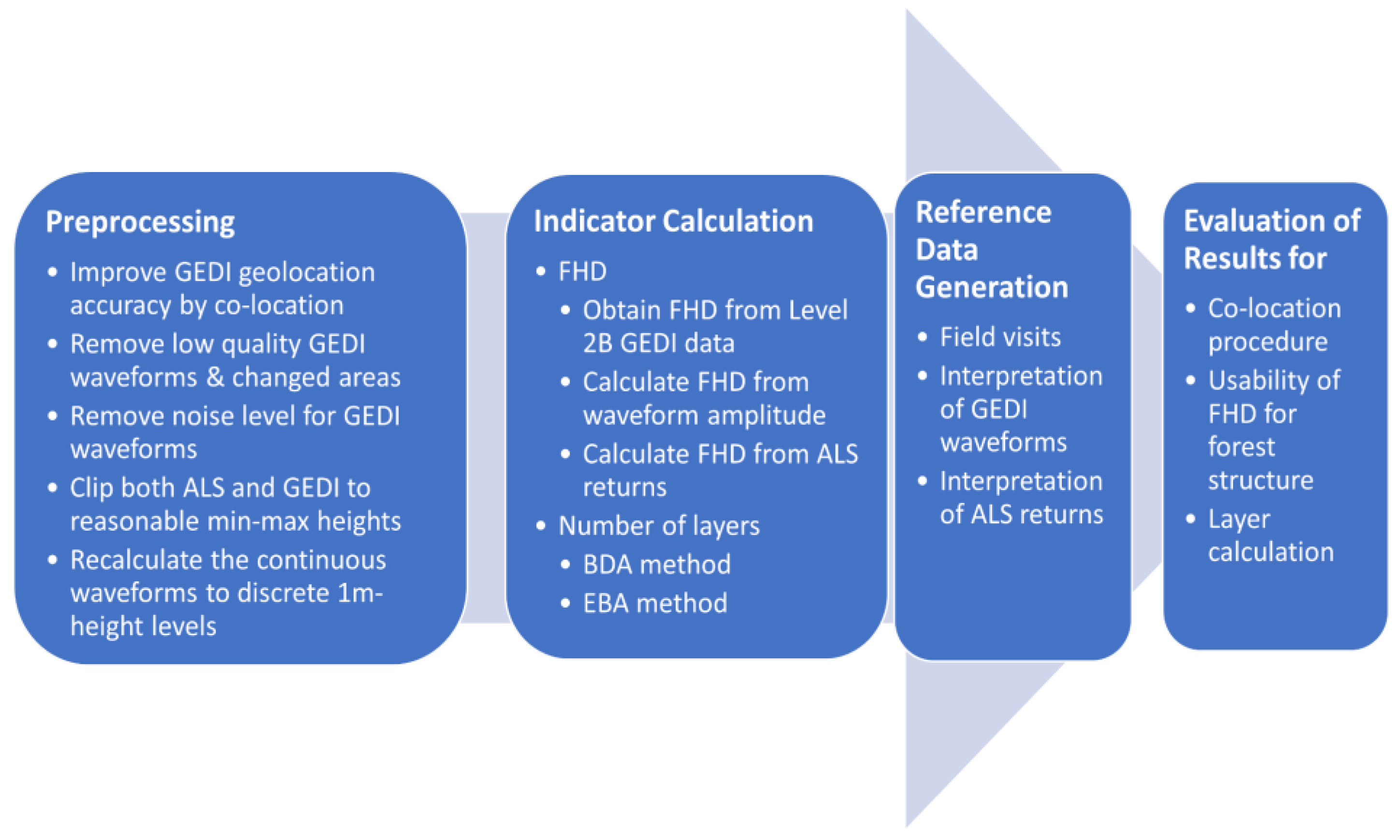
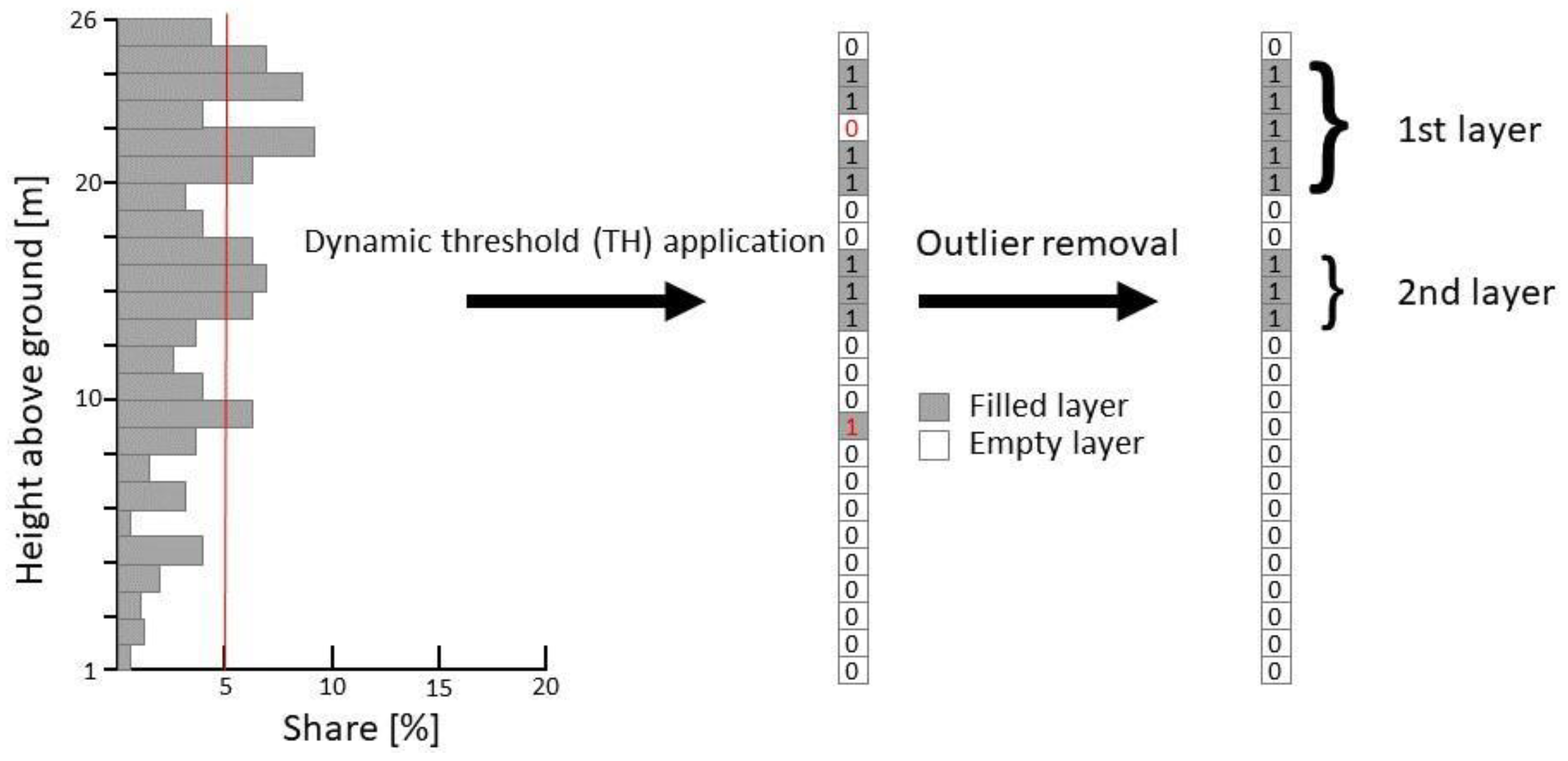
2.2.1. Pre-Processing
- Quality flag = 1 (4618);
- Waveforms with terrain height within accuracy limits. Due to the steep terrain, inaccuracies with respect to the terrain’s height occur. In order not to impact the analysis, these outliers (>2*stdv) were discarded from further analysis (4174);
- Acquisition during leaf-on season (June–October 2019 and 2020) (2911);
- Degrade flag = 0 (2911);
- Data overlapping the ALS coverage (1734);
- Within areas, where no changes between 2018 and 2020 occurred (1725);
- Footprints, where GEDI or ALS estimate heights above ground of 50 m or more, are removed to account for artefacts (e.g., from birds) (1692).
2.2.2. Calculation of Indicators for Vertical Forest Structure from Waveforms
2.2.3. Reference Data Generation
3. Results
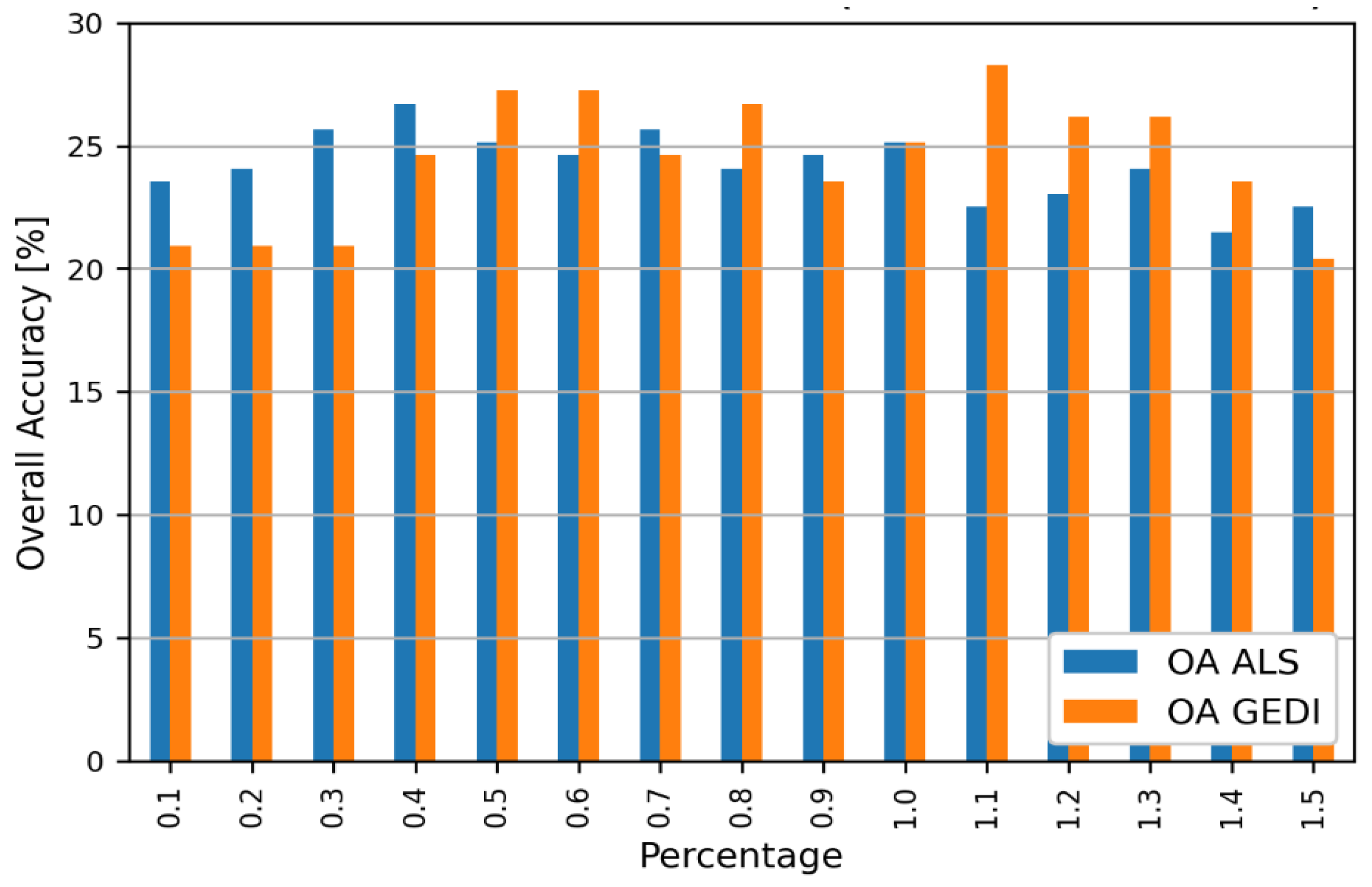
3.1. Results of Co-Location
3.2. Results for Vertical Forest Structure Assessment
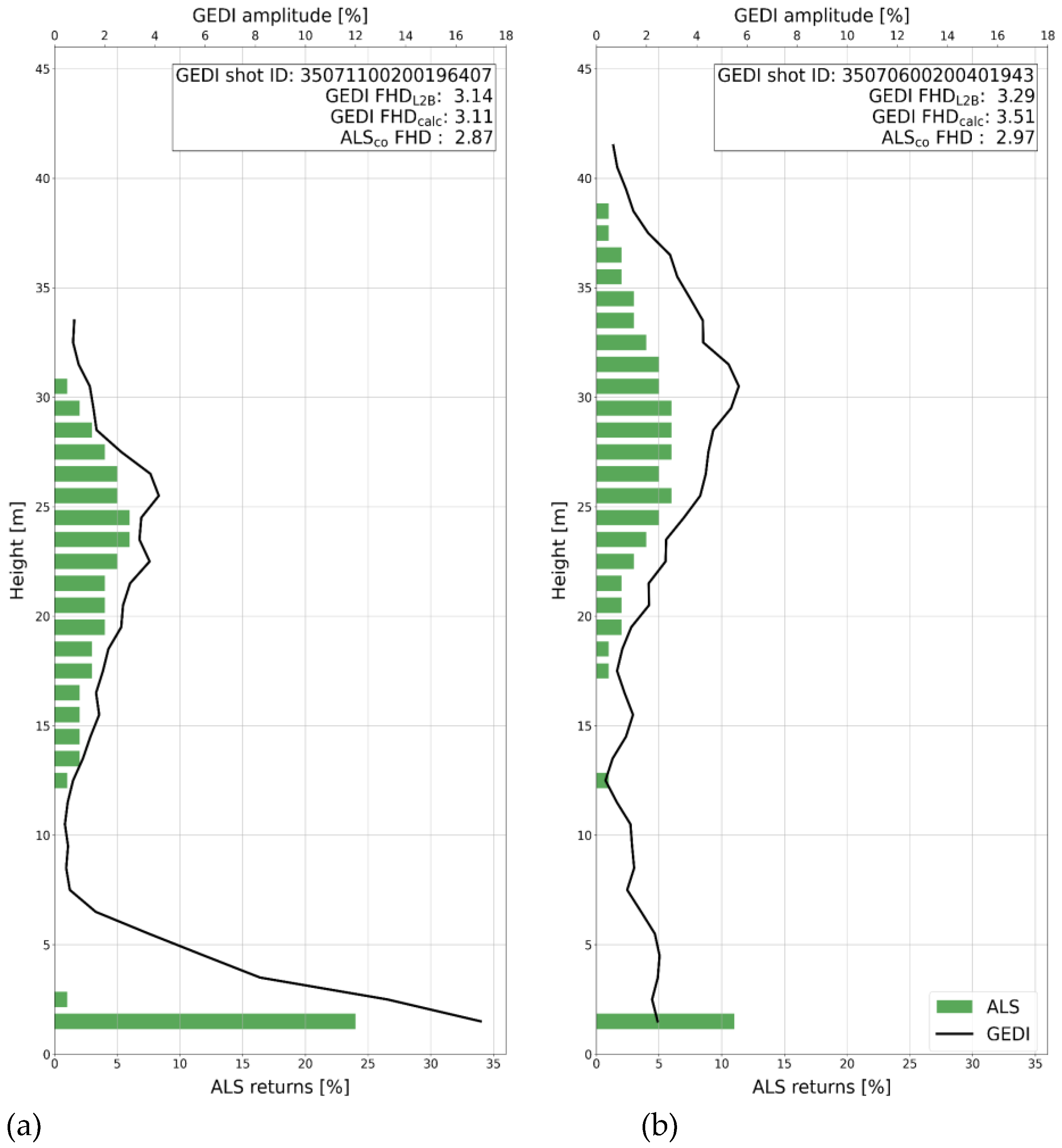
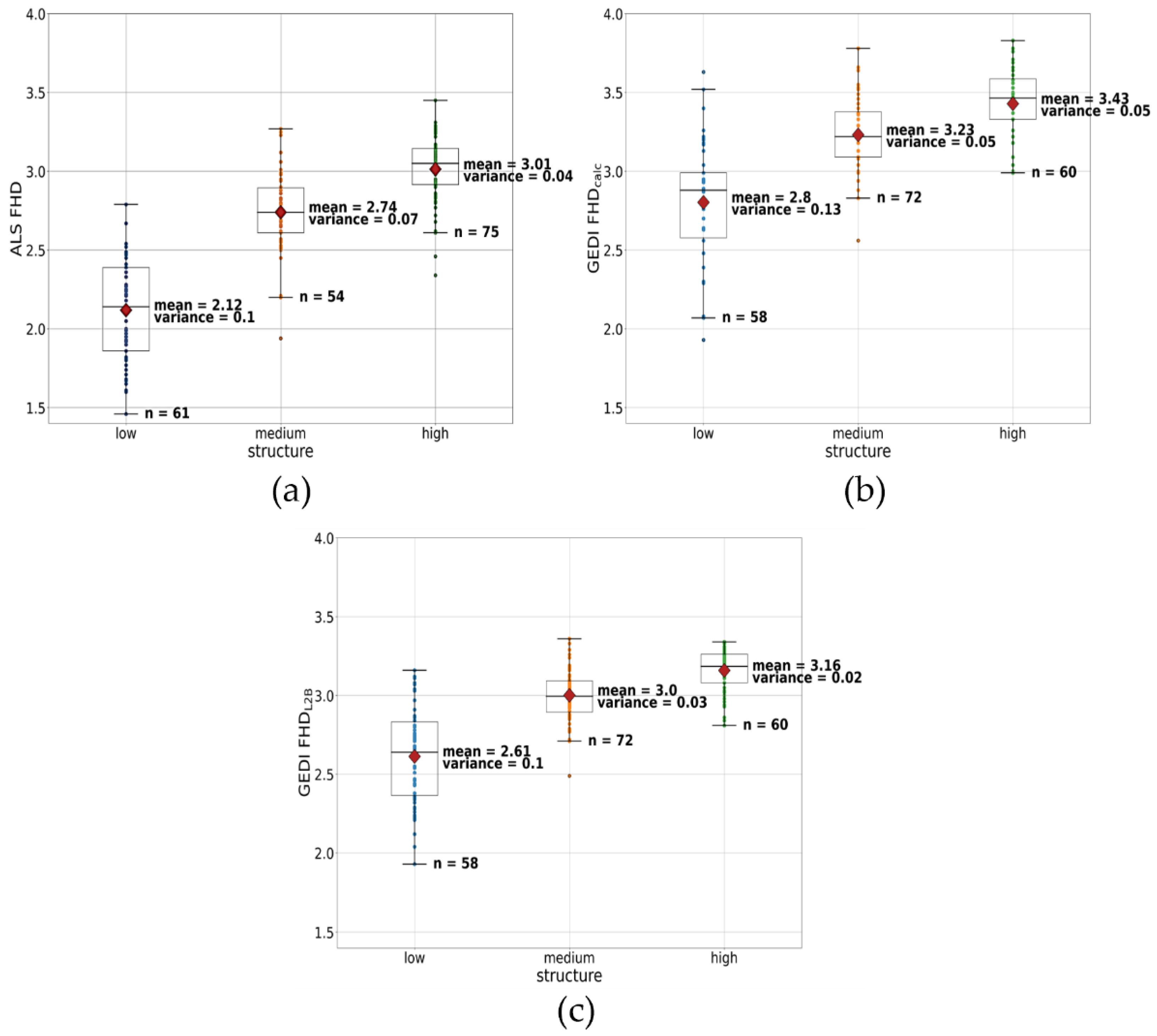
3.2.1. Results for Indicator “FHD”
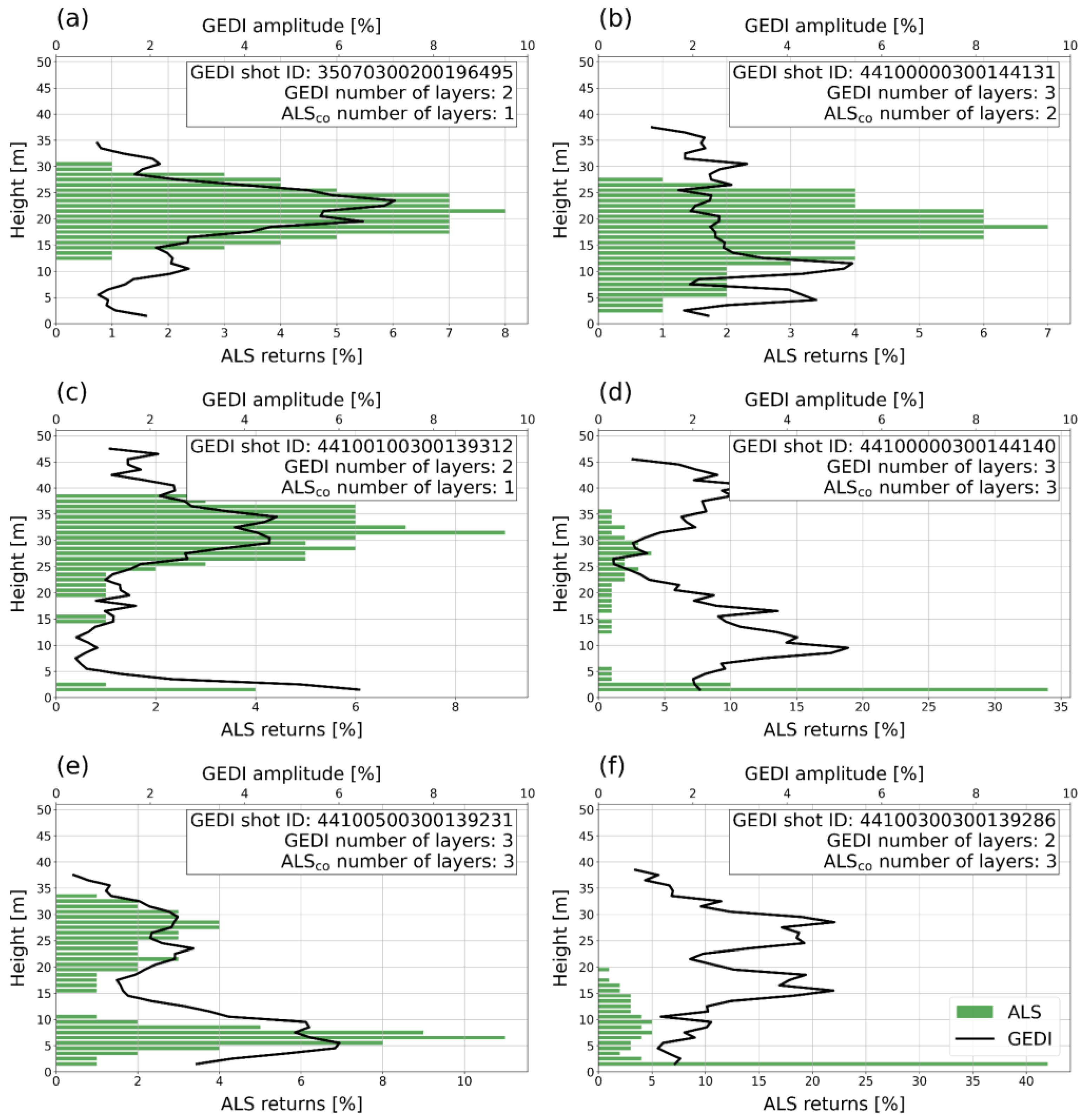
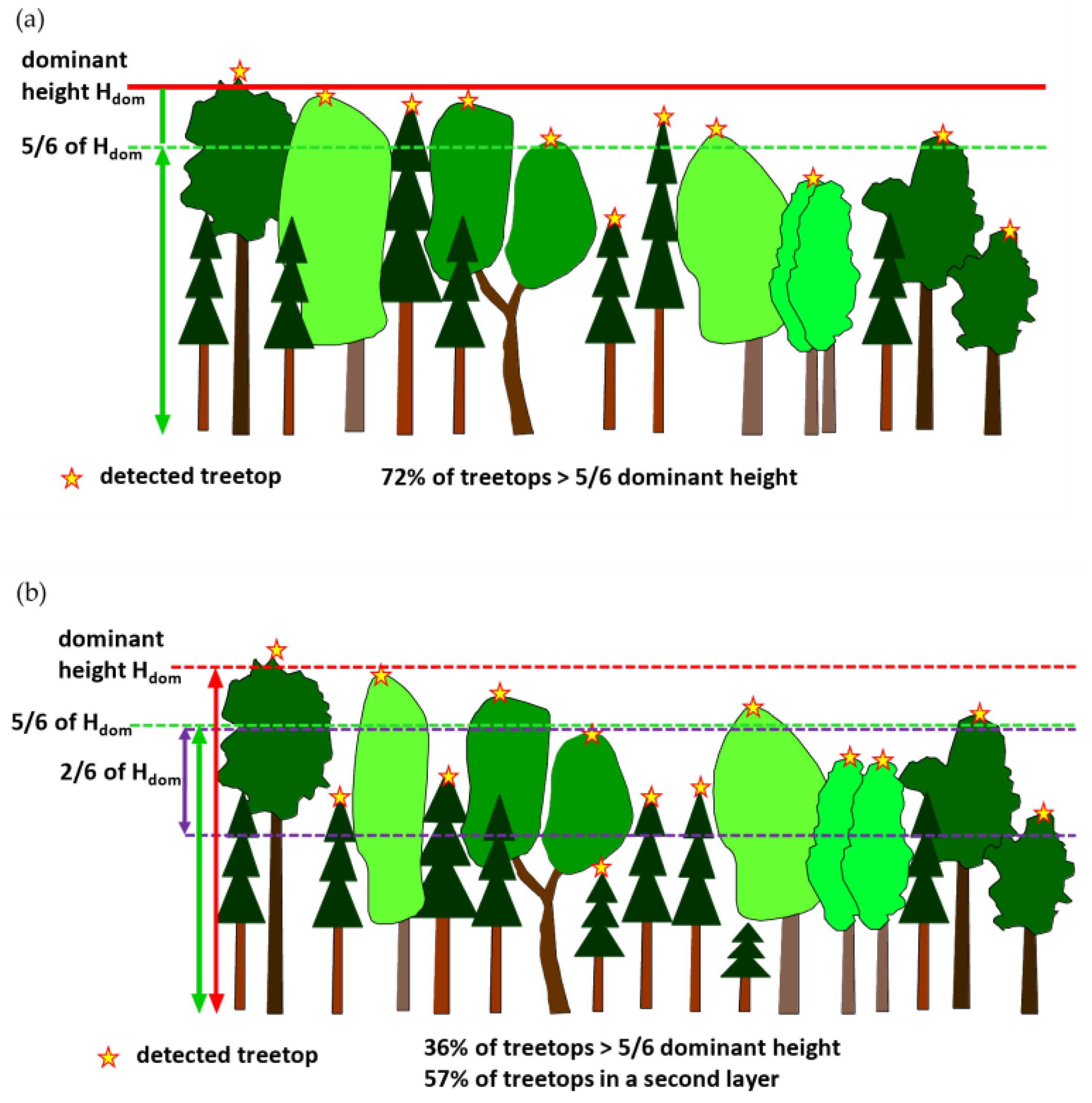
3.2.2. Results for “Number of Layers” Indicator
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Orbit No. | Shift x | Shift y | R2 |
|---|---|---|---|
| 02056 02 | −10.0 | −10.0 | −0.00013 |
| 02578 03 | 0 | −10.0 | −0.016344 |
| 02713 02 | −6.0 | 9.0 | 0.765259 |
| 03143 03 | 9 | 9 | 0.14292 |
| 03372 03 | 1 | 3 | 0.780396 |
| 03507 02 | −6.0 | 9.0 | 0.805535 |
| 04410 03 | −6.0 | −2.0 | 0.845933 |
| 05173 03 | −5.0 | 6.0 | 0.623483 |
| 06119 03 | −10.0 | 9.0 | −0.011138 |
| 07705 03 | 9.0 | −10.0 | 0.266957 |
| 07766 03 | 3.0 | 1.0 | 0.707449 |
| 08633 02 | −2.0 | −10.0 | −0.000612 |
| 08694 02 | 9.0 | −6.0 | −0.00683 |
| 09093 03 | 8.0 | 1. | 0.830865 |
| 10313 03 | −7.0 | 0.0 | −0.009003 |
| 13119 03 | 6.0 | −1.0 | 0.330467 |
| 13180 03 | 3.0 | −2.0 | 0.54763 |
| 13241 03 | −10.0 | −1.0 | −0.021584 |
| 13879 02 | −1.0 | 7.0 | 0.682199 |
| 13940 02 | 5.0 | 9.0 | −0.008227 |
| 14001 02 | −10 | 9.0 | 0.734022 |
| 15086 03 | 6.0 | 9.0 | 0.475214 |
| 15419 02 | −2.0 | 0 | 0.871305 |
References
- Mitchard, E.T.A. The Tropical Forest Carbon Cycle and Climate Change. Nature 2018, 559, 527–534. [Google Scholar] [CrossRef] [PubMed]
- Fischer, R.; Knapp, N.; Bohn, F.; Shugart, H.H.; Huth, A. The Relevance of Forest Structure for Biomass and Productivity in Temperate Forests: New Perspectives for Remote Sensing. Surv. Geophys. 2019, 40, 709–734. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Zenner, E.K.; Hibbs, D.E. A New Method for Modeling the Heterogeneity of Forest Structure. For. Ecol. Manag. 2000, 129, 75–87. [Google Scholar] [CrossRef]
- Spies, T.A.; Franklin, J.F. Gap Characteristics and Vegetation Response in Coniferous Forests of the Pacific Northwest. Ecology 1989, 70, 543–545. [Google Scholar] [CrossRef]
- Buongiorno, J.; Dahir, S.; Lu, H.C.; Lin, C.R. Tree Size Diversity and Economic Returns in Uneven-Aged Forest Stands. For. Sci. 1994, 40, 83–103. [Google Scholar] [CrossRef]
- MacArthur, R.H.; MacArthur, J.W. On Bird Species Diversity. Ecology 1961, 42, 594–598. [Google Scholar] [CrossRef]
- Thomas, C.D.; Cameron, A.; Green, R.E.; Bakkenes, M.; Beaumont, L.J.; Collingham, Y.C.; Erasmus, B.F.N.; de Siqueira, M.F.; Grainger, A.; Hannah, L.; et al. Extinction Risk from Climate Change. Nature 2004, 427, 145–148. [Google Scholar] [CrossRef]
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote Sensing for Biodiversity Science and Conservation. Trends Ecol. Evol. 2003, 18, 306–314. [Google Scholar] [CrossRef]
- Jetz, W.; Wilcove, D.S.; Dobson, A.P. Projected Impacts of Climate and Land-Use Change on the Global Diversity of Birds. PLOS Biol. 2007, 5, e157. [Google Scholar] [CrossRef]
- Bergen, K.M.; Goetz, S.J.; Dubayah, R.O.; Henebry, G.M.; Hunsaker, C.T.; Imhoff, M.L.; Nelson, R.F.; Parker, G.G.; Radeloff, V.C. Remote Sensing of Vegetation 3-D Structure for Biodiversity and Habitat: Review and Implications for Lidar and Radar Spaceborne Missions: Vegetation 3-D Structure for Biodiversity. J. Geophys. Res. Biogeosci. 2009, 114, G00E06. [Google Scholar] [CrossRef]
- Manakos, I.; Braun, M.; Manakos, I. Land Use and Land Cover Mapping in Europe: Practices & Trends; Remote Sensing and Digital Image Processing; Springer: Dordrecht, The Netherlands, 2014; ISBN 978-94-007-7969-3. [Google Scholar]
- European Environment Agency. Copernicus Land Monitoring Service High Resolution Land Cover Characteristics: Tree-Cover/Forest and Change 2015–2018. User Manual; 68, 2021. Available online: https://land.copernicus.eu/user-corner/technical-library/forest-2018-user-manual.pdf (accessed on 2 January 2023).
- Lang, N.; Kalischek, N.; Armston, J.; Schindler, K.; Dubayah, R.; Wegner, J.D. Global canopy height regression and uncertainty estimation from GEDI LIDAR waveforms with deep ensembles. Remote Sens. Environ. 2022, 268, 112760. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-Resolution Laser Ranging of the Earth’s Forests and Topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Lin, X.; Xu, M.; Cao, C.; Dang, Y.; Bashir, B.; Xie, B.; Huang, Z. Estimates of Forest Canopy Height Using a Combination of ICESat-2/ATLAS Data and Stereo-Photogrammetry. Remote Sens. 2020, 12, 3649. [Google Scholar] [CrossRef]
- Chi, H.; Sun, G.; Huang, J.; Guo, Z.; Ni, W.; Fu, A. National Forest Aboveground Biomass Mapping from ICESat/GLAS Data and MODIS Imagery in China. Remote Sens. 2015, 7, 5534–5564. [Google Scholar] [CrossRef]
- Hilbert, C.; Schmullius, C. Influence of Surface Topography on ICESat/GLAS Forest Height Estimation and Waveform Shape. Remote Sens. 2012, 4, 2210–2235. [Google Scholar] [CrossRef]
- Qi, W.; Lee, S.-K.; Hancock, S.; Luthcke, S.; Tang, H.; Armston, J.; Dubayah, R. Improved Forest Height Estimation by Fusion of Simulated GEDI Lidar Data and TanDEM-X InSAR Data. Remote Sens. Environ. 2019, 221, 621–634. [Google Scholar] [CrossRef]
- Schneider, F.D.; Ferraz, A.; Hancock, S.; Duncanson, L.I.; Dubayah, R.O.; Pavlick, R.P.; Schimel, D.S. Towards Mapping the Diversity of Canopy Structure from Space with GEDI. Environ. Res. Lett. 2020, 15, 115006. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M.; et al. Biomass Estimation from Simulated GEDI, ICESat-2 and NISAR across Environmental Gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Rishmawi, K.; Huang, C.; Zhan, X. Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sens. 2021, 13, 442. [Google Scholar] [CrossRef]
- Adam, M.; Urbazaev, M.; Dubois, C.; Schmullius, C. Accuracy Assessment of GEDI Terrain Elevation and Canopy Height Estimates in European Temperate Forests: Influence of Environmental and Acquisition Parameters. Remote Sens. 2020, 12, 3948. [Google Scholar] [CrossRef]
- Spracklen, B.; Spracklen, D.V. Determination of Structural Characteristics of Old-Growth Forest in Ukraine Using Spaceborne LiDAR. Remote Sens. 2021, 13, 1233. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Pascual, A. Using GEDI Lidar Data and Airborne Laser Scanning to Assess Height Growth Dynamics in Fast-Growing Species: A Showcase in Spain. For. Ecosyst. 2021, 8, 14. [Google Scholar] [CrossRef]
- Dwiputra, A. Detailed Land Cover Mapping in a Seasonally Dry Tropical Forest Landscape Using Multiple Sensor Types. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 2021. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance Evaluation of GEDI and ICESat-2 Laser Altimeter Data for Terrain and Canopy Height Retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Duncker, P.S.; Barreiro, S.M.; Hengeveld, G.M.; Lind, T.; Mason, W.L.; Ambrozy, S.; Spiecker, H. Classification of Forest Management Approaches: A New Conceptual Framework and Its Applicability to European Forestry. Ecol. Soc. 2012, 17, 51. [Google Scholar] [CrossRef]
- Meyer, P.; Aljex, M.; Culmsee, H.; Feldmann, E.; Glatthorn, J.; Leuschner, C.; Schneider, H. Quantifying Old-Growthness of Lowland European Beech Forests by a Multivariate Indicator for Forest Structure. Ecol. Indic. 2021, 125, 107575. [Google Scholar] [CrossRef]
- Burrascano, S.; Keeton, W.S.; Sabatini, F.M.; Blasi, C. Commonality and Variability in the Structural Attributes of Moist Temperate Old-Growth Forests: A Global Review. For. Ecol. Manag. 2013, 291, 458–479. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial Laser Scanning in Forest Ecology: Expanding the Horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The Use of Terrestrial LiDAR Technology in Forest Science: Application Fields, Benefits and Challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Bauhus, J.; Puettmann, K.; Messier, C. Silviculture for Old-Growth Attributes. For. Ecol. Manag. 2009, 258, 525–537. [Google Scholar] [CrossRef]
- Wirth, C.; Messier, C.; Bergeron, Y.; Frank, D.; Fankhänel, A. Old-Growth Forest Definitions: A Pragmatic View. In Old-Growth Forests: Function, Fate and Value; Wirth, C., Gleixner, G., Heimann, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 11–33. ISBN 978-3-540-92706-8. [Google Scholar]
- Zimble, D.A.; Evans, D.L.; Carlson, G.C.; Parker, R.C.; Grado, S.C.; Gerard, P.D. Characterizing Vertical Forest Structure Using Small-Footprint Airborne LiDAR. Remote Sens. Environ. 2003, 87, 171–182. [Google Scholar] [CrossRef]
- Leiterer, R.; Torabzadeh, H.; Furrer, R.; Schaepman, M.E.; Morsdorf, F. Towards Automated Characterization of Canopy Layering in Mixed Temperate Forests Using Airborne Laser Scanning. Forests 2015, 6, 4146–4167. [Google Scholar] [CrossRef]
- Karna, Y.K.; Penman, T.D.; Aponte, C.; Bennett, L.T. Assessing Legacy Effects of Wildfires on the Crown Structure of Fire-Tolerant Eucalypt Trees Using Airborne LiDAR Data. Remote Sens. 2019, 11, 2433. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Smith, A.M.S.; Gessler, P.E.; Hudak, A.T.; Vierling, L.A.; Evans, J.S. The Influence of Conifer Forest Canopy Cover on the Accuracy of Two Individual Tree Measurement Algorithms Using Lidar Data. Can. J. Remote Sens. 2008, 34, S338–S350. [Google Scholar] [CrossRef]
- De Assis Barros, L. Assessing Set Aside Old-Growth Forests with Airborne LiDAR Metrics; University of Northern British Columbia: Prince George, BC, Canada, 2019; Available online: https://chinookcomfor.ca/wp-content/uploads/2020/07/1st_Manuscript_Barros_20_09_2019.pdf (accessed on 14 December 2022).
- Sparks, A.M.; Smith, A.M.S. Accuracy of a LiDAR-Based Individual Tree Detection and Attribute Measurement Algorithm Developed to Inform Forest Products Supply Chain and Resource Management. Forests 2022, 13, 3. [Google Scholar] [CrossRef]
- Park, S.-H.; Jung, H.-S.; Lee, S.; Kim, E.-S. Mapping Forest Vertical Structure in Sogwang-Ri Forest from Full-Waveform Lidar Point Clouds Using Deep Neural Network. Remote Sens. 2021, 13, 3736. [Google Scholar] [CrossRef]
- Yu, J.-W.; Yoon, Y.-W.; Baek, W.-K.; Jung, H.-S. Forest Vertical Structure Mapping Using Two-Seasonal Optic Images and LiDAR DSM Acquired from UAV Platform through Random Forest, XGBoost, and Support Vector Machine Approaches. Remote Sens. 2021, 13, 4282. [Google Scholar] [CrossRef]
- Latifi, H.; Heurich, M.; Hartig, F.; Müller, J.; Krzystek, P.; Jehl, H.; Dech, S. Estimating Over- and Understorey Canopy Density of Temperate Mixed Stands by Airborne LiDAR Data. Forestry 2016, 89, 69–81. [Google Scholar] [CrossRef]
- Kane, V.R.; Bakker, J.D.; McGaughey, R.J.; Lutz, J.A.; Gersonde, R.F.; Franklin, J.F. Examining Conifer Canopy Structural Complexity across Forest Ages and Elevations with LiDAR Data. Can. J. For. Res. 2010, 40, 774–787. [Google Scholar] [CrossRef]
- Kane, V.R.; Lutz, J.A.; Roberts, S.L.; Smith, D.F.; McGaughey, R.J.; Povak, N.A.; Brooks, M.L. Landscape-Scale Effects of Fire Severity on Mixed-Conifer and Red Fir Forest Structure in Yosemite National Park. For. Ecol. Manag. 2013, 287, 17–31. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Jacquemoud, S.; Gonçalves, G.; Silva, C.; Soares, P.; Tomé, M.; Pereira, L. Airborne Lidar Estimation of Aboveground Forest Biomass in the Absence of Field Inventory. Remote Sens. 2016, 8, 653. [Google Scholar] [CrossRef]
- Mayrhofer, S.; Kirchmeir, H.; Weigand, E.; Mayrhofer, E. Assessment of Forest Wilderness in Kalkalpen National Park. J. Prot. Mt. Areas Res. 2015, 7, 30–40. [Google Scholar] [CrossRef]
- Kirchmeir, H.; Kovarovic, A. Nomination Dossier to the UNESCO for the Inscription on the World Heritage List “Primeval Beech Forests of the Carpathians and Other Regions of Europe” as Extension to the Existing Natural World Heritage Site “Primeval Beech Forests of the Carpathians and the Ancient Beech Forests of Germany”; Klagenfurt. 2016. Available online: https://whc.unesco.org/document/159695 (accessed on 2 January 2023).
- Tang, H.; Armston, J. Algorithm Theoretical Basis Document (ATBD) for GEDI L2B Footprint Canopy Cover and Vertical Profile Metrics; Goddard Space Flight Centre: Greenbelt, MD, USA, 2019. Available online: https://lpdaac.usgs.gov/documents/588/GEDI_FCCVPM_ATBD_v1.0.pdf (accessed on 2 January 2023).
- NovAtel SPAN® IMU-FSAS; Canada. 2016. Available online: https://hexagondownloads.blob.core.windows.net/public/Novatel/assets/Documents/Papers/FSAS/FSAS.pdf. (accessed on 22 December 2022).
- Kutchartt, E.; Pedron, M.; Pirotti, F. Assessment of Canopy and Ground Height Accuracy from GEDI LiDAR over Steep Mountain Areas. SPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 3, 431–438. [Google Scholar] [CrossRef]
- Roy, D.P.; Kashongwe, H.B.; Armston, J. The Impact of Geolocation Uncertainty on GEDI Tropical Forest Canopy Height Estimation and Change Monitoring. Sci. Remote Sens. 2021, 4, 100024. [Google Scholar] [CrossRef]
- Ni, W.; Zhang, Z.; Sun, G. Assessment of Slope-Adaptive Metrics of GEDI Waveforms for Estimations of Forest Aboveground Biomass over Mountainous Areas. J. Remote Sens. 2021, 2021, 9805364. [Google Scholar] [CrossRef]
- Blair, J.B.; Hofton, M.A. Modeling Laser Altimeter Return Waveforms over Complex Vegetation Using High-Resolution Elevation Data. Geophys. Res. Lett. 1999, 26, 2509–2512. [Google Scholar] [CrossRef]
- Hancock, S.; Armston, J.; Hofton, M.; Sun, X.; Tang, H.; Duncanson, L.I.; Kellner, J.R.; Dubayah, R. The GEDI Simulator: A Large-Footprint Waveform Lidar Simulator for Calibration and Validation of Spaceborne Missions. Earth Space Sci. 2019, 6, 294–310. [Google Scholar] [CrossRef]
- Atkins, J.W.; Walter, J.A.; Stovall, A.E.L.; Fahey, R.T.; Gough, C.M. Power Law Scaling Relationships Link Canopy Structural Complexity and Height across Forest Types. Funct. Ecol. 2022, 36, 713–726. [Google Scholar] [CrossRef]
- Tarmu, T.; Laarmann, D.; Kiviste, A. Mean Height or Dominant Height—What to Prefer for Modelling the Site Index of Estonian Forests? For. Stud. 2020, 72, 121–138. [Google Scholar] [CrossRef]
- West, P.W. Stand Measurement. In Tree and Forest Measurement; Springer: Cham, Switzerland, 2015; pp. 71–95. ISBN 978-3-319-14707-9. [Google Scholar]
- Schardt, M.; Granica, K.; Hirschmugl, M.; Deutscher, J.; Mollatz, M.; Steinegger, M.; Gallaun, H.; Wimmer, A.; Linser, S. The Assessment of Forest Parameters by Combined LiDAR and Satellite Data over Alpine Regions—EUFODOS Implementation in Austria. For. J. 2015, 61, 3–11. [Google Scholar] [CrossRef]
- Quiros, E.; Polo, M.-E.; Fragoso-Campon, L. GEDI Elevation Accuracy Assessment: A Case Study of Southwest Spain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5285–5299. [Google Scholar] [CrossRef]
- Shannon, E.; Finley, A.; Hayes, D.; Noralez, S.; Weiskittel, A.; Cook, B.; Babcock, C. Quantifying and Correcting Geolocation Error in Sampling LiDAR Forest Canopy Observations Using High Spatial Accuracy ALS: A Case Study Involving GEDI. arXiv 2022. [Google Scholar] [CrossRef]

| Classification | ||||||
|---|---|---|---|---|---|---|
| Class | 1 | 2 | 3 | Total | PA (%) | |
| Reference | 1 | 24 | 9 | 11 | 45 | 53.3 |
| 2 | 9 | 18 | 39 | 66 | 27.3 | |
| 3 | 6 | 22 | 52 | 80 | 73.6 | |
| Total | 39 | 49 | 102 | 190 | ||
| UA (%) | 61.5 | 36.7 | 51.0 | OA = 49.5 | ||
| Classification | ||||||
|---|---|---|---|---|---|---|
| Class | 1 | 2 | 3 | Total | PA (%) | |
| Reference | 1 | 5 | 22 | 12 | 39 | 12.8 |
| 2 | 0 | 26 | 53 | 79 | 32.9 | |
| 3 | 0 | 19 | 53 | 72 | 73.6 | |
| Total | 5 | 67 | 118 | 190 | ||
| UA (%) | 100 | 38.8 | 44.9 | OA = 44.2 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirschmugl, M.; Lippl, F.; Sobe, C. Assessing the Vertical Structure of Forests Using Airborne and Spaceborne LiDAR Data in the Austrian Alps. Remote Sens. 2023, 15, 664. https://doi.org/10.3390/rs15030664
Hirschmugl M, Lippl F, Sobe C. Assessing the Vertical Structure of Forests Using Airborne and Spaceborne LiDAR Data in the Austrian Alps. Remote Sensing. 2023; 15(3):664. https://doi.org/10.3390/rs15030664
Chicago/Turabian StyleHirschmugl, Manuela, Florian Lippl, and Carina Sobe. 2023. "Assessing the Vertical Structure of Forests Using Airborne and Spaceborne LiDAR Data in the Austrian Alps" Remote Sensing 15, no. 3: 664. https://doi.org/10.3390/rs15030664
APA StyleHirschmugl, M., Lippl, F., & Sobe, C. (2023). Assessing the Vertical Structure of Forests Using Airborne and Spaceborne LiDAR Data in the Austrian Alps. Remote Sensing, 15(3), 664. https://doi.org/10.3390/rs15030664










