Ensemble Machine Learning for Mapping Tree Species Alpha-Diversity Using Multi-Source Satellite Data in an Ecuadorian Seasonally Dry Forest
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
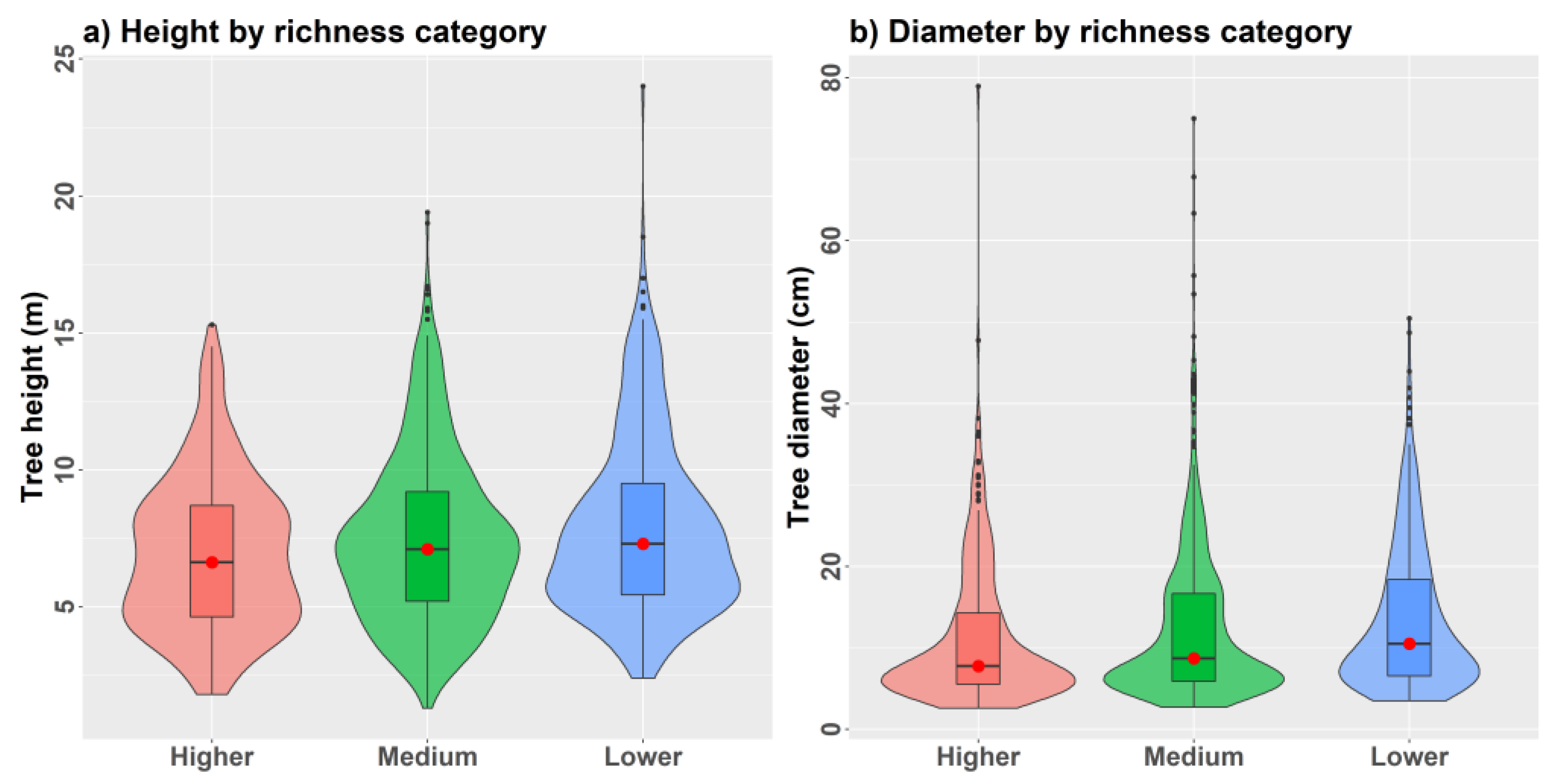
2.2. Tree Data
2.3. Remotely Sensed Data
| Var. Abbrev. | Spectral Range (nm) | Description | Equation | Ref. |
|---|---|---|---|---|
| b1 | 440–510 | Blue | - | - |
| b2 | 520–590 | Green | - | - |
| b3 | 630–685 | Red | - | - |
| b4 | 690–730 | Red-edge | - | - |
| b5 | 760–850 | NIR | - | - |
| ndvi | - | Normalized difference vegetation index | [41] | |
| ndvir | - | Red-edge normalized difference vegetation index | [42] | |
| gndvi | - | Green normalized difference vegetation index | [43] | |
| rg | - | Red–green simple ratio | [44] | |
| sr | - | Simple ratio | [45] | |
| sre | - | Red-edge simple ratio | [43] | |
| mtvi2 | - | Modified triangular vegetation index | [40] | |
| rtvi | - | Red-edge triangular vegetation index | [46] |
2.4. Diversity Indices
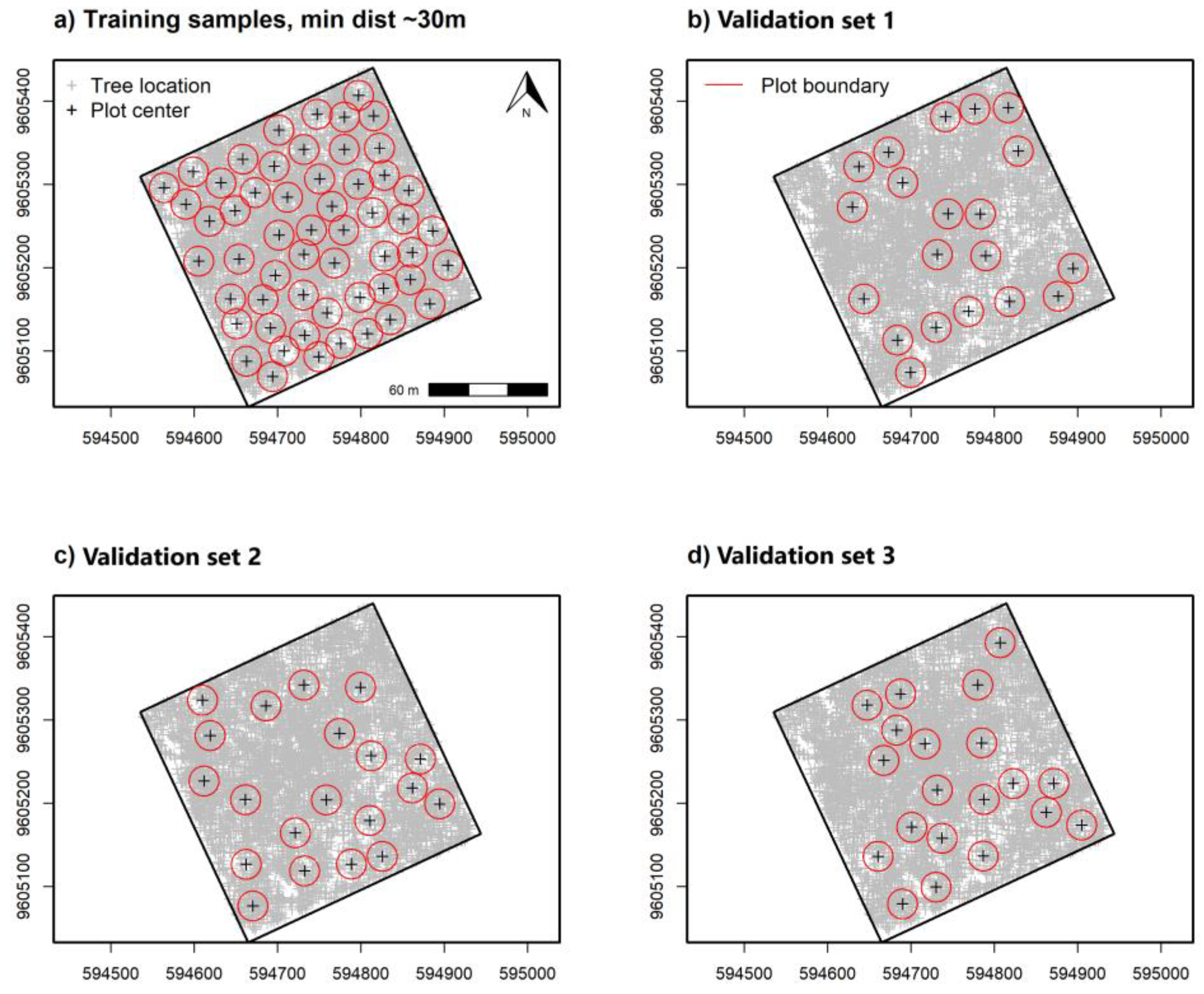
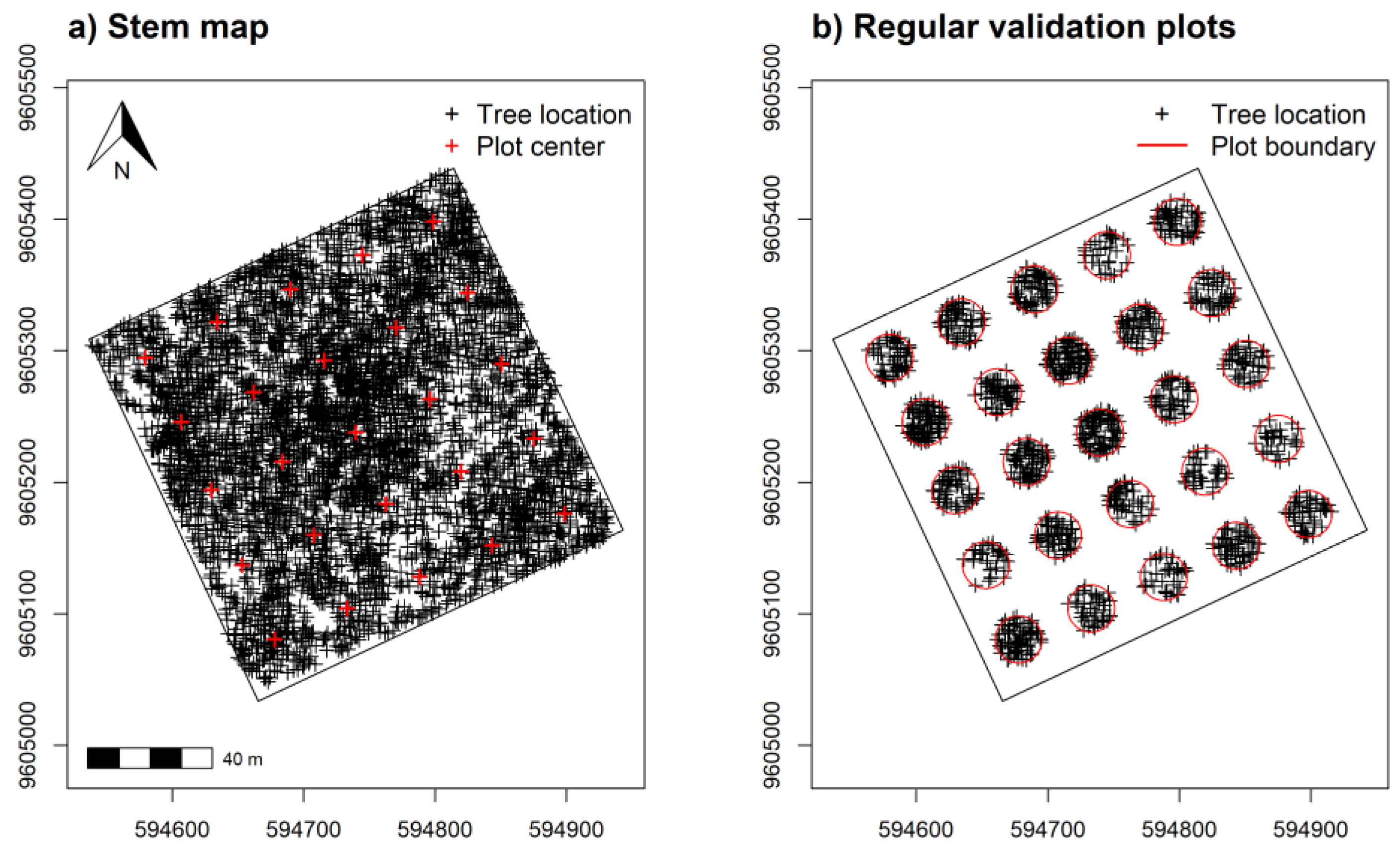
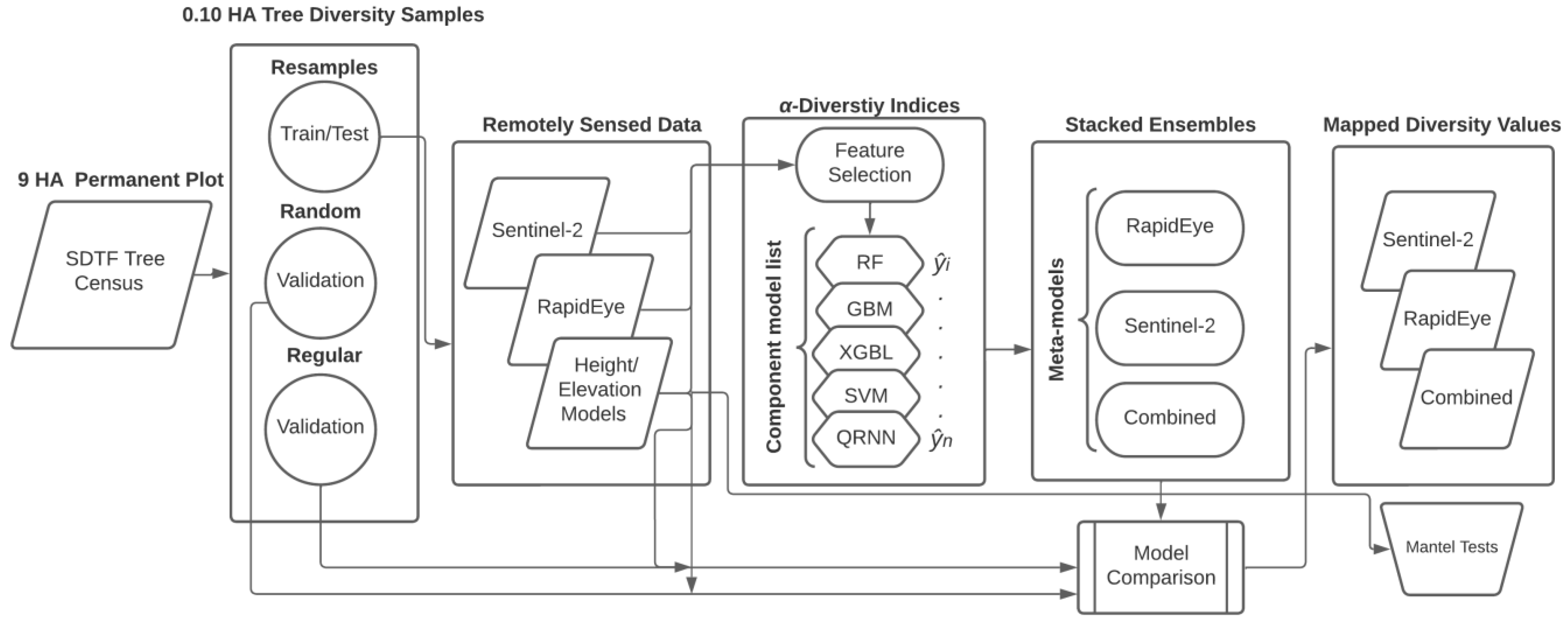
2.5. Sample Design
2.6. Ensemble Models
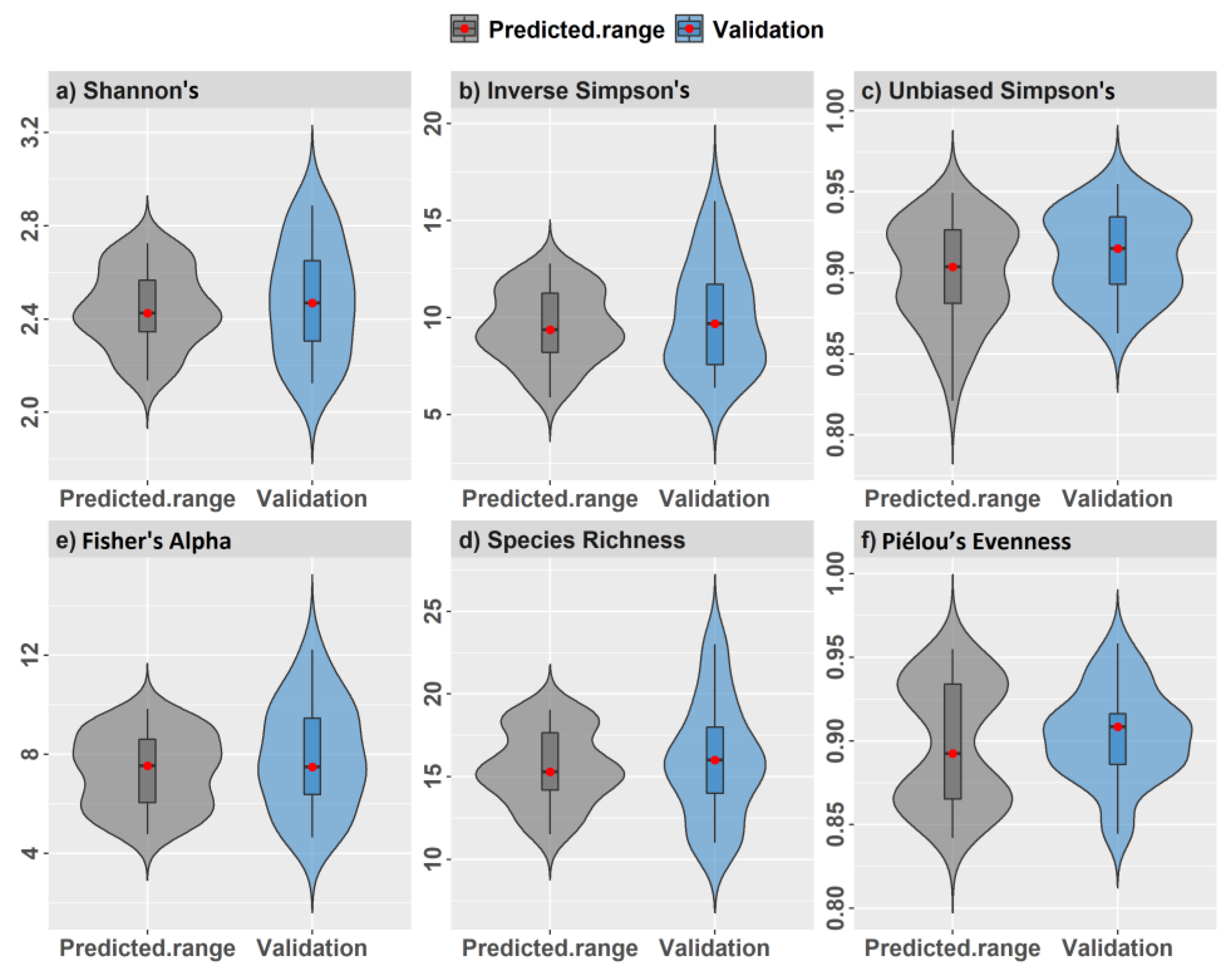
2.7. Data Analysis and Model Validation
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foody, G.M.; Cutler, M.E.K. Mapping the species richness and composition of tropical forest from remotely sensed data with neural networks. Ecol. Model. 2006, 195, 37–42. [Google Scholar] [CrossRef]
- Rocchini, D.; Balkenhol, N.; Carter, G.A.; Foody, G.M.; Gillespie, T.W.; He, K.S.; Kark, S.; Levin, N.; Lucas, K.; Luoto, M.; et al. Remotely sensed spectral heterogeneity as a proxy of species diversity: Recent advances and open challenges. Ecol. Inform. 2010, 5, 318–329. [Google Scholar] [CrossRef]
- Bustamonte, M.M.C.; Roitman, I.; Aide, T.M.; Alencar, A.; Anderson, L.O.; Aragão, L.; Asner, G.P.; Barlow, J.; Berenguer, E.A.; Chambers, J.; et al. Toward an integrated monitoring framework to assess the effect of tropical forest degradation and recovery on carbon stocks and biodiversity. Glob. Change Biol. 2016, 22, 92–109. [Google Scholar] [CrossRef] [PubMed]
- Ganivet, E.; Bloomberg, M. Towards rapid assessment of tree species diversity and structure in fragmented tropical forests: A review of perspectives offered by remotely-sensed and field-based data. For. Ecol. Manag. 2019, 432, 40–53. [Google Scholar] [CrossRef]
- Banda-R, K.; Delgado-Salinas, A.; Dexter, K.G.; Linares-Palomino, R.; Oliveira-Filho, A.; Prado, D.; Pullan, M.; Quintana, C.; Riina, R.; Weintritt, J.; et al. Plant diversity patterns in neotropical dry forests and their conservation implications. Science 2016, 353, 1385–1387. [Google Scholar]
- Miles, L.; Newton, A.C.; Defries, R.S.; Ravilious, C.; May, I.; Blyth, S.; Kapos, V.; Gordon, J.D. A global overview of the conservation status of tropical dry forests. J. Biogeogr. 2006, 33, 491–505. [Google Scholar] [CrossRef]
- García Millán, V.E.; Sánchez-Azofeifa, A.; Málvarez García, G.C.; Rivard, B. Quantifying tropical dry forest succession in the Americas using CHRIS/PROBA. Remote Sens. Environ. 2014, 144, 120–136. [Google Scholar] [CrossRef]
- González-M, R.; García, H.; Isaacs, P.; Cuadros, H.; López-Camacho, R.; Rodríguez, N.; Pérez, K.; Mijares, F.; Castaño-Naranjo, A.; Jurado, R.; et al. Disentangling the environmental heterogeneity, floristic distinctiveness and current threats of tropical dry forests in Colombia. Environ. Res. Lett. 2018, 13, 045007. [Google Scholar] [CrossRef]
- Linares-Palomino, R. Phytogeography and floristics of seasonally dry tropical forest in Peru. In Neotropical Savannas and Seasonally Dry Forests; Pennington, T.R., Ratter, J.A., Eds.; CRC Press: Boca Raton, FL, USA, 2006; pp. 257–280. [Google Scholar]
- Manchego, C.E.; Hildebrandt, P.; Cueva, J.; Espinosa, C.I.; Stimm, B.; Günter, S. Climate change versus deforestation: Implications for tree species distribution in the dry forests of southern Ecuador. PLoS ONE 2017, 12, e0190092. [Google Scholar] [CrossRef]
- Cueva Ortiz, J.; Espinosa, C.I.; Dahik, C.Q.; Mendoza, Z.A.; Ortiz, E.C.; Gusmán, E.; Weber, M.; Hildebrandt, P. Influence of anthropogenic factors on the diversity and structure of a dry forest in the central part of the Tumbesian Region (Ecuador-Perú). Forests 2019, 10, 31. [Google Scholar] [CrossRef]
- Cueva-Ortiz, J.; Espinosa, C.I.; Aguirre-Mendoza, Z.; Gusmán-Montalván, E.; Weber, M.; Hildebrandt, P. Natural regeneration in the Tumbesian dry forest: Identification of the drivers affecting abundance and diversity. Sci. Rep. 2020, 10, 9786. [Google Scholar] [CrossRef] [PubMed]
- Rossi, C.; Kneubühler, M.; Schütz, M.; Schaepman, M.E.; Haller, R.M.; Risch, A.C. Remote sensing of spectral diversity: A new methodological approach to account for spatio-temporal dissimilarities between plan communities. Ecol. Indic. 2021, 130, 108106. [Google Scholar] [CrossRef]
- Cavender-Bares, J.; Schnelder, F.D.; Santos, M.J.; Armstrong, A.; Carnaval, A.; Dahlin, K.M.; Fatoyinbo, L.; Hurtt, G.C.; Schimel, D.; Townsend, P.A.; et al. Integrating remote sensing with ecology and evolution to advance biodiversity conservation. Nat. Ecol. Evol. 2022, 6, 506–519. [Google Scholar] [CrossRef] [PubMed]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The global ecosystem dynamics investigation: High resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Marselis, S.; Keil, P.; Case, J.M.; Dubayah, R. The use of GEDI canopy structure for explaining variation in tree species richness in natural forests. Environ. Res. Lett. 2022, 17, 045003. [Google Scholar] [CrossRef]
- Castagneyrol, B.; Jactel, H. Unraveling plant-animal diversity relationships: A meta-regression analysis. Ecology 2012, 93, 2115–2124. [Google Scholar] [CrossRef] [PubMed]
- Barton, P.S.; Westgate, M.J.; Lane, P.W.; MacGregor, C.; Lindenmayer, D.B. Robustness of habitat-based surrogates of animal diversity: A multitaxa comparison over time. J. Appl. Ecol. 2014, 51, 1434–1443. [Google Scholar] [CrossRef]
- Cruz-Salazar, B.; Ruiz-Montoya, L.; Ramírez-Marcial, N.; García-Bautista, M. Relationship between genetic variation and diversity of tree species in tropical forests in the Ocote Biosphere Reserve, Chiapas, Mexico. Trop. Conserv. Sci. 2021, 14, 1940082920978143. [Google Scholar] [CrossRef]
- Wu, J.; Li, H.; Wan, H.; Wang, Y.; Sun, C.; Zhou, H. Analyzing the relationship between animal diversity and remote sensing vegetation parameters: The case of Xinjiang, China. Sustainability 2021, 13, 9897. [Google Scholar] [CrossRef]
- Roy, D.P.; Kashongwe, H.B.; Armston, J. The impact of geolocation uncertainty on GEDI tropical forest canopy height estimation and change monitoring. Sci. Remote Sens. 2021, 4, 1000024. [Google Scholar] [CrossRef]
- Fricker, G.A.; Wolf, J.A.; Saatchi, S.S.; Gillespie, T.W. Predicting spatial variations of tree species richness in tropical forests from high-resolution remote sensing. Ecol. Appl. 2015, 25, 1776–1789. [Google Scholar] [CrossRef]
- Daly, A.J.; Baetens, J.M.; Baets, B.D. Ecological diversity: Measuring the unmeasurable. Mathematics 2018, 6, 119. [Google Scholar] [CrossRef]
- Jost, L. The relation between evenness and diversity. Diversity 2010, 2, 207–232. [Google Scholar] [CrossRef]
- Ontoy, D.S.; Padua, R.N. Measuring species diversity for conservation biology: Incorporating social and ecological importance of species. Biodivers. J. 2014, 5, 387–390. [Google Scholar]
- Soto-Navarro, C.A.; Harfoot, M.; Hill, S.L.L.; Campbell, J.; Mora, F.; Campos, C.; Pretorius, C.; Pascual, U.; Kapos, V.; Allison, H.; et al. Towards a multidimensional biodiversity index for national application. Nat. Sustain. 2021, 4, 933–942. [Google Scholar] [CrossRef]
- Morris, E.K.; Caruso, T.; Buscot, F.; Fischer, M.; Hancock, C.; Maier, T.S.; Meiners, T.; Müller, C.; Obermaier, E.; Prati, D.; et al. Choosing and using diversity indices: Insights for ecological applications from the German Biodiversity Exploratories. Ecol. Evol. 2014, 4, 3514–3524. [Google Scholar] [CrossRef] [PubMed]
- Palmer, M.W.; Earls, P.G.; Hoagland, B.W.; White, P.S.; Wohlgemuth, T. Quantitative tools for predicting species lists. Environmetrics 2002, 13, 121–137. [Google Scholar] [CrossRef]
- Rocchini, D. Effects of spatial and spectral resolution in estimating ecosystem α-diversity by satellite imagery. Remote Sens. Environ. 2007, 111, 423–434. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A. Remote sensing of terrestrial plant biodiversity. Remote Sens. Environ. 2019, 231, 111218. [Google Scholar] [CrossRef]
- Ochoa-Franco, A.P.; Valdez-Lazalde, J.R.; Ángeles-Pérez, G.; Santos-Posadas, H.M.; Hernádez-Stefanoni, J.L.; Valdez-Hernández, J.I.; Pérez-Rodríguez, P. Beta-diversity modeling and mapping with LiDAR and multispectral sensors in a semi-evergreen tropical forest. Forests 2019, 10, 419. [Google Scholar] [CrossRef]
- George-Chacon, S.P.; Dupuy, J.M.; Peduzzi, A.; Hernandez-Stefanoni, J.L. Combining high resolution satellite imagery and lidar data to model woody plant species diversity of tropical dry forests. Ecol. Indic. 2019, 101, 975–984. [Google Scholar] [CrossRef]
- Lieske, D.J.; Schmid, M.S.; Mahoney, M. Ensembles of ensembles: Combining predictions from multiple machine learning methods. In Machine Learning for Ecology and Sustainable Natural Resource Management; Humphries, G.R.W., Magness, D.R., Huettmann, F., Eds.; Springer Nature: Cham, Switzerland, 2018; pp. 109–122. [Google Scholar]
- Civantos-Gómez, I.; García-Algarra, J.; García-Callejas, D.; Galeano, J.; Godoy, O.; Bartomeus, I. Fine scale prediction of ecological community composition using a two-step sequential machine learning ensemble. PLoS Comput. Biol. 2021, 17, e1008906. [Google Scholar] [CrossRef] [PubMed]
- Unger, M.; Homeier, J.; Lueschner, C. Relationship among leaf area index, below canopy light availability and tree diversity along a transect from tropical lowland to montane forest in NE Ecuador. Trop. Ecol. 2013, 54, 33–45. [Google Scholar]
- Espinosa, C.I.; Jara-Guerrero, A.; Cisneros, R.; Sotomayor, J.D.; Escribano-Ávila, G. Reserva Ecológica Arenillas ¿un refugio de diversidad biológica o una isla en extinción. Ecosistemas 2016, 25, 5–12. [Google Scholar] [CrossRef]
- Instituto Espacial Ecuatoriano (IEE). Memoria Técnica Cantón Huaquillas, Proyecto: Generación de Geoinformación Para la Gestió del Territorio a Nivel Nacional Escala 1:25.000; Clima e Hidrología; Instituto Espacial Ecuatoriano (IEE): Guayaquil, Ecuador, 2012; 20p. [Google Scholar]
- Sierra, R. Propuesta Preliminar de un Sistema de Clasificación de Vegetación para el Ecuador Continental; Proyecto INEFAN/GEF-BIRF y EcoCiencia; Editorial Rimana: Quito, Ecuador, 1999. [Google Scholar]
- Espinosa, C.I.; De la Cruz, M.; Jara-Guerrero, A.; Gusmán, E.; Escudero, A. The effects of individual tree species on species diversity in a tropical dry forest change throughout ontogeny. Ecography 2015, 39, 329–337. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–357. [Google Scholar] [CrossRef]
- Rouse, J.W.; Hass, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the vernal advancement and retrogradation (Green Effect) of natural vegetation. In NASA/GSFC Type III Final Report; Greenbelt: MD, USA, 1973; 371p. [Google Scholar]
- Gitelson, A.; Merzlyak, M.N. Spectral reflectance changes associates with autumn senescence of Aesculus hippocastum L. and Acer platanoides L. leaves. Spectral features and relation to chlorophyll estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Birth, G.; McVey, G. Measuring the color of growing turn with a reflectance spectrometer. Agron. J. 1969, 60, 640–643. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Chen, P.; Tremblay, N.; Wang, J.; Vigneaulta, P. New index for crop canopy fresh biomass estimation. Spectrosc. Spectr. Anal. 2010, 30, 512–517. [Google Scholar]
- Ma, X.; Mahecha, M.D.; Migliavacca, M.; van der Plas, F.; Benavides, R.; Ratcliffe, S.; Kattge, J.; Richter, R.; Musavi, T.; Baeten, L.; et al. Inferring plant functional diversity from space: The potential of Sentinel-2. Remote Sens. Environ. 2019, 233, 111368. [Google Scholar] [CrossRef]
- Chrysafis, I.; Korakis, G.; Kyriazopoulos, A.P.; Mallinis, G. Predicting tree species diversity using geodiversity and Sentinel-2 multi-seasonal spectral information. Sustainability 2020, 12, 9250. [Google Scholar] [CrossRef]
- Xie, Q.; Dash, J.; Huete, A.; Jiang, A.; Yin, G.; Ding, Y.; Peng, D.; Hall, C.C.; Brown, L.; Shi, Y.; et al. Retrieval of crop biophysical parameters from Sentinel-2 remote sensing imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 187–195. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W. Application of a weighted infrared-red vegetation index for estimating leaf area index by correcting for soil moisture. Remote Sens. Environ. 1988, 29, 25–27. [Google Scholar] [CrossRef]
- Boegh, E.; Seogaard, H.; Broge, N.; Hasager, C.B.; Jensen, N.O.; Schelde, N.O.; Thomsen, A. Airborne multispectral data for quantifying leaf area index, nitrogen concentration, and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
- Nagendra, H.; Rocchini, D.; Ghate, R.; Sharma, B.; Pareeth, S. Assessing plant diversity in a dry tropical forest: Comparing the utility of Landsat and Ikonos satellite images. Remote Sens. 2010, 2, 478–496. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Dupuy, J.M.; Johnson, K.D.; Birdsey, R.; Tun-Dzul, F.; Peduzzi, A.; Caamal-Sosa, J.P.; Sánchez-Santos, G.; López-Merlín, D. Improving species diversity and biomass estimates of tropical dry forests using airborne LiDAR. Remote Sens. 2014, 6, 4741–4763. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. 2021. Available online: https://www.R-project.org/ (accessed on 10 June 2022).
- Oksanen, J.; Blanchet, F.G.; Friendly, M.; Kindt, R.; Legendre, P.; McGlinn, D.; Minchin, P.R.; O’Hara, R.B.; Simpson, G.L.; Solymos, P.; et al. Vegan: Community Ecology Package. R package version 2.5-7. 2020. Available online: https://CRAN.R-project.org/package=vegan (accessed on 10 June 2022).
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Simpson, E.H. Measurement of diversity. Nature 1949, 163, 688. [Google Scholar] [CrossRef]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Hurlbert, S.H. The nonconcept of species diversity: A critique and alternative parameters. Ecology 1971, 52, 577–586. [Google Scholar] [CrossRef]
- Fisher, R.A.; Corbet, A.S.; Williams, C.B. The relation between the number of species and the number of individuals in a random sample of animal population. J. Anim. Ecol. 1943, 12, 42–58. [Google Scholar] [CrossRef]
- Piélou, E.C. The measurement of diversity in different types of biological collections. J. Theor. Biol. 1966, 13, 131–144. [Google Scholar] [CrossRef]
- Magurran, A.E. Measuring Biological Diversity; Blackwell Publishing: Malden, MA, USA, 2004. [Google Scholar]
- Jost, L. What do we mean by diversity: The path towards quantification. Métode 2018, 9, 55–61. [Google Scholar] [CrossRef]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. R Package Version 3.5-15. 2022. Available online: https://CRAN.R-project.org/package=raster (accessed on 10 June 2022).
- Evans, J.S. _spatialEco_. R package version 1.3-6. 2021. Available online: https://github.com/jeffreyevans/spatialEco (accessed on 10 June 2022).
- Deane-Mayer, Z.A.; Knowles, J.E. caretEnsemble: Ensembles of caret models 2019, R Package 2.0.1. Available online: https://CRAN.R-project.org/package=caretEnsemble (accessed on 10 June 2022).
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F. Toward an optimal SVM classification system for hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3374–3385. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V.N. Support vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Taylor, J.W. A quantile regression neural network approach to estimating the conditional density of multiperiod returns. J. Forecast. 2000, 19, 299–311. [Google Scholar] [CrossRef]
- Kuhn, M. caret: Classification and Regression Training 2017, R Package Version 6.0-78. Available online: https://CRAN.R-project.org/package=caret (accessed on 10 June 2022).
- Biecek, P. DALEX: Explainers for Complex Predictive Models in R. J. Mach. Learn. Res. 2018, 19, 3245–3249. Available online: https://jmlr.org/papers/v19/18-416.html (accessed on 8 September 2022).
- Mantel, N. The detection of disease clustering and a generalized regression approach. Cancer Res. 1967, 27, 209–220. [Google Scholar]
- Rocchini, D.; Boyd, D.S.; Féret, J.-B.; Foody, G.M.; He, K.S.; Lausch, A.; Negendra, H.; Wegmann, M.; Pettorelli, N. Satellite remote sensing to monitor species diversity: Potential and pitfalls. Remote Sens. Ecol. Conserv. 2016, 2, 25–36. [Google Scholar] [CrossRef]
- Jara-Guerrero, A.; De La Cruz, M.; Espinosa, C.I.; Méndez, M.; Escudero, A. Does spatial heterogeniety blur the signatura of dispersal sindormes on spatial patterns of woody species? A test in a tropical dry forest. Oikos 2015, 124, 1360–1366. [Google Scholar] [CrossRef]
- Jara-Guerrero, A.; González-Sánchez, D.; Escudero, A.; Espinosa, C.I. Chronic disturbance in a tropical dry forest: Disentangling direct and indirect pathways behind the loss of plant richness. Front. For. Glob. Change 2021, 4, 723985. [Google Scholar] [CrossRef]
- Marselis, A.M.; Tang, H.; Armston, J.; Abernethy, K.; Alonso, A.; Barbier, N.; Bissiengou, P.; Jeffery, K.; Kenfack, D.; Labriére, N.; et al. Exploring the relation between remotely sensed vertical canopy structure and tree species diversity in Gabon. Environ. Res. Lett. 2019, 14, 094013. [Google Scholar] [CrossRef]
- Sun, H.; Hu, J.; Wang, J.; Zhou, J.; Lv, L.; Nie, J. RSPD: A novel remote sensing index of plant biodiversity combining the spectral variation hypothesis and productivity hypothesis. Remote Sens. 2021, 13, 3007. [Google Scholar] [CrossRef]
- Redowan, M. Spatial patter of tree diversity and evenness across forest types in Majella National Park, Italy. For. Ecosyst. 2015, 2, 24. [Google Scholar] [CrossRef]
- Marselis, S.M.; Abernethy, K.; Alfonso, A.; Armston, J.; Baker, T.R.; Bastin, J.-F.; Bogaert, J.; Boyd, D.S.; Boeckx, P.; Chazdon, R.; et al. Evaluating the potential of full-waveform lidar for mapping pan-tropical tree species richness. Global Ecol. Biogeogr. 2020, 29, 1799–1816. [Google Scholar] [CrossRef]



| Var. Abbrev. | Spectral Range (nm) | Description | Equation | Ref. |
|---|---|---|---|---|
| b2 | 458–523 | Blue | - | - |
| b3 | 543–578 | Green | - | - |
| b4 | 650–680 | Red | - | - |
| b5 | 698–713 | Red-edge 1 | - | - |
| b6 | 733–748 | Red-edge 2 | - | - |
| b7 | 773–793 | Red-edge 3 | - | - |
| b8 | 785–900 | Near infrared | - | - |
| b8a | 855–875 | Near infrared narrow | - | - |
| b11 | 1565–1655 | Shortwave infrared 1 | - | - |
| b12 | 2100–2280 | Shortwave infrared 2 | - | - |
| evi | - | Enhanced vegetation index | [50] | |
| ndvi | - | Normalized difference vegetation index | [41] | |
| rndvi | - | Red-edge normalized difference vegetation index | [42] | |
| rg | - | Red–green ratio | [44] | |
| wdvi | - | Weighted difference vegetation index | [51] | |
| lai | - | Leaf area index | [52] | |
| laib | - | Leaf area index | SNAP biophysical processor 2 | [49] |
| fpar | - | Fraction absorbed photosynthetically active radiation | SNAP biophysical processor 2 | |
| fcov | - | Fraction of vegetation cover | SNAP biophysical processor 2 | |
| cab | - | Chlorophyll content of leaf | SNAP biophysical processor 2 | |
| cw | - | Canopy water content | SNAP biophysical processor 2 |
| Diversity Index | Equation | Description | Abbr. |
|---|---|---|---|
| Shannon’s [58] | Uncertainty in predicting a species identity of individuals selected at random, sensitive to variation in rare species | H′ | |
| Simpson’s [59] | Probability that two species taken at random are the same, sensitive to variation as abundant species. Addition of rare species causes minor variation in D1 values | D1 | |
| Inverse Simpson’s [60] | Simpson’s transformation so that high values correspond to increased species diversity | D2 | |
| Unbiased Simpson’s [61] | Probability of any two individuals of the same species being drawn from an infinite community | D3 | |
| Fisher’s alpha [62] | Logarithmic series describing the relationship between the number of species and the number of individuals in those species | A | |
| Species richness [58] | Number of species occurrences in a sample | S | |
| Piélou’s Evenness [63] | The equivalence among species in a community | J |
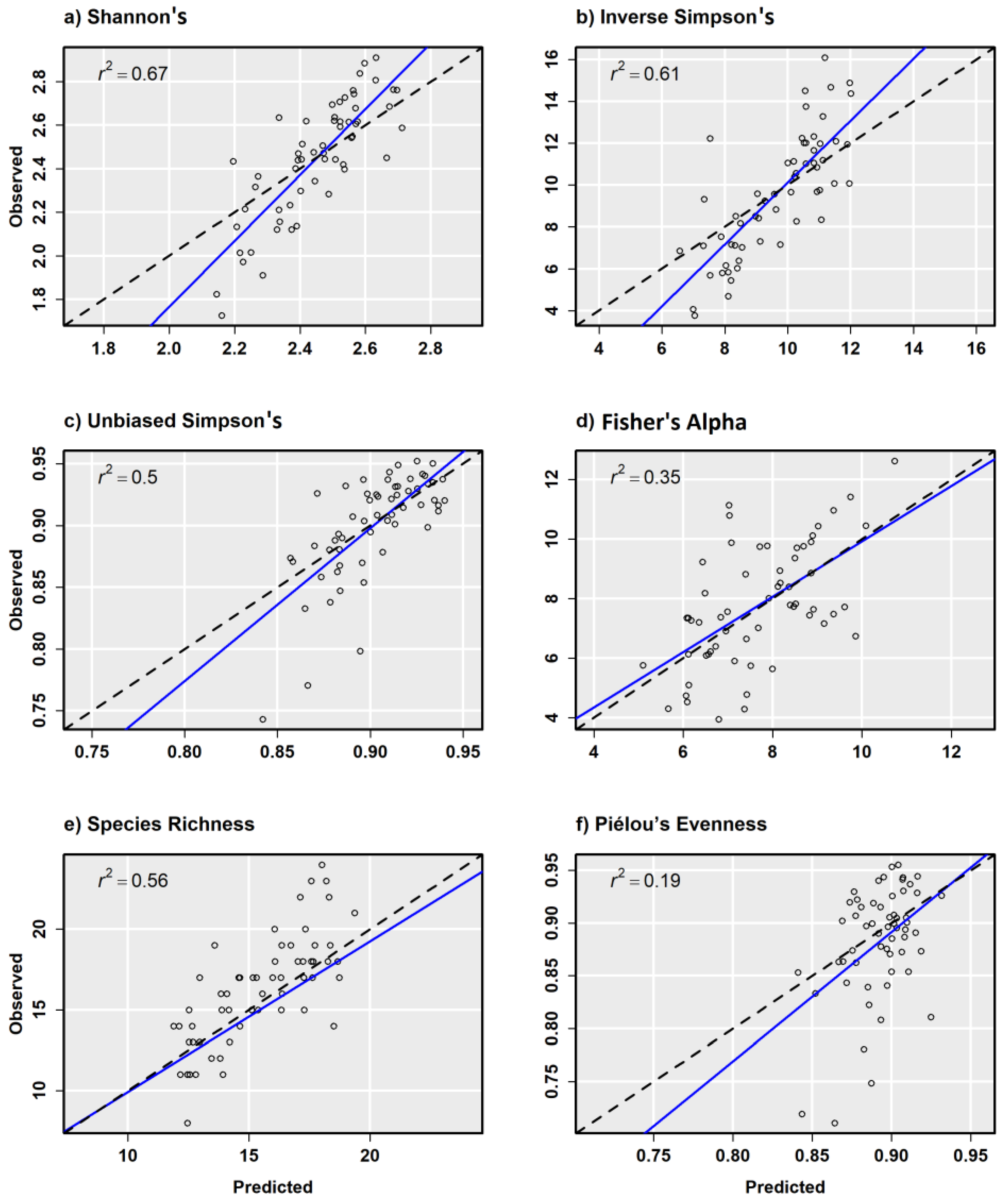
| Dep. Var. | Model | No. Vars 1 | RMSE | R2 | MAE | RMSE SD | R2 SD | MAE SD |
|---|---|---|---|---|---|---|---|---|
| H′ | Sentinel-2 | 28/84 | 0.17 | 0.54 | 0.148 | 0.06 | 0.344 | 0.052 |
| RapidEye | 47/52 | 0.21 | 0.53 | 0.167 | 0.06 | 0.244 | 0.053 | |
| Combined | 10/156 | 0.15 | 0.66 | 0.127 | 0.05 | 0.160 | 0.043 | |
| D2 | Sentinel-2 | 25/84 | 1.95 | 0.53 | 1.660 | 0.64 | 0.282 | 0.578 |
| RapidEye | 30/52 | 2.22 | 0.52 | 1.840 | 0.63 | 0.260 | 0.546 | |
| Combined | 28/156 | 1.94 | 0.41 | 1.590 | 0.39 | 0.231 | 0.34 | |
| D3 | Sentinel-2 | 63/84 | 0.31 | 0.43 | 0.024 | 0.02 | 0.241 | 0.012 |
| RapidEye | 36/52 | 0.03 | 0.47 | 0.023 | 0.02 | 0.331 | 0.015 | |
| Combined | 51/156 | 0.03 | 0.46 | 0.024 | 0.02 | 0.292 | 0.011 | |
| A | Sentinel-2 | 84/84 | 1.67 | 0.35 | 1.40 | 0.52 | 0.203 | 0.455 |
| RapidEye | 50/52 | 2.14 | 0.25 | 1.70 | 0.41 | 0.246 | 0.311 | |
| Combined | 103/156 | 1.50 | 0.60 | 1.21 | 0.49 | 0.246 | 0.413 | |
| S | Sentinel-2 | 77/84 | 2.19 | 0.31 | 2.26 | 0.339 | 0.308 | 0.269 |
| RapidEye | 38/52 | 3.24 | 0.36 | 2.66 | 0.559 | 0.277 | 0.519 | |
| Combined | 43/156 | 2.43 | 0.60 | 2.11 | 1.03 | 0.285 | 0.945 | |
| J | Sentinel-2 | 83/84 | 0.04 | 0.24 | 0.03 | 0.018 | 0.314 | 0.012 |
| RapidEye | 44/52 | 0.04 | 0.22 | 0.04 | 0.017 | 0.207 | 0.011 | |
| Combined | 124/156 | 0.04 | 0.38 | 0.03 | 0.015 | 0.304 | 0.008 |
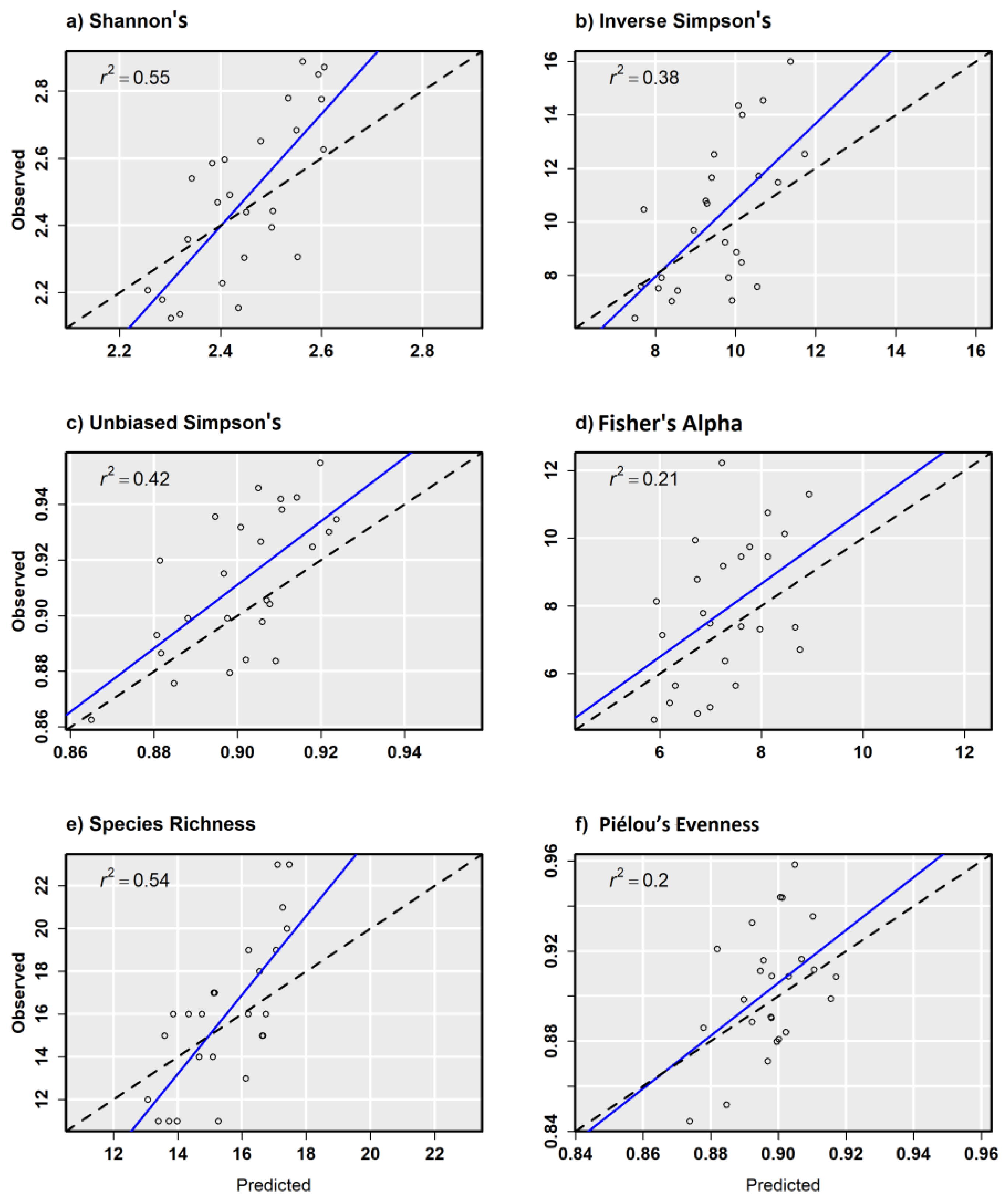
| Dep. Var. | Model | R2 | Adj. R2 | Sigma | F-Stat. | p Value | R2 | Adj. R2 | Sigma | F-Stat. | p-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|
| H′ | Sentinel-2 | 0.52 | 0.51 | 0.153 | 63.3 | <0.001 | 0.24 | 0.21 | 0.216 | 7.4 | 0.012 |
| RapidEye | 0.45 | 0.44 | 0.199 | 47.9 | <0.001 | 0.2 | 0.16 | 0.222 | 5.66 | 0.026 | |
| Combined | 0.67 | 0.67 | 0.155 | 120.0 | <0.001 | 0.54 | 0.52 | 0.168 | 26.92 | <0.001 | |
| D2 | Sentinel-2 | 0.41 | 0.4 | 1.81 | 40.0 | <0.001 | 0.18 | 0.14 | 2.55 | 4.9 | 0.036 |
| RapidEye | 0.44 | 0.43 | 2.18 | 44.8 | <0.001 | 0.35 | 0.32 | 2.27 | 12.4 | 0.002 | |
| Combined | 0.62 | 0.61 | 1.81 | 92.5 | <0.001 | 0.38 | 0.35 | 2.22 | 14.1 | 0.001 | |
| D3 | Sentinel-2 | 0.36 | 0.35 | 0.028 | 32.3 | <0.001 | 0.13 | 0.09 | 0.024 | 3.3 | 0.083 |
| RapidEye | 0.36 | 0.35 | 0.034 | 32.8 | <0.001 | 0.18 | 0.14 | 0.025 | 5 | 0.035 | |
| Combined | 0.5 | 0.49 | 0.03 | 57.7 | <0.001 | 0.42 | 0.4 | 0.02 | 17 | <0.001 | |
| A | Sentinel-2 | 0.20 | 0.19 | 1.63 | 14.8 | <0.001 | 0.20 | 0.17 | 1.95 | 5.9 | 0.023 |
| RapidEye | 0.26 | 0.25 | 1.65 | 21 | <0.001 | 0.29 | 0.26 | 1.26 | 9.3 | 0.005 | |
| Combined | 0.35 | 0.34 | 1.62 | 31.4 | <0.001 | 0.21 | 0.17 | 1.95 | 5.9 | 0.023 | |
| S | Sentinel-2 | 0.54 | 0.54 | 2.15 | 69.2 | <0.001 | 0.45 | 0.42 | 2.69 | 18.5 | <0.001 |
| RapidEye | 0.42 | 0.41 | 2.58 | 41.5 | <0.001 | 0.48 | 0.46 | 2.59 | 21.6 | <0.001 | |
| Combined | 0.56 | 0.55 | 2.26 | 72.5 | <0.001 | 0.54 | 0.52 | 2.43 | 27.3 | <0.001 | |
| J | Sentinel-2 | 0.22 | 0.2 | 0.04 | 15.9 | <0.001 | 0.31 | 0.28 | 0.02 | 10.27 | 0.003 |
| RapidEye | 0.28 | 0.27 | 0.05 | 22.8 | <0.001 | 0.09 | 0.05 | 0.03 | 2.24 | 0.147 | |
| Combined | 0.37 | 0.36 | 0.04 | 34.0 | <0.001 | 0.20 | 0.17 | 0.03 | 5.9 | 0.020 |
| Matrix Comparisons | Control Matrix | Test | Mantel r | p-Value 1 |
|---|---|---|---|---|
| α-Diversity/Geographic dist. | Mantel | 0.05 | 0.13 | |
| α-Diversity/Species comp. | Mantel | 0.39 | <0.001 *** | |
| α-Diversity/Species comp. | Geographic | Partial mantel | 0.39 | <0.001 *** |
| α-Diversity/Forest structure | Mantel | 0.23 | <0.001 *** | |
| α-Diversity/Forest structure | Geographic | Partial mantel | 0.23 | <0.001 *** |
| Species comp./Geographic dist. | Mantel | 0.08 | 0.038 * | |
| Species comp./Geographic dist. | Forest structure | Partial mantel | 0.05 | 0.14 |
| Species comp./Forest structure | Mantel | 0.35 | <0.001 *** | |
| α-Diversity/Sentinel-2 | Mantel | 0.13 | 0.035 * | |
| α-Diversity/Sentinel-2 | Geographic | Partial Mantel | 0.13 | 0.045 * |
| α-Diversity/Sentinel-2 | Forest structure | Partial Mantel | 0.14 | 0.034 * |
| α-Diversity/RapidEye | Mantel | 0.08 | 0.1002 | |
| Species comp./Sentinel- 2 | Mantel | 0.057 | 0.18 | |
| Species comp./RapidEye | Mantel | 0.095 | 0.036 * | |
| Species comp./RapidEye | Forest structure | Partial Mantel | 0.054 | 0.14 |
| Forest structure/Sentinel-2 | Mantel | 0.05 | 0.17 | |
| Forest structure/RapidEye | Mantel | 0.13 | 0.01 ** | |
| Forest structure/RapidEye | Geographic | Partial Mantel | 0.12 | 0.01 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sesnie, S.E.; Espinosa, C.I.; Jara-Guerrero, A.K.; Tapia-Armijos, M.F. Ensemble Machine Learning for Mapping Tree Species Alpha-Diversity Using Multi-Source Satellite Data in an Ecuadorian Seasonally Dry Forest. Remote Sens. 2023, 15, 583. https://doi.org/10.3390/rs15030583
Sesnie SE, Espinosa CI, Jara-Guerrero AK, Tapia-Armijos MF. Ensemble Machine Learning for Mapping Tree Species Alpha-Diversity Using Multi-Source Satellite Data in an Ecuadorian Seasonally Dry Forest. Remote Sensing. 2023; 15(3):583. https://doi.org/10.3390/rs15030583
Chicago/Turabian StyleSesnie, Steven E., Carlos I. Espinosa, Andrea K. Jara-Guerrero, and María F. Tapia-Armijos. 2023. "Ensemble Machine Learning for Mapping Tree Species Alpha-Diversity Using Multi-Source Satellite Data in an Ecuadorian Seasonally Dry Forest" Remote Sensing 15, no. 3: 583. https://doi.org/10.3390/rs15030583
APA StyleSesnie, S. E., Espinosa, C. I., Jara-Guerrero, A. K., & Tapia-Armijos, M. F. (2023). Ensemble Machine Learning for Mapping Tree Species Alpha-Diversity Using Multi-Source Satellite Data in an Ecuadorian Seasonally Dry Forest. Remote Sensing, 15(3), 583. https://doi.org/10.3390/rs15030583






