Spectral Characteristics of the Dynamic World Land Cover Classification
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods
. . . = .
. . . .
FSE10 + FVE10 + FDE10 R10
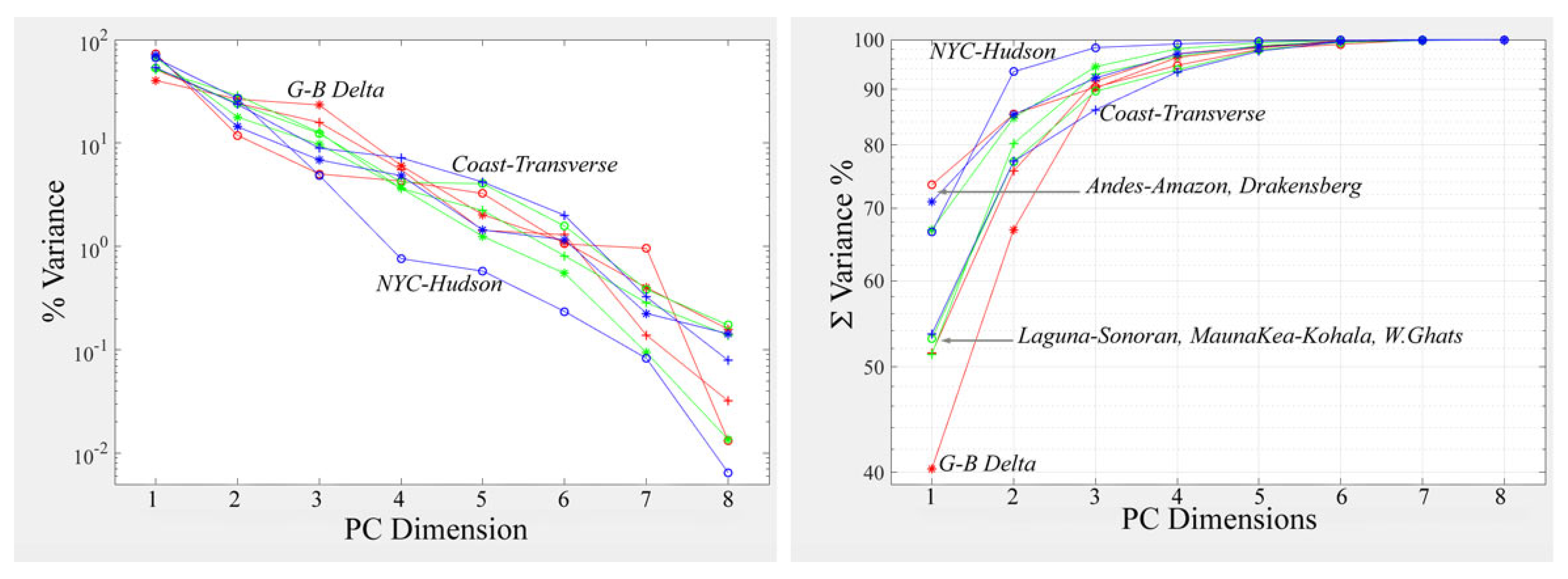
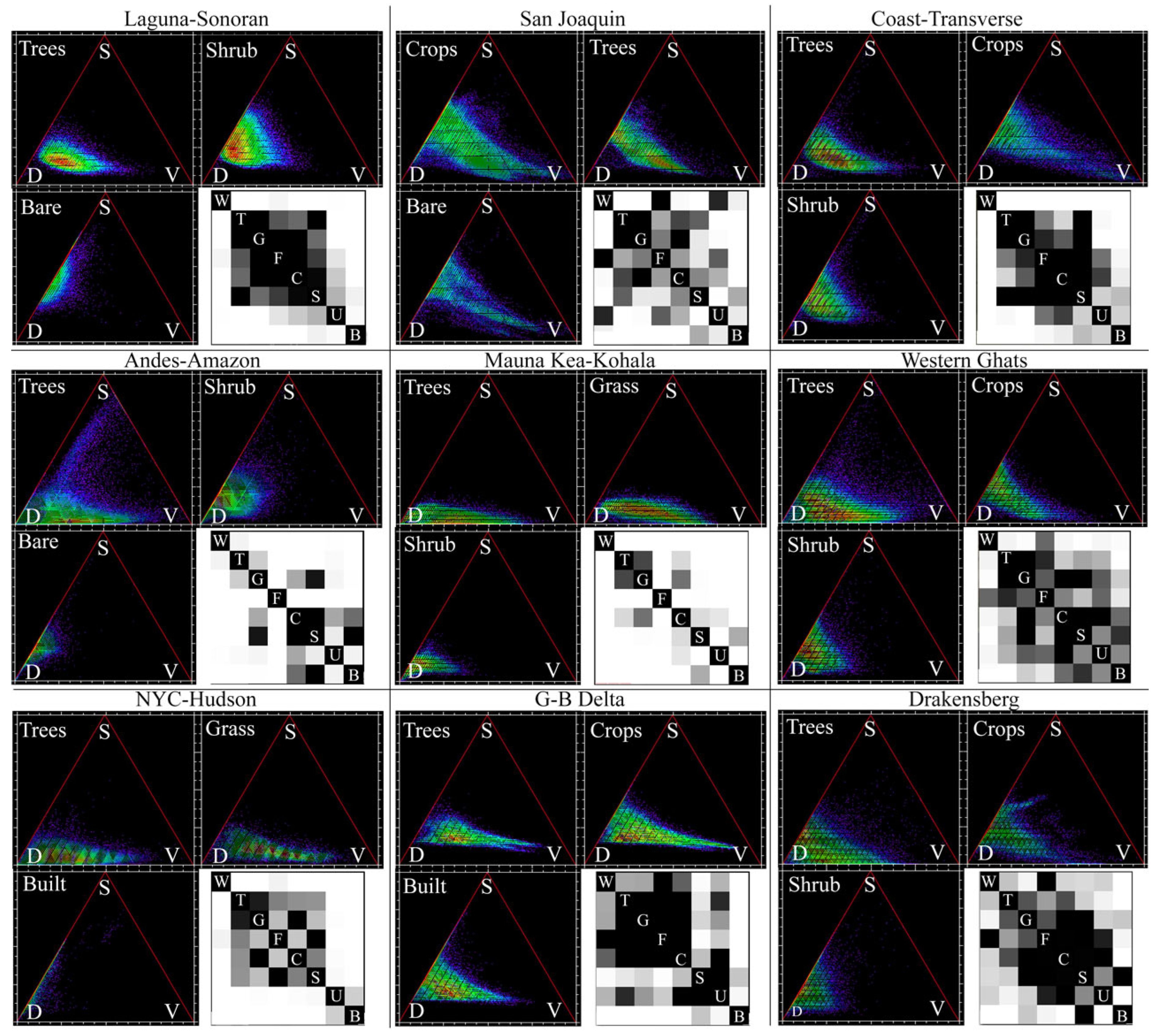
3. Results
4. Discussion
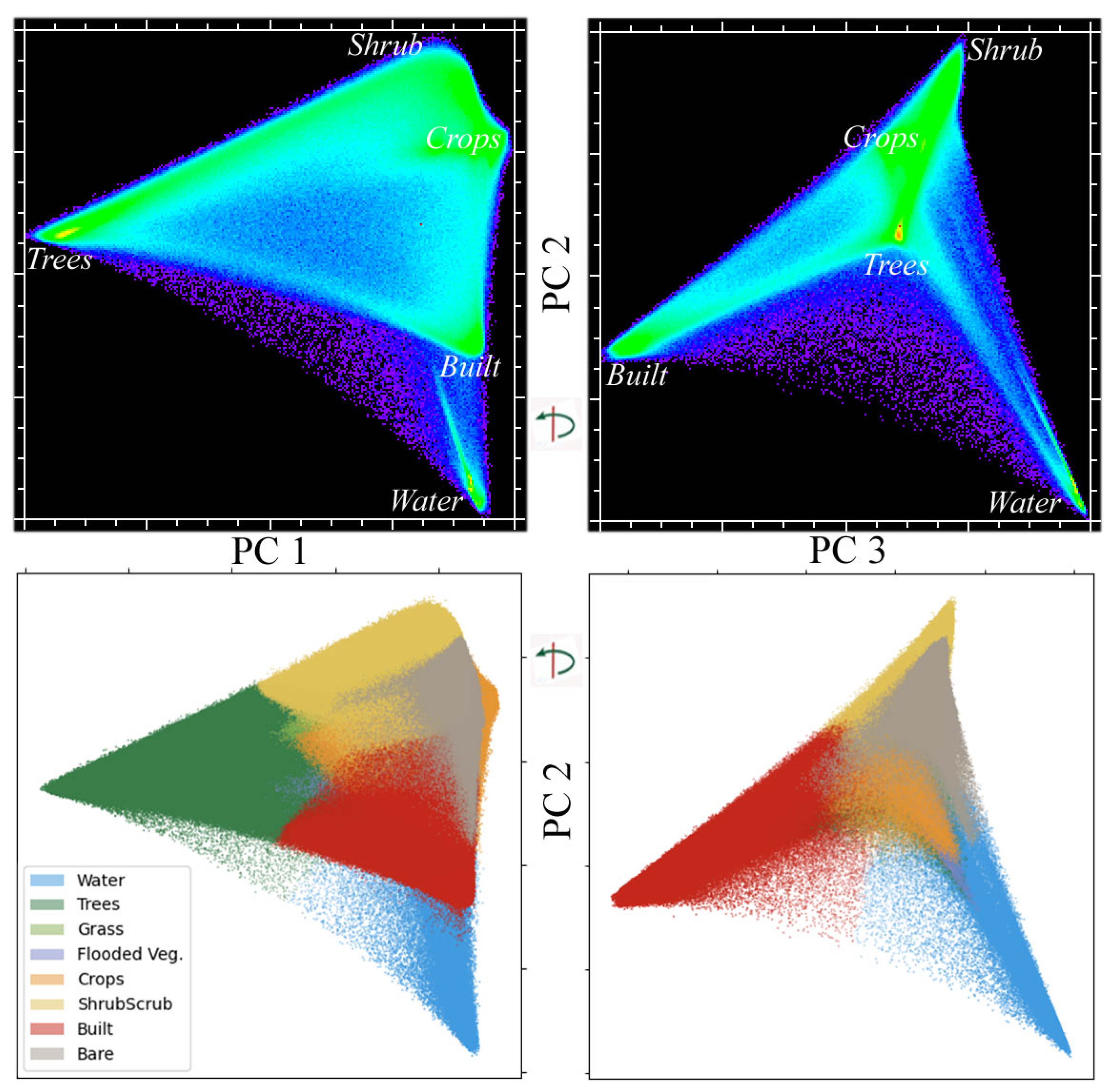
4.1. The SVD Model: Why It Works
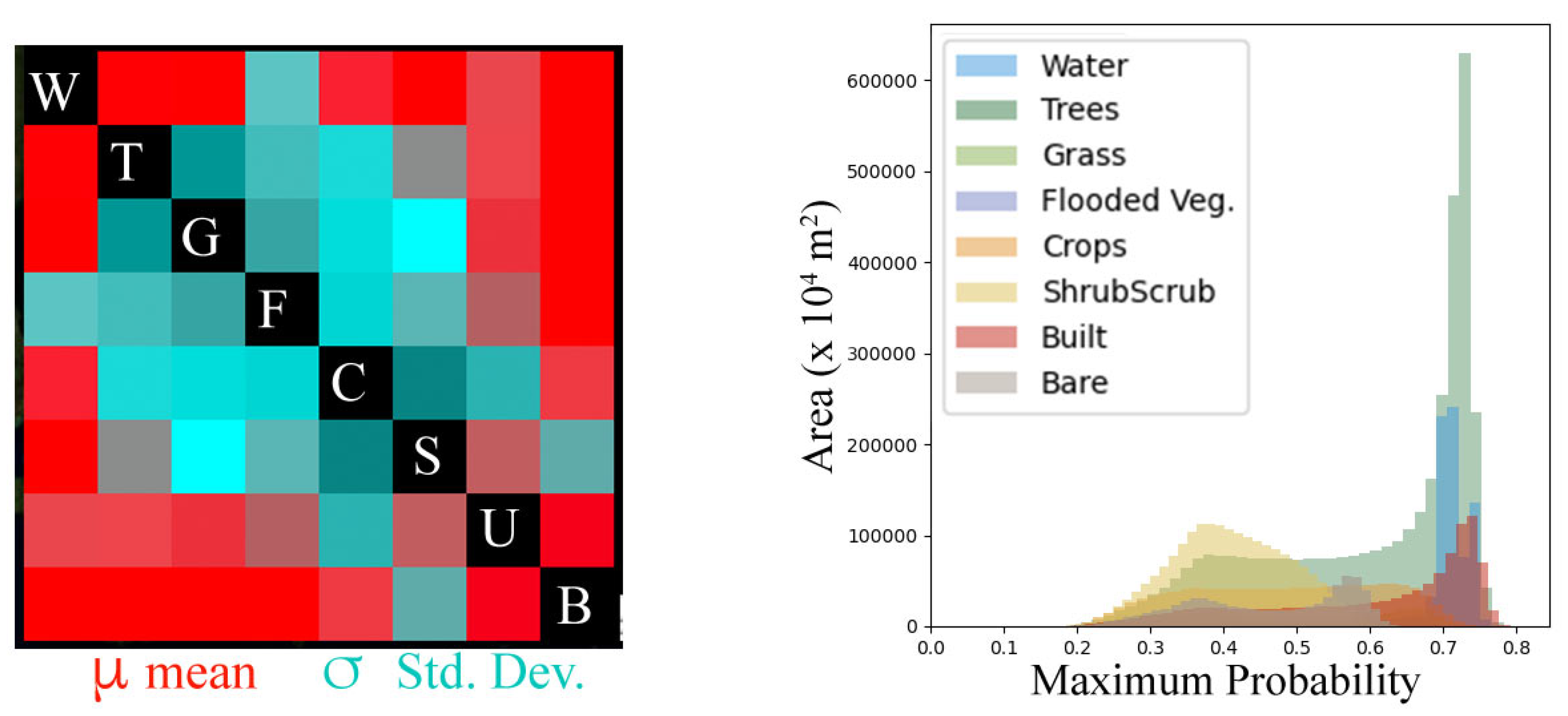
4.2. The Dynamic World Class Probability Continuum
4.3. Spectral Characteristics and Physical Properties of the Dynamic World Classes
4.4. Information Content and Spatial Context
5. Conclusions
- We used a continuous, pixelwise, physical land cover model to characterize a discrete, spatially convolved, statistical land cover classification.
- SVD land cover fractions provided simple, physically meaningful quantification of Dynamic World class similarity and difference.
- Continuous tetrahedral simplices consistently emerged in the Dynamic World class probability space.
- Topology-preserving UMAP manifolds embedded from the Dynamic World probability space revealed further topological structure not obvious from PC feature spaces.
- SVD land cover fractions provided interpretable physical context to the spatio-spectral information used by FCNN-based models.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, C.F.; Brumby, S.P.; Guzder-Williams, B.; Birch, T.; Hyde, S.B.; Mazzariello, J.; Czerwinski, W.; Pasquarella, V.J.; Haertel, R.; Ilyushchenko, S.; et al. Dynamic World, Near Real-Time Global 10 m Land Use Land Cover Mapping. Sci. Data 2022, 9, 251. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical Vegetation Indices for Monitoring Terrestrial Ecosystems Globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Adams, J.B.; Gillespie, A.R. Remote Sensing of Landscapes with Spectral Images: A Physical Modeling Approach; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral Mixture Modeling: A New Analysis of Rock and Soil Types at the Viking Lander 1 Site. J. Geophys. Res. Solid Earth 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in Deserts: I. A Regional Measure of Abundance from Multispectral Images. Remote Sens. Environ. 1990, 31, 1–26. [Google Scholar] [CrossRef]
- Gillespie, A.; Smith, M.; Adams, J.; Willis, S.; Fischer, A.; Sabol, D. Interpretation of Residual Images: Spectral Mixture Analysis of AVIRIS Images, Owens Valley, California. In Proceedings of the Second Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) Workshop, Pasadena, CA, USA, 4–5 June 1990; NASA: Pasadena, CA, USA, 1990; pp. 243–270. [Google Scholar]
- Johnson, P.E.; Smith, M.O.; Taylor-George, S.; Adams, J.B. A Semiempirical Method for Analysis of the Reflectance Spectra of Binary Mineral Mixtures. J. Geophys. Res. Solid Earth 1983, 88, 3557–3561. [Google Scholar] [CrossRef]
- Small, C. The Landsat ETM+ Spectral Mixing Space. Remote Sens. Environ. 2004, 93, 1–17. [Google Scholar] [CrossRef]
- Small, C.; Milesi, C. Multi-Scale Standardized Spectral Mixture Models. Remote Sens. Environ. 2013, 136, 442–454. [Google Scholar] [CrossRef]
- Sousa, D.; Small, C. Global Cross-Calibration of Landsat Spectral Mixture Models. Remote Sens. Environ. 2017, 192, 139–149. [Google Scholar] [CrossRef]
- Sousa, D.; Small, C. Globally Standardized MODIS Spectral Mixture Models. Remote Sens. Lett. 2019, 10, 1018–1027. [Google Scholar] [CrossRef]
- Small, C.; Sousa, D. The Sentinel 2 MSI Spectral Mixing Space. Remote Sens. 2022, 14, 5748. [Google Scholar] [CrossRef]
- Sousa, D.; Small, C. Joint Characterization of Sentinel-2 Reflectance: Insights from Manifold Learning. Remote Sens. 2022, 14, 5688. [Google Scholar] [CrossRef]
- Butterfield, H.; Reynolds, M.; Gleason, M.; Merrifield, M.; Cohen, B.; Heady, W.; Cameron, D. Jack and Laura Dangermond Preserve Integrated Resources Management Plan; The Nature Conservancy: Sacramento, CA, USA, 2019. [Google Scholar]
- Settle, J.J.; Drake, N.A. Linear Mixing and the Estimation of Ground Cover Proportions. Int. J. Remote Sens. 1993, 14, 1159–1177. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Richards, J.A.; Richards, J. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 1999; Volume 3, ISBN 3-642-30061-8. [Google Scholar]
- Swain, P.H.; Davis, S.M. Remote Sensing: The Quantitative Approach. IEEE Trans. Pattern Anal. Mach. Intell. 1981, 3, 713–714. [Google Scholar] [CrossRef]
- Swain, P.H. A Result from Studies of Transformed Divergence. LARS Tech. Rep. 1973. Available online: https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=1041&context=larstech (accessed on 30 December 2022).
- Sousa, D.; Small, C. Multisensor Analysis of Spectral Dimensionality and Soil Diversity in the Great Central Valley of California. Sensors 2018, 18, 583. [Google Scholar] [CrossRef] [PubMed]
- Sousa, D.; Brodrick, P.G.; Cawse-Nicholson, K.; Fisher, J.B.; Pavlick, R.; Small, C.; Thompson, D.R. The Spectral Mixture Residual: A Source of Low-Variance Information to Enhance the Explainability and Accuracy of Surface Biology and Geology Retrievals. J. Geophys. Res. Biogeosciences 2022, 127, e2021JG006672. [Google Scholar] [CrossRef]
- Small, C.; Das, I. The Cryospheric Spectral Mixing Space; AGU: Washington, DC, USA, 2018. [Google Scholar]
- Small, C.; Sousa, D. Joint Characterization of the Cryospheric Spectral Feature Space. Front. Remote Sens. 2021, 2, 55. [Google Scholar] [CrossRef]
- Batty, M.; Longley, P.A. Urban Shapes as Fractals. Area 1987, 19, 215–221. [Google Scholar]
- Small, C.; Milesi, C.; Elvidge, C.; Baugh, K.; Henebry, G.; Nghiem, S. The Land Cover Continuum; Multi-Sensor Characterization of Human-Modified Landscapes. In Proceedings of the EARSeL/NASA Joint Workshop on Land Use and Land Cover, Berlin, Germany, 17–18 March 2014; pp. 17–18. [Google Scholar]





| Hotspot | Date | TileID |
|---|---|---|
| Laguna-Sonoran | 5 April 2022 | L1C_T11SNS_A035445_20220405T182333 |
| San Joaquin | 31 May 2022 | L1C_T11SKA_A036246_20220531T185113 |
| Coast-Transverse | 25 February 2022 | L1C_T10SGD_A025979_20220225T184402 |
| Andes-Amazon | 23 July 2021 | L1C_T18LZL_A031782_20210723T150514 |
| Mauna Kea-Kohala | 12 December 2017 | L1C_T04QHH_A012924_20171212T210918 |
| Western Ghats | 18 February 2020 | L1C_T43PFN_A024326_20200218T051826 |
| NYC-Hudson | 23 July 2021 | L1C_T18TWL_A033041_20211019T154735 |
| G-B Delta | 15 February 2022 | L1C_T46QBM_A034736_20220215T042852 |
| Drakensberg | 16 August 2020 | L1C_T35JRN_A017993_20200816T080232 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Small, C.; Sousa, D. Spectral Characteristics of the Dynamic World Land Cover Classification. Remote Sens. 2023, 15, 575. https://doi.org/10.3390/rs15030575
Small C, Sousa D. Spectral Characteristics of the Dynamic World Land Cover Classification. Remote Sensing. 2023; 15(3):575. https://doi.org/10.3390/rs15030575
Chicago/Turabian StyleSmall, Christopher, and Daniel Sousa. 2023. "Spectral Characteristics of the Dynamic World Land Cover Classification" Remote Sensing 15, no. 3: 575. https://doi.org/10.3390/rs15030575
APA StyleSmall, C., & Sousa, D. (2023). Spectral Characteristics of the Dynamic World Land Cover Classification. Remote Sensing, 15(3), 575. https://doi.org/10.3390/rs15030575







