Reduction in Uncertainty in Forest Aboveground Biomass Estimation Using Sentinel-2 Images: A Case Study of Pinus densata Forests in Shangri-La City, China
Abstract
1. Introduction
- (1)
- To compare different biomass estimation models—the ANN, RF, and the QRNN for estimating the biomass of Pinus densata forests using Sentinel-2 images in Shangri- La City.
- (2)
- To explore the optimal quantile model on each biomass segment to improve the AGB estimation accuracy, and then provide a method to reduce the uncertainties from over-estimation and under-estimation of forest AGB estimation.
2. Materials and Methods
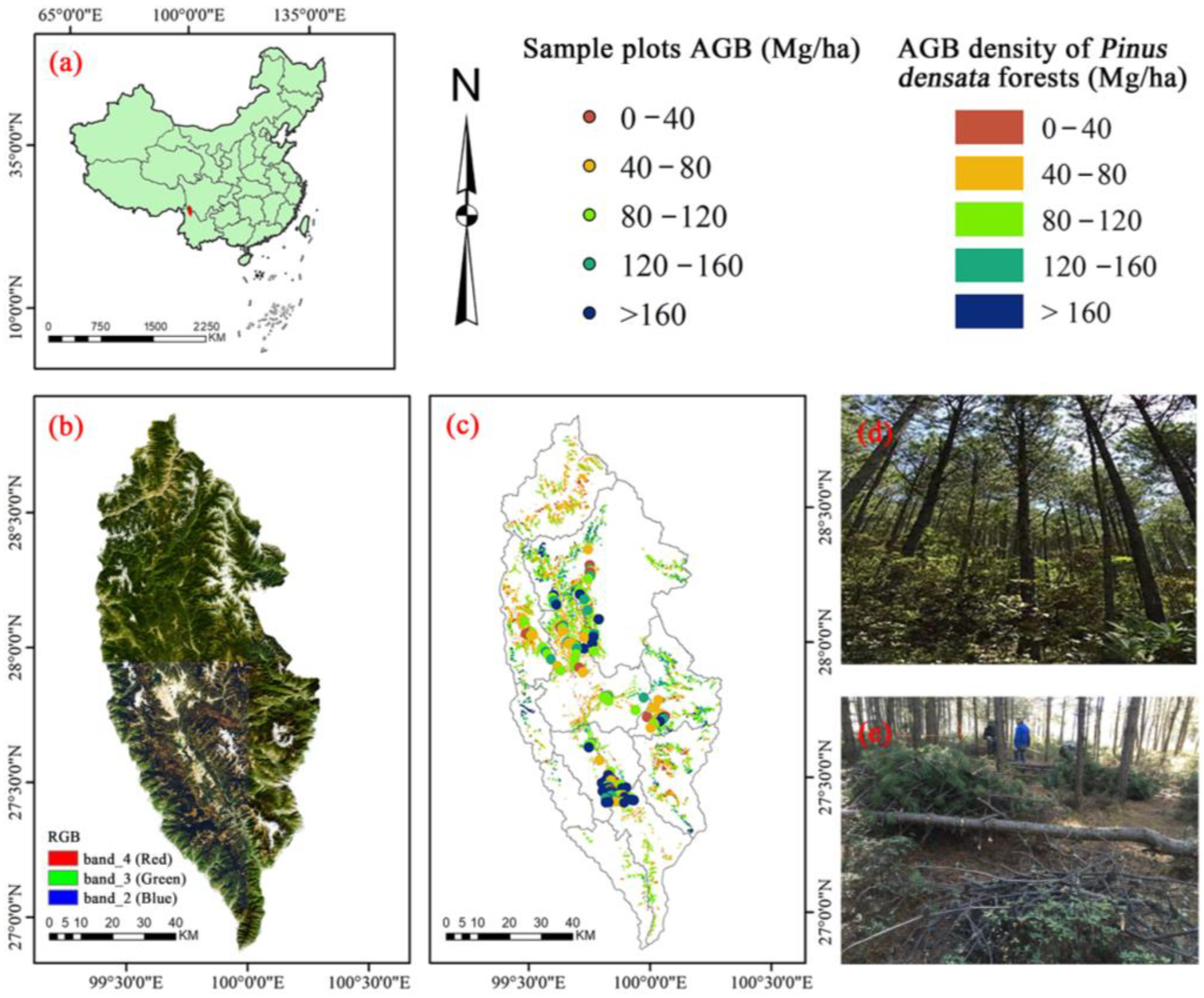
2.1. Study Site
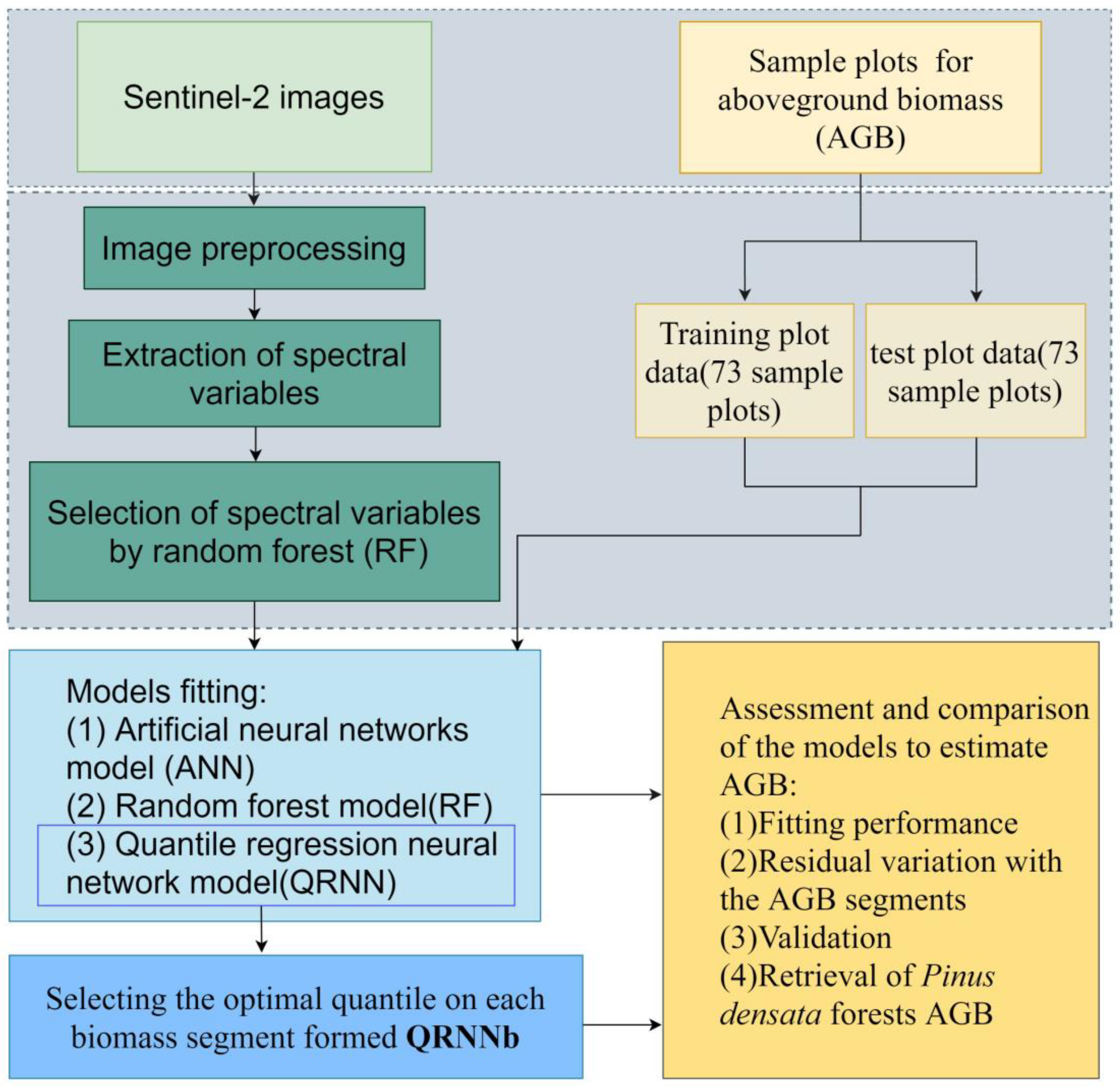
2.2. Flow Chart
2.3. Field Data Collection and Aboveground Biomass Calculation
2.4. Remote Sensing Data and Variables
2.4.1. Pre-Processing of Sentinel-2 Images
2.4.2. Extraction Feature Variables from Remote Sensing
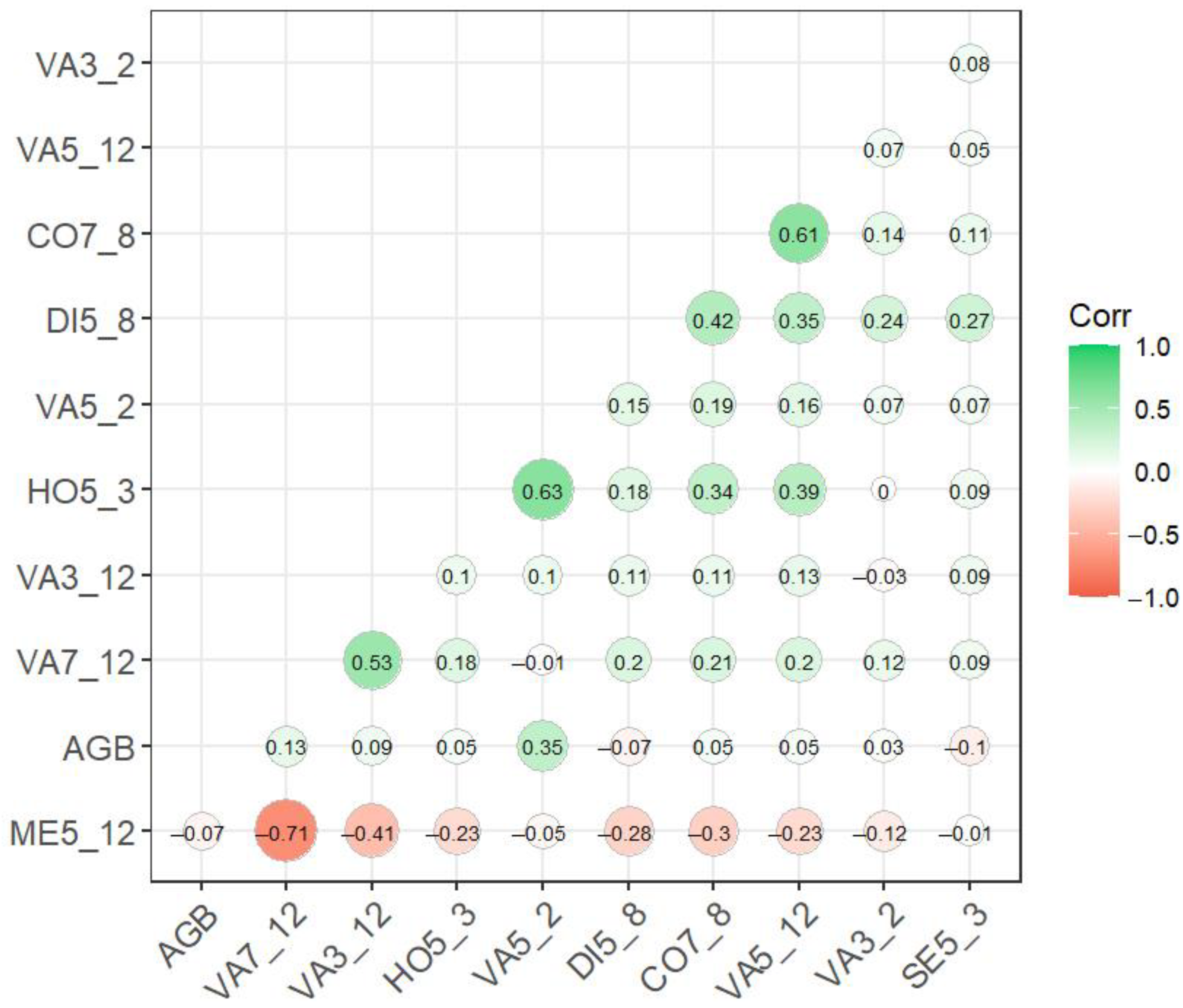
2.4.3. Variables Screening
2.5. Modeling Methods
2.5.1. Random Forests Modeling (RF)
2.5.2. Artificial Neural Networks Model (ANN)
2.5.3. Quantile Regression Neural Network (QRNN)
2.6. Assessment and Validation of the Models
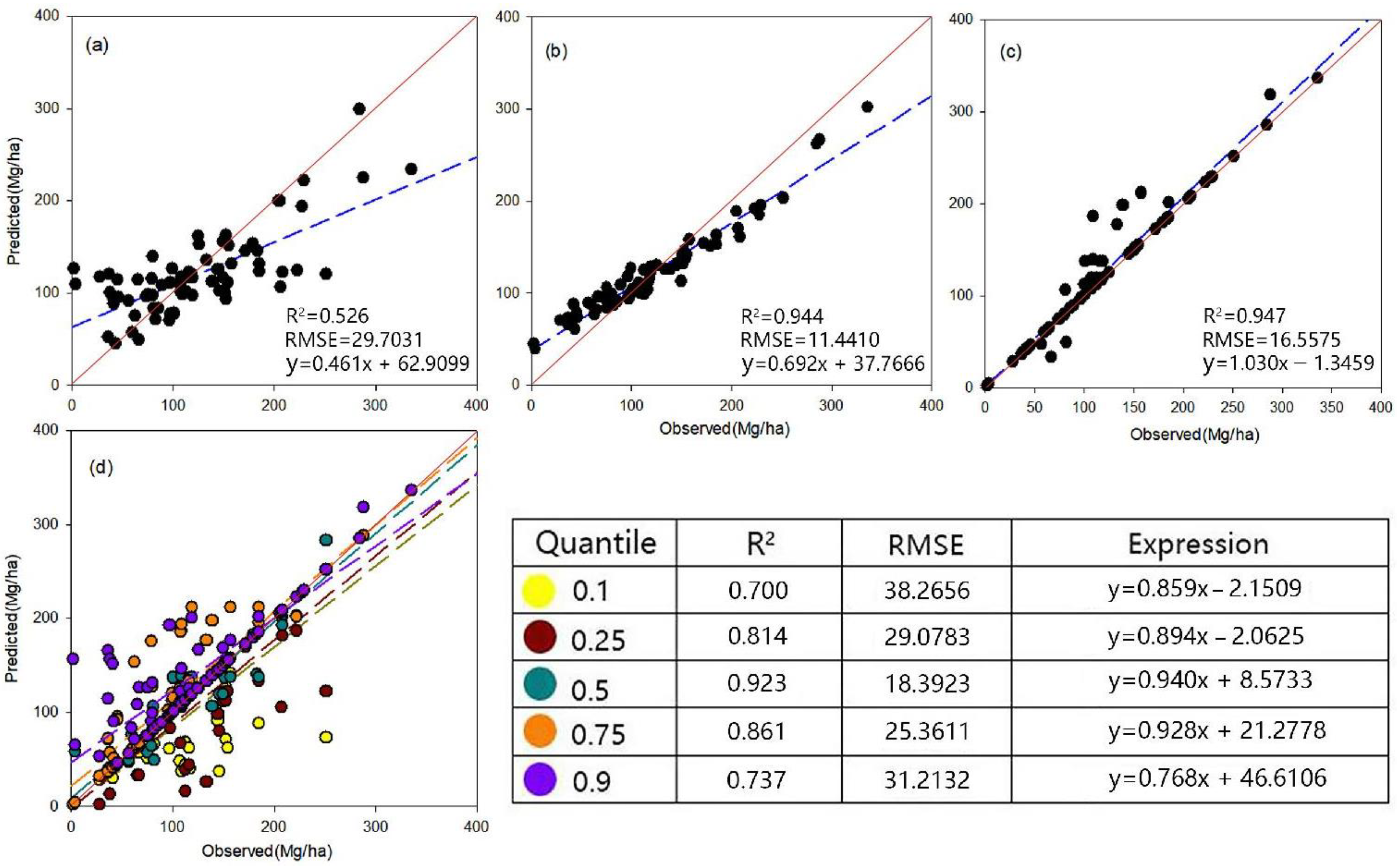
3. Results
3.1. Results of Spectral Variables Screening
3.2. Model Comparison of the Model
3.2.1. Model Fitting
3.2.2. Method Validation
4. Discussion
4.1. Accuracy Comparison
4.2. Data Resource and Variables
4.3. Limitation and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Indices | Models | |||
|---|---|---|---|---|
| ANN | RFs | QRNNb | ||
| R2 | 0–40 | 0.384 | 0.076 | 0.958 |
| 40–80 | 0.022 | 0.200 | 0.889 | |
| 80–120 | 0.050 | 0.241 | 0.430 | |
| 120–160 | 0.031 | 0.302 | 0.234 | |
| >160 | 0.257 | 0.861 | 0.968 | |
| Total | 0.549 | 0.932 | 0.956 | |
| RMSE (Mg/ha) | 0–40 | 6.919 | 8.474 | 1.799 |
| 40–80 | 12.075 | 10.926 | 4.068 | |
| 80–120 | 11.050 | 9.952 | 8.621 | |
| 120–160 | 13.586 | 11,708 | 12.258 | |
| >160 | 52.062 | 22.510 | 2.774 | |
| Total | 51.310 | 19.960 | 16.063 | |
| ME (Mg/ha) | 0–40 | −58.615 | −31.676 | −0.597 |
| 40–80 | −37.525 | −18.002 | 1.489 | |
| 80–120 | −7.131 | −1.365 | −7.131 | |
| 120–160 | 10.183 | 7.239 | −4.231 | |
| >160 | 60.937 | 42.327 | 0.200 | |
| Total | −0.454 | 2.275 | −1.211 | |
| MAE (Mg/ha) | 0–40 | 61.077 | 31.676 | 0.601 |
| 40–80 | 39.856 | 18.243 | 0.941 | |
| 80–120 | 20.327 | 6.905 | 1.455 | |
| 120–160 | 25.946 | 10.825 | 5.084 | |
| >160 | 65.955 | 42.327 | 0.308 | |
| Total | 42.060 | 22.555 | 2.396 | |
References
- Houghton, R.A.; Hackler, J.L.; Lawrence, K.T. The U.S. Carbon budget: Contributions from land-use change. Science 1999, 285, 574–578. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Chen, Q.; Hu, Y.; Du, Z.; Lin, G.; Wang, C.; Huang, Y. Estimation of forest aboveground biomass by using a mixed-effects model. Int. J. Remote Sens. 2021, 42, 8675–8690. [Google Scholar] [CrossRef]
- Sun, S.; Wang, Y.; Song, Z.; Chen, C.; Zhang, Y.; Chen, X.; Chen, W.; Yuan, W.; Wu, X.; Ran, X.; et al. Modelling aboveground biomass carbon stock of the Bohai rim coastal wetlands by integrating remote sensing, terrain, and climate data. Remote Sens. 2021, 13, 4321. [Google Scholar] [CrossRef]
- Wulder, M.A.; Roy, D.P.; Radeloff, V.C.; Loveland, T.R.; Anderson, M.C.; Johnson, D.M.; Healey, S.; Zhu, Z.; Scambos, T.A.; Pahlevan, N.; et al. Fifty years of Landsat science and impacts. Remote Sens. Environ. 2022, 280, 113195. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E.J. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Puliti, S.; Solberg, S.; Næsset, E.; Gobakken, T.; Zahabu, E.; Mauya, E.; Malimbwi, R. Modelling aboveground biomass in Tanzanian miombo woodlands using TanDEM-X world DEM and field data. Remote Sens. 2017, 9, 984. [Google Scholar] [CrossRef]
- Xue, B.W. Lidar and Machine Learning Estimation of Hardwood Forest Biomass in Mountainous and Bottomland Environments. Master’s Thesis, University of Arkansas, Fayetteville, NC, USA, 2015; p. 1274. [Google Scholar]
- Tian, Y.; Huang, H.; Zhou, G.; Zhang, Q.; Tao, J.; Zhang, Y.; Lin, J. Aboveground mangrove biomass estimation in Beibu Gulf using machine learning and UAV remote sensing. Sci. Total Environ. 2021, 781, 146816. [Google Scholar] [CrossRef]
- Vaglio, L.G.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Frate, F.D.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- Listopad, C.M.C.S.; Drake, J.B.; Masters, R.E.; Weishampel, J.F. Portable and airborne small footprint LiDAR: Forest canopy structure estimation of fire managed plots. Remote Sens. 2011, 3, 1284–1307. [Google Scholar] [CrossRef]
- Spriggs, R.; Coomes, D.; Jones, T.; Caspersen, J.; Vanderwel, M. An alternative approach to using LiDAR remote sensing data to predict stem diameter distributions across a temperate forest landscape. Remote Sens. 2017, 9, 944. [Google Scholar] [CrossRef]
- Cutler, M.E.J.; Boyd, D.S.; Foody, G.M.; Vetrivel, A. Estimating tropical forest biomass with a combination of SAR image texture and Landsat TM data: An assessment of predictions between regions. ISPRS J. Photogramm. Remote Sens. 2012, 70, 66–77. [Google Scholar] [CrossRef]
- El Hage, M.; Villard, L.; Huang, Y.; Ferro-Famil, L.; Koleck, T.; Le Toan, T.; Polidori, L. Multicriteria accuracy assessment of digital elevation models (DEMs) produced by airborne P-band polarimetric SAR tomography in tropical rainforests. Remote Sens. 2022, 14, 4173. [Google Scholar] [CrossRef]
- Quegan, S.; Le Toan, T.; Chave, J.; Dall, J.; Exbrayat, J.-F.; Minh, D.H.T.; Lomas, M.; D’ Alessandro, M.M.; Paillou, P.; Papathanassiou, K.; et al. The European space agency BIOMASS Mission: Measuring forest above-ground biomass from space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef]
- El Idrissi Essebtey, S.; Villard, L.; Borderies, P.; Koleck, T.; Burban, B.; Le Toan, T. Long-term trends of P-Band temporal decorrelation over a tropical dense forest-experimental results for the BIOMASS mission. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R.; Pardini, M.; Quiñones, M.J.; Hoekman, D.; Ferro-Famil, L.; Goodenough, D.; Chen, H.; Tebaldini, S.; Neumann, M.; et al. Forest Applications. In Polarimetric Synthetic Aperture Radar: Principles and Application; Remote Sensing and Digital Image, Processing; Hajnsek, I., Desnos, Y.-L., Eds.; Springer International Publishing: Cham, Germany, 2021; pp. 59–117. ISBN 978-3-030-56504-6. [Google Scholar]
- López-Serrano, P.M.; Cárdenas, D.; José, L.; Corral-Rivas, J.J.; Jiménez, E.; López-Sánchez, C.A.; Vega-Nieva, D.J. Modeling of aboveground biomass with Landsat 8 OLI and machine learning in temperate forests. Forests 2019, 11, 11. [Google Scholar] [CrossRef]
- Zeng, N.; Ren, X.L.; He, H.L.; Zhang, L.; Zhao, D.; Ge, R.; Li, P.; Niu, Z.G. Estimating grassland aboveground biomass on the Tibetan Plateau using a random forest algorithm. Ecol. Indic. 2019, 102, 479–487. [Google Scholar] [CrossRef]
- Sagang, L.B.T.; Ploton, P.; Sonké, B.; Poilvé, H.; Couteron, P.; Barbier, N. Airborne Lidar sampling pivotal for accurate regional AGB predictions from multispectral images in forest-Savanna landscapes. Remote Sens. 2020, 12, 1637. [Google Scholar] [CrossRef]
- SUHET. Sentinel-2 User Handbook; European Space Agency: Paris, France, 2013. [Google Scholar]
- Chen, Y.; Guerschman, J.; Shendryk, Y.; Henry, D.; Harrison, M.T. Estimating pasture biomass using Sentinel-2 imagery and machine learning. Remote Sens. 2021, 13, 603. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Abdullah, H.; Skidmore, A.K.; Darvishzadeh, R.; Heurich, M.; Pettorelli, N.; Disney, M. Sentinel-2 accurately maps green-attack stage of European spruce bark beetle (Ips typographus L.) compared with Landsat-8. Remote Sens. Ecol. Conserv. 2018, 5, 87–106. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.Q.L.; Batchily, K.B.; Leeuwen, W.V. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Kalaitzidis, C.; Zianis, D.; Heinzel, V. A Review of Vegetation Indices for the Estimation of Biomass. In Proceedings of the 29th Symposium of the European Association of Remote Sensing Laboratories, Chania, Greece; IOS Press Ebook: Amsterdam, The Netherlands, 2009; pp. 201–208. [Google Scholar] [CrossRef]
- Safari, A.; Sohrabi, H. Integration of synthetic aperture radar and multispectral data for aboveground biomass retrieval in Zagros oak forests, Iran: An attempt on Sentinel imagery. Int. J. Remote Sens. 2020, 41, 8069–8095. [Google Scholar] [CrossRef]
- Luan, P.V.; Everardo, C.M.; do Amaral, C.H.; Christopher, M.U.; NealeZution, G.I.; Filgueiras, R.; Fernando, C.E. Potential of using spectral vegetation indices for corn green biomass estimation based on their relationship with the photosynthetic vegetation sub-pixel fraction. Agric. Water Manag. 2020, 236, 106155. [Google Scholar] [CrossRef]
- David, R.M.; Rosser, N.J.; Donoghue, D.N.M. Improving above ground biomass estimates of Southern Africa dryland forests by combining Sentinel-1 SAR and Sentinel-2 multispectral imagery. Remote Sens. Environ. 2022, 282, 113232. [Google Scholar] [CrossRef]
- Lu, D.S. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2007, 27, 1297–1328. [Google Scholar] [CrossRef]
- Kuplich, T.M.; Curran, P.J.; Atkinson, P.M. Relating SAR image texture to the biomass of regenerating tropical forests. Int. J. Remote Sens. 2011, 26, 4829–4854. [Google Scholar] [CrossRef]
- Wang, X.Q.; Pang, Y.; Zhang, Z.J.; Yuan, Y. Forest Aboveground Biomass Estimation Using SPOT-5 Texture Indices and Spectral Derivatives. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec, QC, Canada, 13–18 July 2014; pp. 2830–2833. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground biomass estimation using multi-sensor data synergy and machine learning algorithms in a dense tropical forest. Appl. Geogr. 2018, 96, 29–40. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Su, H.Y.; Shen, W.J.; Wang, J.R.; Ali, A.; Li, M. Machine learning and geostatistical approaches for estimating aboveground biomass in Chinese subtropical forests. For. Ecosyst. 2020, 7, 64. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 34, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Arsalan, G.; Soheil, Z.; Reza, M.A.; Meisam, A.; Mohammadzadeh, A.; Sadegh, J. Ghrobanian-Mangrove ecosystem mapping using Sentinel-1 and Sentinel-2 Satellite images and random forest algorithm in Google Earth Engine. Remote Sens. 2021, 13, 2565. [Google Scholar] [CrossRef]
- Jiang, F.; Kutia, M.; Ma, K.; Chen, S.; Long, J.; Sun, H. Estimating the aboveground biomass of coniferous forest in Northeast China using spectral variables, land surface temperature and soil moisture. Sci. Total Environ. 2021, 785, 147335. [Google Scholar] [CrossRef]
- Zeng, P.; Zhang, W.; Li, Y.; Shi, J.; Wang, Z. Forest total and component above-ground biomass (AGB) estimation through C- and L-band polarimetric SAR data. Forests 2022, 13, 442. [Google Scholar] [CrossRef]
- Lourenço, P.; Godinho, S.; Sousa, A.; Gonçalves, A.C. Estimating tree aboveground biomass using multispectral satellite-based data in Mediterranean agroforestry system using random forest algorithm. Remote Sens. Appl. Soc. Environ. 2021, 23, 100560. [Google Scholar] [CrossRef]
- Ou, G.L.; Lv, Y.Y.; Xu, H.; Wang, G.X. Improving forest aboveground biomass estimation of Pinus densata forest in Yunnan of southwest China by spatial regression using Landsat 8 images. Remote Sens. 2019, 11, 2750. [Google Scholar] [CrossRef]
- Axelsson, C.; Skidmore, A.K.; Schlerf, M.; Fauzi, A.; Verhoef, W. Hyperspectral analysis of mangrove foliar chemistry using PLSR and support vector regression. Int. J. Remote Sens. 2012, 34, 1724–1743. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D.; Sun, J. Artificial neural network-based ionospheric delay correction method for satellite-based augmentation systems. Remote Sens. 2022, 14, 676. [Google Scholar] [CrossRef]
- Beaudoin, A.; Hall, R.J.; Castilla, G.; Filiatrault, M.; Villemaire, P.; Skakun, R.; Guindon, L. Improved k-NN mapping of forest attributes in northern Canada using spaceborne L-Band SAR, multispectral and LiDAR data. Remote Sens. 2022, 14, 1181. [Google Scholar] [CrossRef]
- Yadav, S.; Padalia, H.; Sinha, S.K.; Srinet, R.; Chauhan, P. Above-ground biomass estimation of Indian tropical forests using X band Pol-InSAR and Random Forest. Remote Sens. Appl. Soc. Environ. 2021, 21, 100462. [Google Scholar] [CrossRef]
- Joshua, O.L.; Chinenye, A.L.; Adewale, G.A. Multi-layer perceptron artificial neural network (MLP-ANN) prediction of biomass higher heating value (HHV) using combined biomass proximate and ultimate analysis data. Model. Earth Syst. Environ. 2022, 8, 3177–3191. [Google Scholar] [CrossRef]
- Vahedi, A.A. Artificial neural network application in comparison with modeling allometric equations for predicting above-ground biomass in the Hyrcanian mixed-beech forests of Iran. Biomass Bioenergy 2016, 88, 66–76. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yua, M.; Bai, Y.; Zhang, L. A comparison of two models with Landsat data for estimating above-ground grassland biomass in Inner Mongolia, China. Ecol. Model. 2009, 220, 1810–1818. [Google Scholar] [CrossRef]
- Yang, S.; Feng, Q.; Liang, T.; Liu, B.; Zhang, W.; Xie, H. Modeling grassland above-ground biomass based on artificial neural network and remote sensing in the Three-River Headwaters Region. Remote Sens. Environ. 2018, 204, 448–455. [Google Scholar] [CrossRef]
- Taylor, J.W. A quantile regression neural network approach to estimating the conditional density of multiperiod returns. J. Forecast. 2000, 19, 299–311. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Cade, B.S.; Noon, B.R. A gentle introduction to quantile regression for ecologists. Front. Ecol. Environ. 2003, 1, 412–420. [Google Scholar] [CrossRef]
- Julien, L. A quantile regression study of climate change in Chicago, 1960–2010. SIAM Undergrad. Res. Online 2012, 5, 148–165. [Google Scholar] [CrossRef]
- Cannon, A.J. Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Comput. Geosci. 2011, 37, 1277–1284. [Google Scholar] [CrossRef]
- Cannon, A.J. Non-crossing nonlinear regression quantiles by monotone composite quantile regression neural network, with application to rainfall extremes. Stoch. Environ. Res. Risk Assess. 2018, 32, 3207–3225. [Google Scholar] [CrossRef]
- He, Y.; Li, H. Probability density forecasting of wind power using quantile regression neural network and kernel density estimation. Energy Convers. Manag. 2018, 164, 374–384. [Google Scholar] [CrossRef]
- Dong, M.; Wu, D.; Fu, X.; Deng, H.; Wu, G. Regional-scale analysis on the strengths, weaknesses, opportunities, and threats in sustainable development of Shangri-La County. Int. J. Sustain. Dev. World Ecol. 2014, 22, 171–177. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Y.; Huang, Y.; Jarvis, D.; Sato, K.; Kato, K.; Tsuyuzaki, H.; Chen, L.; Long, C. Genetic diversity analysis of hulless barley from Shangri-la region revealed by SSR and AFLP markers. Genet. Resour. Crop Evol. 2011, 59, 1543–1552. [Google Scholar] [CrossRef]
- Wang, B.; Mao, J.F.; Jie, G.; Wei, Z.; Wang, X.R. Colonization of the Tibetan plateau by the homoploid hybrid pine Pinus densata. Mol. Ecol. 2011, 20, 3796–3811. [Google Scholar] [CrossRef] [PubMed]
- Compilation Committee of Yunnan Forest. Yunnan Forest; Yunnan Science and Technology Press: Kunming, China; China Forestry Publishing House: Beijing, China, 1986. [Google Scholar]
- Zhang, J.; Lu, C.; Xu, H.; Wang, G. Estimating aboveground biomass of Pinus densata-dominated forests using Landsat time series and permanent sample plot data. J. For. Res. 2019, 30, 1689–1706. [Google Scholar] [CrossRef]
- Ou, G.L.; Li, C.; Lv, Y.Y.; Wei, A.C.; Xiong, H.X.; Xu, H.; Wang, G.X. Improving aboveground biomass estimation of Pinus densata forests in Yunnan using Landsat 8 imagery by incorporating age dummy variable and method comparison. Remote Sens. 2019, 11, 738. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.Q.; Chhin, S.; Zhang, J.; Duan, A. Disentangling the effects of stand and climatic variables on forest productivity of Chinese fir plantations in subtropical China using a random forest algorithm. Agric. For. Meteorol. 2021, 304–305, 108412. [Google Scholar] [CrossRef]
- Roy, N.; Pal, A.; Dey, A.; Das, S. Applications of artificial intelligence in machine learning: Review and Prospect. Int. J. Comput. Appl. 2015, 115, 31–41. [Google Scholar] [CrossRef]
- Stathakis, D. How many hidden layers and nodes? Int. J. Remote Sens. 2009, 30, 2133–2147. [Google Scholar] [CrossRef]
- Tiryaki, S.; Aydın, A. An artificial neural network model for predicting compression strength of heat treated woods and comparison with a multiple linear regression model. Constr. Build. Mater. 2014, 62, 102–108. [Google Scholar] [CrossRef]
- Babcock, C.; Finley, A.O.; Bradford, J.B.; Kolka, R.; Birdsey, R.; Ryan, M.G. LiDAR-based prediction of forest biomass using hierarchical models with spatially varying coefficients. Remote Sens. Environ. 2015, 169, 113–127. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, G.; Deng, L.; Tang, Z.; Wang, K.; Sun, W.; Shangguan, Z. Prediction of aboveground grassland biomass on the Loess Plateau, China, using a random forest algorithm. Sci. Rep. 2017, 7, 6940. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Li, G.; Wang, M.; Fan, Z. Analyzing the uncertainty of estimating forest aboveground biomass using optical imagery and spaceborne LiDAR. Remote Sens. 2019, 11, 722. [Google Scholar] [CrossRef]
- Zhu, X.L.; Liu, D.S. Improving forest aboveground biomass estimation using seasonal Landsat NDVI time-series. J. Photogramm. Remote Sens. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Examining the potential of Sentinel-2 MSI spectral resolution in quantifying above-ground biomass across different fertilizer treatments. ISPRS J. Photogramm. Remote Sens. 2015, 110, 55–65. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High-density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Exploring the inclusion of Sentinel-2 MSI texture metrics in above-ground biomass estimation in the community forest of Nepal. Geocarto Int. 2019, 35, 1832–1849. [Google Scholar] [CrossRef]
- Kelsey, K.; Neff, J. Estimates of aboveground biomass from texture analysis of Landsat imagery. Remote Sens. 2014, 6, 6407–6422. [Google Scholar] [CrossRef]
- Xu, H.; Yue, C. Study on Forest Landscape Change and Forest Biomass Estimation in Shangri-La Based on Remote Sensing Technology; Yunnan Science and Technology Press: Kunming, China, 2014. [Google Scholar]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Xie, F.; Shu, Q.; Zi, L.; Wu, R.; Wu, Q.; Wang, H.; Liu, Y.; Ji, Y. Remote sensing estimation of Pinus densata aboveground biomass based on k-NN nonparametric model. Acta Agric. Univ. Jiangxiensis 2018, 40, 743–750. [Google Scholar]
- Li, L.; Zhou, X.S.; Chen, L.; Chen, L.; Zhang, Y.; Liu, Y. Estimating urban vegetation biomass from Sentinel-2A image data. Forests 2020, 11, 125. [Google Scholar] [CrossRef]
- Lu, D.S.; Batistella, M.; Moran, E. Satellite estimation of aboveground biomass and impacts of forest stand structure. Photogramm. Eng. Remote Sens. 2005, 71, 967–974. [Google Scholar] [CrossRef]
- Chang, J.S.; Shoshany, M. Mediterranean Shrublands Biomass Estimation Using Sentinel-1 and Sentinel-2. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar] [CrossRef]
- Masjedi, A.; Zhao, J.Q.; Thompson, A.M.; Yang, K.W.; Flatt, J.E.; Crawford, M.M.; Ebert, D.S.; Tuinstra, M.R.; Hammer, G.; Chapman, S. Sorghum Biomass Prediction Using UAV-Based Remote Sensing Data and Crop Model Simulation. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Freeman, E.A.; Moisen, G.G. An Application of Quantile Random Forests for Predictive Mapping of Forest Attributes. In Proceedings of the New Directions in Inventory Techniques & Applications Forest Inventory & Analysis (FIA) Symposium, Portland, OR, USA, 8–10 December 2015; p. 362. [Google Scholar]
- Pham, T.D.; Le, N.N.; Ha, N.T.; Nguyen, L.V.; Xia, J.; Yokoya, N.; To, T.T.; Trinh, H.X.; Kieu, L.Q.; Takeuchi, W. Estimating Mangrove Above-Ground Biomass Using Extreme Gradient Boosting Decision Trees Algorithm with Fused Sentinel-2 and ALOS-2 PALSAR-2 Data in Can Gio Biosphere Reserve, Vietnam. Remote Sens. 2020, 12, 777. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Xu, M.; Liu, R.; Chen, J.M.; Liu, Y.; Shang, R.; Ju, W.; Wu, C.; Huang, W. Retrieving leaf chlorophyll content using a matrix-based vegetation index combination approach. Remote Sens. Environ. 2019, 224, 60–73. [Google Scholar] [CrossRef]


| Variables | Fitting Data (n = 73) | Test Data (n = 73) | All Data (n = 146) | |
|---|---|---|---|---|
| Minimum | H (m) | 2.2 | 2.9 | 2.2 |
| Dg (cm) | 2.9 | 4.9 | 2.9 | |
| AGB (Mg/ha) | 2.1 | 11.1 | 2.1 | |
| Maximum | H (m) | 24.3 | 19.5 | 24.3 |
| Dg (cm) | 41.3 | 24.7 | 41.3 | |
| AGB (Mg/ha) | 335.9 | 344.4 | 344.4 | |
| Mean | H (m) | 10.0 | 10.3 | 10.1 |
| Dg (cm) | 14.6 | 15.0 | 14.8 | |
| AGB (Mg/ha) | 120.7 | 122.2 | 121.5 | |
| Standard deviation | H (m) | 3.8 | 3.7 | 3.7 |
| Dg (cm) | 6.3 | 4.5 | 5.5 | |
| AGB (Mg/ha) | 67.5 | 79.9 | 73.7 | |
| Image ID | Acquisition Date | Central Longitude (Degree) | Central Latitude (Degree) | Solar Elevation | Solar Azimuth | Mean Cloud Amount (%) |
|---|---|---|---|---|---|---|
| S2A_MSIL1C_20161124T040102_N0204_R004_T47RNK_20161124T040118 | 24 November 2016 | 99.5513 | 26.6257 | 1.0249 | 162.1176 | 12.6 |
| S2A_MSIL1C_20161124T040102_N0204_R004_T47RNL_20161124T040118 | 24 November 2016 | 99.5557 | 27.5287 | 1.0249 | 162.2853 | 25.6 |
| S2A_MSIL1C_20161124T040102_N0204_R004_T47RNM_20161124T040118 | 24 November 2016 | 99.5604 | 28.4315 | 1.0249 | 162.4446 | 41.7 |
| S2A_MSIL1C_20161124T040102_N0204_R004_T47RPL_20161124T040118 | 24 November 2016 | 100.5684 | 27.5209 | 1.0249 | 163.4582 | 15.1 |
| S2A_MSIL1C_20161124T040102_N0204_R004_T47RPL_20161124T040118 | 24 November 2016 | 100.5815 | 28.4235 | 1.0249 | 163.6144 | 38.5 |
| Data Sources | SV | Definitions of SV | Number of SV |
|---|---|---|---|
| Sentinel-2 | Original band | b2—blue, b3—green, b4—red, b5—vegetation red edge, b6—vegetation red edge, b7—vegetation red edge, b8—NIR, b9—water vapor, b10—SWIR-cirrus, b11—SWIR, b12—SWIR | 11 |
| Vegetation indices | Normalized difference vegetation index (NDVI), atmospherically resistant vegetation index (ARVI), difference vegetation index (DVI), ratio vegetation index (RVI), vegetation index of soil adjustment ratio (SARV), oil adjusted vegetation index (SAVI), modified soil vegetation index (MSAVI), short infrared temperature vegetation index (MVI5), mid-infrared temperature vegetation index (MVI7), transformation vegetation index (TVI), nonlinear vegetation index (NLI), perpendicular vegetation Index (PVI), infrared vegetation index (II), optimization simple ratio index (MSR), simple vegetation index (SR), brightness vegetation index (B), temperature vegetation index (W), greenness vegetation index (G), normalized difference vegetation index using R and G bands (ND43), normalized difference vegetation index using band 6 and band 7 (ND67), normalized difference vegetation index using band 5, band 6, and band 3 (ND563) | 21 | |
| Image transformations | The first three components from the tasseled cap transform (K T transform) and the first three principal components of principal component analysis (PCA) | 6 | |
| Texture measures | Grey-level co-occurrence matrix-based texture measures including the mean, angular second moment, contrast, correlation, dissimilarity, entropy, homogeneity, and variance using moving window sizes of 3 × 3, 5 × 5, and 7 × 7 pixels | 96 |
| Indices | Models | |||
|---|---|---|---|---|
| ANN | RFs | QRNNb | ||
| R2 | 0–40 | 0.105 | 0.402 | 0.961 |
| 40–80 | 0.043 | 0.094 | 0.757 | |
| 80–120 | 0.167 | 0.598 | 0.430 | |
| 120–160 | 0.277 | 0.385 | 0.671 | |
| >160 | 0.480 | 0.857 | 0.867 | |
| Total | 0.602 | 0.936 | 0.943 | |
| RMSE (Mg/ha) | 0–40 | 8.341 | 6.818 | 1.733 |
| 40–80 | 11.948 | 11.624 | 6.019 | |
| 80–120 | 10.421 | 7.242 | 9.851 | |
| 120–160 | 11.915 | 10.987 | 8.034 | |
| >160 | 43.555 | 23.215 | 22.052 | |
| Total | 48.180 | 19.396 | 18.203 | |
| ME (Mg/ha) | 0–40 | −44.364 | −30.845 | 1.035 |
| 40–80 | −33.623 | −19.38 | 7.029 | |
| 80–120 | −0.338 | 2.093 | 2.683 | |
| 120–160 | 13.741 | 8.230 | −6.861 | |
| >160 | 44.386 | 34.321 | −11.617 | |
| Total | −1.507 | 1.927 | −1.419 | |
| MAE (Mg/ha) | 0–40 | 48.400 | 30.846 | 1.035 |
| 40–80 | 36.041 | 19.438 | 7.090 | |
| 80–120 | 11.213 | 5.720 | 5.926 | |
| 120–160 | 18.874 | 18.482 | 9.202 | |
| >160 | 47.465 | 34.321 | 11.618 | |
| Total | 32.066 | 21.271 | 8.357 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhou, B.; Liu, Y.; Wu, Y.; Tang, J.; Xu, W.; Wang, L.; Ou, G. Reduction in Uncertainty in Forest Aboveground Biomass Estimation Using Sentinel-2 Images: A Case Study of Pinus densata Forests in Shangri-La City, China. Remote Sens. 2023, 15, 559. https://doi.org/10.3390/rs15030559
Li L, Zhou B, Liu Y, Wu Y, Tang J, Xu W, Wang L, Ou G. Reduction in Uncertainty in Forest Aboveground Biomass Estimation Using Sentinel-2 Images: A Case Study of Pinus densata Forests in Shangri-La City, China. Remote Sensing. 2023; 15(3):559. https://doi.org/10.3390/rs15030559
Chicago/Turabian StyleLi, Lu, Boqi Zhou, Yanfeng Liu, Yong Wu, Jing Tang, Weiheng Xu, Leiguang Wang, and Guanglong Ou. 2023. "Reduction in Uncertainty in Forest Aboveground Biomass Estimation Using Sentinel-2 Images: A Case Study of Pinus densata Forests in Shangri-La City, China" Remote Sensing 15, no. 3: 559. https://doi.org/10.3390/rs15030559
APA StyleLi, L., Zhou, B., Liu, Y., Wu, Y., Tang, J., Xu, W., Wang, L., & Ou, G. (2023). Reduction in Uncertainty in Forest Aboveground Biomass Estimation Using Sentinel-2 Images: A Case Study of Pinus densata Forests in Shangri-La City, China. Remote Sensing, 15(3), 559. https://doi.org/10.3390/rs15030559










