Abstract
As a prerequisite for many 3D visualization tasks, point cloud registration has a wide range of applications in 3D scene reconstruction, pose estimation, navigation, and remote sensing. However, due to the limited overlap of point clouds, the presence of noise and the incompleteness of the data, existing feature-based matching methods tend to produce higher outlier matches, thus reducing the quality of the registration. Therefore, the generation of reliable feature descriptors and the filtering of outliers become the key to solving these problems. To this end, we propose a multi-local-to-global registration (MLGR) method. First, in order to obtain reliable correspondences, we design a simple but effective network module named the local geometric network (LG-Net), which can generate discriminative feature descriptors to reduce the outlier matches by learning the local latent geometric information of the point cloud. In addition, we propose a multi-local-to-global registration strategy to further filter outlier matches. We compute the hypothetical transformation matrix from local patch matches. The point match evaluated as an inlier under multiple hypothetical transformations will receive a higher score, and low-scoring point matches will be rejected. Finally, our method is quite robust under different numbers of samples, as it does not require sampling a large number of correspondences to boost the performance. The numerous experiments on well-known public datasets, including KITTI, 3DMatch, and ModelNet, have proven the effectiveness and robustness of our method. Compared with the state of the art, our method has the lowest relative rotation error and relative translation error on the KITTI, and consistently leads in feature matching recall, inlier ratio, and registration recall on 3DMatch under different numbers of point correspondences, which proves the robustness of our method. In particular, the inlier ratio is significantly improved by 3.62% and 4.36% on 3DMatch and 3DLoMatch, respectively. In general, the performance of our method is more superior and robust than the current state of the art.
1. Introduction
Point cloud registration is a fundamental but challenging research topic in the field of computer 3D vision. There are many potential applications, such as 3D scene reconstruction, AR/VR, laser radar remote sensing (LRRTS), and autonomous driving [1,2,3,4]. For example, in the field of remote sensing, data come from a variety of sensors, such as LIDAR, satellites, drones, and cameras, and the point cloud data generated by these sensors usually suffer from positional bias, attitude differences, and temporal differences. Only when these inconsistent data are aligned can they be used for downstream tasks. The goal of point cloud registration is to find the optimal spatial transformation that accurately aligns point clouds from different data sources in the same coordinate system [5]. In recent years, with the development and popularization of laser scanning, radar, and other detection technologies, point cloud as a unique form of expression in the field of 3D vision has received more and more attention. Point cloud alignment is a prerequisite for other tasks, such as point cloud classification and segmentation, so it is necessary to investigate the reduction of errors in point cloud alignment and the enhancement of the stability of alignment methods.
The most classic method in point cloud registration is the iterative closest point (ICP) algorithm [6]. Its core idea involves iteratively optimizing the alignment of point clouds by alternating between two steps. Firstly, it identifies the closest point in the target point set for each point in the source point set. Then, by minimizing the distances between these corresponding points, it continuously adjusts the transformation to refine the alignment of the point clouds progressively, ensuring convergence to the optimal alignment through iterations. From ICP, many improvement methods [7,8,9,10] have emerged. These approaches iteratively optimize point cloud alignment, achieving higher precision registration, and enhancing the accuracy and stability of alignments. In the domain of point cloud registration, ICP and its derivative methods stand as powerful and effective tools.
However, the classical ICP algorithm tends to have a slower convergence speed due to its linear convergence rate. Another issue is that alignment accuracy may be affected by deficiencies within point sets, such as noise, outliers, and limited overlap, which are common occurrences during real-world data collection [11]. With the development of deep learning, learning-based point cloud registration has been widely studied [12]. Compared with non-learning methods, learning-based methods are less sensitive to noise, point cloud density, and outlier, and have higher robustness. The more popular ones are correspondence-based registration [13] and end-to-end registration [14]. The advantage of the correspondence-based method is that it can provide a robust and accurate correspondence search, and then achieve accurate alignment results by the simple RANSAC method. The advantage of the end-to-end learning method is the uniformity, which can directly realize the point cloud alignment without the help of other methods.
Our approach follows the correspondence-based methodology, typically involving two primary stages [15]. First, obtain point correspondences. Older methods, such as the ICP algorithm [11], identify the closest point pair in the source point cloud and target point cloud as a match. The other one is to determine the correspondence based on the feature descriptors [16,17,18,19,20], and point pairs with similar features will be matched. This is further divided into hand-crafted descriptors and learning-based descriptors. In recent years, with the boom in deep learning, learned descriptors have shown better results. Subsequently, an algorithm such as SVD is used to compute the transformation matrix between the two point clouds.
A more recent and popular approach is to train neural networks to extract feature descriptions [21,22,23,24,25,26] and determine the correspondence based on their similarity, and, finally, use a robust estimator [27,28], e.g., random sample consensus (RANSAC), to evaluate the rigid transformation matrix. However, due to the natural non-overlapping area between the point clouds, the correspondence obtained by this method inevitably has outliers, which are especially prominent when the overlapping area of two point clouds is small. In addition, the RANSAC-based evaluation method often requires a large number of iterations to obtain acceptable results, and this method also receives outliers in the low overlap scenario. Our baseline, GeoTransformer [29], improves the alignment results by adding manually calculated local geometric information to the network; however, it is not flexible to use a uniform geometric information embedding method in different scenarios. Therefore, how to extract robust and accurate feature descriptions and avoid incorrect correspondence due to outliers become the key to solving this problem.
In this paper, we propose a new coarse-to-fine registration strategy for point cloud registration. Inspired by most of these efforts [29,30,31,32,33], our method first downsamples the point clouds to obtain sparse points, and the sparse points as the centre are combined with its domain to form patches. In the coarse registration phase, we obtain the initial sparse point correspondences and then extend these correspondences to local patch matches, so we obtain a series of local patch correspondences. In the fine matching phase, we compute the hypothetical transformations matrix based on the patch correspondences, and apply each scheme to the global and evaluate it. Only the point correspondence that is evaluated as an inline match in multiple schemes will be used to compute the final transformation matrix.
An existing method [29] uses a transformer for global information exchange to generate feature descriptors. In contrast, we add a local feature aggregation module. It was shown in [34] that local feature aggregation can increase the discriminative nature of feature descriptors, which is useful for computing reliable correspondences. We build a local geometric network (LG-Net) for discovering local features. We use the LG-Net to mine local potential geometric information while using the transformer for global information exchange for the generation of accurate correspondence. In addition, choosing reliable correspondence is crucial to avoid outlier matches. GeoTransformer [29] proposes a local-to-global registration (LGR) method, which generates a transformation matrix from the local dense point correspondences, and then evaluates it on the global dense point correspondences, selecting the scheme with the highest number of inlier matches. Correspondence scores evaluated as inlier matches are retained; otherwise, they are considered as outlier matches and masked. However, the limitation of this approach is that the correspondences obtained by the neural network are not absolutely correct, which means that some real inlier matches may be mistaken for outlier matches and filtered. For this reason, we propose a more reliable multi-local-to-global registration (MLGR) method based on the LGR. The difference is that, instead of choosing the single scheme with the most evaluated inlier matches as the global correspondence scheme, we vote on the top-k schemes. If a point correspondence is evaluated as inlier mathing in all k schemes, this means that it is more reliable and we will keep its correspondence score. Correspondences that are evaluated as inlier mathing in only a few schemes will have their scores weakened, and correspondences that are evaluated as outlier mathing in all k schemes will be masked. Our MLGR can filter outlier matching better and has better robustness than selecting a single local solution.
The main contributions of this paper are as follows:
- We design and add a local feature aggregation module (LG-Net) based on the geometric transformer. Our design is simple and efficient, and improves the overall performance with little overhead. While using the attention mechanism for global information exchange, local features are aggregated to increase feature diversity and make the generated feature descriptors more distinguishable. This will be conducive to obtaining more accurate correspondences, thus reducing the probability of outlier matching.
- We design a multi-local-to-global registration (MLGR) strategy to filter outlier matches. In LGR, the evaluated single correspondence scheme with the most inlier matches is used directly to compute the global transformation matrix. However, there are instances where outlier correspondence is incorrectly evaluated as inlier mathing in this process. For this reason, we propose MLGR, where we pick the top-k correspondence schemes with the most inlier matching. Correspondence scores that are evaluated as inlier matching in all k schemes will be maintained, the ones that are evaluated as inlier matching in just a few schemes will be lowered, and the rest will be masked as outlier matching. Reliable correspondences will be retained and the weight of unreliable correspondences will be reduced as well as filtered. In this way, we effectively filter outlier matching and improve the stability of the registration.
- Our method is quite robust under different sample numbers, which outperforms the state of the art on KITTI and 3DMatch with the highest registration accuracy. It improves the inlier ratio by 3.62% and 4.36% on 3DMatch and 3DLoMatch, respectively. With the number of point correspondences decreasing, the results of the other methods either become unacceptable or drop dramatically, while our method maintains good results, reflecting the robustness of our method.
2. Related Work
There has been extensive research on how to align two-frame point cloud [35,36,37,38,39]. Alignment is broadly divided into two categories: optimization-based methods and deep learning-based methods. Compared with the traditional optimization-based methods [11], deep learning-based methods [18,40,41] have better performance in today’s research. The research in this paper is based on deep learning, so here we mainly discuss the related methods. Some of the more popular methods are correspondence-based methods and end-to-end-learning approach methods, which we will discuss in detail in the following paragraphs. In this paper, our approach is correspondence-based.
The correspondence-based approach first extracts the correspondence between the two points and then uses a robust attitude estimator, such as RANSAC, to iteratively sample the correspondences in the set until a satisfactory solution is obtained. Extracting reliable feature descriptors is essential for finding an accurate correspondence between two point clouds. Thanks to the development of deep learning models, the learned feature descriptors have made impressive progress compared with the traditional hand-crafted ones [42,43]. Predator [26] uses attentional mechanisms to study alignment in low-overlap scenarios. PerfectMatch [21] proposes a descriptor for compactly learning local features for 3D point cloud matching. D3Feat [25] processes point clouds using 3D fully convolutional networks, which allows dense prediction of detection scores and feature descriptions for each point. FCGF [22] uses the Minsky convolution method and is able to produce outstanding high-resolution features. Spinnet [44] is able to learn feature descriptors with rotational invariance, high descriptiveness, and strong generalization performance. YOHO [45] leverages group equivariant feature learning to attain rotation invariance, showcasing remarkable resilience against variations in point density and noise interference. CoFiNet [30] extracts hierarchical correspondences from coarse to fine without keypoint detection. GeoTransformer [29] enhances the discriminatory nature of feature descriptors by adding computed geometric features to the network. These methods commonly use deep learning as a tool for feature extraction, hoping to evaluate correspondences by learning discriminative feature descriptions.
The basic idea of the end-to-end-learning approach is to transform the alignment problem into a regression problem. The scheme solves the alignment problem using a neural network, where the input is a two-frame point cloud and the output is a transformation matrix that aligns the two-frame point cloud. DCP [46] uses feature similarity to establish pseudo-correspondences for SVD-based transform estimation. RPM-Net [19] utilizes Sinkhorn layers and annealing to generate discriminative matching maps. Refs. [47,48] integrate cross-entropy methods into deep models for robust alignment. RIENet [49] uses structural differences between source and pseudo-target neighborhoods for internal confidence assessment. With Transformer’s powerful feature representation, RegTR [50] effectively aligns large indoor scenes in an end-to-end manner. Ref. [4] proposed a matching normalization layer for robust alignment in a real-world 6D object pose estimation task. More end-to-end models, such as [28,41,51,52], also have impressive accuracy.
Our approach is based on correspondence. The accuracy of correspondences depends on the model’s performance. However, the model’s learning capability is limited, and the correspondences it generates may not be entirely accurate. As a result, incorrect correspondences might be mistakenly identified as inlier matches, and the ground truth correspondences may also be misjudged and excluded as outlier matches. Although research on learning-based descriptors has largely improved the accuracy of correspondences, outlier matches are still inevitably produced in large and complex scenarios, reducing the quality of the alignment. Traditional outlier filtering methods such as RANSAC and its variants often require a large number of iterations to obtain acceptable results, which is too costly in time and ineffective in scenes with high outlier ratios. Another approach [28,53] uses a deep robust estimator, which identifies and rejects outliers by additionally training a classification network. PointDSC [27] proposed a clustering network guided by spatial consistency for distinguishing between inlier and outlier. SC2-PCR [54] proposed a second-order spatial compatibility metric to calculate the similarity between matching pairs, which considers global compatibility rather than local consistency between matching pairs, thus enabling a more accurate measure of the difference between correct and incorrect matches. As our baseline, GeoTransformer [29] proposes a local-to-global registration strategy that is 100 times faster than RANSAC with comparable alignment accuracy, and does not require the training of additional networks to filter outlier matches.
3. Methods
Given source point clouds and target point clouds , our goal is to estimate the optimal rigid transformation matrix that aligns the overlapping regions of the two point clouds. is the rotation matrix and is the translation matrix. The transformation matrix can be obtained by solving the following equation:
where denotes the ground-truth correspondences between point clouds and point clouds . In this paper, our goal is to investigate the generation of reliable putative correspondences and then estimate the transformation matrix.
The general flow of our method is roughly as follows. First, we downsample the point clouds to obtain two layers of sampled points (sparse and dense). Too many samples will cause redundant computation and be no help in improving the quality of the alignment, so the downsampling is necessary. During this process, the initial features of the point clouds are extracted. Then, the features of sparse points will enter our LG-Net to learn the local geometric features, and the feature descriptors are generated by the self-attention and cross-attention mechanisms, and then the sparse point correspondences are computed based on the descriptors. Finally, we extend this correspondence to dense points in a neighborhood of sparse points to form patch correspondences, generate a series of hypothetical transformations based on the patch correspondences, and then estimate the globally optimal transformation matrix with our multi-local-to-global registration strategy. The general framework of our network is shown in Figure 1.
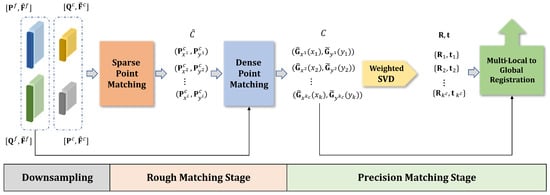
Figure 1.
The input point clouds is downsampled into dense and sparse points. High-quality sparse point correspondences are obtained after LG-Net and attention mechanism. Then, the sparse point correspondences are propagated to dense points. Finally, the transformation matrix is computed with the multi-local-to-global registration strategy.
3.1. Sparse Point Matching with LG-Net
Following our baseline [29], we use Kpconv-FPN [55,56] to implement point clouds downsampling and feature extraction. We utilize the grid downsampling method to reduce the number of points, while largely preserving the inherent shape characteristics of the point clouds and retaining spatial structural information. This method is notably efficient, ensuring a relatively uniform distribution of sampled points. Moreover, it allows controlling the point spacing by adjusting the grid size. A large amount of point clouds data results in a large number of computations with both outlier and redundant information. In fact, we can estimate the correspondence with fewer points, while helping to lighten the network input and improve the time efficiency.
The point clouds are downsampled to obtain a coarse-resolution layer and a high-density layer, while initial features of the point clouds are generated in the process. For the coarse-resolution point clouds, i.e., sparse points, we denote and , and for the dense layer, i.e., dense points, we denote and . Their features are denoted as , and , .
For points in the coarse resolution layer of the source point clouds, we use a point-to-node grouping strategy to construct a patch, :
Note that if the nearest neighbor of the sparse point is empty, it will not be used to construct a patch. For the features of the points in , we denote them as . Similarly, for the target point clouds, we also calculate and denote and features .
3.1.1. Local Geometric Network
There is a loss of original pose information during the transition from low to high latitudes, which makes the learned feature descriptors not discriminative [29], especially when facing scenes with a large number of structural repetitions and local similarities; however, the fuzzy feature descriptor might result in incorrect correspondences. When the number of point correspondences is too small, the difficulty of registration increases dramatically, as shown in Figure 2, while the registration recall of these methods decreases dramatically when the number of point correspondences decreases, which is due to the non-robust correspondences. Some methods encode the location by explicit coordinate embedding, and GeoTransformer [29] improves the discriminative nature of the feature descriptor by adding relative position information to the transformer. The limitation of these methods is that they are more sensitive to noise, outliers, density variations, and overlap rates. In scenes with low density and noise, their effectiveness will be significantly diminished, preventing them from achieving the desired results. To address this problem, we advocate the use of learning methods to obtain information about the underlying geometric structure of the point clouds. For this purpose, we designed the local geometric network (LG-Net) module to improve its discriminative ability at the feature level.
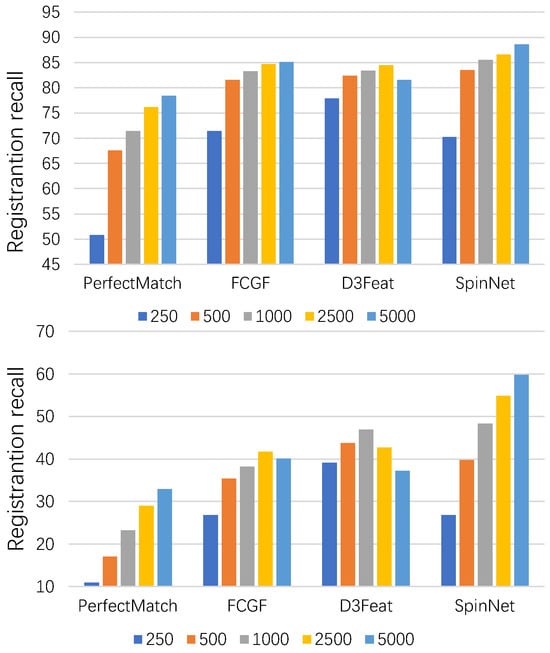
Figure 2.
Registration recall of previous methods on 3DMatch (top) and 3DLoMatch (bottom). The numbers 250, 500, 1000, 2500, and 5000 indicate the number of correspondences, respectively. It can be observed that, as the number of correspondences decreases, the registration recall of these methods decreases dramatically. A stable registration method should be robust to the number of samples, which is the main direction of our research.
In the work of [29], the network coarse matching module has the following components: self-attention module with geometric structure embedding; cross-attention module; and sparse point matching module. The transformer structure with geometric information encoded enhances the discriminative nature of the generated features, allowing them to achieve the desired match at the coarse alignment stage. However, this method still has limitations and it is inflexible to use a uniform structure to encode geometric information in different scenarios. For this reason, we added a network to the original method to mine the local potential geometric information, hoping to improve the accuracy of coarse alignment, as will be demonstrated in the experimental section.
We designed a local geometric network dedicated to learning local potential geometric information. Figure 3 illustrates our local geometric network architecture. Because the network operates on local data, it does not cause much computational cost. First we compute the distance map between sparse points, for in , and we perform the following operations:
where denotes the distance from point to point . Then, the features of the k nearest neighbor sparse points of each sparse point will be used as the input to the local geometric network:
where denotes the set of k sparse point features of the nearest neighbors of point , and denotes the features corresponding to the k points. denotes the multi-layer perceptron with shared weights and denotes concatenation operation. denotes the output of the local geometric network.
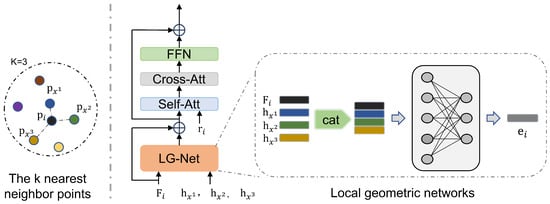
Figure 3.
Local geometric network (LG-Net) structure diagram. We add LG-Net to the original self-attention and cross-attention mechanisms to learn local geometric features and generate discriminative feature descriptors, thus producing robust correspondences.
3.1.2. Self-Attention
Self-attention mechanisms have been shown to be effective but powerful in many works [26,29]. In this paper, we use the self-attentive mechanism to capture long-range features while preserving the geometric structure embedding [29]:
where is input of the self-attention layer, and denotes the output matrix. denotes the attention map. We follow the method of [29] and add geometric information to the attention calculation. , , , and denote the respective projection matrices.
In the above step, we are performing the calculation of the source point clouds, . We do the same step for the target point clouds, .
3.1.3. Cross-Attention
We use the cross-attention mechanism to facilitate information exchange between the source point clouds and the target point clouds. The input feature matrix is denoted as , , for , , respectively. the output feature matrix, , of can be computed as follows:
by alternating the computation of attention between patches within two point clouds, the consistency between them is found. This method is able to estimate robust correspondences.
The Gaussian correlation matrix is used to evaluate the point match score. This is done by normalizing and and computing a matrix with , and finally performing a double normalization:
Finally, select the largest entries in as the sparse point correspondences:
3.2. Dense Point Matching with MLGR
After the coarse alignment stage, we obtain the correspondence of patch, and the next step is to match the points in patch. We integrate all the point matches with high confidence.
We use the optimal transport layer to calculate the correspondence of the dense points in the patch. We first compute a cost matrix, :
where denotes the matching score of point and point . denotes the feature dimension of dense points. To maintain the one-to-one correspondence, an extra row and column are added to and filled with learnable parameters. Finally, compute the soft assignment matrix using the Sinkhorn algorithm and remove the extra row and column to obtain . We treat as the matrix of scores of points used for matching and extract the top-k point correspondence:
We integrate all as the set of point correspondences for global registration .
Multi-Local-to-Global Registration
The presence of noise, data incompleteness, etc., will inevitably lead to outlier matches. Existing approaches to outlier filtering, for example, the RANSAC approach, is computationally expensive and slow to converge. Some deep robust estimators require an additional network to be trained. Inspired by [29], our method summarizes the global alignment scheme from multiple localities and achieves RANSAC-free and robust alignment. Figure 4 illustrates our alignment strategy with multiple local solutions to the global.
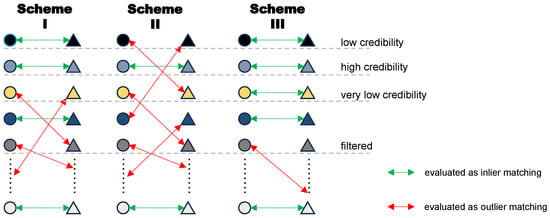
Figure 4.
Multi-local-to-global registration strategy. Circles and triangles with the same color represent pairs of points where correspondence exists. We evaluate the correspondence in different transformation schemes, and correspondences that are evaluated as inlier matching in multiple schemes will receive higher scores (e.g., bottom, last row), and, conversely, correspondences with low scores will be filtered (e.g., penultimate row).
The method of [29] uses the scheme with the most inlier matches as the global registration scheme. However, this strategy is not applicable in all scenarios. In addition, global transformation summarized from multiple hypothetical transformation schemes is more robust and representative than the alignment from a single local-to-global alignment. We believe that if the correspondence of a pair of points is judged to be an inlier matching in multiple hypothetical transformation schemes, then it will have higher confidence and eventually be used to perform global registration. We thus propose a multi-local-to-global registration method. The distinction lies in our approach: rather than selecting a single scheme with the highest count of evaluated inlier matches as the global correspondence scheme, we employ a voting mechanism for the top-k schemes. If a point correspondence is assessed as an inlier match in all k schemes, it indicates higher reliability, and we maintain its correspondence score. Correspondences evaluated as inlier matches in only a few schemes will have their scores attenuated, while those assessed as outlier matches in all k schemes will be disregarded. The flow of our algorithm is shown in Algorithm 1.
In the local alignment phase, we align the points in the patch to obtain multiple hypothetical alignment schemes :
where denotes the weight in the weighted SVD algorithm, and its value is equal to the confidence score in . Then, we apply the hypothetical transformations to the global points and unify the number of their inlier matches. As stated before, our method aligns with multiple localities:
where is the acceptance radius. We evaluate each hypothetical scheme by counting the number of its inlier matches according to Equation (15), select the schemes with the most inlier matches, and combine them together. The weights corresponding to the outlier matches in each scheme will be masked and updated to . Finally, we compute the average of the weights:
where denotes the updated weight of the selected schemes with the most inlier matches. Using this method, the degradation of alignment quality due to outlier matches can be better avoided. The weights of reliable matches will be maintained, while the weights of unreliable matches will be weakened or masked. We thus achieve registration from multi-local-to-global:
We then iteratively (iter = 7) re-estimate the transformations with surviving internal matches by solving Equation (16). In our experiments, our multi-local-to-global registration exceeds the alignment accuracy of RANSAC in some scenarios and does not require a large number of iterative computations, such as RANSAC-50k.
| Algorithm 1 Multi-local-to-global registration |
 |
4. Experiments
In this section, we perform experiments and comparisons on several datasets to validate the superiority of our method, including the indoor datasets 3DMatch and 3DLoMatch, the outdoor dataset KITTI, and the synthetic dataset ModelNet. We first tested the metrics RRE, RTE, and RR on KITTI and ModelNet40 to evaluate the effectiveness of the proposed method. Subsequently, we tested the metrics such as FMR, IR, and RR with different numbers of point correspondences on the 3DMatch dataset to evaluate the stability of the proposed method.
4.1. Experimental Settings
The structure of our network is basically the same as GeoTransformer, with the difference that we add the LG-Net module, and, for each sparse point, we pick sparse points closest to itself as inputs to the module. As in [29], the LG-Net module will be interleaved 3 times with the self-attention module and the cross-attention module. In the multi-local-to-global registration module, we select the top scheme with the most inlier matches to vote for high-confidence point correspondences. If the number of programs is less than three, we will select as many schemes as possible.
We trained 40 epochs on 3DMacth and 3DLoMatch, 80 epochs on KITTI, and 200 epochs on ModelNet40 using the Adam optimizer. The batch size is 1, and the weight decay is . The learning rate starts from and decays exponentially by 0.05 every epoch on 3DMatch and 4DMatch, every 5 epochs on ModelNet40, and every 4 epochs on KITTI. Other parameter settings are consistent with GeoTransformer unless otherwise noted. We implemented the project using PyTorch and ran all experiments on a server with an Intel i5 12490F CPU and an RTX3090 GPU.
4.2. Evaluation Metric
4.2.1. Evaluation Metric on KITTI
We reported in the RTE, RRE, and RR in the KITTI dataset. They are defined as follows: the relative translation error (RTE) is the euclidean distance between the estimated translational vector and the true translational vector, which measures the differences between the predicted and the ground-truth translation vectors:
where denotes the translation matrix of the aligned two-frame point clouds, and denotes the translation matrix that aligns the two frames of the point clouds under ground truth.
The relative rotation error (RRE) is the geodesic distance between the estimated rotation matrix and the ground-truth rotation matrix, which measures the differences between the predicted and the ground-truth rotation matrices:
where denotes the rotation matrix and denotes the ground-truth rotation matrix.
Registration recall is the percentage of successful registrations that satisfies both the rotation and translation error thresholds:
4.2.2. Evaluation Metric on 3DMatch
We report FMR, IR, and RR in 3DMatch, where the inlier ratio (IR) is the assumed corresponding fraction of residuals below a certain determined value after the ground-truth transformation:
Feature matching recall (FMR) is the percentage of point cloud pairs with inliers above a certain threshold, which measures the potential success during the registration:
Registration recall (RR): the proportion of point cloud pairs whose transformation error is less than a certain threshold.
4.2.3. Evaluation Metric on ModelNet40
We reported two metrics: RRE and RTE. In our ModelNet40 evaluation, their definitions are consistent with the above.
4.3. Evaluation on KITTI
KITTI odometry [57] is a typical outdoor scene dataset consisting of LiDAR scans, which we use to evaluate our method. KITTI odometry includes 11 outdoor scenes, and provides GPS ground truth. The dataset is divided in the following way: scenarios 0–5 are used to train our network, 6–7 are the validation set, and 8–10 are the test set. We adopt the operational procedure of [29]. In this experiment, the ICP algorithm is only used for ground-truth pose refinement: the ground-truth poses are refined with ICP and we only use point cloud pairs that are at least 10 m away for evaluation.
We compared 10 existing advanced methods, as in Table 1: 3DFeat-Net [58], FCGF [22], D3Feat [25], SpinNet [44], Predator [26], CoFiNet [30], and GeoTransformer (RANSAC-50k) [29] were evaluated with RANSAC-50k, and FMR [59], DGR [28], HRegNet [60], and GeoTransformer (LGR) were evaluated with the RANSAC-free method.

Table 1.
Registration results on KITTI odometry. Bold numbers indicate the best, underlined numbers indicate the second best, and “” denotes approximate value.
Among all the RANSAC-based methods, our method has a lower RRE and RTE compared with the state-of-the-art method, proving that our designed LG-Net module can improve the alignment accuracy. Our method shows good generalization in large outdoor scenes.
Our method also has the smallest RRE and RTE among all the RANSAC-free based methods. Our proposed MLGR strategy beats LGR in alignment accuracy and outperforms all the RANSAC-based methods, proving that our MLGR can effectively improve the alignment accuracy, and our method does not require a large number of iterations, as in the case of RANSAC.
4.4. Evaluation on ModelNet40
ModelNet40 consists of 40 categories of CAD models. We follow [29] using the dataset after its processing, which includes 4194 models for training, 1002 models for validation, and 1146 models for testing. We categorized them into ModelNet with and ModelLoNet with by overlapping settings, and evaluated them in the case of large rotational amplitude () and small rotational amplitude (), respectively. Similarly, we removed the 8 categories (i.e., bottle, bowl, cone, cup, flower pot, lamp, tent, and vase) whose poses are ambiguous.
We compare our method with the methods in Table 2, which are RPM-Net [19], RGM [52], Predator [26], CoFiNet [30], and GeoTransformer [29], respectively. RPM-Net [19] and RGM [52], which are end-to-end based registration methodology, Predator [26], and CoFiNet [30] are evaluated using the RANSAC-50k to estimate the transformation matrix. For GeoTransformer [29] and our method, we use the RANSAC-free method. Predator, CoFiNet, GeoTransformer, and ours use KPConv as the network backbone, and all models are trained with 200 epochs.

Table 2.
Registration results on ModelNet40. Bold numbers indicate the best and underlined numbers indicate the second best.
In the case of small rotation settings, RPM-Net, RGM, GeoTransformer, etc., do not differ much and seem to be saturated on ModelNet; our method goes a step further and reduces the RRE and RTE. On ModelLoNet, which is a low overlap scenario, our method performs as well as GeoTransformer, showing strong competitiveness.
With large rotation settings, the alignment task becomes much more difficult, and the rotation and translation errors of other methods increase dramatically with unsatisfactory results. Both our method and GeoTransformer show good robustness and maintain high accuracy at both low overlap and large rotations.
4.5. Evaluation on 3DMatch and 3DLoMatch
There are 62 scenes in the 3DMatch dataset, of which 46 scenes are used for training, 8 for validation, and 8 for testing. In this paper, we use the processed dataset in [26]. The difference between 3DMatch and 3DLoMatch is that the overlap of the test sample data in 3DMatch is greater than 30%, and the overlap of the 3DLoMatch test sample data is between 10% and 30%. When the overlap rate is low, the registration becomes more difficult. Figure 5 shows the registration results of our method on 3DMatch.
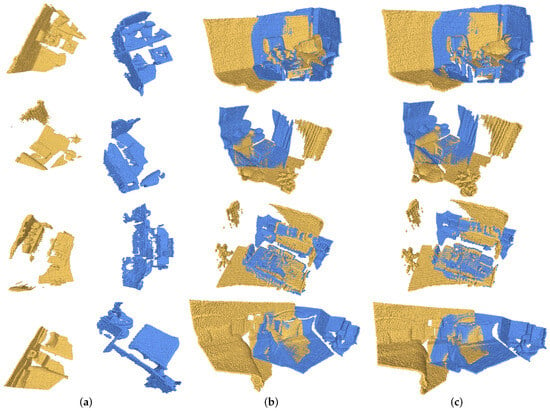
Figure 5.
Registration visualization on 3DMatch, The input (a) image shows the original point clouds pose, and, to make it easier to distinguish between the two point clouds, we have pulled the two point clouds apart by a distance. Ground truth (b) denotes ground truth pose. Output (c) shows the point clouds pose after alignment.
We first compared our method with the current state of the art: PerfectMatch [21], FCGF [22], D3Feat [25], SpinNet [44], Predator [26], YOHO [45], CoFiNet [30], and GeoTransformer [29] in Table 3. We evaluated the metrics FMR, IR, and RR in the case of having different numbers of correspondences. All methods use the RANSAC-50k to evaluate the transformation matrix.

Table 3.
Evaluation results on 3DMatch and 3DLoMatch. Bold numbers indicate the best and underlined numbers indicate the second best.
On the left side of Table 3 are shown the results on 3DMatch. In the 3DMatch dataset, our method achieves the highest inlier ratio, which is significantly ahead of other methods. Compared with the baseline method, the inlier ratio improves by 3.62% on average, and the feature matching recall and registration recall improve by 0.3% to 0.7% and 0.1% to 1.2%, respectively. Our method shows the most significant improvement in the inlier ratio, being the only method to achieve more than 80% of the mean value in the evaluation of the 3DMacth dataset.
The results of 3DLoMatch are shown on the right side of Table 3. Compared with the state-of-the-art methods, our method improves on IR by an average of 4.36%, which greatly exceeds other methods. In the comparison of FMR and RR, our method beats all methods except GeoTransformer.
We notice that some previous methods have seen their FMR, IR, and RR decrease when the number of point correspondences decreases, indicating that they are more sensitive to low-sample data. From Table 3, we can observe that, unlike these methods, our method still maintains high RR and FMR in the case of a low number of correspondences. In particular, as the number of correspondences decreases, our IR shows an increasing trend. Our LG-Net module provides more information about the local structure of the point clouds, which makes the obtained correspondences more accurate, and thus exhibits strong robustness.
Our method achieves the best results on the 3DMatch dataset, outperforming state-of-the-art methods. Compared with GeoTransformer, the test results of our method on 3DLoMatch are slightly insufficient, partly due to the increased difficulty of registration and partly due to the inadequacy of our method in the low overlap case. However, compared with other methods on 3DLoMatch, our method is still competitive in the low overlap scenario, and our method is ahead of GeoTransformer in inlier recall, which means that our method is more robust and proves that our improvement is effective.
We subsequently add a comparison with the RANSAC-free estimator in Table 4. We use the RANSAC (top) and weighted SVD (middle) estimators for FCGF, D3Feat, SpinNet, Predator, CoFiNet, and GeoTransformer, respectively; the number of points corresponding to the two estimators is 5000 and 250, respectively. Finally, we compare CoFiNet, GeoTransformer, and the proposed approach with RANSAC-free (bottom).

Table 4.
Registration results w/o RANSAC on 3DMatch and 3DLoMatch. Bold numbers indicate the best and underlined numbers indicate the second best.
When we use the RANSAC estimator, our method achieves an RR of 91.9% on 3DMatch, which is almost the same as GeoTransformer (RANSAC-50k), and 71.3% on 3DLoMatch, and our method outperforms all the methods out of GeoTransformer (RANSAC-50k) to achieve second place.
We changed the estimator to the weighted SVD and reduced the number of correspondences to 250, which greatly increased the difficulty of the registration. The previous methods either failed to achieve reasonable results or suffered severe performance degradation. Our method still has an RR of 87.4% on 3DMatch, outperforming other methods. Our RR is 58.6% on 3DLoMatch, which is close to Predator with RANSAC.
When using multi-local-to-global registration, our results on 3DMatch outperform all methods using RANSAC except GeoTransformer (RANSAC-50k) and are very close to GeoTransformer (RANSAC-50k). In the comparison without RANSAC, our RR is 91.8%, which outperforms CoFiNet with LGR and GeoTransformer (LGR). Our method also shows good applicability on 3DLoMatch, with an RR of 72.0%, which exceeds our results using RANSAC, but does not require a large number of iterative computations, as in RANSAC. Figure 6 shows the quantization results of our method comparing GeoTransformer on 3DMatch.

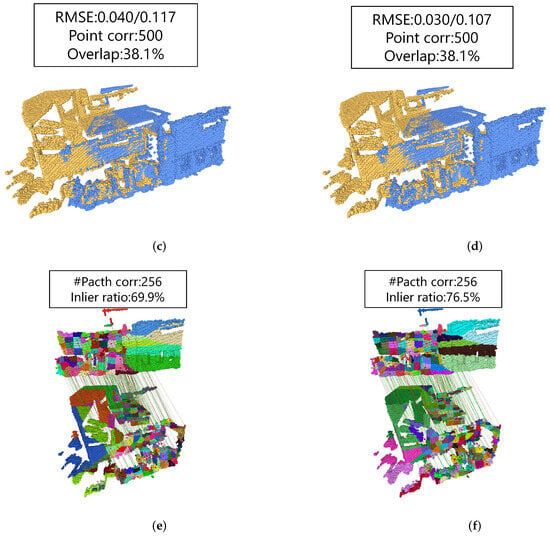
Figure 6.
The visualization results of GeoTransformer and MLGR on the 3DMatch dataset. RMSE (m) includes two values, the left one being the error for this sample and the right one being the average error tested on the dataset. Point corr indicates the quantity of point correspondences. Overlap represents the overlap rate between the two point clouds. Patch corr denotes the quantity of patch correspondences, and the colors of different patches vary. Compared with GeoTransformer, the average value of our RMSE is smaller. (a) input; (b) ground truth; (c) GeoTransformer-pose; (d) MLGR-pose; (e) GeoTransformer-patch correspondences; and (f) MLGR-patch correspondences.
4.6. Ablation Study
We have conducted extensive ablation studies to understand the role of the modules we designed. GeoTransformer is used as the baseline for comparison with our method. We use RANSAC, LGR, and MLGR, respectively, to compare our method experimentally with the baseline. The experimental results on 3DMatch are shown in Table 5.

Table 5.
Ablation experiments on 3DMatch. The results are measured in %. Bold numbers indicate the best and underlined numbers indicate the second best.
The transformation matrix is first estimated using RANSAC. Our method adds a local feature aggregation module (LG-Net) compared with the baseline only, but substantially improves inlier recall and leads the baseline in metrics such as FMR and RR. As we describe, our module enhances feature diversity, which produces more accurate correspondences and reduces the probability of outlier matching.
Subsequently, we apply LGR and our proposed MLGR to estimate the transformation matrix, respectively. In the LGR-based comparison, compared with the baseline, our method exhibits higher FMR and IR, which means that the correspondence obtained by our method is more accurate. After using MLGR, both the baseline and our method show improvement in all indicators. The results after using MLGR for the baseline are comparable to its results using RANSAC, yet our MLGR does not require many iterative calculations. As shown in Table 5, our proposed method has a significant performance improvement compared with the baseline, fully proving its superiority.
The ablation experiments on the KITTI dataset are presented in Table 6. Similarly, GeoTransformer serves as the baseline, and RANSAC, LGR, and MLGR are used to test both the baseline and our method.

Table 6.
Ablation experiments on KITTI. Bold numbers indicate the best and underlined numbers indicate the second best.
In the RANSAC-based testing, our method achieved lower RET and RRE compared with the baseline. Similarly, when estimating the transformation matrix using LGR, our method also exhibited smaller error values. Upon using MLGR, both the baseline and our method reached their respective optimal values, yet, overall, our method performed better. It is evident that incorporating the local feature aggregation module (LG-Net) already enhanced module performance, and, with the use of our MLGR, the registration accuracy reached its peak.
After conducting ablation experiments on the 3DMatch and KITTI datasets, we proceeded to study certain parameters within our proposed module. Firstly, in the LG-Net module, we investigated the effect of different numbers of nearest neighbor points on the experimental results, as shown in Table 7. When the number of nearest neighbor points , RR drops significantly, for this reason, we only studied the three cases where , with the best results when .

Table 7.
Ablation study of the number of nearest neighbor points in LG-Net. Bold numbers indicate the best and underlined numbers indicate the second best.
We then evaluated the effect of the number of iterations, , on the results at the refinement step of the multi-local-to-global registration, as shown in Figure 7. We increased from 1 to 10, and RR increased with the number of iterations, eventually approaching saturation at . In this paper, we chose for the experiment for better equilibrium accuracy and speed.
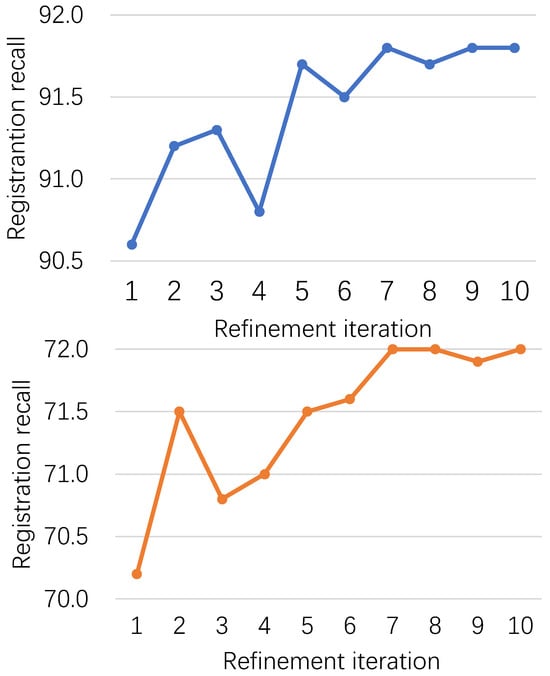
Figure 7.
Ablation study of the pose refinement on 3DMatch (top) and 3DLoMatch (bottom). Pose refinement continuously improves results and saturates after 7 iterations.
5. Conclusions and Limitations
During the registration process, monotonic feature descriptors often lead to outlier matching. In this paper, we add a simple and efficient local feature aggregation module in transformer, which makes the generated feature descriptors more diversified, which is helpful to generate accurate correspondences and reduce the probability of outlier matching. In addition, blindly enhancing the learning capability of a model to generate more accurate correspondences in order to reduce the probability of outlier matching is unrealistic. This is due to the inevitable presence of noise and outliers in point clouds data. Therefore, we propose a strategy to evaluate the correspondences generated by the model. Unreliable matches are masked, further filtering outlier matches. Finally, we conducted experiments on both outdoor and indoor datasets, and the experimental results demonstrate the superiority of our method, which still guarantees good results in large and complex scenes. Our method achieved the best results on the 3DMatch, KITTI, and ModelNet datasets, while demonstrating strong competitiveness on 3DLoMatch and ModelLoNet datasets. In addition, our method maintains high-quality registration results, all with different sample sizes, showing strong stability, which is not found in other methods, validating the effectiveness of our improvement. However, we notice that, compared with state-of-the-art methods, our approach still has room for improvement in low-overlap scenarios. We plan to address these issues in our next phase of work. Our aim is to enhance registration stability while achieving high-precision alignment, and to conduct a more comprehensive investigation.
Author Contributions
Conceptualization, Y.M.; funding acquisition, Y.C. and X.Y.; investigation, Y.M.; methodology, Y.C. and Y.M.; project administration, Y.C.; software, Y.M.; supervision, Y.C., B.Y., W.X., Y.W., D.Z. and X.Y.; validation, Y.M.; visualization, Y.M.; writing—original draft, Y.M.; writing—review & editing, Y.C., B.Y., W.X., Y.W., D.Z. and X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Scientific Research Foundation of Wuhan Institute of Technology under Grant No. 21QD53, the Innovation Fund of Hubei Key Laboratory of Intelligent Robot under Grant No. HBIRL202107, the Science and Technology Research Project of Education Department of Hubei Province under Grant No. Q20221501, the National Natural Science Foundation of China under Grant No. 62102268, the Stable Supporting Program for Universities of Shenzhen under Grant No. 20220812102547001, the Research Foundation of Shenzhen Polytechnic University under Grants No. 6022312044K, 6023310030K and 6021310008K.
Data Availability Statement
All datasets used in this study are publicly available. The KITTI dataset is available at KITTI Vision Benchmark Suite (https://www.cvlibs.net/datasets/kitti/eval_odometry.php, accessed on 17 September 2023), the 3DMatch dataset is available at Prodata (https://github.com/prs-eth/OverlapPredator, accessed on 17 September 2023), and the ModelNet dataset is available at ShapeNet (https://shapenet.cs.stanford.edu/media/modelnet40_ply_hdf5_2048.zip, accessed on 17 September 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zheng, Y.; Li, Y.; Yang, S.; Lu, H. Global-PBNet: A novel point cloud registration for autonomous driving. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22312–22319. [Google Scholar] [CrossRef]
- Bash, E.A.; Wecker, L.; Rahman, M.M.; Dow, C.F.; McDermid, G.; Samavati, F.F.; Whitehead, K.; Moorman, B.J.; Medrzycka, D.; Copland, L. A Multi-Resolution Approach to Point Cloud Registration without Control Points. Remote Sens. 2023, 15, 1161. [Google Scholar] [CrossRef]
- Song, Y.; Shen, W.; Peng, K. A novel partial point cloud registration method based on graph attention network. Vis. Comput. 2023, 39, 1109–1120. [Google Scholar] [CrossRef]
- Dang, Z.; Wang, L.; Guo, Y.; Salzmann, M. Learning-based point cloud registration for 6d object pose estimation in the real world. In Proceedings of the Computer Vision–ECCV 2022: 17th European Conference, (Proceedings, Part I), Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 19–37. [Google Scholar]
- Mei, G.; Poiesi, F.; Saltori, C.; Zhang, J.; Ricci, E.; Sebe, N. Overlap-guided gaussian mixture models for point cloud registration. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikola, HI, USA, 2–7 January 2023; pp. 4511–4520. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1991; SPIE: Bellingham, WA, USA, 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Pottmann, H.; Huang, Q.X.; Yang, Y.L.; Hu, S.M. Geometry and convergence analysis of algorithms for registration of 3D shapes. Int. J. Comput. Vis. 2006, 67, 277–296. [Google Scholar] [CrossRef]
- Bouaziz, S.; Tagliasacchi, A.; Pauly, M. Sparse iterative closest point. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 2013; Volume 32, pp. 113–123. [Google Scholar]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Pomerleau, F.; Colas, F.; Siegwart, R.; Magnenat, S. Comparing ICP variants on real-world data sets: Open-source library and experimental protocol. Auton. Robot. 2013, 34, 133–148. [Google Scholar] [CrossRef]
- Zhang, J.; Yao, Y.; Deng, B. Fast and robust iterative closest point. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3450–3466. [Google Scholar] [CrossRef]
- Yin, P.; Yuan, S.; Cao, H.; Ji, X.; Zhang, S.; Xie, L. Segregator: Global Point Cloud Registration with Semantic and Geometric Cues. arXiv 2023, arXiv:2301.07425. [Google Scholar]
- Zhang, Z.; Lyu, E.; Min, Z.; Zhang, A.; Yu, Y.; Meng, M.Q.H. Robust Semi-Supervised Point Cloud Registration via Latent GMM-Based Correspondence. Remote Sens. 2023, 15, 4493. [Google Scholar] [CrossRef]
- Cheng, X.; Yan, S.; Liu, Y.; Zhang, M.; Chen, C. R-PCR: Recurrent Point Cloud Registration Using High-Order Markov Decision. Remote Sens. 2023, 15, 1889. [Google Scholar] [CrossRef]
- Hu, E.; Sun, L. VODRAC: Efficient and robust correspondence-based point cloud registration with extreme outlier ratios. J. King Saud-Univ. Comput. Inf. Sci. 2023, 35, 38–55. [Google Scholar] [CrossRef]
- Wei, P.; Yan, L.; Xie, H.; Huang, M. Automatic coarse registration of point clouds using plane contour shape descriptor and topological graph voting. Autom. Constr. 2022, 134, 104055. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, F.; Tao, W. Detarnet: Decoupling translation and rotation by siamese network for point cloud registration. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22 February–1 March 2022; Volume 36, pp. 401–409. [Google Scholar]
- Yuan, W.; Eckart, B.; Kim, K.; Jampani, V.; Fox, D.; Kautz, J. Deepgmr: Learning latent gaussian mixture models for registration. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, (Proceedings, Part V 16), Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 733–750. [Google Scholar]
- Yew, Z.J.; Lee, G.H. Rpm-net: Robust point matching using learned features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 11824–11833. [Google Scholar]
- Wang, J.; Wu, B.; Kang, J. Registration of 3D point clouds using a local descriptor based on grid point normal. Appl. Opt. 2021, 60, 8818–8828. [Google Scholar] [CrossRef] [PubMed]
- Gojcic, Z.; Zhou, C.; Wegner, J.D.; Wieser, A. The perfect match: 3D point cloud matching with smoothed densities. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5545–5554. [Google Scholar]
- Choy, C.; Park, J.; Koltun, V. Fully convolutional geometric features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 2 November 2019; pp. 8958–8966. [Google Scholar]
- Poiesi, F.; Boscaini, D. Learning general and distinctive 3D local deep descriptors for point cloud registration. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 3979–3985. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Birdal, T.; Ilic, S. PPF-FoldNet: Unsupervised learning of rotation invariant 3d local descriptors. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 602–618. [Google Scholar]
- Bai, X.; Luo, Z.; Zhou, L.; Fu, H.; Quan, L.; Tai, C.L. D3feat: Joint learning of dense detection and description of 3D local features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 6359–6367. [Google Scholar]
- Huang, S.; Gojcic, Z.; Usvyatsov, M.; Wieser, A.; Schindler, K. Predator: Registration of 3D point clouds with low overlap. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4267–4276. [Google Scholar]
- Bai, X.; Luo, Z.; Zhou, L.; Chen, H.; Li, L.; Hu, Z.; Fu, H.; Tai, C.L. Pointdsc: Robust point cloud registration using deep spatial consistency. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15859–15869. [Google Scholar]
- Choy, C.; Dong, W.; Koltun, V. Deep global registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 2514–2523. [Google Scholar]
- Qin, Z.; Yu, H.; Wang, C.; Guo, Y.; Peng, Y.; Xu, K. Geometric transformer for fast and robust point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11143–11152. [Google Scholar]
- Yu, H.; Li, F.; Saleh, M.; Busam, B.; Ilic, S. Cofinet: Reliable coarse-to-fine correspondences for robust pointcloud registration. Adv. Neural Inf. Process. Syst. 2021, 34, 23872–23884. [Google Scholar]
- Rocco, I.; Cimpoi, M.; Arandjelović, R.; Torii, A.; Pajdla, T.; Sivic, J. Neighbourhood consensus networks. In Advances in Neural Information Processing Systems; Springer: Berlin/Heidelberg, Germany, 2018; Volume 31. [Google Scholar]
- Zhou, Q.; Sattler, T.; Leal-Taixe, L. Patch2pix: Epipolar-guided pixel-level correspondences. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4669–4678. [Google Scholar]
- Huang, X.; Mei, G.; Zhang, J.; Abbas, R. A comprehensive survey on point cloud registration. arXiv 2021, arXiv:2103.02690. [Google Scholar]
- Han, D.; Pan, X.; Han, Y.; Song, S.; Huang, G. Flatten transformer: Vision transformer using focused linear attention. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2023; pp. 5961–5971. [Google Scholar]
- Cheng, L.; Chen, S.; Liu, X.; Xu, H.; Wu, Y.; Li, M.; Chen, Y. Registration of laser scanning point clouds: A review. Sensors 2018, 18, 1641. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Guan, D.; Zheng, X.; Chen, Z.; Pan, L. SD-CapsNet: A Siamese Dense Capsule Network for SAR Image Registration with Complex Scenes. Remote Sens. 2023, 15, 1871. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. Point cloud registration based on one-point ransac and scale-annealing biweight estimation. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9716–9729. [Google Scholar] [CrossRef]
- Brightman, N.; Fan, L.; Zhao, Y. Point cloud registration: A mini-review of current state, challenging issues and future directions. AIMS Geosci. 2023, 9, 68–85. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, Q.; Fan, X.; Gong, M.; Ma, W.; Miao, Q. Panet: A point-attention based multi-scale feature fusion network for point cloud registration. IEEE Trans. Instrum. Meas. 2023, 72, 2512913. [Google Scholar] [CrossRef]
- Wang, Y.; Solomon, J.M. Prnet: Self-supervised learning for partial-to-partial registration. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Li, J.; Zhang, C.; Xu, Z.; Zhou, H.; Zhang, C. Iterative distance-aware similarity matrix convolution with mutual-supervised point elimination for efficient point cloud registration. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, (Proceedings, Part XXIV 16), Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 378–394. [Google Scholar]
- Chen, S.; Nan, L.; Xia, R.; Zhao, J.; Wonka, P. PLADE: A plane-based descriptor for point cloud registration with small overlap. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2530–2540. [Google Scholar] [CrossRef]
- Salti, S.; Tombari, F.; Di Stefano, L. SHOT: Unique signatures of histograms for surface and texture description. Comput. Vis. Image Underst. 2014, 125, 251–264. [Google Scholar] [CrossRef]
- Ao, S.; Hu, Q.; Yang, B.; Markham, A.; Guo, Y. Spinnet: Learning a general surface descriptor for 3D point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–23 June 2021; pp. 11753–11762. [Google Scholar]
- Wang, H.; Liu, Y.; Dong, Z.; Wang, W. You only hypothesize once: Point cloud registration with rotation-equivariant descriptors. In Proceedings of the 30th ACM International Conference on Multimedia, Nashville, TN, USA, 19–25 June 2022; pp. 1630–1641. [Google Scholar]
- Wang, Y.; Solomon, J.M. Deep closest point: Learning representations for point cloud registration. In Proceedings of the IEEE/CVF international Conference on Computer Vision, New Orleans, LA, USA, 19–24 June 2019; pp. 3523–3532. [Google Scholar]
- Jiang, H.; Xie, J.; Qian, J.; Yang, J. Planning with learned dynamic model for unsupervised point cloud registration. arXiv 2021, arXiv:2108.02613. [Google Scholar]
- Jiang, H.; Shen, Y.; Xie, J.; Li, J.; Qian, J.; Yang, J. Sampling network guided cross-entropy method for unsupervised point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 6128–6137. [Google Scholar]
- Shen, Y.; Hui, L.; Jiang, H.; Xie, J.; Yang, J. Reliable inlier evaluation for unsupervised point cloud registration. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2022; Volume 36, pp. 2198–2206. [Google Scholar]
- Yew, Z.J.; Lee, G.H. Regtr: End-to-end point cloud correspondences with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 6677–6686. [Google Scholar]
- Liu, W.; Wang, C.; Bian, X.; Chen, S.; Li, W.; Lin, X.; Li, Y.; Weng, D.; Lai, S.H.; Li, J. AE-GAN-Net: Learning invariant feature descriptor to match ground camera images and a large-scale 3D image-based point cloud for outdoor augmented reality. Remote Sens. 2019, 11, 2243. [Google Scholar] [CrossRef]
- Fu, K.; Liu, S.; Luo, X.; Wang, M. Robust point cloud registration framework based on deep graph matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2021; pp. 8893–8902. [Google Scholar]
- Pais, G.D.; Ramalingam, S.; Govindu, V.M.; Nascimento, J.C.; Chellappa, R.; Miraldo, P. 3DRegNet: A deep neural network for 3D point registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7193–7203. [Google Scholar]
- Chen, Z.; Sun, K.; Yang, F.; Tao, W. Sc2-pcr: A second order spatial compatibility for efficient and robust point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13221–13231. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Thomas, H.; Qi, C.R.; Deschaud, J.E.; Marcotegui, B.; Goulette, F.; Guibas, L.J. Kpconv: Flexible and deformable convolution for point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6411–6420. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Yew, Z.J.; Lee, G.H. 3DFeat-Net: Weakly supervised local 3D features for point cloud registration. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 607–623. [Google Scholar]
- Huang, X.; Mei, G.; Zhang, J. Feature-metric registration: A fast semi-supervised approach for robust point cloud registration without correspondences. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11366–11374. [Google Scholar]
- Lu, F.; Chen, G.; Liu, Y.; Zhang, L.; Qu, S.; Liu, S.; Gu, R. Hregnet: A hierarchical network for large-scale outdoor lidar point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16014–16023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).