A Multi-Source-Data-Assisted AUV for Path Cruising: An Energy-Efficient DDPG Approach
Abstract
:1. Introduction
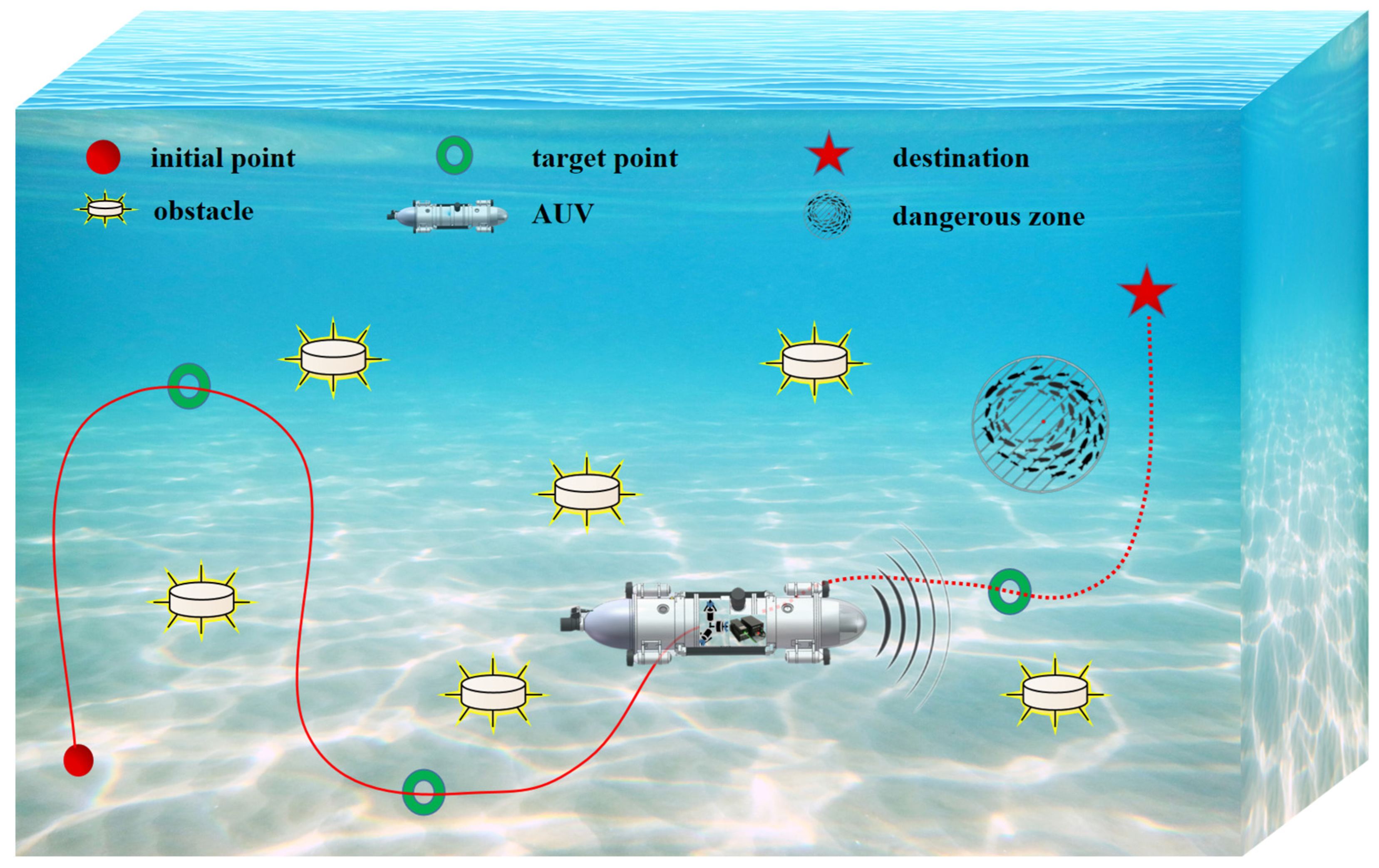
- A novel approach is introduced that utilizes remote sensing data to tackle the local minima inherent in APF. This methodology is suitable for 2D and 3D environments.
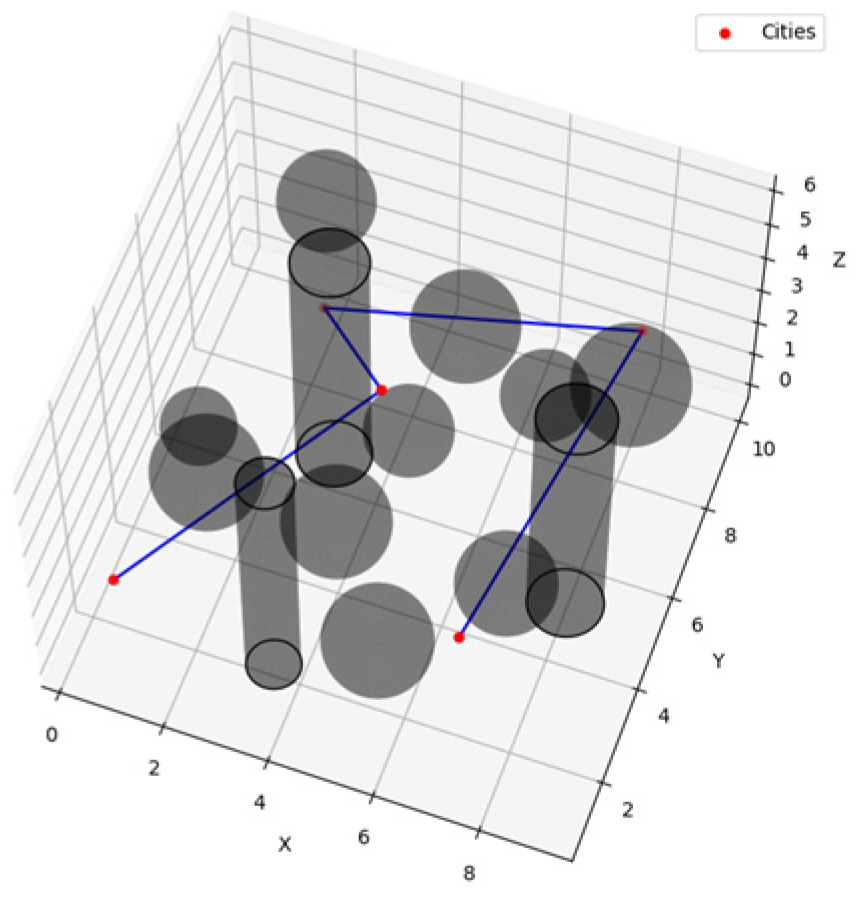
- Determining an optimal cruising sequence among multiple objectives has been likened to the traveling salesman problem (TSP). This paper proposes the TSP-IAPF method, which substitutes the Euclidean distance in the TSP with the IAPF path distance between two points. As a result, it automatically generates a cruise sequence with the shortest path across all target points.
- This paper introduces an algorithm combining the IAPF with DDPG, integrating multi-resource data from the gyroscope, accelerometer, rangefinder, and energy consumption. By embedding this multi-source data into an IAPF-DDPG-driven motion control system, the resultant path ensures safe navigation across all target points while emphasizing energy efficiency and trajectory smoothness.
2. Related Works
3. Problem Formulation
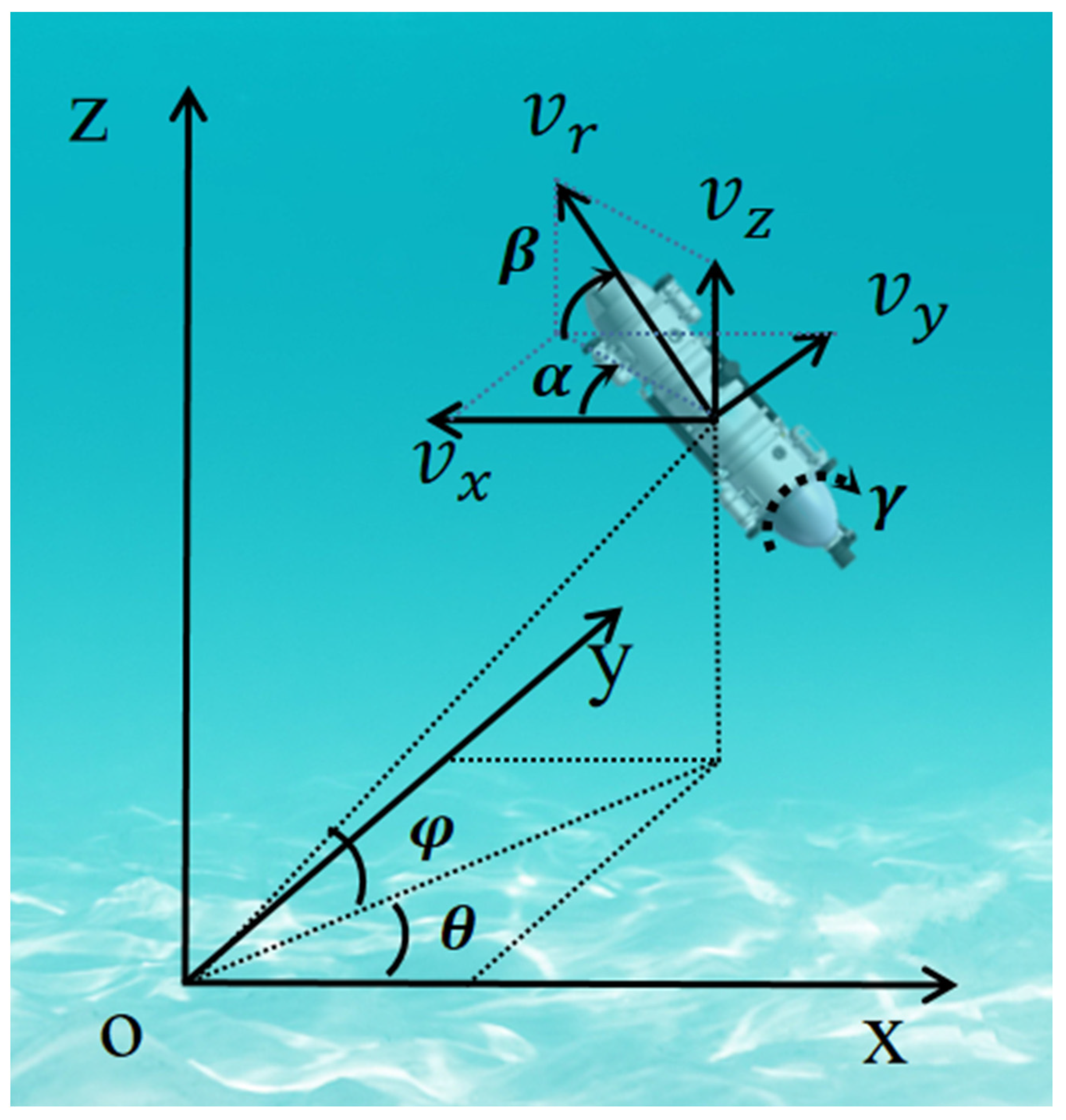
3.1. Kinematics and Dynamics Models
3.2. Energy Consumption Model
4. Method
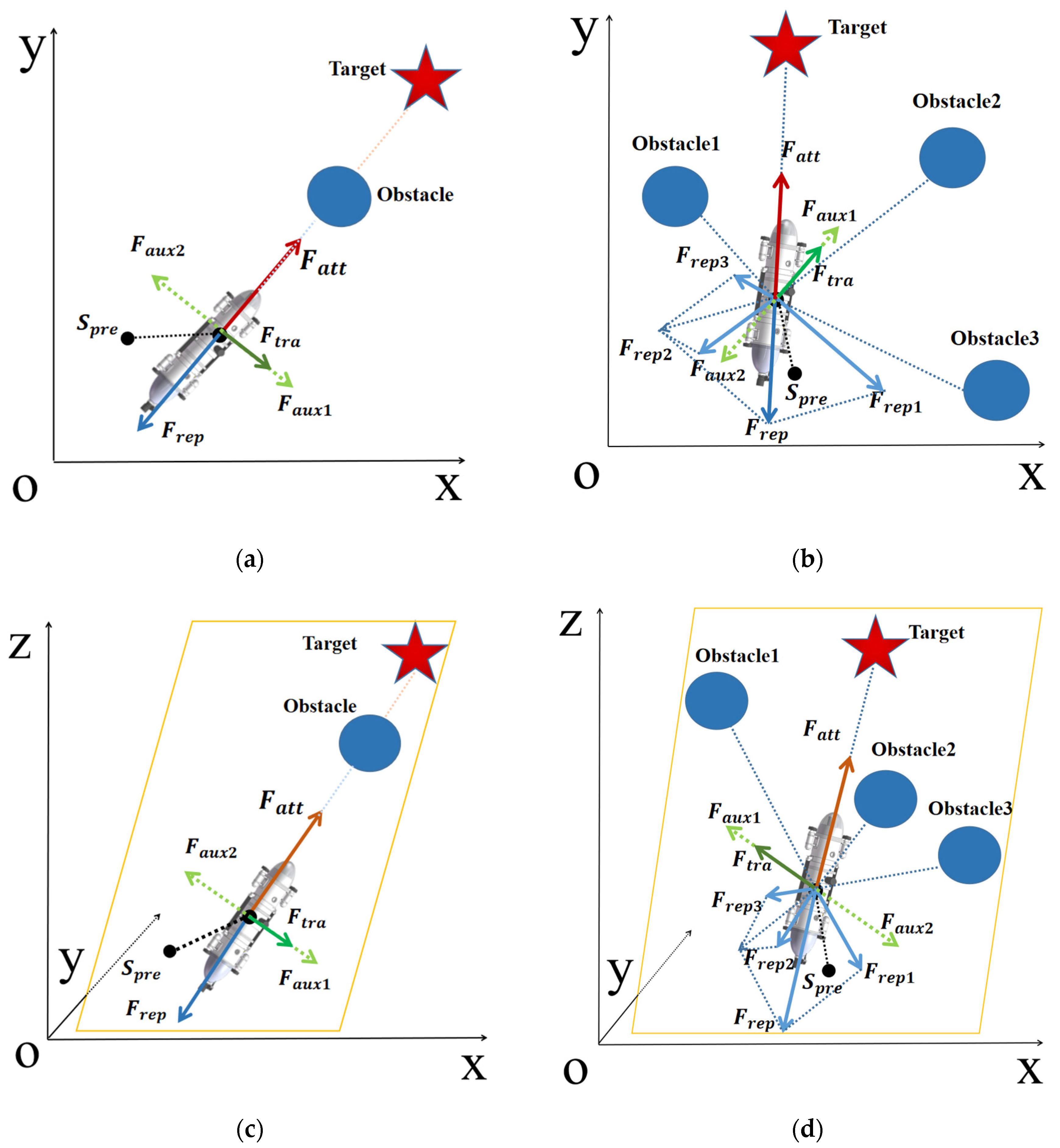
4.1. Improved Artificial Potential Field
4.1.1. Improved Method for Inaccessible Target
4.1.2. Improved Method for Local Minima
4.2. Traveling Salesman Problem
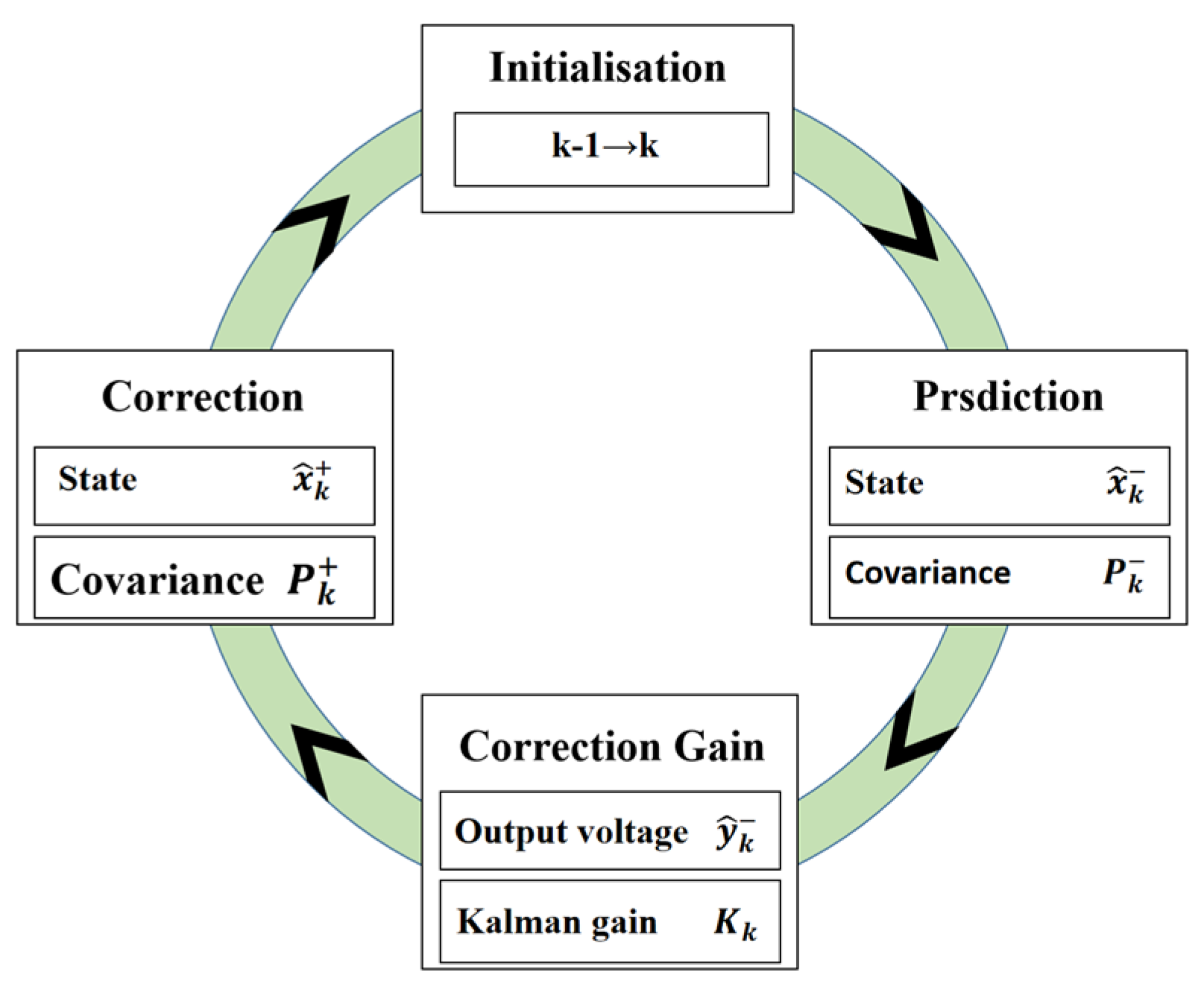
4.3. Utilization of Inertial Devices
4.4. Markov Decision Process
- 1.
- State at the step.
- 2.
- State at the step.
- 3.
- Reward at the step.
4.5. AUV Motion-Planning Method based on DDPG Algorithm
4.5.1. DDPG
4.5.2. AUV Motion-Planning Model Based on DDPG Algorithm with Multi-Source Data
4.5.3. State Space
4.5.4. Action Space
4.5.5. Reward Function
4.5.6. Mixed Noise
| Algorithm 1. Multi-source-data-assisted AUV for path cruising based on the DDPG algorithm. |
 |
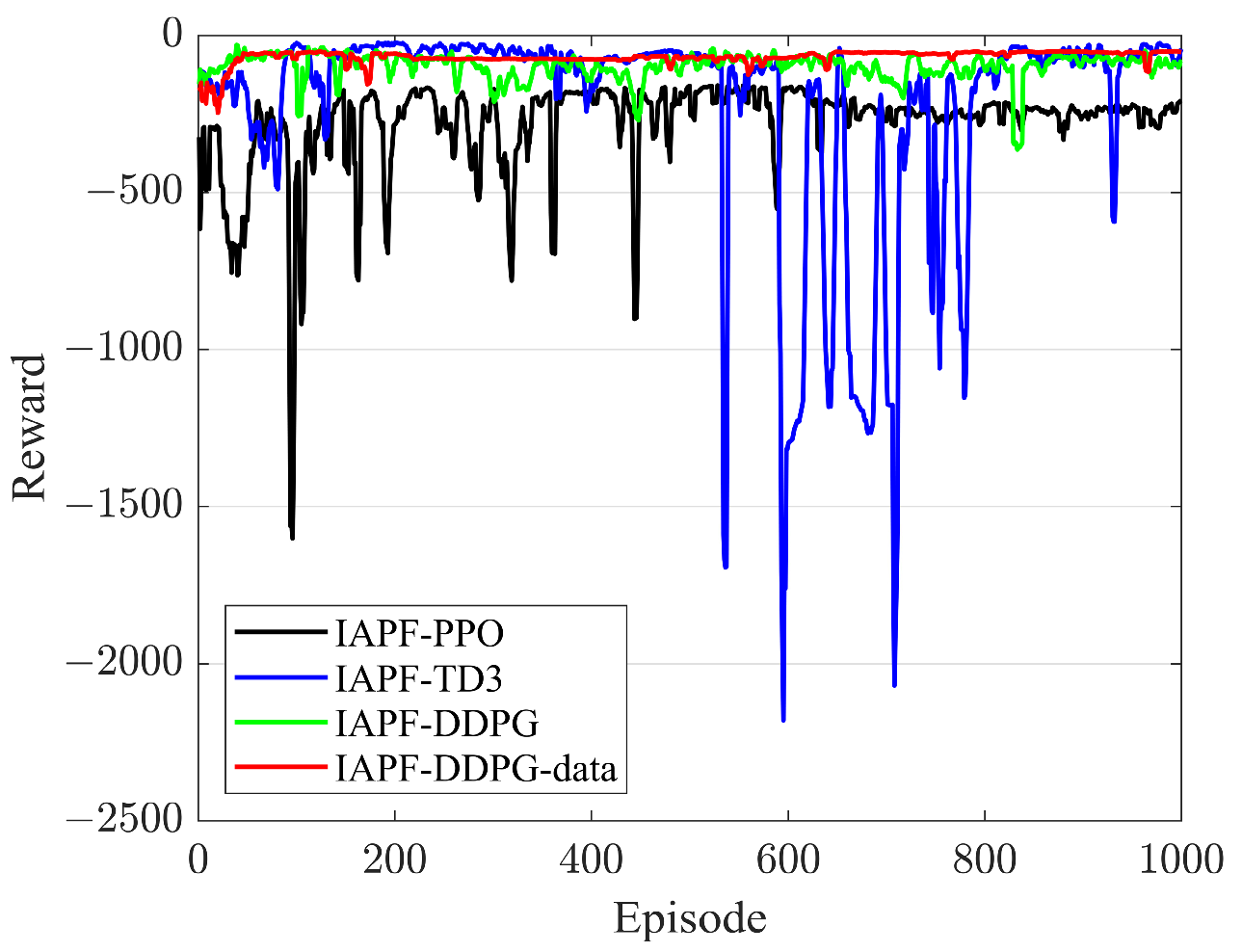
5. Simulation Results
5.1. Target Point Cruise Sequence
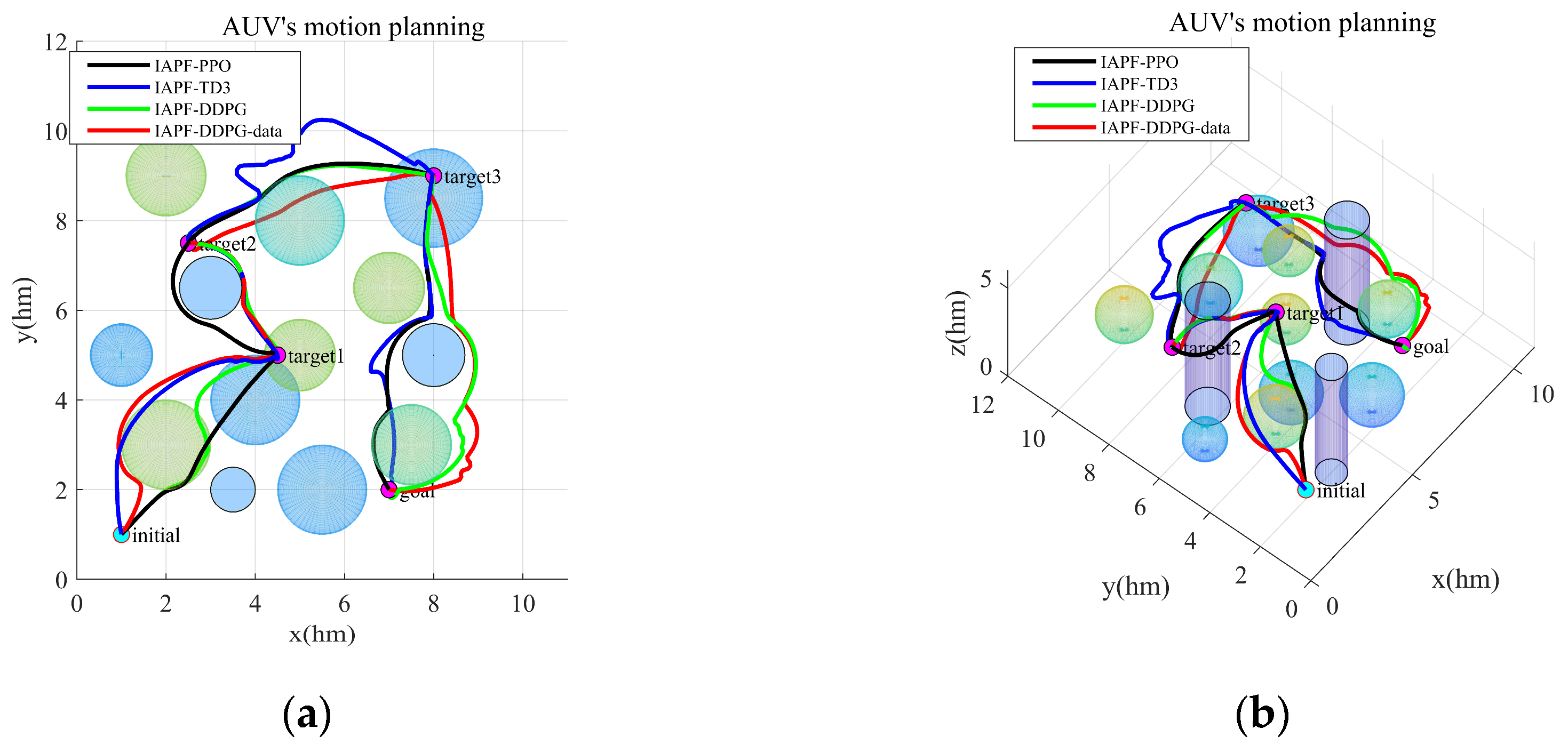
5.2. Motion Planning for Multiple Target Points
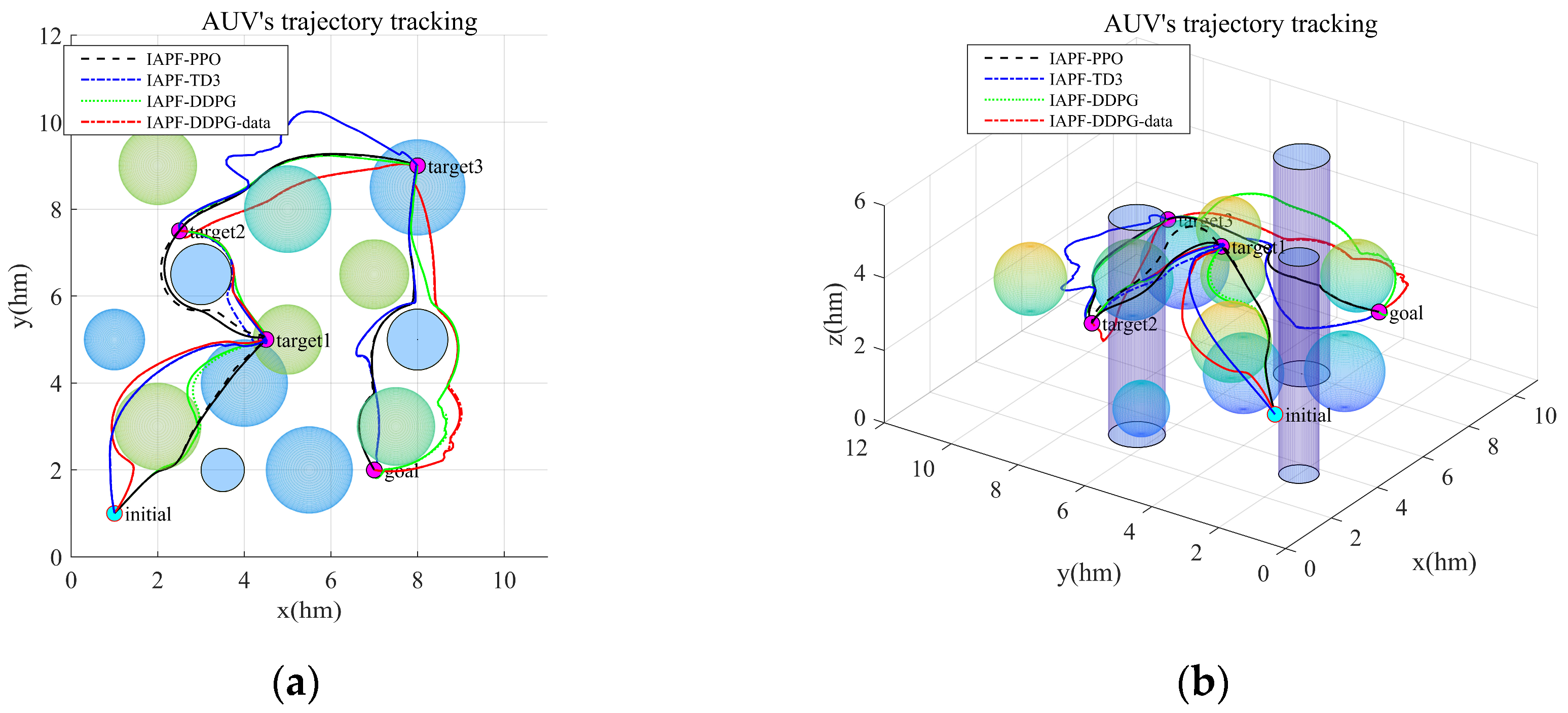
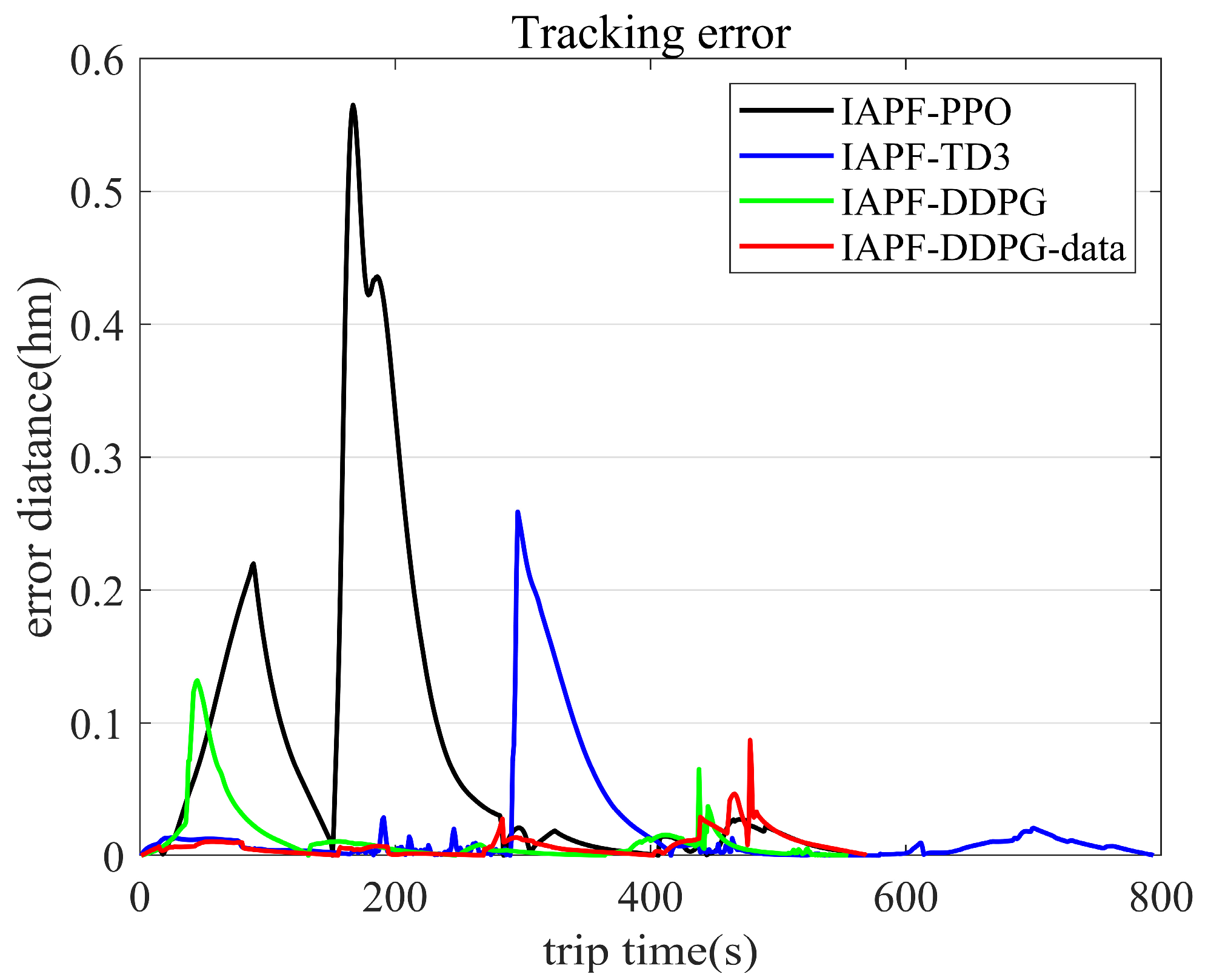
5.3. Trajectory Tracking and Path Optimization with Remote Sensing Information
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sahoo, A.; Dwivedy, S.K.; Robi, P. Advancements in the field of autonomous underwater vehicle. Ocean Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Stankiewicz, P.; Tan, Y.T.; Kobilarov, M. Adaptive sampling with an autonomous underwater vehicle in static marine environments. J. Field Robot. 2021, 38, 572–597. [Google Scholar] [CrossRef]
- Du, J.; Song, J.; Ren, Y.; Wang, J. Convergence of broadband and broadcast/multicast in maritime information networks. Tsinghua Sci. Technol. 2021, 26, 592–607. [Google Scholar] [CrossRef]
- Cao, X.; Ren, L.; Sun, C. Research on obstacle detection and avoidance of autonomous underwater vehicle based on forward-looking sonar. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Wang, J.; Jiang, C.; Wei, W.; Ren, Y. AUV-Assisted Node Repair for IoUT Relying on Multi-Agent Reinforcement Learning. IEEE Internet Things J. 2023. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, W.; Li, S.; Zhu, X. Energy optimised D* AUV path planning with obstacle avoidance and ocean current environment. J. Navig. 2022, 75, 685–703. [Google Scholar] [CrossRef]
- Cao, X.; Chen, L.; Guo, L.; Han, W. AUV Global Security Path Planning Based on a Potential Field Bio-Inspired Neural Network in Underwater Environment. Intell. Autom. Soft Comput. 2021, 27, 391–407. [Google Scholar] [CrossRef]
- Zhu, D.; Cao, X.; Sun, B.; Luo, C. Biologically inspired self-organizing map applied to task assignment and path planning of an AUV system. IEEE Trans. Cogn. Dev. Syst. 2017, 10, 304–313. [Google Scholar] [CrossRef]
- Hao, K.; Zhao, J.; Li, Z.; Liu, Y.; Zhao, L. Dynamic path planning of a three-dimensional underwater AUV based on an adaptive genetic algorithm. Ocean Eng. 2022, 263, 112421. [Google Scholar] [CrossRef]
- Lin, C.; Han, G.; Du, J.; Bi, Y.; Shu, L.; Fan, K. A path planning scheme for AUV flock-based Internet-of-Underwater-Things systems to enable transparent and smart ocean. IEEE Internet Things J. 2020, 7, 9760–9772. [Google Scholar] [CrossRef]
- Yu, X.; Chen, W.-N.; Hu, X.-M.; Gu, T.; Yuan, H.; Zhou, Y.; Zhang, J. Path planning in multiple-AUV systems for difficult target traveling missions: A hybrid metaheuristic approach. IEEE Trans. Cogn. Dev. Syst. 2019, 12, 561–574. [Google Scholar] [CrossRef]
- Ma, X.; Yanli, C.; Bai, G.; Liu, J. Multi-AUV collaborative operation based on time-varying navigation map and dynamic grid model. IEEE Access 2020, 8, 159424–159439. [Google Scholar] [CrossRef]
- Wei, W.; Wang, J.; Fang, Z.; Chen, J.; Ren, Y.; Dong, Y. 3U: Joint design of UAV-USV-UUV networks for cooperative target hunting. IEEE Trans. Veh. Technol. 2022, 72, 4085–4090. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, P.; Du, B.; Dong, B.; Zhang, W. AUV path tracking with real-time obstacle avoidance via reinforcement learning under adaptive constraints. Ocean Eng. 2022, 256, 111453. [Google Scholar] [CrossRef]
- Bu, F.; Luo, H.; Ma, S.; Li, X.; Ruby, R.; Han, G. AUV-Aided Optical—Acoustic Hybrid Data Collection Based on Deep Reinforcement Learning. Sensors 2023, 23, 578. [Google Scholar] [CrossRef]
- Yang, P.; Cao, X.; Xi, X.; Du, W.; Xiao, Z.; Wu, D. Three-dimensional continuous movement control of drone cells for energy-efficient communication coverage. IEEE Trans. Veh. Technol. 2019, 68, 6535–6546. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, N.; Wu, W. A hybrid path planning algorithm considering AUV dynamic constraints based on improved A* algorithm and APF algorithm. Ocean Eng. 2023, 285, 115333. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Zhang, S.; Zheng, R.; Dong, S. Multi-AUV adaptive path planning and cooperative sampling for ocean scalar field estimation. IEEE Trans. Instrum. Meas. 2022, 71, 9505514. [Google Scholar] [CrossRef]
- Guo, J.; Hou, Y.; Liang, X.; Yang, H.; Xiong, Y. Mission-driven path planning and design of submersible unmanned ship with multiple navigation states. Ocean Eng. 2022, 263, 112363. [Google Scholar] [CrossRef]
- Wen, J.; Yang, J.; Wang, T. Path planning for autonomous underwater vehicles under the influence of ocean currents based on a fusion heuristic algorithm. IEEE Trans. Veh. Technol. 2021, 70, 8529–8544. [Google Scholar] [CrossRef]
- Yang, H.; Teng, X. Mobile robot path planning based on enhanced dynamic window approach and improved a algorithm. J. Robot. 2022, 2022, 2183229. [Google Scholar] [CrossRef]
- Yu, X.; Chen, W.-N.; Gu, T.; Yuan, H.; Zhang, H.; Zhang, J. ACO-A*: Ant colony optimization plus A* for 3-D traveling in environments with dense obstacles. IEEE Trans. Evol. Comput. 2018, 23, 617–631. [Google Scholar] [CrossRef]
- Sun, B.; Zhu, D.; Tian, C.; Luo, C. Complete coverage autonomous underwater vehicles path planning based on glasius bio-inspired neural network algorithm for discrete and centralized programming. IEEE Trans. Cogn. Dev. Syst. 2018, 11, 73–84. [Google Scholar] [CrossRef]
- Xing, T.; Wang, X.; Ding, K.; Ni, K.; Zhou, Q. Improved Artificial Potential Field Algorithm Assisted by Multisource Data for AUV Path Planning. Sensors 2023, 23, 6680. [Google Scholar] [CrossRef]
- Cao, X.; Sun, C.; Yan, M. Target search control of AUV in underwater environment with deep reinforcement learning. IEEE Access 2019, 7, 96549–96559. [Google Scholar] [CrossRef]
- Jiang, D.; Huang, J.; Fang, Z.; Cheng, C.; Sha, Q.; He, B.; Li, G. Generative adversarial interactive imitation learning for path following of autonomous underwater vehicle. Ocean Eng. 2022, 260, 111971. [Google Scholar] [CrossRef]
- Zhu, G.; Shen, Z.; Liu, L.; Zhao, S.; Ji, F.; Ju, Z.; Sun, J. AUV Dynamic Obstacle Avoidance Method Based on Improved PPO Algorithm. IEEE Access 2022, 10, 121340–121351. [Google Scholar] [CrossRef]
- Chu, Z.; Wang, F.; Lei, T.; Luo, C. Path planning based on deep reinforcement learning for autonomous underwater vehicles under ocean current disturbance. IEEE Trans. Intell. Veh. 2022, 8, 108–120. [Google Scholar] [CrossRef]
- Hadi, B.; Khosravi, A.; Sarhadi, P. Deep reinforcement learning for adaptive path planning and control of an autonomous underwater vehicle. Appl. Ocean Res. 2022, 129, 103326. [Google Scholar] [CrossRef]
- Su, N.; Wang, J.-B.; Zeng, C.; Zhang, H.; Lin, M.; Li, G.Y. Unmanned-Surface-Vehicle-Aided Maritime Data Collection Using Deep Reinforcement Learning. IEEE Internet Things J. 2022, 9, 19773–19786. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Phillips, A.; Haroutunian, M.; Murphy, A.J.; Boyd, S.; Blake, J.; Griffiths, G. Understanding the power requirements of autonomous underwater systems, Part I: An analytical model for optimum swimming speeds and cost of transport. Ocean Eng. 2017, 133, 271–279. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Lanfeng, Z.; Mingyue, K. 3D obstacle-avoidance for a unmanned aerial vehicle based on the improved artificial potential field method. J. East China Norm. Univ. 2022, 2022, 54. [Google Scholar]
- Ding, K.; Wang, X.; Hu, K.; Wang, L.; Wu, G.; Ni, K.; Zhou, Q. Three-dimensional morphology measurement of underwater objects based on the photoacoustic effect. Opt. Lett. 2022, 47, 641–644. [Google Scholar] [CrossRef] [PubMed]
- Butler, B.; Verrall, R. Precision Hybrid Inertial/Acoustic Navigation System for a Long-Range Autonomous Underwater Vehicle. Navigation 2001, 48, 1–12. [Google Scholar] [CrossRef]
- Zeng, Z.; Lian, L.; Sammut, K.; He, F.; Tang, Y.; Lammas, A. A survey on path planning for persistent autonomy of autonomous underwater vehicles. Ocean Eng. 2015, 110, 303–313. [Google Scholar] [CrossRef]
- Suh, Y.S. Attitude estimation by multiple-mode Kalman filters. IEEE Trans. Ind. Electron. 2006, 53, 1386–1389. [Google Scholar] [CrossRef]
- Campestrini, C.; Heil, T.; Kosch, S.; Jossen, A. A comparative study and review of different Kalman filters by applying an enhanced validation method. J. Energy Storage 2016, 8, 142–159. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Zeng, F.; Wang, C.; Ge, S.S. A survey on visual navigation for artificial agents with deep reinforcement learning. IEEE Access 2020, 8, 135426–135442. [Google Scholar] [CrossRef]
- Wang, X.; Gu, Y.; Cheng, Y.; Liu, A.; Chen, C.P. Approximate policy-based accelerated deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1820–1830. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Wan, K.; Gao, X.; Zhai, Y.; Wang, Q. Deep reinforcement learning approach with multiple experience pools for UAV’s autonomous motion planning in complex unknown environments. Sensors 2020, 20, 1890. [Google Scholar] [CrossRef] [PubMed]




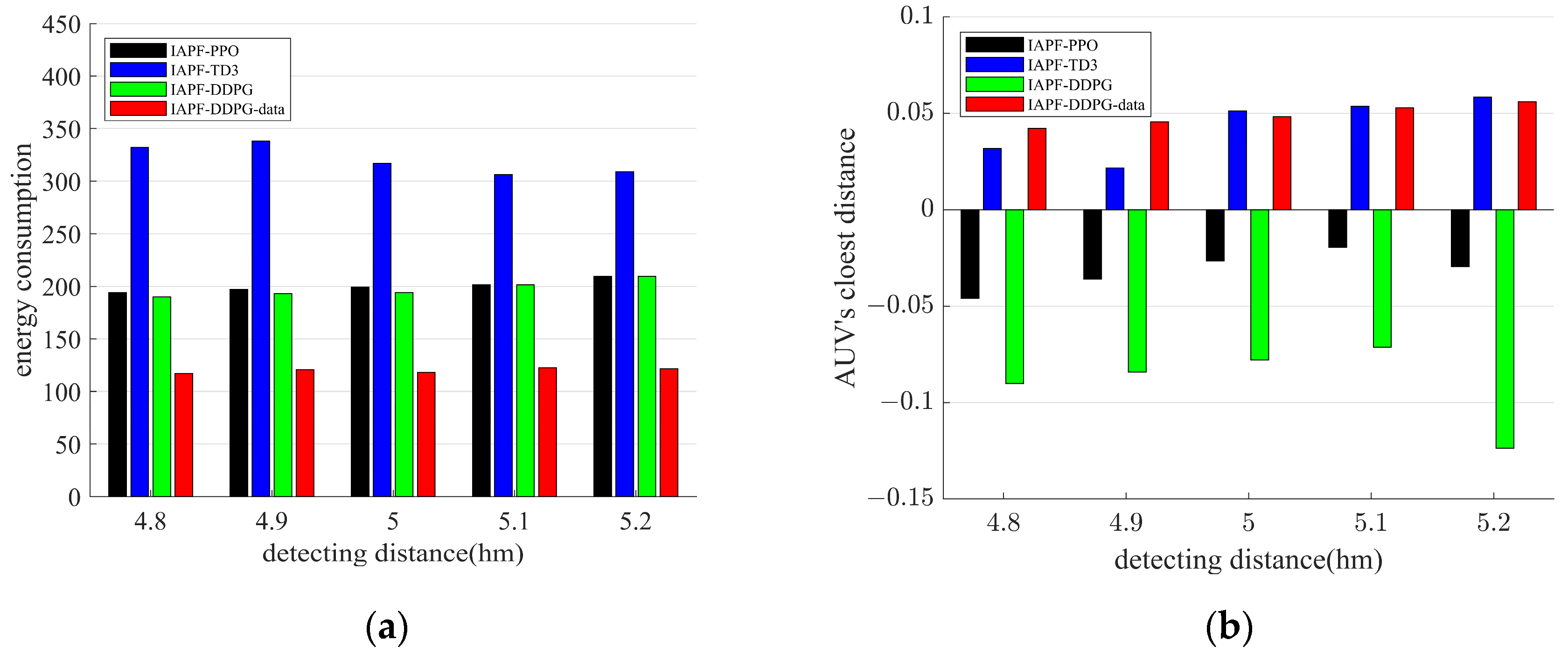
| Category | Parameter Name | Parameter Values |
|---|---|---|
| Mechanical parameters | Velocity | 1~10 m/s (0.01~0.10 hm/s) |
| Steering angle | −40°/s~40°/s | |
| Attack angle | −40°/s~40°/s | |
| Pitch angle | −50°~50° | |
| Hyperparameter | Experience replay buffer | 2 × 106 |
| Batch size | 128 | |
| Max episode | 1000 | |
| Max step | 500 | |
| Actor learning rate | 0.001 | |
| Critic learning rate | 0.001 | |
| Soft update rate | 0.01 |
| Name | IAPF-PPO | IAPF-TD3 | IAPF-DDPG | IAPF-DDPG-Data |
|---|---|---|---|---|
| es | 188.242749 | 317.011388 | 194.030737 | 118.264115 |
| cd | −0.027284 | 0.051236 | −0.077943 | 0.048216 |
| as | 1.903563 | 13.984265 | 4.003103 | 2.922921 |
| aa | 1.876285 | 11.784965 | 1.243111 | 0.945653 |
| Me | 50.000018 | 50.000018 | 50.000018 | 50.000018 |
| Mv | 10.000000 | 10.000000 | 10.000000 | 10.000000 |
| Ma | 4.499984 | 9.000000 | 9.000000 | 4.999958 |
| pl | 25.692477 | 31.369528 | 26.293851 | 27.032355 |
| rt | 545 | 957 | 553 | 567 |
| Name | IAPF-PPO | IAPF-TD3 | IAPF-DDPG | IAPF-DDPG-Data |
|---|---|---|---|---|
| es | 162.028648 | 991.704624 | 282.105936 | 176.921956 |
| cd | −0.041092 | −0.095522 | −0.024499 | 0.007177 |
| as | 3.365245 | 7.667607 | 3.385832 | 2.942140 |
| aa | 1.313024 | 2.552670 | 1.649219 | 1.101778 |
| Me | 50.000018 | 50.000018 | 50.000018 | 50.000018 |
| Mv | 9.979185 | 10.000000 | 10.000000 | 10.000000 |
| Ma | 5.637515 | 9.000000 | 9.000000 | 9.000000 |
| pl | 28.723478 | 36.953162 | 26.600114 | 27.097279 |
| rt | 1052 | 1252 | 1160 | 1012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, T.; Wang, X.; Ding, K.; Ni, K.; Zhou, Q. A Multi-Source-Data-Assisted AUV for Path Cruising: An Energy-Efficient DDPG Approach. Remote Sens. 2023, 15, 5607. https://doi.org/10.3390/rs15235607
Xing T, Wang X, Ding K, Ni K, Zhou Q. A Multi-Source-Data-Assisted AUV for Path Cruising: An Energy-Efficient DDPG Approach. Remote Sensing. 2023; 15(23):5607. https://doi.org/10.3390/rs15235607
Chicago/Turabian StyleXing, Tianyu, Xiaohao Wang, Kaiyang Ding, Kai Ni, and Qian Zhou. 2023. "A Multi-Source-Data-Assisted AUV for Path Cruising: An Energy-Efficient DDPG Approach" Remote Sensing 15, no. 23: 5607. https://doi.org/10.3390/rs15235607
APA StyleXing, T., Wang, X., Ding, K., Ni, K., & Zhou, Q. (2023). A Multi-Source-Data-Assisted AUV for Path Cruising: An Energy-Efficient DDPG Approach. Remote Sensing, 15(23), 5607. https://doi.org/10.3390/rs15235607






